- ... Morais
-
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... co-orbital
![[*]](/icons/foot_motif.gif)
- The word
co-orbital, which has here its literal meaning of shares the orbit with,
is also generally
used whenever referring to any nearby orbits.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... by
![[*]](/icons/foot_motif.gif)
- Note that
Eq. (3) implies that at L4 (or L5), a=a1 and
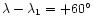 (or
(or
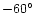 )
and follows from the fact that
the three-body potential at
L4 (or L5) is of keplerian type but with a larger mean motion.
)
and follows from the fact that
the three-body potential at
L4 (or L5) is of keplerian type but with a larger mean motion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... axis
![[*]](/icons/foot_motif.gif)
-
Here we refer to a semi-major axis obeying the approximate
relation
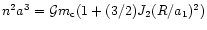 which follows
from the fact that the oblateness potential is of nearly keplerian type
but with a larger mean motion (see Greenberg 1981).
which follows
from the fact that the oblateness potential is of nearly keplerian type
but with a larger mean motion (see Greenberg 1981).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... write
![[*]](/icons/foot_motif.gif)
- There is an obvious error in the
definition of c[l] in Paper I (Eq. (36)).
This only takes the unit value when l=0 and when
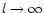 ,
as can easily be confirmed in Fig. 1b from the same paper.
,
as can easily be confirmed in Fig. 1b from the same paper.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
system
![[*]](/icons/foot_motif.gif)
- Here, we took into account Uranus' oblate shape by
adding the terms
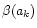 (recall definition of function
(recall definition of function 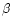 in Eq. (26)) to Akk and -Bkk (the diagonal terms of matrices
A and -B which we introduced in Sect. 2.3).
in Eq. (26)) to Akk and -Bkk (the diagonal terms of matrices
A and -B which we introduced in Sect. 2.3).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
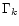 )
)![[*]](/icons/foot_motif.gif)
- In our calculations we
ignored the contribution
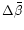 (given by Eq. (71)) due to
Uranus' oblate shape as in general this is unimportant (cf. last paragraph
of Sect. 3.2.2).
(given by Eq. (71)) due to
Uranus' oblate shape as in general this is unimportant (cf. last paragraph
of Sect. 3.2.2).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... regions
![[*]](/icons/foot_motif.gif)
- The use of more
accurate values for the eigen-frequencies from Laskar (1988) does
not cause any significant alteration in the location of these
secular resonances.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.