

Up: Conditions for shock revival
Subsections
8 Mass and energy conservation in the gain region
Mass and energy conservation in the gain region between
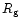 and
and
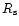 determine the early postbounce
evolution of the supernova shock. For example, the shock is pushed outward
when the matter that falls through the shock stays hot and piles up on top
of the neutron star, forming an extended envelope instead of being
accreted into the dense core quickly after efficient energy loss in the
neutrino cooling layer below
determine the early postbounce
evolution of the supernova shock. For example, the shock is pushed outward
when the matter that falls through the shock stays hot and piles up on top
of the neutron star, forming an extended envelope instead of being
accreted into the dense core quickly after efficient energy loss in the
neutrino cooling layer below
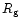 .
Similarly, strong neutrino
heating in the gain region causes an increase of the postshock pressure
and thus drives an expansion of the shock. On the other hand, enhanced
neutrino emission will extract mass and/or energy from the layer which
supports the supernova shock. The consequence will be a retraction of the
shock in radius. These effects need to be accounted for by an appropriate discussion of the
delayed explosion mechanism. A steady-state picture is certainly not adequate.
.
Similarly, strong neutrino
heating in the gain region causes an increase of the postshock pressure
and thus drives an expansion of the shock. On the other hand, enhanced
neutrino emission will extract mass and/or energy from the layer which
supports the supernova shock. The consequence will be a retraction of the
shock in radius. These effects need to be accounted for by an appropriate discussion of the
delayed explosion mechanism. A steady-state picture is certainly not adequate.
8.1 Mass in the gain region
The mass
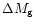 in the gain region can be calculated as
volume integral over the density:
in the gain region can be calculated as
volume integral over the density:
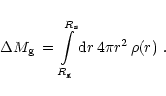 |
(96) |
with the density 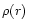 given by Eq. (59). Alternatively,
since the latter equation is the exact
solution for hydrostatic equilibrium, one can use
given by Eq. (59). Alternatively,
since the latter equation is the exact
solution for hydrostatic equilibrium, one can use
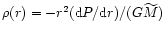 with P(r)from Eq. (60). Defining the coefficients
with P(r)from Eq. (60). Defining the coefficients
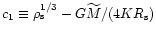 and
and
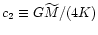 ,
one finds:
,
one finds:
In deriving the second form of Eq. (97), use was made of
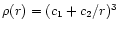 .
Moreover, with
.
Moreover, with
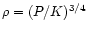 the
density in Eq. (97) can be substituted by the pressure P.
Note that the quantities
the
density in Eq. (97) can be substituted by the pressure P.
Note that the quantities
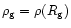 and
and
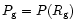 at the gain
radius must be expressed by the exact relations of Eqs. (59) and
(60), respectively. They depend on the postshock state of the matter
as do the coefficients c1 and c2.
The gain radius
at the gain
radius must be expressed by the exact relations of Eqs. (59) and
(60), respectively. They depend on the postshock state of the matter
as do the coefficients c1 and c2.
The gain radius
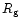 is given by Eq. (66). It is also
a function of the conditions immediately behind the shock. Writing the
postshock temperature in terms of the postshock pressure via Eq. (56),
is given by Eq. (66). It is also
a function of the conditions immediately behind the shock. Writing the
postshock temperature in terms of the postshock pressure via Eq. (56),
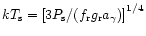 ,
and using Eqs. (39), (43), (44) and
(53)-(55) with typical values
,
and using Eqs. (39), (43), (44) and
(53)-(55) with typical values
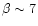 ,
,
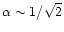 ,
,
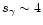 ,
and
,
and
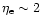 (the exact values of these parameters are not essential for the discussion and
affect the result rather insensitively),
one gets in case of
(the exact values of these parameters are not essential for the discussion and
affect the result rather insensitively),
one gets in case of
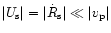 :
:
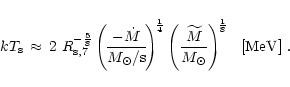 |
(98) |
Inserting this in Eq. (66) and using
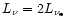 yields
yields
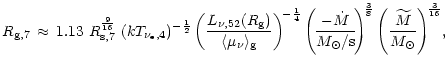 |
|
|
(99) |
where the neutrino luminosity at the gain radius,
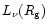 ,
is given by Eq. (76).
,
is given by Eq. (76).
Instead of the exact expression of Eq. (97) an approximation for
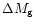 is sometimes preferable. Performing the integration of
Eq. (96) with the approximate density profile of Eq. (63),
one finds
is sometimes preferable. Performing the integration of
Eq. (96) with the approximate density profile of Eq. (63),
one finds
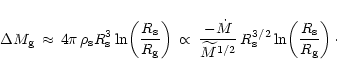 |
(100) |
Here
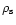 was written in terms of
was written in terms of
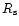 by
making use of
by
making use of
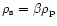 and Eq. (44).
Moreover, from Eq. (99) one can deduce that
and Eq. (44).
Moreover, from Eq. (99) one can deduce that
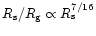 for
for
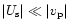 .
An increase of the shock radius
therefore means that
.
An increase of the shock radius
therefore means that
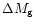 will also grow.
will also grow.
The rate at which the mass in the gain region changes in time due to a
shift of the upper and lower boundaries of this region but also due to a
variation of the density of the stellar medium, is determined as
the total time derivative of Eq. (96):
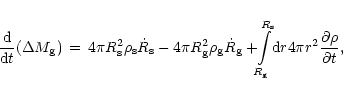 |
(101) |
where
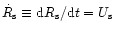 is the shock velocity and
is the shock velocity and
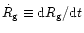 the velocity of the gain radius. When the integration in Eq. (101)
is carried out to a radius infinitesimally smaller than
the velocity of the gain radius. When the integration in Eq. (101)
is carried out to a radius infinitesimally smaller than
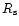 with the help of Eq. (2), one obtains
with the help of Eq. (2), one obtains
with
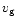 and
and
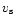 being the velocities of the
stellar medium at the gain radius and just behind the shock, respectively.
The lower expression was derived by using the shock jump condition for the
mass flow, Eq. (36), and the definitions
being the velocities of the
stellar medium at the gain radius and just behind the shock, respectively.
The lower expression was derived by using the shock jump condition for the
mass flow, Eq. (36), and the definitions
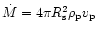 and
and
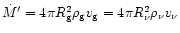 as introduced in Sect. 7.
Equation (102) shows that the mass in the gain region can change
because of inflow and outflow of gas but also due to the motion of the
boundaries
as introduced in Sect. 7.
Equation (102) shows that the mass in the gain region can change
because of inflow and outflow of gas but also due to the motion of the
boundaries
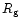 and
and
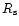 .
Knowing the initial mass in this layer,
.
Knowing the initial mass in this layer,
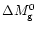 ,
Eq. (102) allows one to calculate the value at later times.
,
Eq. (102) allows one to calculate the value at later times.
8.2 Energy in the gain region
Since the postshock matter is effectively in hydrostatic equilibrium
(see Sect. 5) the kinetic energy is negligible
compared to the internal energy and the gravitational potential energy,
and the total energy in the gain region is therefore given by
 |
(103) |
To evaluate the right hand side, one substitutes
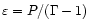 ,
which relates the internal energy density
,
which relates the internal energy density
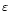 and the pressure Pfor an ideal gas, with the adiabatic index
and the pressure Pfor an ideal gas, with the adiabatic index 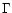 being typically between 4/3 and 5/3, depending on whether relativistic or nonrelativistic particles, respectively, dominate
the pressure. In addition making use of hydrostatic equilibrium (Eq. (47))
or, alternatively, applying the virial theorem, one finds
being typically between 4/3 and 5/3, depending on whether relativistic or nonrelativistic particles, respectively, dominate
the pressure. In addition making use of hydrostatic equilibrium (Eq. (47))
or, alternatively, applying the virial theorem, one finds
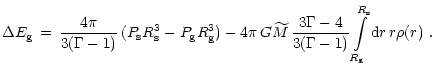 |
|
|
(104) |
The second term is the gravitational potential energy times
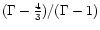 .
An exact expression for the integral
is obtained when Eq. (59) is used for
.
An exact expression for the integral
is obtained when Eq. (59) is used for 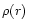 :
:
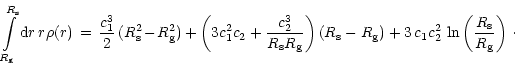 |
|
|
(105) |
The coefficients c1 and c2 were already defined in Sect. 8.1.
For the following discussion an approximation of this integral
is sufficient. It can be derived by employing the approximate power law
profile for the density, Eq. (63):
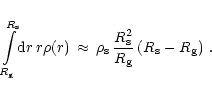 |
(106) |
The rate at which the total energy in the gain region changes with time
can be calculated as the time derivative of Eq. (103).
With the definition
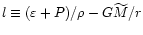 one finds
one finds
where
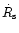 and
and
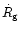 have the same meaning
as in Eq. (101).
The partial derivatives in the integral can be substituted by
Eqs. (2) and (4). Making additional use of
Eqs. (5) and (6) and of
have the same meaning
as in Eq. (101).
The partial derivatives in the integral can be substituted by
Eqs. (2) and (4). Making additional use of
Eqs. (5) and (6) and of
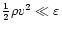 yields
yields
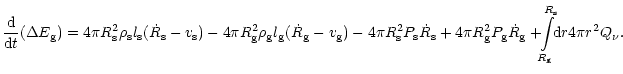 |
|
|
(108) |
Now employing the continuity equation for the mass flow across the shock,
Eq. (36),
and replacing the integral for the energy exchange with neutrinos
between
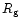 and
and
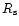 by
by
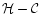 as given
in Eqs. (82) and (87), one ends up with
as given
in Eqs. (82) and (87), one ends up with
The mass accretion rates 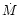 and
and 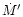 account for the inflow
of matter into the gain region through the shock and for the mass that
is advected through the gain radius, respectively
(see Sect. 7 and discussion after Eq. (102)).
Equation (109) means that the total energy in the gain region
changes due to active mass motions,
account for the inflow
of matter into the gain region through the shock and for the mass that
is advected through the gain radius, respectively
(see Sect. 7 and discussion after Eq. (102)).
Equation (109) means that the total energy in the gain region
changes due to active mass motions,
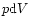 work associated
with these mass motions, the movement of the boundaries, and neutrino
heating.
work associated
with these mass motions, the movement of the boundaries, and neutrino
heating.
Making use of
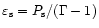 ,
,
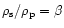 ,
and Eq. (39),
one finds for
,
and Eq. (39),
one finds for
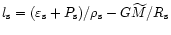 :
:
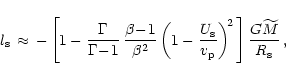 |
(110) |
where Eq. (43) with
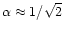 was employed for
was employed for
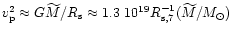 erg
erg g-1.
Because of hydrostatic equilibrium a simple relation exists between
g-1.
Because of hydrostatic equilibrium a simple relation exists between
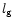 and
and
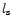 .
With
.
With
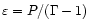 and
Eqs. (56) and (59) one obtains
and
Eqs. (56) and (59) one obtains
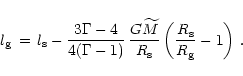 |
(111) |
Using the more general density-pressure relation
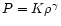 instead of Eq. (56), and the corresponding
hydrostatic density profile of Eq. (62), leads to
instead of Eq. (56), and the corresponding
hydrostatic density profile of Eq. (62), leads to
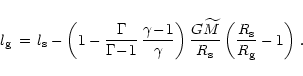 |
(112) |
For
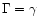 ,
this gives
,
this gives
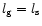 .
.


Up: Conditions for shock revival
Copyright ESO 2001
![]() in the gain region can be calculated as
volume integral over the density:
in the gain region can be calculated as
volume integral over the density:
![]() is sometimes preferable. Performing the integration of
Eq. (96) with the approximate density profile of Eq. (63),
one finds
is sometimes preferable. Performing the integration of
Eq. (96) with the approximate density profile of Eq. (63),
one finds
![]() ,
,
![]() ,
and Eq. (39),
one finds for
,
and Eq. (39),
one finds for
![]() :
: