

Up: Conditions for shock revival
Subsections
6 Heating and cooling
To discuss energy deposition and emission of neutrinos exterior to the
neutrinosphere, one starts with the energy equation for
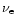 plus
plus
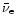 ,
which is
,
which is
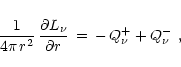 |
(68) |
where
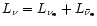 and
and 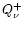 and
and 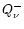 are the heating and cooling rates of the
stellar medium as given by Eqs. (28) and (31), respectively.
In writing Eq. (68), stationarity was assumed for the neutrinos,
which is justified because the neutrino emission of the accreting
neutrino star changes on a timescale which is typically longer than other
relevant timescales of the discussed problem.
From Eq. (68) the net effect of heating or cooling
in a layer between radii r1 and r2 can be deduced as
are the heating and cooling rates of the
stellar medium as given by Eqs. (28) and (31), respectively.
In writing Eq. (68), stationarity was assumed for the neutrinos,
which is justified because the neutrino emission of the accreting
neutrino star changes on a timescale which is typically longer than other
relevant timescales of the discussed problem.
From Eq. (68) the net effect of heating or cooling
in a layer between radii r1 and r2 can be deduced as
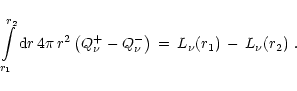 |
(69) |
Refering to Eqs. (23) and (27), a suitable spectral
and flavor average for the absorption coefficient of
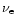 and
and
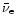 can be defined as
can be defined as
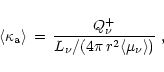 |
(70) |
when
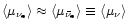 is used. Plugging this into Eq. (68) gives
is used. Plugging this into Eq. (68) gives
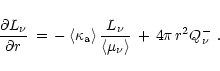 |
(71) |
The neutrino luminosity as a function of radius 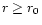 is the general solution of Eq. (71):
is the general solution of Eq. (71):
The first exponential factor represents the absorption damping of the
luminosity in the shell between r0 and r, the
second exponential factor the reabsorption of neutrinos emitted
at r' in the layer enclosed by radii r' and r.
6.1 Heating and cooling between
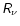 and
and
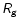
Here the lower boundary of the considered volume is the neutrinosphere at
radius
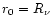 .
Since both
.
Since both
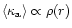 (cf. Eqs. (70)
and (28)) and
(cf. Eqs. (70)
and (28)) and
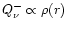 (cf. Eq. (31))
are steep functions of the radius in the region between
(cf. Eq. (31))
are steep functions of the radius in the region between 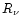 and
and
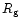 ,
where the density drops exponentially, most of the absorption
and emission occurs in the immediate vicinity of the neutrinosphere.
Therefore the neutrino luminosity at the gain radius,
,
where the density drops exponentially, most of the absorption
and emission occurs in the immediate vicinity of the neutrinosphere.
Therefore the neutrino luminosity at the gain radius,
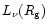 ,
can be approximated by the limit for
,
can be approximated by the limit for
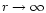 of Eq. (72), and
the integral
of Eq. (72), and
the integral
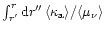 can be replaced by
can be replaced by
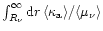 .
This leads to
.
This leads to
To evaluate the exponential damping factor,
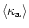 is
expressed by Eq. (70), making use of Eq. (28) and
is
expressed by Eq. (70), making use of Eq. (28) and
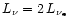 .
The neutrino spectrum is assumed not to change
outside the neutrinosphere. With Eq. (50) the integral over the
density profile becomes
.
The neutrino spectrum is assumed not to change
outside the neutrinosphere. With Eq. (50) the integral over the
density profile becomes
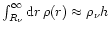 .
Employing Eqs. (51) and (52), one finds
.
Employing Eqs. (51) and (52), one finds
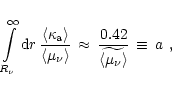 |
(74) |
where
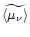 denotes a radial average of
the flux factor
denotes a radial average of
the flux factor
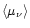 in the layer between
in the layer between 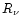 and
and
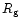 .
The energy loss integral is calculated with Eq. (31) where
.
The energy loss integral is calculated with Eq. (31) where
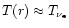 is used near the neutrinosphere. With
is used near the neutrinosphere. With
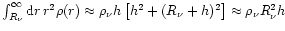 (because
(because
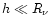 ,
cf. Eq. (51)) and Eqs. (51) and (52) this leads to:
,
cf. Eq. (51)) and Eqs. (51) and (52) this leads to:
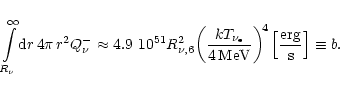 |
(75) |
Equation (73) now becomes
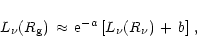 |
(76) |
and the total energy exchange between 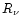 and
and
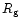 according to Eq. (69) therefore is
according to Eq. (69) therefore is
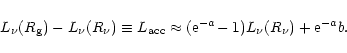 |
(77) |
Since
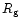 separates the layer of neutrino cooling from the
one of neutrino heating, the region between
separates the layer of neutrino cooling from the
one of neutrino heating, the region between 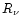 and
and
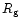 must lose energy by neutrino emission.
Therefore the neutrino luminosity at
must lose energy by neutrino emission.
Therefore the neutrino luminosity at
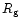 must be larger than
must be larger than
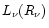 ,
and
,
and
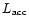 represents the luminosity associated with the
accretion of matter through the gain radius onto the surface of
the nascent neutron star. The requirement
represents the luminosity associated with the
accretion of matter through the gain radius onto the surface of
the nascent neutron star. The requirement
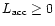 constrains the luminosity of the neutron star core relative to the
product
constrains the luminosity of the neutron star core relative to the
product
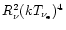 by the inequality
by the inequality
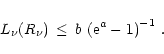 |
(78) |
Provided the core luminosity can be expressed in terms of blackbody emission
of temperature
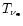 ,
,
the consistency condition translates into the relation
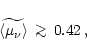 |
(80) |
which is satisfied above the neutrinosphere in the layer between 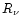 and
and
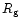 .
.
6.2 Heating and cooling between
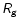 and
and
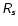
For reasons of simplicity it will be assumed that in the layer bounded by
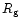 and
and
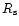 nuclei are completely disintegrated
into free nucleons. Disregarding the occurrence of
nuclei are completely disintegrated
into free nucleons. Disregarding the occurrence of 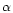 particles, in
particular, is certainly an approximation which becomes invalid when the
temperature drops below about 1
particles, in
particular, is certainly an approximation which becomes invalid when the
temperature drops below about 1 MeV, i.e., when the shock is at large
radii, typically around 300
MeV, i.e., when the shock is at large
radii, typically around 300 km (see Bethe 1993, 1995, 1996a-c, 1997). The presence of
km (see Bethe 1993, 1995, 1996a-c, 1997). The presence of 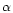 particles reduces the neutrino heating, because
electron neutrinos and antineutrinos are absorbed only on nucleons, but energy
released by the recombination of
particles reduces the neutrino heating, because
electron neutrinos and antineutrinos are absorbed only on nucleons, but energy
released by the recombination of 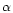 's during shock expansion supports
the shock at a later stage and contributes to the energy budget of the explosion. Since
in the context of this paper we do not attempt to calculate the explosion
energy, but are interested in a qualitative discussion of the revival phase
of the stalled shock, the recombination of nucleons to
's during shock expansion supports
the shock at a later stage and contributes to the energy budget of the explosion. Since
in the context of this paper we do not attempt to calculate the explosion
energy, but are interested in a qualitative discussion of the revival phase
of the stalled shock, the recombination of nucleons to 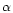 particles
is probably not a crucial issue.
particles
is probably not a crucial issue.
As will be demonstrated below, the optical depth between
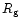 and
and
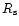 is small such that
is small such that
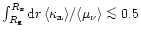 .
Therefore
the reabsorption probability of emitted neutrinos is also small and an
approximation to the solution of Eq. (72) at the shock position is
.
Therefore
the reabsorption probability of emitted neutrinos is also small and an
approximation to the solution of Eq. (72) at the shock position is
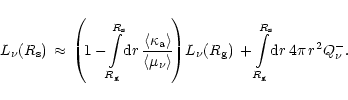 |
(81) |
The net energy deposition is found to be
Since in the layer bounded by
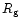 and
and
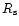 neutrino
heating takes place,
neutrino
heating takes place,
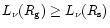 (this will also be verified below).
Expanding the exponential damping factors only to lowerst
order in the exponent implies a slight overestimation of the energy
input into the stellar medium by neutrinos (because the luminosity entering
at
(this will also be verified below).
Expanding the exponential damping factors only to lowerst
order in the exponent implies a slight overestimation of the energy
input into the stellar medium by neutrinos (because the luminosity entering
at
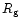 is assumed to decay linearly through the layer), but also
the energy loss by neutrinos is overestimated, because the reabsorption
of emitted neutrinos is not included.
is assumed to decay linearly through the layer), but also
the energy loss by neutrinos is overestimated, because the reabsorption
of emitted neutrinos is not included.
Using 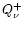 from Eq. (28) in Eq. (70),
from Eq. (28) in Eq. (70),
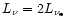 ,
and the density profile from
Eq. (63), one finds for the first integral in Eq. (82):
,
and the density profile from
Eq. (63), one finds for the first integral in Eq. (82):
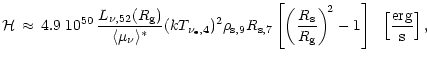 |
|
|
(83) |
where
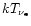 was again treated as a constant,
was again treated as a constant,
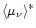 defines an average value of the flux factor in the layer between
defines an average value of the flux factor in the layer between
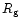 and
and
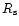 ,
and
,
and
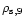 is the
density behind the shock in units of
is the
density behind the shock in units of 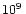 g
g cm-3.
The second integral in Eq. (82) is evaluated with
cm-3.
The second integral in Eq. (82) is evaluated with 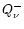 from Eq. (31) and the temperature and density relations from
Eq. (63):
from Eq. (31) and the temperature and density relations from
Eq. (63):
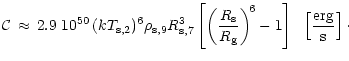 |
|
|
(84) |
Employing the gain condition, Eq. (33), and again making use of
Eq. (63), one gets
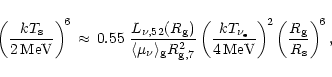 |
(85) |
which serves to rewrite Eq. (84) as
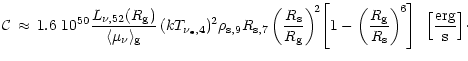 |
|
|
(86) |
Combining Eqs. (83) and (86) gives the net energy
transfer to the stellar medium in the gain region:
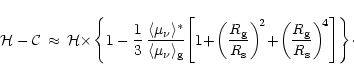 |
(87) |
Since
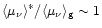 and
and
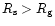 ,
typically
,
typically
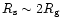 ,
we verify that
,
we verify that
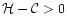 and therefore
and therefore
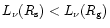 ,
as expected for the neutrino heating region.
For
,
as expected for the neutrino heating region.
For
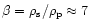 (Eq. (41))
and
(Eq. (41))
and
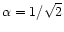 ,
Eq. (44) yields for the postshock
density
,
Eq. (44) yields for the postshock
density
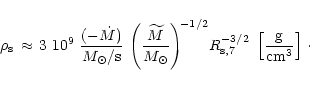 |
(88) |
Using this and
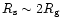 in Eq. (83)
leads to
in Eq. (83)
leads to
For sufficiently small accretion rates 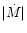 this is less than
about 0.5, and the assumption made before Eq. (81) is verified,
i.e., the reabsorption of neutrinos emitted in the gain region can be
neglected.
this is less than
about 0.5, and the assumption made before Eq. (81) is verified,
i.e., the reabsorption of neutrinos emitted in the gain region can be
neglected.


Up: Conditions for shock revival
Copyright ESO 2001
![]() plus
plus
![]() ,
which is
,
which is
![]() .
Since both
.
Since both
![]() (cf. Eqs. (70)
and (28)) and
(cf. Eqs. (70)
and (28)) and
![]() (cf. Eq. (31))
are steep functions of the radius in the region between
(cf. Eq. (31))
are steep functions of the radius in the region between ![]() and
and
![]() ,
where the density drops exponentially, most of the absorption
and emission occurs in the immediate vicinity of the neutrinosphere.
Therefore the neutrino luminosity at the gain radius,
,
where the density drops exponentially, most of the absorption
and emission occurs in the immediate vicinity of the neutrinosphere.
Therefore the neutrino luminosity at the gain radius,
![]() ,
can be approximated by the limit for
,
can be approximated by the limit for
![]() of Eq. (72), and
the integral
of Eq. (72), and
the integral
![]() can be replaced by
can be replaced by
![]() .
This leads to
.
This leads to
![]() and
and
![]() nuclei are completely disintegrated
into free nucleons. Disregarding the occurrence of
nuclei are completely disintegrated
into free nucleons. Disregarding the occurrence of ![]() particles, in
particular, is certainly an approximation which becomes invalid when the
temperature drops below about 1
particles, in
particular, is certainly an approximation which becomes invalid when the
temperature drops below about 1![]() MeV, i.e., when the shock is at large
radii, typically around 300
MeV, i.e., when the shock is at large
radii, typically around 300![]() km (see Bethe 1993, 1995, 1996a-c, 1997). The presence of
km (see Bethe 1993, 1995, 1996a-c, 1997). The presence of ![]() particles reduces the neutrino heating, because
electron neutrinos and antineutrinos are absorbed only on nucleons, but energy
released by the recombination of
particles reduces the neutrino heating, because
electron neutrinos and antineutrinos are absorbed only on nucleons, but energy
released by the recombination of ![]() 's during shock expansion supports
the shock at a later stage and contributes to the energy budget of the explosion. Since
in the context of this paper we do not attempt to calculate the explosion
energy, but are interested in a qualitative discussion of the revival phase
of the stalled shock, the recombination of nucleons to
's during shock expansion supports
the shock at a later stage and contributes to the energy budget of the explosion. Since
in the context of this paper we do not attempt to calculate the explosion
energy, but are interested in a qualitative discussion of the revival phase
of the stalled shock, the recombination of nucleons to ![]() particles
is probably not a crucial issue.
particles
is probably not a crucial issue.
![]() and
and
![]() is small such that
is small such that
![]() .
Therefore
the reabsorption probability of emitted neutrinos is also small and an
approximation to the solution of Eq. (72) at the shock position is
.
Therefore
the reabsorption probability of emitted neutrinos is also small and an
approximation to the solution of Eq. (72) at the shock position is
![]() from Eq. (28) in Eq. (70),
from Eq. (28) in Eq. (70),
![]() ,
and the density profile from
Eq. (63), one finds for the first integral in Eq. (82):
,
and the density profile from
Eq. (63), one finds for the first integral in Eq. (82):