

Up: Conditions for shock revival
Subsections
4 The characteristic radii
The neutrinospheric radius 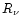 ,
the gain radius
,
the gain radius
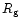 and
the transition radius of the EoS properties,
and
the transition radius of the EoS properties,
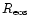 ,
will be formally defined below. They are characteristic of the atmospheric
structure in the postshock region, which determines, together with the
infall region ahead of the shock, the shock radius
,
will be formally defined below. They are characteristic of the atmospheric
structure in the postshock region, which determines, together with the
infall region ahead of the shock, the shock radius
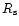 and the
shock velocity
and the
shock velocity
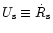 .
.
4.1 The neutrinosphere
The neutrinosphere relevant for the discussion in the following sections
is the "energy-sphere'', where neutrinos decouple energetically
from the stellar background. It usually does not coincide with the
sphere of last scattering, the
so-called "transport-sphere'', outside of which the neutrino distribution
becomes strongly forward peaked (for a detailed discussion, see Janka 1995).
Only inside their energy-sphere neutrinos can be considered to be roughly
in thermodynamic equilibrium with the stellar medium.
Besides neutrino-nucleon scattering, which is important for all
neutrinos, electron neutrinos
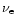 and electron antineutrinos
and electron antineutrinos
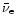 interact via frequent charged-current absorption and emission reactions with
nucleons, whereas muon and tau neutrinos and antineutrinos do not. Therefore the
energy-spheres of electron neutrinos and antineutrinos are typically
located farther out in the star at larger radii than those of muon and
tau neutrinos.
interact via frequent charged-current absorption and emission reactions with
nucleons, whereas muon and tau neutrinos and antineutrinos do not. Therefore the
energy-spheres of electron neutrinos and antineutrinos are typically
located farther out in the star at larger radii than those of muon and
tau neutrinos.
The energy deposition in the gain region, however, is clearly dominated
by
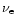 and
and
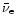 .
For this reason one can concentrate on their
transport properties and neglect muon and tau neutrinos and antineutrinos in
the discussion. Scattering off nucleons acts on all neutrinos equally.
The charged-current absorption reactions of
.
For this reason one can concentrate on their
transport properties and neglect muon and tau neutrinos and antineutrinos in
the discussion. Scattering off nucleons acts on all neutrinos equally.
The charged-current absorption reactions of
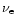 and
and
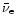 on neutrons
and protons, respectively, yield an even larger contribution to the total opacity.
The opacities of
on neutrons
and protons, respectively, yield an even larger contribution to the total opacity.
The opacities of
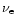 and
and
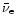 are nearly equal, because
are nearly equal, because
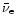 absorption and emission (Eq. (18)) is similarly
frequent as
absorption and emission (Eq. (18)) is similarly
frequent as
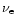 absorption and emission (Eq. (17))
as long as positrons are abundant, i.e., the stellar
atmosphere is hot and electrons are not very degenerate.
Therefore the transport-spheres and energy-spheres of electron neutrinos and antineutrinos are all close together and it is justified to consider only one, "the'', neutrinosphere
at radius
absorption and emission (Eq. (17))
as long as positrons are abundant, i.e., the stellar
atmosphere is hot and electrons are not very degenerate.
Therefore the transport-spheres and energy-spheres of electron neutrinos and antineutrinos are all close together and it is justified to consider only one, "the'', neutrinosphere
at radius 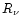 .
Of course, the real situation is more complex and there
is no definite radius interior to which neutrinos are in
equilibrium at the local thermodynamical conditions and diffuse, and exterior
to which they are decoupled from the background and stream freely. The
transition between these two limits is continuous and in case of neutrinos,
whose reaction rates are strongly energy dependent, it is also a function
of the neutrino energy.
.
Of course, the real situation is more complex and there
is no definite radius interior to which neutrinos are in
equilibrium at the local thermodynamical conditions and diffuse, and exterior
to which they are decoupled from the background and stream freely. The
transition between these two limits is continuous and in case of neutrinos,
whose reaction rates are strongly energy dependent, it is also a function
of the neutrino energy.
The spectral temperature of electron neutrinos will be taken equal to the gas
temperature at the assumed neutrinosphere,
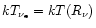 .
Detailed
simulations of neutrino transport show that electron antineutrinos
have somewhat more energetic spectra. A typical result (e.g., Bruenn 1993; Janka 1991a) is
.
Detailed
simulations of neutrino transport show that electron antineutrinos
have somewhat more energetic spectra. A typical result (e.g., Bruenn 1993; Janka 1991a) is
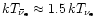 ,
which will be used below. The fact that
,
which will be used below. The fact that
 and
and
 spectra are found to be different in detailed models is an indication that the picture drawn above is overly simplified. Nevertheless
it is sufficiently accurate for the analysis in this paper. Note that in general the
neutrino luminosity
spectra are found to be different in detailed models is an indication that the picture drawn above is overly simplified. Nevertheless
it is sufficiently accurate for the analysis in this paper. Note that in general the
neutrino luminosity 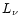 can not be related to the neutrinospheric temperature
by the Stefan-Boltzmann law for blackbody emission of a sphere with radius
can not be related to the neutrinospheric temperature
by the Stefan-Boltzmann law for blackbody emission of a sphere with radius 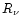 ,
,
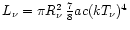 .
This formula is frequently
taken for the combined luminosity of neutrinos plus antineutrinos, assuming their
chemical potentials to be zero. However, the effective temperature
.
This formula is frequently
taken for the combined luminosity of neutrinos plus antineutrinos, assuming their
chemical potentials to be zero. However, the effective temperature
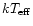 ,
which should be used in the Stefan-Boltzmann law, is typically not equal to the
spectral temperature
,
which should be used in the Stefan-Boltzmann law, is typically not equal to the
spectral temperature 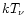 (for a discussion, see Janka 1995).
Transport simulations show that due to non-equilibrium effects the difference can
be quite significant. For this reason two parameters,
(for a discussion, see Janka 1995).
Transport simulations show that due to non-equilibrium effects the difference can
be quite significant. For this reason two parameters, 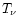 and
and 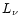 ,
will be retained here to describe the spectrum and the luminosity of the neutrinos emitted from the neutrinosphere.
Moreover, the radius of the neutrinosphere will be considered as the position in the star
where the mean value of the cosine of the neutrino propagation angle relative to
the radial direction has a value of 0.25 (see Eq. (26) and Janka 1991a,b, 1995).
,
will be retained here to describe the spectrum and the luminosity of the neutrinos emitted from the neutrinosphere.
Moreover, the radius of the neutrinosphere will be considered as the position in the star
where the mean value of the cosine of the neutrino propagation angle relative to
the radial direction has a value of 0.25 (see Eq. (26) and Janka 1991a,b, 1995).
Keeping in mind the simplifications associated with the concept of the
neutrinosphere, the radius 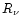 can be defined by the requirement that the
effective optical depth to energy exchange for neutrinos with average energy is
can be defined by the requirement that the
effective optical depth to energy exchange for neutrinos with average energy is
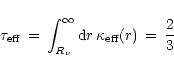 |
(13) |
(Suzuki 1989). The effective opacity
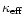 in case of
in case of
 and
and
 is defined from the scattering opacity
is defined from the scattering opacity
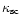 and the
absorption opacity
and the
absorption opacity
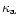 as
as
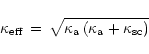 |
(14) |
(Rybicki & Lightman 1979; Shapiro & Teukolsky 1983; Suzuki 1989). Using Eqs. (10) and (11) one obtains for
the effective opacity, again averaged over the spectrum of the energy flux
which is supposed to have Fermi-Dirac shape with zero degeneracy,
in case of electron neutrinos the expression
and in case of electron antineutrinos the analogue result with
 being replaced by
being replaced by
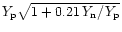 .
Since nuclei are nearly completely dissociated into free nucleons and
.
Since nuclei are nearly completely dissociated into free nucleons and
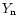 is larger than
is larger than 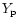 ,
i.e.,
,
i.e.,
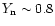 and
and
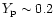 ,
but
,
but
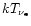 is usually somewhat lower than
is usually somewhat lower than
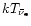 ,
i.e.,
,
i.e.,
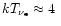 MeV and
MeV and
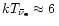 MeV, we verify the above statement that the
effective opacities of
MeV, we verify the above statement that the
effective opacities of
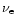 and
and
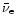 are approximately equal.
Assuming equal luminosities,
are approximately equal.
Assuming equal luminosities,
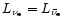 ,
a suitable average
value for the effective opacity therefore is
,
a suitable average
value for the effective opacity therefore is
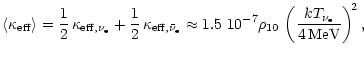 |
|
|
(16) |
where the composition dependent term in the weighted average has been
approximated by 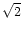 .
Knowing the density profile
.
Knowing the density profile 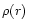 ,
the
density
,
the
density
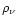 at the neutrinosphere can be determined by using
Eqs. (16) in (13).
at the neutrinosphere can be determined by using
Eqs. (16) in (13).
4.2 The gain radius
Heating and cooling of the gas outside the neutrinosphere mainly
proceed via the charged-current absorption and emission processes
of
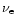 and
and
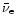 (Bethe & Wilson 1985; Bethe 1993, 1995, 1997):
(Bethe & Wilson 1985; Bethe 1993, 1995, 1997):
To leading order in the particle energies, the cross sections for neutrino
and electron/positron absorption, respectively, are
At the considered densities and temperatures, fermion phase space blocking
and dense-medium effects can be safely ignored, and electrons are
relativistic (
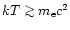 ). The heating
rate
). The heating
rate
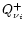 of the stellar medium by neutrinos
of the stellar medium by neutrinos 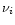 is given by
is given by
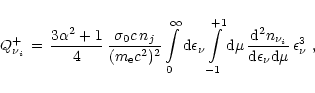 |
(21) |
where nj is the number density of the target nucleons (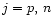 ),
and
),
and
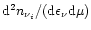 the neutrino distribution,
the neutrino distribution,
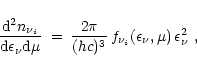 |
(22) |
with
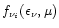 being the neutrino phase space occupation
function at some radius r, which depends on the neutrino energy
being the neutrino phase space occupation
function at some radius r, which depends on the neutrino energy
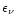 and the cosine of the angle of neutrino propagation
relative to the radial direction,
and the cosine of the angle of neutrino propagation
relative to the radial direction,
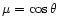 .
In Eq. (22)
the factor h in the denominator is Planck's constant. Introducing
Eq. (22) into Eq. (21) and performing
the phase space integration over all energies and angles yields
.
In Eq. (22)
the factor h in the denominator is Planck's constant. Introducing
Eq. (22) into Eq. (21) and performing
the phase space integration over all energies and angles yields
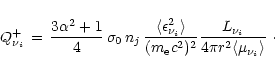 |
(23) |
Here the neutrino luminosity 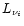 ,
the average squared neutrino
energy
,
the average squared neutrino
energy
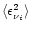 ,
and the mean value of the cosine of
the propagation angle,
,
and the mean value of the cosine of
the propagation angle,
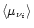 ,
are calculated from the
neutrino phase space occupation function
,
are calculated from the
neutrino phase space occupation function
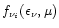 by
by
The quantity
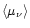 is also called flux factor and can be
understood as the ratio of the neutrino energy flux,
is also called flux factor and can be
understood as the ratio of the neutrino energy flux,
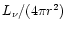 ,
to the neutrino energy density times c. Typically,
it is close to 0.25 near the neutrinosphere of
,
to the neutrino energy density times c. Typically,
it is close to 0.25 near the neutrinosphere of
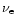 and
and
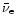 and
approaches unity when the neutrino distribution get more and more forward
peaked in the limit of free streaming with increasing distance from the
neutrinosphere (Janka 1991b, 1992, 1995).
The total heating rate
and
approaches unity when the neutrino distribution get more and more forward
peaked in the limit of free streaming with increasing distance from the
neutrinosphere (Janka 1991b, 1992, 1995).
The total heating rate 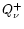 is the sum of the contributions from
is the sum of the contributions from
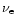 and
and
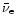 :
:
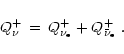 |
(27) |
To derive a simple expression, one can
again assume that
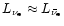 ,
,
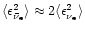 ,
and
that the
,
and
that the
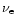 spectrum has
Fermi-Dirac shape with zero degeneracy, i.e.,
spectrum has
Fermi-Dirac shape with zero degeneracy, i.e.,
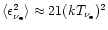 .
In addition, the equality
.
In addition, the equality
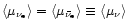 is reasonably well
fulfilled because the opacities of electron neutrinos and antineutrinos are very
similar and therefore the neutrinospheres of both of them are nearly at
the same radius. Putting everything together, the heating rate per unit volume
is derived as
is reasonably well
fulfilled because the opacities of electron neutrinos and antineutrinos are very
similar and therefore the neutrinospheres of both of them are nearly at
the same radius. Putting everything together, the heating rate per unit volume
is derived as
The numerical factor gives the rate in MeV per baryon, r7 is the radius in
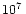 cm, and
cm, and
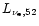 the
the
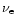 luminosity normalized to
10
luminosity normalized to
10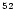 erg/s. In the layers where most of the heating and cooling between
neutrinosphere and shock take place, nuclei are nearly fully dissociated into
free nucleons (Bethe 1993, 1995, 1997; Thompson 2000) and
erg/s. In the layers where most of the heating and cooling between
neutrinosphere and shock take place, nuclei are nearly fully dissociated into
free nucleons (Bethe 1993, 1995, 1997; Thompson 2000) and
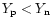 ,
therefore
using
,
therefore
using
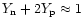 in the last expression is a reasonable approximation.
in the last expression is a reasonable approximation.
The cooling rate of the stellar gas by emission of
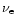 and
and
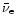 is calculated as
is calculated as
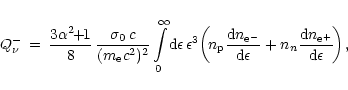 |
(29) |
where use was made of Eq. (20), and the distributions of
relativistic electrons and positrons are given by
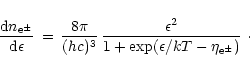 |
(30) |
T(r) is the local gas temperature and
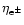 the degeneracy parameter
of electrons or positrons, defined as the ratio of the chemical potential to the
temperature. A factor of 2 was taken into account as the statistical weight
for positive and negative spin states. Inserting Eq. (30) into
Eq. (29) one gets for the cooling rate per unit volume
the degeneracy parameter
of electrons or positrons, defined as the ratio of the chemical potential to the
temperature. A factor of 2 was taken into account as the statistical weight
for positive and negative spin states. Inserting Eq. (30) into
Eq. (29) one gets for the cooling rate per unit volume
where the numerical factor is the rate in MeV per nucleon when
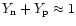 and the equilibrium relation
and the equilibrium relation
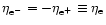 with
with
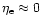 are used.
The latter approximation is good in the shock-heated layers because the
electron fraction
are used.
The latter approximation is good in the shock-heated layers because the
electron fraction
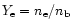 and thus the electron degeneracy
is rather low and
and thus the electron degeneracy
is rather low and
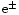 pairs are abundant.
pairs are abundant.
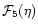 is the Fermi integral for
relativistic particles,
is the Fermi integral for
relativistic particles,
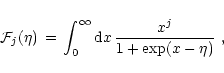 |
(32) |
with
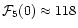 .
(Useful formulae for sums and
differences of these Fermi integrals can be found in Bludman & Van Riper 1978,
and simple approximations in Takahashi et al. 1978.)
.
(Useful formulae for sums and
differences of these Fermi integrals can be found in Bludman & Van Riper 1978,
and simple approximations in Takahashi et al. 1978.)
Heating balances cooling at the gain radius, i.e., the gain radius  has to fulfill the condition
has to fulfill the condition
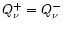 by definition.
With Eqs. (28) and (31) one obtains the following relation:
by definition.
With Eqs. (28) and (31) one obtains the following relation:
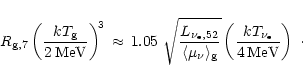 |
(33) |
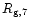 is the gain radius in units of 107 cm and
is the gain radius in units of 107 cm and
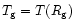 the temperature at the gain radius.
Depending on the position of the gain radius,
the temperature at the gain radius.
Depending on the position of the gain radius,
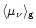 is a
factor somewhere between 0.25 (value at the neutrinosphere) and unity
(limit for
is a
factor somewhere between 0.25 (value at the neutrinosphere) and unity
(limit for
 ).
).
4.3 The EoS transition radius
It is interesting to consider the conditions for which the pressure is
dominated by nonrelativistic nucleons or radiation plus
relativistic
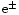 pairs (
pairs (
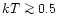 MeV).
In the first case
MeV).
In the first case
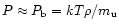 ,
if nuclei are fully dissociated into free nucleons. In the latter case
,
if nuclei are fully dissociated into free nucleons. In the latter case
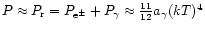 ,
when
,
when
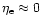 is again assumed for the electron degeneracy and the
constant is
is again assumed for the electron degeneracy and the
constant is
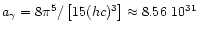 MeV-3cm-3.
Setting
MeV-3cm-3.
Setting 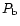 equal to
equal to 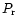 gives
gives
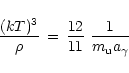 |
(34) |
or, using the temperature
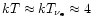 MeV (compare Fig. 2),
MeV (compare Fig. 2),
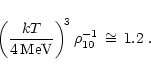 |
(35) |
This means that the transition from the baryon-dominated to the
radiation-dominated regime occurs at a density significantly below that
of the neutrinosphere. The latter is typically above 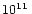 g/cm3.
When the electron degeneracy is negligibly small, the contributions of
relativistic and nonrelativistic gas components
to the pressure are equal for a value of the radiation entropy per nucleon of
g/cm3.
When the electron degeneracy is negligibly small, the contributions of
relativistic and nonrelativistic gas components
to the pressure are equal for a value of the radiation entropy per nucleon of
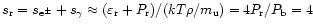 .
Since the energy density of relativistic particles is
.
Since the energy density of relativistic particles is
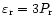 ,
whereas
,
whereas
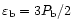 for nonrelativistic particles, the relativistic electrons-positron pairs
and photons dominate the energy density at such conditions. The main
contribution to the entropy, however, then still comes from nucleons and nuclei
(cf. Fig. 8 in Woosley et al. 1986).
for nonrelativistic particles, the relativistic electrons-positron pairs
and photons dominate the energy density at such conditions. The main
contribution to the entropy, however, then still comes from nucleons and nuclei
(cf. Fig. 8 in Woosley et al. 1986).
4.4 The shock radius and infall region
Conservation of the mass flow, momentum flow and energy flow across the
discontinuity of the shock front is expressed by the three
Rankine-Hugoniot conditions
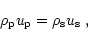 |
(36) |
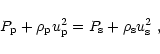 |
(37) |
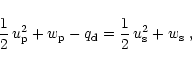 |
(38) |
where the indices p and s denote quantities just ahead and behind the shock,
respectively (see Fig. 2),
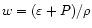 is the enthalpy per unit mass,
is the enthalpy per unit mass,
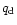 the nuclear binding energy per unit mass absorbed by
photodisintegration of nuclei within the shock front,
and
the nuclear binding energy per unit mass absorbed by
photodisintegration of nuclei within the shock front,
and
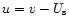 the fluid velocity
relative to the shock when
the fluid velocity
relative to the shock when
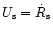 is the
shock velocity and v the gas velocity relative to the center of the star.
Note that in the infall region v has negative sign.
is the
shock velocity and v the gas velocity relative to the center of the star.
Note that in the infall region v has negative sign.
With the definition
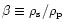 ,
Eq. (36) gives
,
Eq. (36) gives
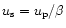 ,
which can
be used to eliminate
,
which can
be used to eliminate
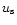 from Eq. (37).
For a strong shock, i.e.,
from Eq. (37).
For a strong shock, i.e.,
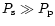 ,
this yields
,
this yields
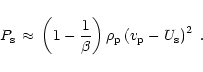 |
(39) |
Combining Eqs. (36)-(38) one further finds
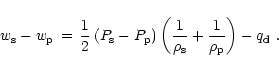 |
(40) |
With
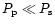 ,
,
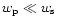 and
and
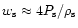 for the
radiation-dominated gas in the postshock region, Eq. (40)
can be rewritten as
for the
radiation-dominated gas in the postshock region, Eq. (40)
can be rewritten as
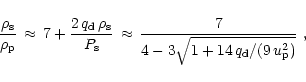 |
(41) |
where in the second transformation Eq. (39) was used to replace
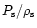 .
This shows that for a relativistic gas
the density jump in a strong shock is a factor of 7. Energy consumed by
photodissociation of nuclei increases the density contrast between preshock
and postshock region (Thompson 2000).
In a more general treatment, retaining
.
This shows that for a relativistic gas
the density jump in a strong shock is a factor of 7. Energy consumed by
photodissociation of nuclei increases the density contrast between preshock
and postshock region (Thompson 2000).
In a more general treatment, retaining
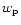 and taking into account
the (subdominant) contributions from nonrelativistic nucleons to the gas pressure behind the
shock (but still using
and taking into account
the (subdominant) contributions from nonrelativistic nucleons to the gas pressure behind the
shock (but still using
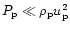 in the infall region) one also derives the right hand side of
Eq. (41), now with the expression
in the infall region) one also derives the right hand side of
Eq. (41), now with the expression
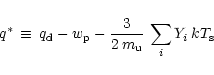 |
(42) |
instead of
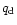 in the denominator. This means that the density
discontinuity is also affected by the preshock enthalpy and the thermal pressure
of nucleons and nuclei behind the shock (the nuclear composition is accounted
for by the sum of the number fractions,
in the denominator. This means that the density
discontinuity is also affected by the preshock enthalpy and the thermal pressure
of nucleons and nuclei behind the shock (the nuclear composition is accounted
for by the sum of the number fractions, 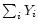 ).
Considering
).
Considering
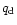 to be several
MeV/
to be several
MeV/
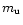 ,
,
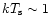 MeV, and the preshock medium to be
dominated by relativistic, degenerate electrons in which case
MeV, and the preshock medium to be
dominated by relativistic, degenerate electrons in which case
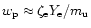 with an electron chemical
potential
with an electron chemical
potential
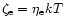 of a few MeV, one can see that all terms in
Eq. (42) are of the same order and therefore equally important.
of a few MeV, one can see that all terms in
Eq. (42) are of the same order and therefore equally important.
The preshock region is not affected by the postshock conditions. Because
the shock moves supersonically relative to the medium ahead of it,
sound waves cannot transport information in this direction. The matter
there falls into the shock with a significant fraction of the
free-fall velocity,
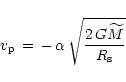 |
(43) |
with
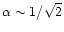 (Bethe 1990, 1993; Bruenn 1993).
Ahead of the shock free nucleons are absent and therefore
(Bethe 1990, 1993; Bruenn 1993).
Ahead of the shock free nucleons are absent and therefore
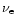 and
and
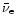 absorption does not play a role, but neutrinos interact with nuclei by coherent
scatterings. The opacity of the latter reaction scales roughly with N2/A when Nis the neutron number and A the mass number of the nuclei, and the total neutrino
opacity of the preshock medium turns out to be close to the result of
Eq. (12). Therefore the momentum transfer by neutrinos was again taken
into account by using
absorption does not play a role, but neutrinos interact with nuclei by coherent
scatterings. The opacity of the latter reaction scales roughly with N2/A when Nis the neutron number and A the mass number of the nuclei, and the total neutrino
opacity of the preshock medium turns out to be close to the result of
Eq. (12). Therefore the momentum transfer by neutrinos was again taken
into account by using
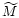 instead of M in Eq. (43).
Plugging Eq. (43) into the rate at which mass falls into the shock,
instead of M in Eq. (43).
Plugging Eq. (43) into the rate at which mass falls into the shock,
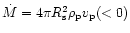 ,
gives the density just above the shock:
,
gives the density just above the shock:
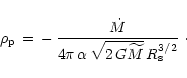 |
(44) |
On the other hand, if the original presupernova material has a density
distribution
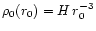 with H being a constant, then
mass conservation yields a density at the footpoint of the shock at time t
after the start of the collapse of
with H being a constant, then
mass conservation yields a density at the footpoint of the shock at time t
after the start of the collapse of
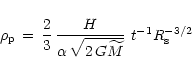 |
(45) |
(Bethe 1990, 1993; see also Cooperstein et al. 1984). Comparing
Eqs. (44) and (45) one finds that the rate at which mass
crosses the shock in this case is
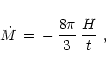 |
(46) |
which depends on the structure of the progenitor star through the constant
H and decreases with time.


Up: Conditions for shock revival
Copyright ESO 2001
![]() ,
the gain radius
,
the gain radius
![]() and
the transition radius of the EoS properties,
and
the transition radius of the EoS properties,
![]() ,
will be formally defined below. They are characteristic of the atmospheric
structure in the postshock region, which determines, together with the
infall region ahead of the shock, the shock radius
,
will be formally defined below. They are characteristic of the atmospheric
structure in the postshock region, which determines, together with the
infall region ahead of the shock, the shock radius
![]() and the
shock velocity
and the
shock velocity
![]() .
.
![]() and electron antineutrinos
and electron antineutrinos
![]() interact via frequent charged-current absorption and emission reactions with
nucleons, whereas muon and tau neutrinos and antineutrinos do not. Therefore the
energy-spheres of electron neutrinos and antineutrinos are typically
located farther out in the star at larger radii than those of muon and
tau neutrinos.
interact via frequent charged-current absorption and emission reactions with
nucleons, whereas muon and tau neutrinos and antineutrinos do not. Therefore the
energy-spheres of electron neutrinos and antineutrinos are typically
located farther out in the star at larger radii than those of muon and
tau neutrinos.
![]() and
and
![]() .
For this reason one can concentrate on their
transport properties and neglect muon and tau neutrinos and antineutrinos in
the discussion. Scattering off nucleons acts on all neutrinos equally.
The charged-current absorption reactions of
.
For this reason one can concentrate on their
transport properties and neglect muon and tau neutrinos and antineutrinos in
the discussion. Scattering off nucleons acts on all neutrinos equally.
The charged-current absorption reactions of
![]() and
and
![]() on neutrons
and protons, respectively, yield an even larger contribution to the total opacity.
The opacities of
on neutrons
and protons, respectively, yield an even larger contribution to the total opacity.
The opacities of
![]() and
and
![]() are nearly equal, because
are nearly equal, because
![]() absorption and emission (Eq. (18)) is similarly
frequent as
absorption and emission (Eq. (18)) is similarly
frequent as
![]() absorption and emission (Eq. (17))
as long as positrons are abundant, i.e., the stellar
atmosphere is hot and electrons are not very degenerate.
Therefore the transport-spheres and energy-spheres of electron neutrinos and antineutrinos are all close together and it is justified to consider only one, "the'', neutrinosphere
at radius
absorption and emission (Eq. (17))
as long as positrons are abundant, i.e., the stellar
atmosphere is hot and electrons are not very degenerate.
Therefore the transport-spheres and energy-spheres of electron neutrinos and antineutrinos are all close together and it is justified to consider only one, "the'', neutrinosphere
at radius ![]() .
Of course, the real situation is more complex and there
is no definite radius interior to which neutrinos are in
equilibrium at the local thermodynamical conditions and diffuse, and exterior
to which they are decoupled from the background and stream freely. The
transition between these two limits is continuous and in case of neutrinos,
whose reaction rates are strongly energy dependent, it is also a function
of the neutrino energy.
.
Of course, the real situation is more complex and there
is no definite radius interior to which neutrinos are in
equilibrium at the local thermodynamical conditions and diffuse, and exterior
to which they are decoupled from the background and stream freely. The
transition between these two limits is continuous and in case of neutrinos,
whose reaction rates are strongly energy dependent, it is also a function
of the neutrino energy.
![]() .
Detailed
simulations of neutrino transport show that electron antineutrinos
have somewhat more energetic spectra. A typical result (e.g., Bruenn 1993; Janka 1991a) is
.
Detailed
simulations of neutrino transport show that electron antineutrinos
have somewhat more energetic spectra. A typical result (e.g., Bruenn 1993; Janka 1991a) is
![]() ,
which will be used below. The fact that
,
which will be used below. The fact that
![]() and
and
![]() spectra are found to be different in detailed models is an indication that the picture drawn above is overly simplified. Nevertheless
it is sufficiently accurate for the analysis in this paper. Note that in general the
neutrino luminosity
spectra are found to be different in detailed models is an indication that the picture drawn above is overly simplified. Nevertheless
it is sufficiently accurate for the analysis in this paper. Note that in general the
neutrino luminosity ![]() can not be related to the neutrinospheric temperature
by the Stefan-Boltzmann law for blackbody emission of a sphere with radius
can not be related to the neutrinospheric temperature
by the Stefan-Boltzmann law for blackbody emission of a sphere with radius ![]() ,
,
![]() .
This formula is frequently
taken for the combined luminosity of neutrinos plus antineutrinos, assuming their
chemical potentials to be zero. However, the effective temperature
.
This formula is frequently
taken for the combined luminosity of neutrinos plus antineutrinos, assuming their
chemical potentials to be zero. However, the effective temperature
![]() ,
which should be used in the Stefan-Boltzmann law, is typically not equal to the
spectral temperature
,
which should be used in the Stefan-Boltzmann law, is typically not equal to the
spectral temperature ![]() (for a discussion, see Janka 1995).
Transport simulations show that due to non-equilibrium effects the difference can
be quite significant. For this reason two parameters,
(for a discussion, see Janka 1995).
Transport simulations show that due to non-equilibrium effects the difference can
be quite significant. For this reason two parameters, ![]() and
and ![]() ,
will be retained here to describe the spectrum and the luminosity of the neutrinos emitted from the neutrinosphere.
Moreover, the radius of the neutrinosphere will be considered as the position in the star
where the mean value of the cosine of the neutrino propagation angle relative to
the radial direction has a value of 0.25 (see Eq. (26) and Janka 1991a,b, 1995).
,
will be retained here to describe the spectrum and the luminosity of the neutrinos emitted from the neutrinosphere.
Moreover, the radius of the neutrinosphere will be considered as the position in the star
where the mean value of the cosine of the neutrino propagation angle relative to
the radial direction has a value of 0.25 (see Eq. (26) and Janka 1991a,b, 1995).
![]() can be defined by the requirement that the
effective optical depth to energy exchange for neutrinos with average energy is
can be defined by the requirement that the
effective optical depth to energy exchange for neutrinos with average energy is
![]() and
and
![]() (Bethe & Wilson 1985; Bethe 1993, 1995, 1997):
(Bethe & Wilson 1985; Bethe 1993, 1995, 1997):
![]() and
and
![]() is calculated as
is calculated as
![]() has to fulfill the condition
has to fulfill the condition
![]() by definition.
With Eqs. (28) and (31) one obtains the following relation:
by definition.
With Eqs. (28) and (31) one obtains the following relation:
![]() pairs (
pairs (
![]() MeV).
In the first case
MeV).
In the first case
![]() ,
if nuclei are fully dissociated into free nucleons. In the latter case
,
if nuclei are fully dissociated into free nucleons. In the latter case
![]() ,
when
,
when
![]() is again assumed for the electron degeneracy and the
constant is
is again assumed for the electron degeneracy and the
constant is
![]() MeV-3cm-3.
Setting
MeV-3cm-3.
Setting ![]() equal to
equal to ![]() gives
gives
![]() ,
Eq. (36) gives
,
Eq. (36) gives
![]() ,
which can
be used to eliminate
,
which can
be used to eliminate
![]() from Eq. (37).
For a strong shock, i.e.,
from Eq. (37).
For a strong shock, i.e.,
![]() ,
this yields
,
this yields