5 Variability of instrumental lines

The activity of isotopes contributing to the COMPTEL background (except for the primordial radio-isotopes ⁴⁰K and ²⁰⁸Tl) in general varies in time. They are produced by interactions of primary and secondary cosmic-ray particles and radiation-belt (SAA) particles within the instrument material. The intensity of each of these particle species, and hence the level of activation, changes in time due to orbit details (e.g. the satellite's altitude, the geomagnetic cut-off rigidity, the SAA radiation dose) and the solar cycle. The activity of a specific radioactive isotope then results from the competing processes of activation (production) and decay.

The variation of the activity of a specific isotope is complex in general. If the isotope's half-life T_1/2 and the typical time-scale(s) $\tau$ for the intensity variation of the particle population(s) producing it are very different, however, the activity variations can be described rather simply. For $T_{1/2} \ll \tau$, the isotope's activity approximatly follows the incident cosmic-ray particle intensity and its orbital variation (see Sect. 5.2). This is, e.g., the case for short-lived isotopes ( $T_{1/2} \stackrel{\textstyle _<}{_{\sim}}$ a few minutes) produced by primary cosmic-ray particles or neutrons, such as ²D and ²⁸Al. For $T_{1/2} \gg \tau$, a long-term build-up occurs since the activated nuclei do not decay away between consecutive SAA transits (see Sect. 5.1). This is, e.g., the case for long-lived isotopes ( $T_{1/2} \gg 90$ min, i.e. the orbital period) produced during SAA passages (which occur 6-8 times each day), such as ²²Na and ²⁴Na. Intermediate half-lifes produce more complicated variability.

The long-term and orbital variations of spectral features are useful in identifying their physical origin. Spectral features arising from primordial radioactivity will show no variation. Prompt and short-lived components will vary with incident cosmic-ray intensity, i.e. on time-scales shorter than an orbital period. In addition, prompt and short-lived components may also vary over long time-scales if their production is sensitive to changes in the cosmic-ray intensity due to the solar cycle or the orbit altitude. Spectral features due to long-lived isotopes will exhibit variations on time-scales that reflect their half-life as well as the changes in SAA dosage. With regard to a spectral feature not yet identified, these long-term variations provide a crude estimate of its half-life. With regard to a tentatively identified isotope, comparison of its time-dependent activity with an empirical model serves as an important cross-check for the correctness of its identification.

  
5.1 Long-term variation

The long-term variation of the activity of long-lived radio-nuclides arises from the combined effects of the isotopes' decay and the time history of the activation episodes during SAA transits. Activation outside the SAA by cosmic-ray particles is negligible (see e.g. Kurfess et al. 1989), since the average daily fluence due to SAA particles by far exceeds that of cosmic-ray particles. The count rate in the CAL-units can be used to model the production of long-lived radio-nuclides (Varendorff et al. 1997, hereafter referred to as "activity model''). The small plastic scintillators (thickness 3 mm, diameter 12 mm) of the CAL-units are sensitive to protons and other charged particles, but insensitive to secondary $\gamma$-ray photons. They therefore provide a measure of the charged-particle flux at the instrument (Snelling et al. 1986). The trigger rates of the two CAL-units above both a low and a high threshold value are available for all times, including SAA transits. Most other instrument systems are switched off during SAA passages, including the veto shields which therefore cannot be used as charged particle monitors for the activity model. The high-threshold trigger rate of CAL-unit B ( ${r}_{\rm BH}$) is most useful because it is the least affected by noise and long-term efficiency degradation. Only telemetry data gaps interrupt this measure of the cosmic-ray intensity.

To achieve continuous information on the charged-particle flux during every SAA passage, the activity model employs a neural net to describe ${r}_{\rm BH}$ as a function of orbit altitude, geographic longitude and latitude, time since launch (to include variations due to the solar cycle), and orientation (azimuth and zenith) of the satellite relative to its velocity vector (to account for asymmetries in the incident SAA-proton flux, see e.g. Watts et al. 1989). The number of nuclei of a specific isotope as a function of time, N(t), is then given by:

 

$$N(t + \delta t) N(t) \cdot {\rm e}^{-\lambda \cdot \delta t} + N_{\rm new}(t)$$ =

$${\rm and}$$ (2)

$$N_{\rm new}(t) \alpha \cdot \delta t \cdot ({r}_{\rm BH}(t) - {r}_{\rm BH,0})$$ =

where the time interval $\delta t$ usually is 16.384 s, $\lambda = \ln 2 / T_{1/2}$ is the decay constant of the isotope with half-life T_1/2, $\alpha$ is the proportionality factor between the CAL-unit trigger rate and the isotope activation, and ${r}_{\rm BH,0}$ is the value of ${r}_{\rm BH}$outside the SAA. The isotope activity A(t) then is

$$A(t) = \lambda \cdot N(t).$$ (3)

The value of $\alpha$ is not well known as it depends on the cross-sections for the production of the isotope in the telescope material, particularly in the D1 detector. For each isotope, a scaling factor, which is the product of $\alpha$ and the efficiency for triggering a background event (see Sect. 6), must be determined from a measurement of the event rate from the COMPTEL data.

Figure 8: The measured event rates due to the long-lived isotopes 22Na, 24Na, 52Mn, and 57Ni, the short-lived isotopes 2D and 28Al, and the primordial isotopes 40K and 208Tl as a function of time for the first 6 years (May 1991 through July 1997) of the CGRO mission for imaging event selections. In addition, the predictions of the normalized activity model for the long-lived isotopes is depicted with solid grey lines

Figure 9: The altitude of the CGRO orbit as a function of time from May 1991 through July 1997. The two reboosts of the orbit around TJD 9280 (Oct.-Dec. 1993) and TJD 10560 (Apr.-May 1997) are clearly seen. The rapid decay of the orbit at the beginning of the mission results from the increased drag of the expanded atmosphere at solar maximum

A comparison of the measured event rates due to the long-lived isotopes ²²Na, ²⁴Na, ⁵²Mn, and ⁵⁷Ni with the predictions of the normalized activity model from May 1991 through July 1997 is depicted in the left panels of Fig. 8. In addition, the long-term variation determined for the event rates arising from the short-lived isotopes ²D and ²⁸Al, as well as from the primordial radio-nuclides ⁴⁰K and ²⁰⁸Tl are shown in the right panels of Fig. 8. These rates were obtained from the study of the galactic ²⁶Al 1.8 MeV line emission, which requires a measure of the isotopes' background contributions for each observation period (see Appendix B.2) under imaging event selections (see Appendix A.2). The scatter of the eight sets of event rates, particularly those for the primordial radio-isotopes ⁴⁰K and ²⁰⁸Tl, is larger than what is expected from statistics alone. Part of the additional scatter is expected from intrinsic inadequacies of the fitting procedure (such as the correction for the Earth-horizon angle selection, see Appendix B.2) and of the fit models employed (these cannot account for all structures in the E₂ and $E_{\rm tot}$ spectra, which particularly affects weak components, see below and Appendix B). Partly, however, the additional scatter may be attributed to known physical effects. Due to the precession of the satellite orbit the radiation dose from SAA transits may vary considerably between observation periods. In addition, the orientation of the satellite relative to the anisotropic SAA-particle flux affects the radiation dose in the D1 detector, which is the major source of instrumental line background. The resulting differences in SAA radiation dose between observation periods contribute to the scatter in the event rates of the long-lived isotopes. Since the CAL-units are located half-way between the D1 and D2 detectors, shielding effects due to surrounding spacecraft materials may result in less variation in ${r}_{\rm BH}$ than in the D1 radiation dose, so that the activity model would underpredict this variation. Orientation effects may also result in variations of the effective cosmic-ray particle flux between observation periods and add some scatter to the event rates of short-lived isotopes.

The long-term variation of the long-lived isotopes reflects the variation of the SAA radiation dose, which depends, among other parameters, on orbit altitude and solar cycle. ²⁴Na is the best tracer of the changing intensity of the encountered SAA-particle fluxes, as it is the strongest component of the line background and has a half-live of about 15 h. From the beginning of the mission until the first reboost (around TJD 9280), the decay of the orbital altitude (see Fig. 9) results in a monotonic decrease of the incident SAA-particle fluxes. The SAA radiation dose increased after the first reboost; the effect of the slow decrease of the orbital altitude is probably more than compensated by the solar cycle, which proceeded towards solar minimum, resulting in the observed net increase of SAA radiation dose over time. The second reboost (around TJD 10560) again resulted in a significant increase of activation during SAA passages. The long-term variation of the ⁵²Mn and ⁵⁷Ni event rates is similar to that of ²⁴Na, since the half-lifes of these isotopes are of the same order. The long-term behaviour of the ²²Na event rate is quite different. Its 2.6 y half-life is significantly longer than the typical time-scale of the changes in SAA radiation dose. Therefore ²²Na never reaches an equilibrium between activation and decay, but is continuously built up, with the two reboosts resulting in increases in the slope of the ²²Na activity trend.

The fact that the activity model reproduces the long-term variation of the event rates from long-lived isotopes confirms the model assumptions, in particular that activation predominantly occurs during SAA transits. The model can also verify the isotope identifications, as the activity of an isotope depends, among other parameters, on its half-life (see Eqs. (2) and (3)).

The background produced by the short-lived isotopes ²D and ²⁸Al is not expected to be influenced by SAA radiation dose, rather, any long-term trends will arise from variations in the average cosmic-ray intensity. The count rate in the 2.22 MeV line does not exhibit any significant long-term variation. The orbital variation of the event rate in the 2.22 MeV line (Weidenspointner et al. 1996) is similar to that of the fast-neutron flux ( ${E}_{\rm n} > 12.8$ MeV) in the D1 detector (Morris et al. 1995a), as discussed in Sect. 5.2. In addition, Morris et al. (1995a) demonstrated that the solar cycle variation of the fast-neutron flux is much less than its orbit variation. It is therefore expected that the relatively weak solar cycle dependence of the 2.22 MeV line is dominated by the much greater orbital variations, which presumably accounts for much of the observed scatter. Similar to ²D, the isotope ²⁸Al is predominantly produced by thermal-neutron captures. Hence ²⁸Al is expected to exhibit the same long-term variation as ²D. However, the low count rate from ²⁸Al exhibits a slight, increasing trend, hinting at deficiencies of the fit models and/or contributions from yet unidentified isotopes.

The activity of the primordial radio-nuclides ⁴⁰K and ²⁰⁸Tl is constant over the duration of the mission. Both data sets are consistent with this fact, although a small long-term increase may be present for ²⁰⁸Tl. Again, this apparent increase may be due to deficiencies of the fitting procedure and/or due to yet unidentified line background components.

The activity model can not only be used to predict the number of nuclei activated during SAA passages, but also to estimate the average daily SAA-proton fluence from the daily increase in the number of proton-produced nuclei. For example, based on the measured ²²Na event rate a daily average SAA-proton fluence ( ${E}_{\rm p} > 100$ MeV) of 2.3 10⁵ protons cm^-2 was inferred by Varendorff et al. (1997) for the beginning of the mission during solar maximum at an altitude of 440 km. Considering the uncertainties in this measurement, and the large altitude gradient of the SAA-proton flux (Stassinopoulos 1989), this value is in good agreement with the prediction of 5 10⁵ protons cm^-2 for an altitude of 462 km (Dyer et al. 1994).

  
5.2 Variation with cosmic-ray intensity

The prompt instrumental background closely tracks the local, instantaneous cosmic-ray intensity, which can, e.g., be parameterized by a geomagnetic cut-off rigidity. Another way of parameterizing the incident cosmic-ray intensity is to use the count rate of the anti-coincidence domes of the COMPTEL instrument, referred to as "veto rate'' in the following. To a good approximation, the prompt background components vary in proportion to the incident cosmic-ray intensity as monitored by the veto rate. The best example of this are ²D and ²⁸Al (Fig. 10), determined for CDG event selections (see Appendix A.1). In the following discussion, "veto rate'' and "incident cosmic-ray intensity'' are therefore used interchangeably. In contrast to prompt background components, the activity of the primordial radio-isotopes ⁴⁰K and ²⁰⁸Tl is independent of incident cosmic-ray intensity and hence does not vary with veto rate. The activity variation of long-lived isotopes such as ²²Na with veto rate is complex and depends on the isotopes' half-life as well as on the geophysical environment. Similar to the study of the long-term variation, the study of the variation of the event rate of a background component with cosmic-ray intensity can be helpful in identifying the responsible isotope.

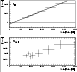Figure 10: The veto rate variation of the count rate due the background isotopes 2D and 28Al as measured for CDG event selections. The dashed line is a linear fit to the measured 2D event rate

In the following, the physical origin of the complex and - in general - non-linear variation of the event rate of long-lived isotopes with incident cosmic-ray intensity as monitored by veto rate is illustrated with the isotope ²²Na, which has a half-life of 2.6 y. To investigate the variation of a line background component with veto rate over a given time period the events are sorted in energy spectra, one for each of a set of veto rate intervals, according to the veto rate value at the time the events were recorded. The event rate due to the background isotope under study is then determined for each veto rate bin in an iterative line fitting procedure described in Appendix B.1. Each of these rates represents the "average'' event rate due to the isotope in a given veto rate interval over a given time period.

The veto rate variation of the event rate due to ²²Na over relatively short periods of time, during which the geophysical environment did not change significantly, is illustrated in Fig. 11 for data from 1991-1993 (CGRO Phases I and II) and from 1994-1995 (CGRO Cycle 4). To a good approximation, the ²²Na event rate is independent of veto rate, as expected for a half-life of 2.6 years. The average ²²Na event rate increased with time due to the build-up of this isotope during successive SAA passages (see Fig. 8). An increasing background contribution is also observed for long-lived isotopes with shorter half-lifes, such as ²⁴Na with T_1/2 = 15 h. However, due to a correlation between the encountered geomagnetic cut-off rigidity and the time since the last SAA transit, there is some correlation between the event rate of these isotopes and veto rate, which is generally complex even over relatively short periods of time. Nevertheless, the following conclusions drawn from the veto rate variation of the ²²Na event rate apply to long-lived isotopes with shorter half-lifes such as ²⁴Na as well.

Figure 11: The count rate from 22Na, determined under CDG event selections, as a function of veto rate for data from 1991-1993 and from 1994-1995

Figure 12: The count rate from 22Na, determined under CDG event selections, as a function of veto rate for data from 1991-1996

The average variation of the event rate arising from ²²Na over the extended time period from 1991-1996 (CGRO Phase I through Cycle 5), during which the geophysical environment changed significantly due to the first reboost (see Fig. 9) and the solar cycle, is depicted in Fig. 12. Typically, a bump-like feature, hereafter referred to as the veto rate bump, appears at low veto rate values when studying the veto rate variation of the background contribution of long-lived isotopes over extended periods of time that include at least one reboost. This is even true for an isotope such as ²²Na, whose event rate is independent of veto rate over short periods of time. It must be emphasized, however, that changes in the geophysical environment do not always produce a bump-like feature, but rather result in a complex, non-linear variation of the contribution from long-lived background components with veto rate.

Figure 13: The variation of the normalized veto rate frequency distribution with time, exemplified for veto dome 2. Depicted are the normalized veto rate frequency distributions, in units of 16.384 s time intervals (superpackets, SP) per veto rate bin, for the time periods 1991/1992 (thin black line), 1994/1995 (grey line), and 1997/1998 (thick black line)

To understand the origin of the veto rate bump it is necessary to realize that the changing geophysical environment not only affects the activity of long-lived isotopes (see Fig. 8), but also the veto rate frequency distribution, mostly due to variations of the incident cosmic-ray intensity with orbit altitude and solar cycle. This is illustrated in Fig. 13, depicting the normalized veto rate frequency distributions for the time periods 1991/1992, 1994/1995, and 1997/1998 (i.e. CGRO Phase I, Cycle 4, and Cycle 7, respectively). For clarity, the distributions for other Phases/Cycles were omitted as they are fully consistent with the trend described in the following. The generic veto rate distribution is characterized by a pronounced peak at low veto rates, with a flat tail extending to higher veto rate values. To a good approximation, the time variation of this generic veto rate frequency distribution can be described by a slow but steady shift of the peak to higher veto rate values, with some slight changes of the shape of the distribution such as an increasing extension of the tail.

Figure 14: Illustration of the origin of the veto rate bump. Features such as the veto rate bump result from the combined effects of the time variation of the isotope activity (see Fig. 8) and of the veto rate frequency distribution (see Fig. 13), as explained in detail in the text

As is illustrated in Fig. 14, the veto rate bump is nothing more than an artifact of the combined effects of the long-term variation in the activity of long-lived isotopes (see Fig. 8) and of the long-term shift of the veto rate frequency distribution (see Fig. 13). For simplicity, let us consider a long-lived isotope whose activity is independent of veto rate over periods of time during which the geophysical conditions do not change, such as ²²Na. Let us further consider a combination of two such time intervals of equal duration from early and late in the mission. Late in the mission the isotope activity is higher than early in the mission, and the veto rate distribution is shifted to higher veto rate values. The two sets of data are represented by the two bars in Fig. 14, with the grey-shading indicating the veto rate distribution in terms of the number of 16.384 s sampling intervals (superpackets, see Footnote 4) per veto rate interval, i.e. dark grey indicates that the corresponding veto rate values occurred more often (compare Fig. 13). The average activity (determined as described above) then increases from interval 1 through interval 4 as the late-mission data become relatively more important. In interval 5 both sets of data contribute equally and the average activity is the mean of the individual activities. Finally, only data from the late mission contribute to veto rate interval 6. The net result for the average activity exhibits a general tendency to increase with increasing veto rate with a pronounced bump superimposed - similar to what has been measured for ²²Na (compare to Fig. 12). It can easily be demonstrated, following the above example, that the veto rate bump is an almost universal indicator for the presence of radio-isotopes with half-lifes ranging from several minutes to several years when combining data covering extended periods of time during which the geophysical environment inevitably changed. However, the veto rate bump cannot be used to estimate the half-life of an isotope, as can be done with the activity model. Also, it should be noted that non-linear variations of the event rate due to a long-lived isotope with veto rate other than the veto rate bump are to be expected once the isotope activity decreases and/or the veto rate frequency distribution shifts towards lower values as the mission continues.

Among other things, a detailed understanding of the variation of the background contribution of long-lived isotopes with veto rate is necessary for a reliable measurement of the cosmic diffuse gamma-ray background (CDG) at MeV energies. The COMPTEL analyses make use of the variable nature of the instrument background to isolate the CDG signal, which is assumed to be constant (see e.g. Kappadath et al. 2000; Weidenspointner et al. 2001). In particular, above about 4 MeV the instrumental background is exclusively due to prompt processes. These are also present in the background at lower energies, but with large contributions from long-lived radioactive isotopes. Because prompt background components vary, to a good approximation, linearly with incident cosmic-ray intensity as monitored by veto rate, they can be eliminated from the data by an extrapolation technique (Kappadath et al. 1996). In contrast, the event rate of long-lived isotopes does not vary linearly with veto rate. The contributions of long-lived isotopes must therefore be subtracted, as a function of veto rate, before the veto rate extrapolation (Weidenspointner 1999). The validity of a veto rate extrapolation for removing prompt instrumental backgrounds thus depends on the absence of any long-lived background components, since only then can the event rate be assumed to vary linearly with veto rate. Subtraction of non-prompt background components after the veto rate extrapolation is only possible for constant background components, such as primordial radioactivity.