

Up: Accretion discs models with
Subsections
In a steady state Keplerian accretion disc where the viscosity is
given by Eq. (2), the mass accretion rate 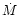 is linked to
the surface density
is linked to
the surface density 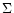 by the relation
by the relation
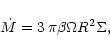 |
(A.1) |
where 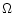 is the Keplerian angular velocity and R the
radius. The surface density is
is the Keplerian angular velocity and R the
radius. The surface density is
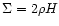 ,
with
,
with 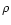 being
the mass density and H the total pressure scale height, which is
determined from the equation of hydrostatic equilibrium
being
the mass density and H the total pressure scale height, which is
determined from the equation of hydrostatic equilibrium
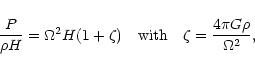 |
(A.2) |
where 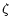 represents the effect of self-gravity.
The total pressure P
is the sum of the gas pressure
represents the effect of self-gravity.
The total pressure P
is the sum of the gas pressure 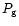 and of the
radiation pressure
and of the
radiation pressure 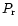 :
:
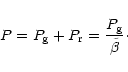 |
(A.3) |
We draw 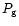 from the perfect gas equation
from the perfect gas equation
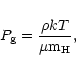 |
(A.4) |
where T is the midplane temperature and 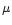 the mean
mass per particle
in units of the proton mass. The disc temperature in the equatorial
plane is fixed by the balance Q+=Q- between viscous heating
(Frank et al. 1992)
the mean
mass per particle
in units of the proton mass. The disc temperature in the equatorial
plane is fixed by the balance Q+=Q- between viscous heating
(Frank et al. 1992)
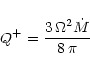 |
(A.5) |
and radiative losses (Hubeny 1990)
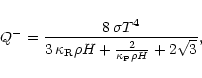 |
(A.6) |
where
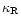 and
and
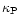 are respectively the Rosseland
and Planck mean
opacities (in cm2g-1). The general
expression for the radiative pressure is then
are respectively the Rosseland
and Planck mean
opacities (in cm2g-1). The general
expression for the radiative pressure is then
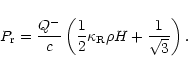 |
(A.7) |
Note that in the optically thick limit the radiation
pressure tends
to its LTE value (labeled with an asterisk)
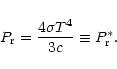 |
(A.8) |
The above equation set can in fact be reduced to a system of two
non linear algebraic equations with 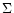 as the unknown. From
Eqs. (A.1)-(A.7), the
first equation is
as the unknown. From
Eqs. (A.1)-(A.7), the
first equation is
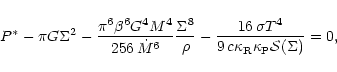 |
(A.9) |
where the function
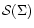 is
is
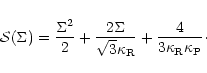 |
(A.10) |
The second equation is obtained from Eqs. (A.1),
(A.5)
and (A.6)
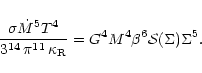 |
(A.11) |
We can follow the method
described in Huré (1998) to solve the system of Eqs. (A.9)
and (A.11). Note that the solution is valid in all
cases: optically thick or thin, pressure dominated by gas or radiation,
self-gravitating or not.
If we set
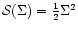 in
Eqs. (A.9) and (A.11), and omit the last term
of Eq. (A.9) we recover the optically thick limit (
in
Eqs. (A.9) and (A.11), and omit the last term
of Eq. (A.9) we recover the optically thick limit (
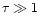 ),
and there is a single equation to solve:
),
and there is a single equation to solve:
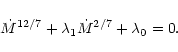 |
(A.12) |
The coefficients 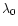 and
and 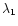 are respectively
are respectively
Note that the solution of Eq. (A.12) must satisfy
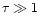 .
.
In the optically thin limit (
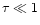 ),
),
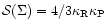 and the last term of
Eq. (A.9) is identical to
and the last term of
Eq. (A.9) is identical to
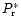 .
There is also a single
equation to solve, namely
.
There is also a single
equation to solve, namely
| |
|
![$\displaystyle \left[4 \, \pi G \rho + \left( \frac{16 \sigma \kappa_{\rm P}}{3
\beta G^{2/3} M^{2/3}}T^4 \right)^{6/5} \right] \dot{M}^2$](/articles/aa/full/2001/09/aa10256/img165.gif) |
|
| |
|
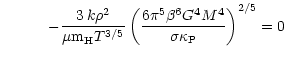 |
(A.14) |
and its solution must be such that
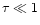 .
.


Up: Accretion discs models with
Copyright ESO 2001
![]() is linked to
the surface density
is linked to
the surface density ![]() by the relation
by the relation
![]() in
Eqs. (A.9) and (A.11), and omit the last term
of Eq. (A.9) we recover the optically thick limit (
in
Eqs. (A.9) and (A.11), and omit the last term
of Eq. (A.9) we recover the optically thick limit (
![]() ),
and there is a single equation to solve:
),
and there is a single equation to solve:
![]() ),
),
![]() and the last term of
Eq. (A.9) is identical to
and the last term of
Eq. (A.9) is identical to
![]() .
There is also a single
equation to solve, namely
.
There is also a single
equation to solve, namely