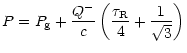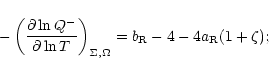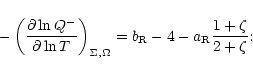Up: Accretion discs models with
Setting
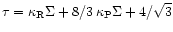 ,
and differentiating
Eq. (A.6) while keeping
,
and differentiating
Eq. (A.6) while keeping 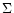 constant, we obtain
constant, we obtain
where
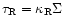 and
and
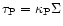 are the total Rosseland and Planck
optical thicknesses respectively, and
are the total Rosseland and Planck
optical thicknesses respectively, and
Note that this expression does not depend on the actual viscosity
prescription. For Thompson scattering, we have simply
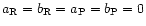 ,
and for free-free opacity,
,
and for free-free opacity,
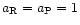 and
and
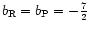 .
For a
combination of both sources, we have
.
For a
combination of both sources, we have
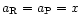 and
and
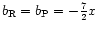 where
where
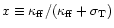 .
.
To compute the derivative
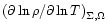 ,
we use the two different
expressions of the total pressure at the midplane. First, by
differentiation of Eq. (A.2), keeping
,
we use the two different
expressions of the total pressure at the midplane. First, by
differentiation of Eq. (A.2), keeping 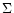 and
and
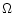 constant, we have
constant, we have
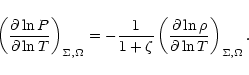 |
(B.2) |
Note that
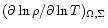 is
always negative. Second, from Eq. (A.3) which is written
is
always negative. Second, from Eq. (A.3) which is written
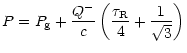 |
|
|
(B.3) |
and setting
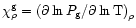 ,
,
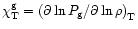 and
and
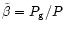 ,
we have
,
we have
Combining now Eqs. (B.2) and (B.4), we find
| |
|
![$\displaystyle -\left( \frac{ \partial \ln \rho }{\partial \ln T}
\right)_{\Sigm...
...ght) a_{\rm R}
\frac{\tau_{\rm R}}{\tau_{\rm R} + \frac{4}{\sqrt{3}}} \right] =$](/articles/aa/full/2001/09/aa10256/img191.gif) |
|
| |
|
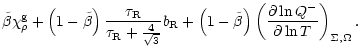 |
|
| |
|
|
(B.5) |
Finally, from Eqs. (B.1) and (B.5) and after
rearrangement
and so Eq. (B.1) becomes
It is then easy to derive from Eq. (B.7) the following
asymptotic expressions:
- in the optically thick limit (
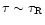 and
and
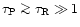 )
)
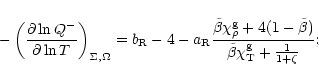 |
(B.8) |
- in the radiative pressure dominated limit (
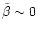 )
)
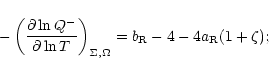 |
(B.9) |
- in the gas pressure dominated limit (
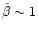 )
)
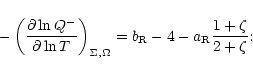 |
(B.10) |
- in the optically thin limit (
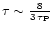 and
and
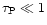 )
)
| |
- |
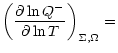 |
|
| |
- |
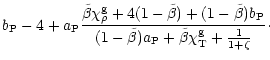 |
(B.11) |


Up: Accretion discs models with
Copyright ESO 2001
![]() ,
and differentiating
Eq. (A.6) while keeping
,
and differentiating
Eq. (A.6) while keeping ![]() constant, we obtain
constant, we obtain
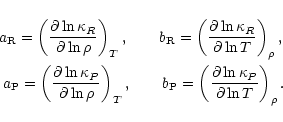
![]() ,
we use the two different
expressions of the total pressure at the midplane. First, by
differentiation of Eq. (A.2), keeping
,
we use the two different
expressions of the total pressure at the midplane. First, by
differentiation of Eq. (A.2), keeping ![]() and
and
![]() constant, we have
constant, we have