The laboratory experiment which is the most pertinent to studies of
hydrodynamical instabilities in differentially rotating flows is the
Couette-Taylor experiment: a fluid is sheared between two cylinders rotating at
different speeds. Only a few experiments have been run in the case
where the angular momentum increases outwards, as in a Keplerian
disc, but from the torque measurements that are available, it
appears that the turbulent viscosity scales as
This prescription was originally proposed by Lynden-Bell & Pringle (1974)
and some aspects of it have been discussed in later papers (De Freitas
Pacheco & Steiner 1976; Thompson et al. 1977; Lin & Papaloizou 1980; Williams 1980; Hubeny 1990). It has been recently revived by Biermann & Duschl (1998; see also Duschl et al. 2000) on the
grounds that the only relevant scales in a Keplerian disc are the angular velocity
and the radius, since they contain all the information about the rotation and
the curvature of the flow. These authors make the sensible choice of
equating the parameter ![]() with the inverse of the critical Reynolds number
with the inverse of the critical Reynolds number ![]() ,
which they assume to be the same as in plane-parallel shear flows (i.e.
,
which they assume to be the same as in plane-parallel shear flows (i.e.
![]() and therefore
and therefore
![]() ).
).
However, in the following we shall use a smaller value for
this ![]() -parameter, which is derived from the Couette-Taylor
experiment. The only experimental data available, in the case where
angular momentum increases outwards, are those
obtained by Wendt (1933) and Taylor (1936),
in which the inner cylinder is at rest; from these one derives
-parameter, which is derived from the Couette-Taylor
experiment. The only experimental data available, in the case where
angular momentum increases outwards, are those
obtained by Wendt (1933) and Taylor (1936),
in which the inner cylinder is at rest; from these one derives
![]() .
This value
is compatible with the critical gradient
Reynolds number which characterizes these experiments
(see Richard & Zahn 1999):
.
This value
is compatible with the critical gradient
Reynolds number which characterizes these experiments
(see Richard & Zahn 1999):
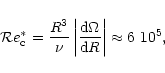 |
(3) |
One important property of this ![]() -viscosity is that it depends
only on the radius in a Keplerian disc, and does not involve local physical
conditions. On the contrary, the standard
-viscosity is that it depends
only on the radius in a Keplerian disc, and does not involve local physical
conditions. On the contrary, the standard
![]() -prescription (Shakura & Sunyaev 1973) depends on the local
values of the pressure scale height H and sound velocity
-prescription (Shakura & Sunyaev 1973) depends on the local
values of the pressure scale height H and sound velocity ![]() (taken in a broad sense -
it is the Alfvén velocity if magnetic pressure dominates):
(taken in a broad sense -
it is the Alfvén velocity if magnetic pressure dominates):
The ![]() -prescription has been designed such that the Mach number is smaller than unity for
-prescription has been designed such that the Mach number is smaller than unity for
![]() .
In contrast, subsonic turbulence
is not guaranteed with the
.
In contrast, subsonic turbulence
is not guaranteed with the ![]() -prescription. This restriction on
subsonic turbulent velocities is dictated by the fact that supersonic
turbulence would be highly dissipative and therefore difficult to
sustain. Moreover, the turbulent viscosity used here has been measured in a
liquid, and its application to compressible fluids can only be justified in the
subsonic range. Therefore one has to check whether the
-prescription. This restriction on
subsonic turbulent velocities is dictated by the fact that supersonic
turbulence would be highly dissipative and therefore difficult to
sustain. Moreover, the turbulent viscosity used here has been measured in a
liquid, and its application to compressible fluids can only be justified in the
subsonic range. Therefore one has to check whether the ![]() -prescription
predicts subsonic turbulence in a given disc.
By making the reasonable assumption that the vorticity
-prescription
predicts subsonic turbulence in a given disc.
By making the reasonable assumption that the vorticity
![]() of the turbulent eddies is of order
of the turbulent eddies is of order ![]() (
(![]() and
and
![]() denoting respectively the typical velocity and length scales of
turbulence), and setting
denoting respectively the typical velocity and length scales of
turbulence), and setting
![]() ,
the
Mach number in a
,
the
Mach number in a ![]() -disc is given by
-disc is given by
Copyright ESO 2001