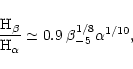Up: Accretion discs models with
Subsections
Let us now examine under which conditions the 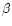 -prescription
allows for subsonic turbulence in geometrically thin
accretion discs in active galactic nuclei (AGN),
evolved binary systems (EBS) and young stellar objects (YSO).
For this first exploration, we will be content with the usual
one-dimensional steady state approach to compute the sound speed and the aspect ratio, the
vertical structure being reduced to vertical averages.
The reader can find the relevant equation set in Appendix A.
-prescription
allows for subsonic turbulence in geometrically thin
accretion discs in active galactic nuclei (AGN),
evolved binary systems (EBS) and young stellar objects (YSO).
For this first exploration, we will be content with the usual
one-dimensional steady state approach to compute the sound speed and the aspect ratio, the
vertical structure being reduced to vertical averages.
The reader can find the relevant equation set in Appendix A.
In a stationary Keplerian disc characterized by a steady accretion rate 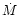 ,
the surface density
,
the surface density 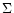 is determined by the conservation of mass
and momentum:
is determined by the conservation of mass
and momentum:
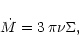 |
(7) |
ignoring a correcting factor which is negligible sufficiently far from
the center (see Frank et al. 1992).
Applying the 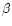 -prescription (2), we find
-prescription (2), we find
where
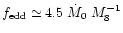 is the Eddington
factor (around 0.1 typically),
M = M8 108
is the Eddington
factor (around 0.1 typically),
M = M8 108
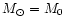
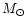 ,
,
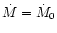
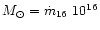 g/s
g/s
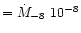
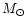 /yr,
/yr,
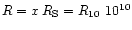 cm
cm
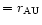 AU (
AU (
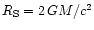 being the Schwarzschild radius of the black hole), and
being the Schwarzschild radius of the black hole), and
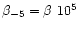 .
These dimensionless variables are well suited to
describe the three families of discs quoted above.
Note that Eq. (8) is quite
general and does not depend on the vertical structure.
.
These dimensionless variables are well suited to
describe the three families of discs quoted above.
Note that Eq. (8) is quite
general and does not depend on the vertical structure.
Thermal equilibrium between radiative cooling and viscous heating
provides another equation. Assuming that the disc is optically thick,
we have (Frank et al. 1992):
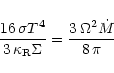 |
(9) |
where 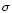 is the Stefan constant and
is the Stefan constant and
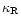 the Rosseland mean
opacity.
the Rosseland mean
opacity.
In gas pressure supported discs, the hydrostatic equation
yields directly the mid-plane temperature T:
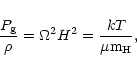 |
(10) |
with the usual notations for the gas pressure 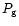 ,
the density
,
the density 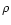 ,
the Boltzmann constant k, the molecular
weight
,
the Boltzmann constant k, the molecular
weight 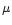 and the mass of the hydrogen atom
and the mass of the hydrogen atom  .
It then follows from
Eqs. (6), (8),
(9) and (10)
that the turbulent Mach number in those
discs is
.
It then follows from
Eqs. (6), (8),
(9) and (10)
that the turbulent Mach number in those
discs is
Note the relatively strong dependence of the Mach
number on the viscosity parameter and
its weak dependence on the opacity and specially the radius.
We conclude that the 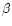 -prescription is
certainly applicable to gas pressure dominated
accretion discs around forming stars, white dwarfs, neutrons
stars and stellar black holes, but not to such discs around
supermassive black holes, where this prescription would imply
supersonic turbulence.
-prescription is
certainly applicable to gas pressure dominated
accretion discs around forming stars, white dwarfs, neutrons
stars and stellar black holes, but not to such discs around
supermassive black holes, where this prescription would imply
supersonic turbulence.
The innermost part of accretion discs may be dominated by
radiation pressure if they reach a sufficiently high temperature;
this occurs for instance in
standard discs surrounding black holes or compact objects. In such a case, the
hydrostatic equation is written
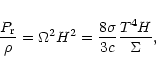 |
(12) |
and therefore, according to (9),
H depends only on the accretion rate, and not on the viscosity
prescription:
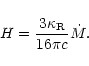 |
(13) |
Thus the Mach number is given by
meaning that turbulence is expected to be subsonic in the
inner part of radiation pressure dominated discs.
![\begin{figure}
\includegraphics[width=8.6cm,clip]{hurerichardzahn.fig1.eps}
\end{figure}](/articles/aa/full/2001/09/aa10256/Timg83.gif) |
Figure 1:
Disc thickness versus radius for a 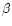 -disc
with -disc
with
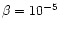 ( solid line) and for a standard disc with
( solid line) and for a standard disc with
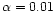 ( dashed line), for =1
( dashed line), for =1 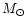 and
and
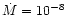
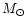 /yr /yr |
In this paper, we restrict ourselves to Keplerian discs, which are
necessarily geometrically thin, i.e. 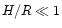 .
Eq. (6) shows that the
turbulent Mach number increases as the aspect ratio decreases; therefore
the disc cannot be thinner than
.
Eq. (6) shows that the
turbulent Mach number increases as the aspect ratio decreases; therefore
the disc cannot be thinner than
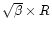 .
One easily finds from
Eq. (11) that
.
One easily finds from
Eq. (11) that
within the gas pressure dominated regions.
It is interesting again to make
the comparison with standard discs. Using power law solutions of
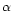 -discs (Huré 1998) and Eq. (15), we obtain
-discs (Huré 1998) and Eq. (15), we obtain
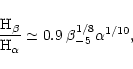 |
(16) |
indicating that 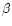 -discs globally should have about the same shape
as standard
-discs globally should have about the same shape
as standard 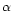 -discs. This is confirmed
in Fig. 1, where we have plotted the disc
thickness computed from vertically averaged equations with realistic
opacities and equations of state, for the two
viscosity laws and for M=1
-discs. This is confirmed
in Fig. 1, where we have plotted the disc
thickness computed from vertically averaged equations with realistic
opacities and equations of state, for the two
viscosity laws and for M=1  and
and
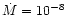
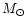 /yr which could represent both a YSO disc and a EBS disc.
In the innermost part of AGN, where the radiation pressure dominates,
the disc thickness is independent of the viscosity prescription, as
we have already pointed out, and therefore
/yr which could represent both a YSO disc and a EBS disc.
In the innermost part of AGN, where the radiation pressure dominates,
the disc thickness is independent of the viscosity prescription, as
we have already pointed out, and therefore
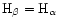 .
We thus conclude that, despite the flaring,
.
We thus conclude that, despite the flaring, 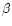 -discs are
expected to be thin and
Keplerian, provided that the accretion rate does not reach too
large values. Note that
-discs are
expected to be thin and
Keplerian, provided that the accretion rate does not reach too
large values. Note that 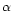 -discs are subject to the same constraint.
-discs are subject to the same constraint.


Up: Accretion discs models with
Copyright ESO 2001
![]() -prescription
allows for subsonic turbulence in geometrically thin
accretion discs in active galactic nuclei (AGN),
evolved binary systems (EBS) and young stellar objects (YSO).
For this first exploration, we will be content with the usual
one-dimensional steady state approach to compute the sound speed and the aspect ratio, the
vertical structure being reduced to vertical averages.
The reader can find the relevant equation set in Appendix A.
-prescription
allows for subsonic turbulence in geometrically thin
accretion discs in active galactic nuclei (AGN),
evolved binary systems (EBS) and young stellar objects (YSO).
For this first exploration, we will be content with the usual
one-dimensional steady state approach to compute the sound speed and the aspect ratio, the
vertical structure being reduced to vertical averages.
The reader can find the relevant equation set in Appendix A.
![]() ,
the surface density
,
the surface density ![]() is determined by the conservation of mass
and momentum:
is determined by the conservation of mass
and momentum:
![]() -prescription is
certainly applicable to gas pressure dominated
accretion discs around forming stars, white dwarfs, neutrons
stars and stellar black holes, but not to such discs around
supermassive black holes, where this prescription would imply
supersonic turbulence.
-prescription is
certainly applicable to gas pressure dominated
accretion discs around forming stars, white dwarfs, neutrons
stars and stellar black holes, but not to such discs around
supermassive black holes, where this prescription would imply
supersonic turbulence.
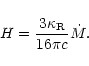
![\begin{figure}
\includegraphics[width=8.6cm,clip]{hurerichardzahn.fig1.eps}
\end{figure}](/articles/aa/full/2001/09/aa10256/Timg83.gif)
![]() .
Eq. (6) shows that the
turbulent Mach number increases as the aspect ratio decreases; therefore
the disc cannot be thinner than
.
Eq. (6) shows that the
turbulent Mach number increases as the aspect ratio decreases; therefore
the disc cannot be thinner than
![]() .
One easily finds from
Eq. (11) that
.
One easily finds from
Eq. (11) that