4 Warm H $_\mathsf{2}$

Table 3 lists the observed fluxes of the lines. The most intense lines are the S(0) ( $J=2 \rightarrow 0$) and S(1) ( $J=3 \rightarrow 1$) lines, with typical fluxes of 0.5-1 10^-19 and 1-2 10^-19 W cm^-2, respectively. Unfortunately, the S(2) line was only observed in the two clouds already discussed in detail by Rodríguez-Fernández et al. (2000). The S(3) line is very weak and it has only been detected in the sources with more intense S(1) emission. Even in some sources which show emission in the S(4) and S(5) lines, the S(3) line has not been detected. This is due to strong dust absorption produced by the solid state band of the silicates at $9.7~\mu$m (Martín-Pintado et al. 1999a).

The pure rotational lines of   arise due to electric quadrupole transitions. The quadrupole transition probabilities are small (Turner et al. 1977) and thus the rotational lines remain optically thin. In this case, the column density of the upper level involved in a transition from level i to level j can be obtained from the line fluxes F_ij of Table 3 using the following expression:

$$N_i=\displaystyle{\frac{\lambda_{ij}}{hc} \frac{4\pi F_{ij} {\rm e}^{\tau_{ij}}}{\Omega_{ij}A_{ij}}}$$

where $\lambda_{ij}$ and A_ij are the wavelength and the quadrupole probability of the transition, and $\tau_{ij}$ and $\Omega_{ij}$ are the dust opacity and the aperture at $\lambda_{ij}$, respectively. Since the column densities are averaged on the ISO apertures, in the case of extended sources (assumed homogeneous), it is not necessary to apply any additional correction to account for the different ISO apertures (see also Rodríguez-Fernández et al. 2000).

4.1 Extinction and ortho-to-para ratio

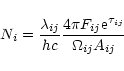
Figure 4 shows the population diagrams for one of the sources for which more than four lines were detected: M -0.32-0.19.

Figure 4: Population diagrams for M -0.32-0.19 without any extinction correction (circles) and corrected for 15 (squares), 30 (triangles), and 45 mag (stars) of visual extinction ( $A_{\rm V}$). We have assumed the relative extinctions derived toward the Galactic center by Lutz (1999). Note that a smooth curve is obtained with $A_{\rm V}\sim 30$ mag

It shows, for each observed line, the logarithm of the upper level population divided by both the rotational and nuclear spin degeneracy, i.e. 3(2J+1) for the ortho levels (odd J) and (2J+1) for the para levels (even J). The filled circles show the populations without any extinction correction. One can see that the population in the J=5 level is lower than expected from the interpolation from the other levels. As discussed in Rodríguez-Fernández et al. (2000), this fact can be used to estimate the total extinction caused by the dust located between the observer and the emitting region. Once an extinction law is assumed, we can correct the line intensities by increasing the visual extinction until the column density in any level (in particular that in the J=5 level) is consistent with the column densities derived for the other levels, i.e. until the population diagrams are smooth curves.

We have used the extinction law derived by Lutz (1999) towards the Galactic center using hydrogen recombination lines. This extinction law differs from that of Draine (1989) for silicate-graphite mixtures of grains in that there is no deep minimum at $\sim \,$$7~\mu$m and there is a slightly higher value for the $A_{9.7\mu{\rm m}}/A_{\rm V}$ ratio, where $A_{\rm V}$ the visual extinction (at 0.55  $\mu{\rm m}$) and $A_{9.7\mu{\rm m}}$ is the extinction at 9.7  $\mu{\rm m}$. For instance, in the case of M -0.32-0.19 one sees that 15 mag of visual extinction (squares in Fig. 4) is a lower limit to the extinction while 45 mag (stars in Fig. 4) is an upper limit. The best result is obtained for a visual extinction of around 30 mag (triangles). Using this method for the other sources with more than four lines detected, we also derive a visual extinction of $\sim \,$30. This value should be considered as a lower limit to the actual extinction for the sources where the S(3) line was not detected. It is not possible to know how much of this extinction is caused by material in the line-of-sight towards the GC (foreground extinction) and how much is intrinsic to the GC clouds. Nevertheless, a visual extinction of $\sim \,$30 mag is in agreement with the average foreground extinction as measured by Catchpole et al. (1990) using stars counts and suggests that the emission can arise from the clouds surfaces (see also Pak et al. 1996). In the other sources where we cannot estimate the extinction from our data we have applied a correction of $A_{\rm V}=30$ mag. For those clouds located farther from the center of the Galaxy and/or the Galactic plane, we have corrected the observed fluxes by 15 mag (see Table 4). This value was derived by Rodríguez-Fernández et al. (2000) by analyzing the far infrared dust emission toward two sources in the "Clump 2" and the $l=1.5^{\circ}$ complexes. In any case, the extinction correction has a minor impact in the main results of this paper (see below). Figure 5 shows the extinction corrected population diagrams for all the sources presented in this paper.

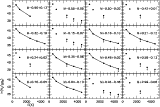Figure 5: Population diagrams for all the sources corrected for the extinctions listed in Table 4. The filled circles are connected when more than three lines are detected. Arrows indicate upper limits. The error-bars are smaller than the circles (even taking into account both calibration and Gaussian fitting errors)

The values of extinction required to give a smooth population diagram would be somewhat smaller if the ortho-to-para (OTP) ratio were lower than the local thermodynamic equilibrium (LTE) ratio. This is obvious since the method to derive the extinction depends mainly on the extinction at the wavelength of an ortho level (J=5). Non-equilibrium OTP ratios measured with the lowest rotational lines has been found in two clouds of our sample (Rodríguez-Fernández et al. 2000). Unfortunately, for the clouds presented in this paper, it is difficult to estimate the OTP ratio since the S(2) line has not been observed and the S(3) line is completely extincted in most of them. Current data do not show any evidence for a non-equilibrium OTP ratio, but we cannot rule it out a priori. For instance, assuming OTP ratios of $\sim \,$2 we still can find a smooth population diagrams, i.e. without the typical zig-zag shape characteristic of non-equilibrium OTP ratios (see e.g. Fuente et al. 1999). In this case, the extinction would be of $\sim \,$20-25 mag instead of 30 mag. On the contrary, assuming OTP ratios of $\sim \,$1 one finds, in general, rather artificial diagrams, which suggests that OTP ratios as low as $\sim \,$1 are not compatible with the data. Although one must bear in mind these considerations, in the following we assume that the OTP ratios are LTE.

4.2 H $_\mathsf{2}$ column densities and excitation temperatures

Table 4 lists the results derived from the lines after applying the extinction corrections.

 

 

Table 4: Total column densities and rotational temperatures between the J=3 and the J=2 levels (T₃₂) and between the J=7 and the J=6 levels (T₇₆) after correcting for extinction. Numbers in parentheses are $1\sigma$ errors of the last significant digits as derived from the fluxes errors in the Gaussian fits of the lines

Source	$A_{\rm V}$	T32	T76	$N_{\ensuremath {\rm H_2} }$(T32)
		K	K	1022 cm-2
M -0.96+0.13	15	157(6)	-	1.10(9)
M -0.55-0.05	30	135(5)	-	2.7(3)
M -0.50-0.03	30	135(4)	-	2.3(2)
M -0.42+0.01	30	167(6)	-	1.03(8)
M -0.32-0.19	30	188(5)	650(90)	1.03(5)
M -0.15-0.07	30	136(6)	-	2.6(4)
M +0.16-0.10	30	157(7)	900(200)	1.17(13)
M +0.21-0.12	30	186(13)	670(110)	0.64(7)
M +0.24+0.02	30	163(2)	-	1.73(6)
M +0.35-0.06	30	195(11)	700(200)	0.66(5)
M +0.48+0.03	30	174(7)	$\leq$600	1.03(9)
M +0.58-0.13	30	149(5)	-	1.3(2)
M +0.76-0.05	30	181(4)	-	1.77(8)
M +0.83-0.10	30	178(5)	550(60)	1.59(6)
M +0.94-0.36	15	146(7)	-	0.95(10)
M +2.99-0.06	15	152(3)	-	1.40(9)

The excitation temperature derived from the J=3 and J=2 levels (T₃₂) is between 130 and 200 K while the excitation temperature derived from the J=7and J=6 levels (T₇₆) is $\sim \,$500-700 K. The temperatures are only 15-20% larger than those one obtains without any extinction correction. For the four clouds in which the S(4) and S(5) lines were undetected, we derive T₃₂ of $\sim \,$135-150 K, clearly lower than the temperature derived for the sources where the S(4) and S(5) lines were detected. There is no clear dependence of T₃₂ on the distance to the Galactic center. However, it is noteworthy that the two clouds with lower T₃₂ are located in the Sgr C complex, one of them in the non-thermal filament.

Obviously, T₃₂ lacks of physical sense if the ortho- and para- abundances are not in equilibrium. As mentioned, we can obtain smooth population diagrams assuming OTP ratios lower than the LTE ratio. The temperature T₃₂ derived in this case ( $T_{32}^{\rm corr}$) is higher than the one derived directly from the observations (T₃₂). For instance, assuming OTP ratios $\sim \,$2 one obtains a $T_{32}^{\rm corr}$ which is $\sim \,$10% larger than T₃₂.

It is possible to estimate the total warm column densities ( $N_{\ensuremath {\rm H_2} }$) by extrapolating the populations in the J=2 level to the J=1 and J=0 levels at the temperature T₃₂. The derived warm $N_{\ensuremath {\rm H_2} }$ are listed in Table 4 and should be considered lower limits to the actual amount of warm molecular gas since the lowest levels can be populated with colder, although still warm, gas. The total column density of warm varies from source to source but it is typically of 1-2 10²² cm^-2. These column densities are only a factor of 1.2 higher than those one would obtain without any extinction correction. Thus, in regard to the derived gas temperatures and total column densities, the extinction correction is not critical. On the other hand, extrapolating the column densities in the J=6 and J=7 to lower levels at the temperature T₇₆, one finds that the amount of gas at $\sim \,$600 K is less than 1% of the column densities measured at $\sim \,$150 K. The total column densities at temperatures $T_{32}^{\rm corr}$assuming an OTP ratio of $\sim \,$2 are lower than those of Table 4 by a factor of 1.8. Note, that in this case the total column density should be derived extrapolating the observed population in the J=3 to the J=1 level and the population in the J=2 to the J=0 levels, as two different species at temperature $T_{32}^{\rm corr}$. Of course, these column densities are still lower limits to the actual warm column densities.

These results are the first direct estimation of the column densities and the structure of the warm gas in the GC clouds. They show the presence of large column densities of warm molecular gas with large temperature gradients (150-700 K), extending the results derived by Hüttemeister et al. (1993) from their NH₃ data.