5 Discussion

5.1 Warm H $_\mathsf{2}$ to CO and NH₃ ratios

As mentioned in Sect. 2.2, we cannot identify which velocity components seen in CO are associated to the warm . Furthermore, the bulk of the CO seen in the $J=1\rightarrow 0$ and $J=2 \rightarrow 1$ lines do not show the characteristics of warm CO associated to the warm (see Sect. 3). In the following, we will estimate the ratio of the warm column densities observed with ISO to the column densities derived from the CO using LVG calculations. We have added the column densities of each velocity component in every source. These total column densities are listed in Table 5.

 

 

Table 5: Total column densities of derived from . Fraction of warm $N_{\ensuremath {\rm H_2} }$ as measured with ISO to the total $N_{\ensuremath {\rm H_2} }$ derived from . Abundances of NH₃ in the warm and cold components (see text)

Source	$N_{\ensuremath {\rm H_2} }$$^{\rm CO}$	$N_{\ensuremath {\rm H_2} }$ $^{\rm warm}$/ $N_{\ensuremath {\rm H_2} }$$^{\rm CO}$	X(NH3) $_{\rm warm}$	X(NH3) $_{\rm cold}$
	1022 cm-2
M -0.96+0.13	0.6-1.1	1	3.7 10-7	4.9 10-6
M -0.55-0.05	4.3-6.0	0.45
M -0.50-0.03	2.4-3.0	0.77	2.6 10-8	1.6 10-7
M -0.42+0.01	2.1-3.4	0.29	8.3 10-8	2.9 10-8
M -0.32-0.19	1.1-2.2	0.45	1.8 10-8	3.1 10-7
M -0.15-0.07	6.6-8.4	0.31	2.4 10-7	2.7 10-7
M +0.16-0.10	3.7-4.9	0.24
M +0.21-0.12	0.8-1.5	0.41
M +0.24+0.02	4.8-7.1	0.24	1.3 10-7	8.9 10-7
M +0.35-0.06	1.7-2.7	0.25
M +0.48+0.03	3.2-3.6	0.28
M +0.58-0.13	3.1-3.9	0.33
M +0.76-0.05	6.6-8.6	0.21
M +0.83-0.10	4.8-6.5	0.25		3.4 10-8
M +0.94-0.36	1.3-2.9	0.33		6.7 10-7
M +2.99-0.06	1.0-2.1	0.65		9.0 10-7

One can compare the maximum column densities derived from CO to the column densities listed in Table 4 to derive a lower limit to the fraction of warm molecular gas with respect to the gas emitting in CO. These ratios are given in Table 5 for all the molecular clouds. We find that the warm is about $\sim \,$30% of the column densities measured from CO. For a few clouds the fraction of warm gas is as high as 77% (M -0.50-0.03) or even $\sim \,$100% for M -0.96+0.13. This implies that, for two clouds all the CO emission should arise from warm gas.

Table 5 also lists the NH₃ abundances in the warm (X(NH₃) $_{\rm warm}$) and cold components (X(NH₃) $_{\rm cold}$). The X(NH₃) $_{\rm warm}$has been derived from the column densities of warm ammonia (Hüttemeister et al. 1993) and our warm column densities. We find that, X(NH₃) $_{\rm warm}$ is within a range of 3 10^-8 to 4 10^-7. On the other hand, X(NH₃) $_{\rm cold}$ has been derived from the cold ammonia column densities of Hüttemeister et al. and the column densities derived from the data. In this case, we have taken into account only the velocity components with NH₃ emission and we have assumed that, in average, $\sim \,$70% of the gas traced by CO is cold gas. With these assumptions, X(NH₃) $_{\rm cold}$ varies between 4 10^-8 and 6 10^-6, being the average value $\sim \,$5 10^-7. This is similar to the abundance in the warm component, and approximately 10 times higher than the "typical" interstellar ammonia abundance (Irvine et al. 1987). The high NH₃ abundances in the cold gas point to the existence of a cold post-shocked gas component as suggested by Hüttemeister et al. (1998) to explain the SiO emission in the GC clouds.

5.2 Heating mechanism

What is the heating mechanism that produces such a large amount of warm molecular gas in the GC? Shocks have been invoked to explain the widespread distribution and the large abundances of refractory molecules like SiO (Martín-Pintado et al. 1997; Hüttemeister et al. 1998), the high temperatures observed in NH₃ (Wilson et al. 1982; Güsten et al. 1985) and the non-equilibrium ortho-to-para ratio of two sources in our sample (Rodríguez-Fernández et al. 2000). The high NH₃ abundance derived in the previous section points to a mechanical heating mechanism since the ammonia molecule is easily photo-dissociated by ultraviolet radiation. The small column densities of warm dust in these clouds also points to a mechanical heating mechanism (Martín-Pintado et al. 1999a).

On the other hand, in some of the clouds we have detected line emission from ionized species like Neii, Neiii or Oiii, that should arise in an Hii region ionized by ultraviolet (UV) photons (Martín-Pintado et al. 1999a, 2000). This implies that, at least in those clouds, there must be a PDR in the interface between the Hii region and the molecular material. Large scale emission of the v=1-0 S(1) line has also been interpreted as arising from PDRs of density $n \sim10^4$ cm^-3 and incident far-UV flux of $G_0 \sim10^3$ (in units of 1.6 10^-3 ergscm^-2s^-1) in the clouds surfaces (Pak et al. 1996). The total visual extinction of $\sim \,$30 mag derived for the clouds of our sample matches the expected foreground extinction and suggest that the pure-rotational emission could also arise in the surfaces of the clouds as the ro-vibrational lines.

We have compared the population diagrams obtained for the GC clouds with the same type of diagrams predicted by models of C-shocks, J-Shocks and PDRs. Figure 6a shows the comparison between the predictions of a C-Shock from Draine et al. (1983), a J-Shock from Hollenbach & McKee (1989), and the data for M -0.32-0.19.

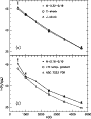Figure 6: a) Population diagram for M -0.32-0.19 (open squares) corrected for 30 mag of visual extinction. The errorbars represent upper limits to the flux calibration uncertainties (see text). For comparison, it also displays the population diagrams derived from the model of Draine et al. (1983) of a shock with velocity $\sim \,$12 kms-1 and preshock density 106 cm-3 (circles and dashed lines). Triangles and long-dashed lines are used to plot the population diagram derived from the J-shock model of Hollenbach & McKee (1989) for a velocity of 50 kms-1 and a preshock density of 106 cm-3. b) Comparison of the population diagram derived for M +0.16-0.10 (open squares) with the results of Fuente et al. (1999) for the NGC 7023 PDR (triangles and dashed line) and the population diagram one obtains integrating the H2 emission along the temperature and H2 abundance gradient derived by Burton et al. (1990) for a PDR with density of 106 cm-3 and G0=104 (open circles)

The S(1) to S(5) lines (squares) can be explained with both a C-Shock with velocity of $\sim \,$12 kms^-1 acting on gas with preshock density of 10⁶ cm^-3 (circles) or a J-Shock of 50 kms^-1 and preshock density of 10⁶ cm^-3 (triangles). However, the observed emission in the S(0) line is $\sim \,$3 times larger than the predicted by both models.

Figure 6b shows the population diagram for M +0.16-0.10 (squares) versus the prototypical reflection nebula NGC 7023 (triangles). As discussed by Fuente et al. (1999), the emission from this source is well fitted by the PDR model of Burton et al. (1990, 1992) with G₀=10⁴ and n=10⁶ cm^-3 although with an OTP ratio of 1.5-2. Comparing the NGC 7023 population diagram with M +0.16-0.10, one finds that the agreement is excellent for the S(4) and S(5) lines but it is not so good for the lowest lines, even taking into account the non-equilibrium OTP ratio found in NGC 7023. In particular, the GC clouds exhibit more emission in the lowest lines than expected from the PDR model for G₀=10⁴ and n=10⁶ cm^-3. In contrast, the v=1-0 S(1) intensity predicted by this PDR model is a factor of $\sim \,$10 larger than observed by Pak et al. (1996). This fact would imply that the vibrational line emission is more diluted in a 3' beam than the pure-rotational lines in the SWS beam or that the PDR models do not apply.

In any case, the observed curvature of the population diagrams seems to be in good agreement with the predicted temperature gradient in a PDR. In Fig. 6b, we also show the population diagram one obtains integrating the emission in LTE with the temperature and abundance profiles along the G₀=10⁴ and n=10⁶ cm^-3 PDR model of Burton et al. (1990). The result differs from that of Burton et al. in that we do not take into account any radiative pumping, which affects mainly to higher levels than those involved in the S(0) and S(1) lines. Although the GC emission is $\sim \,$3 times larger, it is evident that the shape of the population diagram is very similar to that observed.

With regard to those sources where the S(4) and S(5) were not detected, the upper limits imply that if they are PDR-excited the density must be somewhat lower than n=10⁶ cm^-3, or if shock-excited, the shock velocity should be slightly lower than those of the models ploted in Fig. 6.

Both shock and PDR models suggest densities as high as 10⁶ cm^-3 and fail to explain the observed intensity of the S(0) emission and to less extend the S(1) line. The densities implied by the models seem somewhat large, but it looks like the   traces two components: a hot ($\sim \,$500 K) and dense ( $\stackrel{<}{\scriptstyle \sim}$10⁶ cm^-3) component necessary to explain the observed S(4) and S(5) lines, and a warm component ($\sim \,$150 K) traced by the S(0) and S(1) lines. To match the measured $J=2 \rightarrow 1$/ $J=1\rightarrow 0$ and   ratios the warm   component should have densities of $\sim \,$10³ cm^-3  (see Sect. 3). The hot and dense gas would have $J=2 \rightarrow 1$/ $J=1\rightarrow 0$ ratios of $\sim \,$4-5 but it would emit mainly in the high-J CO lines. In any case, the column density of hot and dense gas is very small to make it detectable in the low-J CO lines when mixed with the colder and less dense gas that dominates the emission of these lines.

To explain the derived $T_{32}\sim150$ K is necessary to invoke PDRs with $G_0 \sim10^3$ and $n \sim10^3$ cm^-3, but to obtain the observed intensities $\sim \,$20 of such PDRs are needed. J-shock models do not predict temperatures as low as 150 K. Moreover, the high velocities required to explain our data are difficult to reconcile with the observations. C-shocks could explain the observed S(0) and S(1) emission with, at least, 10 shocks with velocities as low as $\sim \,$7 kms^-1 and n=10⁶ cm^-3 (even more shock fronts are needed for lower gas densities). In addition, dissipation of supersonic turbulence could heat the gas to temperatures of $\sim \,$150 K (Wilson et al. 1982; Güsten et al. 1985) and thus, could contribute to the emission in the two lowest lines. The origin of the turbulence would be the movement of dense clumps in a less dense interclump medium due to the differential Galactic rotation and the tidal disruption of the clumps.

The heating rate by dissipation of supersonic turbulence can be estimated as

$${\Gamma \sim3.5~10^{28}\,v_{\rm t}^3 \,n_{\ensuremath{\rm H_2} } (1 {\rm pc}/ l)~{\rm erg}\,{\rm s}^{-1}\,{\rm cm}^{-3}}$$

(Black 1987), where l and $v_{\rm t}$ are the spatial scale and the velocity of the turbulence, respectively. Taking $v_{\rm t}\sim15$ kms^-1 (the typical linewidths of GC clouds), l=5 pc, and $n_{\ensuremath{\rm H_2} }=10^3$ cm^-3, one obtains $\Gamma \sim5\,10^{-22}$ ergs^-1cm^-3. For the conditions of the warm gas, $T\sim150$ K and $n_{\ensuremath{\rm H_2} }\sim10^3$ cm^-3, the cooling is expected to be dominated by   and CO. Le Bourlot et al. (1999) has recently estimated the cooling rate by   ( $\Lambda_{\ensuremath{\rm H_2} }$) for a wide range of parameters. For the warm gas component of the GC clouds we obtain $\Lambda_{\ensuremath{\rm H_2} } \sim3~10^{-22}$ ergs^-1cm^-3, which is comparable to the CO cooling rate (see e.g. Goldsmith & Langer 1978) Thus, comparing heating and cooling rates, one finds that the dissipation of supersonic turbulence could account for the heating of the warm component.

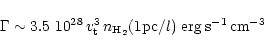
In summary, several agents could heat the warm component, while the hot component should trace the densest gas in the GC clouds heated by a PDR or a shock. For instance, if the inhomogeneous structure revealed in the Sgr B2 envelope by interferometric NH₃ observations (Martín-Pintado et al. 1999b) is common in the GC, and due to evolved massive stars as they propose, both C-shocks of $\sim \,$10 kms^-1 (shell expansion) and PDRs (stellar radiation) would be present. However, it is not possible to rule out mechanical heating by large scale shocks. In fact, the high fraction of warm derived for M -0.96+0.13 and the fact that the CO component with positive velocities apparently does not contribute to the emission suggests this kind of heating since, at this galactic longitude, shocks are expected at negative velocities due to the intersection of x₁ and x₂ orbits in the context of a barred potential (Binney et al. 1991).