Unstable interaction of gravity-inertial waves with Rossby waves with application to solar system atmospheres

J. F. McKenzie; T. B. Doyle

doi:10.1051/0004-6361/200913453

Home

All issues

Volume 509 (January 2010)

A&A, 509 (2010) L11

Full HTML

Free Access

Issue		A&A Volume 509, January 2010


Article Number		L11
Number of page(s)		3
Section		Letters
DOI		https://doi.org/10.1051/0004-6361/200913453
Published online		28 January 2010

A&A 509, L11 (2010)

LETTER TO THE EDITOR

Unstable interaction of gravity-inertial waves with Rossby waves with application to solar system atmospheres

J. F. McKenzie^1,2 - T. B. Doyle³

1 - King's College, University of Cambridge, UK
2 - School of Mathematical Sciences, University of KwaZulu-Natal, South Africa
3 - Materials Research Division, iThemba LABS, Somerset West, South Africa

Received 12 October 2009 / Accepted 12 January 2010

Abstract
This letter reports on the important features of an analysis of the combined theory of gravity - inertial - Rossby waves on a $\beta$ -plane in the Boussinesq approximation. In particular, it is shown that the coupling between higher frequency gravity - inertial waves and lower frequency Rossby waves, arising from the accumulated influences of the $\beta$ effect, stratification characterized by the Väisäla - Brunt frequency N, the Coriolis frequency f, and the component of vertical propagation wave number k_z, may lead to an unstable coupling between buoyancy - inertial modes with westward propagating Rossby waves. ``Supersonic'' fast rotators (such as Jupiter) are predicted to be unstable in a fairly narrow band of latitudes around their equators. The Earth is moderately supersonic and exhibits instability within about $34^\circ$ of its equator. Slow ``subsonic'' rotators (e.g. Mercury, Venus, and the Sun's corona) are unstable at all latitudes except those very close to the poles where the $\beta$ effect vanishes.

Key words: hydrodynamics - instabilities - planets and satellites: atmospheres - waves

1 Introduction

A brief report is presented on an instability which may have important consequences in the dynamics of rotating planetary atmospheres. The structure of each planetary atmosphere is unique, with properties determined by momentum balance and heating and cooling processes in the presence of heat conduction/transport and viscous stresses. The complex basic state of each planetary atmosphere (exosphere) is beyond the scope of this letter. Instead we assume a highly idealized situation in which the atmosphere is characterized by a density scale height H (determined by g and the temperature T) rotating with a frequency $\Omega$ which, together with the planetary radius R, define a dimensionless (rotational Mach or Froude) number $M_{\rm eq}=\Omega R/\sqrt{g H}$ , which plays a critical role in the stability problem. The present analysis is governed by the dispersion equation for coupled inertial-gravity-Rossby waves on a $\beta$ -plane in the Boussinesq approximation. Under certain circumstances the coupling between westward propagating ``higher'' frequency inertial-gravity waves and ``lower'' frequency Rossby waves drives the system unstable, with growth rates of order days. The stability analysis indicates that rapidly rotating planets (e.g. Jupiter) are unstable within a fairly narrow belt of latitudes around their equators, whereas slowly rotating atmospheres (e.g. Venus and Mercury) are unstable at all latitudes except near the poles. Earth and Mars are ``transonic'' and are unstable within latitudes of about $34^\circ$ and $39^\circ$ , respectively.

2 Dispersion equation and stability analysis

The instability condition and the growth rate, arising from the unstable coupling between buoyancy-inertial modes and Rossby waves, follow from the existence of complex roots for $\omega$ in the ``mid-latitude'' dispersion equation (Longuet-Higgins 1968; Pedlosky 1987; Gill 1982; and more recently McKenzie 2009) given by

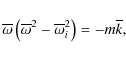
$\begin{displaymath}\overline{\omega}\left(\overline{\omega}^2-\overline{\omega}_i^2\right)=-m\overline{k}, \end{displaymath}$

(1)

where

$\begin{displaymath}\overline{\omega}_i^2\equiv1+\overline{k}^2, \end{displaymath}$

(2)

and

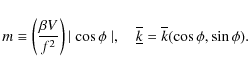
$\begin{displaymath}m\equiv\left(\frac{\beta V}{f^2}\right){\mid\cos \phi \mid, \... ...\overline{\underline{k}}}=\overline{k}(\cos \phi, \sin \phi). \end{displaymath}$

(3)

Here $f=2\Omega \sin \theta_{\rm o}$ is the Coriolis frequency (with $\theta_{\rm o}$ the latitude of the $\beta$ -plane), $\overline{\omega}=\omega/f$ is the normalized wave frequency, and $\overline{k}=k/(f/V)$ is the normalized horizontal wave number, where $k =\sqrt{k_x^2+k_y^2}$ ), and V is a characteristic gravity - inertial speed given by

V=N/k_z.

(4)

Here k_z is the vertical component of the wave number vector $\underline{k}$ and N is the Väisäla - Brunt frequency, defined (Lighthill 1980) by

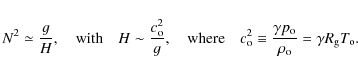
$\begin{displaymath}N^2\simeq\frac{g}{H},\quad \textrm{with} \quad H\sim \frac{c_... ...ac{\gamma p_{\rm o}}{\rho_{\rm o}}=\gamma R_{\rm g} T_{\rm o}. \end{displaymath}$

(5)

in which H is the density scale height, $p_{\rm o}$ is the pressure, $\rho_{\rm o}$ the density, $c_{\rm o}$ the velocity of sound, $\gamma$ the adiabatic constant, $R_{\rm g}$ the gas constant and $T_{\rm o}$ the temperature.

We emphasize that although the assumed basic state is highly idealized, the instability analysis may, nevertheless, capture conditions on spherical shells in which N and $T_{\rm o}$ may be regarded as constants, and for horizontal length scales consistent with the $\beta$ -plane approximation. The analysis may, moreover, also apply to latitudinally sheared zonal flows (as is evident in the banded structure of Jupiter) in which the wave frequency $\omega$ is replaced by its Doppler shifted counterpart (see e.g. Mekki and McKenzie 1977).

In defining the coupling parameter m in Eqs. (1) and (3) we have taken the modulus of $\cos \phi$ and assigned a minus sign in the right hand side of the dispersion equation (Eq. (1)) to make it applicable to waves propagating in the second or third quadrants, corresponding to a westward component of propagation (since plane waves are proportional to $\exp i(\omega t-\underline{k}.\underline{x}))$ and with $\omega >0$ ). The coupling parameter m is, in fact, the quantity $\epsilon$ , as defined by Gill (1982). This parameter is normally regarded as small because the Rossby wave frequency is generally very much smaller than the gravity-inertial wave frequency. In the present work this approximation is not used and situations where the wave frequencies of these modes may overlap in certain bands of wave number are included. It will be noted that in the absence of the $\beta$ -effect ( $\beta=2\Omega \cos \theta_{\rm o}/R$ , where R is the radius of the body) Eq. (1) reduces to the inertial - gravity mode dispersion relation, namely,

$\begin{displaymath}\overline{\omega}=\pm \overline{\omega}_i, \end{displaymath}$

(6)

for wave frequencies $\omega\ll N$ , but for $\omega>f$ . Whereas for very low frequencies, $\omega\ll f$ the dispersion equation goes over to that of the Rossby wave, namely,

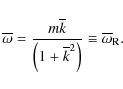
$\begin{displaymath}\overline{\omega}=\frac{m\overline{k}}{\left(1+\overline{k}^2\right)}\equiv\overline{\omega}_{\rm R}. \end{displaymath}$

(7)

The coupled dispersion equation (Eq. (1)) gives two positive roots for $\overline {\omega }$ ; one of which represents a Rossby wave, whose frequency is increased above its uncoupled value $\overline{\omega}_{\rm R}$ , and the other is an inertial - gravity wave, whose frequency is decreased below its uncoupled value $\overline{\omega}_i$ . The third root yields a negative value for $\overline {\omega }$ (with $\overline{\omega} < -\overline{\omega}_i$ ) corresponding to an eastward propagating gravity-inertial wave. As the coupling ( $m\overline{k}$ ) increases the two positive roots move towards each other and coalesce where the right hand side of Eq. (1) is equal to the minimum value of the left hand side, namely, $-2\overline{\omega}_i^3/3\sqrt{3}$ , which occurs at $\overline{\omega}=\overline{\omega}_i/\sqrt{3}\equiv\overline{\omega}_m$ . A further increase in $m\overline{k}$ leads to complex conjugate roots (corresponding to instability) given approximately by

$\begin{displaymath}\overline{\omega}-\overline{\omega}_m=\pm\frac{i\overline{k}^... ...t[m-F(\overline{k})\right]^{1/2}\equiv \pm i\overline{\gamma}, \end{displaymath}$

(8)

where

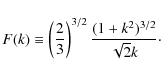
$\begin{displaymath}F(k)\equiv\left(\frac{2}{3}\right)^{3/2}\frac{(1+k^2)^{3/2}}{\sqrt{2} k}\cdot \end{displaymath}$

(9)

This approximation to the complex conjugate roots follows directly from the Taylor expansion of the LHS of Eq. (1) in the neighbourhood of the double root, at $\bar{\omega}-\bar{\omega}_m$ [neglecting terms of O $(\bar{\omega} = \bar{\omega}_m)^3$ ]. Since $F(\overline{k})$ has a minimum value of 1 at $\overline{k}^2=1/2$ the condition for instability is simply

m>1.

(10)

When this is satisfied there is a band of unstable wave numbers lying between the two roots of

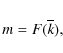
$\begin{displaymath}m=F(\overline{k}), \end{displaymath}$

(11)

given approximately by

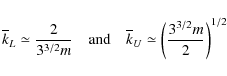
$\begin{displaymath}\overline{k}_L\simeq \frac{2}{3^{3/2} m} \quad \textrm{and} \quad \overline{k}_U\simeq \left(\frac{3^{3/2} m}{2}\right)^{1/2} \end{displaymath}$

(12)

for m just moderately greater than unity. The central frequency of the instability (occurring at $\overline{k}^2=1/2$ ) is the local Coriolis frequency divided by $\sqrt{2}$ , i.e. $f/\sqrt{2}$ , and the corresponding growth rate is $(m-1)^{1/2}/\sqrt{3}= \overline{\gamma}$ . The solutions (real roots) of Eq. (1) for westward propagation are shown in Fig. 1, for the stable regime (m<1), the unstable regime (m>1) cases, and for the critical case m=1. The dashed line in the figure is the locus of $\overline {\omega }=\overline {\omega }_i/\sqrt {3}$ . The instability growth rate $\overline {\gamma }$ , as a function of $\overline {k}$ , for different values of the coupling parameter m>1 is shown in Fig. 2, in which the solid curves (exact solutions)may be compared with the dashed curves (approximate solutions), showing that the latter is accurate only near marginal stability ( $\overline{\gamma}=0$ ).

$\begin{figure} \par\includegraphics[width=7.2cm,clip]{13453fg1.eps}\vspace*{-1.5mm} \vspace{-1mm} \end{figure}$

Figure 1:

The diagnostic diagram, ( $\overline {\omega }$ , $\overline {k}$ ) plot, for the coupled modes, including a stable case (m=1/2), an unstable case (m=2), and the critical case (m=1). The higher frequency curve segments (above the locus $\overline {\omega }=\overline {\omega }_i/\sqrt {3}$ ) describe the gravity - inertial mode, and the lower frequency segments the Rossby mode. The coupling of these modes leads to a convective instability for m> 1.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=7.2cm,clip]{13453fg2.eps} \end{figure}$	Figure 2: The normalized growth rate $\overline {\gamma }$ as a function of $\overline {k}$ for m = 1.2, 2 and 3. The solid and dashed curves are derived, respectively, from the exact complex conjugate roots of Eq. (1)) and from the approximate form given by Eq. (8).
Open with DEXTER

The instability condition m>1 may be written as

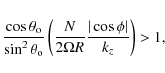
$\begin{displaymath}\frac{\cos \theta_{\rm o}}{\sin^2 \theta_{\rm o}}\left(\frac{N}{2\Omega R}\frac{\vert\cos \phi \vert}{k_z}\right)>1, \end{displaymath}$

(13)

which, on squaring, translates into a bi-quadratic for $\sin^2 \theta_{\rm o}$ . This may be cast in the interesting form:

$\begin{displaymath}\theta_{\rm o}\leq\theta_{\rm c}, \end{displaymath}$

(14)

$\begin{displaymath}\sin\theta_{\rm c}=\frac{1}{2\sqrt{2}M}\left[\sqrt{1+16M^2}-1\right]^{1/2}, \end{displaymath}$

(15)

and

$\begin{displaymath}M_{\rm eq}\equiv\frac{\Omega R}{NH}=\frac{\Omega R}{\sqrt{gH}... ...uiv M_{\rm eq}\left(\frac{k_z H}{\vert\cos \phi\vert}\right), \end{displaymath}$

(16)

where again H is the density scale height. The expressions for $M_{\rm eq}$ follow from the definitions of Eq. (5) for N, H and $c_{\rm o}$ . Note that the Lamb parameter $\epsilon = 2(\Omega R)^2/gH$ introduced by Longuet-Higgins (1968) is related to the rotational Mach number by $\epsilon=4M_{\rm eq}^2$ . The Mach number $M_{\rm eq}$ plays a critical role in the instability condition. This is shown in Fig. 3 as the region below the curve of the critical latitudes $\theta _{\rm c}$ as a function of an equivalent Mach number M, defined by relations (14)-(16), in terms of $M_{\rm eq}$ and the configuration of the wave, through the parameter $k_zH/\vert\cos \phi\vert$ .

$\begin{figure} \par\includegraphics[width=7.2cm,clip]{13453fg3.eps} \end{figure}$	Figure 3: The instability condition, relations [13-16], with the critical latitude $\theta _{\rm c}$ as a function of the effective rotational Mach number, M, separating the parameter space into stable and unstable regions.
Open with DEXTER

3 Application to planetary atmospheres

The results of the present analysis, as shown in Fig. 3, predict that for supersonically rotating planets ( $M_{\rm eq}>1$ ), such as the outer giants (e.g. Jupiter), instability is confined to a fairly narrow belt of latitudes around their equators. For subsonically rotating bodies (e.g. the Sun, Mercury and Venus), for which $M_{\rm eq}\ll 1$ , instability occurs at almost all latitudes, with the fastest growing mode near their equators. The Earth and Mars are ``transonic'' planets for which $\theta_\textrm{c}$ is around $34^\circ$ and $39^\circ$ , respectively. Note that in the ``hypersonic'' Jupiter instability is confined to approximately $12^{\rm o}$ about its equator. The present analysis breaks down near the equator where the Coriolis frequency goes to zero. In this region a special treatment is required as a consequence of the development of a waveguide system (Moore & Philander 1977; Cane & Sarachik 1976; and Maas & Harlander 2007). These analyses indicate that ``globally'' the instability disappears, while ``locally'' it may still exist within a JWKB approximation. This point requires further study and clarification.

Finally we note that a similar analysis pertains to oceans except that the effective Mach number M in the instability condition (Eq. (14)) is now given by

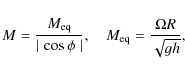
$\begin{displaymath}M=\frac{M_{\rm eq}}{\mid\cos \phi\mid}, \quad M_{\rm eq}=\frac{\Omega R}{\sqrt{gh}}, \end{displaymath}$

(17)

where h is the ocean depth and $\sqrt{gh}$ is the shallow water speed. In an Earth's ocean of depth h=6 km this speed is roughly 250 m/s, yielding $M_{\rm eq}\simeq 1.9$ . Purely westward propagating waves ( ${\mid}\cos \phi{\mid}=1$ ) are, therefore, unstable in a band of latitudes of about $25^\circ$ of the equator.

Since this instability feeds off rotational kinetic energy and gravitational buoyancy its nonlinear evolution may play an important role in atmospheric and ocean dynamics over time scales of, or less than, a few planetary days.

Acknowledgements

J.F. McK. wishes to thank the Pei-Ling Chan Chair, Department of Physics, University of Alabama, for support, and J.F. McK. and T.B.D. thank the Foundation for Research and Development of South Africa (under Grant number 2053776) for support.

References

Cane, M. A., & Sarachik, E. S. 1976, J. Mar. Res., 35, 395 [Google Scholar]
Gill, A. E. 1982, Atmosphere-Ocean Dynamics, International Geophys. Ser. 30 [Google Scholar]
Lighthill, J. 1980, Waves in Fluids (Cambridge University Press) [Google Scholar]
Longuet-Higgins, M. S. 1968, Phil. Trans. Roy. Soc., 262, 511 [Google Scholar]
Maas, L. R. M., & Harlander, U. 2007, J. Fluid Mech., 570, 47 [NASA ADS] [CrossRef] [Google Scholar]
McKenzie, J. F. 2009, Ann. Geophys., 27, 4221 [NASA ADS] [CrossRef] [Google Scholar]
Mekki, O. M., & McKenzie, J. F. 1977, Phil. Trans. R. Soc. London Ser. A, 287, 115 [NASA ADS] [CrossRef] [Google Scholar]
Moore, D. W., & Philander, S. G. H. 1977, Modelling of the tropic ocean circulation. In The Sea (Chap. 8), ed. Goldberg et al. (New York: Inter- science) [Google Scholar]
Pedlosky, J. 1987, Geophys. Fluid Dynamics (Springer Verlag) [Google Scholar]

All Figures

$\begin{figure} \par\includegraphics[width=7.2cm,clip]{13453fg1.eps}\vspace*{-1.5mm} \vspace{-1mm} \end{figure}$	Figure 1: The diagnostic diagram, ( $\overline {\omega }$ , $\overline {k}$ ) plot, for the coupled modes, including a stable case (m=1/2), an unstable case (m=2), and the critical case (m=1). The higher frequency curve segments (above the locus $\overline {\omega }=\overline {\omega }_i/\sqrt {3}$ ) describe the gravity - inertial mode, and the lower frequency segments the Rossby mode. The coupling of these modes leads to a convective instability for m> 1.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.2cm,clip]{13453fg2.eps} \end{figure}$	Figure 2: The normalized growth rate $\overline {\gamma }$ as a function of $\overline {k}$ for m = 1.2, 2 and 3. The solid and dashed curves are derived, respectively, from the exact complex conjugate roots of Eq. (1)) and from the approximate form given by Eq. (8).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.2cm,clip]{13453fg3.eps} \end{figure}$	Figure 3: The instability condition, relations [13-16], with the critical latitude $\theta _{\rm c}$ as a function of the effective rotational Mach number, M, separating the parameter space into stable and unstable regions.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Cane, M. A., & Sarachik, E. S. 1976, J. Mar. Res., 35, 395 [Google Scholar]

[2] Gill, A. E. 1982, Atmosphere-Ocean Dynamics, International Geophys. Ser. 30 [Google Scholar]

[3] Lighthill, J. 1980, Waves in Fluids (Cambridge University Press) [Google Scholar]

[4] Longuet-Higgins, M. S. 1968, Phil. Trans. Roy. Soc., 262, 511 [Google Scholar]

[5] Maas, L. R. M., & Harlander, U. 2007, J. Fluid Mech., 570, 47 [NASA ADS] [CrossRef] [Google Scholar]

[6] McKenzie, J. F. 2009, Ann. Geophys., 27, 4221 [NASA ADS] [CrossRef] [Google Scholar]

[7] Mekki, O. M., & McKenzie, J. F. 1977, Phil. Trans. R. Soc. London Ser. A, 287, 115 [NASA ADS] [CrossRef] [Google Scholar]

[8] Moore, D. W., & Philander, S. G. H. 1977, Modelling of the tropic ocean circulation. In The Sea (Chap. 8), ed. Goldberg et al. (New York: Inter- science) [Google Scholar]

[9] Pedlosky, J. 1987, Geophys. Fluid Dynamics (Springer Verlag) [Google Scholar]