A&A 493, 727-734 (2009)
DOI: 10.1051/0004-6361:200810472
Deconvolution with shapelets
P. Melchior - R. Andrae - M. Maturi - M. Bartelmann
Zentrum für Astronomie, ITA, Universität Heidelberg,
Albert-Ueberle-Str. 2, 69120 Heidelberg, Germany
Received 27 June 2008 / Accepted 12 September 2008
Abstract
Aims. We seek a shapelet-based scheme for deconvolving galaxy images from the PSF that leads to unbiased shear measurements.
Methods. Based on the analytic formulation of convolution in shapelet space, we constructed a procedure to recover the unconvolved shapelet coefficients under the assumption that the PSF is perfectly known. Using specific simulations, we test this approach and compare it to other published approaches.
Results. We show that convolution in shapelet space leads to a shapelet model of order
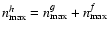 ,
with
,
with
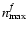 and
and
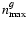 being the maximum orders of the intrinsic galaxy and the PSF models, respectively. Deconvolution is hence a transformation that maps a certain number of convolved coefficients onto a generally smaller number of deconvolved coefficients. By inferring the latter number from data, we construct the maximum-likelihood solution for this transformation and obtain unbiased shear estimates with a remarkable amount of noise reduction compared to established approaches. This finding is particularly valid for complicated PSF models and low S/N images, which renders our approach suitable for typical weak-lensing conditions.
being the maximum orders of the intrinsic galaxy and the PSF models, respectively. Deconvolution is hence a transformation that maps a certain number of convolved coefficients onto a generally smaller number of deconvolved coefficients. By inferring the latter number from data, we construct the maximum-likelihood solution for this transformation and obtain unbiased shear estimates with a remarkable amount of noise reduction compared to established approaches. This finding is particularly valid for complicated PSF models and low S/N images, which renders our approach suitable for typical weak-lensing conditions.
Key words: techniques: image processing - gravitational lensing - methods: data analysis
Shapelets have been proposed as an orthonormal set of two-dimensional functions to quantify shapes of galaxy images (Refregier 2003). They have several convenient mathematical properties that suggest their use in measurements of weak gravitational lensing (Refregier & Bacon 2003). Their application to data with low signal-to-noise ratio, however, is hampered by several problems. First, their enormous flexibility allows shapelets to represent random noise patterns well, which generates their tendency to escape into high orders and to overfit noisy images. Second, this same property affects not only the order, but also the spatial scale of the best-fitting shapelet model. The scale sizes of the shapelets decomposing noisy images are thus likely to be too high.
These drawbacks are inherent properties of the shapelet method and have to be addressed to effectively use them in astronomical image processing. At first sight, it seems natural to limit the order of the shapelets from above to avoid overfitting and to limit the scale from above to prevent shapelets from creeping into the noise.
On the other hand, convolution with the PSF alters the shape and spatial extent of imaged objects, leaving an imprint on the maximum shapelet order and the scale size.
Guided by these considerations, we address the question of how the maximum order and the spatial scale of a shapelet decomposition should be determined in cases where PSF convolution significantly modifies the object's appearance? This question aims at applications of shapelets in weak-lensing measurements, where the situation is particularly delicate because typically very small and noisy images are convolved with structured, incompletely known PSF kernels with scales similar to those of the imaged objects. How can deconvolution schemes be constructed in this case to find significant and unbiased shear estimates?
We show in Sect. 2 and in the Appendix that mathematical sum rules exist for the shapelet orders and the squared spatial scales of original image, kernel, and convolved image. We then proceed in Sect. 3 to devise an algorithm respecting these sum rules as closely as possible, which leads to a deconvolution scheme based on the (possibly weighed) pseudo-inverse of a rectangular rather than the inverse of a quadratic convolution matrix. In Sect. 4, we demonstrate by means of simulations with different signal-to-noise levels and PSF kernels that our algorithm does indeed perform very well and that it leads in most realistic cases to substantially improved results compared to previously proposed methods. Our conclusions are summarized in Sect. 5.
2 Convolution in shapelet space
A two-dimensional function
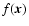 ,
e.g. a galaxy image, is decomposed into a set of shapelet modes by projection,
,
e.g. a galaxy image, is decomposed into a set of shapelet modes by projection,
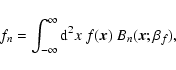 |
(1) |
where
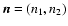 is a two-dimensional index and
is a two-dimensional index and 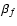 is called scale size. The
two-dimensional shapelet basis function
is called scale size. The
two-dimensional shapelet basis function
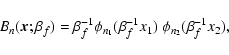 |
(2) |
is related to the one-dimensional Gauss-Hermite polynomial
![\begin{displaymath}
\phi_{n}(x) = \left[2^n \pi^{\frac{1}{2}} n!\right]^{-\frac{1}{2}}\ H_n(x)\
{\rm e}^{-\frac{x^2}{2}},
\end{displaymath}](/articles/aa/full/2009/02/aa10472-08/img27.gif) |
(3) |
with Hn(x) the Hermite polynomial of order n.
From the coefficients one can then reconstruct a shapelet model
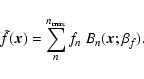 |
(4) |
The number of shapelet modes - often expressed in terms of the maximum shapelet order
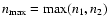 - and the scale size have to be determined by an optimization algorithm (Melchior et al. 2007; Massey & Refregier 2005), which minimizes the modulus of the residuals
- and the scale size have to be determined by an optimization algorithm (Melchior et al. 2007; Massey & Refregier 2005), which minimizes the modulus of the residuals
 ,
or from empirical relations based on other measures of the object like FWHM or major and minor axes (Kuijken 2006; Chang et al. 2004).
,
or from empirical relations based on other measures of the object like FWHM or major and minor axes (Kuijken 2006; Chang et al. 2004).
A convolution
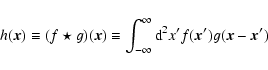 |
(5) |
can be performed analytically in shapelet space.
According to Eq. (1), the functions f, g, and h are represented by sets of shapelet states fn, gn, and hn with scale sizes 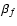 ,
,
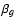 ,
and
,
and 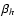 .
.
Refregier (2003) and Refregier & Bacon (2003) showed that the coefficients of the convolved image
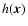 are given by
are given by
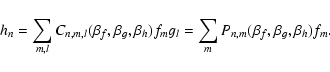 |
(6) |
Formally, this is an ordinary matrix equation,
hence
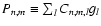 is called convolution matrix. The value of
is called convolution matrix. The value of
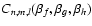 and thus the entire convolution matrix can be computed analytically.
and thus the entire convolution matrix can be computed analytically.
However, there is no clear statement of the scale size 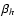 and, in particular, of the maximum order
and, in particular, of the maximum order
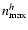 of the convolved object h. In appendix A we prove that the so-called natural choice (Refregier 2003)
of the convolved object h. In appendix A we prove that the so-called natural choice (Refregier 2003)
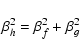 |
(8) |
is indeed the correct choice for 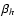 and that the maximum order of the convolved object is given by
and that the maximum order of the convolved object is given by
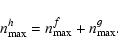 |
(9) |
While this result gives the highest possible mode of the convolved object that could contain power, it does not tell us whether it does indeed have power, as this depends primarily on the ratio of scales
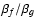 entering
Pn,m. This is demonstrated in Fig. 1, where we show the result of a convolution of a function that is given by a pure B4 mode with a kernel represented by a pure B2 mode. From this it becomes obvious that in a wide region around
entering
Pn,m. This is demonstrated in Fig. 1, where we show the result of a convolution of a function that is given by a pure B4 mode with a kernel represented by a pure B2 mode. From this it becomes obvious that in a wide region around
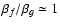 ,
power is transfered to all even modes up to n=6 (odd modes vanish because of parity, cf. Eq. (A.5) and the following discussion). If either
,
power is transfered to all even modes up to n=6 (odd modes vanish because of parity, cf. Eq. (A.5) and the following discussion). If either
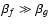 or
or
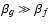 ,
the highest order of the larger object is also the highest effective order of the convolved object. Thus, we can generalize Eq. (9),
,
the highest order of the larger object is also the highest effective order of the convolved object. Thus, we can generalize Eq. (9),
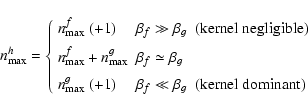 |
(10) |
where the option (+1) is taken if required by parity.
For most cases, in particular for weak gravitational lensing, PSF and object scales are comparable, which means that we must not neglect the power transfer to higher modes.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{0472fig1.eps}
\end{figure}](/articles/aa/full/2009/02/aa10472-08/Timg45.gif) |
Figure 1:
One-dimensional convolution
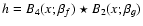 .
We plot the modulus of hn with n even (all odd modes have vanishing power), normalized by .
We plot the modulus of hn with n even (all odd modes have vanishing power), normalized by
 . . |
| Open with DEXTER |
3 How to deconvolve
While the correct values for 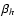 and
and
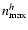 are clarified now, it is not obvious how these results need to be used in deconvolving real data. We first comment on possible ways to undo the convolution and then discuss our finding in the light of measurement noise.
are clarified now, it is not obvious how these results need to be used in deconvolving real data. We first comment on possible ways to undo the convolution and then discuss our finding in the light of measurement noise.
As Refregier & Bacon (2003) have already discussed, there are two ways to deconvolve from the PSF in shapelet space:
- -
- inversion of the convolution matrix: according to Eq. (6), one can solve for the unconvolved coefficients;
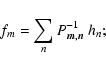 |
(11) |
- -
- fit with the convolved basis system (Massey & Refregier 2005; Kuijken 1999): This modifies Eq. (4) such that it directly minimizes the residuals of
 w.r.t. its shapelet model
w.r.t. its shapelet model
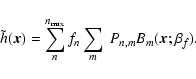 |
(12) |
The second method is generally applicable but slow because the convolution has to be applied at each iteration step of the decomposition process. On the other hand, the first approach reduces deconvolution to a single step after the shapelet decomposition and is therefore computationally more efficient.
According to Eq. (9), P is not square and thus not invertible as suggested by Eq. (11). To cope with this, we need to replace the inverse P-1 by the pseudo-inverse
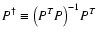 such that the equation now reads as
such that the equation now reads as
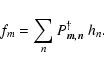 |
(13) |
What seems as a drawback at first glance is effectively beneficial. Conceptually, this is now the least-squares solution of Eq. (6), recovering the most probable unconvolved coefficients from the set of noisy convolved coefficients. The underlying assumption of Gaussian noise in the coefficients hn holds for the most usual case of background-dominated images for which the pixel noise is Gaussian.
Correlations among the coefficients hn, which arise from non-constant pixel weights or pixel correlations, can be accounted for by introducing the coefficient covariance matrix
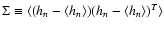 ,
which alters Eq. (7) to read
,
which alters Eq. (7) to read
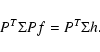 |
(14) |
Maximizing the likelihood for recovering the correct unconvolved coefficients leads to the weighted pseudo-inverse
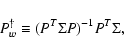 |
(15) |
which replaces 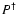 in Eq. (13).
in Eq. (13).
However, both approaches (direct inversion, Eq. (11), or least-squares solution, Eq. (13)) would fail if P was rank-deficient. Refregier & Bacon (2003) argue that convolution with the PSF amounts to a projection of high-order modes onto low-order modes and therefore P can become singular. This is only true for very simple kernels (e.g. the Gaussian-shaped mode of order 0) with rather large scales. In fact, Eq. (10) tells us that convolution carries power from all available modes of f to modes up to order
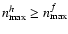 ,
hence P is generally not rank-deficient. In practice we did not have problems in constructing P-1 or
,
hence P is generally not rank-deficient. In practice we did not have problems in constructing P-1 or 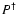 when using realistic kernels. We therefore see no hindrance in employing the matrix-inversion scheme and will use it in the course of this paper.
when using realistic kernels. We therefore see no hindrance in employing the matrix-inversion scheme and will use it in the course of this paper.
Up to here, we have discussed (de-)convolution entirely in shapelet space, where this problem is now completely solved. For the following line of reasoning, we further assume that the kernel is perfectly known and can be described by a shapelet model.
Critical issues still arise at the transition from pixel to shapelet space. There are no intrinsic values of
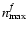 and
and 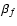 .
Even if they existed, they would not be directly accessible to a measurement. While the first statement stems from trying to model a highly complicated galaxy or stellar shape with a potentially completely inappropriate function set, the second statement arises from pixelation and measurement noise occurring in the detector.
.
Even if they existed, they would not be directly accessible to a measurement. While the first statement stems from trying to model a highly complicated galaxy or stellar shape with a potentially completely inappropriate function set, the second statement arises from pixelation and measurement noise occurring in the detector.
However, the pixelated version of the shape can be described by a shapelet model, with an accuracy that depends on the noise level and the pixel size. Consider for example a galaxy whose light distribution strictly follows a Sérsic profile. Modeling the cusp and the wide tails of this profile with the shapelet basis functions would require an infinite number of modes. But pixelation effectively removes the central singularity of the Sérsic profile and turns the continuous light distribution into a finite number of light measures, such that it is in principle describable by a finite number of shapelet coefficients. Pixel noise additionally limits the spatial region within which the tails of Sérsic profile remain noticeable, hence the number of required shapelet modes.
Consequently, shapelet implementations usually determine
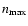 by some significance measure of the model (
by some significance measure of the model (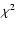 in Melchior et al. 2007; Massey & Refregier 2005) or - similarly - fix
in Melchior et al. 2007; Massey & Refregier 2005) or - similarly - fix
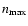 at a value that seems reasonable for capturing the general features of the shape (e.g. Refregier & Bacon 2003; Kuijken 2006).
at a value that seems reasonable for capturing the general features of the shape (e.g. Refregier & Bacon 2003; Kuijken 2006).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0472fig2.eps}
\end{figure}](/articles/aa/full/2009/02/aa10472-08/Timg57.gif) |
Figure 2:
Sketch of the effect of a convolution on the power of shapelet coefficients. The detailed shape of the curves is neither realistic nor important, but typical shapelet models show decreasing coefficient power with increasing order n. The noise regime (represented by the gray area) is constant in the case of uncorrelated noise. |
| Open with DEXTER |
Figure 2 schematically highlights an important issue of a significance-based ansatz.
When the power in a shapelet coefficient is lower than the power of the noise, it is considered insignificant, and the shapelet series is truncated at this mode (in Fig. 2, fn may be limited to 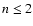 and hn to
and hn to 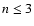 ).
Since convolution with a flux-normalized kernel does not change the overall flux or - as the shapelet decomposition is linear - the total coefficient power but generally increases the number of modes, the signal-to-noise ratio (S/N) of each individual coefficient is lowered on average. Thus, after convolution, more coefficients will be considered insignificant and will be disregarded.
).
Since convolution with a flux-normalized kernel does not change the overall flux or - as the shapelet decomposition is linear - the total coefficient power but generally increases the number of modes, the signal-to-noise ratio (S/N) of each individual coefficient is lowered on average. Thus, after convolution, more coefficients will be considered insignificant and will be disregarded.
This is equivalent to the action of a convolution in pixel space, where some objects' flux is distributed over a larger area. If the noise is independent of the convolution, demanding a certain S/N threshold results in a smaller number of significant pixels.
The main point here is that we try to measure hn from data and from this fn by employing Eq. (13). But if we truncate hn too early, at an order
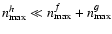 ,
the resulting unconvolved coefficients fn are expected to be biased even if the convolution kernel is perfectly described. The reason for this is that, by truncating, we assume that any higher-order coefficient is zero on average, while in reality it is non-zero, but just smaller than the noise limit. Every estimator formed from these coefficients is thus likely biased itself.
,
the resulting unconvolved coefficients fn are expected to be biased even if the convolution kernel is perfectly described. The reason for this is that, by truncating, we assume that any higher-order coefficient is zero on average, while in reality it is non-zero, but just smaller than the noise limit. Every estimator formed from these coefficients is thus likely biased itself.
In turn, if we knew
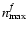 ,
we could go to the order demanded by Eq. (9) and the deconvolution would map many noise-dominated high-order coefficients back onto lower-order coefficients. This way, we would not cut off coefficient power, and our coefficient set would remain unbiased. Unfortunately, this approach comes at a price. First, the resulting shapelet models are often massively overfitted, and second, obtaining unbiased fn requires the knowledge of
,
we could go to the order demanded by Eq. (9) and the deconvolution would map many noise-dominated high-order coefficients back onto lower-order coefficients. This way, we would not cut off coefficient power, and our coefficient set would remain unbiased. Unfortunately, this approach comes at a price. First, the resulting shapelet models are often massively overfitted, and second, obtaining unbiased fn requires the knowledge of
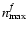 .
The first problem can be addressed by averaging over a sufficient number of galaxies, while the second one can indeed be achieved by checking the S/N of the recovered fn after deconvolution. The average number of significant deconvolved coefficients gives an indication of the typical complexity of the imaged objects as they would be seen in a measurement without convolution, but using the particular detector characterized by its pixel size and noise level.
.
The first problem can be addressed by averaging over a sufficient number of galaxies, while the second one can indeed be achieved by checking the S/N of the recovered fn after deconvolution. The average number of significant deconvolved coefficients gives an indication of the typical complexity of the imaged objects as they would be seen in a measurement without convolution, but using the particular detector characterized by its pixel size and noise level.
3.3 Unbiased deconvolution method
The previous consideration guides us to set up a deconvolution procedure that yields unbiased deconvolved coefficients. Again, we assume that the kernel can be perfectly modeled by shapelet series with finite order
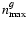
![[*]](/icons/foot_motif.gif) .
.
- -
- Given the noise level and the pixel size of the images, we initially guess
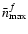 for each individual galaxy;
for each individual galaxy;
- we set the lower bounds
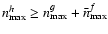 and
and
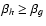 ;
;
- -
- we decompose each galaxy by minimizing the decomposition
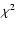 under these constraints. A value of
under these constraints. A value of
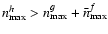 is used only if
is used only if 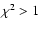 otherwise. This yields hn and
otherwise. This yields hn and 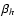 ;
;
- -
- by inverting Eq. (8), we obtain
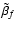 ;
;
- -
- using the maximum orders and scale sizes for f, g, and h in addition to gn, we can form the convolution matrix P according to Eq. (7);
- -
- by forming
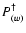 and applying Eq. (13), we reconstruct
and applying Eq. (13), we reconstruct
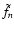 ;
;
- -
- by propagating the coefficient errors from the decomposition through the same set of steps, we investigate the number of significant coefficients and should find
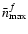 if our initial guess was correct.
if our initial guess was correct.
Given the demanded accuracy, it might be necessary to adjust the guess
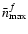 and reiterate the steps above. For the initial guess, it is inevitable to split the data set in magnitude bins, because the best value for
and reiterate the steps above. For the initial guess, it is inevitable to split the data set in magnitude bins, because the best value for
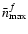 clearly depends on the intrinsic brightness. Further splitting (according to apparent size or brightness profile etc.) may be advantageous, too.
clearly depends on the intrinsic brightness. Further splitting (according to apparent size or brightness profile etc.) may be advantageous, too.
4 Deconvolution microbenchmark
There exists a growing number of shapelet-based decomposition and deconvolution approaches published in the literature. In this section we show that the method proposed here is indeed capable of inferring unbiased unconvolved coefficients. Moreover, employing the least-squares solution given by Eq. (13) results in a considerable noise reduction, which is to be expected from this ansatz.
At first, we want to emphasize that the simulations we use in this section are highly simplistic. Their only purpose is to investigate how well a certain decomposition/deconvolution scheme can recover the unconvolved coefficients. By understanding the performance of different approaches, we acquire the knowledge for treating more realistic cases.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0472fig3.eps}
\end{figure}](/articles/aa/full/2009/02/aa10472-08/Timg70.gif) |
Figure 3:
Example of simulated galaxies used in our testbed: a) intrinsic galaxy model with 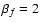 and flux equaling unity; b) after applying a shear
and flux equaling unity; b) after applying a shear
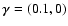 ;
c) after convolving with PSFb from Fig. 4 with ;
c) after convolving with PSFb from Fig. 4 with 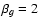 .
The bottom panels show c) after addition of Gaussian noise of zero mean and variance .
The bottom panels show c) after addition of Gaussian noise of zero mean and variance
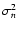 :
d) moderate noise, :
d) moderate noise,
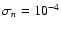 ;
e) high noise, ;
e) high noise,
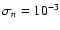 ;
f) is the shapelet reconstruction of e). The scale is logarithmic. ;
f) is the shapelet reconstruction of e). The scale is logarithmic. |
| Open with DEXTER |
The construction of simulated galaxy images is visualized in Fig. 3. As intrinsic function we use a polar shapelet model with
f0,0=f2,0=c, where c is chosen such that the model has unit flux. Then, 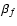 is varied between 1.5 and 4. Given its ring-shaped appearance, this model is not overly realistic but also not too simple, and circularly symmetric. We apply a mild shear of
is varied between 1.5 and 4. Given its ring-shaped appearance, this model is not overly realistic but also not too simple, and circularly symmetric. We apply a mild shear of
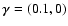 ,
thus populate coefficients of order
,
thus populate coefficients of order
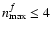 ,
and convolve with five different realistic kernels g (cf. Fig. 4) in shapelet space (employing Eqs. (8) and (9) with
,
and convolve with five different realistic kernels g (cf. Fig. 4) in shapelet space (employing Eqs. (8) and (9) with
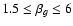 ). The pixelated version of the convolved object is then subject to N realizations of Gaussian noise with constant variance.
). The pixelated version of the convolved object is then subject to N realizations of Gaussian noise with constant variance.
Each of these simulated galaxy images is decomposed into shapelets again, yielding hn, using the code by Melchior et al. (2007), where the optimization is constrained by fixing either
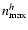 or
or 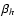 ,
or both. The observed coefficients hn are then deconvolved from the kernel g.
,
or both. The observed coefficients hn are then deconvolved from the kernel g.
As a diagnostic for the correctness of the deconvolved coefficients, we estimate the gravitational shear from the quadrupole moments Qij of the light distribution (Bartelmann & Schneider 2001),
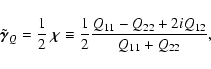 |
(16) |
where Qij is computed as a linear combination of all available deconvolved coefficients (Melchior et al. 2007; Bergé 2005).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0472fig4.eps}
\end{figure}](/articles/aa/full/2009/02/aa10472-08/Timg74.gif) |
Figure 4:
The kernels used in our benchmark: a) model of PSF2 from STEP1 (Heymans et al. 2006) with
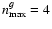 ;
b) model of PSF3 from STEP1 with ;
b) model of PSF3 from STEP1 with
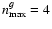 ;
c) airy disk model with ;
c) airy disk model with
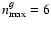 ;
d) model from a raytracing simulation of a space-bourne telescope's PSF with ;
d) model from a raytracing simulation of a space-bourne telescope's PSF with
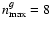 and
and
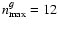 (shown here). The scale is logarithmic.
(shown here). The scale is logarithmic. |
| Open with DEXTER |
We investigate five different approaches that differ in the choice of
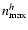 ,
,
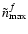 or the reconstruction of
or the reconstruction of 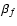 .
The different choices are summarized in Table 1.
.
The different choices are summarized in Table 1.
F ULL is the method we propose here (cf. Sect. 3.3), and for the following tests we set
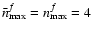 .
S IGNIFIC is a variant of F ULL, which bounds the decomposition order by the kernel order because coefficients beyond that are often insignificant, but makes use of our guess on
.
S IGNIFIC is a variant of F ULL, which bounds the decomposition order by the kernel order because coefficients beyond that are often insignificant, but makes use of our guess on
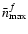 .
.
S AME is similar to the one used by Kuijken (2006) with two differences. As discussed above, we employ the matrix inversion scheme (Eq. (11) since P is square for this method) instead of fitting the convolved shapelet basis functions, and in our implementation 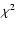 is minimized with respect to a continuous parameter
is minimized with respect to a continuous parameter 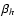 ,
while Kuijken (2006) finds the best-fitting
,
while Kuijken (2006) finds the best-fitting
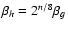 with some integer n. Without knowing the increase of shapelet orders due to convolution given by Eq. (9), this represents the best-defined deconvolution approach.
with some integer n. Without knowing the increase of shapelet orders due to convolution given by Eq. (9), this represents the best-defined deconvolution approach.
Refregier & Bacon (2003) state that the approach C ONSTS CALE delivers the best results in their analysis. N MAX2, however, is an approach inspired by the naïve assumption that such a decomposition scheme catches the essential shear information without being affected by overfitting.
Table 1:
Overview of the parameter choices of the investigated methods.
The first set of simulations comprises galaxy models with peak S/N between 45 and 220 with a median of 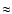 90 (an example is shown in Fig. 3d). For each value of
90 (an example is shown in Fig. 3d). For each value of 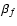 and
and 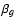 ,
we created N=100 noise realizations. These high S/N values are more typical of galaxy morphology studies than of weak lensing, but we can see the effect of the convolution best. In this regime, problems with the deconvolution method immediately become apparent.
,
we created N=100 noise realizations. These high S/N values are more typical of galaxy morphology studies than of weak lensing, but we can see the effect of the convolution best. In this regime, problems with the deconvolution method immediately become apparent.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0472fig5.eps}
\end{figure}](/articles/aa/full/2009/02/aa10472-08/Timg82.gif) |
Figure 5:
Recovered shear
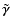 and intrinsic scale size
and intrinsic scale size
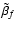 in a moderate-noise simulation (
in a moderate-noise simulation (
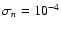 , ,
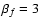 ,
PSFb) as functions of the kernel scale ,
PSFb) as functions of the kernel scale 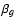 .
In each panel the horizontal dashed line shows the true value of the quantity and the vertical dotted line shows the true value for .
In each panel the horizontal dashed line shows the true value of the quantity and the vertical dotted line shows the true value for 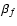 as reference. Errorbars (which are often too small to be visible) exhibit the standard deviation of the mean of N=100 realizations. For visualization purposes, each method is slightly offset along
as reference. Errorbars (which are often too small to be visible) exhibit the standard deviation of the mean of N=100 realizations. For visualization purposes, each method is slightly offset along 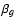 .
Simulations with different PSF models or .
Simulations with different PSF models or 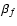 are qualitatively equivalent.
are qualitatively equivalent. |
| Open with DEXTER |
Considering Fig. 5, we can ascertain that F ULL, S IGNIFIC, and S AME perform quite well, while C ONSTS CALE and N MAX2 are clearly in trouble. This is not too surprising. By construction, N MAX2 truncates the shapelet series at
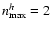 ,
hence misses all information contained in higher-order coefficients. One has to recall that the sheared model already has
,
hence misses all information contained in higher-order coefficients. One has to recall that the sheared model already has
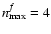 ,
and after convolution with PSFb (
,
and after convolution with PSFb (
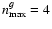 ), it arrives at
), it arrives at
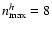 .
N MAX2 tries to undo the deconvolution with less information than contained in both sheared model and kernel individually. This is an enormously underconstrained attempt and leads to unpredictable behavior.
C ONSTS CALE assumes that
.
N MAX2 tries to undo the deconvolution with less information than contained in both sheared model and kernel individually. This is an enormously underconstrained attempt and leads to unpredictable behavior.
C ONSTS CALE assumes that 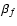 can be approximated by
can be approximated by 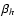 ,
so
,
so
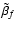 must be an increasing function of
must be an increasing function of 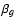 (see bottom panel of Fig. 5). According to Eq. (8), this ansatz is only applicable if
(see bottom panel of Fig. 5). According to Eq. (8), this ansatz is only applicable if 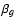 is negligible. For very small kernel scales, we can indeed see a tendency to converge to the correct solution, but for all other situations, this choice is manifestly non-optimal. Because of the clearly problematic behavior of C ONSTS CALE and N MAX2, we exclude these two methods from the further investigation.
is negligible. For very small kernel scales, we can indeed see a tendency to converge to the correct solution, but for all other situations, this choice is manifestly non-optimal. Because of the clearly problematic behavior of C ONSTS CALE and N MAX2, we exclude these two methods from the further investigation.
This situation is very similar for other choices of 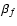 and other PSF models. To work out the general trends of the three remaining methods, we average over all scales
and other PSF models. To work out the general trends of the three remaining methods, we average over all scales 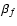 and
and 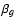 and plot the results in dependence of the PSF model.
and plot the results in dependence of the PSF model.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0472fig6.eps}
\end{figure}](/articles/aa/full/2009/02/aa10472-08/Timg86.gif) |
Figure 6:
Recovered shear
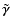 and intrinsic scale size
and intrinsic scale size
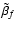 (in units of the true scale size
(in units of the true scale size 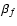 )
in the moderate-noise simulations in dependence on the PSF models from Fig. 4 (subscripts denote )
in the moderate-noise simulations in dependence on the PSF models from Fig. 4 (subscripts denote
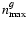 ). Each data point represents the mean of the quantity for all available values of ). Each data point represents the mean of the quantity for all available values of 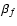 and
and 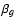 (in total 60 independent combinations), and errorbars show the standard deviation of the mean. For visualization purposes, each method is slightly offset horizontally with respect to the others.
(in total 60 independent combinations), and errorbars show the standard deviation of the mean. For visualization purposes, each method is slightly offset horizontally with respect to the others. |
| Open with DEXTER |
The top and middle panels of Fig. 6 confirm that all remaining methods yield essentially unbiased estimates of the shear, although we notice a mild tendency of S AME and S IGNIFIC to underestimate
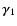 .
This indicates that truncation of the decomposition order
.
This indicates that truncation of the decomposition order
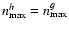 might be insufficient for high S/N images. That this underestimation is absent at higher kernel orders confirms this interpretation.
might be insufficient for high S/N images. That this underestimation is absent at higher kernel orders confirms this interpretation.
Within the errors, the recovered scale size
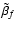 is rather unbiased (see the bottom panel of 6). For S AME and S IGNIFIC, we can see a clear shift of
is rather unbiased (see the bottom panel of 6). For S AME and S IGNIFIC, we can see a clear shift of
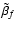 for PSFc. The reason for this lies in the large spatial extent and wide wings of the Airy disk model in combination with a low
for PSFc. The reason for this lies in the large spatial extent and wide wings of the Airy disk model in combination with a low
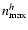 .
Since the entries of P depend in a nonlinear way on
.
Since the entries of P depend in a nonlinear way on 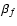 ,
this shift affects the recovery of the shear and leads to slightly poorer results.
,
this shift affects the recovery of the shear and leads to slightly poorer results.
From this initial simulation with moderate noise, we can conclude that one should respect Eq. (8) and must not truncate the shapelet series of hn severely.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0472fig8.eps}
\end{figure}](/articles/aa/full/2009/02/aa10472-08/Timg90.gif) |
Figure 8:
Distance in shapelet space 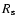 between the mean deconvolved and the true intrinsic coefficients in dependence of the PSF model for the three methods F ULL ( top panel), S IGNIFIC ( middle panel), and S AME ( bottom panel). The mean is computed by averaging over all available values of
between the mean deconvolved and the true intrinsic coefficients in dependence of the PSF model for the three methods F ULL ( top panel), S IGNIFIC ( middle panel), and S AME ( bottom panel). The mean is computed by averaging over all available values of 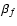 and
and 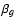 (in total 60 independent combinations). Shown are the results for the moderate-noise simulations (solid line) and the high-noise simulations (dotted line).
(in total 60 independent combinations). Shown are the results for the moderate-noise simulations (solid line) and the high-noise simulations (dotted line). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0472fig9.eps}
\end{figure}](/articles/aa/full/2009/02/aa10472-08/Timg91.gif) |
Figure 9:
Recovered shear
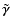 and intrinsic scale size
and intrinsic scale size
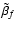 (in units of the true scale size
(in units of the true scale size 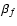 )
in the high-noise simulations in dependence on the S/N of the convolved galaxy. The binning (dotted lines) is defined by the octiles of the S/N distribution, therefore all bins contain the mean values of approx. 7 combinations of )
in the high-noise simulations in dependence on the S/N of the convolved galaxy. The binning (dotted lines) is defined by the octiles of the S/N distribution, therefore all bins contain the mean values of approx. 7 combinations of 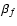 , ,
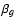 for each PSF model, in total
for each PSF model, in total 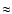 35 independent settings. The data are plotted at the center of the bins and the methods are slightly offset horizontally for visualization purposes. Color code is as explained in Fig. 6. 35 independent settings. The data are plotted at the center of the bins and the methods are slightly offset horizontally for visualization purposes. Color code is as explained in Fig. 6. |
| Open with DEXTER |
We now consider a realistic weak-lensing situation by increasing the noise level by a factor of 10, hence
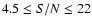 (cf. Fig. 3e). To partly compensate for the higher noise, we increase the number of realizations to N=1000.
(cf. Fig. 3e). To partly compensate for the higher noise, we increase the number of realizations to N=1000.
Considering Fig. 7, we can confirm that the shear estimates from these three methods are also not significantly biased for very noisy images. However, for S AME we can see a remarkable drop in the mean of
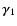 and a drastic increase in the noise in
and a drastic increase in the noise in
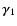 and
and
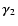 with the kernel order. Both findings are probably related to using P-1 instead of
with the kernel order. Both findings are probably related to using P-1 instead of 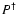 when performing the deconvolution.
In contrast to the two methods we are proposing here, S AME uses
when performing the deconvolution.
In contrast to the two methods we are proposing here, S AME uses
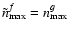 (cf. Table 1). For the typical weak-lensing scenario - characterized by
(cf. Table 1). For the typical weak-lensing scenario - characterized by
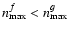 ,
where all methods create a substantial amount of overfitting, cf. Fig. 3f - this assumes finding a higher number of significant deconvolved coefficients than are actually available. These additional, noise-dominated coefficients affect Qij and
,
where all methods create a substantial amount of overfitting, cf. Fig. 3f - this assumes finding a higher number of significant deconvolved coefficients than are actually available. These additional, noise-dominated coefficients affect Qij and
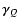 (cf. Eq. (16)). Therefore, these quantities become rather noisy themselves. Given that those high-order coefficients contain mostly arbitrary pixel noise that does not have a preferred direction, they also tend to dilute the available shear information from the lower-order coefficients, which explains the drop in
(cf. Eq. (16)). Therefore, these quantities become rather noisy themselves. Given that those high-order coefficients contain mostly arbitrary pixel noise that does not have a preferred direction, they also tend to dilute the available shear information from the lower-order coefficients, which explains the drop in
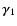 .
The estimate for
.
The estimate for
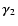 is not affected, as its true value was zero anyway.
is not affected, as its true value was zero anyway.
The superior behavior of F ULL and S IGNIFIC in these low S/N simulations can also be seen more directly. As measure of the decomposition quality, we calculate the distance in shapelet space between the mean deconvolved coefficients
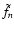 and the true input coefficients fn,
and the true input coefficients fn,
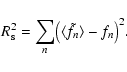 |
(17) |
Figure 8 confirms that, as long as the kernel order is small, all three methods perform quite similarly. But when the kernel order increases, S AME tries to recover a quadratically increasing number of deconvolved coefficients whose individual significance is lowered at the same time. On the other hand, F ULL and S IGNIFIC make use of the redundancy of the overdetermined coefficient set, which is created by applying a rectangular matrix P in Eq. (6). As a direct consequence of computing the least-squares solution via 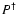 ,
the higher the number of convolved coefficients and the lower the number of significant intrinsic coefficients, the better these intrinsic coefficients can be recovered from noisy measurements. This explains the decrease in
,
the higher the number of convolved coefficients and the lower the number of significant intrinsic coefficients, the better these intrinsic coefficients can be recovered from noisy measurements. This explains the decrease in 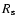 with the kernel order for these two methods.
with the kernel order for these two methods.
However, F ULL also does not perform perfectly. The bottom panel of Fig. 7 reveals a bias on
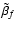 ,
independent of the PSF model. The reason for this is again overfitting. As F ULL goes to higher orders than S IGNIFIC and S AME, it is even more affected by the pixel noise. As the decomposition determines
,
independent of the PSF model. The reason for this is again overfitting. As F ULL goes to higher orders than S IGNIFIC and S AME, it is even more affected by the pixel noise. As the decomposition determines 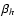 by minimizing
by minimizing 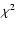 ,
,
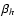 tends to become larger because this allows the model to fit a larger (increasingly noise-dominated) area, which reduces the overall residuals and thus
tends to become larger because this allows the model to fit a larger (increasingly noise-dominated) area, which reduces the overall residuals and thus 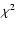 .
S IGNIFIC and S AME behave similarly when the kernel order - and hence the decomposition order - becomes larger.
.
S IGNIFIC and S AME behave similarly when the kernel order - and hence the decomposition order - becomes larger.
To prevent the shapelet models from creeping into the noisy areas around the object, it seems useful to constrain 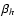 not only from below but also from above. In addition to a guess on
not only from below but also from above. In addition to a guess on
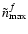 ,
we therefore impose a constraint
,
we therefore impose a constraint
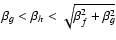 .
Inferring both should be feasible when investigating observational data.
.
Inferring both should be feasible when investigating observational data.
As our simulations comprise galaxy models of varying S/N![[*]](/icons/foot_motif.gif) , it is illustrative to present the deconvolution results in S/N bins.
Figure 9 confirms that the two methods we propose here are very robust against image degradation. This is remarkable, since many weak-lensing pipelines (and also S AME in this paper) suffer from an underestimation of the shear, which becomes increasingly prominent with decreasing S/N (Massey et al. 2007). Our statement from above, in which we related this drop to the high number of insignificant coefficients obtained from a deconvolution using S AME, is further supported by this figure. It is obvious that - independent of the kernel model - a low S/N in pixel space results in a low S/N in shapelet space. By obtaining the least-squares solution for the fn, F ULL and S IGNIFIC boost the significance of the recovered coefficients and thus perform better in the low S/N regime. The reason why
, it is illustrative to present the deconvolution results in S/N bins.
Figure 9 confirms that the two methods we propose here are very robust against image degradation. This is remarkable, since many weak-lensing pipelines (and also S AME in this paper) suffer from an underestimation of the shear, which becomes increasingly prominent with decreasing S/N (Massey et al. 2007). Our statement from above, in which we related this drop to the high number of insignificant coefficients obtained from a deconvolution using S AME, is further supported by this figure. It is obvious that - independent of the kernel model - a low S/N in pixel space results in a low S/N in shapelet space. By obtaining the least-squares solution for the fn, F ULL and S IGNIFIC boost the significance of the recovered coefficients and thus perform better in the low S/N regime. The reason why
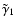 from F ULL is consistently but insignificantly lower than the estimates from S AME is still somewhat unclear. A possible reason is the generally higher number of shapelet coefficients hn for F ULL and thus a more noticeable noise contamination.
from F ULL is consistently but insignificantly lower than the estimates from S AME is still somewhat unclear. A possible reason is the generally higher number of shapelet coefficients hn for F ULL and thus a more noticeable noise contamination.
5 Conclusions
Based on an analytic consideration of shapelet convolution, we have studied algorithms for the PSF deconvolution of galaxy images in shapelet space. The starting point are sum rules for shapelet convolution, showing that the intrinsic shapelet orders of PSF and image add up in the convolved image and that the squares of their scales are also added. We suggest an algorithm respecting these sum rules as well as possible in the presence of noise, whose central step is the deconvolution of the convolved image with the pseudo-inverse of the convolution matrix. Applications to simulated images have shown that our algorithm performs very well and, in many cases noticeably better, than previously suggested methods.
We identify three main reasons for the improved performance:
- As the sum rule for the shapelet order shows, the convolution transports power to higher shapelet modes. The mean signal-to-noise ratio of the convolved coefficients is thus reduced. Our reduction of the order during the deconvolution increases the signal-to-noise without the need for calibration.
- The sum rules typically require a much higher shapelet order than the
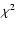 minimization, in particular if the PSF model is structured. Many of the high-order coefficients are thus highly insignificant. The significance of the coefficients is re-established by the reduction to the order
minimization, in particular if the PSF model is structured. Many of the high-order coefficients are thus highly insignificant. The significance of the coefficients is re-established by the reduction to the order
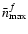 ,
which is chosen such that the shapelet expansion contains only significant coefficients. Fortunately,
,
which is chosen such that the shapelet expansion contains only significant coefficients. Fortunately,
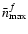 mainly depends on the signal-to-noise ratio of the galaxy, and this dependence is rather weak. Many different galaxy shapes can be deconvolved with the same
mainly depends on the signal-to-noise ratio of the galaxy, and this dependence is rather weak. Many different galaxy shapes can be deconvolved with the same
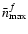 ,
so binning the galaxies into broad signal-to-noise bins will suffice.
,
so binning the galaxies into broad signal-to-noise bins will suffice.
- The STEP-2 project (Massey et al. 2007) has shown that shear measurements generally depend strongly on the galaxy brightness. Our algorithm seems to have the advantage of lowering the influence of pixel noise in a well-defined manner.
We shall proceed to study the performance of our algorithm in shear measurements under realistic conditions.
Acknowledgements
PM wants to thank Thomas Erben, Alex Boehnert, Ludovic van Waerbeke, and Marco Lombardi for very fruitful discussions. P.M. is supported by the DFG Priority Programme 1177. M.M. is supported by the Transregio-Sonderforschungsbereich TRR 33 of the DFG.
Appendix A: Convolution scale and order
For simplicity we restrict ourselves to the one-dimensional case. From Eqs. (1) and (5) it is apparent that
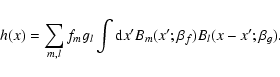 |
(A.1) |
We define
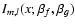 as the integral in Eq. (A.1) and decompose it into shapelets with scale size
as the integral in Eq. (A.1) and decompose it into shapelets with scale size 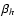 and maximum order N,
and maximum order N,
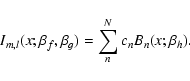 |
(A.2) |
Considering Eqs. (2), (3) and (A.1), we recognize that N cannot be infinite but is determined by the highest modes of the expansions of f and g, which we will call M and L, respectively. Restricting ourselves to these modes and dropping all unnecessary constants, we can proceed,
where we expanded
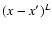 in the last step. By employing Eq. (8) and substituting
in the last step. By employing Eq. (8) and substituting
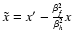 ,
we can split the exponential,
,
we can split the exponential,
Again, we expand
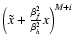 ,
which yields the desired expression
,
which yields the desired expression
where we inserted
![$C_j \equiv \int {\rm d}\tilde{x}~\tilde{x}^j \exp\left[-\frac{\beta_h^2}{2\beta_f^2\beta_g^2}\tilde{x}^2\right]$](/articles/aa/full/2009/02/aa10472-08/img115.gif) .
Apart from the omitted constants, the second line of A.5 is the definition of
.
Apart from the omitted constants, the second line of A.5 is the definition of
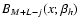 (cf. Eqs. (2) and (3)), which shows that the natural choice is justified. Moreover, as j runs from 0 to M+i, we see that the maximum order N is indeed M+L, as we claimed in Eq. (9). Since Cj=0 if j is odd, the only states with non-vanishing power have the same parity as M+L.
(cf. Eqs. (2) and (3)), which shows that the natural choice is justified. Moreover, as j runs from 0 to M+i, we see that the maximum order N is indeed M+L, as we claimed in Eq. (9). Since Cj=0 if j is odd, the only states with non-vanishing power have the same parity as M+L.
In summary, the natural choice is inherited from the Gaussian weighting function in Eq. (3) and the maximum order the result of a product of polynomials.
- Bartelmann, M., & Schneider,
P. 2001, Phys. Rep., 340, 291 [NASA ADS] [CrossRef]
(In the text)
-
Bergé, J. 2005, An introduction to shapelets based weak
lensing image processing, 1s [NASA ADS]t edn.
- Chang, T.-C.,
Refregier, A., & Helfand, D. J. 2004, ApJ, 617, 794 [NASA ADS] [CrossRef]
- Heymans, C., Van
Waerbeke, L., Bacon, D., et al. 2006, MNRAS, 368, 1323 [NASA ADS] [CrossRef]
(In the text)
- Kuijken, K.
1999, A&A, 352, 355
- Kuijken, K.
2006, A&A, 456, 827 [NASA ADS] [CrossRef] [EDP Sciences]
- Massey, R.,
Heymans, C., Bergé, J., et al. 2007, MNRAS, 376, 13 [NASA ADS] [CrossRef]
(In the text)
- Massey, R.,
& Refregier, A. 2005, MNRAS, 363, 197 [NASA ADS] [CrossRef]
- Melchior,
P., Meneghetti, M., & Bartelmann, M. 2007, A&A, 463,
1215 [NASA ADS] [CrossRef] [EDP Sciences]
- Refregier, A.
2003, MNRAS, 338, 35 [NASA ADS] [CrossRef]
(In the text)
- Refregier,
A., & Bacon, D. 2003, MNRAS, 338, 48 [NASA ADS] [CrossRef]
(In the text)
Copyright ESO 2009
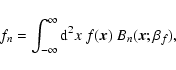
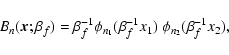
![\begin{displaymath}
\phi_{n}(x) = \left[2^n \pi^{\frac{1}{2}} n!\right]^{-\frac{1}{2}}\ H_n(x)\
{\rm e}^{-\frac{x^2}{2}},
\end{displaymath}](/articles/aa/full/2009/02/aa10472-08/img27.gif)
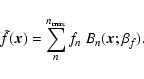
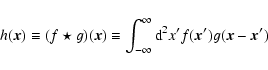
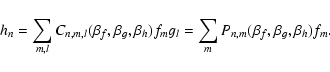
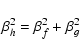
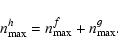
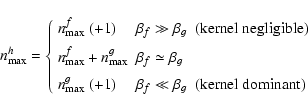
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{0472fig1.eps}
\end{figure}](/articles/aa/full/2009/02/aa10472-08/Timg45.gif)
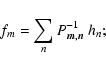
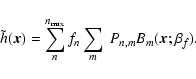
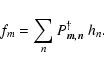
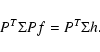
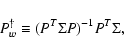
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0472fig2.eps}
\end{figure}](/articles/aa/full/2009/02/aa10472-08/Timg57.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0472fig3.eps}
\end{figure}](/articles/aa/full/2009/02/aa10472-08/Timg70.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0472fig5.eps}
\end{figure}](/articles/aa/full/2009/02/aa10472-08/Timg82.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0472fig6.eps}
\end{figure}](/articles/aa/full/2009/02/aa10472-08/Timg86.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0472fig7.eps}
\end{figure}](/articles/aa/full/2009/02/aa10472-08/Timg87.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0472fig8.eps}
\end{figure}](/articles/aa/full/2009/02/aa10472-08/Timg90.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0472fig9.eps}
\end{figure}](/articles/aa/full/2009/02/aa10472-08/Timg91.gif)
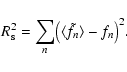
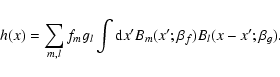
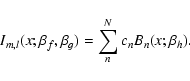
![$\displaystyle \int {\rm d}x^\prime (x^\prime )^M \exp\left[-\frac{x^{\prime 2}}...
...^2}\right] (x-x^\prime )^L \exp\left[-\frac{(x-x^\prime )^2}{2\beta_g^2}\right]$](/articles/aa/full/2009/02/aa10472-08/img105.gif)
![$\displaystyle =\!\!\sum_{i=0}^L (-1)^{L+1}\left(\begin{array}{c} L \\ i \end{a...
...[-\frac{(x-x^\prime)^2}{2\beta_g^2}\!-\!\frac{(x^\prime)^2}{2\beta_f^2}\right],$](/articles/aa/full/2009/02/aa10472-08/img106.gif)
![$\displaystyle \sum_{i=0}^L (-1)^{L+1}\left(\begin{array}{c} L \\ i \end{array}\right)x^{L-i}\exp\left[-\frac{x^2}{2\beta_h^2}\right]$](/articles/aa/full/2009/02/aa10472-08/img110.gif)
![$\displaystyle \times\int {\rm d}\tilde{x}~\left(\tilde{x}+\frac{\beta_f^2}{\bet...
...ight)^{M+i} \exp\left[-\frac{\beta_h^2}{2\beta_f^2\beta_g^2}\tilde{x}^2\right].$](/articles/aa/full/2009/02/aa10472-08/img111.gif)
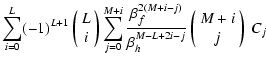
![$\displaystyle \times
\left(\frac{x}{\beta_h}\right)^{M+L-j}\exp\left[-\frac{x^2}{2\beta_h^2}\right],$](/articles/aa/full/2009/02/aa10472-08/img114.gif)