A&A 491, 713-730 (2008)
DOI: 10.1051/0004-6361:200810704
C. J. Walcher1,2 - F. Lamareille5,12 - D. Vergani5,6 - S. Arnouts2,3 - V. Buat2 - S. Charlot1 - L. Tresse2 - O. Le Fèvre2 - M. Bolzonella5 - J. Brinchmann4, 23 - L. Pozzetti5 - G. Zamorani5 - D. Bottini6 - B. Garilli6 - V. Le Brun2 - D. Maccagni6 - B. Milliard2 - R. Scaramella7,8 - M. Scodeggio6 - G. Vettolani7 - A. Zanichelli7 - C. Adami2 - S. Bardelli5 - A. Cappi5 - P. Ciliegi5 - T. Contini12 - P. Franzetti6 - S. Foucaud13 - I. Gavignaud14 - L. Guzzo15 - O. Ilbert16 - A. Iovino15 - H. J. McCracken1,11 - B. Marano17 - C. Marinoni18 - A. Mazure2 - B. Meneux24,25 - R. Merighi5 - S. Paltani19,20 - R. Pellò12 - A. Pollo21 - M. Radovich22 - E. Zucca5 - C. Lonsdale9 - C. Martin10
1 -
Institut d'Astrophysique de Paris, CNRS, Université Pierre & Marie Curie, UMR 7095, 98 bis Boulevard Arago, 75014 Paris, France
2 -
Laboratoire d'Astrophysique de Marseille (UMR6110), CNRS-Université de Provence, 38 rue Frederic Joliot-Curie, 13388 Marseille Cedex 13, France
3 -
Canada France Hawaii Telescope corporation, Mamalahoa Hwy, Kamuela, HI-96743, USA
4 -
Centro de Astrofísica da Universidade do Porto, Rua das Estrelas, 4150-762, Porto, Portugal
5 -
INAF-Osservatorio Astronomico di Bologna, via Ranzani 1, 40127, Bologna, Italy
6 -
IASF-INAF, via Bassini 15, 20133, Milano, Italy
7 -
IRA-INAF, via Gobetti 101, 40129, Bologna, Italy
8 -
INAF-Osservatorio Astronomico di Roma, via di Frascati 33, 00040, Monte Porzio Catone, Italy
9 -
University of California, San Diego 9500 Gilman Dr. La Jolla, CA 92093-0424, USA
10 -
California Institute of Technology, MC 405-47, 1200 East California Boulevard, Pasadena, CA 91125, USA
11 -
Observatoire de Paris, LERMA, 61 Avenue de l'Observatoire, 75014, Paris, France
12 -
Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de Toulouse, CNRS, 14 avenue Edouard Belin, 31400 Toulouse, France
13 -
School of Physics & Astronomy, University of Nottingham, University Park, Nottingham, NG72RD, UK
14 -
Astrophysical Institute Potsdam, An der Sternwarte 16, 14482, Potsdam, Germany
15 -
INAF-Osservatorio Astronomico di Brera, via Brera 28, 20021, Milan, Italy
16 -
Institute for Astronomy, 2680 Woodlawn Dr., University of Hawaii, Honolulu, Hawaii, 96822, USA
17 -
Università di Bologna, Dipartimento di Astronomia, via Ranzani 1, 40127, Bologna, Italy
18 -
Centre de Physique Théorique, UMR 6207 CNRS-Université de Provence, 13288 Marseille, France
19 -
Integral Science Data Centre, ch. d'Écogia 16, 1290, Versoix, Switzerland
20 -
Geneva Observatory, ch. des Maillettes 51, 1290, Sauverny, Switzerland
21 -
The Andrzej Soltan Institute for Nuclear Studies, ul. Hoza 69, 00-681 Warszawa, Poland
22 -
INAF-Osservatorio Astronomico di Capodimonte, via Moiariello 16, 80131, Napoli, Italy
23 -
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden,
The Netherlands
24 -
Max-Planck-Institut fur Extraterrestrische Physik, Giessenbachstrasse, 85748 Garching b. Muenchen, Germany
25 -
Universitats-Sternwarte, Scheinerstrasse 1, 81679 Muenchen, Germany
Received 29 July 2008 / Accepted 11 September 2008
Abstract
Measuring the build-up of stellar mass is one of the main
objectives of studies of galaxy evolution. Traditionally, the mass
in stars and the star formation rates have been measured by different
indicators, such as photometric colours, emission lines,
and the UV and IR emission.
We intend to show that it is possible to derive the physical parameters
of galaxies from their broad-band spectral energy distribution
out to a redshift of 1.2. This method has the potential to yield
the physical parameters of all galaxies in a single field in a
homogeneous way, thus overcoming problems with the sample size
that particularly plague methods relying on spectroscopy.
We use an extensive dataset, assembled in the context of the VVDS
survey, which reaches from the UV to the IR and covers a sample of
84 073 galaxies over an area of 0.89 deg2. We also use a library
of 100 000 model galaxies with a wide variety of star formation
histories (in particular including late bursts of star formation).
We find that we can determine the physical parameters stellar mass, age,
and star formation rate with good confidence. We validate the
star formation rate
determination in particular by comparing it to a sample of
spectroscopically observed galaxies with an emission-line measurement.
While the attenuation in the galaxies shows more scatter,
the mean over the sample is unbiased. Metallicity, however, cannot be
measured from rest-frame optical photometry alone. As a first application
we use our sample to build the number density function of galaxies as
a function of stellar mass, specific star formation rate, and redshift.
We are then able to study whether the stellar mass function at a later
time can be predicted from the stellar mass function and star formation
rate distribution at an earlier time. We find that, between redshifts
of 1.02 and 0.47, the predicted growth in stellar mass from star formation
agrees with the observed one. However, the predicted stellar mass density
for massive galaxies is lower than observed, while the mass density of
intermediate mass galaxies is overpredicted. This
apparent discrepancy can be explained by major and minor mergers.
Indeed, when comparing with a direct measurement of the major merger
rate from the VVDS survey, we find that major mergers can account for
about half of the mass build-up at the massive end. Minor
mergers are very likely to contribute the missing fraction.
Key words: surveys - galaxies: evolution - galaxies: photometry - galaxies: general
Traditionally, astronomers have tackled the wide variety in the appearance of galaxies by classification. The one by Hubble (1936) with extensions is still, of course, the one most used for its simplicity. At higher redshifts, classifications have been based on red vs. blue colours (e.g. Lilly et al. 1995; Bell et al. 2004), spectral type (e.g. Tresse et al. 1996), morphological information (e.g. Brinchmann et al. 1998), or principal component analysis of the spectra (e.g. De Lapparent 2003). All these classifications exploit those quantities that are directly observable in the respective surveys. Their relation to the physical properties of galaxies has made them immensely useful for galaxy evolution studies. The colour bimodality and the number density evolution of the different colour classes in particular, have provided a very useful way to study galaxy evolution from large samples. The usefulness of other classifications, such as the classification into four SED-types described and used in Zucca et al. (2006) and Tresse et al. (2007) remains underexplored.
However, it needs to be kept in mind that a classification in terms of observed quantities does not fully represent the fundamental physical differences between galaxies. The colour bimodality, for example, draws its usefulness from the notion that red galaxies are passive; i.e. the observed colour is related to the underlying physical parameter ``recent star formation history'' (SFH). Much work has been done to understand and quantify the contamination from star-forming, but highly extincted, galaxies to the red sequence (e.g. Wolf et al. 2005; Franzetti et al. 2007).
While classification thus has provided a framework and an important tool for galaxy studies, it is clear that galaxies cannot be divided uniquely into well-defined ``species'' as in Linnaean taxonomy (Linné 1735). If anything, it is the underlying continuum of physical properties that allows to measure and understand their evolution. It is also only in terms of this continuum of physical properties that the results from different datasets become comparable.
One of the fundamental physical concepts is the SFH of galaxies.
This is hard to come by in its entirety from archaeological study
alone (see Panter et al. 2007, for a recent attempt on local
galaxies from the Sloan Digital Sky Survey, SDSS). As a first
attempt, the SFH can be parameterized in SFR![]() (star formation rate,
recent SFH) and M* (stellar mass, integrated SFH). The SSFR
(specific star formation rate, SSFR = SFR/M*) is also often
used as an alternative to the
SFR. It represents the ratio of recent and past SFH of a galaxy (see also
Kennicutt et al. 2003, for the b parameter). Indeed, recent studies
have shown that, in the parameter space of log (M*) and log (SSFR),
the blue cloud of the colour bimodality becomes a star-forming sequence
(e.g. Brinchmann et al. 2004; Salim et al. 2004; Zheng et al. 2007;
Feulner et al. 2005; Elbaz et al. 2007; Noeske et al. 2007;
Wyder et al. 2007). Star formation rates for galaxies with low
SFRs have been hard to quantify, as star formation rate indicators,
such as emission lines and infrared (IR) flux, become hard to
measure at low SFRs.
(star formation rate,
recent SFH) and M* (stellar mass, integrated SFH). The SSFR
(specific star formation rate, SSFR = SFR/M*) is also often
used as an alternative to the
SFR. It represents the ratio of recent and past SFH of a galaxy (see also
Kennicutt et al. 2003, for the b parameter). Indeed, recent studies
have shown that, in the parameter space of log (M*) and log (SSFR),
the blue cloud of the colour bimodality becomes a star-forming sequence
(e.g. Brinchmann et al. 2004; Salim et al. 2004; Zheng et al. 2007;
Feulner et al. 2005; Elbaz et al. 2007; Noeske et al. 2007;
Wyder et al. 2007). Star formation rates for galaxies with low
SFRs have been hard to quantify, as star formation rate indicators,
such as emission lines and infrared (IR) flux, become hard to
measure at low SFRs.
This study aims at establishing a method of deriving the physical parameters of galaxies by fitting their rest frame optical spectral energy distributions out to redshift 1.2. This method has two advantages over the complementary approach of measuring each physical parameter by its own tracer: 1) it allows physical properties to be derived in a homogeneous way for all galaxies in a given sample; and 2) the derived parameters are all internally consistent for one specific galaxy. Finally, as the method uses only photometric data points, it has the potential to help in the exploitation of the information from future large photometric surveys.
One of the corner-stones of the present method is the trust that can be put in the stellar population model that predicts the shape of the SED and relates it to the underlying physical properties. Earlier, systematic work has concentrated mostly on galaxies in the local universe (e.g. Brinchmann & Ellis 2000). Salim et al. (2005, 2007) exploited the comprehensive data from the SDSS and the Galex mission to demonstrate that fits of stellar population model SEDs to observed broad-band SEDs do yield results that agree with those from more classical tracers of physical properties, in particular emission lines. Johnson et al. (2007) have used Galex, SDSS and Spitzer data to further test the consistency of the predictions from stellar population models with the observed data, concentrating in particular on the effects of dust. Schawinski et al. (2007) have developed a method for recovering star formation history parameters using broadband photometry from the UV to the near-IR and combine it with information from spectral absorption indices. They show that the combination can help to break degeneracies between the parameters age, mass, dust and metallicity. Burgarella et al. (2005) have combined the Galex and IRAS surveys to build multi-wavelengths, broadband SEDs that are again compared to the predictions of a stellar population model. They particularly show that for a sample selected in the far infrared (FIR), where the galaxies are by definition dominated by dust, the attenuation estimate derived from a fit to the optical data alone can be off by as much as a factor of 100. Finally, Iglesias-Paramo et al. (2007) have extended these studies to a redshift range between 0.2 and 0.7, showing that the results obtained from SED fitting can be used to study the cosmic evolution of star formation rate and dust content. For recent studies exploiting SED fitting at high redshift to obtain stellar masses, we refer to e.g. Maraston et al. (2006), Berta et al. (2008) and references therein.
Throughout the paper we quote AB magnitudes (Oke 1974) and use
a cosmology where H0 = 70 km s-1 Mpc-1,
![]() ,
and
,
and
![]() .
.
We wish to determine the physical parameters, such as M* and SFR (see Table 1), for the galaxies in our sample by fitting observed SEDs with model SEDs from stellar population synthesis models.
We first remind the reader that
the spectral energy distribution (SED) of a stellar
population at time t can be written as
Table 1: Parameter definitions.
In principle Eq. (1) can be solved directly,
see e.g. Panter et al. (2007), Ocvirk et al. (2006),
Walcher et al. (2006) (references can also be found
in Cid-Fernandez 2007).
While this approach avoids prior assumptions on the functional form
of
![]() ,
degeneracies and problems with
the accuracy of the stellar population model are difficult to control.
Another classical approach, that of minimizing
,
degeneracies and problems with
the accuracy of the stellar population model are difficult to control.
Another classical approach, that of minimizing ![]() over a
number of precomputed model SEDs, yields a single best-fit
model star formation history. While in principle
over a
number of precomputed model SEDs, yields a single best-fit
model star formation history. While in principle ![]() statistics
also provide confidence regions, these can be inappropriate for
two reasons in the present case: 1) unsuitable model; and
2) overlooked degeneracies.
statistics
also provide confidence regions, these can be inappropriate for
two reasons in the present case: 1) unsuitable model; and
2) overlooked degeneracies.
We therefore opt here for the method recently adopted by e.g.
Kauffmann et al. (2003), Brinchmann et al. (2004), and Salim et al. (2007).
This is based on a Bayesian understanding of probabilities and was
first proposed in Kauffmann et al. (2003, see Appendix A of that paper for
a rigorous treatment of the method). Put in words, we assume that
| (2) |
The probabilities for each model are then marginalized over
all parameters except the one we want to derive, which yields
a probability distribution function (PDF). The median of this
distribution and its confidence regions are then
used to derive a robust estimate of value and error
for the parameter that is to be determined. Degeneracies
are immediately visible as distorted (non-Gaussian) PDFs
or large confidence regions for a particular parameter.
This method is ``Bayesian'' because we use a pre-computed
library of model galaxies, thus introducing
our prior knowledge (or belief) about the functional form
of
![]() into the finally resulting probability
(see Fig. 1 for our prior assumptions).
It is particularly important to use a suitable prior on
into the finally resulting probability
(see Fig. 1 for our prior assumptions).
It is particularly important to use a suitable prior on
![]() and
and
![]() to avoid systematic biases.
In particular, an artificially narrow distribution of
star formation histories (e.g. excluding secondary bursts)
will affect the results. Obviously this is the case for
the resulting physical property, i.e. if the ``true'' parameter
combination does not exist in the library. However, the
uncertainties are also affected, as these will be
underestimated if a degenerate parameter combination lacks
from the library.
Similar approaches to fit broad-band SEDs have been used with success
in the literature, see e.g. Finlator et al. (2007) and
Blanton & Roweis (2007).
Examples at higher redshifts include Sawicki & Yee (1998) for the
Hubble deep field and Yan et al. (2006) who go out to redshift 6.
to avoid systematic biases.
In particular, an artificially narrow distribution of
star formation histories (e.g. excluding secondary bursts)
will affect the results. Obviously this is the case for
the resulting physical property, i.e. if the ``true'' parameter
combination does not exist in the library. However, the
uncertainties are also affected, as these will be
underestimated if a degenerate parameter combination lacks
from the library.
Similar approaches to fit broad-band SEDs have been used with success
in the literature, see e.g. Finlator et al. (2007) and
Blanton & Roweis (2007).
Examples at higher redshifts include Sawicki & Yee (1998) for the
Hubble deep field and Yan et al. (2006) who go out to redshift 6.
The first step is thus to precompute a large library of 100 000 stochastic representations of star formation histories (SFHs), with varying parameters describing the underlying SFH, dust attenuation, metallicity, and the strength and number of bursts. Secondary bursts can be produced by a number of mechanisms: accretion and cooling of gas (see e.g. Birnboim et al. 2007), close encounters (e.g. Barton et al. 2000) and mergers (e.g. Mihos & Hernquist 1996), infall into clusters (e.g. Marcillac et al. 2007) and more. It is therefore important to allow for such secondary bursts in the library of pre-computed SFHs. Note that our SFHs are parameterized functions and are not based on explicit, self-consistent modelling of galaxy evolution. Each one of these SFHs corresponds to a fictitious ``model galaxy'', which is the term we will use throughout this paper. Photometric properties of each model galaxy are readily derived from (red-shifted) model spectra by convolving with instrumental filter response functions.
Our ultimate goal is to derive the galaxies' physical properties
to understand their evolution. When constructing our
library of star formation histories, we therefore also compute
such parameters, which are not input parameters to the
computation of the library. Figure 1 shows the
prior distributions of the input parameters formation time,
time of the last burst, metallicity, exponent factors for the
underlying SFH (
![]() ,
where t is
in Gyr) and attenuation
,
where t is
in Gyr) and attenuation ![]()
![]() (
(
![]() ,
and
,
and ![]() is the effective wavelength of the V-band), as well as
the prior distribution of the derived parameters mean
mass-weighted age, mean light-weighted age (r-band),
star formation rate in the mean over the last 100 Myr and stellar mass.
See also Eq. (1) and Table 1
for definitions of the parameters.
It is important to realise that the prior
on the library changes with redshift, as model galaxies that
have ages older than the universe at any given redshift need
to be excluded from the fitting. A library therefore needs to
be carefully constructed, so the prior changes relatively little
with redshift. In Fig. 1 we show the prior
at the two redshifts that bracket our study.
is the effective wavelength of the V-band), as well as
the prior distribution of the derived parameters mean
mass-weighted age, mean light-weighted age (r-band),
star formation rate in the mean over the last 100 Myr and stellar mass.
See also Eq. (1) and Table 1
for definitions of the parameters.
It is important to realise that the prior
on the library changes with redshift, as model galaxies that
have ages older than the universe at any given redshift need
to be excluded from the fitting. A library therefore needs to
be carefully constructed, so the prior changes relatively little
with redshift. In Fig. 1 we show the prior
at the two redshifts that bracket our study.
![\begin{figure}
\par\mbox{\resizebox{8.8cm}{!}{\includegraphics[]{0704f1a.ps}}\resizebox{8.8cm}{!}{\includegraphics[]{0704f1b.ps}} }\end{figure}](/articles/aa/full/2008/45/aa10704-08/Timg43.gif) |
Figure 1:
Prior distribution of parameters in the
library of stochastic star formation histories we are using.
These are from bottom to top and from left to right: the mean
r-band weighted age
|
| Open with DEXTER | |
We use a preliminary version of the stellar population model described in
detail in Charlot & Bruzual (2007, CB07).
Although the reader is referred to this paper for details,
we state some important points.
1) The model covers the full wavelength range from 900 Å to
10 ![]() m in stellar light emission for a wide range of age between 0.1 Myr
and 20 Gyr and for metallicities between a fifth and twice solar.
This wide coverage
of parameter space is highly desirable for coping with the large dataset
over a large redshift interval that we intend to study.
2) As shown by Maraston (2005, M05) and Maraston et al. (2006),
it is important to correctly treat the emission from the stars that
are in the thermally-pulsing asymptotic giant branch (TP-AGB) phase
of stellar evolution. TP-AGB stars are especially important at a
redshift of 1, where many galaxy spectra are dominated by emission
from these intermediate age stars. The
CB07 models include an updated treatment of this evolutionary phase
from the models of Marigo & Girardi (2007). This also is the main
improvement in our context over the Bruzual & Charlot
(2003, BC03) model. 3) The initial mass function (IMF) is an adjustable parameter of
the model and we
follow BC03 in choosing a Chabrier (2003b) IMF. The spectral
properties obtained using the above IMF are similar to those obtained
using the Kroupa (2001) IMF. We adopt the Chabrier
IMF because it is physically motivated and provides a better fit
to counts of low-mass stars and brown dwarfs in the Galactic disc
(Chabrier 2001, 2002, 2003a).
m in stellar light emission for a wide range of age between 0.1 Myr
and 20 Gyr and for metallicities between a fifth and twice solar.
This wide coverage
of parameter space is highly desirable for coping with the large dataset
over a large redshift interval that we intend to study.
2) As shown by Maraston (2005, M05) and Maraston et al. (2006),
it is important to correctly treat the emission from the stars that
are in the thermally-pulsing asymptotic giant branch (TP-AGB) phase
of stellar evolution. TP-AGB stars are especially important at a
redshift of 1, where many galaxy spectra are dominated by emission
from these intermediate age stars. The
CB07 models include an updated treatment of this evolutionary phase
from the models of Marigo & Girardi (2007). This also is the main
improvement in our context over the Bruzual & Charlot
(2003, BC03) model. 3) The initial mass function (IMF) is an adjustable parameter of
the model and we
follow BC03 in choosing a Chabrier (2003b) IMF. The spectral
properties obtained using the above IMF are similar to those obtained
using the Kroupa (2001) IMF. We adopt the Chabrier
IMF because it is physically motivated and provides a better fit
to counts of low-mass stars and brown dwarfs in the Galactic disc
(Chabrier 2001, 2002, 2003a).
Before applying the method to real data it is necessary to check
for its internal consistency, as well as intrinsic degeneracies, in
particular because we are applying it to objects with varying
redshifts. To this end we carried out a set of simulations in
which we attempted to recover the known properties of our
galaxies from artificially downgraded SEDs. We first produce
a representation of each model SED with added noise,
by assuming a signal-to-noise (S/N) ratio and Gaussian errors,
which we call a ``pseudo-galaxy''. This procedure thus concentrates
on the effect of measurement errors. We then
fit every pseudo-galaxy with the original model catalogue,
excluding the model galaxy that was used to generate this
particular pseudo-galaxy.
The pseudo-galaxy SEDs are produced over the same photometric bands
that will be used later on real data, i.e. NUV,
B, V, R, I, u*,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
J, K,
3.6
,
J, K,
3.6 ![]() m, 4.5
m, 4.5 ![]() m (see below, Sect. 3).
m (see below, Sect. 3).
![\begin{figure}
\par\includegraphics[width=9cm]{0704f2a.ps}\\
\includegraphics[width=9cm]{0704f2b.ps}\\
\includegraphics[width=9cm]{0704f2c.ps}
\end{figure}](/articles/aa/full/2008/45/aa10704-08/Timg50.gif) |
Figure 2:
Results of fits to noised ``pseudo-galaxies'' produced
from the library of star formation histories. The plots show the fitted
parameters vs. those in the original library over a range in redshift.
Note that stellar mass M* and mean age |
| Open with DEXTER | |
We do not attempt here to show the effects of varying observing
conditions or varying data coverage. We concentrate only on
the limitations that are intrinsic to the method, even
for a perfect model and 14 photometric bands. The simulation results
obtained for a constant S/N of 10 in all bands at the two ends of
our redshift range are shown in Fig. 2. The mean and
scatter of the distributions are given in Table 2.
In the case of the parameter age of the beginning of star formation
![]() ,
the distribution of original versus fitted
properties shows a general point: this parameter is not
a well-defined quantity in terms of a measurement, it is an
input model parameter
,
the distribution of original versus fitted
properties shows a general point: this parameter is not
a well-defined quantity in terms of a measurement, it is an
input model parameter![]() . This is why the mean light-weighted
age
. This is why the mean light-weighted
age ![]() age
age![]() is usually introduced to measure
the ``age'' of a galaxy. For
is usually introduced to measure
the ``age'' of a galaxy. For ![]() age
age![]() and stellar
mass M*, our method is known to be robust, as is confirmed by the
results shown in Fig. 2. This has been exploited in several
papers, some examples have been listed in the introduction.
While the SSFR is also generally
well-constrained, there is a minimal SSFR threshold at
SSFR
and stellar
mass M*, our method is known to be robust, as is confirmed by the
results shown in Fig. 2. This has been exploited in several
papers, some examples have been listed in the introduction.
While the SSFR is also generally
well-constrained, there is a minimal SSFR threshold at
SSFR ![]() 10-12, under which the fitted SSFR shows a plateau.
This is due to the fact that the SSFR is mainly determined by the
UV-optical colours. However, these colours do not change very much
with SSFR anymore when the SSFR sinks below this threshold value.
This limit is due to a physical property of the SEDs and depends
only very weakly on the assumed S/N ratio.
Note that all age-related properties, i.e. M*,
10-12, under which the fitted SSFR shows a plateau.
This is due to the fact that the SSFR is mainly determined by the
UV-optical colours. However, these colours do not change very much
with SSFR anymore when the SSFR sinks below this threshold value.
This limit is due to a physical property of the SEDs and depends
only very weakly on the assumed S/N ratio.
Note that all age-related properties, i.e. M*, ![]() age
age![]() ,
SFR and
,
SFR and
![]() show a smaller scatter at higher redshift.
This is due to the fact that the age of the universe is smaller,
thus limiting the possible diversity in SFHs. This in turn reduces
degeneracies.
While metallicity and attenuation parameter show large scatter,
it is noteworthy that they are not biased. Thus, for a large
sample, mean values can be considered representative.
show a smaller scatter at higher redshift.
This is due to the fact that the age of the universe is smaller,
thus limiting the possible diversity in SFHs. This in turn reduces
degeneracies.
While metallicity and attenuation parameter show large scatter,
it is noteworthy that they are not biased. Thus, for a large
sample, mean values can be considered representative.
It is noteworthy that the biases and uncertainties on the fitted parameters do not change significantly over our redshift range. There is some reduction in scatter, that is mostly due to the exclusion of models that are older than the age of the universe. Thus, the total possible age range of a galaxy at redshift 1.2 is less than half of what it is a z=0.1, which in turn reduces degeneracies between different SFHs.
In the remainder of this paper, we concentrate on the properties
stellar mass M*, star formation rate in the mean over the
last 100 Myr SFR and attenuation parameter ![]() .
First, these
allow the SFH of galaxies to be reconstructed
and second the simulations just presented show that at least
in principle useful measurements should be obtainable for these.
.
First, these
allow the SFH of galaxies to be reconstructed
and second the simulations just presented show that at least
in principle useful measurements should be obtainable for these.
We now apply the SED-fitting method to a large, multi-wavelength dataset. Our extensive data were combined from a number of different surveys that provide multi-wavelength observations over the VVDS-F02 field of view as described below.
Our primary starting point are the data from the F02 field of the
VIMOS/VLT deep survey (VVDS), centred on RA = 2
![]() 26
26
![]() and
Dec = -04
and
Dec = -04
![]() 30
30
![]() over an area of
over an area of ![]() deg2.
This provides us with deep photometry from the CFHT/CFH12K camera
in the B, V, R, and I bands with
limiting magnitudes of 26.5, 26.2, 25.9, and 25.0, respectively
(McCracken et al. 2003; Le Fèvre et al. 2004, http://cencosw.oamp.fr/).
Additionally, deep NIR imaging down to limits of
deg2.
This provides us with deep photometry from the CFHT/CFH12K camera
in the B, V, R, and I bands with
limiting magnitudes of 26.5, 26.2, 25.9, and 25.0, respectively
(McCracken et al. 2003; Le Fèvre et al. 2004, http://cencosw.oamp.fr/).
Additionally, deep NIR imaging down to limits of
![]() and
and
![]() is available for part of the sample (160 arcmin2,
Iovino et al. 2005). We also use the photometry from the
Canada-France-Hawaii Telescope Legacy Survey (CFHTLS,
http://www.cfht.hawaii.edu/Science/CFHTLS) field D1 over an
area of 1 deg2, in the version of the data release T0003.
The data processing of the CFHTLS ``deep fields'' will be
described in McCracken et al. (2008, in preparation). All
objects in this sample have u*,
is available for part of the sample (160 arcmin2,
Iovino et al. 2005). We also use the photometry from the
Canada-France-Hawaii Telescope Legacy Survey (CFHTLS,
http://www.cfht.hawaii.edu/Science/CFHTLS) field D1 over an
area of 1 deg2, in the version of the data release T0003.
The data processing of the CFHTLS ``deep fields'' will be
described in McCracken et al. (2008, in preparation). All
objects in this sample have u*,
![]() ,
,
![]() ,
,
![]() ,
,
![]() photometry down to limiting magnitudes
of 26.5, 26.4, 26.1, 25.9, and 25.0, respectively.
photometry down to limiting magnitudes
of 26.5, 26.4, 26.1, 25.9, and 25.0, respectively.
We use the VVDS spectroscopic data acquired with the
VIsible Multi-Object Spectrograph (VIMOS, Le Fèvre et al. 2003)
installed at the ESO-VLT. These spectra give us spectroscopic
redshifts for 8981 galaxies over ![]() 0.5 deg2
between
0.5 deg2
between
![]() and
and
![]() (Le Fèvre et al. 2005).
Four redshift classes have been established to represent the quality
of each spectroscopic redshift measurement, corresponding to confidence
levels of
(Le Fèvre et al. 2005).
Four redshift classes have been established to represent the quality
of each spectroscopic redshift measurement, corresponding to confidence
levels of ![]() 55% (class 1),
55% (class 1),
![]() 81% (class 2),
81% (class 2), ![]() 97%
(class 3), and
97%
(class 3), and ![]() 99% (class 4)
(Le Fèvre et al. 2005). The success in measuring redshifts
depends somewhat on the spectral features that can be measured (see
Ilbert et al. 2005, for a detailed analysis).
For a more detailed description of the spectra themselves, see
Sect. 3.2.
99% (class 4)
(Le Fèvre et al. 2005). The success in measuring redshifts
depends somewhat on the spectral features that can be measured (see
Ilbert et al. 2005, for a detailed analysis).
For a more detailed description of the spectra themselves, see
Sect. 3.2.
The F02 field was observed as part of the GALEX (Martin et al.
2005) Deep Imaging Survey in two channels (FUV 1530 Å and
NUV 2310 Å). We restrict the analysis to the central 1![]() diameter region of the GALEX field of view, which provides higher
uniformity (Morrissey et al. 2005). In this region, number counts
are 80% complete at 24.5 (AB system) in the FUV and NUV bands
(Xu et al. 2005). The typical point-spread function (PSF) has
a FWHM of 5
diameter region of the GALEX field of view, which provides higher
uniformity (Morrissey et al. 2005). In this region, number counts
are 80% complete at 24.5 (AB system) in the FUV and NUV bands
(Xu et al. 2005). The typical point-spread function (PSF) has
a FWHM of 5
![]() .
Because of the high source density and
relatively large PSF in these images, many sources cannot be
deblended by source extraction algorithms. After a simple match between
the CFHTLS optical catalogue and the GALEX photometry as derived
from the pipeline, 45% of the UV objects have a double optical
identification. In the case of the distant universe and for
deep Galex pointings, simple associations with the closest or
brightest optical counterpart are thus clearly susceptible to
high uncertainties.
.
Because of the high source density and
relatively large PSF in these images, many sources cannot be
deblended by source extraction algorithms. After a simple match between
the CFHTLS optical catalogue and the GALEX photometry as derived
from the pipeline, 45% of the UV objects have a double optical
identification. In the case of the distant universe and for
deep Galex pointings, simple associations with the closest or
brightest optical counterpart are thus clearly susceptible to
high uncertainties.
Table 2: Simulation results: mean offset, rms scatter.
We therefore use a
new approach to derive the photometry catalogues. Prior locations
of potential UV emitters are determined from the optical sources
in the field (objects with u<26.5). Then each prior point source
is convolved with the GALEX PSF. The flux in one pixel of the
GALEX image is considered to be the sum of the contributions of
all the priors and a mean background. This parametric model is
optimal in the Poisson-noise regime. Individual fluxes are then
assigned to each prior through a Maximum likelihood estimation.
The method will be described in full detail in a forthcoming paper
(Arnouts et al., in prep; see also Martin et al. 2007b).
The reliability limit of the method has been
estimated to be at a magnitude of 25.5. Those objects visible
in the optical that are not detected in the NUV are
assigned zero flux and a conservative error estimate of 0.23 ![]() Jy.
Jy.
The F02 field has also been observed as the XMM-LSS field of the
Spitzer Wide-area InfraRed Extragalactic
survey (SWIRE, Lonsdale et al. 2003), a large programme completed
during the first year of the Spitzer Space Observatory.
Infrared photometry in the IRAC 3.6, 4.5, 5.8 and 8.0 ![]() m
is thus available. We use the source catalogue
as released by the SWIRE team
(http://swire.ipac.caltech.edu/swire/swire.html),
with detection limits at 5
m
is thus available. We use the source catalogue
as released by the SWIRE team
(http://swire.ipac.caltech.edu/swire/swire.html),
with detection limits at 5![]() of 5.0, 9.0, 43.0, 40.0
of 5.0, 9.0, 43.0, 40.0 ![]() Jy,
respectively.
Throughout the following we use the fluxes through the SWIRE aperture 2,
i.e. with radius of 1
Jy,
respectively.
Throughout the following we use the fluxes through the SWIRE aperture 2,
i.e. with radius of 1
![]() 9, as recommended by the data release paper.
9, as recommended by the data release paper.
Matching between all catalogues but the new UV catalogue is
done inside the VVDS database CENCOS (LeBrun et al. 2008,
in prep., http://cencosw.oamp.fr/). Matching is performed
according to spatial distance
alone; the match radii have been optimized according to the
spatial resolution of the data and are 0.5
![]() between
CFHTLS and VVDS photometry and 1
between
CFHTLS and VVDS photometry and 1
![]() between VVDS and
Swire photometry. The new NUV photometry being based on direct
redistribution of flux according to optical priors from the
CFHTLS data, matching is easily done by reference to the ID
of the optical prior.
between VVDS and
Swire photometry. The new NUV photometry being based on direct
redistribution of flux according to optical priors from the
CFHTLS data, matching is easily done by reference to the ID
of the optical prior.
A combined multi-wavelength catalogue from the same field and
based on the same data has already been used to measure the
stellar mass density evolution based on a sample selected
in the SWIRE 3.6 ![]() m band (Arnouts et al. 2007).
m band (Arnouts et al. 2007).
The VVDS observing programme was designed to obtain spectroscopic redshifts
for galaxies between
![]() and
and
![]() (see Le Fèvre et al. 2005). The spectra have a resolution of R = 227 and typical
signal-to-noise of 5 (see Fig. 5 of Le Fèvre et al. 2005), thus
optimizing the number of objects observed. The observed wavelength
range goes from 5500 to 9500 Å. However, fringing and sky lines
can considerably impair the spectra redwards of 8000 Å.
(see Le Fèvre et al. 2005). The spectra have a resolution of R = 227 and typical
signal-to-noise of 5 (see Fig. 5 of Le Fèvre et al. 2005), thus
optimizing the number of objects observed. The observed wavelength
range goes from 5500 to 9500 Å. However, fringing and sky lines
can considerably impair the spectra redwards of 8000 Å.
Albeit not comparable in quality to the spectra of the Sloan
Digital Sky Survey (SDSS), such spectra from a survey of much
higher redshift galaxies also contain information that can
be extracted. First, for galaxies with emission lines, one
can reliably identify
Seyfert 1 nuclei (Gavignaud et al. 2006), which are excluded
from the present sample. Second, the VVDS team has adapted the
platefit programme designed for the SDSS (Tremonti et al.
2004) to the lower resolution VVDS spectra (Lamareille et al.
2008). This software yields continuum subtracted emission line
fluxes. For this paper we are
in particular interested in the H![]() line (for objects
between redshift of 0.0 and 0.44) and
the [OII] line
(for objects between redshift of 0.48 and 1.2).
On average, the errors on the detected lines are 20% and 30% for
[OII] and H
line (for objects
between redshift of 0.0 and 0.44) and
the [OII] line
(for objects between redshift of 0.48 and 1.2).
On average, the errors on the detected lines are 20% and 30% for
[OII] and H![]() ,
respectively. We here
only use these emission line measurements as a check on the
reliability of the SED fitting. A detailed study of the
physical properties of VVDS galaxies from their emission lines
will be undertaken in Vergani et al. (2008, in prep.).
,
respectively. We here
only use these emission line measurements as a check on the
reliability of the SED fitting. A detailed study of the
physical properties of VVDS galaxies from their emission lines
will be undertaken in Vergani et al. (2008, in prep.).
An important issue when comparing spectral and photometric information is the effect of a mismatch between the aperture used to extract the photometry and the spectra. However, this effect is less severe in the VVDS than in lower redshift surveys for two reasons. 1) The VVDS is based on long-slit spectra and extraction apertures are optimized to contain all the visible flux along the slit. For this reason alone, aperture biases are much smaller than for fiber-based spectral extraction. 2) Most of the galaxies are small on the sky due to their distance.
Correction factors (in the following called ``normalization'')
for the VVDS were derived by synthesizing photometry from
the spectra using the instrumental response functions of the
instrument. These aperture normalizations are released to the
public together with the spectra. In the VVDS R band we find
a median normalization factor over the full sample of
![]() with an rms of 0.5.
This normalization factor is almost independent
of the redshift and size of the object on the sky. The largest
contributors to the scatter in this factor are the different
observing conditions, as the survey spectra were assembled
over an extended period of time. The physical properties of a
galaxy change with radius. Therefore the stellar populations
probed by a photometry that includes all light from a galaxy
and those populations probed by a spectrum that was taken over
only a fraction of the light from the same galaxy can in
principle be biased. As we find no dependence of the normalization
factor on either size of the galaxy or its
colour, we made no further attempt to correct for such issues.
with an rms of 0.5.
This normalization factor is almost independent
of the redshift and size of the object on the sky. The largest
contributors to the scatter in this factor are the different
observing conditions, as the survey spectra were assembled
over an extended period of time. The physical properties of a
galaxy change with radius. Therefore the stellar populations
probed by a photometry that includes all light from a galaxy
and those populations probed by a spectrum that was taken over
only a fraction of the light from the same galaxy can in
principle be biased. As we find no dependence of the normalization
factor on either size of the galaxy or its
colour, we made no further attempt to correct for such issues.
We define two subsamples of objects for different purposes. Our first sample, which we call the ``photometric sample'' is designed to be as complete as possible, providing a comprehensive view of galaxy properties over the age of the universe. The second sample, which we call the ``spectroscopic sample'', is designed to provide us with secure spectroscopic data, in order to test the validity of our approach.
The ``photometric sample'' comprises all objects that have
been detected at
![]() in the VVDS
data over the
area covered by the F02 field. At this flux limit, the VVDS
and CFHTLS data are complete. For all of these objects we
have spectroscopically calibrated photometric redshifts
from Ilbert et al. (2006) with an accuracy of
in the VVDS
data over the
area covered by the F02 field. At this flux limit, the VVDS
and CFHTLS data are complete. For all of these objects we
have spectroscopically calibrated photometric redshifts
from Ilbert et al. (2006) with an accuracy of
![]() for objects brighter than
for objects brighter than
![]() .
We cut this sample at a redshift
of 1.2. The reddest band regularly available for all
galaxies, the CFHTLS
.
We cut this sample at a redshift
of 1.2. The reddest band regularly available for all
galaxies, the CFHTLS
![]() band, corresponds to
roughly 4000 Å at this redshift. Redwards of this
wavelength, the SED is dominated by stars from the
main-sequence turnoff, thus allowing the mean age of a
galaxy to be effectively probed. Bluewards of 4000 Å, the
SED starts to be dominated by stars that emit strongly
in the UV, i.e. O and B stars, which are in turn only associated
with the recent star formation. At redshifts higher
than 1.2 we would thus enter a totally different
regime, where the SED is constrained by restframe UV
information only (see e.g. Law et al. 2007) and where
the SED does not provide a reliable measure of the
mean age or stellar mass of a galaxy. If NIR photometric
data are available for an entire sample, there is no
other obstacle to prevent the extension of the
present methods to higher redshifts.
band, corresponds to
roughly 4000 Å at this redshift. Redwards of this
wavelength, the SED is dominated by stars from the
main-sequence turnoff, thus allowing the mean age of a
galaxy to be effectively probed. Bluewards of 4000 Å, the
SED starts to be dominated by stars that emit strongly
in the UV, i.e. O and B stars, which are in turn only associated
with the recent star formation. At redshifts higher
than 1.2 we would thus enter a totally different
regime, where the SED is constrained by restframe UV
information only (see e.g. Law et al. 2007) and where
the SED does not provide a reliable measure of the
mean age or stellar mass of a galaxy. If NIR photometric
data are available for an entire sample, there is no
other obstacle to prevent the extension of the
present methods to higher redshifts.
Our photometric sample contains 84 073 galaxies.
All of them have B, V, R, I, u*,
![]() ,
,
![]() ,
,
![]() ,
,
![]() photometry;
39% are detected in the NUV, 5% in J, 17% in K, 29% in the IRAC 3.6 and
4.5
photometry;
39% are detected in the NUV, 5% in J, 17% in K, 29% in the IRAC 3.6 and
4.5 ![]() m bands
simultaneously. Eight hundred twenty-five
objects are detected in all bands
from NUV to 4.5
m bands
simultaneously. Eight hundred twenty-five
objects are detected in all bands
from NUV to 4.5 ![]() m.
Our total photometric catalogue is built on the available
photometry in the observed optical wavelength. The total
area covered by the combined photometric catalogue is thus
the cross-section between the CFHTLS D1
photometry and the VVDS photometry, i.e. 0.89 deg2.
m.
Our total photometric catalogue is built on the available
photometry in the observed optical wavelength. The total
area covered by the combined photometric catalogue is thus
the cross-section between the CFHTLS D1
photometry and the VVDS photometry, i.e. 0.89 deg2.
For the ``spectroscopic sample'' our goal is to assess how feasible it is to recover physical parameters for galaxies from population synthesis models. Starting from the photometric sample, we therefore restrict ourselves to objects with spectra and with VVDS redshift classes with a confidence level greater than or equal to 81% (classes 2, 3 and 4). This is a compromise between our wishes to avoid overly biasing ourselves to galaxies with spectral features that make redshift measurements more secure and to avoid fitting galaxies under completely wrong assumptions.
After matching and excluding galaxies with redshifts
higher than 1.2, we have a total sample of 5753 galaxies
in the spectroscopic sample.
Out of these, all have by definition observed optical
photometry in the B, V, R, I, u*,
![]() ,
,
![]() ,
,
![]() ,
,
![]() bands, as well as spectra in the
observed optical wavelength region. Additionally, 67%
are detected in the NUV, while an additional 17% have
upper flux limits. Twelve percent and 48% are detected
in J and K,
respectively. Finally, while 45% are detected in the
IRAC 3.6 and 4.5
bands, as well as spectra in the
observed optical wavelength region. Additionally, 67%
are detected in the NUV, while an additional 17% have
upper flux limits. Twelve percent and 48% are detected
in J and K,
respectively. Finally, while 45% are detected in the
IRAC 3.6 and 4.5 ![]() m simultaneously, only 3% are also
detected in the 8.0
m simultaneously, only 3% are also
detected in the 8.0 ![]() m band due to the shallower
detection limit. Out of our total 5753 objects, 212 are
detected in all bands from the NUV to 4.5
m band due to the shallower
detection limit. Out of our total 5753 objects, 212 are
detected in all bands from the NUV to 4.5 ![]() m.
Additionally, as described in Sect. 3.2,
information on emission lines properties is available
for all objects from their spectra.
For reference, the redshift distributions of our two
samples are shown in Fig. 3.
m.
Additionally, as described in Sect. 3.2,
information on emission lines properties is available
for all objects from their spectra.
For reference, the redshift distributions of our two
samples are shown in Fig. 3.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[width=1\hsize]{0704f3.ps}}
\end{figure}](/articles/aa/full/2008/45/aa10704-08/Timg71.gif) |
Figure 3: Redshift distribution of the 5753 galaxies in the ``spectroscopic sample'' (dashed line), i.e. with secure spectroscopic redshifts, and of the 84 073 galaxies in the ``photometric sample'' (full line), i.e. with high quality photometric redshifts. |
| Open with DEXTER | |
We now describe the results of applying the method described in Sect. 2.1 to the data as described in Sect. 3 using the model library as described in Sect. 2.1.
We first checked, whether the observed and the model galaxies are similar in their photometric properties. We find that, in general, the range of observed and modelled colours do cover the same loci in parameter space. This confirms that the stellar population model is a good representation of real galaxies over all the redshifts probed in this paper. Furthermore, as the density distribution of observed and model galaxies in each region of parameter space is similar, we also have some reality check on the assumptions that went into our prior distribution, as presented in Sect. 2.1.
In Fig. 4 we show one of our checks. As can be seen from the figure, the loci of data (photometric sample) and model library colours move with redshift. This is to be expected, as the rest frame wavelength region observed through a particular filter depends on redshift. For most redshifts, the locus of data and model galaxies overlap. However, for one specific redshift, i.e. for a redshift of 0.7, the contours indicating the locus of the model library move differently from the locus of the data - f or the colour combination we show here. A very similar effect is also seen in data accumulated for use in the DEEP2 survey (Salim, private communication). At redshift 0.7, the models are bluer than the data in g-r, and redder than the data in r-i. This shift of approximately 0.5 mag in the r-band is mostly observed for blue (young) galaxies. It can be explained if there is a restframe wavelength region in which the flux is underpredicted by the stellar population model.
The observed r-band ranges from 5600 to 6900 Å, approximately. This samples a rest frame wavelength region between 3300 and 4050 Å at a redshift of 0.7. It has been shown (Wild et al. 2007) that the BC03 models overpredict the strength of the Balmer break for young galaxies. As there has been little change in this wavelength region in the preliminary version of CB07 we are using, we assume that this is just another manifestation of the same model limitation. For each object we therefore exclude the filters that draw more than 5% of the total light from the so-defined restframe wavelength region from any later analysis. We have verified that excluding those photometric bands from the fit avoids a bias in the results towards younger ages and higher SFRs.
We also exclude the bands measuring flux at wavelengths longer
than 4 ![]() m due to possible contamination from hot dust or
PAH emission. The bands used for the
fitting at each redshift are summarised in Table 3.
m due to possible contamination from hot dust or
PAH emission. The bands used for the
fitting at each redshift are summarised in Table 3.
![\begin{figure}
\par\resizebox{18cm}{!}{\includegraphics[width=1\hsize]{0704f4.ps}}
\end{figure}](/articles/aa/full/2008/45/aa10704-08/Timg72.gif) |
Figure 4: Overlap between the loci in colour-colour space of data and models. The observed data are in grey shading, while model galaxies are shown as solid contours. In general the overlap between the loci covered by the observation and the model library is good. However, this plot suggests that the spectral region between restframe wavelengths 3300 to 4050 Å is not correctly reproduced by this preliminary version of the CB07 stellar population model. We have verified that similar problems do not occur at other wavelengths. |
| Open with DEXTER | |
Table 3: Bands used in the fitting.
To apply the Bayesian method, we calculated
![]() for every combination of object and model galaxy
in our two samples and in the library. As
for every combination of object and model galaxy
in our two samples and in the library. As ![]() is a
measure of the ``goodness-of-fit'', we can also use the
minimum
is a
measure of the ``goodness-of-fit'', we can also use the
minimum ![]() we find for each object to gauge
the applicability of our model to our data.
we find for each object to gauge
the applicability of our model to our data.
From the fit results on the photometric sample, we find
that, in general, the model can be said to reproduce the
available data fairly. The median reduced
![]() is 1.35, while the mean is 4.4, excluding outliers that
have
is 1.35, while the mean is 4.4, excluding outliers that
have
![]() (see Fig. 5).
We explicitly note here that the distribution in
(see Fig. 5).
We explicitly note here that the distribution in
![]() would be somewhat tighter if we had multiplied all error values
by a constant factor as done e.g. in Ilbert et al. (2006)
and Iovino et al. (2005). Out of our photometric sample
of 84073 galaxies, 0.4%, 2.0% and 7% have
would be somewhat tighter if we had multiplied all error values
by a constant factor as done e.g. in Ilbert et al. (2006)
and Iovino et al. (2005). Out of our photometric sample
of 84073 galaxies, 0.4%, 2.0% and 7% have
![]() larger than 500, 100 and 20, respectively. A browse through
such poorly fit objects shows that outliers can be caused
by a combination of two effects.
1) While for such a large survey, uniform procedures of
data reduction and matching are clearly necessary, there
are always objects where such standard procedures
fail (e.g. extended objects, catalogue mismatches, blended
targets, Sey2 AGN, and unusual targets)
2) Due to the high quality and wide wavelength coverage of
the data we use, the model reaches its limits.
larger than 500, 100 and 20, respectively. A browse through
such poorly fit objects shows that outliers can be caused
by a combination of two effects.
1) While for such a large survey, uniform procedures of
data reduction and matching are clearly necessary, there
are always objects where such standard procedures
fail (e.g. extended objects, catalogue mismatches, blended
targets, Sey2 AGN, and unusual targets)
2) Due to the high quality and wide wavelength coverage of
the data we use, the model reaches its limits.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[width=1.0\hsize]{0704f5.ps}}
\end{figure}](/articles/aa/full/2008/45/aa10704-08/Timg75.gif) |
Figure 5:
Cumulative distribution of reduced |
| Open with DEXTER | |
Example fits to the photometry are shown in Fig. 6
for two objects that are detected in all bands from the NUV to 8 ![]() m.
m.
Stellar masses for the VVDS spectroscopic sample have been derived by Pozzetti et al. (2007, P07) by an SED-fitting technique essentially identical to ours. In particular these authors have tested the influence of the prior distribution of SFHs on the derived stellar masses. It is of interest to verify that the stellar masses derived in the present paper are compatible with those of P07. To that end we determined the physical properties of the galaxies not only with the CB07 models, but also with the BC03 ones, as these were used in P07. Otherwise our setup was left unchanged. We used the masses from P07 that were determined from models allowing for secondary bursts. We find that our results agree with those of P07 to within 10%, as expected.
Without independent kinematic data, there is no direct way to assess how correct in an absolute sense the stellar masses are that we determine. Di Serego Alighieri et al. (2005) find, however, that the Chabrier (2003b) IMF we use results in masses consistent with the dynamical ones. An in-depth comparison of the effects of using different stellar population models (BC03 and M05) on the determined stellar masses can be found in Van der Wel et al. (2006). These authors use dynamically determined masses as a benchmark. They find that BC03 and M05 models bracket the mass value determined dynamically, with offsets of the order of a factor 2. Also, the use of complex SFHs, as done in the models used here, can significantly improve the correctness of the resulting stellar masses. As the contribution of the TP-AGB stars to the total infrared light in the CB07 model is intermediate between the BC03 and the M05 models, and as we are allowing for secondary bursts in the SFH, we expect our stellar masses to be robust and correct in an absolute sense.
![\begin{figure}
\par\mbox{\resizebox{8.8cm}{!}{\includegraphics[]{0704f6a.ps}}\resizebox{8.8cm}{!}{\includegraphics[]{0704f6b.ps}} }\end{figure}](/articles/aa/full/2008/45/aa10704-08/Timg76.gif) |
Figure 6:
Two example SEDs that were observed and
detected in all bands from the NUV to the 4.5 |
| Open with DEXTER | |
The robustness of stellar mass measurements in a relative sense is
more easily assessed. First, photometric data in the J and
K bands or at 3.5 ![]() m (collectively referred to as near-infrared,
NIR) is available only for a part of our sample. A thorough discussion
of the uncertainties in stellar mass arising from limitations in data
coverage and from the use of different priors can be found in P07.
From our own sample we confirm the finding of P07 that exclusion of
the NIR data leads to an overestimation of the stellar mass at the
high-mass end of the sample. When correlating this bias in the
estimation of M* with other physical parameters, we find that the
strongest correlation is with SSFR. The mean ratios of masses determined
without NIR data to the masses derived with NIR data are 2.8, 1.50,
1.0 for bins of log (SSFR) of [-16, -13], [-13, -10], [-10, -8], respectively.
These correction factors are independent of redshift, within the
uncertainties.
Similarly to P07, we correct for this effect by dividing the masses
of objects that have not been observed in the NIR by these ratios.
This approach relies on the assumption that the objects that
have not been observed in the NIR have the same properties as those
that have been observed.
m (collectively referred to as near-infrared,
NIR) is available only for a part of our sample. A thorough discussion
of the uncertainties in stellar mass arising from limitations in data
coverage and from the use of different priors can be found in P07.
From our own sample we confirm the finding of P07 that exclusion of
the NIR data leads to an overestimation of the stellar mass at the
high-mass end of the sample. When correlating this bias in the
estimation of M* with other physical parameters, we find that the
strongest correlation is with SSFR. The mean ratios of masses determined
without NIR data to the masses derived with NIR data are 2.8, 1.50,
1.0 for bins of log (SSFR) of [-16, -13], [-13, -10], [-10, -8], respectively.
These correction factors are independent of redshift, within the
uncertainties.
Similarly to P07, we correct for this effect by dividing the masses
of objects that have not been observed in the NIR by these ratios.
This approach relies on the assumption that the objects that
have not been observed in the NIR have the same properties as those
that have been observed.
Finally, we mention that a direct comparison of the new CB07 models to the standard BC03 models shows a rather modest offset in stellar mass. This offset changes with the measured SSFR of the galaxy, in the sense that the masses determined using BC03 for objects with an intermediate SSFR (-12 < log (SSFR) < -9) are in the mean more massive by 50% than those determined using CB07. These are the objects where the TP-AGB stars are most likely to contribute significantly to the light in the NIR bands. Objects with lower or higher SSFRs do not show this offset. Our results agree with the findings of Maraston et al. (2005, 2006), who for the first time showed the significant effect of the TP-AGB phase of stellar evolution on the derived stellar masses.
From the fit results we can show the relation between
SFR and ![]() .
Figure 7 presents
.
Figure 7 presents ![]() as a function of star formation rate in 4 different redshift
bins. The two quantities show a broad relation in all the
4 redshift bins. In our two lowest redshift bins we
sample a comparatively small volume, thus missing rare,
high star formation rate objects (see Ilbert et al. 2005).
On the other
hand, we are sampling brighter galaxies at higher redshift.
That we observe different populations of galaxies
at different cosmic epochs (Tresse et al. 2007)
affects the mean measured attenuation. On the other hand,
the scatter remains large at every epoch, translating the
diversity of galaxy properties.
as a function of star formation rate in 4 different redshift
bins. The two quantities show a broad relation in all the
4 redshift bins. In our two lowest redshift bins we
sample a comparatively small volume, thus missing rare,
high star formation rate objects (see Ilbert et al. 2005).
On the other
hand, we are sampling brighter galaxies at higher redshift.
That we observe different populations of galaxies
at different cosmic epochs (Tresse et al. 2007)
affects the mean measured attenuation. On the other hand,
the scatter remains large at every epoch, translating the
diversity of galaxy properties.
We also plot, for reference, the relation between SFR and ![]() as
inferred from the dependence of the Balmer decrement on star formation
rate found by
Sullivan et al. (2001) in a sample of nearby galaxies.
These authors also explicitly note the large
scatter around the mean relation. For simplicity, we converted
H
as
inferred from the dependence of the Balmer decrement on star formation
rate found by
Sullivan et al. (2001) in a sample of nearby galaxies.
These authors also explicitly note the large
scatter around the mean relation. For simplicity, we converted
H![]() /H
/H![]() into E(B-V) using the formulae described in
Reynolds et al. (1997), which relies on the Osterbrock (1989)
interstellar extinction curve. The necessary conversion does not
depend sensitively on the adopted dust prescription, because of
the small wavelength leverage involved. To convert E(B-V) to
into E(B-V) using the formulae described in
Reynolds et al. (1997), which relies on the Osterbrock (1989)
interstellar extinction curve. The necessary conversion does not
depend sensitively on the adopted dust prescription, because of
the small wavelength leverage involved. To convert E(B-V) to
![]() we additionally assume RV = 3.1 (see e.g. Cardelli
1989). Although our measurement of the attenuation concerns the
stellar continuum, and the Sullivan et al. (2001) measurement is
based on emission lines, the general agreement shown in
Fig. 7 can be
considered to be quite good, in particular in light of the intrinsic
uncertainty on the attenuation parameter as described in
Sect. 2.2.
We additionally plot several literature relations in the lowest
redshift bin: from Hopkins et al. (2001, their Eq. (3)), based on
the Balmer decrement of local starburst galaxies (dot-dashed);
from Buat et al. (2007, dashed line, their Fig. 7), based
on the ratio of the total infrared luminosity over the UV luminosity of a local sample of galaxies bright in the far
infrared and on relations given in Hirashita
et al. (2003); from Choi et al. (2006, dotted line, their
Sect. 5.2.1), who derive their attenuation estimate from a
comparison of the optical SFR to the FIR SFR, again based on
a sample of starburst galaxies. Finally, in the uppermost redshift
bin, we also show the relation we determine from Burgarella
et al. (2007, dashed line, their Fig. 6), again using
Hirashita et al. (2003). While we note that we tend to
measure lower SFRs at the same attenuation values, this is
most probably due to the literature relations
having been derived for samples with a restricted range in SFR.
Indeed, all these last relations are based on samples, where
strongly star-forming galaxies are well represented by selection.
we additionally assume RV = 3.1 (see e.g. Cardelli
1989). Although our measurement of the attenuation concerns the
stellar continuum, and the Sullivan et al. (2001) measurement is
based on emission lines, the general agreement shown in
Fig. 7 can be
considered to be quite good, in particular in light of the intrinsic
uncertainty on the attenuation parameter as described in
Sect. 2.2.
We additionally plot several literature relations in the lowest
redshift bin: from Hopkins et al. (2001, their Eq. (3)), based on
the Balmer decrement of local starburst galaxies (dot-dashed);
from Buat et al. (2007, dashed line, their Fig. 7), based
on the ratio of the total infrared luminosity over the UV luminosity of a local sample of galaxies bright in the far
infrared and on relations given in Hirashita
et al. (2003); from Choi et al. (2006, dotted line, their
Sect. 5.2.1), who derive their attenuation estimate from a
comparison of the optical SFR to the FIR SFR, again based on
a sample of starburst galaxies. Finally, in the uppermost redshift
bin, we also show the relation we determine from Burgarella
et al. (2007, dashed line, their Fig. 6), again using
Hirashita et al. (2003). While we note that we tend to
measure lower SFRs at the same attenuation values, this is
most probably due to the literature relations
having been derived for samples with a restricted range in SFR.
Indeed, all these last relations are based on samples, where
strongly star-forming galaxies are well represented by selection.
Our plot of SFR vs. ![]() is at least
qualitatively similar to Fig. 1 in Calzetti (2007).
Finally, Salim et al. (2007) also find that on the whole
the attenuation as measured
from SED fitting agrees reasonably well with the one determined
from accurate modelling of the emission lines, although the SED
fitting value is less tightly constrained.
is at least
qualitatively similar to Fig. 1 in Calzetti (2007).
Finally, Salim et al. (2007) also find that on the whole
the attenuation as measured
from SED fitting agrees reasonably well with the one determined
from accurate modelling of the emission lines, although the SED
fitting value is less tightly constrained.
In the median over the sample, the attenuation at the wavelength
of H![]() is a factor of 3.
This is consistent with the mean extinction
of the H
is a factor of 3.
This is consistent with the mean extinction
of the H![]() line for local samples of galaxies, which
is very roughly 1 mag (Kennicutt 1998), i.e. a factor of 2.5.
line for local samples of galaxies, which
is very roughly 1 mag (Kennicutt 1998), i.e. a factor of 2.5.
We conclude that, while the extinction measurement on a galaxy by galaxy basis is uncertain, it can be considered to be realistic in the average over the photometric sample. This last statement is consistent with the results from simulations shown in Sect. 2.1.
![\begin{figure}
\par\includegraphics[angle=0,width=17cm]{0704f7.ps}
\end{figure}](/articles/aa/full/2008/45/aa10704-08/Timg78.gif) |
Figure 7:
Relation between SFR and attenuation |
| Open with DEXTER | |
We now use the spectroscopic subsample to check whether
we can trust the SFRs as derived from the photometry.
Here we are interested in the SFRs we
can derive for the galaxies in the spectroscopic
sample from the H![]() and OII emission lines.
The spectra themselves contain more information,
which has been used in Vergani et al. (2007) and
Franzetti et al. (2007). We emphasise that we redetermine
the physical properties of the objects using the redshifts
as determined directly from the spectra for this comparison.
Because we use identical redshifts, our comparison
bears on the physical relation between both
methods to determine SFRs.
and OII emission lines.
The spectra themselves contain more information,
which has been used in Vergani et al. (2007) and
Franzetti et al. (2007). We emphasise that we redetermine
the physical properties of the objects using the redshifts
as determined directly from the spectra for this comparison.
Because we use identical redshifts, our comparison
bears on the physical relation between both
methods to determine SFRs.
SFRs for the spectroscopic sample have been determined
in Vergani et al. (2008, in prep.). In order to obtain the
SFRs from the OII line, these authors use the
calibration presented by Moustakas et al. (2006). This
has the advantage of also utilising the information contained in
the B-band absolute magnitude, thus accounting, at least statistically,
for the effects of dust attenuation and varying metallicity
on the derived SFR. Nevertheless, using this calibration
at higher redshifts assumes that the correlations between
B-band luminosity and attenuation/metallicity do not change
significantly with redshift.
The H![]() SFRs were derived
using the standard Kennicutt (1998) formula.
SFRs were derived
using the standard Kennicutt (1998) formula.
The correlation between the SFR determined in this way and
the SFR determined from the SED fit is shown in Fig. 8 for both emission lines. The total number of
objects in these plots (grey plus signs) is 2776 (for
OII) and 679 (for H![]() ), and 52% (OII)
and 45% (H
), and 52% (OII)
and 45% (H![]() )
of those are considered to be of
high quality (black plus signs), as determined in Vergani
et al. (2008). If we define catastrophic failures as
objects with log (
)
of those are considered to be of
high quality (black plus signs), as determined in Vergani
et al. (2008). If we define catastrophic failures as
objects with log (
![]() /
/
![]() ),
the percentage of such catastrophic failures for the total
sample is 11% and 10% for OII and H
),
the percentage of such catastrophic failures for the total
sample is 11% and 10% for OII and H![]() ,
respectively. Excluding catastrophic failures, we obtain:
the median of log(
,
respectively. Excluding catastrophic failures, we obtain:
the median of log(
![]() /
/
![]() )
is 0.07 and the scatter in log is 0.71. The median of
log (
)
is 0.07 and the scatter in log is 0.71. The median of
log (
![]() /
/
![]() )
is -0.02 and the scatter in log is 0.62.
Thus, both determinations appear to be consistent.
)
is -0.02 and the scatter in log is 0.62.
Thus, both determinations appear to be consistent.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[]{0704f8a.ps}}\\
\resizebox{8.8cm}{!}{\includegraphics[]{0704f8b.ps}}
\end{figure}](/articles/aa/full/2008/45/aa10704-08/Timg84.gif) |
Figure 8:
Relation between SFRs as determined from
the photometry and as determined from the H |
| Open with DEXTER | |
Nevertheless, two important caveats need to be mentioned that should in principle hamper the direct comparison of the two SFR indicators.
First, star formation is episodic (e.g. Glazebrook et al. 1999).
However, the UV light of stellar populations fades more
slowly than the emission line flux, thus the UV gives
the average star formation rate over a longer period of time.
In our case the SFR as derived from the photometry is an average over the
last 100 Myr, while emission lines tend to disappear soon after a
burst on a timescale of 10-20 Myr. Thus, the typical duration of a
star formation burst will influence how well these two measures of
SFR can be intercompared. We can empirically estimate the size of
this effect using the following recipe. In the interest
of higher and less biased statistics, we go back to a sample including
ALL spectra that were measured in the F02 here.
There are in total 8981 spectra in the F02. Out of these, 3758 have
successfully measured emission lines (either [OII] or H![]() );
yet, according to the photometric fit, 7040 have an SFR
above log (SFR) = -0.2
);
yet, according to the photometric fit, 7040 have an SFR
above log (SFR) = -0.2![]() .
At face value, this factor of
.
At face value, this factor of ![]() 2
difference between the number of photometrically star-forming galaxies
and those with detectable emission lines could be accounted for if the
typical duration of a burst is half the time over which the SFR is averaged,
i.e. 50 Myr. Then, the SFRs as measured from the emission lines would
need to be scaled down by a factor 0.5 to yield the same average SFR
as the one used in the SED fit. The true correction is probably smaller
than indicated by this number, as there are a number of other
reasons, why objects might not have a measured emission line. Among
these reasons are faint emission lines, extraction problems,
misalignment of the slit and more.
2
difference between the number of photometrically star-forming galaxies
and those with detectable emission lines could be accounted for if the
typical duration of a burst is half the time over which the SFR is averaged,
i.e. 50 Myr. Then, the SFRs as measured from the emission lines would
need to be scaled down by a factor 0.5 to yield the same average SFR
as the one used in the SED fit. The true correction is probably smaller
than indicated by this number, as there are a number of other
reasons, why objects might not have a measured emission line. Among
these reasons are faint emission lines, extraction problems,
misalignment of the slit and more.
Objects that have only upper limits on the strength of
the emission line are shown as grey symbols in Fig. 8.
The SFR values were obtained by converting the flux value corresponding
to the ![]() detection limit into a SFR.
This verifies that their photometrically determined SFR is
compatible with emission below our detection threshold for
most objects. In the same context,
the scatter in Fig. 8
is dominated by the catastrophic failures that can
be seen as a spur of objects for which the
detection limit into a SFR.
This verifies that their photometrically determined SFR is
compatible with emission below our detection threshold for
most objects. In the same context,
the scatter in Fig. 8
is dominated by the catastrophic failures that can
be seen as a spur of objects for which the
![]() is
much lower than
is
much lower than
![]() .
It is possible that
these catastrophic failures represent objects for which
star formation has just begun and where most of the newly
formed stars are heavily obscured, thus having no impact
on the observed SED (compare Da Cunha et al. 2008).
.
It is possible that
these catastrophic failures represent objects for which
star formation has just begun and where most of the newly
formed stars are heavily obscured, thus having no impact
on the observed SED (compare Da Cunha et al. 2008).
Second, while the sample has been cleaned for Sey1 AGN,
the selection of type 2 AGN from the VVDS spectra is still
in progress and we have not eliminated these objects
from our sample. Locally the fraction of light in the
[OII] and H![]() line emitted by AGN
is 30% and 25% respectively. These values have been computed
from the catalogue of galaxies analysed in Brinchman et al. (2004).
These numbers give a very rough estimate of the possible
contribution that Sey2 AGN would have to the total emission in
the respective emission lines.
line emitted by AGN
is 30% and 25% respectively. These values have been computed
from the catalogue of galaxies analysed in Brinchman et al. (2004).
These numbers give a very rough estimate of the possible
contribution that Sey2 AGN would have to the total emission in
the respective emission lines.
If we applied the derived corrections, the median offset in
log(
![]() /
/
![]() )
in
dex would be changed from -0.02 to -0.47.
We conclude that overall the SFRs as derived from the two completely
independent tracers agree with each other inside the, considerable,
measurement uncertainties. This conclusion has also been reached
in studies of the local universe (Salim et al. 2007; Treyer et al.
2007).
)
in
dex would be changed from -0.02 to -0.47.
We conclude that overall the SFRs as derived from the two completely
independent tracers agree with each other inside the, considerable,
measurement uncertainties. This conclusion has also been reached
in studies of the local universe (Salim et al. 2007; Treyer et al.
2007).
While not presented here, we point forward to Wild et al. (in prep.), in which a direct comparison between the continuum properties of the spectra and the SED fitting properties is undertaken for a subclass of galaxies, the post-starburst galaxies. There we find again that the SED properties are entirely consistent with the completely independent spectral measurement.
In the last section we have derived M* and SFR for a sample of 84 073 galaxies in a redshift interval between 0 and 1.2. This is the first catalogue to hold such information for such many galaxies and for galaxies with star formation rates too low to have detectable emission lines or IR emission. We now proceed to take a first look at the information that this catalogue provides on the evolution of star formation and stellar mass over redshift. More in-depth studies of these issues will be undertaken in the forthcoming papers by Lamareille et al. (2008, in prep.) and Vergani et al. (2008, in prep.). From now on we split our sample into four redshift bins that are approximately equally spaced in cosmic time, i.e. 1.5 Gyr wide. The respective lower, and upper redshifts are: [0.21, 0.37], [0.37, 0.57], [0.57, 0.83], [0.83, 1.20].
While the completeness in a particular photometric band can
be judged empirically, this is not possible for the
completeness in derived parameters, such as M*
and SFR. We therefore use an alternative
approach to derive an estimate of the completeness of our
photometric sample. We first note that our ability to detect
a specific galaxy will depend on its stellar mass, on the
mass-to-light ratio, and on the shape of the SED
(see e.g. Ilbert et al. 2004, for an in-depth discussion on the effect of this
bias on the determination of luminosity functions). The two
last parameters are determined by the ratio of recent to total
star formation history of the galaxy, which is conveniently
parameterized in terms of the specific star formation rate
SSFR = SFR/M*. We assumed from the beginning that our
library of model galaxies is representative of the population
of galaxies at the redshifts surveyed in this paper. Figure 9 shows the percentage of model galaxies
brighter than
![]() as a function of M*,
SSFR and redshift. It need not be emphasised that we cannot
correct for incompleteness using the completeness array as
this would imply the assumption that we not only sample
the parameter space of real galaxies, but actually know
the relative densities of the galaxies in this parameter space.
For comparison we also plot the 80% completeness limit
derived empirically by Meneux et al. (2007) for the VVDS data, however for a magnitude limit at
as a function of M*,
SSFR and redshift. It need not be emphasised that we cannot
correct for incompleteness using the completeness array as
this would imply the assumption that we not only sample
the parameter space of real galaxies, but actually know
the relative densities of the galaxies in this parameter space.
For comparison we also plot the 80% completeness limit
derived empirically by Meneux et al. (2007) for the VVDS data, however for a magnitude limit at
![]() .
This
mass limit is compatible with Fig. 9, if one
takes into account that the real distribution of galaxies
in SSFR is non-uniform, with most observed galaxies lying
in the two uppermost dex of the plot. Note also that the
spacing between the iso-completeness lines in the plot
depends strongly on the assumed prior and cannot
be directly compared to the real data.
.
This
mass limit is compatible with Fig. 9, if one
takes into account that the real distribution of galaxies
in SSFR is non-uniform, with most observed galaxies lying
in the two uppermost dex of the plot. Note also that the
spacing between the iso-completeness lines in the plot
depends strongly on the assumed prior and cannot
be directly compared to the real data.
For later use we now define the completeness limit
in M* to be where we are 50% complete in the
model catalogue, marginalized over all SSFRs.
According to this criterion, the completeness limits are
at log (![]() ) = 9.2, 9.6, 10.0 for
z = 0.5, 0.7, 1.0,
respectively. This would correspond to the redshift bins
[0.37, 0.57], [0.57, 0.83], [0.83, 1.2], again respectively.
) = 9.2, 9.6, 10.0 for
z = 0.5, 0.7, 1.0,
respectively. This would correspond to the redshift bins
[0.37, 0.57], [0.57, 0.83], [0.83, 1.2], again respectively.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[]{0704f9.ps}}
\end{figure}](/articles/aa/full/2008/45/aa10704-08/Timg89.gif) |
Figure 9:
Percentage of model galaxies in our library
that have
|
| Open with DEXTER | |
In Fig. 10 we show our measurement
of the space density ![]() of galaxies as a function
of M*, SSFR and
redshift for a large sample of galaxies and for all
star formation rates. In the following we call
of galaxies as a function
of M*, SSFR and
redshift for a large sample of galaxies and for all
star formation rates. In the following we call ![]() the ``Mass-SFR function'' analoguous to the
widely used luminosity function. The space density
of objects was derived using the classical
the ``Mass-SFR function'' analoguous to the
widely used luminosity function. The space density
of objects was derived using the classical
![]() method (Schmidt 1968;
Felten 1976) for luminosity functions. This weights
galaxies according to the fraction of the survey volume
in which they could have been observed, given their
brightness and the shape of their SED. In our case, we
simply scale the best-fit model to the observed galaxy
magnitude and shift it in redshift to determine the
total redshift path in which the galaxy would be
seen, given the survey magnitude limits.
The comoving volume sampled by the survey between the
lower and upper redshift limits of the bin was
computed following Carroll et al. (1992). The area
covered on the sky is
method (Schmidt 1968;
Felten 1976) for luminosity functions. This weights
galaxies according to the fraction of the survey volume
in which they could have been observed, given their
brightness and the shape of their SED. In our case, we
simply scale the best-fit model to the observed galaxy
magnitude and shift it in redshift to determine the
total redshift path in which the galaxy would be
seen, given the survey magnitude limits.
The comoving volume sampled by the survey between the
lower and upper redshift limits of the bin was
computed following Carroll et al. (1992). The area
covered on the sky is
![]() deg2.
deg2.
The objects with measured SSFR below 10-14 yr-1 were set to 10-14 yr-1. As shown in Sect. 2.2, the lower limit where we can trust the measurement of the SSFR is at roughly 10-12 yr-1. A dashed line shows this limit. The apparent ``sequence'' at 10-14 yr-1 is therefore not real!
The upper limit to the SSFR at 10-8 per year is
intrinsic to our definition of SSFR. The SFR of
a model galaxy is defined as the stellar mass it formed
in the last 108 years divided by the time elapsed,
i.e. 108 years. The maximum value for a SFR according
to this definition occurs when the galaxy has formed all
of its stars in the last 108 years. If we denote
the present stellar mass by
![]() ,
we
therefore obtain for the maximum SSFR:
,
we
therefore obtain for the maximum SSFR:
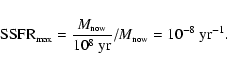 |
(3) |
The measurement of the Mass-SFR function bears on many topics that are currently actively studied. Its value as a fundamental measurement to constrain galaxy evolution is underpinned by recent theoretical work, such as e.g. Cattaneo et al. (2007). However, a detailed discussion of the implications of Fig. 10 and a detailed comparison to the literature is beyond the scope of this work. It will be undertaken in forthcoming papers (Lamareille et al., Vergani et al. 2008, in prep.). In the next section we only concentrate on one possible application.
![\begin{figure}
\par\includegraphics[]{0704f10.ps}
\end{figure}](/articles/aa/full/2008/45/aa10704-08/Timg95.gif) |
Figure 10:
Space density of objects with
different M* and SFRs as a function
of redshift and as determined from SED fitting.
As shown in Sect. 2.2, the lower limit
where we can trust the measurement of the SSFR is at
roughly 10-12 yr-1. The horizontal dashed line
shows this limit. The objects with measured SSFR below
10-14 yr-1 have been set to 10-14 yr-1.
The apparent ``sequence'' a 10-14 yr-1 is
therefore not real! The lowest isodensity contour
is 10-5 Mpc-3/log (M*)/log (SSFR) and
the contours are spaced by a factor 10. Typical 1 |
| Open with DEXTER | |
We use the Mass-SFR function for a useful test of the
merger rate in the universe. To that end we use the
Mass-SFR function in an upper redshift bin to predict the mass
function in the lower redshift bin. If galaxies grew only
through star formation, this predicted mass function should
be consistent with the measured one. In Fig. 11 we
show the observed mass function at each redshift as a solid
line. No errorbars are shown, as the formal statistical
uncertainties are very small. However, we note explicitly that
the mass function we determine is not measured with the same
precision as the one published in P07. In particular,
the mass function in Fig. 11 shows a number
of objects with stellar masses higher than
![]() .
Such high stellar masses are not seen in P07 or in the
local mass functions of Cole et al. (2001) or
Bell et al. (2003). These objects could possibly be Galactic stars
or QSOs contaminating our purely photometric sample. Further
uncertainties arise in
particular at the high-mass end of the mass function,
because we are based on photometric redshifts.
Objects whose redshift has been strongly overestimated
will appear to be intrinsically more luminous than
they are in reality. They thus will artificially swell the
high-mass end of the mass function.
The percentage of catastrophic redshift failures has been
well-quantified and is 5.5% for a sample selected at
.
Such high stellar masses are not seen in P07 or in the
local mass functions of Cole et al. (2001) or
Bell et al. (2003). These objects could possibly be Galactic stars
or QSOs contaminating our purely photometric sample. Further
uncertainties arise in
particular at the high-mass end of the mass function,
because we are based on photometric redshifts.
Objects whose redshift has been strongly overestimated
will appear to be intrinsically more luminous than
they are in reality. They thus will artificially swell the
high-mass end of the mass function.
The percentage of catastrophic redshift failures has been
well-quantified and is 5.5% for a sample selected at
![]() (Ilbert et al. 2006).
In our photometric sample (
(Ilbert et al. 2006).
In our photometric sample (
![]() )
this percentage is expected to be somewhat higher.
On the other hand, the percentage of objects out of the
total sample that have stellar masses above
)
this percentage is expected to be somewhat higher.
On the other hand, the percentage of objects out of the
total sample that have stellar masses above
![]() is 4% and 1% for the two bins at
0.37<z<0.57 and
0.57<z<0.83,
respectively. We conclude that catastrophic redshift failures
make the high-mass end of our stellar mass function
uncertain. It is beyond the scope of this paper to remedy this;
however, under the assumption that the catastrophic failures
redistribute themselves evenly in redshift space, we can
draw conclusions about the relative evolution of the mass
function at masses below
is 4% and 1% for the two bins at
0.37<z<0.57 and
0.57<z<0.83,
respectively. We conclude that catastrophic redshift failures
make the high-mass end of our stellar mass function
uncertain. It is beyond the scope of this paper to remedy this;
however, under the assumption that the catastrophic failures
redistribute themselves evenly in redshift space, we can
draw conclusions about the relative evolution of the mass
function at masses below
![]() ,
as the
fraction of objects from catastrophic failures becomes
small below this limit.
,
as the
fraction of objects from catastrophic failures becomes
small below this limit.
![\begin{figure}
\par\resizebox{8.6cm}{!}{\includegraphics[]{0704f11.ps}}
\end{figure}](/articles/aa/full/2008/45/aa10704-08/Timg99.gif) |
Figure 11: Mass functions as observed and predicted in different redshift bins. The solid line is the observed mass function for the bin shown. The dashed line is the mass function predicted from the higher redshift bin for the current bin. The dotted line is the mass function from Pozzetti et al. (2007). The vertical lines are the corresponding limits of completeness in stellar mass. No errorbars are shown, because the formal statistical uncertainties are very small compared to the systematic uncertainties discussed in the text. |
| Open with DEXTER | |
Given the stellar mass M*i and the SFR SFRi at
time t, the stellar mass of galaxy i at time
![]() is simply
is simply
A useful check on this procedure comes from directly
comparing the observed evolution of the total mass
density to the predicted one. The evolution in total
mass density (summed between the completeness limit
in mass given in Sect. 5.1 and
M* = 1011.8 ![]() )
)
![]() is
given in Table 4. The agreement between
the predicted and the observed evolution can be deemed
satisfactory, given the uncertainties in our mass function.
These values can also be compared to the total growth
in mass density as measured by Arnouts et al. (2007).
From the value given by these authors for the stellar
mass growth between z=1.2 and z=0, we infer a mass growth of
is
given in Table 4. The agreement between
the predicted and the observed evolution can be deemed
satisfactory, given the uncertainties in our mass function.
These values can also be compared to the total growth
in mass density as measured by Arnouts et al. (2007).
From the value given by these authors for the stellar
mass growth between z=1.2 and z=0, we infer a mass growth of
![]()
![]() Mpc-3 for the same total time
interval as used in our paper, i.e. 3 Gyr, and the same field, thus
minimizing our exposure to cosmic variance. While this is a factor
of 3 below our estimate, it must be born in mind that the
Arnouts et al. (2007) growth rate value assumes that the growth
in the mass density is linear with time. However, it is known and
can be seen in their Fig. 13 that the mass growth is faster
at higher redshift. Thus, for our case, the Arnouts et al. (2007)
value is a lower limit, which may alleviate some of the
discrepancy. Indeed, the total mass growth between
z=1.2 and z=0as found by Arnouts et al. (2007) is
Mpc-3 for the same total time
interval as used in our paper, i.e. 3 Gyr, and the same field, thus
minimizing our exposure to cosmic variance. While this is a factor
of 3 below our estimate, it must be born in mind that the
Arnouts et al. (2007) growth rate value assumes that the growth
in the mass density is linear with time. However, it is known and
can be seen in their Fig. 13 that the mass growth is faster
at higher redshift. Thus, for our case, the Arnouts et al. (2007)
value is a lower limit, which may alleviate some of the
discrepancy. Indeed, the total mass growth between
z=1.2 and z=0as found by Arnouts et al. (2007) is
![]()
![]() Mpc-3, much closer to our value of
Mpc-3, much closer to our value of
![]()
![]() Mpc-3.
Mpc-3.
Table 4: Observed versus predicted evolution in stellar mass density.
In Fig. 11 we show, besides the observed mass function, the mass function as determined from evolution of the observed Mass-SFR function at higher redshift. We omit the lowest possible redshift bin, as the directly observed stellar mass function suffers from selection effects at the massive end due to limitations in the probed volume. Several effects are noteworthy in Fig. 11:
Similar analyses were performed in Bell et al. (2007) and in Martin et al. (2007a,b).
Bell et al. (2007) base themselves on SFRs derived
from 24 ![]() m data, i.e. a very different SFR tracer.
They discuss the evolution of the mass function in
a similar way to ours, i.e. predicting the mass function
in the lower redshift bin from the mass function and
SSFR distribution in the higher redshift bin. They use
this approach to ascertain that the growth of the mass
in the red sequence of galaxies has to be dominated by
the quenching of star formation in blue sequence galaxies.
They also state that they find generally good agreement
between the predicted and observed total mass functions.
Close scrutiny of their Fig. 4, however, hints at
an opposite trend to the one we find, i.e. the mass
function tends to be overpredicted at high masses
and underpredicted at intermediate masses. Whether
this difference could be attributed to a slight
underestimate (overestimate) of stellar masses at
lower (higher) redshifts as mentioned in Bell
et al. (2007) remains open.
m data, i.e. a very different SFR tracer.
They discuss the evolution of the mass function in
a similar way to ours, i.e. predicting the mass function
in the lower redshift bin from the mass function and
SSFR distribution in the higher redshift bin. They use
this approach to ascertain that the growth of the mass
in the red sequence of galaxies has to be dominated by
the quenching of star formation in blue sequence galaxies.
They also state that they find generally good agreement
between the predicted and observed total mass functions.
Close scrutiny of their Fig. 4, however, hints at
an opposite trend to the one we find, i.e. the mass
function tends to be overpredicted at high masses
and underpredicted at intermediate masses. Whether
this difference could be attributed to a slight
underestimate (overestimate) of stellar masses at
lower (higher) redshifts as mentioned in Bell
et al. (2007) remains open.
The comparison to Martin et al. (2007a) will be discussed in the next section.
We now quantify the evolution in stellar mass. In each bin of
the mass function, we compute the following measure of the
difference between the predicted mass function
![]() and the originally measured mass
functions
and the originally measured mass
functions
![]() :
:
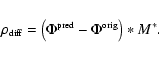 |
(5) |
Table 5: Stellar mass in mergers as a function of redshift.
When comparing the predicted and the measured mass functions,
it is natural to ask where the mass goes that is overpredicted
at intermediate galaxy masses and where the mass comes
from that is underpredicted at the highest galaxy masses?
A simple physical link between both is provided by merging,
i.e. the notion that some or all of the stellar mass that is
overpredicted in intermediate mass galaxies must go to the
most massive galaxies. A similar argument has been presented e.g.
in Brinchman & Ellis (2000). Then,
![]() and
and
![]() should be equal and provide a direct
measure of the stellar mass growth stemming from merger processes.
Given the high uncertainties in
should be equal and provide a direct
measure of the stellar mass growth stemming from merger processes.
Given the high uncertainties in
![]() and
and
![]() ,
our results are compatible with this
picture. Our best estimate for the stellar mass density involved
in mergers between z=1.02 and z=0.47 would then be
,
our results are compatible with this
picture. Our best estimate for the stellar mass density involved
in mergers between z=1.02 and z=0.47 would then be
![]()
![]() Mpc-3.
Mpc-3.
We can directly compare this result with the same quantity
measured by another, independent method in de Ravel et al.
(2008). These authors have used the spectra of the VVDS to
directly measure the fraction of physically associated pairs
of galaxies. This can be used to derive a completely
independent measure of the stellar mass density that is
involved in major mergers. In the redshift bin [1.0, 0.4],
they derive a value of
![]()
![]() Mpc-3.
The factor 2 difference between both values can be
understood when considering that de Ravel et al.
(2008) measure the merger rate from galaxies with roughly
equal mass (
Mpc-3.
The factor 2 difference between both values can be
understood when considering that de Ravel et al.
(2008) measure the merger rate from galaxies with roughly
equal mass (
![]() mag), i.e. the major merger
rate. Taken at face value, this would imply that the
contribution of minor and major mergers to the total mass
growth of massive galaxies is of similar size.
mag), i.e. the major merger
rate. Taken at face value, this would imply that the
contribution of minor and major mergers to the total mass
growth of massive galaxies is of similar size.
Martin et al. (2007a) derive quantitative measures for
the mass growth in the blue sequence (i.e. through star
formation) and for the mass flux to the red sequence
(i.e. due to quenching and mergers) of
![]()
![]() yr-1 Mpc-3 and
yr-1 Mpc-3 and
![]()
![]() yr-1 Mpc-3, respectively. They
also note explicitly that these two values are
surprisingly close to each other. For a
time interval of 3 Gyr, this would be equivalent to
a mass flux of
yr-1 Mpc-3, respectively. They
also note explicitly that these two values are
surprisingly close to each other. For a
time interval of 3 Gyr, this would be equivalent to
a mass flux of ![]() 108
108 ![]() Mpc-3.
However, the identification of massive galaxies
with the red sequence and of less massive galaxies
with the blue sequence is clearly an oversimplification
so we simply conclude with the statement that
these two mass fluxes (from intermediate-mass galaxies
to high-mass galaxies and from the blue to the red
sequence) are comprised within a factor of 2.
Mpc-3.
However, the identification of massive galaxies
with the red sequence and of less massive galaxies
with the blue sequence is clearly an oversimplification
so we simply conclude with the statement that
these two mass fluxes (from intermediate-mass galaxies
to high-mass galaxies and from the blue to the red
sequence) are comprised within a factor of 2.
That massive galaxies cannot grow by star formation, but must grow through mergers, has also been found by Drory & Alvarez (2008), who follow a very similar line of argument as the one presented here.
We have used multi-wavelength data from the Vimos VLT Deep Survey
and the Galex, CFHTLS and Swire surveys to derive the
physical properties of a sample of 84 073 galaxies at redshifts
between 0 and 1.2. We used a technique in which we use e
![]() as a measure of probability and thus build the
probability distribution function over parameters such as
stellar mass, star formation rate and attenuation. This
procedure yields a best estimate of every physical parameter,
plus associated errorbars.
as a measure of probability and thus build the
probability distribution function over parameters such as
stellar mass, star formation rate and attenuation. This
procedure yields a best estimate of every physical parameter,
plus associated errorbars.
We have shown that we can derive accurate measures of M*,
SFR and
![]() .
In particular the measured SFRs are not based on
auxiliary data such as the FIR emission or emission lines and
are thus per definition internally consistent with the other
physical parameters. From independent measurements of the
star formation rate as derived from the [OII]
line emission we were
able to independently test our derived SFR values and we found
good agreement.
.
In particular the measured SFRs are not based on
auxiliary data such as the FIR emission or emission lines and
are thus per definition internally consistent with the other
physical parameters. From independent measurements of the
star formation rate as derived from the [OII]
line emission we were
able to independently test our derived SFR values and we found
good agreement.
We have used our catalogue of physical properties to present the
number density of galaxies as a function of SSFR
and M*. It is particularly convenient that we
depend only on one, easily understood selection criterion, i.e.
![]() .
There is no other threshold in a specific
emission line or UV/IR photometric band.
.
There is no other threshold in a specific
emission line or UV/IR photometric band.
We finally used the measured M* and SFRs in four different redshift bins to predict the stellar mass function that would be observed at a later cosmic time. We find that the predicted evolution in the total mass density agrees with the observed one within the uncertainties. However, star formation alone cannot account for the evolution in the shape of the mass function, as the stellar mass density of intermediate mass galaxies is overpredicted, whereas the density of the most massive galaxies is underpredicted. This indicates that objects with intermediate masses must transform into objects with high masses. The most likely physical cause for this is merging. Indeed, when comparing our results with a direct measure of the major merger rate, we find that approximately half of the mass growth is due to major mergers, while the other half is due to minor mergers.
Acknowledgements
C.J.W. is supported by the MAGPOP Marie Curie EU Research and Training Network. This research was developed within the framework of the VVDS consortium. The VLT-VIMOS observations were carried out on guaranteed time (GTO) allocated by the European Southern Observatory (ESO) to the VIRMOS consortium, under a contractual agreement between the Centre National de la Recherche Scientifique of France, heading a consortium of French and Italian institutes, and ESO, to design, manufacture, and test the VIMOS instrument. Based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT), which is operated by the National Research Council (NRC) of Canada, the Institut National des Science de l'Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS.