A&A 491, 363-377 (2008)
DOI: 10.1051/0004-6361:200810122
N. Ota1,2,![]() - K. Murase3 - T. Kitayama4 - E. Komatsu5 - M. Hattori6 - H. Matsuo7 - T. Oshima8 -
Y. Suto9 - K. Yoshikawa10
- K. Murase3 - T. Kitayama4 - E. Komatsu5 - M. Hattori6 - H. Matsuo7 - T. Oshima8 -
Y. Suto9 - K. Yoshikawa10
1 - Max-Planck-Institut für extraterrestrische Physik, Giessenbachstraße, 85748 Garching, Germany
2 - Institute of Space and Astronautical Science,
Japan Aerospace Exploration Agency, 3-1-1 Yoshinodai, Sagamihara, Kanagawa 229-8510, Japan
3 - Saitama University, Shimo-Okubo 255, Sakura, Saitama 338-8570, Japan
4 - Toho University, 2-2-1 Miyama, Funabashi, Chiba 274-8510, Japan
5 - The University of Texas at Austin, 2511 Speedway, RLM 15.306, Austin, TX 78712, USA
6 - Tohoku University, Aramaki, Aoba, Sendai 980-8578, Japan
7 - National Astronomical Observatory of Japan, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
8 - Nobeyama Radio Observatory, Minamimaki, Minamisaku, Nagano 384-1805, Japan
9 - The University of Tokyo, Tokyo 113-0033, Japan
10 - Center for Computational Physics, University of Tsukuba,
Tsukuba, Ibaraki 305-8577, Japan
Received 5 May 2008 / Accepted 28 August 2008
Abstract
Context. We present the results of our analysis of long Suzaku observations (149 ks and 122 ks for XIS and HXD, respectively) of the most X-ray luminous galaxy cluster, RX J1347.5-1145, at z=0.451.
Aims. To understand the gas physics of a violent, cluster merger, we study physical properties of the hot (![]() 20 keV) gas clump in the south-east (SE) region discovered previously by Sunyaev-Zel'dovich (SZ) effect observations. Using hard X-ray data, a signature of non-thermal emission is also explored.
20 keV) gas clump in the south-east (SE) region discovered previously by Sunyaev-Zel'dovich (SZ) effect observations. Using hard X-ray data, a signature of non-thermal emission is also explored.
Methods. We perform single as well as multi-temperature fits to the Suzaku XIS spectra. The Suzaku XIS and HXD, and the Chandra ACIS-I data are then combined to examine the properties of the hot gas component in the SE region. We finally look for non-thermal emission in the Suzaku HXD data.
Results. The single-temperature model fails to reproduce the 0.5-10 keV continuum emission and Fe-K lines measured by XIS simultaneously. A two-temperature model with a very hot component improves the fit, although the XIS data can only provide a lower limit to the temperature of the hot component. In the Suzaku HXD data, we detect hard X-ray emission above the background in the 12-40 keV band at the 9![]() level; however, the significance becomes marginal when the systematic error in the background estimation is included. With the joint analysis of the Suzaku and Chandra data, we determine the temperature of the hot gas in the SE region to be
25.3+6.1-4.5 (statistical; 90% confidence level)
+6.9-9.5 (systematic; 90% confidence level) keV, which is in an excellent agreement with the previous joint analysis of the SZ effect in radio and the Chandra X-ray data. This is the first time that the X-ray analysis alone provides a good measurement of the hot component temperature in the SE region, which is possible because of Suzaku's unprecedented sensitivity over the wide X-ray band. These results indicate strongly that RX J1347.5-1145 has undergone a recent, violent merger. The spectral analysis shows that the SE component is consistent with being thermal. We measure the 3
level; however, the significance becomes marginal when the systematic error in the background estimation is included. With the joint analysis of the Suzaku and Chandra data, we determine the temperature of the hot gas in the SE region to be
25.3+6.1-4.5 (statistical; 90% confidence level)
+6.9-9.5 (systematic; 90% confidence level) keV, which is in an excellent agreement with the previous joint analysis of the SZ effect in radio and the Chandra X-ray data. This is the first time that the X-ray analysis alone provides a good measurement of the hot component temperature in the SE region, which is possible because of Suzaku's unprecedented sensitivity over the wide X-ray band. These results indicate strongly that RX J1347.5-1145 has undergone a recent, violent merger. The spectral analysis shows that the SE component is consistent with being thermal. We measure the 3![]() upper limit to the non-thermal flux,
upper limit to the non-thermal flux,
![]() in the 12-60 keV band, which provides a limit on the inverse Compton scattering of relativistic electrons off the CMB photons. Combining this limit with the discovery of a radio mini halo in this cluster at 1.4 GHz, which measures the synchrotron radiation, we find a lower limit to the strength of the intracluster magnetic field, such that
in the 12-60 keV band, which provides a limit on the inverse Compton scattering of relativistic electrons off the CMB photons. Combining this limit with the discovery of a radio mini halo in this cluster at 1.4 GHz, which measures the synchrotron radiation, we find a lower limit to the strength of the intracluster magnetic field, such that
![]() .
.
Key words: galaxies: clusters: individual: RX J1347.5-1145 - galaxies: intergalactic medium - X-rays: galaxies: clusters - cosmology: observations
RX J1347.5-1145 is one of the most extensively studied
distant clusters of galaxies, located at z=0.451, which is also
known as the most X-ray luminous cluster of galaxies on the sky. The
bolometric luminosity of RX J1347.5-1145 is
![]() (Schindler et al. 1997).
(Schindler et al. 1997).
The previous multi-wavelength observations have shown that RX J1347.5-1145 has an unusually violent merger activity, which makes this cluster an ideal target for probing the intracluster gas physics and non-thermal phenomena associated with the cluster merger at high redshifts.
The global temperature of the intracluster medium (ICM) of RX J1347.5-1145 is as high as 9-14 keV, as indicated from observations with several X-ray satellites (Allen et al. 2002; Gitti et al. 2007b; Ettori et al. 2001; Schindler et al. 1997). This cluster was classified as a ``cooling-flow'' cluster because of its centrally peaked X-ray surface brightness profile as well as its high mass accretion rate estimated at the center (Allen et al. 2002; Schindler et al. 1997).
Table 1: Log of Suzaku observations of RX J1347.5-1145.
The most striking feature of RX J1347.5-1145 is the presence
of an extremely hot, ![]() 20 keV, gas clump in the south-east (SE)
region. This component was discovered by radio observations of the
Sunyaev-Zel'dovich (SZ) effect towards RX J1347.5-1145 at
150 GHz as the prominent substructure of the SZ effect in the SE
region, about
20 keV, gas clump in the south-east (SE)
region. This component was discovered by radio observations of the
Sunyaev-Zel'dovich (SZ) effect towards RX J1347.5-1145 at
150 GHz as the prominent substructure of the SZ effect in the SE
region, about
![]() off at its the center (Komatsu et al. 2001).
Kitayama et al. (2004) performed a detailed joint analysis of
the SZ effect decrement data at 150 GHz (Komatsu et al. 2001),
increment data at 350 GHz (Komatsu et al. 1999), and the Chandra ACIS-S3 X-ray data (Allen et al. 2002), and
determined the temperature of the hot gas clump to be in excess of
20 keV, which is much higher than the average temperature of the ambient gas.
off at its the center (Komatsu et al. 2001).
Kitayama et al. (2004) performed a detailed joint analysis of
the SZ effect decrement data at 150 GHz (Komatsu et al. 2001),
increment data at 350 GHz (Komatsu et al. 1999), and the Chandra ACIS-S3 X-ray data (Allen et al. 2002), and
determined the temperature of the hot gas clump to be in excess of
20 keV, which is much higher than the average temperature of the ambient gas.
The coexistence of the cool and hot ICM in the central region indicates a complex dynamical evolution of the system, such as a recent merger. In the optical band, the cluster center is dominated by two cD galaxies. The dark matter distribution has also been studied by the gravitational lensing effect (e.g. Fischer & Tyson 1997; Sahu et al. 1998; Halkola et al. 2008; Cohen & Kneib 2002; Allen et al. 2002; Bradac et al. 2008; Miranda et al. 2008). An elongated, almost bimodal distribution was found (Bradac et al. 2008), which also implies that a cluster merger has occurred. Another line of evidence for a merger is the discovery of a radio mini halo at the cluster center (Gitti et al. 2007a), which suggests the presence of relativistic particles powered by the merger and the cooling flow.
The X-ray data from the ROSAT satellite (Schindler et al. 1997) failed to identify the hot component in the SE region, because its X-ray sensitivity did not extend to such a high temperature. RX J1347.5-1145 was considered to be a relaxed, non-merging cluster until the SZ effect revealed evidence of a violent merger. This example shows the importance of having sensitivity to high temperatures well in excess of 10 keV.
Such a high temperature component appears normal in merging clusters.
Another, perhaps the most famous, example is the Bullet cluster
(1E0657-56), in which hot gas substructure was also
found (Markevitch et al. 2002). The analysis of the temperature
structure in merging clusters is a powerful tool for understanding the
gas physics in extreme conditions. While X-ray spectroscopy has
been used widely in this type of study, it is not easy to measure
precisely the temperature of very hot (![]() keV) gas, since the majority of
X-ray imaging spectroscopic observations are limited to the energy
band below 10 keV, and therefore cannot measure a spectral cut-off at
kT that is characteristic of the thermal bremsstrahlung emission.
keV) gas, since the majority of
X-ray imaging spectroscopic observations are limited to the energy
band below 10 keV, and therefore cannot measure a spectral cut-off at
kT that is characteristic of the thermal bremsstrahlung emission.
To overcome this difficulty, Kitayama et al. (2004) used the fact
that the SZ effect is sensitive to arbitrary high temperature gas, and
performed a joint analysis of the SZ effect and X-ray images. They
determined the temperature of the SE excess component in
RX J1347.5-1145 to be ![]() keV, while the Chandra
X-ray spectroscopy, whose sensitivity degrades significantly beyond
7 keV, provided a lower limit of 22 keV. This is amongst the hottest gas
detected to date. Based on the numerical simulations by
Takizawa (1999), Kitayama et al. (2004) suggested that
RX J1347.5-1145 had experienced a recent merger at the
collision speed of
keV, while the Chandra
X-ray spectroscopy, whose sensitivity degrades significantly beyond
7 keV, provided a lower limit of 22 keV. This is amongst the hottest gas
detected to date. Based on the numerical simulations by
Takizawa (1999), Kitayama et al. (2004) suggested that
RX J1347.5-1145 had experienced a recent merger at the
collision speed of
![]() ,
which is similar to
that measured for the Bullet cluster
(Mastropietro & Burkert 2007; Nusser 2008; Milosavljevic et al. 2007; Springel & Farrar 2007). This result indicates that
RX J1347.5-1145 is almost identical to the Bullet
cluster, except for its viewing angle.
,
which is similar to
that measured for the Bullet cluster
(Mastropietro & Burkert 2007; Nusser 2008; Milosavljevic et al. 2007; Springel & Farrar 2007). This result indicates that
RX J1347.5-1145 is almost identical to the Bullet
cluster, except for its viewing angle.
The conclusion of Kitayama et al. (2004) was based on SZ data from high-resolution mapping observations of the SZ effect (the highest resolution ever achieved to date; Komatsu et al. 2001,1999). However, the precision of these SZ observations is still limited because of technological reasons; thus, high-precision X-ray observations whose sensitivity goes well beyond 10 keV are required to obtain reliable estimates of physical properties, such as temperature and merging velocity.
The unprecedented sensitivity of the Suzaku satellite (Mitsuda et al. 2007) to hard X-ray emission well over 10 keV offers a wonderful opportunity to study violent merger events. In this paper, we present an analysis of the temperature structure and non-thermal, high-energy component of the distant cluster RX J1347.5-1145 with the onboard instruments, the X-ray Imaging Spectrometer (XIS; Koyama et al. 2007), and the Hard X-ray Detector (HXD; Kokubun et al. 2007; Takahashi et al. 2007). These instruments provide high-sensitivity spectroscopic observations in a wide energy band up to several tens of keV. Combined with the Chandra data, we determine the temperature of the SE clump only from the X-ray spectroscopy, and discuss its physical properties. We also constrain, for the first time, the non-thermal hard X-ray emission and estimate the magnetic-field strength in RX J1347.5-1145.
Throughout this paper, we adopt a cosmological model with the matter
density
![]() ,
the cosmological constant
,
the cosmological constant
![]() ,
and the Hubble constant
,
and the Hubble constant
![]() ,
which are consistent with the WMAP 5-year
results (Komatsu et al. 2008; Dunkley et al. 2008). At the
cluster redshift (z=0.451),
,
which are consistent with the WMAP 5-year
results (Komatsu et al. 2008; Dunkley et al. 2008). At the
cluster redshift (z=0.451),
![]() corresponds to
5.74 kpc. Unless otherwise specified, quoted errors indicate the 90%
confidence intervals.
corresponds to
5.74 kpc. Unless otherwise specified, quoted errors indicate the 90%
confidence intervals.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0122f1.eps} %
\end{figure}](/articles/aa/full/2008/44/aa10122-08/Timg26.gif) |
Figure 1: Suzaku XIS-0 image of RX J1347.5-1145 in the 0.5-10 keV band. The spectral integration regions for the cluster and the background are indicated with the solid and dashed circles, respectively. The two corners of the CCD chip illuminated by 55Fe calibration sources are excluded from the image. |
| Open with DEXTER | |
Long observations of RX J1347.5-1145 were completed twice
in the Suzaku AO-1 period. During the observations, XIS and
HXD were operated in their normal modes. To prioritize the HXD
effective area, the target was observed at the HXD nominal aim-point
(i.e.
![]() off-axis relative to the XIS). The total
exposure time after data filtering was 149 ks/122 ks for XIS/HXD. The
summary of observations is given in Table 1.
off-axis relative to the XIS). The total
exposure time after data filtering was 149 ks/122 ks for XIS/HXD. The
summary of observations is given in Table 1.
The XIS consists of four X-ray CCD cameras: three front-illuminated
CCDs (XIS-0, -2, -3: 0.4-12 keV) and one back-illuminated CCD
(XIS-1: 0.2-12 keV), and covers a field of view of
![]() .
The ``Spaced Charge Injection'' option
was not applied. The energy resolution was
.
The ``Spaced Charge Injection'' option
was not applied. The energy resolution was ![]() 160 eV at 6 keV
(FWHM) at the time of observations. As shown in Fig. 1,
the X-ray emission from the cluster is clearly detected. The X-ray
peak position (13:47:30.3, -11:45:00.9) is consistent with that
derived from Chandra observations (13:47:30.6, -11:45:09.3) and within the
accuracy of the attitude determination of Suzaku
(typically
160 eV at 6 keV
(FWHM) at the time of observations. As shown in Fig. 1,
the X-ray emission from the cluster is clearly detected. The X-ray
peak position (13:47:30.3, -11:45:00.9) is consistent with that
derived from Chandra observations (13:47:30.6, -11:45:09.3) and within the
accuracy of the attitude determination of Suzaku
(typically
![]() ;
Uchiyama et al. 2008).
;
Uchiyama et al. 2008).
The non-imaging HXD covers a wide bandpass of 10-600 keV with PIN
diodes (10-60 keV) and GSO scintillator (40-600 keV). We used
the PIN data in the analysis presented in this paper. The narrow field-of-view of
![]() (FWHM) and the low background level of the
PIN spectral data enabled us to study the hard X-ray emission from the
cluster up to several tens of keV, which is ideal for studying a violent
merger event. The bias voltage from one of four high-voltage units
was reduced from the nominal value of 500 V to 400 V. As a result
the total effective area of the HXD/PIN decreased by a few percent
to just above 20 keV. This effect was incorporated into the detector response
functions.
(FWHM) and the low background level of the
PIN spectral data enabled us to study the hard X-ray emission from the
cluster up to several tens of keV, which is ideal for studying a violent
merger event. The bias voltage from one of four high-voltage units
was reduced from the nominal value of 500 V to 400 V. As a result
the total effective area of the HXD/PIN decreased by a few percent
to just above 20 keV. This effect was incorporated into the detector response
functions.
We used the cleaned event files created by the pipeline processing
version 2.0, and performed the data analysis using HEASOFT
version 6.3.1. The XIS data was filtered according to the following
criteria: the Earth elevation angle
![]() ,
the day-Earth
elevation angle
,
the day-Earth
elevation angle
![]() ,
and the satellite outside the South
Atlantic Anomaly (SAA). The HXD data were filtered according to the
following criteria: the Earth elevation angle
,
and the satellite outside the South
Atlantic Anomaly (SAA). The HXD data were filtered according to the
following criteria: the Earth elevation angle
![]() ,
the
geomagnetic cut-off rigidity (COR) > 6 GV, and the satellite outside
the SAA.
,
the
geomagnetic cut-off rigidity (COR) > 6 GV, and the satellite outside
the SAA.
The XIS spectra were extracted from a circular region within a radius
of 5
![]() that is centered at the X-ray peak position (see
Fig. 1). The background spectra were accumulated from the
circular region within a 3
that is centered at the X-ray peak position (see
Fig. 1). The background spectra were accumulated from the
circular region within a 3
![]() radius which is almost entirely free of
cluster emission. Since the background contributes to 10-15% of
the total spectrum continuum level, the systematic error due to the background
uncertainty is small. To confirm this, we checked the positional
dependence of the background spectra by analyzing the blank-sky data
obtained during the
radius which is almost entirely free of
cluster emission. Since the background contributes to 10-15% of
the total spectrum continuum level, the systematic error due to the background
uncertainty is small. To confirm this, we checked the positional
dependence of the background spectra by analyzing the blank-sky data
obtained during the ![]() 90 ks North Ecliptic Pole observation on
2006 February 10, and found that it was lower than 7%
of the background spectrum continuum level for all four
sensors of XIS. Therefore, the background does not affect our
spectral analysis within the statistical errors.
90 ks North Ecliptic Pole observation on
2006 February 10, and found that it was lower than 7%
of the background spectrum continuum level for all four
sensors of XIS. Therefore, the background does not affect our
spectral analysis within the statistical errors.
The energy response files were generated by using the FTOOLS
task, xisrmfgen. To take into account the vignetting
effect of the X-ray telescopes (XRT; Serlemitsos et al. 2007)
and a decrease in the low-energy efficiency due to the contaminating
material on the optical blocking filter of the XIS, the auxiliary
response files (arfs) were calculated by using xissimarfgen
(Ishisaki et al. 2007). We assumed that the X-ray surface
brightness distribution of the cluster was represented by the double
![]() -model: our reanalysis of the Chandra ACIS-I image
yields the two core radii given by rc1=24 kpc and
rc2=94 kpc, the same slope parameter,
-model: our reanalysis of the Chandra ACIS-I image
yields the two core radii given by rc1=24 kpc and
rc2=94 kpc, the same slope parameter,
![]() ,
for both
components, and a surface brightness ratio of
S1/S2 =8.1 at the
center (see Fig. 9b). Since the spatial distribution
of RX J1347.5-1145 is compact compared with the typical
size of the Suzaku's Point Spread Function (PSF), its
detailed features do not affect our spectral
analysis significantly: if we compare the above arf files with those produced
by using a point-like source or an exposure-corrected Chandra
image as an input source distribution, these three kinds of arfs
agree to within 3%, and provide consistent spectral parameters to within the
present calibration uncertainty of the Suzaku telescope (see
also Appendix A).
,
for both
components, and a surface brightness ratio of
S1/S2 =8.1 at the
center (see Fig. 9b). Since the spatial distribution
of RX J1347.5-1145 is compact compared with the typical
size of the Suzaku's Point Spread Function (PSF), its
detailed features do not affect our spectral
analysis significantly: if we compare the above arf files with those produced
by using a point-like source or an exposure-corrected Chandra
image as an input source distribution, these three kinds of arfs
agree to within 3%, and provide consistent spectral parameters to within the
present calibration uncertainty of the Suzaku telescope (see
also Appendix A).
The hard X-ray spectra were accumulated from all units of the PIN
diodes. The PIN detector background was subtracted by using the
Non-X-ray Background (NXB) files![]() provided by the HXD instrument team. Since precise modeling of the
background is crucial for measuring the hard X-ray flux, we describe
the method of background subtraction in Sect. 4. In
the spectral fitting, we used the PIN response
function
provided by the HXD instrument team. Since precise modeling of the
background is crucial for measuring the hard X-ray flux, we describe
the method of background subtraction in Sect. 4. In
the spectral fitting, we used the PIN response
function![]() that was
appropriate for the epoch of observations.
that was
appropriate for the epoch of observations.
To examine the global temperature structure of RX J1347.5-1145, we attempted to reproduce the observed XIS spectra in the 0.5-10 keV band by fitting the APEC thermal emission model.
The angular size of the X-ray emission is fairly compact and nearly
90% of the total emission originates in the central r<2' region, which
is comparable to the spatial resolution of the Suzaku XRT
(Half Power Diameter
![]() ;
Serlemitsos et al. 2007).
We use the extraction radius of 5
;
Serlemitsos et al. 2007).
We use the extraction radius of 5
![]() ;
more than 97% of
the photons from RX J1347.5-1145 have therefore been collected.
;
more than 97% of
the photons from RX J1347.5-1145 have therefore been collected.
The XIS spectra with high photon statistics allowed us to measure the
global temperature in two different ways: (1) by a APEC model fit to
the 0.5-10 keV spectra; and (2) by using the intensity ratio of two
Fe emission lines, i.e. (He-like Fe K![]() )/(H-like Fe
K
)/(H-like Fe
K![]() ), as an indicator of the ``ionization'' temperature. By
comparing the two results of these methods, we examined
whether the emission could be modeled by
a single-temperature gas, or the data had to be described
instead by a model of more complex temperature structure.
), as an indicator of the ``ionization'' temperature. By
comparing the two results of these methods, we examined
whether the emission could be modeled by
a single-temperature gas, or the data had to be described
instead by a model of more complex temperature structure.
For the analysis (1) (APEC model), we fitted the APEC model to the
observed 0.5-10 keV XIS spectra, where the redshift and Galactic
hydrogen column density were fixed at z=0.451 and
![]() (Dickey & Lockman 1990),
respectively. The metal abundance table in
Anders & Grevesse (1989) was assumed. The spectral bins in the
1.7-1.9 keV range were excluded due to the large calibration errors
in the Si-edge structure. To take into account the
uncertainty in the thickness of the contaminating material, the
absorption column densities of oxygen and carbon (
(Dickey & Lockman 1990),
respectively. The metal abundance table in
Anders & Grevesse (1989) was assumed. The spectral bins in the
1.7-1.9 keV range were excluded due to the large calibration errors
in the Si-edge structure. To take into account the
uncertainty in the thickness of the contaminating material, the
absorption column densities of oxygen and carbon (![]() and
and
![]() )
were included in the spectral model by fixing the ratio
to
)
were included in the spectral model by fixing the ratio
to
![]() .
There was a potential
uncertainty in the absolute energy scale of approximately 10-20 eV, as
indicated by the analysis of the 55Fe calibration source
spectra; the gain offset for each XIS sensor was therefore included in the
fitting model.
.
There was a potential
uncertainty in the absolute energy scale of approximately 10-20 eV, as
indicated by the analysis of the 55Fe calibration source
spectra; the gain offset for each XIS sensor was therefore included in the
fitting model.
Table 2: Single-temperature APEC model parameters fit to the XIS spectra taken by four sensors (XIS-0, XIS-1, XIS-2, XIS-3), and the result from the simultaneous fit to all of the sensors (XIS-0, 1, 2, 3).
Table 3: The instrumental calibration parameters from the APEC model fit simultaneously to the XIS-0, 1, 2, and 3.
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=8cm,clip]{0122f2a.eps} \includegraphics[angle=-90,width=8cm,clip]{0122f2b.eps} }
\end{figure}](/articles/aa/full/2008/44/aa10122-08/Timg45.gif) |
Figure 2:
a) Observed XIS spectra (
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=8cm,clip]{0122f3a.eps} \includegraphics[angle=-90,width=8cm,clip]{0122f3b.eps} }
\end{figure}](/articles/aa/full/2008/44/aa10122-08/Timg46.gif) |
Figure 3:
a) Observed XIS spectra in the 4-5.5 keV band. The spectra
taken by four sensors, XIS-0 (black), 1 (red), 2 (green), and 3 (blue), are shown separately. The solid lines in the upper panels
are the best-fitting continuum plus two Gaussian models. In the
bottom panel the residuals of the fit in units of the number of
standard deviations are shown. b) Line ratio (He-like Fe
K |
| Open with DEXTER | |
Since all four sensors yield consistent APEC parameters (see
Table 2), we show the results from the simultaneous fit
to all of the sensors (XIS-0, XIS-1, XIS-2, and XIS-3) hereafter. When
performing the simultaneous fit, the normalizations of XIS-1, XIS-2,
and XIS-3 relative to that of XIS-0 were also treated as free
parameters. We find the temperature and the metal abundance of
kT=12.86+0.08-0.25 keV and
Z=0.33+0.03-0.02 solar,
respectively. The unabsorbed flux and luminosity in the 0.5-10 keV
band are
![]() ,
and
,
and
![]() ,
respectively. The
estimated bolometric X-ray luminosity is
,
respectively. The
estimated bolometric X-ray luminosity is
![]() .
In Table 3, we
list the instrumental calibration parameters. In the following
analysis, we use the best-fit values for the relative
normalization factors, the carbon column densities, and the gain
offsets.
.
In Table 3, we
list the instrumental calibration parameters. In the following
analysis, we use the best-fit values for the relative
normalization factors, the carbon column densities, and the gain
offsets.
Figure 2 shows the observed XIS spectra. Figure 2b is a
zoomed version of this figure for the region around the redshifted He-like Fe K![]() and
H-like Fe K
and
H-like Fe K![]() lines at about 4.6 keV and 4.8 keV,
respectively. We find clear detections of both lines. Also shown is
the best-fit single-temperature APEC thermal plasma model. The
single-temperature model fails to reproduce the He-like line. The reduced
lines at about 4.6 keV and 4.8 keV,
respectively. We find clear detections of both lines. Also shown is
the best-fit single-temperature APEC thermal plasma model. The
single-temperature model fails to reproduce the He-like line. The reduced
![]() from the single-temperature fit is
from the single-temperature fit is
![]() ;
the single-temperature model is therefore rejected at the 99.3% confidence level.
;
the single-temperature model is therefore rejected at the 99.3% confidence level.
We then attempted to fit the XIS spectra with the NEI (non-equilibrium
ionization collisional plasma) model. We found that the NEI model
did not improve the fit to the He-like Fe K![]() line and the
quality of the fit in the entire energy range was similar to the
12.9 keV APEC model: the resulting
line and the
quality of the fit in the entire energy range was similar to the
12.9 keV APEC model: the resulting ![]() from the NEI model fit was
1340 for 1208 degrees of freedom. The best-fit ionization
timescale of
from the NEI model fit was
1340 for 1208 degrees of freedom. The best-fit ionization
timescale of
![]() is also long sufficiently for
the system to reach the equilibrium state (Masai 1994),
and the assumption that the system is in a non-equilibrium state
cannot therefore be justified. From these results, we conclude that the
single-temperature NEI model fails to describe the observed XIS
spectra.
is also long sufficiently for
the system to reach the equilibrium state (Masai 1994),
and the assumption that the system is in a non-equilibrium state
cannot therefore be justified. From these results, we conclude that the
single-temperature NEI model fails to describe the observed XIS
spectra.
For the analysis (2) (the line-ratio method), we model the observed XIS spectra in the 4-5.5 keV band as the sum of the following components: (i) the APEC model with the metal abundance reset to 0 for the continuum
emission; (ii) two Gaussian functions for the two major Fe lines at
4.6 and 4.8 keV; and (iii) another Gaussian line at 5.4 keV for the
blend of the He-like Ni-K![]() and He-like Fe-K
and He-like Fe-K![]() lines. In
Fig. 3a, we show the results of this fit. This model provides an
acceptable fit to the data with
lines. In
Fig. 3a, we show the results of this fit. This model provides an
acceptable fit to the data with
![]() ,
or a
probability of finding higher
,
or a
probability of finding higher ![]() values than observed is 11.4%.
values than observed is 11.4%.
This model provides the line ratio, (He-like Fe K![]() )/(H-like Fe
K
)/(H-like Fe
K![]() ), of 1.05(0.92-1.34). Figure 3b shows the
temperature dependence of the line ratio predicted by the APEC model,
folded with the XRT+XIS response functions. From this, we find
kT=10.4(9.1-11.4) keV, which is significantly different from that
found in the analysis (1),
kT=12.86(12.61-12.94) keV, suggesting
that the ICM cannot be explained by the single-temperature
model. Therefore, the ICM is more likely to be in the form of
multi-temperature plasma, which we explore in
Sect. 3.2.
), of 1.05(0.92-1.34). Figure 3b shows the
temperature dependence of the line ratio predicted by the APEC model,
folded with the XRT+XIS response functions. From this, we find
kT=10.4(9.1-11.4) keV, which is significantly different from that
found in the analysis (1),
kT=12.86(12.61-12.94) keV, suggesting
that the ICM cannot be explained by the single-temperature
model. Therefore, the ICM is more likely to be in the form of
multi-temperature plasma, which we explore in
Sect. 3.2.
Since the iron lines are emitted mostly from low-temperature gas (see
Sect. 3.2), the line energies and widths are useful
probes of (i) the gas bulk motion; and (ii) the turbulence in the
cluster core. For (i), the observed centroid energies of the iron
lines are consistent with those expected from the 10 keV APEC model
(6.69 and 6.97 keV in the rest frame) and the cluster redshift, to
within the 90% statistical error of 10 eV. As shown in
Table 3, there is the gain offset of 15 eV when averaged over
the four XIS sensors, and we simply assign the 90% systematic error of
15 eV to the XIS energy scale. By adding the statistical and
systematic errors in quadrature, the 90% upper limit to the
line-of-sight bulk velocity relative to z=0.451 is estimated to be
![]() .
For (ii), we find no significant line
broadening: the 90% upper limit to the Gaussian width of the He-like
K
.
For (ii), we find no significant line
broadening: the 90% upper limit to the Gaussian width of the He-like
K![]() line is measured to be
line is measured to be
![]() eV. Since the measured
Gaussian width is the sum of the thermal Doppler broadening,
eV. Since the measured
Gaussian width is the sum of the thermal Doppler broadening,
![]() (
(
![]() eV for kT=10 keV), and the broadening due
to a turbulent velocity,
eV for kT=10 keV), and the broadening due
to a turbulent velocity,
![]() ,
i.e.
,
i.e.
![]() ,
an upper limit to the
turbulent velocity dispersion is measured to be
,
an upper limit to the
turbulent velocity dispersion is measured to be
![]() .
Therefore, from the
analysis of the iron lines we found no significant bulk velocity and
turbulent velocity, which is consistent with the view that the
low-temperature gas in the cluster core is relatively relaxed. The
derived upper limits are also comparable to those obtained for the
core of the Centaurus cluster (Ota et al. 2007).
If velocity structure on small (
.
Therefore, from the
analysis of the iron lines we found no significant bulk velocity and
turbulent velocity, which is consistent with the view that the
low-temperature gas in the cluster core is relatively relaxed. The
derived upper limits are also comparable to those obtained for the
core of the Centaurus cluster (Ota et al. 2007).
If velocity structure on small (
![]() )
spatial scales
exists, the signals may be diluted due to the wide PSF of Suzaku. However, it is not easy to study the detailed spatial
structure in RX J1347.5-1145 because its angular size is
small.
)
spatial scales
exists, the signals may be diluted due to the wide PSF of Suzaku. However, it is not easy to study the detailed spatial
structure in RX J1347.5-1145 because its angular size is
small.
![\begin{figure}
\par\mbox{ \includegraphics[angle=-90,width=7.5cm,clip]{0122f4a.eps} \includegraphics[angle=-90,width=7.5cm,clip]{0122f4b.eps} }
\end{figure}](/articles/aa/full/2008/44/aa10122-08/Timg62.gif) |
Figure 4:
a) Two-temperature APEC model fit to the observed XIS
spectra. The spectra taken by four sensors, XIS-0 (black), 1 (red),
2 (green), and 3 (blue), are shown separately. The solid lines in
the upper panel show the sum of two APEC models with different
temperatures, while the dashed lines show the low-temperature (upper
curves) and high-temperature (lower curves) components separately,
convolved with the telescope and the detector response functions.
In the bottom panel the residuals of the fit in units of the number
of standard deviations are shown. b) Blow-up of the XIS spectra
in the 4-5.5 keV band. The two-temperature model fits both the
He-like and H-like Fe K |
| Open with DEXTER | |
Table 4: Two-temperature APEC model parameters fit to the XIS spectra in the 0.5-10 keV and 4.0-5.5 keV bands.
Given that the single-temperature model failed to describe the observed XIS spectra, we explored the two-temperature model consisting of two APEC models with different temperatures, as a simplest example of multi-temperature plasma. The results of the fit to the two-temperature model are shown in Fig. 4 and Table 4, where the metal abundances of the two components are assumed to be equal.
From the fit to the 0.5-10 keV spectra, we found that the
low-temperature component had the temperature of
![]() keV
keV![]() , whereas we only found a lower bound to
the temperature of the high-temperature component as
, whereas we only found a lower bound to
the temperature of the high-temperature component as
![]() keV. This two-temperature model yielded an acceptable
goodness-of-fit: the reduced
keV. This two-temperature model yielded an acceptable
goodness-of-fit: the reduced ![]() was
was
![]() ,
or the
probability of finding higher
,
or the
probability of finding higher ![]() values than observed was 3.9%.
In comparison with the single-temperature APEC model, the fit has
improved to a confidence level of more than the 99.99% according to the
F-test (
values than observed was 3.9%.
In comparison with the single-temperature APEC model, the fit has
improved to a confidence level of more than the 99.99% according to the
F-test (
![]() for two additional parameters).
Restricting the energy range to 4.0-5.5 keV did not change the
parameters significantly (see the lower row of Table 4). The
reduced
for two additional parameters).
Restricting the energy range to 4.0-5.5 keV did not change the
parameters significantly (see the lower row of Table 4). The
reduced ![]() is
is
![]() ,
or the probability of finding
higher
,
or the probability of finding
higher ![]() values than observed was 7.6%.
values than observed was 7.6%.
Since the observed Fe K![]() lines should be totally dominated by
the low-temperature gas (see Fig. 4b), one
may compare
lines should be totally dominated by
the low-temperature gas (see Fig. 4b), one
may compare
![]() keV and the temperature
derived from the line ratio,
kT=10.4(9.1-11.4) keV (see
Sect. 3.1), directly. These two estimates were in an
excellent agreement, which provides support to the two-temperature
interpretation of the ICM of RX J1347.5-1145.
keV and the temperature
derived from the line ratio,
kT=10.4(9.1-11.4) keV (see
Sect. 3.1), directly. These two estimates were in an
excellent agreement, which provides support to the two-temperature
interpretation of the ICM of RX J1347.5-1145.
Although the XIS data provide a lower bound to the temperature of the hotter component (see Table 4), they cannot provide an upper bound. We found that this was because the two-temperature model is too simple to be realistic. More detailed modeling of the hotter component, including a joint analysis of the Suzaku HXD data and the spatially-resolved Chandra data, is given in Sect. 5.
For the PIN diodes of HXD for the energy band of 12-60 keV, the background is composed of the following three components: (i) the non-X-ray background (NXB); (ii) cosmic X-ray background (CXB); and (iii) bright point-like sources within the detector field-of-view. Of these, the NXB dominates the observed flux, particularly for faint, hard, X-ray sources, such as clusters of galaxies.
Since the NXB has a significant time-variability, the reproducibility of the NXB is the most important factor in the measurements of the hard X-ray flux from clusters of galaxies. In Sect. 4.1, the systematic error due to NXB is carefully examined. In Sect. 4.2, the CXB model is calculated. In Sect. 4.3, the point source fluxes are estimated from the XMM-Newton observations of the same field.
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=7.5cm,clip]{0122f5a.eps}\includegraphics[angle=-90,width=7.5cm,clip]{0122f5b.eps} }
\end{figure}](/articles/aa/full/2008/44/aa10122-08/Timg72.gif) |
Figure 5: Observed PIN spectra during two observing periods of RX J1347.5-1145. a) Seq: 801013010; and b) Seq: 801013020.In each panel Data, NXB, and (Data-NXB) are shown with the black crosses, red crosses, and green circles, respectively. |
| Open with DEXTER | |
Table 5:
PIN count rates measured in the 12-40 keV and 40-60 keV bands.
The quoted errors are 1![]() statistical errors.
statistical errors.
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=7.5cm,clip]{0122f6a.eps} \includegraphics[angle=-90,width=7.5cm,clip]{0122f6b.eps} }
\end{figure}](/articles/aa/full/2008/44/aa10122-08/Timg97.gif) |
Figure 6:
Observed light curves of the PIN 12-40 keV count rates
during two observing periods. a) Seq: 801013010; and b) Seq:
801013020. In the upper panels, the Data and NXB rates are shown by
black and red crosses, respectively. In the bottom panels,
(Data-NXB) is shown by the green circles. The error bars show
the 1 |
| Open with DEXTER | |
The latest report from the instrument
team![]() indicates that
the reproducibility of the PIN NXB model for data processed
by the version 2 pipeline was typically 3% (1
indicates that
the reproducibility of the PIN NXB model for data processed
by the version 2 pipeline was typically 3% (1![]() ).
This estimate is based upon systematic comparisons between the NXB
model and the PIN data during the Earth occultation in a trend
archive. We check below the validity of assigning the 3% systematic
error to our PIN analysis.
).
This estimate is based upon systematic comparisons between the NXB
model and the PIN data during the Earth occultation in a trend
archive. We check below the validity of assigning the 3% systematic
error to our PIN analysis.
In Fig. 5, we show comparisons between the observed PIN data
(hereafter ``Data'') and the NXB model in two observing periods, (a)
Seq: 801013010; and (b) Seq: 801013020. In Table 5 we
summarize the count rates in the 12-40 keV and 40-60 keV bands. The
excess signal was detected in Data-NXB at energies below 30 keV
during both observing periods. The difference in Data-NXB between
two observing periods was well below the NXB itself:
![]() .
However, the difference was marginally (
.
However, the difference was marginally (![]() 2
2![]() )
inconsistent with zero compared with its statistical error,
)
inconsistent with zero compared with its statistical error,
![]() ,
which could indicate some residual time variability.
,
which could indicate some residual time variability.
In general, variations in the NXB intensity depend primarily on the
satellite's passage of the SAA and the COR
(Kokubun et al. 2007). To study these effects, we binned the PIN
spectra under the following different conditions: elapsed time after
the passage of the SAA,
![]() s, and
s, and
![]() s, and three different COR
[GV] ranges of
s, and three different COR
[GV] ranges of
![]() ,
,
![]() ,
and
,
and
![]() .
This analysis indicated that there was a trend to obtain a
higher count rate for TSAA<6000 s compared with TSAA>6000 s, and a
higher count rate for a smaller COR. However, the differences in the
count rates were below 3% of the NXB intensity in each case.
.
This analysis indicated that there was a trend to obtain a
higher count rate for TSAA<6000 s compared with TSAA>6000 s, and a
higher count rate for a smaller COR. However, the differences in the
count rates were below 3% of the NXB intensity in each case.
To study the reproducibility of the NXB further, Data and NXB were compared during periods of Earth occultation.
The Earth is known to be dark in hard X-rays and the Earth occultation data can be regarded as representing the NXB for the PIN observations. As a result,
Data and NXB during Earth occultation show good agreement, and
Data-NXB is consistent with zero. From these studies, we conclude
that the systematic error in the NXB model is fairly small
(![]() 1%).
1%).
In summary, the accuracy of the PIN NXB model is consistent with that found in the latest report from the instrument team. Therefore, we adopt the instrument team's estimate of the systematic error, 3%, and propagate this through our spectral analysis of the HXD/PIN data.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{0122f7.eps}\end{figure}](/articles/aa/full/2008/44/aa10122-08/Timg106.gif) |
Figure 7: Observed PIN spectrum minus the nominal NXB model (Data-NXB; black), the simulated CXB model (red), and the point source contribution estimated from the XMM-Newton observations of the same field (green). |
| Open with DEXTER | |
We calculate the CXB spectrum in the PIN band by assuming a power-law
model with an exponential cut-off at 40 keV, as previously reported
from the HEAO-1 A2 (Boldt 1987). Since
the PIN detector response assumes a uniform distribution of emission
over ![]()
![]()
![]() on the sky, the CXB model for a 4 square
degree field in units of
on the sky, the CXB model for a 4 square
degree field in units of
![]() is
given by
is
given by
The resulting simulated CXB spectrum is shown in Fig. 7. To
calculate the CXB spectrum the integration time of 100 Ms was assumed;
the statistical error of the simulated spectrum is negligibly
small. The CXB count rates in the 12-40 keV and 40-60 keV bands are
given by
![]() and
and
![]() ,
respectively, which amount to about 6.1% and 1.2% of the NXB,
respectively.
,
respectively, which amount to about 6.1% and 1.2% of the NXB,
respectively.
Based upon the ASCA observations, Kushino et al. (2002) found that the CXB fluctuation in the 2-10 keV band is ![]() 6%,
which can be attributed to the Poisson noise of the source count
within
6%,
which can be attributed to the Poisson noise of the source count
within
![]() .
By scaling the HEAO-1
result of 2.8% with the equation
.
By scaling the HEAO-1
result of 2.8% with the equation
![]() ,
where
,
where ![]() and S are the effective
solid angle of the observation and upper cut-off flux of detectable
discrete sources in the field of view,
respectively (Condon 1974), Kawano et al. (2008)
calculated the 1
and S are the effective
solid angle of the observation and upper cut-off flux of detectable
discrete sources in the field of view,
respectively (Condon 1974), Kawano et al. (2008)
calculated the 1![]() fluctuation of CXB to be 9.2% for the
fluctuation of CXB to be 9.2% for the
![]() 100 ks HXD/PIN observations. The CXB fluctuation
over the 30
100 ks HXD/PIN observations. The CXB fluctuation
over the 30
![]() scale was therefore small compared with the NXB systematic error.
scale was therefore small compared with the NXB systematic error.
We next estimated the hard X-ray flux of point sources inside the
field-of-view of HXD/PIN from the 30 ks XMM-Newton/PN data of
the same field (Observation ID: 0112960101). The data reduction was
completed in the standard manner with SAS version 7.1.0, and
the periods of background flares were removed with the threshold value
of
![]() in the 12-14 keV band.
in the 12-14 keV band.
With the edetect_chain program, thirty point sources were
detected in the PN image. The photon index for each source was
estimated from the hardness ratio, which was defined to be the ratio of the source
count rates in the 0.5-1.5 keV and 1.5-5 keV band. The background
was subtracted using the blank-sky data
(Carter & Read 2007). The Galactic absorption was assumed in
the calculation. The photon index of
![]() was obtained
for almost all sources that have significant emission in the hard
band. We then simulated the PIN spectrum expected for each source using
a power-law spectrum with
was obtained
for almost all sources that have significant emission in the hard
band. We then simulated the PIN spectrum expected for each source using
a power-law spectrum with ![]() ,
where we include the PIN angular
response function using hxdarfgen.
,
where we include the PIN angular
response function using hxdarfgen.
Figure 7 shows the spectrum of the sum of the detected sources. We found that the contribution from the point sources was totally negligible.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{0122f8.eps}\end{figure}](/articles/aa/full/2008/44/aa10122-08/Timg119.gif) |
Figure 8: Observed PIN spectrum with the background model subtracted (Data-NXB-CXB; the crosses) in the 12-60 keV band. The error bars indicate only the statistical errors. The histogram shows the best-fit APEC thermal plasma model. The bottom panel shows the residuals in units of the number of standard deviations. |
| Open with DEXTER | |
Table 6: Single-temperature APEC model parameters fit to the PIN data in the 12-60 keV band. The systematic error in the NXB model is included in the error estimate.
In Fig. 8, the observed PIN spectrum with NXB and CXB
subtracted is shown. In the 12-40 keV band, we detected the hard X-ray
emission at the 9![]() confidence level. Taking into account the NXB
systematic error, however, the significance of the detection becomes far
lower: the estimated count rate is
confidence level. Taking into account the NXB
systematic error, however, the significance of the detection becomes far
lower: the estimated count rate is
![]() in the 12-40 keV, where the first and
second errors are the 1
in the 12-40 keV, where the first and
second errors are the 1![]() statistical and 1
statistical and 1![]() systematic
uncertainties, respectively. At higher energies, 40-60 keV, the
count rate is
systematic
uncertainties, respectively. At higher energies, 40-60 keV, the
count rate is
![]() (1
(1![]() ); we therefore do not expect significant hard X-ray emission in the 40-60 keV band.
); we therefore do not expect significant hard X-ray emission in the 40-60 keV band.
We next fit the single-temperature APEC model to the background-subtracted PIN spectrum in the 12-60 keV band. The XIS data is not used here. A joint analysis of XIS and HXD/PIN is presented in Sect. 5. The metal abundance was fixed at the best-fit value obtained from the XIS analysis, 0.33 solar. The systematic error in the spectral parameters due to the systematic uncertainty in the NXB model was estimated by changing the normalization factor of the NXB model by +3% or -3% and repeating the fitting procedure.
The results are shown in Fig. 8 and Table 6. We
found that the temperature and normalization of the single-temperature
APEC model were
kT=20.2+21.4-8.0 (+7.7-8.7) keV and
![]() ,
respectively. These parameters are consistent with those obtained from
the XIS data. Therefore, we conclude that the hard X-ray emission
observed with PIN does indeed originate in RX J1347.5-1145.
,
respectively. These parameters are consistent with those obtained from
the XIS data. Therefore, we conclude that the hard X-ray emission
observed with PIN does indeed originate in RX J1347.5-1145.
From the observed PIN count rate and the best-fit
single-temperature APEC model given in Table 2, we estimate
the energy flux to be
![]() in the 12-60 keV (1
in the 12-60 keV (1![]() ). On the other
hand, the previous Beppo-SAX observation of
RX J1347.5-1145 reported detection of the hard X-ray
emission at the
). On the other
hand, the previous Beppo-SAX observation of
RX J1347.5-1145 reported detection of the hard X-ray
emission at the ![]() 1.5
1.5![]() significance level:
significance level:
![]() in the 13-60 keV band
(Ettori et al. 2001), and
in the 13-60 keV band
(Ettori et al. 2001), and
![]() in the 20-80 keV band (Nevalainen et al. 2004). With
the 12.9 keV Raymond-Smith model and the response of the PDS
instrument onboard Beppo-SAX, the pimms program measures the
12-60 keV flux to be
in the 20-80 keV band (Nevalainen et al. 2004). With
the 12.9 keV Raymond-Smith model and the response of the PDS
instrument onboard Beppo-SAX, the pimms program measures the
12-60 keV flux to be
![]() .
(All errors quoted here are 1
.
(All errors quoted here are 1![]() .) The PIN result therefore agrees
with that of the PDS to within their 1
.) The PIN result therefore agrees
with that of the PDS to within their 1![]() margins of error.
margins of error.
In Sect. 3, the Suzaku XIS data indicated the presence of a significant amount of very hot gas. In this section, we study the physical properties of this hot component, such as the amount, temperature, and metal abundance, by performing a joint analysis of the Suzaku data and the spatially-resolved Chandra spectra.
In Sect. 5.1, the properties of the ambient gas are derived from the Chandra data. In Sect. 5.2, the properties of the hot gas component in the SE quadrant are derived from the Suzaku broad-band spectra combined with the Chandra data by means of a multi-temperature model. In Sect. 5.3, we argue that the hot component is described more accurately by thermal gas rather than non-thermal gas, and derive an upper limit to the possible non-thermal emission.
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=7cm,clip]{0122f9a.eps}...
...e*{2mm}
\includegraphics[angle=-90,width=7cm,clip]{0122f9b.eps} }
\end{figure}](/articles/aa/full/2008/44/aa10122-08/Timg130.gif) |
Figure 9:
a) Chandra ACIS-I image in the 0.5-7 keV band. The solid lines show the NW and SE regions. The radius of the circle is 5 |
| Open with DEXTER | |
The deep Chandra ACIS-I data of RX J1347.5-1145 (Obs ID:3592, Date:2003-09-03) was analyzed with CIAO version 3.4 and CALDB version 3.3.0. After removing the periods of high background rates, the net exposure time was 56.1 ks. The backgrounds were estimated from the same detector regions of the blank-sky data, whose normalization factors were determined with the ratios of the 10-12 keV count rates.
Figure 9 shows the Chandra image and the
azimuthally-averaged surface brightness profiles for three different
position angles (![]() -
-
![]() ,
NW:
,
NW:
![]() -
-
![]() ,
and SE:
,
and SE:
![]() -
-
![]() ). The
cluster emission extends out to
). The
cluster emission extends out to
![]() ,
and
significant excess emission is visible in
,
and
significant excess emission is visible in
![]() for the SE quadrant.
for the SE quadrant.
To derive the average temperature profile within
![]() ,
we
extracted the spectra for the following six radial bins in the NW region,
i.e. the region outside of the SE quadrant: 0-4
,
we
extracted the spectra for the following six radial bins in the NW region,
i.e. the region outside of the SE quadrant: 0-4
![]() ,
,
![]() -
-
![]() ,
,
![]() -
-
![]() ,
,
![]() -
-
![]() ,
,
![]() -
-
![]() ,
and
,
and
![]() -
-
![]() .
The radial bins
were chosen such that the temperature profile was measured with
sufficient spatial resolution and a statistical accuracy of
.
The radial bins
were chosen such that the temperature profile was measured with
sufficient spatial resolution and a statistical accuracy of ![]() 20%.
20%.
Figure 10 shows the projected temperature profile, i.e. the
temperature profile determined from the simple APEC model fit to each
radial bin in the NW region. Our estimate of the projected temperature
profile derived from the Chandra ACIS-I data agrees with the
previous Chandra ACIS-S results reported by
Allen et al. (2002) to within the statistical errors,
particularly in the central
![]() region. Based on the ACIS-I spectral simulations, we also confirmed, assuming the same photon
statistics as the present observation, that we could securely determine
the temperature of each bin including the high-temperature (
region. Based on the ACIS-I spectral simulations, we also confirmed, assuming the same photon
statistics as the present observation, that we could securely determine
the temperature of each bin including the high-temperature (![]() 18 keV) regions between 24
18 keV) regions between 24
![]() and 120
and 120
![]() .
.
Since each spectrum is a superposition of the cluster emission from any point along the line of sight, we correct for this effect, or ``deproject'' our observations, by using the PROJCT model in the XSPEC software and fitting the six radial bins simultaneously with the assumption that the temperature distribution is spherically symmetric. As noted by Allen et al. (2002), the metal abundance gradient is marginally detected in the Chandra data; however, the large uncertainty in the metal abundance measurement does not warrant its treatment as a free function. We therefore assume that the metal abundance distribution is uniform and ignore the abundance gradient.
The resulting deprojected temperature profile in the NW region is shown in Fig. 10 and the best-fit parameters are given in Table 7. Henceforth, we refer to the best-fit model presented in Table 7 as the ``6APEC model.''
The 6APEC model in Sect. 5.1 described the average temperature structure of ambient gas, measured from the NW region. We subtracted the flux inferred by this model from the Suzaku data, and studied the nature of the excess emission in the SE quadrant.
We added another APEC model to describe the hot component in the SE
quadrant. We used the best-fit parameters for kT and K given in
Table 7 for the ambient gas (6APEC model), and used the Suzaku data, both the XIS and PIN spectra, to constrain the
temperature,
![]() ,
and the normalization,
,
and the normalization,
![]() ,
of
the excess component in the SE quadrant. As for the metal abundance,
the abundance was assumed to be equal to all of the six radial bins of
ambient gas, as well as to the excess component, i.e. a single
abundance was applied to the entire cluster. We did this because the
metal abundance was not constrained well by the Chandra data.
,
of
the excess component in the SE quadrant. As for the metal abundance,
the abundance was assumed to be equal to all of the six radial bins of
ambient gas, as well as to the excess component, i.e. a single
abundance was applied to the entire cluster. We did this because the
metal abundance was not constrained well by the Chandra data.
We found that the Chandra data tended to infer systematically
higher values for kT and K than the XIS data did. To
correct for the difference between their instrumental calibrations, we
multiplied the 6APEC model by the PLABS model,
![]() ,
with
,
with
![]() (E is the energy of photons), and used the relative
normalization factor of 0.93. In Appendix A, we provide more details on the Suzaku-Chandra cross-calibration.
(E is the energy of photons), and used the relative
normalization factor of 0.93. In Appendix A, we provide more details on the Suzaku-Chandra cross-calibration.
Figure 11 and Table 8 show the results of the
6APEC![]() PLABS + APEC model fit to the XIS (0.5-10 keV) and PIN
(12-60 keV) data. To show the degree of systematic errors due to the
uncertainty in the Suzaku-Chandra cross-calibration, we
also show the parameters for
PLABS + APEC model fit to the XIS (0.5-10 keV) and PIN
(12-60 keV) data. To show the degree of systematic errors due to the
uncertainty in the Suzaku-Chandra cross-calibration, we
also show the parameters for ![]() and 0.03 in Table 8.
From these results, we conclude that the temperature of the excess
emission in the SE quadrant is
and 0.03 in Table 8.
From these results, we conclude that the temperature of the excess
emission in the SE quadrant is
![]() keV, where the first error is statistical and the
latter is systematic (both 90% confidence levels). In Table 8, we also show the fitted parameters when only XIS was used. Due to the high
photon statistics of XIS, the temperature of the SE excess component
can be constrained to be
keV, where the first error is statistical and the
latter is systematic (both 90% confidence levels). In Table 8, we also show the fitted parameters when only XIS was used. Due to the high
photon statistics of XIS, the temperature of the SE excess component
can be constrained to be
![]() keV. However, the spectral cut-off at
keV. However, the spectral cut-off at
![]() keV coincides with the PIN band, which suggests the
importance of the broad-band spectroscopy in the present study. As
for the other quantities, we found from the XIS+PIN joint analysis that
the metal abundance was 0.38(0.35-0.41) solar, and the
absorption-corrected X-ray luminosity of the excess component was
keV coincides with the PIN band, which suggests the
importance of the broad-band spectroscopy in the present study. As
for the other quantities, we found from the XIS+PIN joint analysis that
the metal abundance was 0.38(0.35-0.41) solar, and the
absorption-corrected X-ray luminosity of the excess component was
![]() in the 0.5-10 keV,
and
in the 0.5-10 keV,
and
![]() in the 12-60 keV.
in the 12-60 keV.
Since the determination of
![]() from X-ray spectroscopy
is the central result of this paper, we estimate the other potential
source of systematic errors in our analysis. Specifically, we examine:
(i) the assumption of constant metal abundance for all radii; (ii)
the suitability in the choice of the SE region; and (iii) effects
of the uncertainty in the 6APEC model parameters.
(i) What if the metal abundance of the ambient gas differs from that of
the excess component? What if an abundance gradient
exists in the ambient gas? To explore these possibilities, we
considered the metal abundance of the excess component,
from X-ray spectroscopy
is the central result of this paper, we estimate the other potential
source of systematic errors in our analysis. Specifically, we examine:
(i) the assumption of constant metal abundance for all radii; (ii)
the suitability in the choice of the SE region; and (iii) effects
of the uncertainty in the 6APEC model parameters.
(i) What if the metal abundance of the ambient gas differs from that of
the excess component? What if an abundance gradient
exists in the ambient gas? To explore these possibilities, we
considered the metal abundance of the excess component,
![]() ,
as
well as that of the ambient gas in two larger radial bins,
,
as
well as that of the ambient gas in two larger radial bins,
![]() and
and
![]() ,
as free
parameters, and fitted them simultaneously. We found that
,
as free
parameters, and fitted them simultaneously. We found that
![]() keV,
keV,
![]() solar, and
solar, and
![]() (
(
![]() ), which are
consistent with the values given in Table 8. As for the
metal abundance of the ambient gas, we found that
), which are
consistent with the values given in Table 8. As for the
metal abundance of the ambient gas, we found that ![]() solar and
0.22 solar in
solar and
0.22 solar in
![]() and
and
![]() ,
respectively; (ii) from the Chandra image, we can observe that the excess emission appears to extend over slightly more than the SE
quadrant. How does this affect the determination of
,
respectively; (ii) from the Chandra image, we can observe that the excess emission appears to extend over slightly more than the SE
quadrant. How does this affect the determination of
![]() ?
We repeated our analysis with the SE and NW regions redefined as
?
We repeated our analysis with the SE and NW regions redefined as
![]() -
-
![]() and
and
![]() -
-
![]() ,
respectively. We measured
,
respectively. We measured
![]() keV,
keV,
![]() ,
and
,
and
![]() solar with
solar with
![]() .
Therefore, selecting the SE
region did not affect the best-fit parameters significantly;
(iii) the statistical errors in the 6APEC model parameters had
not been propagated through the spectral fitting of the SE quadrant,
except for the cross-calibration error in the spectral slope, which
was included by varying
.
Therefore, selecting the SE
region did not affect the best-fit parameters significantly;
(iii) the statistical errors in the 6APEC model parameters had
not been propagated through the spectral fitting of the SE quadrant,
except for the cross-calibration error in the spectral slope, which
was included by varying ![]() from 0 to 0.03. To address this, we
completed simultaneous APEC fits to the Chandra spectra in 6 radial bins (without deprojection) as well as to the Suzaku
XIS and PIN spectra, for which we used the 6 APEC models multiplied
by the
from 0 to 0.03. To address this, we
completed simultaneous APEC fits to the Chandra spectra in 6 radial bins (without deprojection) as well as to the Suzaku
XIS and PIN spectra, for which we used the 6 APEC models multiplied
by the
![]() PLABS model, and then added to the additional APEC
model. We found that
PLABS model, and then added to the additional APEC
model. We found that
![]() keV,
keV,
![]() -0.41) solar, and
-0.41) solar, and
![]() -
-
![]() (
(
![]() ). Although the temperature was not well
constrained in this case, it was of a high value.
From these studies we conclude that our estimate,
). Although the temperature was not well
constrained in this case, it was of a high value.
From these studies we conclude that our estimate,
![]() keV, is robust.
keV, is robust.
Finally, as a consistency check, we analyzed the Chandra spectrum
of the SE quadrant (r<5') on its own, without the Suzaku data,
in the same manner. The best-fit parameters for the excess
component were
![]() keV,
keV,
![]() solar, and
solar, and
![]() (
(
![]() ). Therefore, both the Chandra-alone analysis and
the joint Chandra+Suzaku analysis implied that the excess
emission had a temperature in excess of 20 keV
). Therefore, both the Chandra-alone analysis and
the joint Chandra+Suzaku analysis implied that the excess
emission had a temperature in excess of 20 keV![]() .
.
Compared with the results for the Chandra data alone, the joint
Chandra+Suzaku broad-band data analysis yielded a far more
accurate determination of
![]() .
The Suzaku's
unprecedented sensitivity over the wide X-ray band made it possible to determine, for the first time, the temperature of the hot gas in the
ICM solely from the X-ray spectroscopy without the help of SZ effect data.
.
The Suzaku's
unprecedented sensitivity over the wide X-ray band made it possible to determine, for the first time, the temperature of the hot gas in the
ICM solely from the X-ray spectroscopy without the help of SZ effect data.
We had been assuming that the excess hard X-ray emission from the SE quadrant is thermal; could it, however, be non-thermal? If so, our derived temperature must be reconsidered.
To address this question, the XIS and PIN data were re-analyzed in light
of non-thermal emission. While the 6APEC thermal plasma model was again
used for the ambient gas, the APEC model was replaced with a power-law
(PL) spectrum for describing the excess component. We then fitted the new
model, ``6APEC![]() PLABS+PL model'', to the observed XIS and PIN data. The amplitude (normalization), a power-law index,
PLABS+PL model'', to the observed XIS and PIN data. The amplitude (normalization), a power-law index, ![]() ,
of
the non-thermal component, and the metal abundance of the ambient gas
were treated as free parameters.
,
of
the non-thermal component, and the metal abundance of the ambient gas
were treated as free parameters.
Figure 12 shows the results, and Table 9 lists the
best-fit parameters. We found that the power-law index is given by
![]() ,
or more precisely
,
or more precisely
![]() .
The reduced
.
The reduced
![]() of this model,
of this model,
![]() (see Table 9),
was slightly higher than that for the thermal model,
(see Table 9),
was slightly higher than that for the thermal model,
![]() (see Table 8), and negative residuals were seen
in consecutive bins above 22 keV.
(see Table 8), and negative residuals were seen
in consecutive bins above 22 keV.
We examined the non-thermal model more closely. In the XIS band
below 10 keV, the non-thermal model with
![]() and the thermal
APEC model with 25 keV could hardly be distinguished. However, the
observed PIN spectrum was far softer than
and the thermal
APEC model with 25 keV could hardly be distinguished. However, the
observed PIN spectrum was far softer than
![]() ,
the
effective photon index being
,
the
effective photon index being
![]() .
When we fitted
the 6APEC
.
When we fitted
the 6APEC![]() PLABS+PL model to the PIN data alone, the 90% lower
bound on the photon index was found to be
PLABS+PL model to the PIN data alone, the 90% lower
bound on the photon index was found to be
![]()
![]() , which was
significantly above the 90% upper bound on
, which was
significantly above the 90% upper bound on ![]() from the XIS
data,
from the XIS
data,
![]() .
We further checked that fixing the power-law
index to
.
We further checked that fixing the power-law
index to
![]() ,
as predicted from the non-thermal
bremsstrahlung in the strong shock limit (Sarazin & Kempner 2000),
yielded a poor fit to the XIS and PIN data; the reduced
,
as predicted from the non-thermal
bremsstrahlung in the strong shock limit (Sarazin & Kempner 2000),
yielded a poor fit to the XIS and PIN data; the reduced ![]() was
1708 for 1220 degrees of freedom. Therefore, it appears difficult to
explain the SE excess component with the non-thermal PL model.
was
1708 for 1220 degrees of freedom. Therefore, it appears difficult to
explain the SE excess component with the non-thermal PL model.
Given that the excess component was described more accurately by thermal
emission than non-thermal emission, we derived an upper limit to
the non-thermal emission to characterize the SE component. We
fixed the metal abundance and the PL index to be 0.38 solar and
![]() ,
respectively. The 6APEC model, modified by the
,
respectively. The 6APEC model, modified by the
![]() PLABS model, was again used for describing the ambient
gas.
PLABS model, was again used for describing the ambient
gas.
The derived upper limits are given in Table 10. Taking into
account the NXB systematic error of the PIN detector, the 3![]() upper limit to the non-thermal flux in the 12-60 keV,
upper limit to the non-thermal flux in the 12-60 keV,
![]() ,
was estimated to be
,
was estimated to be
![]() from the PIN analysis, and
from the PIN analysis, and
![]() from the XIS+PIN
simultaneous fit. Here, the 1
from the XIS+PIN
simultaneous fit. Here, the 1![]() error was calculated by adding the
1
error was calculated by adding the
1![]() statistical error and the 1
statistical error and the 1![]() systematic error in
quadrature.
systematic error in
quadrature.
Using the deep broad-band observations of RX J1347.5-1145
with Suzaku, the temperature structure has been determined with
particular attention to the extremely hot gas. We have found that a
multi-temperature thermal emission model including a very hot
(
![]() keV) component fits the wide-band spectra
well. We have also placed an upper limit on the non-thermal hard X-ray emission.
keV) component fits the wide-band spectra
well. We have also placed an upper limit on the non-thermal hard X-ray emission.
In Sect. 6.1, our results are compared with previous X-ray and radio observations, and examine further the physical properties of the SE clump. In Sect. 6.2, our results are compared with those for the radio mini halo in this cluster discovered from 1.4 GHz radio observations to estimate the magnetic-field strength in the ICM.
Table 7: Parameters of the ``6APEC model'', including estimates of the deprojected temperature profile from the Chandra ACIS-I data at the six annular bins in the NW region, which excludes the SE quadrant.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{0122f10a.eps} \includegraphics[angle=-90,width=7.5cm,clip]{0122f10b.eps}\end{figure}](/articles/aa/full/2008/44/aa10122-08/Timg197.gif) |
Figure 10: a) Projected (crosses) and deprojected (circles) temperature profiles measured from the Chandra data in the NW region. b) Projected metal abundance profile (crosses). The horizontal dashed and dotted lines show the best-fit constant abundance and the corresponding 90% confidence interval obtained from the deprojection analysis, respectively. We assume that the metal abundance is constant over all radial bins throughout this paper. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{0122f11a.eps} \includegraphics[angle=-90,width=7.5cm,clip]{0122f11b.eps}\end{figure}](/articles/aa/full/2008/44/aa10122-08/Timg198.gif) |
Figure 11:
a) 6APEC |
| Open with DEXTER | |
From the analysis of the Suzaku spectra of
RX J1347.5-1145, the temperature of the SE excess emission
was obtained to be
![]() keV (90% confidence level; the first error being statistical and the second, systematic). This was in an excellent agreement with the previous measurement by Kitayama et al. (2004),
keV (90% confidence level; the first error being statistical and the second, systematic). This was in an excellent agreement with the previous measurement by Kitayama et al. (2004),
![]() keV (68%; statistical only), from a joint analysis of the SZ data
(Komatsu et al. 2001,1999) and the Chandra
ACIS-S3 data (Allen et al. 2002). Here, we compare our
X-ray-only results with their SZ+X-ray results.
keV (68%; statistical only), from a joint analysis of the SZ data
(Komatsu et al. 2001,1999) and the Chandra
ACIS-S3 data (Allen et al. 2002). Here, we compare our
X-ray-only results with their SZ+X-ray results.
We estimate the gas density and gas mass of the SE excess component
from the Suzaku and Chandra data. For simplicity, we
assume that the extremely hot gas is uniformly distributed within a
sphere of a radius
![]() kpc (because the excess is
present in
kpc (because the excess is
present in
![]() ;
Fig. 9b). Using the
measured spectral normalization,
;
Fig. 9b). Using the
measured spectral normalization,
![]() ,
which depends on
,
which depends on
![]() (where
(where
![]() is the volume of the gas and
is the volume of the gas and
![]() ), the electron density,
), the electron density,
![]() ,
and the gas mass,
,
and the gas mass,
![]() ,
are obtained as:
,
are obtained as:
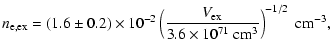 |
(2) | ||
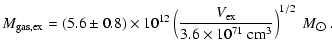 |
(3) |
How does the excess component compare with the remainder of the cluster?
The average (ambient) temperature and gas density for
![]() ,
excluding the SE quadrant, are
,
excluding the SE quadrant, are
![]() keV from the Chandra spectrum and
keV from the Chandra spectrum and
![]() from Eqs. (3)-(5) of
Kitayama et al. (2004), respectively. Thus, the SE clump exhibits
the temperature and the density that are higher than the ambient gas
in the same radial bins by factors of 1.7 and 2.4, respectively. This
means that the excess hot component is over-pressured, and such a
region is expected to be short-lived,
from Eqs. (3)-(5) of
Kitayama et al. (2004), respectively. Thus, the SE clump exhibits
the temperature and the density that are higher than the ambient gas
in the same radial bins by factors of 1.7 and 2.4, respectively. This
means that the excess hot component is over-pressured, and such a
region is expected to be short-lived, ![]() 0.5 Gyr
(Takizawa 1999).
0.5 Gyr
(Takizawa 1999).
As already discussed in Kitayama et al. (2004), the gas properties
can be explained by a fairly recent (within the last 0.5 Gyr or so),
bullet-like high velocity (
![]() )
collision of two massive (
)
collision of two massive (
![]() )
clusters.
)
clusters.
The heat energy of the SE clump is also estimated to be
![]() .
This enormous amount of energy
cannot be easily produced by a central source in the cluster: one
would need an AGN with
.
This enormous amount of energy
cannot be easily produced by a central source in the cluster: one
would need an AGN with
![]() for at least 1 Gyr
and to place the energy into the SE region without any radiative loss. On
the other hand, cluster mergers, which are the most energetic events
in the Universe after the Big Bang, will most naturally explain this
high energy phenomenon. Therefore, our results support a merger
scenario, on the basis of the X-ray spectroscopic data alone without the help of SZ data.
for at least 1 Gyr
and to place the energy into the SE region without any radiative loss. On
the other hand, cluster mergers, which are the most energetic events
in the Universe after the Big Bang, will most naturally explain this
high energy phenomenon. Therefore, our results support a merger
scenario, on the basis of the X-ray spectroscopic data alone without the help of SZ data.
On the basis of our upper limit to the non-thermal hard X-ray emission derived from Suzaku HXD/PIN data, what can be learned about the underlying physics of the cluster X-ray emission?
The non-thermal hard X-ray emission is produced by the inverse Compton (IC) scattering of relativistic electrons off the Cosmic Microwave
Background (CMB) photons, and the same population of electrons also
generate synchrotron radiation. From the exact derivations by
Blumenthal & Gould (1970), equations for the synchrotron emission
at the frequency
![]() and the IC emission at
and the IC emission at
![]() are:
are:
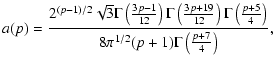 |
(6) | ||
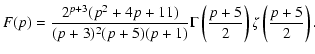 |
(7) |
Table 8:
Spectral parameters for the SE excess component obtained
from the 6APEC ![]() PLABS + APEC model fit to the XIS+PIN data and the XIS data.
PLABS + APEC model fit to the XIS+PIN data and the XIS data.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{0122f12a.eps} \includegraphics[angle=-90,width=7.5cm,clip]{0122f12b.eps}\end{figure}](/articles/aa/full/2008/44/aa10122-08/Timg236.gif) |
Figure 12:
a) 6APEC |
| Open with DEXTER | |
We find
![]() from our limit on the
non-thermal hard X-ray emission for electrons with the IC emission
energy (frequency) of 12 keV (
from our limit on the
non-thermal hard X-ray emission for electrons with the IC emission
energy (frequency) of 12 keV (
![]() Hz).
As for
Hz).
As for
![]() ,
Gitti et al. (2007a) discovered extended
(
,
Gitti et al. (2007a) discovered extended
(![]() 500 kpc) radio emission in RX J1347.5-1145 based on
their low (18
500 kpc) radio emission in RX J1347.5-1145 based on
their low (18
![]() )
resolution VLA observations and higher
(2
)
resolution VLA observations and higher
(2
![]() )
resolution data in the VLA archive. They subtracted the
contribution of discrete radio sources and estimated the total flux
density of the diffuse radio emission to be
)
resolution data in the VLA archive. They subtracted the
contribution of discrete radio sources and estimated the total flux
density of the diffuse radio emission to be
![]() mJy at
mJy at
![]() GHz. Combining these numbers with
Eqs. (4) and (5), a lower bound to the magnetic-field
strength in the ICM is obtained such that
GHz. Combining these numbers with
Eqs. (4) and (5), a lower bound to the magnetic-field
strength in the ICM is obtained such that
![]() for
for
![]() .
The estimation is sensitive to the assumption of p: for example, in the case of p=3,
.
The estimation is sensitive to the assumption of p: for example, in the case of p=3,
![]() .
.
This limit, though weak, is consistent with typical values found for
other clusters,
![]() -
-
![]() ,
based on RXTE and
Beppo-SAX observations (e.g. Rephaeli et al. 2008).
Our result also agrees with results for Suzaku observations of a
merging cluster A3376 at z=0.046,
,
based on RXTE and
Beppo-SAX observations (e.g. Rephaeli et al. 2008).
Our result also agrees with results for Suzaku observations of a
merging cluster A3376 at z=0.046,
![]() (Kawano et al. 2008). However, the previous measurements were derived mostly for nearby (z<0.1) clusters as well as some
medium-redshift clusters, such as A2163 at z=0.20(Rephaeli et al. 2006) and the Bullet cluster at
z=0.296 (Petrosian et al. 2006). Our work provides a constraint
on the cluster magnetic-field strength at a higher redshift,
z=0.451.
(Kawano et al. 2008). However, the previous measurements were derived mostly for nearby (z<0.1) clusters as well as some
medium-redshift clusters, such as A2163 at z=0.20(Rephaeli et al. 2006) and the Bullet cluster at
z=0.296 (Petrosian et al. 2006). Our work provides a constraint
on the cluster magnetic-field strength at a higher redshift,
z=0.451.
We have reported results of an analysis of Suzaku wide-band (0.5-10 keV with XIS and 12-60 keV with HXD/PIN) X-ray spectroscopic observations of the most luminous X-ray cluster, RX J1347.5-1145, at z=0.451, to investigate the temperature structure of the ICM, signatures of a recent violent merger, as well as signatures of the non-thermal emission.
This cluster is known to contain a very hot gas clump that produces
excess emission of the ambient gas that follows
more-or-less the conventional ![]() model
(Kitayama et al. 2004; Komatsu et al. 2001; Allen et al. 2002).
The temperature of this gas clump was not measured accurately
from the previous X-ray spectroscopic observations, because the
sensitivities degraded significantly at energies above 10 keV.
model
(Kitayama et al. 2004; Komatsu et al. 2001; Allen et al. 2002).
The temperature of this gas clump was not measured accurately
from the previous X-ray spectroscopic observations, because the
sensitivities degraded significantly at energies above 10 keV.
Our re-analysis of the Chandra data confirmed the result of previous work, and yielded a poor limit on the temperature of the excess hot
component,
![]() keV (90%
confidence level; statistical). When the hard X-ray data from the Suzaku XIS spectra in the 0.5-10 keV region and the HXD/PIN data in the 12-60 keV were combined with the Chandra data, we finally obtained
a good measurement of the temperature,
25.3+6.1-4.5 (+6.9-9.5) keV (90% confidence level; statistical and
systematic), which was in excellent agreement with that derived from
the previous joint analysis of the SZ effect and X-ray imaging
observations (Kitayama et al. 2004). We emphasize that this is the
first time that X-ray spectroscopic observations alone have enabled a robust analysis of such a high temperature gas component, due to Suzaku's unprecedented sensitivity over the wide X-ray
band.
keV (90%
confidence level; statistical). When the hard X-ray data from the Suzaku XIS spectra in the 0.5-10 keV region and the HXD/PIN data in the 12-60 keV were combined with the Chandra data, we finally obtained
a good measurement of the temperature,
25.3+6.1-4.5 (+6.9-9.5) keV (90% confidence level; statistical and
systematic), which was in excellent agreement with that derived from
the previous joint analysis of the SZ effect and X-ray imaging
observations (Kitayama et al. 2004). We emphasize that this is the
first time that X-ray spectroscopic observations alone have enabled a robust analysis of such a high temperature gas component, due to Suzaku's unprecedented sensitivity over the wide X-ray
band.
Table 9:
Spectral parameters for the SE excess component obtained
from the 6APEC ![]() PLABS+non-thermal power-law (PL) model fit to the XIS+PIN data.
PLABS+non-thermal power-law (PL) model fit to the XIS+PIN data.
Table 10:
Limits on the amplitude (normalization) of a non-thermal
power-law (PL) component with
![]() as the explanation of the
excess hard X-ray emission in the SE quadrant.
as the explanation of the
excess hard X-ray emission in the SE quadrant.
We have found that the broad-band X-ray spectrum is described more accurately
by a thermal plasma model instead of a non-thermal power-law model.
The present result therefore confirms the presence of the hottest thermal gas in the cluster. The most likely explanation for this
phenomena is a recent violent merger at a collision velocity of
![]() 4500 km s-1, similar to that inferred for the Bullet
cluster (Mastropietro & Burkert 2007; Nusser 2008; Milosavljevic et al. 2007; Springel & Farrar 2007).
4500 km s-1, similar to that inferred for the Bullet
cluster (Mastropietro & Burkert 2007; Nusser 2008; Milosavljevic et al. 2007; Springel & Farrar 2007).
The upper bound on the non-thermal flux in the 12-60 keV band,
![]() ,
yields, when
combined with the discovery of a radio mini halo in this
cluster by Gitti et al. (2007a), a lower bound to the ICM
magnetic-field strength,
,
yields, when
combined with the discovery of a radio mini halo in this
cluster by Gitti et al. (2007a), a lower bound to the ICM
magnetic-field strength,
![]() for the electron
index of 2. These constraints provide valuable information on the
non-thermal nature of the cluster gas and the particle acceleration in
a high-redshift universe. However, the accuracy of the present
measurement of the hard X-ray emission is limited by the sensitivity
of the instrument. If the magnetic field in
RX J1347.5-1145 was comparable to that of the other
clusters,
for the electron
index of 2. These constraints provide valuable information on the
non-thermal nature of the cluster gas and the particle acceleration in
a high-redshift universe. However, the accuracy of the present
measurement of the hard X-ray emission is limited by the sensitivity
of the instrument. If the magnetic field in
RX J1347.5-1145 was comparable to that of the other
clusters,
![]() ,
a 50-fold higher
sensitivity would be required to detect non-thermal hard X-ray emission from this cluster.
We expect that future X-ray missions (e.g. NeXT; Takahashi et al. 2008)
will determine the non-thermal X-ray flux more accurately and draw more definitive conclusions.
,
a 50-fold higher
sensitivity would be required to detect non-thermal hard X-ray emission from this cluster.
We expect that future X-ray missions (e.g. NeXT; Takahashi et al. 2008)
will determine the non-thermal X-ray flux more accurately and draw more definitive conclusions.
Before the advent of the Suzaku satellite, it was difficult to
measure the high-temperature (![]() 10 keV) gas in the X-ray band
reliably, due to limited sensitivity. The present paper
demonstrates the power of broad-band X-ray spectroscopy in the
study of gas heating due to a cluster merger, which is
complementary to observations of the SZ effect. In the near future,
we expect the number of merging clusters observed with Suzaku to increase rapidly, which should shed new light on the
physics of these violent mergers.
10 keV) gas in the X-ray band
reliably, due to limited sensitivity. The present paper
demonstrates the power of broad-band X-ray spectroscopy in the
study of gas heating due to a cluster merger, which is
complementary to observations of the SZ effect. In the near future,
we expect the number of merging clusters observed with Suzaku to increase rapidly, which should shed new light on the
physics of these violent mergers.
Acknowledgements
We are grateful to the Suzaku team members for the operation and the instrument calibrations. We also thank H. Böhringer, T. Ohashi, K. Masai, N. Y. Yamasaki, K. Mitsuda, and R. Smith for discussions and comments. NO acknowledges support from the Alexander von Humboldt Foundation in Germany. This work is supported in part by the Grant-in-Aid by the Ministry of Education, Culture, Sports, Science and Technology, 19740112 (NO) and 18740112 (TK). E.K. acknowledges support from an Alfred P. Sloan Research Fellowship.
Because the temperature measurement of very hot gas based on a spectral fit is sensitive to subtle changes in the spectral slope, a precise calibration of the effective area is critical. In the analysis of XIS+HXD spectra (Sect. 5), we have modeled the cluster average emission with Chandra. The cross-calibration between Suzaku/XIS and Chandra/ACIS-I data is therefore mandatory.
If the global cluster spectrum is accumulated from a r<5' circular
region with the Chandra/ACIS-I data, the APEC model fitting infers
kT=14.4(13.6-15.3) keV,
Z=0.45(0.38-0.52) solar,
K=1.47(1.45-
![]() (
(
![]() ), where
z=0.451 and
), where
z=0.451 and
![]() are
adopted. In comparison with the best-fit XIS parameters
(Table 2), the temperature and the normalization are higher
by about 1.5 keV and 7% for the Chandra data. We discuss below the possible reasons for these differences in the light of the Suzaku and Chandra calibration
uncertainties.
are
adopted. In comparison with the best-fit XIS parameters
(Table 2), the temperature and the normalization are higher
by about 1.5 keV and 7% for the Chandra data. We discuss below the possible reasons for these differences in the light of the Suzaku and Chandra calibration
uncertainties.
To simulate the effect of ![]() ,
we multiplied the APEC model
by the PLABS model,
,
we multiplied the APEC model
by the PLABS model,
![]() ,
with
,
with
![]() and fitted this to the
XIS+PIN spectra. The best-fit parameters were derived to be
kT=11.85 keV, Z=0.30 solar, and
and fitted this to the
XIS+PIN spectra. The best-fit parameters were derived to be
kT=11.85 keV, Z=0.30 solar, and
![]() (
(
![]() ). This indicated that the Suzaku
temperature measurement had a systematic error at the level of
). This indicated that the Suzaku
temperature measurement had a systematic error at the level of
![]() 1 keV, although this then had the effect of increasing discrepancy between Suzaku and Chandra data results. The uncertainty in the Suzaku
effective area is therefore unlikely to be a major source of the discrepancy.
1 keV, although this then had the effect of increasing discrepancy between Suzaku and Chandra data results. The uncertainty in the Suzaku
effective area is therefore unlikely to be a major source of the discrepancy.
For example, fitting the Chandra data with the APEC model
multiplied by the
![]() PLABS model leads to
kT=12.89 keV, Z=0.40 solar, and
PLABS model leads to
kT=12.89 keV, Z=0.40 solar, and
![]() (
(
![]() ). Although the metal abundance is
marginally higher, the temperature agrees with that of XIS.
). Although the metal abundance is
marginally higher, the temperature agrees with that of XIS.
By then simultaneously fitting the Chandra and XIS spectra
with the APEC![]() PLABS model, we determined
PLABS model, we determined ![]() and the
relative normalization factor to be
and the
relative normalization factor to be
![]() and
1.07(1.06-1.08), respectively. The best-fit APEC parameters were
kT=12.92 keV, Z=0.35 solar, and
and
1.07(1.06-1.08), respectively. The best-fit APEC parameters were
kT=12.92 keV, Z=0.35 solar, and
![]() (
(
![]() ). The result is plotted in
Fig. A.1.
). The result is plotted in
Fig. A.1.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{0122fa1.eps}\end{figure}](/articles/aa/full/2008/44/aa10122-08/Timg286.gif) |
Figure A.1:
Suzaku/XIS+ Chandra/ACIS-I spectra of
RX J1347.5-1145 (
|
| Open with DEXTER | |