A&A 489, 263-279 (2008)
DOI: 10.1051/0004-6361:200809772
Detailed high-energy characteristics of AXP 1RXS J170849-400910
Probing the magnetosphere using INTEGRAL, RXTE, and XMM-Newton
P. R. den Hartog1 - L. Kuiper1 - W. Hermsen1,2
1 - SRON, Netherlands Institute for Space Research,
Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
2 - Sterrenkundig Instituut Anton Pannekoek, University of Amsterdam,
Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
Received 12 March 2008 / Accepted 10 June 2008
Abstract
1RXS J170849-400910 is one of four anomalous X-ray pulsars
which emit persistent luminous radiation in soft X-rays (<10 keV)
as well as in hard X-rays (>10 keV). In this paper we present
detailed spectral and temporal characteristics over the whole X-ray
band. For this purpose data have been used from INTEGRAL, RXTE and XMM-Newton.
The hard X-ray (>10 keV) time-averaged total spectrum, accumulated
over four years with the imager IBIS-ISGRI onboard INTEGRAL adding up
to 5.2 Ms net exposure, can be described by a power law with a
photon index
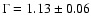 and extends to
and extends to
 175 keV. The 20-175 keV flux is
175 keV. The 20-175 keV flux is
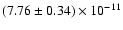 erg cm-2 s-1 which exceeds the 2-10 keV (unabsorbed) flux by a
factor of
erg cm-2 s-1 which exceeds the 2-10 keV (unabsorbed) flux by a
factor of  2.3. No evidence for a spectral break is found below
300 keV. Also, no significant long-term time variability has been
detected above 20 keV on time scales of 1 and 0.5 year. Pulsed
emission is measured with INTEGRAL up to 270 keV, i.e. to much higher
energies than the total emission, with a detection significance of
12.3
2.3. No evidence for a spectral break is found below
300 keV. Also, no significant long-term time variability has been
detected above 20 keV on time scales of 1 and 0.5 year. Pulsed
emission is measured with INTEGRAL up to 270 keV, i.e. to much higher
energies than the total emission, with a detection significance of
12.3 (20-270 keV). The pulse profiles from 0.5 keV up to
270 keV show drastic morphology changes below
(20-270 keV). The pulse profiles from 0.5 keV up to
270 keV show drastic morphology changes below  20 keV. Three
different pulse components can be recognized in these pulse
profiles: 1) a hard pulse peaking around phase 0.8 which contributes
to the pulse profiles above
20 keV. Three
different pulse components can be recognized in these pulse
profiles: 1) a hard pulse peaking around phase 0.8 which contributes
to the pulse profiles above  4 keV; 2) a softer pulse which
peaks around phase 0.4 not contributing in the hard X-ray domain and 3) a very soft pulse component below 2 keV. A combined
time-averaged pulsed spectrum (2.8-270 keV) from INTEGRAL, RXTE-PCA and
HEXTE (collected over nine years) can be described with a soft and a
hard power-law component:
4 keV; 2) a softer pulse which
peaks around phase 0.4 not contributing in the hard X-ray domain and 3) a very soft pulse component below 2 keV. A combined
time-averaged pulsed spectrum (2.8-270 keV) from INTEGRAL, RXTE-PCA and
HEXTE (collected over nine years) can be described with a soft and a
hard power-law component:
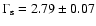 and
and
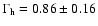 .
In the pulsed spectrum extracted
from a 25.5 ks net exposure XMM-Newton observation we find a
discontinuity between 2 keV and 3 keV. Above these energies the
spectrum is consistent with the spectrum taken with RXTE-PCA. The pulse
profiles and the total-pulsed spectrum prove to be stable over the
whole nine-years time span over which the data have been taken. Also
detailed phase-resolved spectroscopy of the pulsed emission confirms
the long-term stability as the spectra taken at different epochs
connect smoothly. The phase-resolved spectra reveal complex spectral
shapes which do not follow the shape of the total-pulsed
spectrum. The spectral shape gradually changes with phase from a
soft single power law to a complex multi-component shape and then to
a hard single power law. The spectrum switches from a very hard
(
.
In the pulsed spectrum extracted
from a 25.5 ks net exposure XMM-Newton observation we find a
discontinuity between 2 keV and 3 keV. Above these energies the
spectrum is consistent with the spectrum taken with RXTE-PCA. The pulse
profiles and the total-pulsed spectrum prove to be stable over the
whole nine-years time span over which the data have been taken. Also
detailed phase-resolved spectroscopy of the pulsed emission confirms
the long-term stability as the spectra taken at different epochs
connect smoothly. The phase-resolved spectra reveal complex spectral
shapes which do not follow the shape of the total-pulsed
spectrum. The spectral shape gradually changes with phase from a
soft single power law to a complex multi-component shape and then to
a hard single power law. The spectrum switches from a very hard
(
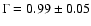 )
to a very soft (
)
to a very soft (
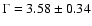 )
single power-law shape within a 0.1-wide phase interval. The
discontinuity measured between 2 keV and 3 keV with XMM-Newton is a
result of a curved component. This component which is most apparent
within phase interval 0.7-0.9 significantly contributes in the
energy range between 4 keV and 20 keV. It has a very steep spectrum
below 5 keV with a photon index
)
single power-law shape within a 0.1-wide phase interval. The
discontinuity measured between 2 keV and 3 keV with XMM-Newton is a
result of a curved component. This component which is most apparent
within phase interval 0.7-0.9 significantly contributes in the
energy range between 4 keV and 20 keV. It has a very steep spectrum
below 5 keV with a photon index
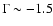 .
From the
phase-resolved spectra we identify three independent components with
different spectral shapes which together can accurately describe all
phase-resolved spectra (2.8-270 keV). The three shapes are a soft
power law (
.
From the
phase-resolved spectra we identify three independent components with
different spectral shapes which together can accurately describe all
phase-resolved spectra (2.8-270 keV). The three shapes are a soft
power law (
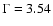 ), a hard power law (
), a hard power law (
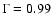 )
and
a curved shape (described with two logparabolic functions). The
phase distributions of the normalizations of these spectral
components form three decoupled pulse profiles. The soft component
peaks around phase 0.4 while the other two components peak around
phase 0.8. The width of the curved component (
)
and
a curved shape (described with two logparabolic functions). The
phase distributions of the normalizations of these spectral
components form three decoupled pulse profiles. The soft component
peaks around phase 0.4 while the other two components peak around
phase 0.8. The width of the curved component ( 0.25 in phase)
is about half the width of the hard component. After 142, 1708
is the second anomalous X-ray pulsar for which such detailed
phase-resolved spectroscopy has been performed. These results give
important constraints showing that three dimensional modeling
covering both the geometry and different production processes is
required to explain our findings.
0.25 in phase)
is about half the width of the hard component. After 142, 1708
is the second anomalous X-ray pulsar for which such detailed
phase-resolved spectroscopy has been performed. These results give
important constraints showing that three dimensional modeling
covering both the geometry and different production processes is
required to explain our findings.
Key words: stars: neutron - X-rays: individuals:
1RXS J170849-400910 -
gamma rays:
observations - X-rays: individuals: 4U 0142+61
1 Introduction
In the past five years, several new developments have changed our view
on anomalous X-ray pulsars (AXPs) drastically (see for a recent
review Kaspi 2007). AXPs are young isolated rotating neutron
stars. Their spin periods and spin derivatives indicate that the
surface magnetic fields of AXPs range from 
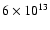 G
to
G
to 
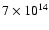 G (assuming a dipole field;
G (assuming a dipole field;
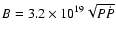 G). The X-ray luminosity of
persistent AXPs can be orders of magnitude higher than explained by
spin-down power. Nowadays, it is generally accepted that AXPs are
powered by magnetic dissipation and that AXPs belong to the magnetar
class (Thompson & Duncan 1995,1996; Duncan & Thompson 1992; Thompson & Duncan 1993; Thompson et al. 2002). To the magnetar class also
belong Soft Gamma-ray Repeaters (SGRs) (Mereghetti et al. 2007; Woods & Thompson 2006). So far, there are in total 13 confirmed
magnetars known.
G). The X-ray luminosity of
persistent AXPs can be orders of magnitude higher than explained by
spin-down power. Nowadays, it is generally accepted that AXPs are
powered by magnetic dissipation and that AXPs belong to the magnetar
class (Thompson & Duncan 1995,1996; Duncan & Thompson 1992; Thompson & Duncan 1993; Thompson et al. 2002). To the magnetar class also
belong Soft Gamma-ray Repeaters (SGRs) (Mereghetti et al. 2007; Woods & Thompson 2006). So far, there are in total 13 confirmed
magnetars known.
Traditionally, AXPs are soft X-ray sources ( 0.5-10 keV) with
thermal-like spectra (
0.5-10 keV) with
thermal-like spectra (
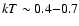 keV) plus a soft
power-law-like component with a photon index
keV) plus a soft
power-law-like component with a photon index
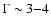 .
This
traditional view changed since the detections of extremely bright and
persistent hard X-ray emission from AXPs by
INTEGRAL (>20 keV Molkov et al. 2004; den Hartog et al. 2004; Revnivtsev et al. 2004). The hard X-ray spectra of these AXPs can be
described with power-law models with photon indices
.
This
traditional view changed since the detections of extremely bright and
persistent hard X-ray emission from AXPs by
INTEGRAL (>20 keV Molkov et al. 2004; den Hartog et al. 2004; Revnivtsev et al. 2004). The hard X-ray spectra of these AXPs can be
described with power-law models with photon indices
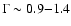 and are observed up to 230 keV
(den Hartog et al. 2008; Kuiper et al. 2004a,2006; den Hartog et al. 2006).
Because no counterparts have been found in the MeV gamma-ray domain by
CGRO-COMPTEL (0.75-30 MeV), these spectra are expected to show
breaks. For AXP 142 den Hartog et al. (2008) measured the first
spectral break in an AXP hard X-ray spectrum. The maximum luminosity
of 142 is estimated to be near 280 keV.
and are observed up to 230 keV
(den Hartog et al. 2008; Kuiper et al. 2004a,2006; den Hartog et al. 2006).
Because no counterparts have been found in the MeV gamma-ray domain by
CGRO-COMPTEL (0.75-30 MeV), these spectra are expected to show
breaks. For AXP 142 den Hartog et al. (2008) measured the first
spectral break in an AXP hard X-ray spectrum. The maximum luminosity
of 142 is estimated to be near 280 keV.
Moreover, Kuiper et al. (2006,2004a) found that a
significant part of the hard X-ray emission is pulsed with spectral
shapes harder than the total-emission spectra. For 142 pulsed
emission was detected up to 160 keV by den Hartog et al. (2008).
These authors performed for 142 a phase-resolved spectral analysis
of the pulsed emission (i.e. without the dominating non-pulsating DC
emission) in a broad band from 0.5 keV to 160 keV exploiting data
from four space missions. In that study den Hartog et al. (2008)
showed that in the pulse profiles at least three different pulse
components can be recognized which appeared to have different
spectra. Therefore, these pulse components are genuinely different
from each other. These findings provide new constraints for modelling
the underlying physical processes responsible for these spectra and
the geometry of the production sites in the AXP
magnetospheres. Theoretical models currently in development
(e.g. Heyl & Hernquist 2005b; Beloborodov & Thompson 2007; Baring & Harding 2007) do so far not
explain these detailed results.
In this paper we present new high-energy results from AXP
1RXS J170849-400910 (hereafter 1708). 1708 has a spin period
of P = 11.0 s and a period derivative of
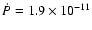 s s-1 (Gavriil & Kaspi 2002). The
characteristic age (
s s-1 (Gavriil & Kaspi 2002). The
characteristic age (
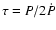 )
dipolar surface
magnetic-field strength of 1708 inferred from these values are 9.0 kyr and
)
dipolar surface
magnetic-field strength of 1708 inferred from these values are 9.0 kyr and
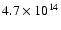 G, respectively. In the 2-10 keV band
its luminosity
G, respectively. In the 2-10 keV band
its luminosity 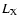 is
is
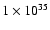 erg s-1, similar to all
other AXPs assuming a distance of 3.8 kpc
(Durant & van Kerkwijk 2006a). Soon after its discovery
(Sugizaki et al. 1997) 1708 has been included in the RXTE
monitoring program of AXPs (Gavriil & Kaspi 2002), providing
a long base-line of observations with a wealth of new information like
timing parameters, pulsed-flux history and glitches (see
e.g. Kaspi et al. 1999; Dib et al. 2008). For this source an
intensity-hardness correlation in the soft X-ray band (<10 keV) is
claimed (Campana et al. 2007; Rea et al. 2007). An indication that this
correlation also holds in the hard X-ray domain
(>10 keV Götz et al. 2007) is not confirmed in this work.
erg s-1, similar to all
other AXPs assuming a distance of 3.8 kpc
(Durant & van Kerkwijk 2006a). Soon after its discovery
(Sugizaki et al. 1997) 1708 has been included in the RXTE
monitoring program of AXPs (Gavriil & Kaspi 2002), providing
a long base-line of observations with a wealth of new information like
timing parameters, pulsed-flux history and glitches (see
e.g. Kaspi et al. 1999; Dib et al. 2008). For this source an
intensity-hardness correlation in the soft X-ray band (<10 keV) is
claimed (Campana et al. 2007; Rea et al. 2007). An indication that this
correlation also holds in the hard X-ray domain
(>10 keV Götz et al. 2007) is not confirmed in this work.
1708 was first detected in the hard X-ray regime (>20 keV) by
Revnivtsev et al. (2004) in a deep INTEGRAL Galactic centre
map. Kuiper et al. (2006) discovered pulsed hard X-ray emission from
this source using RXTE-PCA and HEXTE data. These authors also analysed
early-mission INTEGRAL data adding up to almost 1 Ms effective on-source
exposure and found that the hard X-ray spectrum could be
described by a power-law model with a photon index of
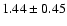 .
Timing analysis revealed significant pulsed emission in
the 20-300 keV band.
.
Timing analysis revealed significant pulsed emission in
the 20-300 keV band.
This work is a continuation of the approach followed in
den Hartog et al. (2008) for AXP 142 applying the same methods now
for 1708. We address again the total high-energy window, using
data collected over four years of INTEGRAL observations adding up to
 5 Ms of on-source exposure, nine years of RXTE monitoring adding
up to an exposure of
5 Ms of on-source exposure, nine years of RXTE monitoring adding
up to an exposure of  600 ks and a
600 ks and a  25 ks
XMM-Newton observation. A significantly improved time-averaged INTEGRAL total
spectrum is presented, as well as those for shorter (
25 ks
XMM-Newton observation. A significantly improved time-averaged INTEGRAL total
spectrum is presented, as well as those for shorter ( 1 year and
1 year and
 0.5 year) data sets to look for possible long-term time
variability. Most importantly, we present the (time-averaged)
total-pulsed spectra as well as (time-averaged) phase-resolved pulsed
spectra from INTEGRAL, RXTE and XMM-Newton.
0.5 year) data sets to look for possible long-term time
variability. Most importantly, we present the (time-averaged)
total-pulsed spectra as well as (time-averaged) phase-resolved pulsed
spectra from INTEGRAL, RXTE and XMM-Newton.
2 Observations and analysis
2.1 INTEGRAL
Table 1:
Summary of the INTEGRAL observations of 1708.
Table 2:
Phase-coherent ephemerides - derived from RXTE-PCA
monitoring data - valid for the analysed INTEGRAL observations.
The INTErnational Gamma-Ray Astrophysics Laboratory (INTEGRAL)
is a hard X-ray/soft gamma-ray (3 keV-8 MeV) mission which has been
operational since October 2002. The payload consists of two main
coded-mask imaging telescopes. 1) IBIS, Imager on Board the
INTEGRAL Satellite (Ubertini et al. 2003), has a wide field of
view (FOV) of
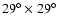 (full-width zero response)
and it has an
(full-width zero response)
and it has an  12
12 angular resolution. The low-energy
detector is called the INTEGRAL Soft Gamma-Ray Imager
(ISGRI; Lebrun et al. 2003) and it is sensitive between
angular resolution. The low-energy
detector is called the INTEGRAL Soft Gamma-Ray Imager
(ISGRI; Lebrun et al. 2003) and it is sensitive between
 20 keV and
20 keV and  300 keV. 2) The Spectrometer for INTEGRAL
(SPI, Vedrenne et al. 2003) has a better spectral resolution but
only a moderate imaging capability with an angular resolution of
300 keV. 2) The Spectrometer for INTEGRAL
(SPI, Vedrenne et al. 2003) has a better spectral resolution but
only a moderate imaging capability with an angular resolution of
 2
2
 5. SPI is sensitive between
5. SPI is sensitive between  20 keV and
20 keV and  8 MeV
and has a FOV of
8 MeV
and has a FOV of
 (full-width zero
response).
(full-width zero
response).
For the best sky map reconstruction INTEGRAL performs observations in
dither patterns (Jensen et al. 2003) besides the occasional staring
observations. Typical pointings (Science Windows, ScWs) last
 1800-3600 s. Due to the limited visibility windows on the
Galactic-centre region, the observations form sets of consecutive
orbital revolutions (Revs). In Table 1 a list of these
sets are given with the total exposure time for the selected ScWs
for which 1708 was within an angle of 14
1800-3600 s. Due to the limited visibility windows on the
Galactic-centre region, the observations form sets of consecutive
orbital revolutions (Revs). In Table 1 a list of these
sets are given with the total exposure time for the selected ScWs
for which 1708 was within an angle of 14
 5 from the pointing
direction of IBIS, as well as the effective on-source exposure, which
is reduced due to off-axis viewing angles.
5 from the pointing
direction of IBIS, as well as the effective on-source exposure, which
is reduced due to off-axis viewing angles.
The region where 1708 is located is often observed with INTEGRAL as
it is  15
15 from the Galactic centre. After four years of
observations the total exposure on this region adds up to 12 Ms taken
in 5161 pointings, after screening for Solar flares and erratic
count-rates due to the passages of the spacecraft through the Earth's
radiation belts. Taking into account the off-axis angles the effective
on-source exposure is 5.2 Ms.
from the Galactic centre. After four years of
observations the total exposure on this region adds up to 12 Ms taken
in 5161 pointings, after screening for Solar flares and erratic
count-rates due to the passages of the spacecraft through the Earth's
radiation belts. Taking into account the off-axis angles the effective
on-source exposure is 5.2 Ms.
2.1.1 INTEGRAL spectra from spatial analysis
The spectral analysis of the IBIS-ISGRI data follows the same
procedures as applied in den Hartog et al. (2008). The shadowgrams of 5161 ScWs are deconvolved into sky images in 20 energy intervals using
the Off-line Scientific Analysis software package version 5.1 (OSA; see Goldwurm et al. 2003). The energy intervals are
exponentially binned between 20 keV and 300 keV. At the source
position of 1708 averaged count rates are determined for all
energy bins. Photon fluxes are generated by normalizing the AXP
count-rates to the Crab count-rates determined from INTEGRAL Crab
observations during Rev. 102, and the Crab spectrum. The spectral
shape of the Crab spectrum we adopted is a curved power-law shape
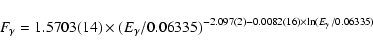 |
(1) |
(Eq. (2) in Kuiper et al. 2006), where
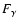 is expressed in ph/(cm2 s MeV) and
is expressed in ph/(cm2 s MeV) and
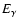 in MeV. For fitting these (and
other) spectra the software package X-spec version 12.3
(Arnaud 1996) and private software are used. All errors
quoted in this paper are 1
in MeV. For fitting these (and
other) spectra the software package X-spec version 12.3
(Arnaud 1996) and private software are used. All errors
quoted in this paper are 1 errors.
errors.
For the INTEGRAL observations up to Rev. 366 SPI spectral analysis is
performed above 140 keV, from where the sensitivity of SPI is
comparable or higher than ISGRI. In the 140 keV-1 MeV energy range
the data were binned in 4 energy bins. From the total-exposure sky maps
source fluxes have been extracted for every energy bin using a maximum
likelihood fitting procedure that considers the instrumental response
of SPI (Knödlseder 2004). Also here the measured flux is
normalized to the Crab spectrum, which has been obtained using SPI
observations of Revs. 43-45.
2.1.2 INTEGRAL timing analyses
For the IBIS-ISGRI timing analysis of AXP 1708 we followed earlier
applied procedures (den Hartog et al. 2008; Kuiper et al. 2006). All
available data taken between Rev. 037 and 485 were used (see
Table 1). Photons were selected only from non-noisy
detector elements that could be illuminated by the source through the
open mask elements by more than 25%. After correcting for
instrumental, onboard processing and ground-station time delays
(Walter et al. 2003), the event arrival times are Solar-system
barycentered (JPL DE200 Solar-system ephemeris) adopting the best
known source position (Israel et al. 2003). The barycentered events
are folded using a phase-connected ephemeris (see
Table 2 and Sect. 2.2 for the ephemeris
creation). The (TDB) time to pulse phase conversion taking into
account consistent phase alignment for each ephemeris is provided by
the following formula:
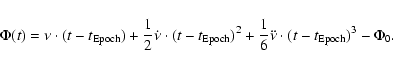 |
(2) |
For the pulse profiles, detection significances are estimated by
applying a Z
 test on bin-free pulse-phase distributions
(Buccheri et al. 1983). Truncated Fourier series with two
harmonics are used to fit the pulse profiles, where the minimum of
these fits are defined as the DC level.
test on bin-free pulse-phase distributions
(Buccheri et al. 1983). Truncated Fourier series with two
harmonics are used to fit the pulse profiles, where the minimum of
these fits are defined as the DC level.
The total-pulsed spectrum is derived by obtaining the number of excess
counts above the DC level from each pulse profile for all considered
energy bands. These excess counts are normalized in Crab units (by
applying the same procedure for the Crab pulsar) and are converted
into photon fluxes using a Crab-pulsar spectrum model (Eq. (3)
in Kuiper et al. 2006);
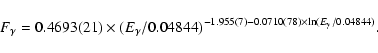 |
(3) |
The analysis to create phase-resolved spectra
(Sect. 3.3.2) is similar. However, for the
phase-resolved spectra only the excess counts within selected phase
intervals are used.
2.2 RXTE
For the timing analysis of the INTEGRAL data the regular monitoring
observations with the Rossi X-ray Timing Explorer (RXTE) during
the INTEGRAL observations are of great importance
(Gavriil & Kaspi 2002), because the INTEGRAL source count rate
is too low to independently detect the pulsation. This is possible
with the data from the Proportional Counter Array
(PCA; Jahoda et al. 1996) aboard RXTE. The PCA is a non-imaging
instrument sensitive in the 2-60 keV energy range and it consists of
five collimated units (PCUs 0-4) with a  1
1 FOV. Using
these RXTE-PCA monitoring data we created accurate phase-connected
ephemerides valid during the INTEGRAL observations. The details of the
ephemerides can be found in Table 2. The pulsar phase
was set arbitrarily to zero where the pulse profile for energies
between
FOV. Using
these RXTE-PCA monitoring data we created accurate phase-connected
ephemerides valid during the INTEGRAL observations. The details of the
ephemerides can be found in Table 2. The pulsar phase
was set arbitrarily to zero where the pulse profile for energies
between  2.5 and 10 keV reached a sharp minimum (see
e.g. Fig. 7B). This is a different choice than made
in Kuiper et al. (2006), resulting in a phase shift in the profiles
of
2.5 and 10 keV reached a sharp minimum (see
e.g. Fig. 7B). This is a different choice than made
in Kuiper et al. (2006), resulting in a phase shift in the profiles
of  0.2.
0.2.
For the study of the pulsed emission of 1708 with RXTE-PCA, we have
used all publicly available data spanning nine years of
observations. The data are analysed in two sets. Set A contains the
data which have been used by Kuiper et al. (2006) and were taken over
a period of almost six years. Most of these data were taken before the
start of the INTEGRAL observations. Set B covers the remaining part of
the publicly available data taken during INTEGRAL operations and span
about three years. All data used in this work have been listed in
Table 3. It can be seen that Set A and B have
similar total exposures on 1708.
The procedures for the RXTE spectral-timing analysis as outlined by
Kuiper et al. (2006), and also applied in den Hartog et al. (2008),
have been followed. The pulse profiles for any selected
energy band can be described sufficiently accurate by truncated
Fourier series with three harmonics above constant DC levels. The
excess (pulsed) counts above these DC levels can then be
converted into flux units using PCU exposure-weighted response
matrices (see e.g. Sect. 3.2 of Kuiper et al. 2006). To derive
unabsorbed PCA time-averaged total-pulsed and phase-resolved spectra,
a Galactic absorption column
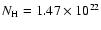 cm-2 was used (fixed value), derived
from XMM-Newton spectral fits (see Sect. 3.1.3).
cm-2 was used (fixed value), derived
from XMM-Newton spectral fits (see Sect. 3.1.3).
The High-Energy X-Ray Timing Experiment (HEXTE, 15-250 keV; Rothschild et al. 1998) aboard RXTE has also been used to extend
the PCA spectral-timing study to higher energies. HEXTE consists of
two independent detector clusters (0 and 1) each with a
 1
1 FOV. HEXTE allows for detailed consistency checks with
the INTEGRAL results obtained for similar energy windows. Due to the
co-alignment of HEXTE and the PCA, the same long monitoring
observations of 1708 can be used for both instruments. Fully
consistent procedures have been applied for the spectral-timing
analysis, including the use of the ephemerides listed in
Table 2, and following the same procedures for deriving
pulsed counts and fluxes of the pulsed emission. On 1708 the total
deadtime corrected exposures for clusters 0 and 1 are 239.04 ks and 259.50 ks, respectively.
FOV. HEXTE allows for detailed consistency checks with
the INTEGRAL results obtained for similar energy windows. Due to the
co-alignment of HEXTE and the PCA, the same long monitoring
observations of 1708 can be used for both instruments. Fully
consistent procedures have been applied for the spectral-timing
analysis, including the use of the ephemerides listed in
Table 2, and following the same procedures for deriving
pulsed counts and fluxes of the pulsed emission. On 1708 the total
deadtime corrected exposures for clusters 0 and 1 are 239.04 ks and 259.50 ks, respectively.
Table 3:
Summary of the RXTE observations of 1708.
2.3 XMM-Newton
XMM-Newton (Jansen et al. 2001) has been operational since early
2000. Onboard are three CCD cameras for X-ray imaging, namely two EPIC
(European Photon Imaging Camera) MOS (Turner et al. 2001) cameras and
one EPIC-PN (Strüder et al. 2001) camera. All cameras have a FOV of
 30
30 and are sensitive in the energy range
and are sensitive in the energy range  0.3-12 keV.
0.3-12 keV.
We have (re)analysed a publicly available 45 ks XMM-Newton observation on
1708. The data were taken in the night of August 28 to 29, 2003
(Obs. Id 0148690101). The data are analysed using SAS v. 7.0 and the
latest calibration files that were available (May 2007). Next, we
considered the EPIC-PN which operated in small-window mode with medium
filter. In this mode the maximum time resolution is 6 ms. These data
are checked for solar (soft proton) flares by creating a light curve
with events with energies larger than 10 keV. A count-rate
distribution was created from this light curve to which a Gaussian was
fitted to determine the mean count rate of the high-energy
photons. Good-Time Intervals (GTIs) were created allowing only time
stamps for which the count rate was lower than 0.078 counts per second
which corresponds to the fitted mean count rate plus three times the
width of the distribution (3 ). The GTIs add up to 25.5 ks of
exposure. All single and double events, i.e. patterns less than and
equal four, are selected within the energy range 0.3 keV to 12 keV. The arrival times of the selected events are barycentered.
). The GTIs add up to 25.5 ks of
exposure. All single and double events, i.e. patterns less than and
equal four, are selected within the energy range 0.3 keV to 12 keV. The arrival times of the selected events are barycentered.
There was no need to correct for pile-up effects as the count rate of
1708 was low enough for the PN in small window mode with medium
filter. To extract the source counts a circular extraction region with
a radius of 35
 was used. As this source is not so bright it
was possible to select a background extraction region from the small
window with a radius of 45
was used. As this source is not so bright it
was possible to select a background extraction region from the small
window with a radius of 45
 .
No out-of-time event correction has
been applied as the effect is approximately 1%. The extracted
spectrum has been binned oversampling the energy resolution by a
factor of three and then rebinned occasionally (for energies
.
No out-of-time event correction has
been applied as the effect is approximately 1%. The extracted
spectrum has been binned oversampling the energy resolution by a
factor of three and then rebinned occasionally (for energies
 5 keV) to ensure a minimum of 25 counts per bin.
5 keV) to ensure a minimum of 25 counts per bin.
For timing analysis, the barycentered events are folded using an
appropriate ephemeris (ephemeris 1 in Table 2). To
create pulsed spectra pulsed excess counts are extracted as described
in Sect. 2.1.2, fitting the pulse profiles with
truncated Fourier series with the first three harmonics above a
constant background.
3 Results
In this section we present results from INTEGRAL, XMM-Newton and RXTE. First,
we present the total (pulsed plus DC) spectrum using INTEGRAL data above
20 keV and look for possible long-term time variability. Then we
derive the complementary XMM-Newton total spectrum below 12 keV. RXTE is a
non-imaging mission and due to the presence of nearby strong sources
and large gradients in the Galactic ridge emission
(Valinia & Marshall 1998), it can in this work only be used for studying
the timing signal of 1708. The pulse profiles are then presented
and compared for all three missions. Finally, the results from
spectral timing analyses in the form of total-pulsed spectra and
phase-resolved spectra for all data sets are presented and discussed
in detail. This leads to the identification of genuinely different
components contributing to the pulsed high-energy emission.
3.1 Total spectra and long-term variability
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{09772fig01.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg48.gif) |
Figure 1:
Total-flux (pulsed + DC) spectra of 1708 collected during
four one-year intervals of INTEGRAL observations, corresponding to
revolution intervals ( from left to right); 037-120, 164-246,
283-366 and 399-485. The upper limits are 2 .
The model
lines are single power-law fits (see Table 4). .
The model
lines are single power-law fits (see Table 4). |
| Open with DEXTER |
3.1.1 INTEGRAL ISGRI persistent time-averaged spectra
and long-term variability
Table 4:
Summary of the power-law model fits to the
INTEGRAL-IBIS-ISGRI total-spectra of 1708 summing observations
taken in intervals of  1 year and for the total exposure.
1 year and for the total exposure.
Listed in Table 1 are eight sets of INTEGRAL observations,
each covering about half a year. 1708 is not bright in hard
X-rays, therefore we first performed the spectral analysis averaging
observations over one-year time intervals to obtain significant flux
values till above 100 keV. The resulting four spectra are shown in
Fig. 1. They can be described satisfactorily with
single power-law models. The fit results are listed in
Table 4. The power-law indices range from
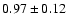 to
to
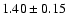 and the 20-150 keV fluxes range from
and the 20-150 keV fluxes range from
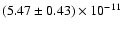 to
to
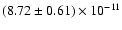 erg cm-2 s-1 which can be seen as a indication for time variability. When we
compare these yearly averages with the long-term four year average
(see Sect. 3.1.2), we find that the spectra taken in
Revs. 037-120 and 399-485 are most deviating from this time-averaged
spectrum, i.e. at the
erg cm-2 s-1 which can be seen as a indication for time variability. When we
compare these yearly averages with the long-term four year average
(see Sect. 3.1.2), we find that the spectra taken in
Revs. 037-120 and 399-485 are most deviating from this time-averaged
spectrum, i.e. at the  2
2 and
and  3
3 level,
respectively (see error contours in Fig. 2).
level,
respectively (see error contours in Fig. 2).
Alternatively, the standard deviations (
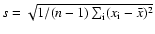 )
for the power-law indices and the 20-150 keV
fluxes relative to the weighted mean are 0.20 and
)
for the power-law indices and the 20-150 keV
fluxes relative to the weighted mean are 0.20 and
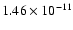 erg cm-2 s-1, respectively. Therefore, the power-law shape is stable
within 18% (1
erg cm-2 s-1, respectively. Therefore, the power-law shape is stable
within 18% (1 )
and the 20-150 keV flux is stable within 22%
(1
)
and the 20-150 keV flux is stable within 22%
(1 ).
).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{09772fig02.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg57.gif) |
Figure 2:
Error contours (
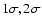 and
and 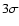 )
of the
power-law model fits to the total spectrum (20-300 keV) for
observations 037-120 and 399-485 compared to the total time-averaged
fit (037-485). Out of the four observations (each averaged over one
year) these two differ most from the four-year time-averaged
spectrum. )
of the
power-law model fits to the total spectrum (20-300 keV) for
observations 037-120 and 399-485 compared to the total time-averaged
fit (037-485). Out of the four observations (each averaged over one
year) these two differ most from the four-year time-averaged
spectrum. |
| Open with DEXTER |
To explore the indication for variability further, we also fitted the
spectra of the half-year long time sets (Table 1) plus
a more recent short, lower-statistics observation (Revs. 534-542,
Feb. 27-Mar. 25, 2007, 173 ScWs, 307 ks effective on-source
exposure) with single power-law models, but over the narrower energy
band 20-70 keV. The results are plotted in
Fig. 3. The 20-70 keV flux measurement for
Revs. 399-431 is the only one that deviates at a 3 level from
the time-average value. Since this is one single 3
level from
the time-average value. Since this is one single 3 deviation
for nine measurements, we consider this only as an indication for time
variability.
deviation
for nine measurements, we consider this only as an indication for time
variability.
The bottom panel of Fig. 3 shows no indication for
significant variation in spectral index, either.
Israel et al. (2007) and Dib et al. (2008) reported the detection
of glitches and candidate glitches of 1708 during the INTEGRAL
operations, the epochs are indicated in Fig. 3. This
figure shows that there is no indication for an obvious change in
spectral slope nor flux triggered by one of the glitches. Possibly
there is a change in spectral slope after the glitch on MJD 53366. However, the difference between
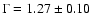 and
and
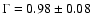 ,
the average values before and after the
glitch, is not significant (2.3
,
the average values before and after the
glitch, is not significant (2.3 ).
).
Götz et al. (2007) analysed part of the INTEGRAL data used in this work,
they did not use Revs. 164-185, 345-366 and 399-431, and claim the
detection of long-term hard X-ray (20-70 keV) variability based on an
indication for lower flux values in the INTEGRAL measurements after the
second candidate glitch (epoch marked in Fig. 3),
correlated with lower fluxes measured with Swift in the 1-10 keV band (their Fig. 1). However, our more complete analysis
including full spectral fitting of the data in stead of using merely
count rates does not confirm the reported trend in the INTEGRAL data for
1708 (see Fig. 3). Therefore, we do not support
the claimed correlated variability between the hard X-ray and soft
X-ray emission from 1708.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{09772fig03.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg60.gif) |
Figure 3:
Fluxes (20-70 keV) and photon indices for the half-year time
sets specified in Table 1 and one shorter observation
(see Sect. 3.1.1). Indicated as horizontal dotted
lines are the time-averaged values with their 1 errors (grey
bands). Glitches and candidate glitches
(Israel et al. 2007; Dib et al. 2008) are indicated as vertical black
and grey lines, respectively.
errors (grey
bands). Glitches and candidate glitches
(Israel et al. 2007; Dib et al. 2008) are indicated as vertical black
and grey lines, respectively. |
| Open with DEXTER |
3.1.2 INTEGRAL time-averaged total spectrum
Combining all the data listed in Table 1 a
time-averaged spectrum is extracted using 5.2 Ms on-source exposure
time (Fig. 4). 1708 has been detected with high
significance up to 175 keV with a 4.2 detection significance
in the 152-175 keV band. Fitting this spectrum with a single power
law yields an excellent fit (
detection significance
in the 152-175 keV band. Fitting this spectrum with a single power
law yields an excellent fit (
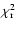 = 1.13 with 14 d.o.f.) with a photon
index
= 1.13 with 14 d.o.f.) with a photon
index
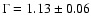 and a 20-150 keV flux of
and a 20-150 keV flux of
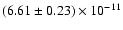 erg cm-2 s-1. Its 20-175 keV luminosity is
erg cm-2 s-1. Its 20-175 keV luminosity is
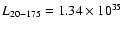 erg s-1 assuming a distance of 3.8 kpc
(Durant & van Kerkwijk 2006a). It is remarkable that there is no hint for
a spectral break up to the highest energies in our INTEGRAL-ISGRI
spectrum, particularly when compared to the reported COMPTEL upper
limits for energies above 750 keV (Kuiper et al. 2006), which impose
a spectral break between 100 keV and 750 keV (see
Fig. 4).
erg s-1 assuming a distance of 3.8 kpc
(Durant & van Kerkwijk 2006a). It is remarkable that there is no hint for
a spectral break up to the highest energies in our INTEGRAL-ISGRI
spectrum, particularly when compared to the reported COMPTEL upper
limits for energies above 750 keV (Kuiper et al. 2006), which impose
a spectral break between 100 keV and 750 keV (see
Fig. 4).
Unfortunately, it turned out that 1708 is not bright enough above
 100 keV to be detected with INTEGRAL-SPI, even for this long
exposure. In Fig. 4 three 2
100 keV to be detected with INTEGRAL-SPI, even for this long
exposure. In Fig. 4 three 2 upper limits
derived from SPI spatial analysis are added. These limits are all
above the extrapolation of the power-law fit to the ISGRI flux values,
contrary to the case of 142, for which SPI upper limits provided
evidence for the presence of a spectral break
(den Hartog et al. 2008).
upper limits
derived from SPI spatial analysis are added. These limits are all
above the extrapolation of the power-law fit to the ISGRI flux values,
contrary to the case of 142, for which SPI upper limits provided
evidence for the presence of a spectral break
(den Hartog et al. 2008).
Following den Hartog et al. (2008) we have fitted all INTEGRAL and
COMPTEL spectral information (including limits) with a logparabolic
function;
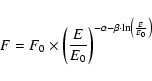 |
(4) |
where E0 (in units keV) is the pivot energy to minimize
correlations between the parameters and F0 is the flux (in units ph cm-2 s-1keV-1) at E0. This function is a power-law if the curvature
parameter 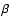 is equal to zero. Assuming this spectral shape we
get an acceptable broad-band (20 keV-30 MeV) fit with best-fit
parameters
is equal to zero. Assuming this spectral shape we
get an acceptable broad-band (20 keV-30 MeV) fit with best-fit
parameters
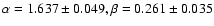 and
and
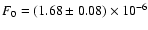 ph cm-2 s-1keV-1 at
E0 = 143.276 keV. The peak energy
ph cm-2 s-1keV-1 at
E0 = 143.276 keV. The peak energy
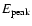 is
287+75-45 keV. This
value lies remarkably close to the peak energy found for 142 (i.e.
279+65-41 keV; den Hartog et al. 2008). In
Fig. 4 both the power-law and the logparabolic fit
are drawn.
is
287+75-45 keV. This
value lies remarkably close to the peak energy found for 142 (i.e.
279+65-41 keV; den Hartog et al. 2008). In
Fig. 4 both the power-law and the logparabolic fit
are drawn.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{09772fig04.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg68.gif) |
Figure 4:
High-energy spectra of 1708. In this figure the following
is plotted: the unabsorbed total spectra of XMM-Newton (<12 keV) and
INTEGRAL (with triangle markers) in black, also in black three COMPTEL
upper limits (Kuiper et al. 2006), three INTEGRAL-SPI upper limits in
grey (with triangle markers); also in grey a power-law fit to the
INTEGRAL-IBIS spectrum, in blue a logparabolic fit to the INTEGRAL-IBIS, SPI
and COMPTEL data, total pulsed spectra of XMM-Newton in black, RXTE-PCA and
HEXTE are shown in blue and aqua, and the total pulsed spectrum of
INTEGRAL-ISGRI in red (with triangle markers). |
| Open with DEXTER |
3.1.3
 total spectrum
total spectrum
For energies below 12 keV we extracted the absorbed total (pulsed +
DC) spectrum using XMM-Newton EPIC-PN data (see Sect. 2.3). In
order to obtain an estimate for the Galactic absorption column
(
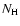 )
we fitted the spectrum globally with a canonical
logparabolic function, including fixed INTEGRAL parameters for the hard
X-ray contribution above
)
we fitted the spectrum globally with a canonical
logparabolic function, including fixed INTEGRAL parameters for the hard
X-ray contribution above  8 keV. We derive an
8 keV. We derive an
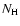 of
of
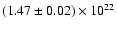 cm-2, which can be compared with
the value (
cm-2, which can be compared with
the value (
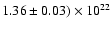 cm-2 obtained by
Rea et al. (2005) fitting the same XMM-Newton data with an absorbed
black-body plus a power-law model. Durant & van Kerkwijk (2006b) used a
model-independent approach analysing X-ray grating spectra taken with
the Reflection Grating Spectrometer (den Herder et al. 2001) onboard
XMM-Newton. Their value for
cm-2 obtained by
Rea et al. (2005) fitting the same XMM-Newton data with an absorbed
black-body plus a power-law model. Durant & van Kerkwijk (2006b) used a
model-independent approach analysing X-ray grating spectra taken with
the Reflection Grating Spectrometer (den Herder et al. 2001) onboard
XMM-Newton. Their value for
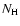 of
of
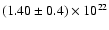 cm-2 is consistent with both estimates. We adopted
cm-2 is consistent with both estimates. We adopted
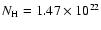 cm-2 in this work for the
XMM-Newton and RXTE analyses. The total unabsorbed spectrum is shown in
Fig. 4. The 2-10 keV unabsorbed flux is
cm-2 in this work for the
XMM-Newton and RXTE analyses. The total unabsorbed spectrum is shown in
Fig. 4. The 2-10 keV unabsorbed flux is
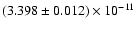 erg cm-2 s-1. The error is statistical only. The
2-10 keV unabsorbed fluxes for
erg cm-2 s-1. The error is statistical only. The
2-10 keV unabsorbed fluxes for
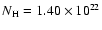 and
and
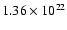 cm-2 are
cm-2 are
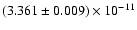 and
and
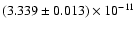 erg cm-2 s-1,
respectively. These values are within 2% of our value.
erg cm-2 s-1,
respectively. These values are within 2% of our value.
3.2 Pulse profiles
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{09772fig05.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg79.gif) |
Figure 5:
IBIS-ISGRI pulse profile of 1708 between 20 keV and 270 keV. This profile has a 12.3 significance using a Z23 test (fit shown as a solid curve). The fitted DC level is indicated
with an horizontal line. The grey lines and the colours indicate
three phase intervals Ph I, II and III (see
Table 6). The colours are consistently used in this
paper in figures showing results of phase-resolved analyses (see
Sect. 3.3.2).
significance using a Z23 test (fit shown as a solid curve). The fitted DC level is indicated
with an horizontal line. The grey lines and the colours indicate
three phase intervals Ph I, II and III (see
Table 6). The colours are consistently used in this
paper in figures showing results of phase-resolved analyses (see
Sect. 3.3.2). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{09772fig06.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg80.gif) |
Figure 6:
Pulse profiles from soft to hard X-rays. XMM-Newton pulse
profiles in the energy range 0.5-12.0 keV are shown in panels A- D. Panels E- H show INTEGRAL pulse profiles in the
energy range 20-270 keV. The differential energy ranges are
indicated in the figures. The phase intervals are indicated as in
Fig. 5. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{09772fig07.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg81.gif) |
Figure 7:
Pulse profiles from RXTE. RXTE-PCA pulse profiles in the energy
range 2.2-63.9 keV are shown in panels A- E.
RXTE-HEXTE pulse profiles are shown in panels F, G and H within the
energy range 14.8-267.6 keV. The phase intervals are indicated as
in Fig. 5. |
| Open with DEXTER |
3.2.1 INTEGRAL and XMM-Newton pulse profiles
Kuiper et al. (2006) showed for the first time pulsed hard X-ray
emission (>10 keV) from 1708 using data from RXTE-PCA, RXTE-HEXTE
and INTEGRAL-ISGRI. For the INTEGRAL pulse profiles  1.4 Ms on-source
exposure was used, resulting in a 5.9
1.4 Ms on-source
exposure was used, resulting in a 5.9 detection for energies
20-300 keV. In this work, we present INTEGRAL pulse profiles using
detection for energies
20-300 keV. In this work, we present INTEGRAL pulse profiles using
 5.2 Ms on-source exposure. The result is a very much improved
pulse profile with a 12.3
5.2 Ms on-source exposure. The result is a very much improved
pulse profile with a 12.3 detection significance
(Z
detection significance
(Z
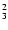 test; Buccheri et al. 1983) for
energies 20-270 keV (Fig. 5). The profile shows a
single pulse which peaks around phase 0.8 with a steep trailing wing
dropping off to the DC level at phase
test; Buccheri et al. 1983) for
energies 20-270 keV (Fig. 5). The profile shows a
single pulse which peaks around phase 0.8 with a steep trailing wing
dropping off to the DC level at phase  1.05 (0.05). On the
leading wing there appears to be a weak pulse or shoulder.
1.05 (0.05). On the
leading wing there appears to be a weak pulse or shoulder.
Presented in Fig. 6E-H are four
exponentially-binned differential INTEGRAL pulse profiles. The profiles
have significances of 6.3 ,
6.8
,
6.8 ,
6.2
,
6.2 and
3.5
and
3.5 ,
respectively, using a Z
,
respectively, using a Z
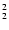 test. All profiles
show single pulses which all peak at phase
test. All profiles
show single pulses which all peak at phase  0.8, like for the
total pulse in Fig. 5.
0.8, like for the
total pulse in Fig. 5.
The complementary high-statistics XMM-Newton pulse profiles at lower
energies (0.5-12 keV) are shown in
Figs. 6A-D. The pulse profile with the lowest
statistics, in panel D, still has a significance of 10.7 (Z
(Z
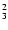 test). The drastic change in morphology moving up in
energy from 0.5 keV up to 270 keV is evident and will be investigated
further. Note that in the timing analysis the pulsed emission has been
detected to higher energies than the total emission in the sky maps.
test). The drastic change in morphology moving up in
energy from 0.5 keV up to 270 keV is evident and will be investigated
further. Note that in the timing analysis the pulsed emission has been
detected to higher energies than the total emission in the sky maps.
3.2.2 RXTE-PCA and RXTE-HEXTE pulse profiles
The RXTE-PCA bridges the observational gap (12-20 keV) in energy between
XMM-Newton and INTEGRAL, with XMM-Newton being sensitive down to  0.5 keV and
INTEGRAL extending the coverage to
0.5 keV and
INTEGRAL extending the coverage to  300 keV. In addition, RXTE-HEXTE
is sensitive over about the same energy band as INTEGRAL-ISGRI.
Analysis of data from these three missions allow for consistency
checks, particularly when the observations are covering the same
epochs and for checks on long-term variability. RXTE observations
set A (Table 3) covers about 6 years (mostly before
the launch of INTEGRAL) and was used by Kuiper et al. (2006). Set B
overlaps in time with the INTEGRAL observations up to December 2006. Therefore, we first compared the time-averaged RXTE-PCA pulse
profiles in 5 differential energy bands for set A with those for
set B. We did not find significant differences in these time averaged
(over years) profile shapes. This is in agreement with the findings
by Dib et al. (2008), who compared the profile shapes for seven
(glitch-free) intervals of the total set A plus B. We should note
that the PCA gain changed over time, what can offer an explanation for
some indications for small changes with time in the profiles as
discussed in Dib et al. (2008).
300 keV. In addition, RXTE-HEXTE
is sensitive over about the same energy band as INTEGRAL-ISGRI.
Analysis of data from these three missions allow for consistency
checks, particularly when the observations are covering the same
epochs and for checks on long-term variability. RXTE observations
set A (Table 3) covers about 6 years (mostly before
the launch of INTEGRAL) and was used by Kuiper et al. (2006). Set B
overlaps in time with the INTEGRAL observations up to December 2006. Therefore, we first compared the time-averaged RXTE-PCA pulse
profiles in 5 differential energy bands for set A with those for
set B. We did not find significant differences in these time averaged
(over years) profile shapes. This is in agreement with the findings
by Dib et al. (2008), who compared the profile shapes for seven
(glitch-free) intervals of the total set A plus B. We should note
that the PCA gain changed over time, what can offer an explanation for
some indications for small changes with time in the profiles as
discussed in Dib et al. (2008).
In order to exploit the maximal statistics, we created pulse profiles
using all available data collected with the PCA and HEXTE over nine
years (see Table 3 and
Sect. 2.2). Before summing the profiles obtained at
different epochs we corrected for the above-mentioned PCA gain drift
in the conversion from channels to energy. In Fig. 7
the RXTE-PCA (panels A-E) and HEXTE (panels F-H) pulse profiles are
presented. The ``lowest-significance'' profiles above  15 keV
(Figs. 7D-H) have significances of
15 keV
(Figs. 7D-H) have significances of
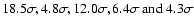 ,
respectively.
,
respectively.
3.2.3 Pulse profile changes with energy
Comparing the profile shapes derived with INTEGRAL
(Fig. 6) with those obtained with the PCA and HEXTE
in similar energy bands (Fig. 7), shows very good
agreement, INTEGRAL achieving the best statistics above 70 keV. Above  20 keV there does not seem to occur significant changes in
morphology with energy. The pulse profiles are statistically similar
which was tested using a combination of a Pearson
20 keV there does not seem to occur significant changes in
morphology with energy. The pulse profiles are statistically similar
which was tested using a combination of a Pearson 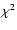 (see
e.g. Sect. 11.2 of Eadie et al. 1971) and a Run test (see
e.g. Sect. 11.3.1 of Eadie et al. 1971).
(see
e.g. Sect. 11.2 of Eadie et al. 1971) and a Run test (see
e.g. Sect. 11.3.1 of Eadie et al. 1971).
Below 20 keV, the situation is different: the XMM-Newton and RXTE-PCA profiles
show strong morphology changes as a function of energy. This has been
noted in a number of earlier publications
(e.g. Kuiper et al. 2006; Sugizaki et al. 1997; Israel et al. 2001). In fact,
the morphology is changing faster with energy than can be seen in the
broad energy bins selected for Figs. 6 and 7. In addition, there are systematic effects
which should be realized when comparing XMM-Newton and PCA profiles. For
example, in the measured energy band 2.2-3.9 keV
(Fig. 7A) one can see in the PCA profile a small
secondary peak at phase  0.8, which is absent in the
corresponding XMM-Newton profile (Fig. 6B). This can
be explained with the significantly coarser energy resolution of the
PCA, accepting more events with photon energy above 4 keV in the band
with measured energies below 4 keV. For the same reason, this
secondary peak at phase 0.8 in the PCA 3.9-8.2 profile
(Fig. 7B) is higher than found in the corresponding
XMM-Newton profile (Fig. 6C), because this pulse
component is maximal for energies above 8 keV. Therefore, a more
accurate comparison can be made between the pulse characteristics
measured with XMM-Newton and the RXTE-PCA by performing phase-resolved
spectroscopy in which the energy resolution is automatically taken
into account (addressed in Sect. 3.3.2).
0.8, which is absent in the
corresponding XMM-Newton profile (Fig. 6B). This can
be explained with the significantly coarser energy resolution of the
PCA, accepting more events with photon energy above 4 keV in the band
with measured energies below 4 keV. For the same reason, this
secondary peak at phase 0.8 in the PCA 3.9-8.2 profile
(Fig. 7B) is higher than found in the corresponding
XMM-Newton profile (Fig. 6C), because this pulse
component is maximal for energies above 8 keV. Therefore, a more
accurate comparison can be made between the pulse characteristics
measured with XMM-Newton and the RXTE-PCA by performing phase-resolved
spectroscopy in which the energy resolution is automatically taken
into account (addressed in Sect. 3.3.2).
Nevertheless, the XMM-Newton and
RXTE-PCA profiles consistently show that the soft X-ray pulse has two
components which peak at phases  0.4 and
0.4 and  0.8. The pulse
peaking at phase
0.8. The pulse
peaking at phase  0.4 is spectrally softer than the pulse peaking
at phase
0.4 is spectrally softer than the pulse peaking
at phase  0.8. As mentioned above, the latter is not visible in
Fig. 6A and B. This peak starts contributing
above
0.8. As mentioned above, the latter is not visible in
Fig. 6A and B. This peak starts contributing
above  4 keV (Figs. 6C and 7B) and is the dominating pulse component
already above
4 keV (Figs. 6C and 7B) and is the dominating pulse component
already above  8 keV up to and including the hard X-ray band.
8 keV up to and including the hard X-ray band.
The soft pulse (peak at phase  0.4) is gradually decreasing in
strength as a function of energy and seems to disappear entirely at
hard X-rays. Finally, there is an indication for a third pulse
component, visible in the XMM profile below 2 keV where the RXTE-PCA has
no sensitivity. This component at phase
0.4) is gradually decreasing in
strength as a function of energy and seems to disappear entirely at
hard X-rays. Finally, there is an indication for a third pulse
component, visible in the XMM profile below 2 keV where the RXTE-PCA has
no sensitivity. This component at phase  1.0 fills up the soft
pulse to a saw-tooth-like profile (Fig. 6A), at
least, there is a sudden, significant change in pulse shape in
comparison to the profile above 2 keV.
1.0 fills up the soft
pulse to a saw-tooth-like profile (Fig. 6A), at
least, there is a sudden, significant change in pulse shape in
comparison to the profile above 2 keV.
3.3 Energy spectra of the pulsed emission
For INTEGRAL-ISGRI, XMM-Newton-PN, RXTE-PCA and RXTE-HEXTE pulsed spectra were
created by analyzing the pulse profiles following the procedure
described in Sect. 2. In Fig. 5 an
example is given of how the pulsed counts are extracted as excess
counts above a flat background level. In this case for 1708, the
 40% pulsed emission in the total INTEGRAL energy band is
separated from the
40% pulsed emission in the total INTEGRAL energy band is
separated from the  60% DC component. For INTEGRAL pulse profiles
for seven exponentially binned energy intervals within 20-300 keV
were created. For XMM-Newton, RXTE-PCA and HEXTE pulse profiles in 20 (0.5-12 keV), 15 (2.7-32.1 keV) and 5 (14.8-267.5 keV) energy
intervals were produced, respectively. In this section we first show
the total-pulsed phase-averaged spectra. Then we show for all three
missions the results of phase-resolved spectroscopy applied for three
broad phase bins selected in the INTEGRAL profile in
Fig. 5. Finally, we show phase-resolved pulsed
spectra for narrow (
60% DC component. For INTEGRAL pulse profiles
for seven exponentially binned energy intervals within 20-300 keV
were created. For XMM-Newton, RXTE-PCA and HEXTE pulse profiles in 20 (0.5-12 keV), 15 (2.7-32.1 keV) and 5 (14.8-267.5 keV) energy
intervals were produced, respectively. In this section we first show
the total-pulsed phase-averaged spectra. Then we show for all three
missions the results of phase-resolved spectroscopy applied for three
broad phase bins selected in the INTEGRAL profile in
Fig. 5. Finally, we show phase-resolved pulsed
spectra for narrow (
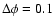 )
phase bins for RXTE-PCA and
INTEGRAL leading to the identification of three spectrally different
components which contribute to the total pulsed emission.
)
phase bins for RXTE-PCA and
INTEGRAL leading to the identification of three spectrally different
components which contribute to the total pulsed emission.
3.3.1 Total-pulsed spectra
In Fig. 4 the time-averaged total-pulsed spectra
are shown for all four instruments using all available exposures. The
flux values from XMM-Newton, RXTE-PCA, RXTE-HEXTE and INTEGRAL are very consistent,
yielding a continuous broad-band spectrum from 0.5 keV up to almost
300 keV. The RXTE-PCA total-pulsed spectrum smoothly bridges the energy
gap between INTEGRAL and XMM-Newton. The RXTE-HEXTE spectrum is in agreement
with the INTEGRAL spectrum and also connects to the RXTE-PCA spectrum.
For RXTE-PCA we first created spectra for sets A and B separately, to
verify whether the time-averaged 1708 spectra differ in the years
before and during the INTEGRAL observations. Within the statistical
errors the spectra appeared to be identical, in flux and shape. This
is in agreement with the recent findings of Dib et al. (2008), who
also concluded that the pulsed emission is very stable over the whole
time span from 1998 until 2006. Therefore, the combined spectrum with
maximal statistics using both sets of data is shown in
Fig. 4 and is further described below.
Fitting INTEGRAL, RXTE-PCA and HEXTE simultaneously with two power-law
components yields an excellent fit for energies above 2.8 keV (see
Table 5). The soft power law has a photon index
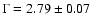 and the hard power law has a photon index
and the hard power law has a photon index
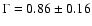 (
(
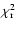 = 0.51, d.o.f. = 22). Fitting the
INTEGRAL spectrum separately it can be described by a single power-law
model with a photon index
= 0.51, d.o.f. = 22). Fitting the
INTEGRAL spectrum separately it can be described by a single power-law
model with a photon index
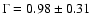 (
(
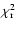 = 0.70, d.o.f. = 5), which is nicely within errors of the combined INTEGRAL-RXTE fit.
= 0.70, d.o.f. = 5), which is nicely within errors of the combined INTEGRAL-RXTE fit.
Table 5:
Spectral-fit parameters of the total-pulsed INTEGRAL, XMM-Newton,
RXTE-PCA and RXTE-HEXTE fits (see Sect. 3.3.1).
To determine the model parameters of the 0.5-12.0 keV XMM-Newton spectrum
the contribution of the hard power-law spectral component (significant
above  5 keV) were added with fixed parameters (as determined from
the INTEGRAL-RXTE fit) to the model and thereby effectively subtracted.
Fitting the 0.5-12.0 keV XMM-Newton spectrum with a power-law yields a
rather poor fit with photon index
5 keV) were added with fixed parameters (as determined from
the INTEGRAL-RXTE fit) to the model and thereby effectively subtracted.
Fitting the 0.5-12.0 keV XMM-Newton spectrum with a power-law yields a
rather poor fit with photon index
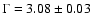 (
(
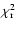 = 1.62, d.o.f. = 15). This photon index is slightly softer than found for
RXTE-PCA. However, the XMM-Newton spectrum in Fig. 4 shows a
discontinuity between 2 and 3 keV, just below the RXTE-PCA energy band.
Phase-resolved spectroscopy in the next section will show that this
discontinuity in the total-pulsed spectrum between 2 and 3 keV is
genuine. Indeed, for energies above 2.8 keV an excellent fit can be
obtained with a power law with a photon index
= 1.62, d.o.f. = 15). This photon index is slightly softer than found for
RXTE-PCA. However, the XMM-Newton spectrum in Fig. 4 shows a
discontinuity between 2 and 3 keV, just below the RXTE-PCA energy band.
Phase-resolved spectroscopy in the next section will show that this
discontinuity in the total-pulsed spectrum between 2 and 3 keV is
genuine. Indeed, for energies above 2.8 keV an excellent fit can be
obtained with a power law with a photon index
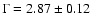 ,
which is in agreement with the RXTE-PCA spectrum above 2.8 keV (in
flux and index, see Table 5). The normalization of the
XMM-Newton spectrum below 2.8 keV is higher than the one above 2.8 keV, but
the spectral shape is the same with an photon index
,
which is in agreement with the RXTE-PCA spectrum above 2.8 keV (in
flux and index, see Table 5). The normalization of the
XMM-Newton spectrum below 2.8 keV is higher than the one above 2.8 keV, but
the spectral shape is the same with an photon index
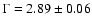 .
.
The XMM-Newton results imply an average pulsed fraction (defined as the pulsed
emission divided by the total emission) of (
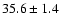 )% for the
2-10 keV band. The INTEGRAL-RXTE fit gives a 20-150 keV pulsed flux of
)% for the
2-10 keV band. The INTEGRAL-RXTE fit gives a 20-150 keV pulsed flux of
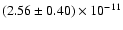 erg cm-2 s-1, resulting in an average pulsed
fraction of (
erg cm-2 s-1, resulting in an average pulsed
fraction of (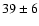 )%. The broad-band 2-10 keV and 20-150 keV
pulsed fractions suggest a fairly constant pulsed fraction over the
total high-energy window. However, in Fig. 4 it can
be seen that the measured pulsed flux (204-300 keV) is on the
extrapolation of the power-law fit to the total spectrum.
At these high energies the pulsed fraction could be as high as 100%.
)%. The broad-band 2-10 keV and 20-150 keV
pulsed fractions suggest a fairly constant pulsed fraction over the
total high-energy window. However, in Fig. 4 it can
be seen that the measured pulsed flux (204-300 keV) is on the
extrapolation of the power-law fit to the total spectrum.
At these high energies the pulsed fraction could be as high as 100%.
3.3.2 Phase-resolved pulsed spectra
The morphology of the 20-270 keV INTEGRAL pulse profile
(Fig. 5) was used to define three broad phase
intervals: Ph I contains the DC level (green coloured in figures);
Ph II contains the shoulder in the INTEGRAL band (blue coloured in
figures); and Ph III contains the main pulse in the INTEGRAL band
(magenta coloured in figures). The phase interval boundaries are
listed in Table 6 and are indicated with vertical lines
and colour bars in Figs. 5-7. In the latter figures is also visible how these
phase intervals relate to the profile shapes at energies below 10 keV.
Table 6:
Selected phase intervals for extraction of high-energy
spectra, using the pulse-shape morphology of the INTEGRAL-IBIS-ISGRI
20-270 keV pulse profile (Fig. 5).
![\begin{figure}
\par\mbox{\includegraphics[width=3.8cm,clip]{09772fig08a.ps}\hspa...
...}\hspace*{1mm}
\includegraphics[width=5.2cm,clip]{09772fig08c.ps} }
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg130.gif) |
Figure 8:
Phase-resolved results for XMM-Newton and RXTE-PCA are presented in
the left and center panels, respectively. These data and the
INTEGRAL (overlapping) results are shown together in the right
panels. Total (except for RXTE), total-pulsed and phase-resolved
pulsed spectra are presented in the top panels. The total spectra
and total-pulsed spectra are plotted in black. The phase resolved
spectra for Ph I, Ph II and Ph III (see Table 6)
are plotted in green, blue and magenta, respectively. The
XMM-Newton pulsed spectra are also indicated with open circle symbols
while the INTEGRAL pulsed spectra are indicated with a triangle
symbols. The data points with arrows indicate that the flux values
have significances less than 1.5 and the positive 1
and the positive 1 error is drawn. In the bottom panels
error is drawn. In the bottom panels 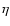 - defined as the fraction
of the total pulsed emission within a phase interval - is shown in
the same colour scheme as the spectra.
- defined as the fraction
of the total pulsed emission within a phase interval - is shown in
the same colour scheme as the spectra. |
| Open with DEXTER |
In the upper panels of Fig. 8 the resulting
pulsed-emission spectra for these three phase intervals are shown, in
each case together with the total-pulsed spectrum, and for XMM-Newton and
INTEGRAL also with the total-emission spectra; XMM-Newton in the upper-left
panel; RXTE-PCA in the top-center panel; and in the top-right panel XMM-Newton,
RXTE-PCA and INTEGRAL together. In the RXTE-PCA analysis we have again
verified that the three phase-resolved spectra for Set A and Set B are
fully consistent: there is no sign for long-term variability in shape
and flux down to the 5%-level.
We first focus on the pulsed-emission spectrum of Ph III which
contains the main hard INTEGRAL pulse. This Ph III spectrum follows the
total-pulsed spectrum in the INTEGRAL band, as expected. However, Ph III
shows below 10 keV a completely different spectral behaviour with
respect to the total-pulsed spectrum. Below 10 keV where the
total-pulsed spectrum turns up towards lower energies, this spectrum
keeps going down steeply.
The pulsed emission of Ph III reaches a minimum in luminosity around  2.5 keV. At lower energies it turns up again. This remarkably
spectral shape is measured consistently with XMM-Newton and RXTE-PCA, as can be
seen in the right panel of Fig. 8 (magenta coloured
data points). Therefore, we can exclude a systematic problem as cause
of this appearance. It is also remarkable how smoothly the combined
XMM-Newton and nine-year-average RXTE-PCA spectra join the four-year-average
INTEGRAL spectrum. This is strong evidence for a very stable
configuration of the production sites of the high-energy emission in
the magnetar magnetosphere over almost a decade.
2.5 keV. At lower energies it turns up again. This remarkably
spectral shape is measured consistently with XMM-Newton and RXTE-PCA, as can be
seen in the right panel of Fig. 8 (magenta coloured
data points). Therefore, we can exclude a systematic problem as cause
of this appearance. It is also remarkable how smoothly the combined
XMM-Newton and nine-year-average RXTE-PCA spectra join the four-year-average
INTEGRAL spectrum. This is strong evidence for a very stable
configuration of the production sites of the high-energy emission in
the magnetar magnetosphere over almost a decade.
It is obviously not straightforward to fit the spectrum of Ph III. We
attempted to make an empirical description to ``quantify'' the
discontinuities using all data points from INTEGRAL, RXTE-PCA and XMM-Newton. We
succeeded in describing the spectrum over the whole 0.5-270 keV band
with a black body and three power-law segments (i.e. one broken power
law plus a power law;
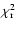 = 0.90 d.o.f. = 29, see
Table 7). The total fit contains a soft thermal
black-body component below 2 keV (
= 0.90 d.o.f. = 29, see
Table 7). The total fit contains a soft thermal
black-body component below 2 keV (
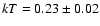 keV). This
component can be due to a tail of the soft pulse which peaks in
Ph II. Above
keV). This
component can be due to a tail of the soft pulse which peaks in
Ph II. Above  2 keV the spectrum drastically hardens. The
spectrum up to the break energy
2 keV the spectrum drastically hardens. The
spectrum up to the break energy
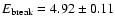 keV
is extremely hard with a photon index
keV
is extremely hard with a photon index
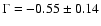 .
After the break a softer power law is required with photon
index
.
After the break a softer power law is required with photon
index
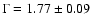 .
Finally, in order to account for the
harder INTEGRAL spectrum a third power law is required with photon index
.
Finally, in order to account for the
harder INTEGRAL spectrum a third power law is required with photon index
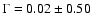 ,
which is dominating above
,
which is dominating above  60 keV. It
is obvious that very different production processes contribute in this
phase interval (Ph III) to the high-energy (pulsed) spectrum.
60 keV. It
is obvious that very different production processes contribute in this
phase interval (Ph III) to the high-energy (pulsed) spectrum.
Fitting only the INTEGRAL spectrum with a power law, a photon index
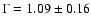 gives the best description.
(Table 7).
gives the best description.
(Table 7).
Also the spectral shape of the pulsed emission in Ph II (centered on
the soft pulse peaking at phase  0.4, blue coloured in figures)
is very different from that of the total-pulsed spectrum.
0.4, blue coloured in figures)
is very different from that of the total-pulsed spectrum.
Table 7:
Spectral-fit parameters for Ph III INTEGRAL, XMM-Newton, RXTE-PCA and
RXTE-HEXTE fits (see Sect. 3.3.2).
The independent XMM-Newton and RXTE-PCA spectra are again fully consistent. A
broad soft component below about 8 keV turns in the RXTE band above 8
keV into a component with power-law index  2, but is not detected
around 20 keV. The flux measurements close to energies as high as 100 keV are likely not related to the softer X-ray components and can be
explained as emission from a tail of the main hard-X-ray INTEGRAL pulse
in Ph III. No sensible model fits can be made to the total combined
Ph II spectrum. A good fit can be obtained considering only
XMM-Newton data, namely with a broken power-law with break energy
2, but is not detected
around 20 keV. The flux measurements close to energies as high as 100 keV are likely not related to the softer X-ray components and can be
explained as emission from a tail of the main hard-X-ray INTEGRAL pulse
in Ph III. No sensible model fits can be made to the total combined
Ph II spectrum. A good fit can be obtained considering only
XMM-Newton data, namely with a broken power-law with break energy
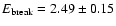 keV, consistent with the energy where in
the total pulsed spectrum the discontinuity was found. Below the break
energy the power-law model has a photon index
keV, consistent with the energy where in
the total pulsed spectrum the discontinuity was found. Below the break
energy the power-law model has a photon index
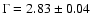 ,
above this energy
,
above this energy
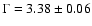 .
.
Ph I contains the left wing of the soft pulse below 8 keV, and
harbours the DC level in the INTEGRAL band (green coloured in
figures). Therefore, no significant flux is measured at hard
X-rays. Also in this case no sensible model combination (black body,
logparabola, power law) can describe the combined
XMM-Newton-RXTE-PCA spectrum. Furthermore, the XMM-Newton spectrum exhibits again a
drastic drop in flux between 2 and 3 keV. The fact that the RXTE-PCA data
points between 2 and 3 keV do not follow this sudden drop, might be
explained with the coarser energy resolution of RXTE-PCA, combined with a
strong gradient in the sensitive area and underlying photon spectrum.
A different way to study the relative contributions of the pulsed
components in the three selected phase intervals as a function of
energy is by plotting the  parameter, defined as the fraction of
the total-pulsed emission. It shows more clearly discontinuities in
the dependence on energy. In the bottom panels of
Fig. 8
parameter, defined as the fraction of
the total-pulsed emission. It shows more clearly discontinuities in
the dependence on energy. In the bottom panels of
Fig. 8  is presented for the different
observations. The bottom panel for XMM-Newton shows that the Ph III
contribution to the pulsed emission is a few percent up to
is presented for the different
observations. The bottom panel for XMM-Newton shows that the Ph III
contribution to the pulsed emission is a few percent up to  2.5 keV. Above 2.5 keV the contribution increases as a function
of energy to
2.5 keV. Above 2.5 keV the contribution increases as a function
of energy to  50% at 10 keV. This picture is fully confirmed by
RXTE, which shows that
50% at 10 keV. This picture is fully confirmed by
RXTE, which shows that  is still increasing above 10 keV up to
is still increasing above 10 keV up to  60% around 30 keV and stabilizes around this value in the
INTEGRAL band.
60% around 30 keV and stabilizes around this value in the
INTEGRAL band.
The opposite can be seen for the contribution to the pulsed flux from
Ph II. A high 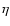 of
of  70%, fairly constant up to
70%, fairly constant up to  3 keV
from where the contribution abruptly decreases to
3 keV
from where the contribution abruptly decreases to  40% at
10 keV. Also this decline is observed with RXTE. The behaviour in the
INTEGRAL band is not clear. Finally, Ph I shows a somewhat similar
trend as Ph II with a significant contribution below
40% at
10 keV. Also this decline is observed with RXTE. The behaviour in the
INTEGRAL band is not clear. Finally, Ph I shows a somewhat similar
trend as Ph II with a significant contribution below  3 keV of
3 keV of
 28%, which decreases to
28%, which decreases to  8% above
8% above  8 keV and only
upper limits in the INTEGRAL band.
8 keV and only
upper limits in the INTEGRAL band.
For XMM-Newton and INTEGRAL the pulsed fraction is shown in
Fig. 9. The pulsed fraction (total-pulsed emission
divided by total emission) of 1708 is around  40% from soft
to hard X-rays (see also Sect. 3.3.1). However, we can
note here, that the pulsed fraction is not constant with energy, but
shows significant variations with energy below 10 keV. In the
INTEGRAL band the error bars are too large to draw firm conclusions. In
Fig. 9 the pulsed fractions for the three phase
intervals are also shown (i.e. emission in Ph I, II or III divided by
total emission). As was also clear from the dependence of
40% from soft
to hard X-rays (see also Sect. 3.3.1). However, we can
note here, that the pulsed fraction is not constant with energy, but
shows significant variations with energy below 10 keV. In the
INTEGRAL band the error bars are too large to draw firm conclusions. In
Fig. 9 the pulsed fractions for the three phase
intervals are also shown (i.e. emission in Ph I, II or III divided by
total emission). As was also clear from the dependence of 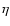 on
energy in Fig. 8, the contribution of the hard X-ray
pulse increases with energy above
on
energy in Fig. 8, the contribution of the hard X-ray
pulse increases with energy above  3 keV, while the pulsed
fractions of the other two phase intervals are decreasing with energy.
3 keV, while the pulsed
fractions of the other two phase intervals are decreasing with energy.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{09772fig09.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg160.gif) |
Figure 9:
The pulsed fractions of 1708 as a function of energy
using XMM-Newton below 10 keV and INTEGRAL above 20 keV. The total pulsed
fraction is drawn in black and plotted in colour are the pulsed
fractions for the three phase intervals (see Table 6). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{09772fig10.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg161.gif) |
Figure 10:
Narrow-band phase-resolved spectroscopy of 1708 using
RXTE-PCA and INTEGRAL-ISGRI data. Each panel shows the spectrum of a phase
interval with
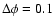 .
The phase intervals are indicated
in the panels. The data points with arrows indicate that the flux
values have significances less than 1.5 .
The phase intervals are indicated
in the panels. The data points with arrows indicate that the flux
values have significances less than 1.5 .
The positive
1 .
The positive
1 errors are drawn. Total spectral fits and the three
components (when contributing significantly) are drawn in black and
grey, respectively (See Sect. 3.3.3 and
Fig. 10).
errors are drawn. Total spectral fits and the three
components (when contributing significantly) are drawn in black and
grey, respectively (See Sect. 3.3.3 and
Fig. 10). |
| Open with DEXTER |
3.3.3 Narrow-band phase resolved pulsed spectra from RXTE
The phase-resolved spectroscopy presented in
Sect. 3.3.2, selecting three broad phase intervals,
unambiguously revealed that spectrally different components contribute
to the total pulsed emission of 1708. A similar conclusion was
earlier reached for AXP 142 (den Hartog et al. 2008). However, the
situation appears to be much more complex for 1708. The
XMM-Newton spectra below  2 keV suggest a soft thermal component,
which is not unexpected. However, this component can not be easily
separated from components with apparently complex spectral shapes
contributing to the total pulsed emission above 2 keV. Therefore, we
exploited the high statistics of the total
2 keV suggest a soft thermal component,
which is not unexpected. However, this component can not be easily
separated from components with apparently complex spectral shapes
contributing to the total pulsed emission above 2 keV. Therefore, we
exploited the high statistics of the total  600 ks of RXTE-PCA data
to explore in more detail the spectral characteristics as a function
of phase above 2 keV and the connection to the INTEGRAL band. We repeated
the phase-resolved spectroscopy but now for 10 narrow bins each
covering 0.1 in phase. Applying the method described in
Sect. 2.2 the 10 phase-resolved spectra have been
extracted and are shown in Fig. 10.
600 ks of RXTE-PCA data
to explore in more detail the spectral characteristics as a function
of phase above 2 keV and the connection to the INTEGRAL band. We repeated
the phase-resolved spectroscopy but now for 10 narrow bins each
covering 0.1 in phase. Applying the method described in
Sect. 2.2 the 10 phase-resolved spectra have been
extracted and are shown in Fig. 10.
The variations in spectral shape with phase are drastic. In the first
4 phase bins between phase 0.0 and 0.4, we see a spectral tail of the
soft component peaking in energy in the XMM-Newton band below 1 keV. These
spectra can be accurately fitted for energies above 2.8 keV with a
single power-law model. The index for the best fit to the sum of the
spectra between phase 0.0 and 0.3 is
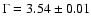 .
In the
phase bins 0.4-0.5 and 0.5-0.6 a significant hardening of the
spectra sets in for energies between about 5 keV and 20 keV. In the
following phase bins 0.6-0.7 and 0.7-0.8, getting closer to the
phase of the main INTEGRAL pulse, evidence is visible for the presence
of the hard power-law component with index
.
In the
phase bins 0.4-0.5 and 0.5-0.6 a significant hardening of the
spectra sets in for energies between about 5 keV and 20 keV. In the
following phase bins 0.6-0.7 and 0.7-0.8, getting closer to the
phase of the main INTEGRAL pulse, evidence is visible for the presence
of the hard power-law component with index  1.0 above 20 keV. This latter hard power-law spectrum is dominating the energy
budget for the last three phase bins. More surprisingly, in the two
phase windows between 0.7 and 0.9, centered on the INTEGRAL main
pulse, a very hard part of the spectrum is apparent in a narrow energy
interval above
1.0 above 20 keV. This latter hard power-law spectrum is dominating the energy
budget for the last three phase bins. More surprisingly, in the two
phase windows between 0.7 and 0.9, centered on the INTEGRAL main
pulse, a very hard part of the spectrum is apparent in a narrow energy
interval above  2 keV. This is most extreme for the phase
interval 0.7-0.8 with a ``local'' photon index
2 keV. This is most extreme for the phase
interval 0.7-0.8 with a ``local'' photon index
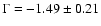 (notice the sign!) up to a break energy
(notice the sign!) up to a break energy
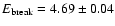 .
Finally, the spectrum for phase interval 0.9-1.0, the
last fraction of the trailing wing of the INTEGRAL main pulse, can be
fitted with a single power law with best-fit photon index
.
Finally, the spectrum for phase interval 0.9-1.0, the
last fraction of the trailing wing of the INTEGRAL main pulse, can be
fitted with a single power law with best-fit photon index
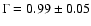 .
Moving only 10% in phase to the next phase interval 0.0-0.1, the hard spectrum ``switches'' and becomes again very soft
with
.
Moving only 10% in phase to the next phase interval 0.0-0.1, the hard spectrum ``switches'' and becomes again very soft
with
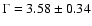 .
.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{09772fig11.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg165.gif) |
Figure 11:
Phase distributions of the normalizations F0 of the three
spectral-model components (see Table 8) taken at
pivot energy
E0 = 15.0433 keV for the 10 narrow phase-interval
spectra. Indicated with crosses and a thin grey line are the
normalizations of the soft power-law component, with triangles and
thick grey line the hard power-law component and with squares and a
black line the composite spectral component. |
| Open with DEXTER |
From Fig. 10 it is evident that different spectral
components contribute to the total pulsed emission and dominate in
different phase intervals. Two components can clearly be identified: a
soft power-law component with index
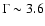 and a hard
power-law component with index
and a hard
power-law component with index
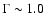 .
Then there appears
to be a third component, dominating in the energy band
.
Then there appears
to be a third component, dominating in the energy band  3 to 20 keV for phases between 0.7 and 0.9. A clear characteristic of this
spectral component is a very steep rise above 2.3 keV (
3 to 20 keV for phases between 0.7 and 0.9. A clear characteristic of this
spectral component is a very steep rise above 2.3 keV (
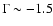 ). We investigated what shape such a third component should
have in order to explain, together with two power-law components, all
spectra in Fig. 10. This shape should give a clear
constraint for any proposed production mechanism.
). We investigated what shape such a third component should
have in order to explain, together with two power-law components, all
spectra in Fig. 10. This shape should give a clear
constraint for any proposed production mechanism.
Table 8:
Model parameters of the three spectral components that are
used to fit the 10 narrow-band phase-resolved RXTE-PCA and INTEGRAL-ISGRI
spectra.
We followed the following procedure. The hard power-law component was
adopted from the best fit to the spectrum for phase 0.9-1.0:
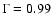 .
Then we investigated empirically what spectral shape,
together with the power-law model with
.
Then we investigated empirically what spectral shape,
together with the power-law model with
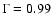 ,
can accurately
describe the spectrum in phase interval 0.7-0.8. This turned out to
be the sum of two logparabolic functions of which the parameters are
given in Table 8. Finally, for the index of the
soft power-law model we adopted the best fit to the summed spectrum in
the phase interval 0.0-0.3:
,
can accurately
describe the spectrum in phase interval 0.7-0.8. This turned out to
be the sum of two logparabolic functions of which the parameters are
given in Table 8. Finally, for the index of the
soft power-law model we adopted the best fit to the summed spectrum in
the phase interval 0.0-0.3:
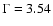 .
.
We now attempted to describe the measured spectral distributions in
the 10 narrow phase intervals in terms of just these three model
shapes with free normalizations. Interestingly, the resulting
total fits are very satisfactory for all narrow phase intervals (see
Fig. 10). The normalizations of the three models are
shown in Fig. 11. Effectively, this figure shows the
pulse profile of each spectral component contributing to the
total-pulsed spectrum, i.e. a complete decoupling based on the
measured spectral and timing characteristics. In
Fig. 10 we show for all 10 spectra the contributions
of the three spectral components to the model fit, but only when
components were statistically required to reproduce the measured
spectra. Figure 11 together with
Fig. 10 show now the characteristics of the three
components which can reproduce together the total pulsed emission, the
pulse shapes and their spectra. Furthermore, we have shown above that
our results indicate that these characteristics are invariant over
almost a decade of observations.
4 Summary
In this paper we have presented new and more detailed characteristics
of 1708 in the hard X-ray/soft gamma-ray regime (>20 keV) using
INTEGRAL-ISGRI and SPI data. Following the approach in our earlier paper
on AXP 142 (den Hartog et al. 2008) we extended the energy window to
lower energies to obtain a broader high-energy view using archival
RXTE and XMM-Newton observations. The emphasis of this work on broad-band
phase-resolved spectroscopy was aimed at the identification of
distinctly different components contributing to the total-pulsed
emission. What follows is a summary of the main results.
1) Using all available INTEGRAL data taken with INTEGRAL ISGRI during
2003-2006 - adding up to 5.2 Ms effective on-source exposure - the
time-averaged 20-175 keV spectrum can be described by a power-law
with photon index
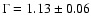 .
The luminosity is
.
The luminosity is
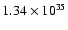 erg s-1 (20-175 keV) adopting a distance of 3.8 kpc
(Sect. 3.1.2, Fig. 4, Table
4).
erg s-1 (20-175 keV) adopting a distance of 3.8 kpc
(Sect. 3.1.2, Fig. 4, Table
4).
2) There is no indication for a spectral break in the
INTEGRAL spectrum up to energies of  175 keV. Including in the
spectral fit earlier published COMPTEL flux upper limits for energies
above 750 keV (Kuiper et al. 2006) and assuming a logparabolic shape
for the spectrum above 20 keV, the maximum luminosity is found for an
energy of
175 keV. Including in the
spectral fit earlier published COMPTEL flux upper limits for energies
above 750 keV (Kuiper et al. 2006) and assuming a logparabolic shape
for the spectrum above 20 keV, the maximum luminosity is found for an
energy of  290 keV (Sect. 3.1.2,
Fig. 4).
290 keV (Sect. 3.1.2,
Fig. 4).
1) In the INTEGRAL data no significant long-term time variability for
energies above 20 keV is found on time scales of one year and half a
year in total flux and spectral index. There is only one measurement
with a  3
3 indication for a flux increase in nine
observations. The total flux (20-150 keV) and the spectral index are
stable within 22% and 18% (both 1
indication for a flux increase in nine
observations. The total flux (20-150 keV) and the spectral index are
stable within 22% and 18% (both 1 ), respectivily ( Sect. 3.1.1, Figs. 1-3).
), respectivily ( Sect. 3.1.1, Figs. 1-3).
2) Our analysis of all available ISGRI data rejects the
claim by Götz et al. (2007) of correlated variability between the
hard X-ray emission measured with ISGRI and soft X-ray emission from
1708 in relation to a (candidate) glitch (Sect. 3.1.1, Fig. 3).
1) ISGRI measures significant pulse profiles for energies up to
270 keV (Sect. 3.2.1,
Figs. 5 and 6).
2) High-energy pulse profiles measured with XMM-Newton, RXTE-PCA and
HEXTE and INTEGRAL-ISGRI over the broad energy band 0.5 keV up to 270 keV
are consistent in morphology when measured in the same differential
energy bands, independent of the epoch of the observation; apparent
differences are either due to statistics or due to differences in
energy response (Sect. 3.2,
Figs. 6 and 7).
3) Fast morphology changes with energy are visible in the
pulse profiles below  20 keV, (earlier noted by
e.g. Kuiper et al. 2006; Sugizaki et al. 1997; Israel et al. 2001) In the
INTEGRAL band the pulse profiles do not show morphology changes ( Sect. 3.2, Figs. 6 and 7).
20 keV, (earlier noted by
e.g. Kuiper et al. 2006; Sugizaki et al. 1997; Israel et al. 2001) In the
INTEGRAL band the pulse profiles do not show morphology changes ( Sect. 3.2, Figs. 6 and 7).
4) Three different pulse components are recognized in the
pulse profiles: a) A hard pulse peaking around phase 0.8; which starts
contributing to the pulse profiles above  4 keV; b) a softer
pulse peaking around phase 0.4; which is not apparent at hard X-rays;
c) a very soft pulse component below 2 keV for which there is an
indication around phase 1 where it fills the pulse profile to a
saw-tooth-like shape (Sect. 3.2.1,
Fig. 6).
4 keV; b) a softer
pulse peaking around phase 0.4; which is not apparent at hard X-rays;
c) a very soft pulse component below 2 keV for which there is an
indication around phase 1 where it fills the pulse profile to a
saw-tooth-like shape (Sect. 3.2.1,
Fig. 6).
1) ISGRI measures the phase-averaged total-pulsed spectrum up to
270 keV which can be described with a power law with photon index
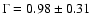 (Sect. 3.3.1,
Fig. 4).
(Sect. 3.3.1,
Fig. 4).
2) The average pulsed fraction in the INTEGRAL band is 39%. Note, that the pulsed flux measured above 200 keV is on the
extrapolation of the total spectrum, consistent with being for 100%
pulsed. Below 10 keV, the pulsed fraction as measured with XMM-Newton is
not constant but varies between  31% and
31% and  48% in a complex
way (Sect. 3.3.1, Figs. 4 and 9).
48% in a complex
way (Sect. 3.3.1, Figs. 4 and 9).
3) The total-pulsed spectrum from 0.5 keV up to 270 keV is
very stable over time-scales of years. Firstly, the pulsed-emission
spectra (2.7-32.1 keV) of two sets of RXTE-PCA data taken six years
before and three years during the INTEGRAL operations, respectively,
appeared to be statistically consistent within a few percent
(see also Dib et al. 2008). Secondly, the summed RXTE-PCA
total-pulsed spectrum joins smoothly that from XMM-Newton at lower
energies, as well as those from RXTE-HEXTE and INTEGRAL at higher energies
(Sect. 3.3.1, Fig. 4).
4) Fitting INTEGRAL, RXTE-PCA and HEXTE simultaneously with two
power-law components yields an excellent fit for energies above 2.8 keV with a soft power-law model with photon index
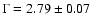 and a hard power-law model with photon index
and a hard power-law model with photon index
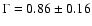 (
(
 = 0.51, d.o.f. = 22). (Sect. 3.3.1,
Table 5).
= 0.51, d.o.f. = 22). (Sect. 3.3.1,
Table 5).
5) The XMM-Newton pulsed spectrum above 2.8 keV is fully
consistent in flux and power-law index with the corresponding
RXTE-PCA spectrum, however, there is a discontinuity in the
XMM-Newton spectrum, a drop in flux, between 2 and 3 keV ( Sect. 3.3.1, Fig. 4).
1) The time-averaged phase-resolved spectra, selecting three broad
phase intervals or narrow 0.1-phase-wide intervals, are connecting
very smoothly over the total 0.5-300 keV energy band from instrument
to instrument: another confirmation of the long-term many-year
stability of the geometry and production mechanisms responsible for
the emission (Sect. 3.3.2, Figs. 8
and 10).
2) The XMM-Newton, RXTE-PCA and INTEGRAL phase-resolved spectra,
selecting three broad phase intervals, have vastly different and
complex spectral shapes, constituting together the total-pulsed
spectrum (Sect. 3.3.2, Fig. 8).
3) Ph III (which contains the main hard INTEGRAL pulse) shows
hardly any contribution to the pulsed spectrum for energies below 2.5 keV (i.e. low 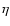 ). This part of the spectrum can be described
by a black-body with a temperature kT of
). This part of the spectrum can be described
by a black-body with a temperature kT of
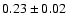 keV. Above
2.5 keV, the energy where the Ph III pulsed emission reaches its
minimum luminosity, the spectral shape becomes very complex: the
spectrum first hardens dramatically (and
keV. Above
2.5 keV, the energy where the Ph III pulsed emission reaches its
minimum luminosity, the spectral shape becomes very complex: the
spectrum first hardens dramatically (and 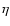 increases) with a
photon index
increases) with a
photon index
 up to a break energy of
up to a break energy of  5 keV, consistently measured with XMM-Newton and RXTE-PCA. After the break
the spectrum softens to a power-law with photon index
5 keV, consistently measured with XMM-Newton and RXTE-PCA. After the break
the spectrum softens to a power-law with photon index
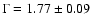 .
In the INTEGRAL band it hardens again to a photon index
.
In the INTEGRAL band it hardens again to a photon index
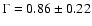 (Sect. 3.3.2,
Fig. 8, Table 7).
(Sect. 3.3.2,
Fig. 8, Table 7).
4) The spectra of Ph I, DC-level in INTEGRAL pulse profile,
and Ph II, ``shoulder'' in INTEGRAL profile and main soft-X-ray pulse,
also appear to be complex. Both spectra are soft with maximum
luminosity below 1 keV and exhibit discontinuities around 2.8 keV, the
energy where we noted a drop in flux in the total-pulsed spectrum of
XMM-Newton. The emissions seem to vanish above 20 keV ( Sect. 3.3.2, Fig. 8).
5) Narrow-band phase-resolved spectroscopy in 10 phase
bins reveals the cause of the complex behaviour of the emission
spectra in the broader phase bins. The 10 spectra show gradual and
sudden changes as a function of phase. The spectral complexity has
become even clearer and is more extreme than seen in the broad-band
phase-resolved spectra (Sect. 3.3.3,
Fig. 10).
6) Each of the 10 pulsed spectra can be accurately described
with a sum (free normalizations) of three components with very
different spectral shapes: a) a soft power-law component with a photon
index
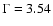 ;
b) a hard power-law component with a photon
index
;
b) a hard power-law component with a photon
index
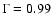 ;
and c) a peculiar curved component which has
been approximated by the sum of two logparabolic functions and
contributes significantly between 4 and 20 keV ( Sect. 3.3.3, Fig. 10,
Table 8).
;
and c) a peculiar curved component which has
been approximated by the sum of two logparabolic functions and
contributes significantly between 4 and 20 keV ( Sect. 3.3.3, Fig. 10,
Table 8).
7) The phase distributions of the normalizations to the
three spectral components represent three decoupled pulse profiles
which together constitute the total pulse profile. The soft component
shows a single peak around phase 0.4. The hard component shows a broad
peak with a significant contribution from phase 0.4 to 1. The curved
component shows a narrower peak ( 0.25 in phase FWHM) which has its
maximum in phase interval 0.7-0.8 (Sect. 3.3.3,
Fig. 11).
0.25 in phase FWHM) which has its
maximum in phase interval 0.7-0.8 (Sect. 3.3.3,
Fig. 11).
5 Discussion
The detailed analysis performed in this work on the high-energy
emission (0.5-300 keV) from 1708 led to similar conclusions as
were reached earlier for AXP 142 (den Hartog et al. 2008). Namely,
that genuinely different pulse components with different spectra
contribute to the total-pulsed emission. In the case of 1708 not
only the variation with energy of the structure of the pulse profiles
could be used to identify these different components, similar to the
case of 142, but also the apparent fine structure in the
phase-resolved spectra provided an efficient means to disentangle the
pulsed emission into different components.
In den Hartog et al. (2008) we discussed the implications of the
derived high-energy characteristics of 142 for models developed in
recent years for explaining the non-thermal, luminous hard X-ray
emission from AXPs: 1) a quantum electro-dynamic model (QED) by
Heyl & Hernquist (2005b,a); 2) a corona model by Beloborodov & Thompson (2007),
further elaborated by Lyubarsky & Eichler (2008) and 3) a resonant
upscattering model by Baring & Harding (2007). We concluded that all
three models have difficulties in explaining many features of the
detailed results (See the discussion in the paper
by den Hartog et al. 2008). A confrontation of these models with our
new results for 1708 leads to similar conclusions. It is apparent
that any attempt to explain the high-energy emission (0.5-300 keV)
should consider a stable (at least over a decade) three-dimensional
geometry taking all relevant angles (the angle between the magnetic
and the spin axis and the viewing angle) into account, as well as the
physical production processes taking place on the surface of the
neutron star and at different sites in the atmosphere and
magnetosphere.
For 1708 our results reveal a clear separation in phase, and
therefore also of the production sites, of all pulsed hard X-ray
emission above 20 keV with photon index
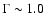 from the
pulsed soft thermal emission below 4 keV. This soft emission can be
described with a black-body spectrum with kT < 0.4 keV and a
power-law spectral tail with photon index
from the
pulsed soft thermal emission below 4 keV. This soft emission can be
described with a black-body spectrum with kT < 0.4 keV and a
power-law spectral tail with photon index
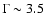 .
Such a
clear separation is consistent with predictions from the QED model by
Heyl (2007). However, the observed total and the pulsed
hard X-ray spectra are harder (index
.
Such a
clear separation is consistent with predictions from the QED model by
Heyl (2007). However, the observed total and the pulsed
hard X-ray spectra are harder (index  1.0) than the photon index
of 1.5 predicted by this model. Contrarily, the clear separation in
phase between the thermal and non-thermal pulses makes an
interpretation of the hard X-ray emission in terms of resonant
magnetic upscattering of the thermal soft photons by
ultra-relativistic electrons, accelerated along either open or closed
magnetic field lines unlikely (proposed in the
Compton-upscattering model by Baring & Harding 2007). At least part of
the thermal target photons should also arrive in the narrow phase
interval of the non-thermal pulse. This problem might be circumvented
if the thermal target photons are part of the isotropic thermal DC
emission, and the thermal pulse at phase 0.4 is not related to the
hard X-ray emission.
1.0) than the photon index
of 1.5 predicted by this model. Contrarily, the clear separation in
phase between the thermal and non-thermal pulses makes an
interpretation of the hard X-ray emission in terms of resonant
magnetic upscattering of the thermal soft photons by
ultra-relativistic electrons, accelerated along either open or closed
magnetic field lines unlikely (proposed in the
Compton-upscattering model by Baring & Harding 2007). At least part of
the thermal target photons should also arrive in the narrow phase
interval of the non-thermal pulse. This problem might be circumvented
if the thermal target photons are part of the isotropic thermal DC
emission, and the thermal pulse at phase 0.4 is not related to the
hard X-ray emission.
As mentioned before, Götz et al. (2007) reported the detection of
correlated variability in hard X-ray flux and spectral index with
similar correlated variations at low-energy X-rays from 1708. This
would imply correlated production processes at the same sites in the
magnetosphere. However, our analysis disproved the claimed variability
in the ISGRI-detected hard X-ray flux.
Very peculiar is the spectral shape of the component which contributes
significantly to the total-pulsed emission from 1708 between 4 keV and
20 keV. It is not obvious what underlying emission processes can
produce such a spectral shape. This component exhibits the most narrow
pulse profile with a width of  0.25 in pulsar phase (FWHM, see
Fig. 11). It appears to be completely separated from
the soft pulse, but it is centered in phase on the hard X-ray pulse
which is about twice as broad. This means that the production site in
the magnetosphere of this curved component is confined to a narrow
region, possibly directed along open or the last closed magnetic-field
lines, similar to different dipole scenarios proposed for radio
pulsars (e.g. Ruderman & Sutherland 1975; Harding & Muslimov 1998; Romani 1996; Arons 1983; Muslimov & Harding 2003; Hirotani 2006; Cheng et al. 1986; Usov & Melrose 1995). Like is the case for radio
pulsars, this geometry appears to be very stable. The RXTE monitoring
observations proved that the pulse profiles and phase resolved spectra
were stable over 9 years. This might indicate that the non-thermal
emission is produced higher-up in the magnetosphere, above the region
closer to the neutron star with a strong twisted (toroidal)
field.
0.25 in pulsar phase (FWHM, see
Fig. 11). It appears to be completely separated from
the soft pulse, but it is centered in phase on the hard X-ray pulse
which is about twice as broad. This means that the production site in
the magnetosphere of this curved component is confined to a narrow
region, possibly directed along open or the last closed magnetic-field
lines, similar to different dipole scenarios proposed for radio
pulsars (e.g. Ruderman & Sutherland 1975; Harding & Muslimov 1998; Romani 1996; Arons 1983; Muslimov & Harding 2003; Hirotani 2006; Cheng et al. 1986; Usov & Melrose 1995). Like is the case for radio
pulsars, this geometry appears to be very stable. The RXTE monitoring
observations proved that the pulse profiles and phase resolved spectra
were stable over 9 years. This might indicate that the non-thermal
emission is produced higher-up in the magnetosphere, above the region
closer to the neutron star with a strong twisted (toroidal)
field.
The detailed results we obtained for AXPs 142 and 1708 clearly
prove that the total persistent high-energy emission from AXPs
consists of DC emission and pulsed emission exhibiting different
spectra (already shown in Kuiper et al. 2006). Furthermore, the
pulsed emission consists of multiple components with different
spectra. As a consequence it does not seem meaningful to make detailed
model fits to just the total AXP spectra to derive a physical
interpretation of the emission. The physical origin and production
site of each different component has to be considered. Examples of
model fitting to the total X-ray spectra of magnetars are recent
applications of the resonant cyclotron scattering model first proposed
by Thompson et al. (2002). Recent developments of this model can be found in
Lyutikov & Gavriil (2006), Güver et al. (2007,2006) and
Fernández & Thompson (2007). This model computes the result of
multiple scatterings of soft photons in the magnetospheres and was
developed to explain the apparently thermal black-body spectra with a
power-law extension to higher energies, as measured for energies below
 10 keV. In the extensive work by Rea et al. (2008)
detailed fits with this model are merely made to the high-energy total
spectra of a comprehensive set of magnetars, including 1708,
leading to interesting estimates of e.g. optical depths and
magnetospheric electron densities at the resonances. However, our
temporal and spectral decoupling of different components in the pulsed
emission (Figs. 10 and 11), shows
that between
10 keV. In the extensive work by Rea et al. (2008)
detailed fits with this model are merely made to the high-energy total
spectra of a comprehensive set of magnetars, including 1708,
leading to interesting estimates of e.g. optical depths and
magnetospheric electron densities at the resonances. However, our
temporal and spectral decoupling of different components in the pulsed
emission (Figs. 10 and 11), shows
that between  4 keV and 20 keV a peculiar curved spectral
component contributes significantly to the pulsed emission, and is
unrelated to the soft thermal emission. This component contributes
also significantly to the total emission detected from 1708 in the
energy interval where the resonant upscattering is effective. Hence,
it will obviously have an adverse impact on the parameter estimations
if this component has not been subtracted. On the other hand, the
resonant cyclotron-scattering model might offer a good explanation for
the soft pulse peaking at phase 0.4. Spectral modeling of the
corresponding spectrum, and separately of the thermal spectrum of the
DC emission will probe the model parameters in different sites in the
magnetosphere.
4 keV and 20 keV a peculiar curved spectral
component contributes significantly to the pulsed emission, and is
unrelated to the soft thermal emission. This component contributes
also significantly to the total emission detected from 1708 in the
energy interval where the resonant upscattering is effective. Hence,
it will obviously have an adverse impact on the parameter estimations
if this component has not been subtracted. On the other hand, the
resonant cyclotron-scattering model might offer a good explanation for
the soft pulse peaking at phase 0.4. Spectral modeling of the
corresponding spectrum, and separately of the thermal spectrum of the
DC emission will probe the model parameters in different sites in the
magnetosphere.
An important parameter to be reproduced by the models is the photon
index of the power-law spectral shape in the hard X-ray window and the
cut-off energy. The index
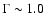 of the non-thermal pulse
and a spectral break at a few hundred keV is consistent with a
bremsstrahlung origin as first proposed in the corona model by
Beloborodov & Thompson (2007). But, further elaboration of the corona model by
Lyubarsky & Eichler (2008) lead to a different hard X-ray spectrum,
namely a superposition of bremsstrahlung radiation from the hot
atmosphere and Comptonization radiation from the extended corona. The
latter produces a hard spectrum up to the MeV band and is inconsistent
with the COMPTEL upper limits at MeV energies. Furthermore, the
stability of the configuration over 9 years is a challenge for the
corona model. For the resonant upscattering model of
Baring & Harding (2007) the predicted photon indexes are considerably
softer and the spectra extend into the MeV range, possibly to
significantly higher gamma-ray energies. In this respect we should
emphasize that we donot see any indication for a break in the
INTEGRAL spectrum (<300 keV) of 1708, more importantly, we donot
know for 1708 and 142 what the shapes of the spectra are above a
few hundred keV. Extreme cases are allowed by the data, e.g. a hard
spectrum with index
of the non-thermal pulse
and a spectral break at a few hundred keV is consistent with a
bremsstrahlung origin as first proposed in the corona model by
Beloborodov & Thompson (2007). But, further elaboration of the corona model by
Lyubarsky & Eichler (2008) lead to a different hard X-ray spectrum,
namely a superposition of bremsstrahlung radiation from the hot
atmosphere and Comptonization radiation from the extended corona. The
latter produces a hard spectrum up to the MeV band and is inconsistent
with the COMPTEL upper limits at MeV energies. Furthermore, the
stability of the configuration over 9 years is a challenge for the
corona model. For the resonant upscattering model of
Baring & Harding (2007) the predicted photon indexes are considerably
softer and the spectra extend into the MeV range, possibly to
significantly higher gamma-ray energies. In this respect we should
emphasize that we donot see any indication for a break in the
INTEGRAL spectrum (<300 keV) of 1708, more importantly, we donot
know for 1708 and 142 what the shapes of the spectra are above a
few hundred keV. Extreme cases are allowed by the data, e.g. a hard
spectrum with index
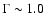 with a sharp cut-off, as well as
with a break or bend with a flat spectrum extending underneath the
COMPTEL upper limits into the MeV or even GeV regions.
with a sharp cut-off, as well as
with a break or bend with a flat spectrum extending underneath the
COMPTEL upper limits into the MeV or even GeV regions.
Similarly hard spectra with
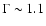 have been measured in
the hard X-ray window up to 60-200 keV for several young
rotation-powered pulsars, e.g. AX J1838.0-0655, PSR J1846-0258,
PSR J1811-1925, PSR J1930+1852 and PSR J1617-5055
(Kuiper et al. 2008; Kuiper & Hermsen 2008). We also know that these
hard power-law spectra donot extrapolate to the MeV range (no
detections by COMPTEL). Furthermore, those young pulsars detected
with COMPTEL in the MeV range, Crab (for a multi-wavelength
analysis similar to this work see Kuiper et al. 2001) and PSR B1509-58
(Kuiper et al. 1999), have flat (
have been measured in
the hard X-ray window up to 60-200 keV for several young
rotation-powered pulsars, e.g. AX J1838.0-0655, PSR J1846-0258,
PSR J1811-1925, PSR J1930+1852 and PSR J1617-5055
(Kuiper et al. 2008; Kuiper & Hermsen 2008). We also know that these
hard power-law spectra donot extrapolate to the MeV range (no
detections by COMPTEL). Furthermore, those young pulsars detected
with COMPTEL in the MeV range, Crab (for a multi-wavelength
analysis similar to this work see Kuiper et al. 2001) and PSR B1509-58
(Kuiper et al. 1999), have flat (
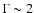 )
spectra at MeV
energies, and started with harder spectra at hard X-ray energies. In
addition, for three millisecond pulsars also an index
)
spectra at MeV
energies, and started with harder spectra at hard X-ray energies. In
addition, for three millisecond pulsars also an index
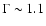 has been measured in the X-ray band up to 25 keV (PSR J0218+4232, PSR B1821-24 and PSR B1937+21; Cusumano et al. 2003; Kuiper et al. 2004b). For one of these
millisecond pulsars, PSR J0218+4232, detection has been claimed even
between 300 MeV and 1 GeV with a soft spectral index of
has been measured in the X-ray band up to 25 keV (PSR J0218+4232, PSR B1821-24 and PSR B1937+21; Cusumano et al. 2003; Kuiper et al. 2004b). For one of these
millisecond pulsars, PSR J0218+4232, detection has been claimed even
between 300 MeV and 1 GeV with a soft spectral index of  2.6
(Kuiper et al. 2000), thus a drastic spectral bend or break is
required between the hard X-rays and the high-energy gamma rays.
These results on young as well as on old millisecond radio pulsars
prove that in dipole fields such hard non-thermal spectra can be
produced in stable configurations. The major difference with the AXPs
is that the energy source for ordinary pulsars is rotational
energy and for AXPs/magnetars magnetic energy. It is interesting to
note that recently during a
2.6
(Kuiper et al. 2000), thus a drastic spectral bend or break is
required between the hard X-rays and the high-energy gamma rays.
These results on young as well as on old millisecond radio pulsars
prove that in dipole fields such hard non-thermal spectra can be
produced in stable configurations. The major difference with the AXPs
is that the energy source for ordinary pulsars is rotational
energy and for AXPs/magnetars magnetic energy. It is interesting to
note that recently during a  50-day outburst magnetar-like bursts
have been reported from a very young rotation-powered pulsar (PSR
J1846-0258) with a strong magnetic field
(Gavriil et al. 2008; Kumar & Safi-Harb 2008).
50-day outburst magnetar-like bursts
have been reported from a very young rotation-powered pulsar (PSR
J1846-0258) with a strong magnetic field
(Gavriil et al. 2008; Kumar & Safi-Harb 2008).
A possible scenario for the persistent high-energy emission from AXPs
seems to emerge in which a soft thermal component, for 1708
peaking at phase 0.4, originates in regions above and close to the
polar cap of the neutron star with resonant cyclotron scattering
offering a physical explanation. A large fraction of the thermal
photons will have a more isotropic distribution. These photons can be
responsible for the soft part of the DC emission spectrum, also with a
resonant cyclotron-scattering origin, but with e.g. different optical
depths and magnetospheric electron densities at the resonances. For
future studies, it will be interesting to accurately derive a spectrum
of just the DC emission for model fitting. Furthermore, the
non-thermal emission might be produced higher up in the outer
magnetosphere, where the magnetic field strengths is in the range
estimated for normal radio pulsars. The required strong current of
electrons and positrons can be sustained by the outward transfer of
magnetic helicity from the inner zone where it is injected. Then the
acceleration of particles and the production of the observed
non-thermal photons has to occur in stable narrow zones along the
curved field lines to produce e.g. the narrow hard X-ray pulse seen
for 1708. In the outer magnetosphere the scenario might resemble
those proposed for the high-energy emission from rotation-powered
pulsars. In fact, the approach taken by Baring & Harding (2007) is a
first attempt along these lines. However, they concluded that the
resonant magnetic Compton upscattering is most effective close to the
magnetar surface.
From only two of the 13 confirmed magnetars radio emission has been
detected and their radio emission properties have been measured in
great detail recently, notably from AXP 1810
(Halpern et al. 2005; Camilo et al. 2006; Kramer et al. 2007) and AXP 1547
(Camilo et al. 2008,2007). These very interesting AXPs show
transient radio emission, which is apparently related to the X-ray
variability (e.g. Ibrahim et al. 2004; Gotthelf & Halpern 2005; Gelfand & Gaensler 2007; Halpern et al. 2008). These radio AXPs appear to be very
highly linearly polarized and have very flat spectra over a wide range
of radio frequencies, very similar characteristics to those of many
young ordinary radio pulsars. Camilo et al. (2008) note that, while
unexpected a priori, it appears that ideas developed to understand the
geometry of emission from ordinary pulsars along open dipolar field
lines also apply to known radio magnetars. However, they also
conclude that both radio AXPs have also variable pulse profiles and
radio flux densities, not typical for young pulsars.
Upon submission of this work, an extensive treatment appeared of pair
creation processes in an ultra-strong magnetic field and particle
heating in a dynamic magnetosphere (Thompson 2008a), as
well as a self-consistent model of the inner accelerator with
implications for pulsed radio emission
(Thompson 2008b). In the first paper Thompson considers
the details of QED processes that create electron-positron pairs in
magnetar fields. He discusses how the pair creation rate in the
open-field circuit and the outer magnetosphere can be strongly
enhanced by instabilities near the light cylinder and how this very
high rate of pair creation on the open magnetic field lines can help
to stabilize a static twist in the closed magnetosphere and to
regulate the loss of magnetic helicity by reconnection at the light
cylinder. In the second paper, one of the possible scenarios for
explaining the rapid radio variability, broad pulses and hard radio
spectra comprises a strongly variable current in the outer
magnetosphere and a high rate of pair creation sustained by a
turbulent cascade. It is interesting to note that stable geometries
are being considered to explain the production of transient radio
emission for AXPs involving high rates of pair creation on the open
magnetic-field lines in the outer magnetosphere. Such scenarios might
also be required to explain the production in the outer magnetosphere
on the orders of magnitude more luminous non-thermal X-ray emission.
Acknowledgements
We thank Jörgen Knödlseder for providing
the SPI upper limits for 1708. This work is supported by NWO,
Netherlands Organisation for Scientific Research. The results are
based on observations with INTEGRAL, an ESA project with instruments
and science data centre funded by ESA member states (especially the PI
countries: Denmark, France, Germany, Italy, Switzerland, Spain), Czech
Republic and Poland, and with the participation of Russia and the
USA. We are grateful to ASI, CEA, CNES, DLR, ESA,
INTA, NASA and OSTC for support. This research has made use of data
obtained through the High-Energy Astrophysics Center Online Service,
provided by the NASA/Goddard Space-Flight Center.
- Arnaud,
K. A. 1996, in Astronomical Data Analysis Software and Systems
V, ASP Conf. Ser., 101, 17
(In the text)
-
Arons, J. 1983, ApJ, 266, 215 [NASA ADS] [CrossRef]
-
Baring, M. G., & Harding, A. K. 2007, Ap&SS, 308,
109 [NASA ADS] [CrossRef]
- Beloborodov, A. M.,
& Thompson, C. 2007, ApJ, 657, 967 [NASA ADS] [CrossRef]
-
Buccheri, R., Bennett, K., Bignami, G. F., et al. 1983,
A&A, 128, 245 [NASA ADS]
(In the text)
- Camilo,
F., Ransom, S. M., Halpern, J. P., et al. 2006,
Nature, 442, 892 [NASA ADS] [CrossRef]
- Camilo,
F., Ransom, S. M., Halpern, J. P., & Reynolds, J.
2007, ApJ, 666, L93 [NASA ADS] [CrossRef]
- Camilo,
F., Reynolds, J., Johnston, S., Halpern, J. P., & Ransom,
S. M. 2008, ApJ, accepted [arXiv:0802.0494]
-
Campana, S., Rea, N., Israel, G. L., Turolla, R., & Zane,
S. 2007, A&A, 463, 1047 [NASA ADS] [CrossRef] [EDP Sciences]
-
Cheng, K. S., Ho, C., & Ruderman, M. 1986, ApJ, 300,
500 [NASA ADS] [CrossRef]
-
Cusumano, G., Hermsen, W., Kramer, M., et al. 2003, A&A,
410, L9 [NASA ADS] [CrossRef] [EDP Sciences]
- den Hartog, P. R., Kuiper,
L., Hermsen, W., & Vink, J. 2004, The Astronomer's Telegram,
293, 1 [NASA ADS]
- den
Hartog, P. R., Hermsen, W., Kuiper, L., et al. 2006,
A&A, 451, 587 [NASA ADS] [CrossRef] [EDP Sciences]
- den
Hartog, P. R., Hermsen, W., Kuiper, L., et al. 2008,
A&A, accepted
- den
Herder, J. W., Brinkman, A. C., Kahn, S. M.,
et al. 2001, A&A, 365, L7 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Dib,
R., Kaspi, V. M., & Gavriil, F. P. 2008, ApJ, 673,
1044 [NASA ADS] [CrossRef]
- Duncan, R. C., &
Thompson, C. 1992, ApJ, 392, L9 [NASA ADS] [CrossRef]
-
Durant, M., & van Kerkwijk, M. H. 2006a, ApJ, 650,
1070 [NASA ADS] [CrossRef]
(In the text)
- Durant, M., & van Kerkwijk,
M. H. 2006b, ApJ, 650, 1082 [NASA ADS] [CrossRef]
(In the text)
- Eadie, W. T.,
Drijard, D., & James, F. E. 1971, Statistical methods in
experimental physics (Amsterdam: North-Holland)
(In the text)
- Fernández, R., &
Thompson, C. 2007, ApJ, 660, 615 [NASA ADS] [CrossRef]
(In the text)
- Gavriil, F. P., Gonzalez,
M. E., Gotthelf, E. V., et al. 2008, Science,
accepted [arXiv:0802.1704]
- Gavriil, F. P., &
Kaspi, V. M. 2002, ApJ, 567, 1067 [NASA ADS] [CrossRef]
(In the text)
-
Gelfand, J. D., & Gaensler, B. M. 2007, ApJ, 667,
1111 [NASA ADS] [CrossRef]
-
Goldwurm, A., David, P., Foschini, L., et al. 2003, A&A,
411, L223 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Gotthelf, E. V., & Halpern, J. P. 2005, ApJ, 632,
1075 [NASA ADS] [CrossRef]
- Götz,
D., Rea, N., Israel, G. L., et al. 2007, A&A, 475,
317 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Güver, T., Özel, F., & Lyutikov, M. 2006, ApJ,
submitted [arXiv:0611405]
- Güver,
T., Özel, F., Gögüs, E., & Kouveliotou, C. 2007,
ApJ, 667, L73 [NASA ADS] [CrossRef]
-
Halpern, J. P., Gotthelf, E. V., Becker, R. H.,
Helfand, D. J., & White, R. L. 2005, ApJ, 632,
L29 [NASA ADS] [CrossRef]
-
Halpern, J. P., Gotthelf, E. V., Reynolds, J., Ransom,
S. M., & Camilo, F. 2008, ApJ, accepted
[arXiv:0711.3780]
- Harding, A. K., &
Muslimov, A. G. 1998, ApJ, 508, 328 [NASA ADS] [CrossRef]
- Heyl,
J. S. 2007, Ap&SS, 308, 101 [NASA ADS] [CrossRef]
(In the text)
- Heyl,
J. S., & Hernquist, L. 2005a, ApJ, 618, 463 [NASA ADS] [CrossRef]
- Heyl,
J. S., & Hernquist, L. 2005b, MNRAS, 362, 777 [NASA ADS] [CrossRef]
- Hirotani, K. 2006, ApJ, 652,
1475 [NASA ADS] [CrossRef]
-
Ibrahim, A. I., Markwardt, C. B., Swank, J. H.,
et al. 2004, ApJ, 609, L21 [NASA ADS] [CrossRef]
- Israel,
G., Oosterbroek, T., Stella, L., et al. 2001, ApJ, 560,
L65 [NASA ADS] [CrossRef]
- Israel,
G. L., Covino, S., Perna, R., et al. 2003, ApJ, 589,
L93 [NASA ADS] [CrossRef]
(In the text)
-
Israel, G. L., Götz, D., Zane, S., et al. 2007,
A&A, 476, L9 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Jahoda, K.,
Swank, J. H., Giles, A. B., et al. 1996, in EUV,
X-Ray, and Gamma-Ray Instrumentation for Astronomy VII, ed. O. H.
Siegmund, & M. A. Gummin, Proc. SPIE, 59
(In the text)
- Jansen, F.,
Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Jensen,
P. L., Clausen, K., Cassi, C., et al. 2003, A&A, 411,
L7 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kaspi,
V. M. 2007, Ap&SS, 308, 1 [NASA ADS] [CrossRef]
(In the text)
- Kaspi,
V. M., Chakrabarty, D., & Steinberger, J. 1999, ApJ, 525,
L33 [NASA ADS] [CrossRef]
-
Knödlseder, J. 2004, in 5th INTEGRAL Workshop on the INTEGRAL
Universe, ed. V. Schoenfelder, G. Lichti, &
C. Winkler, ESA Special Publication, 552, 867
(In the text)
- Kramer,
M., Stappers, B. W., Jessner, A., Lyne, A. G., &
Jordan, C. A. 2007, MNRAS, 377, 107 [NASA ADS] [CrossRef]
- Kuiper,
L., & Hermsen, W. 2008, A&A, in prep.
- Kuiper,
L., Hermsen, W., Krijger, J. M., et al. 1999, A&A,
351, 119 [NASA ADS]
(In the text)
- Kuiper,
L., Hermsen, W., Verbunt, F., et al. 2000, A&A, 359,
615 [NASA ADS]
(In the text)
- Kuiper,
L., Hermsen, W., Cusumano, G., et al. 2001, A&A, 378,
918 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kuiper,
L., Hermsen, W., & Mendez, M. 2004a, ApJ, 613, 1173 [NASA ADS] [CrossRef]
- Kuiper,
L., Hermsen, W., & Stappers, B. 2004b, Adv. Space Res., 33,
507 [NASA ADS] [CrossRef]
- Kuiper,
L., Hermsen, W., den Hartog, P. R., & Collmar, W. 2006,
ApJ, 645, 556 [NASA ADS] [CrossRef]
-
Kuiper, L., Hermsen, W., Klein-Wolt, M., & Wijnands, R. 2008,
The Astronomer's Telegram, 1405, 1 [NASA ADS]
- Kumar,
H. S., & Safi-Harb, S. 2008, ApJ,
accepted[arXiv:0802.1242]
- Lebrun,
F., Leray, J. P., Lavocat, P., et al. 2003, A&A, 411,
L141 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Lyubarsky, Y., & Eichler, D. 2008, ApJ,
submitted[arXiv:0706.3578]
(In the text)
-
Lyutikov, M., & Gavriil, F. P. 2006, MNRAS, 368, 690 [NASA ADS] [CrossRef]
(In the text)
- Mereghetti, S., Esposito, P.,
& Tiengo, A. 2007, Ap&SS, 308, 13 [NASA ADS] [CrossRef]
-
Molkov, S. V., Cherepashchuk, A. M., Lutovinov,
A. A., et al. 2004, Astron. Lett., 30, 534 [NASA ADS] [CrossRef]
-
Muslimov, A. G., & Harding, A. K. 2003, ApJ, 588,
430 [NASA ADS] [CrossRef]
- Rea, N.,
Oosterbroek, T., Zane, S., et al. 2005, MNRAS, 361, 710 [NASA ADS] [CrossRef]
(In the text)
- Rea, N.,
Israel, G. L., Oosterbroek, T., et al. 2007, Ap&SS,
308, 505 [NASA ADS] [CrossRef]
- Rea,
N., Zane, S., Turolla, R., Lyutikov, M., & Gotz, D. 2008, ApJ,
submitted [arXiv:0802.1923]
(In the text)
-
Revnivtsev, M. G., Sunyaev, R. A., Varshalovich,
D. A., et al. 2004, Astron. Lett., 30, 382 [NASA ADS] [CrossRef]
-
Romani, R. W. 1996, ApJ, 470, 469 [NASA ADS] [CrossRef]
-
Rothschild, R. E., Blanco, P. R., Gruber, D. E.,
et al. 1998, ApJ, 496, 538 [NASA ADS] [CrossRef]
(In the text)
- Ruderman, M. A., &
Sutherland, P. G. 1975, ApJ, 196, 51 [NASA ADS] [CrossRef]
-
Strüder, L., Briel, U., Dennerl, K., et al. 2001,
A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Sugizaki, M., Nagase, F., Torii, K., et al. 1997, PASJ, 49,
L25 [NASA ADS]
(In the text)
- Thompson, C. 2008a, ApJ,
submitted [arXiv:0802.2571]
(In the text)
- Thompson, C. 2008b, ApJ,
submitted [arXiv:0802.2572]
(In the text)
- Thompson, C., & Duncan,
R. C. 1993, ApJ, 408, 194 [NASA ADS] [CrossRef]
- Thompson, C., & Duncan,
R. C. 1995, MNRAS, 275, 255 [NASA ADS]
- Thompson, C., & Duncan,
R. C. 1996, ApJ, 473, 322 [NASA ADS] [CrossRef]
- Thompson, C., Lyutikov,
M., & Kulkarni, S. R. 2002, ApJ, 574, 332 [NASA ADS] [CrossRef]
- Turner,
M. J. L., Abbey, A., Arnaud, M., et al. 2001,
A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A,
411, L131 [CrossRef] [EDP Sciences]
(In the text)
- Usov,
V. V., & Melrose, D. B. 1995, Aust. J. Phys., 48,
571 [NASA ADS]
-
Valinia, A., & Marshall, F. E. 1998, ApJ, 505, 134 [NASA ADS] [CrossRef]
(In the text)
-
Vedrenne, G., Roques, J.-P., Schönfelder, V., et al.
2003, A&A, 411, L63 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Walter, R., Favre, P., Dubath, P., et al. 2003, A&A, 411,
L25 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Woods,
P. M., & Thompson, C. 2006, in Compact stellar X-ray
sources, ed. W. Lewin, & M. van der Klis, Cambridge
Astrophys. Ser., 39, 547
Copyright ESO 2008
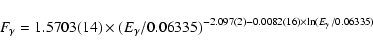
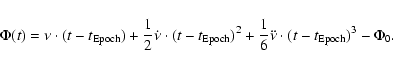
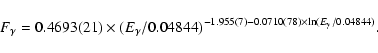
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{09772fig01.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg48.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{09772fig02.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg57.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{09772fig03.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg60.gif)
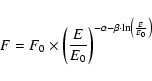
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{09772fig04.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg68.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{09772fig05.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg79.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{09772fig06.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg80.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{09772fig07.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg81.gif)
![\begin{figure}
\par\mbox{\includegraphics[width=3.8cm,clip]{09772fig08a.ps}\hspa...
...}\hspace*{1mm}
\includegraphics[width=5.2cm,clip]{09772fig08c.ps} }
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg130.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{09772fig09.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg160.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{09772fig10.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg161.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{09772fig11.ps}
\end{figure}](/articles/aa/full/2008/37/aa09772-08/Timg165.gif)