A&A 487, 527-532 (2008)
DOI: 10.1051/0004-6361:200809483

On the tidal evolution of the orbits of low-mass satellites around black holes

A. Cadez1 - M. Calvani2 - U. Kostic1


1 - Faculty of Mathematics and Physics, University of Ljubljana, Jadranska 19, 1000 Ljubljana, Slovenia
2 - INAF - Astronomical Observatory of Padova, Vicolo Osservatorio 5, 35122 Padova, Italy

Received 30 January 2008 / Accepted 21 May 2008

Abstract
Context. Low-mass satellites, like asteroids and comets, are expected to be present around the black hole at the Galactic center. We consider small bodies orbiting a black hole, and we study the evolution of their orbits due to tidal interaction with the black hole.
Aims. In this paper we investigate the consequences of the existence of plunging orbits when a black hole is present. We are interested in finding the conditions that exist when capture occurs.
Methods. Earlier analysis of the evolution of classical Keplerian orbits was extended to relativistic orbits around a Schwarzschild black hole.
Results. The main difference between the Keplerian and black hole cases is in the existence of plunging orbits. Orbital evolution, leading from bound to plunging orbits, goes through a ``final'' unstable circular orbit. On this orbit, tidal energy is released on a characteristic black hole timescale.
Conclusions. This process may be relevant for explaining how small, compact clumps of material can be brought onto plunging orbits, where they may produce individual short duration accretion events. The available energy and the characteristic timescale are consistent with energy released and the timescale typical of Galactic flares.

Key words: Galaxy: nucleus - galaxies: active - black hole physics

1 Introduction

Most galaxies, if not all, harbor massive black holes at their center. Some of them manifest their presence in a violent way and show up as active galactic nuclei; others, like the one in our Galaxy, are quiescent. The mass of the black hole at the center of the Milky Way has been estimated as $M_{\rm bh}=3.61$ $\pm$ 0.32 $\times$ $10^6~M_\odot$ from observations with SINFONI (Eisenhauer et al. 2005) confined within a radius of 45 AU. The Galactic center is only $\approx$8 kpc from the Sun and therefore it is the nearest laboratory where we can study the environment of super-massive black holes in detail, see e.g. Alexander (2005), Goldwurm (2007).

The standard assumption for AGNs is that gas accretes onto the black hole forming an accretion disc and releasing energy. On the other hand, some non-active galaxies exhibit short-timescale, low-intensity flaring activity (Genzel et al. 2003; Bélanger et al. 2006; Eckart et al. 2006; Meyer et al. 2006), which could be the result of individual accretion events of small bodies onto the central black hole.

It seems reasonable to assume that stars at the Galactic center are surrounded by planets and by other small orbiting bodies, like asteroids and comets. Such low-mass satellites (LMS) may be stripped off their parent stars by tidal interaction, while they approach the black hole. In this way they contribute to a distribution of low-mass objects that cluster the central black hole. According to Cochran et al. (1995), the Edgeworth-Kuiper belt of our Solar System may still contain as many as $2\times 10^8$objects with radii $\la$10 km. One might therefore expect that LMS will be copiously present all the way down to the black hole.

In this paper we study the evolution of orbits of LMS caused by tidal interaction with the black hole. We extend the analysis presented by Hut (1980,1981,1982) concerning the tidal evolution of close binary systems in the weak friction model in the Newtonian approximation. We show that orbital evolution of these objects leads to capturing orbits by the black hole and argue that tidal interaction can rapidly inject enough energy to explain the energy source of Galactic flares.

2 Low-mass satellites in the Galactic center

2.1 Energy-loss mechanisms

The LMS are injected into the asteroid cloud with low relative velocities with respect to the donor star, therefore their average random velocity is roughly the same as that of stars. In thermodynamic equilibrium, LMS would be expected to reach much higher random velocities; however, it is not difficult to show that such equilibrium cannot be reached, since the relaxation time ta* to exchange energy between stars and LMS is

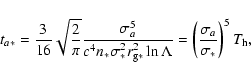\begin{displaymath}% t_{a*}={3\over 16}\sqrt{2\over \pi} {\sigma_{a}^5\over c^4 ... ...bda} = \left ({\sigma_{a} \over \sigma_*}\right )^5 T_{\rm h}, \end{displaymath} (1)

where $\sigma_{a}$ is the random velocity of LMS, n*, $\sigma_*$, and $r_{\rm g*}$ are the density, random velocity, and gravitational radius of stars in the central cluster, $\Lambda$ is the ratio of the maximum and minimum impact parameters, and $T_{\rm h}$ is the non-resonant relaxation time from Hopman & Alexander (2006, hereafter HA06). Since $T_{\rm h}$ is already $\sim$ $10^9~{\rm yr}$, $\sigma_{a}$ cannot increase much before the relaxation time is longer than the Hubble time. This means that LMS do not reach thermodynamic equilibrium random velocities, and the Bondi radius of the LMS mass distribution is approximately the same as that of the stellar distribution, i.e. $r_{\rm B}\sim 2~{\rm pc}$(HA06). However, the direction of angular momentum of such LMS changes on a timescale shorter than $T_{\rm h}$, therefore the distribution of these objects eventually becomes spherically symmetric around the central black hole.

Just like stars, the LMS eventually accrete onto the central black hole. To do so, they must lose orbital energy and/or angular momentum. While stars eventually lose orbital energy by emitting gravitational waves, LMS are not massive enough for this mechanism to play an important role. Considering the gravitational radiation energy loss timescale (Misner et al. 1971, Eq. (36.17b))

 \begin{displaymath}% t_{{\rm GW}}= \frac{5}{256}\frac{M_{\rm bh}}{m}\left( {a\ov... ...}\over c}\ga 10^{14}~{\rm yr}\times \frac{10^{20}~{\rm g}}{m}, \end{displaymath} (2)

where M and $r_{\rm g}({=}GM_{\rm bh}/c^2)$ are the mass and gravitational radius of the black hole, m the mass of the LMS, and $a({>}4~r_{\rm g})$ the radius of its orbit. One finds that satellites with mass less then $10^{23}~{\rm g}$ can circle the central black hole even at $a=4~r_{\rm g}$ for the whole Hubble time.

However, hydrodynamic drag by circum-black-hole cloud might become important in dissipating the energy of LMS. The timescale can be estimated using similar arguments to Narayan (2000) to obtain

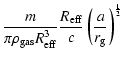                          $\displaystyle % t_{\rm d}$ = $\displaystyle \frac{m}{\pi \rho_{\rm gas}R_{\rm eff}^3}\frac{R_{\rm eff}}{c} \left( \frac{a}{r_{\rm g}}\right)^{\frac{1}{2}}$  
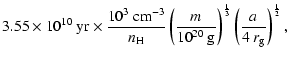  $\textstyle \ga$ $\displaystyle 3.55 \times 10^{10}~{\rm yr} \times\frac{10^3~{\rm cm^{-3}}}{n_{\... ...{\rm g}}\right)^{\frac{1}{3}}\left( \frac{a}{4~r_{\rm g}}\right)^{\frac{1}{2}},$ (3)

where $R_{\rm eff}$ is the effective radius of LMS, and $\rho_{\rm gas}$the density of the interstellar gas. In the second line we assume that the satellite density is $5~{\rm g/cm^3}$, $a=4~r_{\rm g}$, and $\rho_{\rm gas}$ is expressed in terms of hydrogen atom density. The energy loss due to drag strongly depends on the density of the gas and becomes comparable with nonresonant relaxation, if the mass of LMS is below

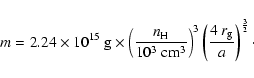\begin{displaymath}% m=2.24 \times 10^{15}~{\rm g}\times \left( \frac{n_{\rm H}}... ...} \right)^3 \left({4~r_{\rm g}\over a}\right )^{3\over 2}\cdot \end{displaymath} (4)

For example, an object circling at the Bondi radius in a gas with density $n_{\rm H}\sim20~{\rm cm^{-3}}$ (Xu et al. 2006) must be less massive than $\sim$$5~{\rm g}$ for hydrodynamic drag to take over. In the very vicinity of the black hole, the gas density may be higher and also the factor  $a/r_{\rm g}$ is much larger, yet, since there is no evidence of an accretion disk (Alexander 2005), it does not seem plausible for these factors to increase enough for hydrodynamic drag to play a very important role.

Since the evolution of orbital parameters is dominated by the process with the shortest timescale, we estimate that nonresonant relaxation occurring on a timescale of $\sim$109 years (HA06) is one of the most important mechanisms until the LMS approaches the black hole to within a few Roche radii, where tidal interaction takes over.

2.2 The population of low-mass satellites

It has been determined by Paumard et al. (2006) that the density of stellar distribution increases as 1/r2 to within the inner 1'' of the Galactic center. At this distance, corresponding to 2 $\times$ $10^5~r_{\rm g}$, there is a sharp drop, interpreted by HA06 as the radius where gravitational radiation extracts orbital energy at a sufficient rate to clean the inner region. Since for low masses gravitational radiation energy loss is negligible, we expect that their density keeps increasing either as $n(r)\propto r^{-7/4}$ (HA06) or as $n(r)\propto r^{-2}$(Paumard et al. 2006) deep down to the very vicinity of the black hole, where tidal effects may extract orbital energy and angular momentum. Note that there are no stars (very few) and no gas (no steady emission lines) in the central region (r<2 $\times$ $10^5~r_{\rm g}$), thus it is likely populated predominantly by low-mass satellites. Hence, we assume that the dynamics of this central cloud is dominated by the exchange of angular momentum by nonresonant relaxation (HA06) and by tidal interaction between the object and the central black hole. As the nonresonant relaxation timescale is roughly position-independent and the tidal interaction grows inversely proportional to a high power of the distance from the black hole, the tidal interaction finally prevails in determining the way in which accretion occurs.

One should expect a fair proportion of LMS to move on highly eccentric, low-periastron orbits. Tidal forces do significant work on such satellites near periastron. This lowers their orbital energy and starts the significant evolution of orbital parameters (Gomboc & Cadez 2005). In this context two classes of such satellites should be taken into account: those that are gravity dominated (i.e. those whose fundamental quadrupole frequency is $\nu_{\rm g} \approx 2 \sqrt{G \rho / 3\pi}$) and those that are solid-state dominated (whose fundamental quadrupole frequency is $\nu_{\rm s}\approx\frac{1}{4}c_{\rm s}/R$). (Here $\rho$ is the density of the body, R its radius and $c_{\rm s}$ the speed of sound.) Taking $c_{\rm s}\approx 5~{\rm km~s}^{-1}$ and $\rho\approx 5~{\rm g\ cm^{-3}}$as typical values, we find that the radius dividing the two classes is close to the radius of the asteroid Ceres. Therefore all gravity-dominated satellites should have about the same fundamental quadrupole frequency, corresponding to the period of about 54 min. All smaller satellites should have shorter fundamental periods. This means that gravity-dominated satellites start rapid tidal evolution when their periastron reaches $r_{\rm p} = (GM_{\rm bh}/(2\pi \nu_{\rm g})^2)^{1/3}\approx 10~r_{\rm g}$. Solid-state dominated bodies may start significant tidal evolution even closer to the black hole.

   
3 Tidal evolution of the orbits

Significant tidal orbital evolution for gravity-dominated solid bodies will start when their periastra reach down to $\approx$9 $r_{\rm g}$. We show, however, that solid-state dominated bodies are also strongly affected by tides and are expected to be heated by them, so that at a certain stage, they are expected to melt and also to become gravity-dominated.

The first stages of tidal evolution of the orbit can be investigated using Hut's formalism for the spin-orbit evolution of the two-body system (Hut 1980,1981,1982), at least until relativistic regime is reached. The evolution is governed by the parameter $\alpha $, which is the ratio of the orbital and rotation angular momentum that the binary would have at stable equilibrium, characterized by a0, the radius of the stable circular orbit and $\omega_0$, the orbital and spin frequency of both bodies. The parameter $\alpha $ is determined by the (conserved) value of the total angular momentum of the system by Eq. (57) given by Hut (1981). We take the spin of both bodies into account, since it has been shown by Fang & Lovelace (2005) that ``the black hole absorbs angular momentum and energy at the same rate as the moon's tidal field sends energy and angular momentum into the hole's horizon''. Thus we generalize Hut's equation to

 \begin{displaymath}% L = \mu(G{\cal M})^{1\over 2}((m_1r_{\rm (1)g}^2R_1^2 + m_2... ...2)/\mu)^{1\over 4}(\alpha^{1\over 4} + \alpha^{-{3\over 4 }}), \end{displaymath} (5)

where m1, R1, $r_{\rm (1)g}$, and m2, R2, $r_{\rm (2)g}$ are the mass, radius, and gyration radius of the two bodies, ${\cal M}=m_1+m_2$ and $\mu=m_1m_2/{\cal M}$.

The (conserved) angular momentum, calculated initially, is

 \begin{displaymath}% L = m_1r_{\rm (1)g}^2R_1^2\omega_1 + m_2r_{\rm (2)g}^2R_2^2\omega_2 + \mu(G{\cal M}r_0)^{1\over 2}, \end{displaymath} (6)

where $\omega_1$ and $\omega_2$ are the two initial spin angular velocities, $h=\mu(G{\cal M}r_0)^{1/2}$ is the initial orbital angular momentum with r0=a(1-e2), and a and e are the semi-major axis and eccentricity of the initial orbit, respectively. Let $m_1\gg m_2$ and $R_1\hspace{2pt} r_{\rm (1)g}\gg R_2\hspace{2pt} r_{\rm (2)g}$and define


    $\displaystyle Z = (m_2r_{\rm (2)g}^2R_2^2)/(m_1r_{\rm (1)g}^2R_1^2)$ (7)
    $\displaystyle Y = h/(m_1r_{\rm (1)g}^2R_1^2\omega_1).$ (8)

Equating Eqs. (5) and (6), we obtain
$\displaystyle % (\mu/m_1)^{3\over 4} (G{\cal M}/R_1^3)^{1\over 2} (1 + Z)^{1\ov... ...alpha^{1\over 4} + \alpha^{-{3\over 4}})= \omega_1(1 + Z\omega_2/\omega_1 + Y).$     (9)

Note that $\Omega_{\rm d} = (G{\cal M}/R_1^3)^{1/2}$ is the angular frequency at which m2 would orbit m1 at its gyration radius. If one assumes that $m_1=M_{\rm bh}$ and m2=m, then $\omega_1/\Omega_{\rm d} = a_{\rm Kerr}/r_{\rm g}c$ where $a_{\rm Kerr}$ is the Kerr angular momentum parameter. Since $M_{\rm bh}\gg m$, we may replace ${\cal M}=M_{\rm bh}$, $\mu =m$ and write R2=R. Finally, from the above equations we obtain

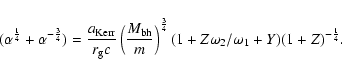\begin{displaymath}% (\alpha^{1\over 4} + \alpha^{-{3\over 4}}) ={ a_{\rm Kerr}\... ...^{3\over 4}(1 + Z\omega_2/\omega_1 + Y) (1 + Z)^{-{1\over 4}}. \end{displaymath} (10)

From this expression it is clear that the angular momentum of the black hole determines $\alpha $; moreover, since $a_{\rm Kerr}/r_{\rm g}c$ is not expected to be exceedingly small and Z and Y are very small, the equation for $\alpha $ is essentially

 \begin{displaymath}% (\alpha^{1\over 4} + \alpha^{-{3\over 4}}) = { a_{\rm Kerr}\over r_{\rm g}c} \left(M_{\rm bh}\over m\right)^{3\over 4}\cdot \end{displaymath} (11)

As the righthand side is very large, it follows that $\alpha $ is either a very small or a very large number. Since, by definition, $\alpha = h_0[(m_1 r_{\rm (1)g}^2 R_1^2+m_2 r_{\rm (2)g}^2 R_2^2)\omega_0]^{-1}$ $\approx$ ${1\over 4}(m/M_{\rm bh})(a_0/r_{\rm g})^2$ it is clear that we are not interested in very high, but in very low values of $\alpha $[*]. Hut was not interested in such orbits. We note that, if $r_{\rm p}(\varepsilon \vert \alpha^\prime)$ is the solution to the Eq. (27) in Hut (1982) for $\alpha^\prime>3$and if $\gamma r_{\rm p}(\varepsilon \vert \alpha)$ is the solution of the same equation for $\alpha<3$ such that $\alpha^\prime$ and $\alpha $ are the two solutions of Eq. (57) in Hut (1981), then a scaling factor $\gamma$ exists, such that both are solutions of the same equation[*]. Therefore both $\alpha $'s solving Eq. (11) produce the same solutions.

The equation for the flow of trajectories in the ( $\tilde r_{\rm p}, e)$ plane for very low values of $\alpha $ is the same as that for very high values of $\alpha $ and can be written using Eq. (27) in Hut (1982)

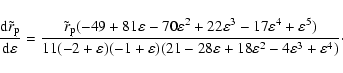\begin{displaymath}% \frac{{\rm d}\tilde r_{\rm p}}{{\rm d}\varepsilon} = \frac{... ...psilon + 18\varepsilon^2 -4\varepsilon^3 +\varepsilon^4)}\cdot \end{displaymath} (12)

Here $\tilde r_{\rm p}=r_{\rm p}/a_0$ is the normalized minimum separation of the two objects at periastron, $\tilde r_{\rm p} = a(1-e)/a_0$. Noting that $\varepsilon=1-e$, where e is the eccentricity of the orbit, the above may be integrated to
 
$\displaystyle % \tilde r_{\rm p} = (21{-}28(1- e ) +18(1 - e)^2 -4 (1 - e)^3 + (1-e)^4)^{2\over 11} e^{4\over 11}\left (1 + e\right )^{-1}\tilde r_{\rm n},$     (13)


  \begin{figure} \par\includegraphics[width=4.1cm,clip]{9483fig1.eps}\hspace*{2mm} \includegraphics[width=4cm,clip]{9483fig2.eps}\end{figure} Figure 1: Orbital evolution tracks in the eccentricity (e)-periastron distance($r_{\rm p}$) plane. Different types of evolution are displayed. Arrows indicate the direction of time. The left panel shows tidal evolution toward stable corotating circular orbits at $r_0^\prime $ = $450~r_{\rm g}$. The right panel is an enlargement of the left bottom part. It shows the evolution of very low orbital angular momentum orbits. (See text for details.) In this example, intended to show the topology of small $\alpha $ tidal evolution, the value of $\alpha $ is arbitrarily taken to be 0.05. Different curves correspond to initial $\tilde r_{\rm p}=25, 50, 100, 200, 250, 400, 600, 800, 1000 $ ( left panel) and $\tilde r_{\rm p}=0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.85, 0.9$ ( right panel).
Open with DEXTER

where $\tilde r_{\rm n}$ is the integration constant. The meaning of these limiting solutions for very small $\alpha $ is illustrated in Fig. 1 by the numerical solution of Eq. (27) in Hut (1982). In this example, where the value of $\alpha $ was chosen equal to 0.05 ( $\alpha^\prime=9720$)[*], the equilibrium radius  $a_0^\prime$ is at $\tilde r_{\rm p}\approx 450$and only orbits with $\tilde r_{\rm p}<0.8$ shrink as they circularize. In Fig. 1, the left panel shows tidal evolution toward stable corotating circular orbits at $r_0^\prime~=450~r_{\rm g}$. These orbits are initially quite eccentric and have low spin (the upper five curves). The remaining orbits start as circular but with large spin. If the initial spin energy is high enough, it can be transferred to orbit, first elongating it and then circularizing again after joining the circularization track (two upper curves starting to the left). If the initial spin energy is not high enough, the circularization track cannot be reached and the orbit keeps elongating at a slower and slower pace (lower two curves). The right panel is an enlargement of the left bottom part. It shows the evolution of very low orbital angular momentum orbits. Very high initial spin angular momentum and energy can be transferred to orbital momentum and energy, leading to higher periastron orbits (the upper three curves). In the case of small initial spin, the orbital evolution starts with orbital energy dissipation by tidal interaction and little angular momentum transfer, leading to less eccentric orbits with shorter and shorter orbital periods. As a result, the orbital angular momentum eventually transfers to spin as the object is forced into faster and faster corotation. As $\alpha^\prime \rightarrow \infty$, the corresponding $a_0^\prime$ also tends to infinity and only the shrinking orbits remain as candidates to bring the body down to the horizon of the black hole. With the solution for $r_{\rm p}$ and noting that


    $\displaystyle h = m(G M_{\rm bh} r_0)^{1\over 2} = m r_{\rm g} c ((1+e) r_{\rm p}/r_{\rm g} )^{1\over 2}$ (14)
    $\displaystyle E = - G M_{\rm bh}m (1 - e)/2r_{\rm p},$ (15)

one can calculate tracks of orbital evolution in the angular momentum - energy plane (see Fig. 2). Using these tracks, one can calculate the evolution of orbital radial turning points.


  \begin{figure} \par\includegraphics[width=6.3cm,clip]{9483fig3.eps}\end{figure} Figure 2: Angular momentum ( $\lambda ={h\over 2 m r_{\rm g} c}$) - orbital energy (E) during the tidal evolution of the orbit for the evolution tracks shown in the right panel of Fig. 1.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=4.2cm,clip]{9483fig4.eps}\includegraphics[width=4.1cm,clip]{9483fig5.eps}\end{figure} Figure 3: The evolution of radial turning points in the Kepler (red) and Schwarzschild effective potentials (black) for the case of a highly eccentric orbit starting with periastron at $9.5~r_{\rm g}$ and apoastron at $110~r_{\rm g}$. The right figure is an enlargement of the final evolution. The gray line indicates the third root of the effective potential equation (Misner et al. 1971).
Open with DEXTER

We do this using both the Keplerian and the black hole effective potentials. For simplicity we only consider the Schwarzschild metric (Fig. 3). The important qualitative difference between the two cases occurs for low values of orbital energy and angular momentum. In the Keplerian case the effective potential guarantees two turning points for all bound orbits, since it has one minimum and no maxima, while in the Schwarzschild case the effective potential has a minimum ( $V_{\rm min}=V(r_{\rm min})$) and also a maximum ( $V_{\rm max}$) at small $r_{\rm max}<r_{\rm min}$ (Misner et al. 1971). Therefore, the inner turning point disappears in a parametric family of orbits, when the effective potential maximum becomes less than the orbital energy. For the parametric family of orbits shown in Fig. 2, this happens when $r_{\rm max}$ is just slightly larger than $4~r_{\rm g}$. In Fig. 3 we then show that, from the point of view of turning points, Schwarzschild orbits do not necessarily circularize, but the inner turning point disappears when the outer one may still be at $\approx$ $20~r_{\rm g}$. The relativistic theory of tidal orbital evolution may produce somewhat different tracks in the $\lambda -E$ plane, yet we believe it is reasonable to expect the results not to change qualitatively, because the exchange between orbital and internal angular momentum and energy occurs very locally in the small volume of the tidally distorted body. In any case, when the total energy of the body closely approaches the maximum value of the effective potential ( $V_{\rm max}$), the body experiences so shallow an effective potential that it does not return to the apoastron, but winds about  $r_{\rm max}$.

   
4 Time scales for tidal evolution

To estimate the timescale for tidal evolution of the orbits, consider the energy loss per orbit as given by Eq. (A10) of Hut (1981)[*]. It can be written as

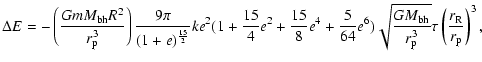$\displaystyle % \Delta E = -\left( {{G m M_{\rm bh}R^2}\over{r_{\rm p}^3}} \rig... ...m bh}}\over{r_{\rm p}^3}}} \tau \left( {{r_{\rm R}}\over{r_{\rm p}}} \right)^3,$     (16)

where $r_{\rm R}=(M_{\rm bh}/m)^{1/3}R$ is the Roche radius. The nonresonant energy timescale is then

 \begin{displaymath}% t_{\rm EN} = - t_{\rm orb}{{GM_{\rm bh}m}\over{2a}}/\Delta E \end{displaymath} (17)

which becomes

 \begin{displaymath}% t_{\rm EN}={64(1+e)^{15\over 2}r_{\rm p}^8\over{9 c^2\sqrt{... ...ce{2pt}e^4+5\hspace{2pt}e^6)k R^2 r_{\rm g} r_{\rm R}^3\tau}}, \end{displaymath} (18)

where $t_{\rm orb}$ is the orbital period, k = 0.75 the apsidal motion constant of the primary (considered as an incompressible fluid), and $\tau$ a constant small time lag (Hut 1981).

Remember, however, that Hut only considers weak tides acting on the deformed body m. Such tides are quite off resonance, and this would not be the case in the proximity of the black hole, where tides would certainly be resonant if the body liquefies. Therefore a better estimate is as follows. For resonant tides the body liquefies. Gomboc & Cadez (2005) obtain the following equation for tidal energy per periastron passage, valid in the limit of high eccentricity,

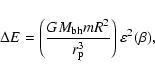\begin{displaymath}% \Delta E = \left({{G M_{\rm bh} mR^2}\over{r_{\rm p}^3}}\right)\varepsilon^2(\beta), \end{displaymath} (19)

with the resonant timescale for tidal evolution,

 \begin{displaymath}% t_{\rm ER} = t_{\rm orb}{{(1-e)r_{\rm p}^2}\over{2R^2\varepsilon^2(\beta)}}, \end{displaymath} (20)

and $\varepsilon^2(\beta)$ is a function that peaks at resonance, i.e. at $\beta \approx 1$. Here $\beta =r_{\rm R}/r_{\rm p}$ is the Roche penetration parameter. For easier comparison we rewrite Eqs. (18) and (20) into a simpler form


  
    $\displaystyle t_{\rm EN} = 1.4\times 10^{11}~{\rm yr}\times\frac{Q f_{\rm EN}(e... ...left(\frac{10~{\rm km}}{R} \right)^2\left(\frac{\rho_0}{\rho}\right)^{7\over 6}$ (21)
    $\displaystyle t_{\rm ER} = 2.9\times 10^{10}~{\rm yr}\times \frac{f_{\rm ER}(e)... ...eft(\frac{10~{\rm km}}{R} \right)^2\left(\frac{\rho_0}{\rho}\right)^{7\over 6},$ (22)

where Q is the resonant damping factor, $\tau=(\omega_0 Q)^{-1}$, $\omega_0=\sqrt{GM_{\rm bh}/r_{\rm R}^3}$, and $\rho_0=1~{\rm g~cm^{-3}}$. The function  $f_{\rm EN}(e)$ is

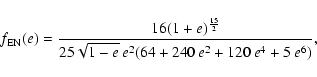\begin{displaymath}% f_{\rm EN}(e) =\frac{16(1+e)^{15\over 2}}{25\sqrt{1-e}\hspa... ...2(64+240\hspace{2pt}e^2+120\hspace{2pt}e^4+5\hspace{2pt}e^6)}, \end{displaymath} (23)

and $f_{\rm ER}(e)$ (valid only for highly eccentric orbits) is

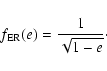\begin{displaymath}% f_{\rm ER}(e) = \frac{1}{\sqrt{1-e}}\cdot \end{displaymath} (24)

Both functions are of order unity on the interval [0.1,0.9]. In Fig. 4 we plot $t_{\rm EN}$ and $t_{\rm ER}$ as a function of $\beta $ for R = 10 km, Q=100 and $\rho =\rho _0$, assuming that the body is liquefied, i.e. gravity-dominated. For example, if an $R=30~{\rm km}$ object with $\rho=5~{\rm g~cm^{-3}}$ is on a $\beta= 2$ orbit, then $t_{\rm ER}=3$ $\times$ $10^{10}~{\rm yr}$ $\times$ (10/30)2 (1/5)7/6= 5.1 $\times$ $10^8~{\rm yr}$; for this case  $t_{\rm EN}$ is approximately twice as long.


  \begin{figure} \par\includegraphics[width=7.55cm,clip]{9483fig6.eps}\end{figure} Figure 4: Resonant and non-resonant timescales as a function of $\beta $ for $\rho =\rho _0$, R=10 km, and Q=100 (see Eqs. (21), (22)).
Open with DEXTER

5 The fate of a small body

Consider now a cold solid object that is scattered on an orbit with a periastron of a few 10 $r_{\rm g}$. Tidal energy loss and the corresponding energy timescale can be accurately calculated using Hut's formalism, since tides on such an object would be well below resonance. However, one must replace the apsidal motion constant kwith a lower value and $\omega_0$ with the higher angular frequency of the quadrupole mode of the solid body. Thus, to obtain the energy time for such a solid body, the timescale in Eq. (18) should be multiplied by the ratio $\left(\nu_{\rm s}/\nu_{\rm g}\right)^3$, to obtain

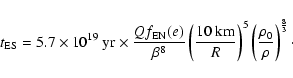\begin{displaymath}% t_{\rm ES} = 5.7\times 10^{19}~{\rm yr}\times\frac{Q f_{\rm... ...R} \right)^{5}\left(\frac{\rho_0}{\rho}\right)^{8\over 3}\cdot \end{displaymath} (25)

The average heating power is
$\displaystyle % P_{\rm heat} = \vert \Delta E\vert/t_{\rm orb} = {1\over 2}GM_{\rm bh}m t_{\rm ES}^{-1}a^{-1},$     (26)

where the last equality follows from Eq. (17). The typical thermal diffusion timescale is $\tau_{\rm solid}=R^2\pi^{-2}D^{-1}$, where D is the thermal diffusion coefficient, which is on the order of $10^{-6}~{\rm m}^2~{\rm s}^{-1}$ for most rocks, so that $\tau_{\rm solid}\approx 3$ $\times$ 105 years for a 10 km object. It is a simple exercise to calculate the central temperature that such an object would reach in equilibrium when the heating power is thermally diffused to the surface, which is black-body radiating. Neglecting the surface temperature, one obtains $T_{\rm c}=P_{\rm heat}(8\pi R \lambda_{\rm c})^{-1}$, where the heat conductivity $\lambda_{\rm c}\approx 1{-}2~{\rm W~m^{-1}~K^{-1}}$ is typical of most rocks. Thus rocks could reach central temperatures on the order of

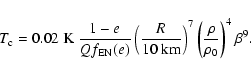\begin{displaymath}% T_{\rm c} = 0.02~{\rm K}\ {1-e\over Q f_{\rm EN}(e)}\left({... ...{\rm km}}\right)^{7}\left({\rho\over \rho_0}\right)^4 \beta^9. \end{displaymath} (27)

Assuming that natural values for Q are a few hundred up to a few thousand, the same as for normal modes of Earth, and noting the extremely steep dependence of $T_{\rm c}$ on R, $\beta $, and $\rho$, one expects a few 10 km rocks to melt ( $T_{\rm c} \ga 3000$ K) at their centers a few hundred thousand years after entering a $\beta \ga 2$ orbit. Melting weakens the body, increases its coupling to tides, and intensifies heating. Therefore, the core melts farther out, but does not essentially increase its temperature, because the convection that sets in is extremely efficient in transporting heat from the center to the remaining solid envelope. This runaway process stops when further melting can no longer weaken the body, i.e. when the body is no longer solid state but gravity-dominated. If melting had started at $\beta \ga 1$, then the body finds itself at tidal resonance, and the pertinent timescale shortens considerably and becomes $T_{\rm ER}$(Eq. (22)). The surface temperature of the body is now determined by the balance between tidal heating and black body cooling, so it can be expressed as

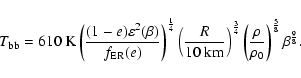\begin{displaymath}% T_{\rm bb}=610~{\rm K} \left ({(1-e)\varepsilon ^2(\beta)\o... ...4}\left({\rho \over \rho_0}\right)^{5\over 8}\beta^{9\over 8}. \end{displaymath} (28)

Because of the 1/4 power in Stefan's law, the black body surface temperature is a slowly varying function of R, $\beta $, and $\rho$. Roughly speaking, it is expected to be just below the boiling temperature of rocky material (a few thousand Kelvin) for melted rocks at a tidal resonance whose size is between about 10 and 100 km. Much smaller rocks would not melt at all, and much larger rocks, moons, and planets would melt farther away from the black hole and would evaporate or split into smaller pieces or drops when reaching the Roche radius. Evidence of a similar tidal melting may also be found in our Solar System (Dermott et al. 1988).

Heating power increases slowly with slowly increasing $\beta $, and the melted body undulates as it moves between periastron and apoastron on an eccentric enough orbit that keeps it outside the Roche radius most of the time.

The above considerations apply until angular momentum transfer becomes important. Angular momentum can be transferred from orbital to spin of the black hole and from orbital to spin of the body. The angular momentum transfer to a Schwarzschild black hole has been studied by Fang & Lovelace (2005) for the case of tidal coupling of a black hole and a circularly orbiting moon. They find that tidal interaction gives rise to orbital angular momentum loss rate (see their Eq. (27)):

 \begin{displaymath}% \dot h={32 \over 5} {m\over M_{\rm bh}}{r_{\rm g}^7\over r^8} h c. \end{displaymath} (29)

In our case $m/M_{\rm bh}$ is so small that the timescale resulting from Eq. (29) is longer than the Hubble time, so this effect is negligible. On the other hand, the angular momentum transfer to the spin of the body can work. We are now considering an already melted electrically conducting object that is constantly elongated by the mounting tidal force. Therefore, its moment of inertia is increasing, while the ever longer object is spinning with the orbital angular velocity. This process only has meaning if the body remains a whole and sufficiently rigid, i.e. if there is a mechanism that distributes angular momentum to all parts of the body. In our case sufficient rigidity can be provided by a frozen-in magnetic field. The necessary field must be strong enough to insure that Alfvén waves can travel the length (l) of the body before the frozen-in magnetic field decays, i.e. $v_{\rm A} \tau_{\rm m}>l$. Here $v_{\rm A}\sim B/\sqrt{\mu_0 \rho}$ is the Alfvén velocity and $\tau_{\rm m} = \sigma \mu_{0} l_{\rm t}^2$ is the magnetic field decay time, where $l_{\rm t}$ is the transverse dimension of the body. Taking a typical value $\sigma\sim 4$ $\times$ $10^6\ \Omega^{-1}~{\rm m}^{-1}$ for the conductivity, one finds that a field of $\sim$ $100~\mu {\rm G}$ is enough to give rigidity to a $100~{\rm km}$ object. Such and much stronger fields have been found in asteroids (Kivelson et al. 1993), so that it is not unreasonable to assume that the LMS in the vicinity of the Galactic black hole also possess it.

Slow orbital angular momentum decay describing the lower part of tracks in Fig. 2 has no dramatic consequences until fully relativistic regime is reached, i.e. until the effective potential maximum starts rapidly dropping with loss of angular momentum. This happens when the inner turning point approaches $r_{\rm max}\approx 4~r_{\rm g}$. The shallow potential no longer returns the body from periastron to apoastron, but the orbit just keeps winding about $r_{\rm max}$ while the constant large tidal tensor, now experienced by the body, keeps squeezing and pulling it apart into a long thread along the orbit, exponentially increasing its internal energy.

We note that the above analysis is an approximation somewhat limited by neglecting dynamical effects and relativistic aspects of tides. As pointed out in Sect. 3, in the relativistic (Schwarzschild) regime, the orbit has no inner turning point when the effective potential maximum becomes less than the orbital energy, leading therefore to capture orbits with orbital energy that may be considerably higher than the orbital energy of the marginally stable orbit. This energy difference is available to do tidal work on the body before entering the final turn down the horizon of the black hole. Since tidal interaction, which transfers energy and angular momentum between spin and orbit, is taking place in a very small region of space-time, it might not be unreasonable to expect that a full relativistic treatment of the problem will not qualitatively change this result, although it is clear that a number of detailed questions still need closer attention. In particular, Hut's analysis should be extended to a relativistic regime above resonance, and the Gomboc & Cadez (2005) analysis would have to include higher order modes, mode splitting due to rotation, and a relativistic regime.

6 Conclusions

In this paper we have investigated the fate of small bodies, like asteroids and comets, that may find themselves on highly eccentric orbits in the vicinity of the Galactic black hole. Extending Hut's analysis of the tidal evolution of close binary systems, we find that they experience very high tides at their periastra, which heat and eventually liquefy them. Those objects that are electrically conductive are likely to have enough magnetic rigidity to efficiently transfer angular momentum from orbit to spin, so that the loss of orbital angular momentum leads to smooth transition from bound to plunging orbits. We propose this as a mechanism that could bring relatively small and condensed clumps of material to the vicinity of the black hole. Such clumps can produce individual accretion events characterized by the time scale of the last circular orbit. The tidal energy released during this process can reach up to 0.1 mc2. This means that both the available energy and the characteristic timescale are consistent with the energy and timescale characteristic of Galactic flares.

Acknowledgements
We acknowledge support from the bilateral protocol of scientific and technological cooperation between Italy and Slovenia. A.C. acknowledges partial support from the grant 1554-501 of the Slovenian Research Foundation. A.C. and M.C. acknowledge the hospitality of the Instituto de Astrofisica de Andalucia (Granada, Spain), where part of this work was done. We thank the anonymous referee for providing comments, which helped improve the contents of this paper.

References

 
Copyright ESO 2008