- ...
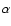
![[*]](/icons/foot_motif.gif)
- The equilibrium orbit is circular with radius a0, so that
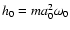 and, since it is co-rotating with the black hole,
and, since it is co-rotating with the black hole,
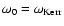 .
With respect to the moment of inertia
of the black hole
.
With respect to the moment of inertia
of the black hole
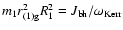 ,
the moment of inertia of the asteroid can be neglected.
According to Ashtekar & Krishnan (2004),
,
the moment of inertia of the asteroid can be neglected.
According to Ashtekar & Krishnan (2004),
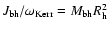 ,
where
,
where 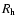 is the horizon radius of the
black hole, which becomes
is the horizon radius of the
black hole, which becomes
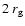 in the limit of small
in the limit of small
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... equation
![[*]](/icons/foot_motif.gif)
- The
exchange
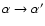 changes the unstable
equilibrium state
changes the unstable
equilibrium state
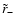 to the attractor
to the attractor
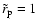 and vice versa with respect to the tracks shown in
Hut (1982).
and vice versa with respect to the tracks shown in
Hut (1982).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
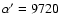 )
)![[*]](/icons/foot_motif.gif)
- This is an unreasonably large
number with respect to our problem, but sufficiently small and
convenient to show the topology of the solution space.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Hut (1981)
![[*]](/icons/foot_motif.gif)
- For the sake of simplicity we
neglect the contribution of work done by the tangential component of
tidal force, which depends on the difference between the orbital and
spin period.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.