A&A 486, 119-130 (2008)
DOI: 10.1051/0004-6361:200809810

The accretion mechanism in low-power radio galaxies

B. Balmaverde¹ - R. D. Baldi² - A. Capetti¹

1 - INAF - Osservatorio Astronomico di Torino, Strada Osservatorio 20, 10025 Pino Torinese, Italy
2 - Università di Torino, via P. Giuria 1, 10125 Torino, Italy

Received 19 March 2008 / Accepted 23 April 2008

Abstract
We study a sample of 44 low-luminosity radio-loud AGN, which represent a range of nuclear radio-power spanning 5 orders of magnitude, to unveil the accretion mechanism in these galaxies. We estimate the accretion rate of gas associated with their hot coronae by analyzing archival Chandra data, to derive the deprojected density and temperature profiles in a spherical approximation. Measuring the jet power from the nuclear radio-luminosity, we find that the accretion power correlates linearly with the jet power, with an efficiency of conversion from rest mass into jet power of $\sim$0.012. These results strengthen and extend the validity of the results obtained by Allen and collaborators for 9 radio galaxies, indicating that hot gas accretion is the dominant process in FR I radio galaxies across their full range of radio-luminosity.

We find that the different levels of nuclear activity are driven by global differences in the structure of the galactic hot coronae. A linear relation links the jet power with the host X-ray surface brightness. This implies that a substantial change in the jet power must be accompanied by a global change in its ISM properties, driven for example by a major merger. This correlation provides a simple widely applicable method to estimate the jet-power of a given object by observing the intensity of its host X-ray emission.

To maintain the mass flow in the jet, the fraction of gas that crosses the Bondi radius reaching the accretion disk must be $\gtrsim$0.002. This implies that the radiative efficiency of the disk must be $\eta \lesssim 0.005$, an indication that accretion in these objects occurs not only at a lower rate, but also at lower efficiency than in standard accretion disks.

Key words: galaxies: active - galaxies: jets - galaxies: elliptical and lenticular, cD - galaxies: ISM

  
1 Introduction

A fundamental problem in studying the physics of active galactic nuclei (AGN) identifying the mechanism that controls the level of activity. More generally, we need to determine why nuclear activity occurs in active galaxies but not in quiescent galaxies, and whether there is a discontinuity in the physical properties of these two galaxy classes. Addressing these points is also important in light of the prominent role that AGN feedback plays in the process of galactic evolution. Furthermore, AGN activity is related to the growth, via accretion, of supermassive black holes (SMBH); the clear evidence for a co-evolution of SMBH and host galaxies, represented by the connections between galaxy physical properties and SMBH mass, implies that the accretion process in AGN has a powerful influence on galaxy evolution.

Several comparisons between the properties of active and quiescent galaxies have been performed with in attempts to isolate the quantities that correlate most significantly with the level of nuclear activity. We limit ourselves to radio-loud galaxies in this paper. Since the research of for example Auriemma et al. (1977) it has been known that the probability of an object to have a radio luminosity above a certain threshold is proportional to its optical luminosity. This was confirmed by studies of the bivariate radio/optical luminosity function of early-type galaxies (Best et al. 2005; Mauch & Sadler 2007). Objects of a given optical luminosity can be associated with radio sources spanning a large range of radio power. Several authors explored the role of environment in setting the level of radio-emission. The fraction of radio-loud AGN is largely independent of the local galaxy density, but a dependence is found on the larger-scale environment (Best 2004). A statistical trend links the amount of dust measured from the absorption features, seen in their optical images, and radio-power (e.g. de Ruiter et al. 2002). Valentijn & Bijleveld (1983) found a positive correlation between the X-ray luminosity of the hosting cluster and the radio-luminosity of the dominant cluster galaxy. Similarly, Burns (1990) showed that central, massive galaxies in clusters or groups of galaxies with a cooling flow are more likely to be radio-loud AGN than galaxies of similar mass that are not centered on a cooling flow, suggesting that concentrated cooling atmospheres can stimulate radio-loud AGN activity. These studies provide statistically important results, but it is still impossible to ascertain from any of these measurements, on an object-by-object basis, whether a galaxy hosts an active nucleus. This implies that we cannot yet associate an observable quantity and, consequently, physical process with the level of nuclear activity.

Substantial progress was reported by Allen et al. (2006). They studied 9 nearby, low-power radio galaxies, selecting objects with well-defined cavities in X-ray emitting gas, which were cospatial with the radio-lobes: these cavities were most likely inflated by radio-jets. They were able to estimate the jet, kinetic power required to inflate the cavities. On the other hand, it was possible, using the same X-ray images, to estimate the amount of hot gas available for accretion onto the SMBH. This analysis revealed a significant correlation between the accretion rate and jet power, which had a dispersion of only 0.16 dex. This represents not only an accurate and powerful method to predict the AGN energy output, but implies that spherical hot-gas, accretion, associated with the hot corona, is the main energy source powering the active nucleus.

We extend the analysis performed by Allen et al. (2006) to two samples of galaxies that host radio-loud nuclei of relatively low-power, which cover almost five orders of magnitude in radio-power. The comparison of accretion properties across the widest possible range of luminosity is clearly the next crucial step in unveiling the connections (and diversities) between galaxies showing different levels of nuclear activity. We examine data for the sample of 29 early-type ``core'' galaxies, selected by Balmaverde & Capetti (2006), and for the sample of 33 FR I radio galaxies, which were extracted from the 3C sample as defined in Chiaberge et al. (1999); in the combined set of galaxies 44 have observational data in the Chandra archive (more details of the sample selection are given in Sect. 2). With respect to Allen et al. (2006) we estimated the jet power using a relation between radio-core luminosity and jet kinetic power derived by Heinz et al. (2007). This relation provides a straightforward, robust measure of the jet power (with an rms error of 0.4 dex), based only on the core power, and enables the number of objects for which accretion and jet power can be compared, to be increased. Furthermore, the range of radio-power that can be studied covers almost five orders of magnitude; this corresponds to the full range of radio-luminosity of FR I, spanning from the faintest level of detectable activity in radio galaxies up to include galaxies whose radio-emission exceeds the luminosity marking the transition between FR I and FR II objects.

  
2 Sample selection and data preparation

Table 1: Basic data and Chandra observations log.

In Capetti & Balmaverde (2005), we focused on a sample of luminous, nearby early-type galaxies to study the link between their host properties and the active nucleus. We used archival HST observations to analyze their surface brightness profiles and to separate these early-type galaxies into core and power-law galaxies on the basis of the slope of their nuclear brightness profiles, following the Nuker scheme (Lauer et al. 1995). We obtained a sub sample of 29 ``core'' galaxies (hereafter CoreG), that is galaxies for which the surface-brightness profiles were fitted with a double power-law of innermost slope $\gamma \leq 0.3$. In Balmaverde & Capetti (2006) we demonstrated that the CoreG hosted a radio-loud nucleus and that they could be considered to be miniature radio galaxies. In fact, they are drawn from the same population of early-type galaxies as the FR I hosts, according to of the surface brightness profiles, and distributions of optical luminosities and black-hole masses, they differ from ``classical'' FR I radio galaxies only in terms of their lower level of nuclear activity.

We combine these CoreG with a sample of low-luminosity radio galaxies of morphology FR I extracted from the 3C catalogue of radio-sources (Bennett 1962) in a way defined by Chiaberge et al. (1999). Three galaxies (namely 3C 270, 3C 272.1, and 3C 274) are in common between the two samples. All 9 galaxies (with the exception of NGC 507) considered by Allen et al. (2006) are in common with our combined FR I/CoreG sample.

We searched for Chandra observations available in the public archive up to August 2007 and found data for 22 of the 33 objects belonging to the FR I sample: with respect to the sample considered by Balmaverde et al. (2006), we were able to add three sources observed, 3C 264, 3C 293, and 3C 442. We found data for 24 of the 29 CoreG: with respect to (Balmaverde & Capetti 2006) newly obtained observations were found for UGC 0968, UGC 7797, UGC 8745. All together, we consider 44 galaxies that have a range of nuclear radio-power covering 5 orders of magnitude. The information on the Chandra observations and basic data for these galaxies are presented in Table 1.

We reduced all data using the Chandra Data analysis CIAO v3.4, with the CALDB version 3.3.0. We reprocessed the data from level 1 to level 2 in the standard way, that is using the CIAO tool acis_process_events, removing bad pixels and applying pixel and PHA randomization. When possible, we improved the rejection of cosmic events for VFAINT mode observations. We rejected time intervals corresponding to high background levels and we filtered by selecting a standard set of ASCA grades (02346).

We modeled the spectra obtained using XSPEC version 12.3.0. We used only events filtered between 0.3 and 8 keV for our analysis and rebinned the spectrum to a minimum of 20 counts per bin to ensure that a $\chi^{2}$ statistics could be applied.

We adopt H₀=75 km s^-1 Mpc^-1 and q₀=0.5.

	Figure 1: Example of the procedure followed to determine the Bondi power for NGC 7898: in the left panel, we show the spectrum extracted in four annuli, centered on the nucleus, that was modeled with a PROJECT*PHA(MEKAL+POWERLAW) law; in the right panel, we show the corresponding deprojected temperature profile of the annuli.
Open with DEXTER

  
3 Calculation of the Bondi accretion rates

Under the assumption of spherical symmetry and negligible angular momentum, the accretion rate onto a SMBH can be estimated by the Bondi (1952) approximation as:

$$\dot{M}_{\rm B}=\pi \; \lambda \; c_{\rm s} \; \rho_{\rm B} \;{r_{\rm B}}^2$$

where $\lambda$ takes the value of 0.25 for an adiabatic index 5/3, $c_{\rm s}$ is the sound speed in the medium ( $c_{\rm s}=\sqrt{\Gamma~k~T~/\mu{ m}_{\rm p}}$) $, r_{\rm B}=\frac{2~G~M_{\rm BH}}{{c_{\rm s}}^2}$ is the Bondi accretion radius, and $\rho_{\rm B}$is the gas density at that radius, ( $\rho=1.13 n_{\rm e} m_{\rm p}$), so that

$$\dot{M}_{\rm B} = \frac{4.52 \pi \lambda G^{2} m_{\rm p}}{\le... ...\right)^{3/2}} n_{\rm e} \; {M_{\rm BH}^2} \; (kT)^{-3/2}\cdot$$

The calculation of the Bondi accretion rate then requires the measurement of three quantities: the electron gas density at the Bondi radius, the gas temperature at the same radius, and the mass of the central black hole.

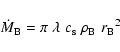
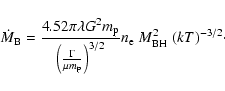
Unfortunately not even the Chandra telescope, which provides presently the highest angular resolution in X-rays, is able to resolve the accretion radius in most galaxies. Different strategies have been devised to estimate the gas and temperature density at the accretion radius. For example, Gliozzi et al. (2003) fitted the electron density profile with a model of gas in isothermal, hydrostatic equilibrium in spherical symmetry. Hardcastle et al. (2007) derived the Bondi power for radio galaxies from the 3CRR catalogue, adopting density and temperature values comparable to that typically measured ( $\rho=5\times 10^5$ m^-3 and kT = 0.7 keV) in nearby FR I. However, the results of Allen et al. (2006) indicated strong departures from equilibrium profiles and large variations in the central gas densities, suggesting that the accretion rates derived with these assumptions can be affected by large errors.

In this work, we determine the Bondi accretion rate following the same technique as Allen et al. (2006) and Bîrzan et al. (2004), which is described in detail below. Briefly, we deproject the temperature and electron density profile, assuming spherical symmetry. We then extrapolate the measured density to the accretion radius and describe the density profile with a power-law, assuming that the temperature is constant inside the innermost measurement radius. Given the temperature, the electron density at the accretion radius, and the black-hole mass, we calculate the Bondi accretion.

3.1 The IGM temperature profile

To characterize the thermal and emissivity properties of the intergalactic hot gas, we extract the spectrum in four annuli (see Fig. 1, left panel) centered on the peak of X-ray emission. Since a X-ray point source associated with the AGN is present in most galaxies, we extract the spectrum of the IG medium avoiding the innermost region within a radius of 1 $\hbox{$.\!\!^{\prime\prime}$ }$5. The outer radius is set to where the diffuse emission reaches the background level.

To measure the dependence of temperature on radius, we deproject the spectra by assuming spherical symmetry and using the PROJECT model in XSPEC. This model projects prolate ellipsoidal shells onto elliptical annuli, calculating the projection matrix of each of the overlying shells onto the area of each annulus and computing the total projected emission on that annulus. The fitting occurs simultaneously for all annuli and, after completion, the model provides the best-fitting temperature and abundance values in each shell (Fig. 1, right panel). We adopt a single-temperature plasma model (MEKAL) and foreground absorption (PHABS), taking into account projection effects, that is the model PROJECT*PHA(MEKAL). The hydrogen column density was tied between annuli and allowed to vary. With this fitting procedure we determine the deprojected profile of temperature. We then assume that the temperature measured inside the innermost annulus (usually bound between 1 $\hbox{$.\!\!^{\prime\prime}$ }$5 and 5 $\hbox{$^{\prime\prime}$ }$ in radius) is a good estimate of the temperature at the Bondi radius (see Table 2).

  
3.2 The electron density profile

We determine the X-ray surface brightness profile (SBP) extracting, the counts in a series of circular annuli centered on the central AGN (see Fig. 2, left panel, for an example; all SBP are shown in the Appendix A (Fig. A.1). When present, we mask the X-ray jet and other unrelated sources; we then subtract the background measured far from the source of interest. To avoid contamination from non-thermal emission due to the central AGN, we exclude the inner 1.5 arcsec region. When a point source is present, we use the PSF libraries to create an image of the PSF for the specific observation. We normalize it to the source flux in a circle of 1 arcsec centered on the peak of the emission and subtract the wings of the PSF brightness profile from the profile of the source.

As a general rule, we extract the X-ray counts from 4 annuli in the first 5 arcsec, then increase the size of the extraction region outward. For weaker sources, we use a coarser sampling of the brightness profile to maintain sufficient signal-to-noise ratio. The next step is to deproject the observed SBP, to derive the number of counts emitted per unit volume as a function of radius. Assuming spherical symmetry, the counts contribution provided by each spherical shell to the inner ones can be determined by pure geometric considerations, following the calculation by Kriss et al. (1983). Briefly, we express the observed SBP as a matrix product between the deprojected count rate in the spherical shell and a weight matrix, defined as the portion of volumes of each overlying shell seen in projection on each annulus.

	Figure 2: Example of the procedure followed in this work to determine the Bondi power for NGC 7898: in the left panel, we present the X-ray surface brightness profile of the galaxy; in the right panel, we show the derived deprojected electron density profile and the power-law extrapolation used to estimate its value at the Bondi radius (marked with a diamond).
Open with DEXTER

Our aim is to compare the observed counts per unit volume, with the theoretical value expected for a thermal plasma of a specific electron density and metal abundances. The XSPEC fitting model provides us with the value of the thermal normalization and the model predicted count rates (deprojected) in each of the annuli. Comparing these values with the counts per unit volume obtained by deprojecting the SBP, we adjust the thermal normalization to recover the counts emitted in each of the circular annuli used for the spatial analysis. The density was then calculated from the normalization of the thermal component, assuming $n_{\rm e}=1.2~n_{\rm H}$ (for a fully-ionized gas). The definition of the thermal normalization is

$$K=\frac{10^{-14}}{4\pi D_{\rm A}^2\left((1+z)^2\right)}\int n_{\rm e} n_{\rm p} {\rm d}V$$

where z is the redshift of the source, $D_{\rm A}$ is the angular-diameter distance at that redshift, $n_{\rm e}$ and $n_{\rm p}$ are the electron and proton number-density, respectively, and the integration is performed over the volume of the projected shells. Assuming a uniform density distribution along the shell, we invert this equation to solve for the electron density. Iterating this procedure for each spherical shell, we obtain the electron density profile (see Fig. 2, right panel, for an example; all profiles are shown in the Appendix A, Fig. A.2).

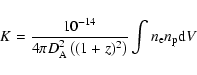
To estimate the gas density at the accretion radii, we perform a fit on the innermost points of the density profile in a power-law form, $n_{\rm e}(r) \sim r^{- \alpha}$, following Allen et al. (2006) and as explained in more detail in Sect. 3.5.

  
3.3 The black-hole mass

The mass of the central black hole can be determined in various ways: when available, we prefer to use the BH mass estimates obtained from direct gas or stellar dynamical measurements listed in Marconi & Hunt (2003).

Otherwise, we derive the SMBH masses using the stellar velocity dispersion (from the HyperLeda database). We apply the relation derived by Tremaine et al. (2002):

$$\log (M_{\rm BH}/M_{\odot})=8.13 + 4.02 \log \left(\sigma / 200~{\rm km}~{\rm s}^{-1}\right),$$

which has an intrinsic dispersion of about 0.23 dex. Alternatively, for the 7 objects for which velocity dispersion measurement is unavailable, we estimate the SMBH mass using the K-band absolute total magnitude (from 2MASS data archive) by using the relation derived by Marconi & Hunt (2003):

$$\log (M_{\rm BH}/M_{\odot}) = 8.21 + 1.13 ~ (\log L_{K} -10.9).$$

The observed scatter in this case is $\sim$0.5 dex.

  
3.4 Error budget

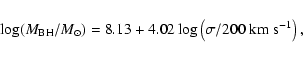
The uncertainties in the results of the deprojection were estimated using a Monte Carlo simulations. We perturbed randomly each point of the SBP with a Gaussian distribution of the perturbations, which had an amplitude determined by the error bar. We obtained 1000 different realizations of the SBP. Each of them was deprojected, and we evaluated, in each shell, the mean value of the counts rate and the scatter. Then we propagate the errors in the calculation of the electron density, taking into account the errors in the counts rate and in the temperature measurement at the accretion radius.

Table 2: Measured Bondi accretion rates and jet power.

Another source of uncertainty is associated with the extrapolation of the electron density to $r_{\rm B}$. This is related to the uncertainties in the parameters of the power-law fit describing the density behavior but also to the choice of the range of radii to be included. We evaluated the differences in $n_{\rm e}$, repeating the extrapolation using from 3 to 6 points of the electron density profile. The adopted value for $n_{\rm e}$ is the average value of these measurements and its uncertainty spans the full range given by the overlap of each individual error bar. This method is graphically explained in Fig. 3.

Figure 3: Example of the procedure followed to determine the density at the Bondi radius in the case of 3C 83.1. The dotted (dashed-dotted) line represents the best-fit linear relation to the density profile obtained by using the innermost 3 (6) density measurements, while the diamond (star) is its extrapolation to the Bondi radius. The adopted value for $n_{\rm e}$ is the filled circle at $r_{\rm B}$.

Open with DEXTER

Concerning uncertainties in the black-hole mass determination, we assume conservatively an error of a factor 3 (0.5 dex), regardless of the method used.

The final error in $P_{\rm B}$ is estimated by propagating the errors of all relevant quantities. We note that since the Bondi accretion power is tied to the electron density, related in turn to radius via the value of $\alpha$, the effective dependence of $P_{\rm B}$ on the black-hole mass is not simply from $M_{\rm BH}^2$, but from $M_{\rm BH}^{2 - \alpha}$. Given that the mean $\alpha$ value estimated (see Table 2) is 1, the propagated uncertainty is essentially linear with the black-hole mass error.

  
3.5 Accretion rate estimates and data quality

The methods presented in the previous sections were applied to every source of our sample to estimate the accretion power. However, the quality of the data is clearly not always sufficient to obtain a measure of $P_{\rm B}$ at a level of accuracy adequate for our purposes. In the following, we describe the quality criteria that we adopted to decide the inclusion or exclusion of a given galaxy from the analysis.

Quality criterion W: weak sources

The first criterion is based on the detection of a sufficient number of photons to obtain a reliable estimate of temperature and to perform the density deprojection. We require at least 100 counts in the region used for the temperature estimate and the presence of at least 5 bins in the surface brightness profile. For this reason, we discard 3C 075, 3C 78, 3C 189, 3C 293, 3C 442, and UGC 7203. The counts in the X-ray image of UGC 7203, only marginally in excess of the background level, are insufficient to measure even its brightness profile. These 6 sources are marked with a W (weak) quality flag in Table 2.

Quality criterion C: complex morphologies

In some cases, the X-ray galaxy morphology is quite complex, far away from the assumption of spherical symmetry on which we based the deprojection technique. This is the case for three galaxies, namely 3C 084 (Perseus A), 3C 317, and NGC 5128 (Cen A) as it can be seen from their respective Chandra images published in the literature (Fabian et al. 2000; Blanton et al. 2003; Kraft et al. 2000). These sources are marked with a C (Complex) quality flag in Table 2.

Quality criterion R: large r$_{\min}$/r$_{\rm B}$ ratio

The Bondi radius of most galaxies in our sample is typically between 10-100 pc, which is always unresolved by Chandra data, with the only exception of UGC 7629 (aka NGC 4472). However, in some cases, the ratio between the minimum radius at which we are able to measure the electron density, $r_{\min}$, and $r_{\rm B}$ is quite large, preventing a reasonable extrapolation of the density profile. For example, in 3C 348, the density at a Bondi radius of 34 pc should be obtained from a measurement at $\sim$10 kpc. All galaxies (namely 3C 028, 3C 346, 3C 348, 3C 438, as well as the core galaxy UGC 9723) with $r_{\rm min}$/ $r_{\rm B} > 100$ are excluded from the analysis at this level, and marked with a R flag.

Quality criterion E: large extrapolation errors

We required that the error in the extrapolation of the logarithm of the electron density to the accretion radius, as described in Sect. 3.4, must be smaller 1. We discarded for this reason 3C 31, 3C 264, and 3C 346 in the FR I sample and UGC 968, UGC 5902, UGC 7797, NGC 1316, and NGC 5419 among the CoreG (all marked with an E).

We note that the errors in $n_{\rm e}$ of the remaining sources are substantially smaller than the adopted threshold and its precise value is therefore not important. Similarly, we also verify that all sources excluded by the R criterion would also fall into this flag category, since the extrapolation over a factor of 100 in radius always produces a large error in $P_{\rm B}$, which indicate that the limit chosen for $r_{\min}$/$r_{\rm B}$ is not important.

To summarize, we have 6 FR I sources and 8 CoreG for with an accurate estimate of the accretion power at the Bondi radius, reported in Table 2, to be added to the 9 sources of the Allen et al. sample, for a total of 23 objects.

Table 3: Correlations summary.

  
4 The jet kinetic power

Several estimators of jet kinetic power in radio galaxies have been devised. A widely used method is based on the link between extended radio emission and jet power (Rawlings & Saunders 1991; Willott et al. 1999) that however suffers from substantial uncertainties (e.g. variations in environment, long-term time variability effects), which are particularly severe when dealing with individual objects. Furthermore, the connection between extended radio emission and $P_{\rm j}$ is calibrated only for FR II radio galaxies and cannot be simply extrapolated to FR I.

Results from X-ray studies with CHANDRA and XMM-Newton demonstrated the ability of a jet associated with an active galactic nucleus to blow cavities or ``bubbles'' in the surrounding X-ray emitting-gas (e.g. Boehringer et al. 1993; Fabian et al. 2000; Forman et al. 2005). These surface brightness depressions associated with radio sources provide us with the most robust and precise estimation of the jet kinetic power (e.g. Churazov et al. 2002), assuming that the jet energy inflates these bubbles at the sound speed.

Measuring the pressure and density of the gas inside the X-ray bubbles, we can calculate the work done by the jet on the surrounding medium to inflate the cavities ( $W\propto pV$). There are different sources of uncertainty in the measurements of cavity energy: the projected bubble size and the shape and composition of the contained plasma. The energy output is probably underestimated for adiabatic losses, cavity disruption, undetected cavities, and the omission of shock energy (e.g. Nusser et al. 2006; Binney et al. 2007). All these factors provide an uncertainty in the jet power of at least a factor of a few. Unfortunately, only a limited number of objects clearly shows surface brightness depressions associated with a radio source.

Heinz et al. (2007) derived a relation between the radio core luminosity $L_\nu$and the jet kinetic power $P_{\rm j}$ using a sample of 15 galaxies that showed jet-driven X-ray cavities. The slope of the relation is determined by theoretical assumption about the jet emission, modeled by a power-law spectrum, while the normalization is obtained empirically. The possible drawbacks of this approach are related to nuclear variability (as opposed to the time-averaged value obtained from the X-ray cavities) and Doppler boosting. Nonetheless, they showed that a significant relation between these two quantities exists in the form:

$$P_{\rm j}=P_0 \left (\frac{L_\nu}{L_0}\right)^{\frac{12}{17}}$$

where P₀ is a constant which has a value $1.0^{+1.3}_{-0.6}\times 10^{44}$ erg s^-1, when L₀ is fixed at $L_0=7\times10^{29}$ erg Hz^-1 s^-1. This relation then provides us with a simple and rather robust (with a scatter of 0.4 dex) estimate of the total jet power based only on the measure of the core power, a quantity available for all sources of our sample, with the only exception of 3C 028.

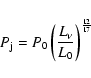
We note that since the research by Heinz et al. (2007), two further measurements of $P_{\rm j}$ based on X-ray cavities have been published (Shurkin et al. 2007). These two objects (namely NGC 1399 and NGC 4649) closely follow the $P_{\rm j}$- $L_{\rm core}$ relation, providing further support of its validity. Given the good agreement we do not need to re-estimate the value of P₀.

5 Results

  
5.1 The connection between jet and accretion power

	Figure 4: Bondi accretion power versus jet power. The stars represent FR I objects, the circles are the CoreG and the triangles represent the objects from Allen et al. sample. We also plot the best-fit linear relation (solid line).
Open with DEXTER

The estimated accretion rates at the Bondi radius in the galaxies of our sample are in the range from $\sim$ $3 \times 10^{-4}$- $4~\times~ 10^{-1}~M_{\odot}$ year^-1, corresponding to an available accretion power of $\sim$ $2~\times~10^{42}$- $2~\times~10^{45}$ erg s^-1

In Fig. 4, we compare the estimated jet power and Bondi accretion power for the 23 objects for which we were able to measure this quantity. The Bondi accretion power and the jet power are strongly correlated, with a Spearman's rank coefficient of $\rho = 0.76$. The probability that this is produced by from a random distribution is only $3\times10^{-5}$. The linear correlation coefficient is instead r = 0.84 (see Table 3 for a summary of the statistical analysis). The best-fit linear relations were derived to be the bisectrix of the fits using the two quantities as independent variables; this followed the suggestion of Isobe et al. (1990) and is the preferable for problems that require the symmetrical treatment of the variables. The best-fit linear relation, weighted for the errors of both the quantities, is

$$\log(P_{\rm j}) = (1.10 \pm 0.11) \times \log(P_{\rm B}) - 1.91 \pm 0.20$$

in 10⁴³ erg s^-1 units. The rms dispersion of the data from the fit is 0.4 dex. Therefore, the jet power is, within the uncertainties, linearly related to the Bondi rate over 3 orders of magnitude with a scatter of less than a factor of 3. Unfortunately, all but 6 FR I had to be excluded from the analysis of the density profile (due partly to the presence of bright point sources and to a larger than average distance) and this prevents being able explore the behavior of the $P_{\rm B}$ vs. $P_{\rm j}$ relation at the high end of radio luminosities of the sample. The efficiency of the conversion between accretion and jet power is 1.2 ^+0.7_-0.4%. We note that the slope found by Allen et al. corresponds, in our notation, to $1.30 \pm0.34$ with a normalization of 2.2 ^+1.0_-0.7 % for $P_{\rm j} = 10^{43}$ erg s^-1, consistent within 1 sigma confidence level with our values.

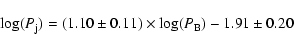
Since the Bondi accretion rate depends on the black-hole mass, the central gas density and temperature, it is important to assess whether the relation between $P_{\rm j}$ and $P_{\rm B}$, discussed above, is driven mostly by only one of these quantities. To estimate these dependences, we compare the jet power with each of these variables separately.

First, we found that there is no correlation between the jet power and the temperature at $r_{\rm B}$. Secondly, we considered how the electron density $n_{\rm e}$ at $r_{\rm B}$ affects the jet power. Figure 5 (left panel) shows a weak correlation between $n_{\rm e}$ and the jet power with a Spearman's rank coefficient of $\rho = 0.29$ (with an associated probability of no correlation of 18%) and a linear correlation coefficient of r = 0.34. The derived relation has a slope of $1.13\pm0.21$.

Thirdly, we correlated $P_{\rm j}$ with the black-hole masses of the 23 objects for which we were able to estimate the accretion rate: Fig. 5 (middle panel) shows a correlation with a slope $\sim$2 and a rms scatter of 0.66 dex. However, we can consider the measurements of mass for all 44 galaxies in the sample, regardless of the possibility to estimate $P_{\rm B}$. In particular, this enables us to include the strongest radio sources, radically changing the picture. The strength of the correlation between $M_{\rm BH}$ and $P_{\rm j}$ is strongly reduced (see Table 3 and Fig. 5, right panel) using the entire sample. Most importantly, we find objects at a given black-hole mass with $P_{\rm j}$ differing by 3 orders of magnitude and indeed the rms scatter of the residual is almost of 1 order of magnitude. This result was presented in Capetti & Balmaverde (2005) where we discussed this issue using the same sample but without the further requirement of the availability of Chandra data: while CoreG define a correlation between $M_{\rm BH}$ and $L_{\rm core}$ (and consequently with $P_{\rm j}$), FR I radio galaxies have much larger radio core luminosities at the similar value of $M_{\rm BH}$ which produces a large scatter in the $P_{\rm j}$- $M_{\rm BH}$ plane.

We conclude that the jet power shows a connection to the Bondi accretion rate, which is stronger than those to $M_{\rm BH}$, $n_{\rm e}$, or T separately. This indicates that $P_{\rm j}$ vs. $P_{\rm B}$ is the primary relation that does not descend from any of these quantities separately.

Figure 5: The electron density at $r_{\rm B}$ versus the jet power ( left panel) for the sub sample of 23 objects for which we are able to measure the accretion power, with the linear best-fit linear relation. Middle panel) black-hole masses versus the jet power for this same sub sample. In the right panel, we compare the linear correlation (dashed line) obtained from the 23 objects (surrounded by a large circle) with that obtained from the entire sample studied (44 objects).

Open with DEXTER

5.2 Jet power and surface brightness profiles

The analysis presented in the previous Section revealed the presence of a strong correlation between the jet power and the central properties of the galaxy, in particular with the gas density and black-hole mass. However, radio galaxies of different power differ also in terms of the global properties of their X-ray emitting hot coronae.

These differences are clearly evident in a comparison of their surface brightness profiles (shown in Fig. 6 for the sub sample of 23 galaxies with estimated $P_{\rm B}$). Their SBP are described well by power-laws, with a relatively small range of slopes ( $\langle \Delta \log{\cal S}$/ $\Delta\log r \rangle = -1.7 \pm 0.6$) while they differ substantially in normalization. The remaining sources of the sample show a similar behavior with an even increased range of intensity. To quantify these differences, we estimated the value of the surface brightness at 1 kpc, (hereafter ${\cal S}_{1~{\rm kpc}}$) a radius accessible for almost all galaxies, by interpolating locally the profile with a power-law. The galaxies of our sample cover 3.5 orders of magnitude in ${\cal S}_{1~{\rm kpc}}$ (see Table 2).

The intensity of the brightness profile at 1 kpc turns out to be strongly correlated with the radio-jet power (see Fig. 6, right panel). The correlation coefficient of this relation is 0.73, the rms is 0.67, and the Spearman rank coefficient is 0.72. The probability, associated with this rank value, that this is produced by a random distribution is $8\times10^{-8}$. The slope of the correlation is $1.17 \pm 0.11$.

A significant advantage of this approach, based simply on the surface brightness profile, is the possibility of including in the analysis also galaxies for which the data were of insufficient quality to estimate the electron density at the Bondi radius. In particular, this enables us to extend the range of jet power probed to 4.5 orders of magnitudes. This is due to two reasons. As already noted, on the one hand, the most luminous radio galaxies did not, in general, have reliable density profiles due to the contamination of the nuclear source and to their average larger distance (e.g. 3C 84 and 3C 346). On the other hand, we find that the objects with the lowest radio luminosity correspond to hot coronae of lower surface brightness, which were then excluded from the analysis due to insufficient count rates in their X-ray images (e.g. UGC 5902 and UGC 9723).

Therefore, the jet power of a given object can be predicted with an rms uncertainty of only a factor of 5 by looking at the intensity of the X-ray emission produced by the galactic hot corona.

Figure 6: Left panel: surface brightness profiles of the 23 objects, zooming into the region around a radius of 1 kpc. They are described well by power laws, with a relatively small range of slopes, while they differ substantially in normalization. Right panel: surface brightness at 1 kpc ( ${\cal S}_{1~{\rm kpc}}$) in units of counts s-1 arcsec-2, versus the jet power for the extended sample of 43 galaxies. The solid line represents the best fit linear relation.

Open with DEXTER

Since the brightness profiles are directly related to the gas electron density, the large range of brightnesses observed reflects the different distributions of hot gas in the centers of these galaxies. A link between brightness profile and jet power is expected because the electron density is one of the critical parameters that, with the BH mass, determine the accretion flow. It must however be noted that, in the case of Bremsstrahlung emission, the expected dependence is in the form $P_{\rm j} \propto {\cal S}_{1~{\rm kpc}}^{0.5}$.

This suggests that our assumption of simple homology in the hot coronae, described only by the normalization of the brightness profile, is probably an over-simplification. Other variables can influence the relation between $P_{\rm j}$ and ${\cal S}_{1~{\rm kpc}}$, for example, a dependence of the SBP shape (e.g. its core radius or outer slope) on luminosity. There is an indication of the existence of a fundamental plane for the X-ray emitting gas, linking the temperature with the surface brightness and half-light (in X-ray) radius (Diehl & Statler 2005). It is likely that a more robust parametrization of the hot corona properties, not simply its intensity at a fixed radius, might reveal an even stronger link with the AGN properties, but this is beyond the scope of this paper.

An alternative explanation for the steeper than expected dependence between brightness profile and jet power originates in a result described by Best et al. (2005). They found that the total mass of gas cooling within an isothermal hot corona is $\dot M_{\rm cool} \propto L_{\rm X}/T$ and that this has the same dependence on black-hole mass as the radio-loud AGN fraction $\dot M_{\rm cool} \propto M_{\rm BH}^{1.5}$. This implies that a linear relation exists between the cooling rate, radio-power, and the X-ray luminosity (and hence with the surface brightness) of the hot corona.

Despite our inability to interpret in detail the correlation between $P_{\rm j}$ and ${\cal S}_{1~{\rm kpc}}$, the phenomenological connection between the brightness profile and jet power has several important ramifications. First of all, considering the galaxies with the highest radio luminosity, we already noted in Fig. 5 (right panel) that they show a substantial upward scatter in the plane comparing radio luminosity and black-hole mass. They effectively break the link between $L_{\rm j}$ and SMBH mass defined by the less luminous radio-sources. However, Fig. 6 (right panel) shows that these bright radio sources are associated with the brightest coronae. Their higher radio luminosity, with respect to other galaxies of similar black-hole mass, is driven by the higher density of their hot ISM, producing a higher accretion rate and a more luminous extended X-ray emission.

Furthermore, the results presented in Sect. 5.1 connect the jet power with the gas properties (and black-hole mass) at the Bondi radius. Conversely, Fig. 6 (right panel) sets a link between the global properties of the hot coronae and the level of AGN activity. The implication of this result is that a substantial variation in the jet power in a given galaxy must be accompanied by a global change in its ISM properties. This can only occur when a dramatic event, such as a major merger, takes place. This is an indication that the accretion flow is stable over significant timescales and that, most likely, the long-term level of jet power remains stable over the interval between major mergers.

Finally, the correlation between $P_{\rm j}$ and ${\cal S}_{1~{\rm kpc}}$ provides us with a simple and rather robust method to estimate the jet power, with an accuracy of better than a factor of $\sim$5, based only on the measurement of the brightness of the hot gas at a fixed radius, 1 kpc for the sample considered here. Clearly, this is applicable to X-ray data of relatively poor quality and/or spatial resolution that would not enable a full spectral fitting and deprojection down to a spatial scale comparable to the Bondi radius. Indeed, this already found a useful application in the context of this work, as it enabled us to understand the properties of the bright FR I. We expect to be able to use this method also, for example, for more distant (and hence more powerful) radio galaxies.

  
6 Constraints on the accretion process and on its radiative efficiency

In Balmaverde & Capetti (2006), we noticed that the X-ray nuclei of CoreG have luminosities of typically $L/L_{\rm {Edd}} \sim 10^{-6}$-10^-9 expressed in fraction of the Eddington luminosity. Furthermore, the tight correlations between radio, optical, and X-ray nuclear emission argue in favor of a jet origin for the nuclear emission. In FR I radio galaxies, the dominant contribution from jet emission is confirmed directly by the high polarization of their optical nuclei (Capetti et al. 2007). This implies that the observed nuclear emission does not originate in the accretion process and the values reported above should be considered as upper limits.

These results add to the already vast literature reporting emission corresponding to a very low fraction of the Eddington luminosity associated with accretion onto supermassive black holes. This prompted the idea that in these objects accretion occurs not only at a low rate but also at a low radiative efficiency, such as in the Advection Dominated Accretion Flows (ADAF, Narayan & Yi 1995). The ADAF models have been rather successful in modeling the observed nuclear spectrum in several galaxies, such as e.g. the Galactic Center and NGC 4258 (Lasota et al. 1996; Narayan & Yi 1995). However, even ADAF models over-predict the observed emission in the nuclei of nearby bright elliptical galaxies (Di Matteo et al. 2000; Loewenstein et al. 2001; Pellegrini 2005).

This suggested the possibility that a substantial fraction of the mass included within the Bondi's accretion radius might not actually reach the central object, thus further reducing the radiative emission from the accretion process. This may be the case in the presence of an outflow (Advection Dominated Inflow/Outflow Solutions, or ADIOS, Blandford & Begelman 1999) or strong convection (Convection Dominated Accretion Flows, or CDAF, Quataert & Gruzinov 2000) in which most gas circulates in convection eddies rather than accreting onto the black hole. These arguments apply also to the galaxies considered here, since the available accretion powers determined in the Sect. 3 exceed by several orders of magnitude the observed nuclear X-ray luminosities $L_{\rm X}$. More quantitatively, the comparison of the values of $L_{\rm X}$ reported in Balmaverde & Capetti (2006) and Balmaverde et al. (2006) and $P_{\rm B}$correspond to typical ratios of $L_{\rm X}$/ $P_{\rm B} \sim 10^{-4}$-10^-5.

In the case of the radio-loud objects considered here, we have further information that can be used to constrain the properties of the accretion process, related to the presence of jets. In fact the mass flowing along the jet, $\dot{m}_{\rm j}$, cannot exceed the mass rate at the radius of accretion disk, $\dot{m}_{\rm disk}$. The jet power, for a matter-dominated jet, can be expressed as $P_{\rm j} \sim \Gamma \dot{m}_{\rm j} c^2$ where $\Gamma$ is the jet Lorentz factor. If we denote with f the fraction of gas crossing the Bondi radius that actually reaches the accretion disk (that is $\dot{m}_{\rm disk} = f \dot{m}_{\rm B}$) and since the correlation between jet and Bondi power gives us

$$P_{\rm j} \sim 0.012 ~~ \dot{m}_{\rm B} c^2,$$

the condition $\dot{m}_{\rm j} < \dot{m}_{\rm disk}$ translates into a lower limit to f as

$$f > 0.012 ~~ \Gamma^{-1}.$$

Assuming the estimate of jet Lorentz for FR I radio galaxies, $\Gamma \sim 5$, derived from Giovannini et al. (2001) this limit becomes

$$f \gtrsim 0.0024.$$

Numerical simulations performed by Zanni et al. (2007) suggest that plasma within the accretion disk can be channeled into the jet with a rather high efficiency, $\dot{m}_{\rm j} \sim 0.2$- $0.55~\dot{m}_{\rm disk}$ from which $f \sim 0.01$.

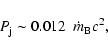
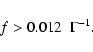
On the other hand, the correlation between the nuclear X-ray luminosities and the radio-core luminosities derived in (Balmaverde & Capetti 2006) sets a limit to the disk emission as

$$\log(L_{\rm X}) < 1.40 + \log \left(\nu L_{\rm R}\right).$$

The X-ray luminosity can be expressed as

$$L_{\rm X} = \eta_{\rm x} \dot{m}_{\rm disk} c^2 = \eta_{\rm x} f \dot{m_{\rm B}} c^2 = 0.012^{-1} \eta_{\rm x} f P_{\rm j}$$

where $\eta_{\rm x}$ is the efficiency of conversion of rest mass into energy radiated within the 2-10 keV band. Taking advantage of the link between radio-core luminosity and jet power discussed in Sect. 4, we obtain:

$$\log L_{\rm X} = 24.84 + \log \left(\eta_{\rm x} f\right) + 12/17 ~~ \log L_{\rm R}$$

leading to

$$\log \left(\eta_{\rm x} f\right) < 5/17 ~~ \log L_{\rm R} -13.74.$$

The limit on $\eta_{\rm x} f$ is most stringent for the objects of lower radio luminosity. For example, for $L_{\rm R} = 10^{27}$ erg/s/Hz this corresponds to $\eta_{\rm x} f < 1.6 ~\times~ 10^{-6}$. When combined to the limit of f obtained above, this implies

$$\eta_{\rm x} < 1.3 \times 10^{-4} ~~ \Gamma \sim 6.5 \times 10^{-4}.$$

To derive the total disk radiative efficiency we have to estimate the bolometric correction corresponding to the 2-10 keV band. This is a complex task, since little is known about the spectral energy distribution of our sources and, in addition, their broad-band nuclear spectrum is dominated by jet emission. Marconi et al. (2004) estimated bolometric corrections at different levels of luminosity by using suitably-built AGN templates and found that the 2-10 keV bolometric correction decreases with decreasing luminosity, down to $\sim$8 for a bolometric luminosity of $\sim$10⁴² erg s^-1. By adopting this value, we derive a bolometric disk radiative efficiency of $\eta \lesssim 0.005$. This limit is substantially smaller than the ``canonical'' value of 0.1 and of the estimates derived from matching the mass function of local SMBH with the AGN relics, $\eta \sim 0.08$ (Shankar et al. 2007; Marconi et al. 2004). This is an indication that accretion in these objects occurs not only at a smaller rate, but also at lower efficiency than in standard accretion disks.

7 Summary and conclusions

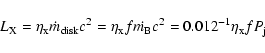
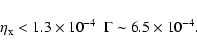
We have presented our results concerning the connection between the accretion rate of hot gas, estimated in the Bondi's spherical approximation, and the jet power in a sample of low-luminosity radio galaxies. The sample was formed by combining radio galaxies with FR I morphology extracted from the 3C catalogue and early-type galaxies with a ``core'' optical brightness profile. Galaxies of this latter sub sample have been shown to represent ``miniature'' radio galaxies, being drawn from the same population of early-type galaxies as the FR I hosts and differing from ``classical'' FR I radio galaxies only in a lower level of nuclear activity. This combined FR I/CoreG sample covers the full range of radio-luminosity of FR I, spanning five orders of magnitude.

In the Chandra public archive, there were observations available for 44 objects of the sample. These data were used to derive profiles of X-ray brightness and of gas temperature that, once deprojected, provided a measurement of the electron gas density at the Bondi radius. When combined with the mass of the central black hole, these values provided us with an estimate of the accretion rate of hot gas, $P_{\rm B}$. The quality and/or spatial resolution of the data was sufficient to obtain a measure of $P_{\rm B}$ at a level of accuracy adequate for our purposes for a sub sample of 23 galaxies.

To estimate the jet power, we took advantage of an empirical relation linking the jet kinetic power, $P_{\rm j}$, to the radio-core luminosity. This method freed us from the need of detecting X-ray cavities inflated by a radio jet to measure its power and enabled us to estimate $P_{\rm j}$ with an rms error of 0.4 dex for all galaxies in our sample.

We found that a tight, linear relation links the accretion with the jet power whose normalization sets the efficiency of the conversion between accretion and jet power to $\sim$1.2%. These results strengthen and extend the validity of the results obtained by Allen et al. (2006) based on the analysis of 9 low-luminosity radio galaxies.

In addition, we found that the jet power is closely connected also with the surface brightness of the X-ray emission, measured at the fixed radius of 1 kpc. This is a simple quantity to measure; it was therefore possible to consider in the analysis all galaxies, including those for which the data were of insufficient quality to estimate the Bondi accretion rate. This method could be extended to objects of the highest radio luminosity, which did not provide useful estimates of $P_{\rm B}$, showing that they are associated with the brightest coronae. This implies that the different levels of radio luminosity are not only associated with nuclear quantities (such as the gas density and black-hole mass) but also to global differences in the structure of the galactic hot coronae. A substantial change in the jet power must be accompanied by a global change in its ISM properties, driven e.g. by a major merger.

At the estimated accretion rates at the Bondi radius, $M_{\rm B}$, even ADAF models substantially over-predict the observed X-ray nuclear emission suggesting that a substantial fraction of the mass crossing the Bondi radius does not reach the central object. On the other hand, the mass rate at the outer radius of the accretion disk must be sufficient to maintain the mass flow along the jet. This requires that at least a mass fraction of $\gtrsim$ $0.0024~M_{\rm B}$ reaches the accretion disk. The X-ray nuclear luminosity corresponding to this accretion rate does not exceed the observed luminosities of the nuclear X-ray sources (having assumed a bolometric correction of 8 for the 2-10 keV band) only when the radiative disk efficiency is $\eta \lesssim 0.005$, substantially smaller than the ``canonical'' value of 0.1. This is an indication that accretion in these objects occurs not only at a smaller rate, but also at lower efficiency than in standard accretion disks.

The picture which emerges is that the accretion of hot gas associated with the host galaxy corona represents the dominant process of fueling for FR I radio galaxies across their full range of radio luminosity, spanning from the faintest level of detectable activity to radio-luminosities marking the transition between FR I and FR II objects. The differences of AGN power across this wide range of luminosity are determined by the available supply of gas, which we found to be closely related to the global properties of the hot corona. These results provide a strong evidence for the presence of a feedback process linking the host galaxy with the active nucleus since the same hot gas that provides the supply to the supermassive black hole is also the repository of the kinetic energy liberated into the ISM by the jets. Clearly, it will be of great interest to explore how the hot gas content is connected to the evolution of the host galaxy and to its merger history.

Another interesting issue is the fate of the gas within the Bondi accretion radius. While on the one handm the spherical accretion provides, a posteriori, a good description of gas inflow in the central regions of these active galaxies, only a small fraction of the gas is allowed to reach the accretion disk.

At small radii, the spherical inflow must therefore break and the bulk of the accreting gas must be removed from its large-scale motion toward the central black hole. The (almost) linear relation between jet power and accretion rate indicates that the efficiency of this mechanism must have only a very weak dependence on the amount of accreting gas. Apparently, also the fraction of gas ultimately launched into the relativistic jet is essentially independent of the jet power. Accounting for this complex phenomenology represents an important challenge if we want to preceed in our understanding of the process of accretion and jet formation in active nuclei.

A crucial question that must also be addressed is which manifestation of an active nucleus can be supported by hot accretion. Although the galaxies considered span a large range of radio power, it is important to establish whether hot accretion is sufficient to power FR II radio galaxies of even higher luminosity or, alternatively, above some threshold an additional source of fuel, possibly associated with an ISM phase of lower temperature. The results presented here refer only to radio-loud AGN that channel a significant fraction of the accretion power into jet kinetic energy. However, hot accretion might also be important in powering radio-quiet AGN. We will explore this possibility in a forthcoming paper.

Acknowledgements

We acknowledge the usage of the HyperLeda database (http://leda.univ-lyon1.fr).

References

• Allen, S. W., Dunn, R. J. H., Fabian, A. C., Taylor, G. B., & Reynolds, C. S. 2006, MNRAS, 372, 21 [NASA ADS] [CrossRef] (In the text)
• Auriemma, C., Perola, G. C., Ekers, R. D., et al. 1977, A&A, 57, 41 [NASA ADS] (In the text)
• Balmaverde, B., & Capetti, A. 2006, A&A, 447, 97 [NASA ADS] [CrossRef] [EDP Sciences] (BC06) (In the text)
• Balmaverde, B., Capetti, A., & Grandi, P. 2006, A&A, 451, 35 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Bennett, A. S. 1962, MmRAS, 68, 163 [NASA ADS] (In the text)
• Best, P. N. 2004, MNRAS, 351, 70 [NASA ADS] [CrossRef] (In the text)
• Best, P. N., Kauffmann, G., Heckman, T. M., et al. 2005, MNRAS, 362, 25 [NASA ADS] [CrossRef]
• Binney, J., Bibi, F. A., & Omma, H. 2007, MNRAS, 377, 142 [NASA ADS] [CrossRef] (In the text)
• Bîrzan, L., Rafferty, D. A., McNamara, B. R., Wise, M. W., & Nulsen, P. E. J. 2004, ApJ, 607, 800 [NASA ADS] [CrossRef] (In the text)
• Blandford, R. D., & Begelman, M. C. 1999, MNRAS, 303, L1 [NASA ADS] [CrossRef] (In the text)
• Blanton, E. L., Sarazin, C. L., & McNamara, B. R. 2003, ApJ, 585, 227 [NASA ADS] [CrossRef] (In the text)
• Boehringer, H., Voges, W., Fabian, A. C., Edge, A. C., & Neumann, D. M. 1993, MNRAS, 264, L25 [NASA ADS] (In the text)
• Bondi, H. 1952, MNRAS, 112, 195 [NASA ADS] (In the text)
• Burns, J. O. 1990, AJ, 99, 14 [NASA ADS] [CrossRef] (In the text)
• Capetti, A., Axon, D. J., Chiaberge, M., et al. 2007, A&A, 471, 137 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Capetti, A., & Balmaverde, B. 2005, A&A, 440, 73 [NASA ADS] [CrossRef] [EDP Sciences] (CB05) (In the text)
• Chiaberge, M., Capetti, A., & Celotti, A. 1999, A&A, 349, 77 [NASA ADS] (In the text)
• Churazov, E., Sunyaev, R., Forman, W., & Böhringer, H. 2002, MNRAS, 332, 729 [NASA ADS] [CrossRef] (In the text)
• de Ruiter, H. R., Parma, P., Capetti, A., Fanti, R., & Morganti, R. 2002, A&A, 396, 857 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Di Matteo, T., Quataert, E., Allen, S. W., Narayan, R., & Fabian, A. C. 2000, MNRAS, 311, 507 [NASA ADS] [CrossRef]
• Diehl, S., & Statler, T. S. 2005, ApJ, 633, L21 [NASA ADS] [CrossRef] (In the text)
• Donzelli, C. J., Chiaberge, M., Macchetto, F. D., et al. 2007, ApJ, 667, 780 [NASA ADS] [CrossRef]
• Fabian, A. C., Sanders, J. S., Ettori, S., et al. 2000, MNRAS, 318, L65 [NASA ADS] [CrossRef] (In the text)
• Forman, W., Nulsen, P., Heinz, S., et al. 2005, ApJ, 635, 894 [NASA ADS] [CrossRef] (In the text)
• Giovannini, G., Cotton, W. D., Feretti, L., Lara, L., & Venturi, T. 2001, ApJ, 552, 508 [NASA ADS] [CrossRef] (In the text)
• Gliozzi, M., Sambruna, R. M., & Brandt, W. N. 2003, A&A, 408, 949 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Hardcastle, M. J., Evans, D. A., & Croston, J. H. 2007, MNRAS, 376, 1849 [NASA ADS] [CrossRef] (In the text)
• Heinz, S., Merloni, A., & Schwab, J. 2007, ApJ, 658, L9 [NASA ADS] [CrossRef] (In the text)
• Isobe, T., Feigelson, E. D., Akritas, M. G., & Babu, G. J. 1990, ApJ, 364, 104 [NASA ADS] [CrossRef] (In the text)
• Kraft, R. P., Forman, W., Jones, C., et al. 2000, ApJ, 531, L9 [NASA ADS] [CrossRef] (In the text)
• Kriss, G. A., Cioffi, D. F., & Canizares, C. R. 1983, ApJ, 272, 439 [NASA ADS] [CrossRef] (In the text)
• Lasota, J.-P., Abramowicz, M. A., Chen, X., et al. 1996, ApJ, 462, 142 [NASA ADS] [CrossRef]
• Lauer, T. R., Ajhar, E. A., Byun, Y.-I., et al. 1995, AJ, 110, 2622 [NASA ADS] [CrossRef] (In the text)
• Loewenstein, M., Mushotzky, R. F., Angelini, L., Arnaud, K. A., & Quataert, E. 2001, ApJ, 555, L21 [NASA ADS] [CrossRef]
• Marconi, A., & Hunt, L. K. 2003, ApJ, 589, L21 [NASA ADS] [CrossRef] (In the text)
• Marconi, A., Risaliti, G., Gilli, R., et al. 2004, MNRAS, 351, 169 [NASA ADS] [CrossRef] (In the text)
• Mauch, T., & Sadler, E. M. 2007, MNRAS, 375, 931 [NASA ADS] [CrossRef]
• Narayan, R., & Yi, I. 1995, ApJ, 444, 231 [NASA ADS] [CrossRef] (In the text)
• Nusser, A., Silk, J., & Babul, A. 2006, MNRAS, 373, 739 [NASA ADS] [CrossRef] (In the text)
• Pellegrini, S. 2005, ApJ, 624, 155 [NASA ADS] [CrossRef]
• Quataert, E., & Gruzinov, A. 2000, ApJ, 539, 809 [NASA ADS] [CrossRef] (In the text)
• Rawlings, S., & Saunders, R. 1991, Nature, 349, 138 [NASA ADS] [CrossRef]
• Shankar, F., Weinberg, D. H., & Miralda-Escude', J. 2007, ArXiv e-prints, 710
• Shurkin, K., Dunn, R. J. H., Gentile, G., Taylor, G. B., & Allen, S. W. 2007, ArXiv e-prints, 710 (In the text)
• Smith, E. P., & Heckman, T. M. 1989, ApJ, 341, 658 [NASA ADS] [CrossRef]
• Tremaine, S., Gebhardt, K., Bender, R., et al. 2002, ApJ, 574, 740 [NASA ADS] [CrossRef] (In the text)
• Valentijn, E. A., & Bijleveld, W. 1983, A&A, 125, 223 [NASA ADS] (In the text)
• Willott, C. J., Rawlings, S., Blundell, K. M., & Lacy, M. 1999, MNRAS, 309, 1017 [NASA ADS] [CrossRef]
• Zanni, C., Ferrari, A., Rosner, R., Bodo, G., & Massaglia, S. 2007, A&A, 469, 811 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)

 

  
Online Material

   
Appendix A

	Figure A.1: The X-ray surface brightness profiles of the 43 galaxies of the sample, having excluded UGC 7203.
Open with DEXTER

	Figure A.1: continued.
Open with DEXTER

	Figure A.1: continued.
Open with DEXTER

	Figure A.2: The electron density profiles of the 30 objects, whose data quality is sufficient to perform the deprojection of the brightness profile (see Sect. 3.5). The solid lines represent the best-fit power-law relation to the density profile.
Open with DEXTER

	Figure A.2: continued.
Open with DEXTER