A&A 485, 127-136 (2008)
DOI: 10.1051/0004-6361:200809440
M. Gonzalez Garcia - J. Le Bourlot - F. Le Petit - E. Roueff
LUTH, Observatoire de Paris and Université Paris 7 Place Jansen, 92190 Meudon, France
Received 23 January 2008 / Accepted 6 March 2008
Abstract
Context. Transfer in lines controls the gas cooling of photon dominated regions (PDR) and provides many of the observational constraints that are available for their modelling.
Aims. The interpretation of infrared and radio observations by the new generation of instruments, such as Herschel, requires sophisticated line radiative-transfer methods. The effect of dust emission on the excitation of molecular species in molecular regions is investigated in detail to explicitly show the origin of various approximations used in the literature. Application to H_2O is emphasised.
Methods. The standard 1D radiative transfer equation is written as a function of the space variable (as opposed to the usual optical depth). This permits to simultaneously consider all pumping contributions to a multi-level species in a non-uniform slab of dust and gas. This treatment is included in the Meudon PDR Code (available at http://aristote.obspm.fr/MIS/).
Results. Infrared emission from hot grains at the edge of the PDR may penetrate deep inside the cloud, providing an efficient radiation source to excite some species at a location where cold grains no longer emit. This leads to non-negligible differences with classical escape probability methods for some lines, e.g. water. Cooling efficiency does not follow directly from line emissivities. The infrared pumping contribution leads to a higher excitation that enhances collisional de-excitation and reduces cooling efficiency.
Key words: ISM: general - line: formation - radiative transfer - methods: numerical - ISM: molecules
The derivation of molecular column densities from molecular emissions requires
detailed radiative transfer treatment of the various emitted transitions. A summary of the various radiative transfer methods can be found in van Zadelhoff et al. (2002). The large velocity gradient technique or escape probability method provides
first-order estimates (van der Tak et al. 2007). A full radiative transfer treatment within a
given assumed geometry provides significantly improved results, and various numerical methods
have been developed such as the accelerated ![]() -iteration method (ALI)
(Hubeny 2001; Chevallier et al. 2003) and, more recently, the coupled escape probability method (CEP)
(Elitzur & Asensio Ramos 2006), which aims to solve the radiative transfer equations exactly.
Monte-Carlo techniques are also highly efficient and allow taking various geometries into account
(Juvela 2005; Bernes 1979). The major difficulties are the computation time and the control of the resulting errors.
-iteration method (ALI)
(Hubeny 2001; Chevallier et al. 2003) and, more recently, the coupled escape probability method (CEP)
(Elitzur & Asensio Ramos 2006), which aims to solve the radiative transfer equations exactly.
Monte-Carlo techniques are also highly efficient and allow taking various geometries into account
(Juvela 2005; Bernes 1979). The major difficulties are the computation time and the control of the resulting errors.
The aim of this paper is to compute the excitation of atomic and molecular species by considering excitation by collisions and pumping due to external radiation fields, as well as internal sources such as dust and lines.
This paper presents the full derivation of the detailed balance equations describing the steady-state level populations of any atomic or molecular system subject to collisions, external and
local (dust and gas) radiation fields. We computed the exact expression of the mean radiation intensity ![]() in Sect. 2, where chemical reactions, inelastic collisions, and
local emission/absorption effects are taken into account. We outline different
approximations corresponding to three different contributions of the monochromatic
intensity in Sect. 3. The energy released in line emissions following
collisional excitation is one of the major cooling processes of the gas. However, the
efficiency of the cooling depends on the ability of the radiation to escape, as described
in Sect. 4.2. We apply the different methods and approximations described
above to the case of the water molecule in Sect. 5.
in Sect. 2, where chemical reactions, inelastic collisions, and
local emission/absorption effects are taken into account. We outline different
approximations corresponding to three different contributions of the monochromatic
intensity in Sect. 3. The energy released in line emissions following
collisional excitation is one of the major cooling processes of the gas. However, the
efficiency of the cooling depends on the ability of the radiation to escape, as described
in Sect. 4.2. We apply the different methods and approximations described
above to the case of the water molecule in Sect. 5.
As already discussed by other authors (van der Tak et al. 2006; Poelman & Spaans 2005; Poelman et al. 2007; Poelman & Spaans 2006), the complicated level structure of H_2O combined with its high permanent dipole moment requires a particularly careful analysis of its excitation and of its subsequent cooling emission transitions. The corresponding implementation in our PDR (photon dominated region) code has been explicitly achieved, complementing the upgrade of ultraviolet radiative transfer by Goicoechea & Le Bourlot (2007).
The case of S140, a well-documented PDR, is specifically addressed as a benchmark of our calculations and permits a detailed comparison with the previous work of Poelman & Spaans (2005, hereafter PS05). Finally, we summarise our results and display our conclusions in Sect. 6. Useful mathematical subtleties are outlined in separate appendices.
In a medium far from LTE, excitation of any given species can only be computed by solving detailed balance equations. Le Petit et al. (2006) have shown that these detailed balance equations
should be written with chemical formation and destruction terms, thus leading
to a fully determined set of equations that does not require the introduction of a conservation equation. For a level i, detailed balance gives
To solve this system, the most difficult term to compute is the mean intensity
![]() ,
which controls radiative excitation. In the following, we deal with a purely 1D plane parallel cloud, as described in Le Petit et al. (2006). At a position
,
which controls radiative excitation. In the following, we deal with a purely 1D plane parallel cloud, as described in Le Petit et al. (2006). At a position ![]() within a cloud,
within a cloud,
![]() is
computed from
is
computed from
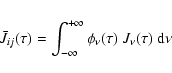
| |
Figure 1: Cloud geometry and sign conventions from Goicoechea & Le Bourlot (2007). |
| Open with DEXTER | |
Since the system of coupled detailed balance equations must be solved
on a common grid, it is mandatory to compute the mean intensity for all
lines on that same grid. Therefore, it is not possible
to use the optical depth in the line as the independent variable as
is usually done for a single line radiative-transfer problem.
All relevant expressions have to be derived using a single common independent
variable for all lines. In all that follows, we use the usual
optical depth in the visible
![]() as our independent variable
(
as our independent variable
(
![]() ).
).
The line profile ![]() is often expressed using a non-dimensional
centred variable
is often expressed using a non-dimensional
centred variable
![]() such that
such that
![]() ,
with
,
with
![]() the line centre frequency and
the line centre frequency and
![]() the Doppler width. However, in a medium with variable
temperature and (potentially) turbulent velocity, this quantity is not
constant as a function of the position in the cloud, and thus it is not possible
to simply exchange integration over position in the cloud
and integration over the line profile.
the Doppler width. However, in a medium with variable
temperature and (potentially) turbulent velocity, this quantity is not
constant as a function of the position in the cloud, and thus it is not possible
to simply exchange integration over position in the cloud
and integration over the line profile.
From the expression of
![]() ,
with T the kinetic temperature,
m the molecular mass, and
,
with T the kinetic temperature,
m the molecular mass, and ![]() the turbulent velocity, we can
define a compound thermal velocity
the turbulent velocity, we can
define a compound thermal velocity
![]() that accounts for all the
(s) position dependent quantities. A natural variable is then
that accounts for all the
(s) position dependent quantities. A natural variable is then
![]() .
The link between profiles is then
.
The link between profiles is then
![]() .
.
For a Gaussian line profile, we have
To compute the mean intensity (3), we need an expression
for the specific intensity ![]() .
It follows from a
formal solution to the 1D radiative transfer equation:
.
It follows from a
formal solution to the 1D radiative transfer equation:
Note that in Eq. (5) the independent variable s is a
``physical'' distance. To introduce the optical depth
![]() ,
we use the following relations:
,
we use the following relations:
We introduce the dust absorption cross section
![]() ,
so
,
so
![]() ,
with
,
with ![]() the
density of nucleons,
the
density of nucleons,
![]() ,
,
![]() ,
,
![]() ;
and following Elitzur & Asensio Ramos (2006), we introduce
;
and following Elitzur & Asensio Ramos (2006), we introduce
![]() ,
where ni is the number density of level i and gi its statistical weight.
,
where ni is the number density of level i and gi its statistical weight.
This leads to an expression of the radiative transfer equation where all
physical constants and atomic and molecular data are clearly separated
from physical variables describing local excitation conditions, i.e.
depending explicitly on position within the cloud:
From Eq. (7) we see that the total optical depth
![]() at frequency
at frequency ![]() has two contributions (Dust and Line),
has two contributions (Dust and Line),
![]() ,
with
,
with
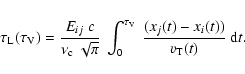
For a cloud of total thickness
![]() ,
the formal solution of Eq. (7) is
,
the formal solution of Eq. (7) is
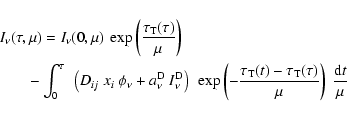
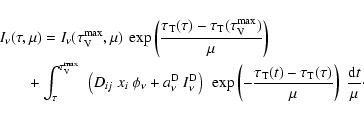
We see that ![]() is the sum of three contributions. The first is
the incident external radiation field attenuated by a factor
is the sum of three contributions. The first is
the incident external radiation field attenuated by a factor
![]() .
By splitting the integral in two, we get a second contribution from the line
emission at t,
.
By splitting the integral in two, we get a second contribution from the line
emission at t,
![]() attenuated
by the difference in total optical depth between the emission
and absorption point, and a third contribution from the dust
emission at t,
attenuated
by the difference in total optical depth between the emission
and absorption point, and a third contribution from the dust
emission at t,
![]() attenuated by the same factor.
These two contributions are summed over the whole cloud.
The arguments of the exponentials are always negative.
attenuated by the same factor.
These two contributions are summed over the whole cloud.
The arguments of the exponentials are always negative.
The mean intensity over line profile is computed from Eqs. (2)
and (3) and
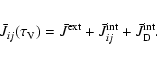
Let us consider an external radiation field that is isotropic on
each side of the cloud
![]() (although possibly different on each side)
plus a contribution perpendicular to the cloud. Such a radiation field keeps the azimutal
symmetry, while allowing for a point source (typically a close-by star) on
the axis. We have
(although possibly different on each side)
plus a contribution perpendicular to the cloud. Such a radiation field keeps the azimutal
symmetry, while allowing for a point source (typically a close-by star) on
the axis. We have
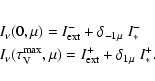
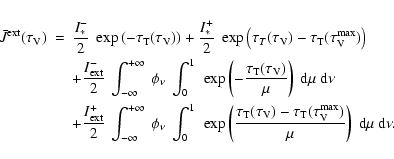
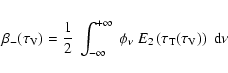
We introduce a step function
![]() such that
such that
![]() if
if
![]() and
and
![]() if
if
![]() .
With this definition, we can use a single function inside
the exponential term, change the sign of the integration over
.
With this definition, we can use a single function inside
the exponential term, change the sign of the integration over ![]() for
negative
for
negative ![]() ,
and write a single sum over t to get
,
and write a single sum over t to get
![\begin{eqnarray*}J_{\rm D}^{\rm int}(\tau_{\rm V})\!=\! \frac{1}{2} \int_{0}^{\t...
...\rm V})}{\mu} \right)~
\frac{{\rm d}\mu}{\mu} \right]~ {\rm d}t.
\end{eqnarray*}](/articles/aa/full/2008/25/aa09440-08/img109.gif)
Using a similar approach, we find
These two kernel functions include all the necessary information
on all radiative processes within the cloud.
They are similar to, but different from, the functions L1 and K1 introduced by Mihalas (1978) in chapter 11, which provides the basis for this discussion. For a given
![]() ,
they are functions of position t and the unknown populations
xi through the contribution of
,
they are functions of position t and the unknown populations
xi through the contribution of
![]() to
to
![]() .
.
From Eqs. (12), (14), and (16) we see that
![]() may be written as
may be written as
In the following, we focus on the effect of computing
![]() using the exact expression of Eq. (14)
and then compare our results to PS05.
using the exact expression of Eq. (14)
and then compare our results to PS05.
We first need to compute L1 and K1 explicitly. This requires a choice of line profile, and in the rest of this paper we use a Gaussian profile.
We need an explicit expression of the line optical depth
![]() .
From
Eqs. (9) and (4) we get
.
From
Eqs. (9) and (4) we get
![\begin{eqnarray*}\tau_{\rm L}(\tau_{\rm V}) = \frac{E_{ij}~ c}{\nu_{\rm c}~ \sqr...
...2}~ \left( \frac{c}{v_{\rm T}(t)} \right)^{2} \right]~ {\rm d}t.
\end{eqnarray*}](/articles/aa/full/2008/25/aa09440-08/img128.gif)
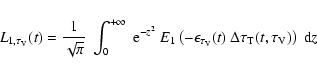
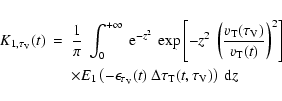
![\begin{eqnarray*}\Delta\tau_{\rm T}(t,\tau_{\rm V}) &=&
\tau_{\rm D}(t)-\tau_{\r...
...(\tau_{\rm V})}{v_{\rm T}(t')}
\right)^{2} \right]~ {\rm d}t'.
\end{eqnarray*}](/articles/aa/full/2008/25/aa09440-08/img132.gif)
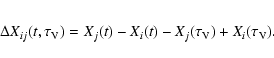
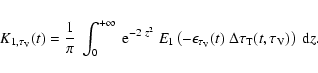
Using how K1 decreases as
![]() increases,
we may evaluate the integration over t in Eq. (17)
using for all functions of t their value at
increases,
we may evaluate the integration over t in Eq. (17)
using for all functions of t their value at
![]() .
First of all, the total optical depth
.
First of all, the total optical depth
![]() between tand
between tand
![]() becomes
becomes
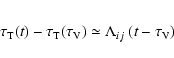
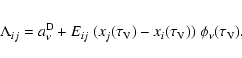
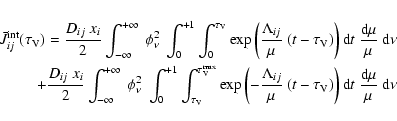
![\begin{eqnarray*}\bar{J}_{ij}^{\rm int}(\tau_{\rm V}) = \frac{D_{ij}~ x_{i}}{2}
...
...}^{\rm max}-\tau_{\rm V})\right)\right]~ {\rm d}\mu~ {\rm d}\nu.
\end{eqnarray*}](/articles/aa/full/2008/25/aa09440-08/img148.gif)
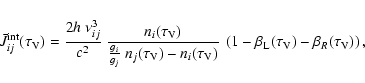
PS05 (Eqs. (3) and (4)) use
However, in the following sections, we use that full expression, using only
the approximate expression of
![]() of Eq. (20)
to simplify the computation of L1. The integration over L1itself is performed using a trapezoidal rule, except in the vicinity of
of Eq. (20)
to simplify the computation of L1. The integration over L1itself is performed using a trapezoidal rule, except in the vicinity of
![]() where L1 has a logarithmic divergence. There we
use an analytic integration of an expansion for the short argument.
where L1 has a logarithmic divergence. There we
use an analytic integration of an expansion for the short argument.
Line profiles can be easily computed from a knowledge of the structure of the cloud - as computed by the code - after the whole iteration has converged. The process is two-stepped: first compute the optical depth at a specific frequency from the ``far'' side of the slab along a ray up to the front. This can be done with Eqs. (8) and (9). Then the formal solution to the transfer equation is computed by using a simple trapezoidal rule that includes three contributions: attenuated radiation from the background (which may reduce to the CMB, but may also include some illuminating source), emission from the dust along the whole path, and emission from the molecules themselves.
The intensity in the line is the contribution from that
single source, integrated over frequency. It is important
to note that potential emission from matter (mainly dust
behind the zone in the cloud where the line forms) is
screened by absorption in the line (followed either by collisional
deexcitation or emission in ![]() steradian) and will
thus not contribute to the underlying background. Therefore, it is
not always possible to compute an integrated line intensity
from observations by simply removing a base line
extending beyond the line. One must have at least a
fair knowledge of the continuum emissivity to compute
the full line emissivity.
steradian) and will
thus not contribute to the underlying background. Therefore, it is
not always possible to compute an integrated line intensity
from observations by simply removing a base line
extending beyond the line. One must have at least a
fair knowledge of the continuum emissivity to compute
the full line emissivity.
This effect can lead to underestimating the line intensity by at least a factor of two for the most intense lines of H_2O. Figure 2 shows the contributions to the total emissivity of the 212 to 101 line in the model of Sect. 5.1 of dust (upper panel) and molecules (lower panel). The dust contribution is high in a tiny slab at the cloud edge where the dust is warm. Deeper into the cloud, its emissivity is lower but remains non vanishing. However, those photons are blocked at line centre (where, in this case, the line optical depth is 1.13) as can be seen from the black area for frequencies close to line centre (up to about two Doppler width). Line emissivity is high on the front side of that high optical depth zone. The decreasing emissivity in the wing is partially offset by a longer optical path, leading to the wing features seen in Fig. 3.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{aa09440-08f2.eps} %
\end{figure}](/articles/aa/full/2008/25/aa09440-08/Timg158.gif) |
Figure 2: Local emissivity of the 202 to 111 transition of H_2O as a function of position in the line (in units of Doppler width) and location on the slab. Upper panel, dust contribution, lower panel line contribution. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.7cm,clip]{figures/9440fig4.ps}\end{figure}](/articles/aa/full/2008/25/aa09440-08/Timg159.gif) |
Figure 3:
H_2O
|
| Open with DEXTER | |
It can be seen that the continuum level is lower under the line than far into the wings, so that a simple linear baseline drawn from the observed continuum misses half of the line signal. Only the strong lines with great optical depth are subject to this bias. However, these are the most likely detectable lines by forthcoming facilities such as the Herschel HIFI instrument. This is shown quantitatively in Fig. 4.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{figures/9440fig5.ps}\end{figure}](/articles/aa/full/2008/25/aa09440-08/Timg160.gif) |
Figure 4: Ratio of real to apparent line emissivity of the lowest lying lines of H_2O as a function of line frequency for model PDR-c. See Sect. 4.1 for details. |
| Open with DEXTER | |
It is customary to compute the cooling contribution of any species by a sum of the energy released by all radiative transitions from an upper level i to a lower level j. However, this approximation is correct only in the limit where excitation is dominated by collisions. This is not the case as soon as the lines become thick, and is particularly erroneous if radiative pumping by infrared dust emission leads to significant excitation. A simple sum would include in the cooling the energy at a given position brought there by a photon originating from somewhere else in the cloud, which never had a chance to release its energy in a kinetic energy form.
The only way to accurately take into account the net energy balance
of the gas is to consider the gains and losses directly through
collisions. This can be illustrated by the example of a two-level atom.
Consider the balance including induced transitions, but
without chemical formation and destruction terms:
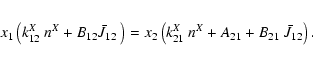
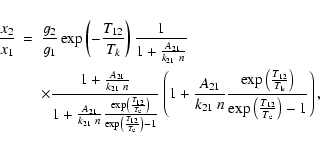
For transitions well below that critical density, the correction factor
(second line of the above expression) simplifies to,
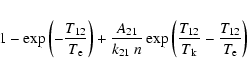
In this section, we compare the formalism proposed here to the results of PS05
on S140, using the same model parameters to the extent possible.
We use four different models, all based on the Meudon PDR code as described in
Le Petit et al. (2006), which differ only by the expression used for
![]() .
PDR-a does not take IR pumping into account,
PDR-b1, and PDR-b2 use Eq. (21) as used
in PS05, and PDR-c uses the formalism of Sect. 2.
PDR-b1 and PDR-b2 differ by the expression of the total dust optical depth used in
Eq. (21):
.
PDR-a does not take IR pumping into account,
PDR-b1, and PDR-b2 use Eq. (21) as used
in PS05, and PDR-c uses the formalism of Sect. 2.
PDR-b1 and PDR-b2 differ by the expression of the total dust optical depth used in
Eq. (21):
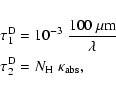
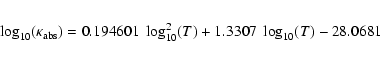
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{figures/9440fig6.ps}\end{figure}](/articles/aa/full/2008/25/aa09440-08/Timg179.gif) |
Figure 5: Ratio of dust opacities used in models PDR-b2 over PDR-b1. |
| Open with DEXTER | |
Table 1: Infrared pumping approximations.
That comparison allows us to understand the effect of IR pumping on physical processes computed in the model. The main input parameters are displayed in Table 2. The chemical network involves about 100 species linked by 1500 reactions. Gas phase elemental abundances are given in Table 3.
Table 2: Physical parameters used to model the PDR of the molecular cloud S140.
Table 3: Gas phase abundances relative to H nuclei.
Figure 6 shows the gas temperature profile resulting from thermal balance.
It ranges from ![]()
![]() at the edge of the cloud, closest to the star, and decreases
to
at the edge of the cloud, closest to the star, and decreases
to ![]()
![]() at cloud centre. The dust temperature ranges from
at cloud centre. The dust temperature ranges from ![]()
![]() to
to
![]()
![]() .
These temperatures are the same in all models, showing that, in
this case, the overall structure is not affected by cooling in infrared lines.
.
These temperatures are the same in all models, showing that, in
this case, the overall structure is not affected by cooling in infrared lines.
Our temperature range is within an order of magnitude of PS05. Roellig et al. (2007) have shown that the gas temperature is a very sensitive output of PDR codes. Thus, given the many differences in the computations, our agreement is satisfactory.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{figures/9440fig7.eps}\end{figure}](/articles/aa/full/2008/25/aa09440-08/Timg205.gif) |
Figure 6: Gas and dust temperature in our S140 models (log scale). The star is to the left of the figure. Higher dust temperature at the edge leads to infrared pumping deeper into the cloud. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.9cm,clip]{figures/9440fig8.eps}\end{figure}](/articles/aa/full/2008/25/aa09440-08/Timg206.gif) |
Figure 7: The H_2O abundance in our S140 models (PDR-abc). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{figures/9440fig9.eps}\end{figure}](/articles/aa/full/2008/25/aa09440-08/Timg207.gif) |
Figure 8: Ortho to para ratio of H_2O in our S140 models. The ratio is set by the balance of chemical formation and destruction alone, with formation proportional to the Boltzman factor. |
| Open with DEXTER | |
Figure 7 shows the H_2O abundance. At
low temperatures (<
![]() ), water is formed by a chain of ion-neutral reactions
initiated by cosmic ray ionization. Closer to the edges, water is destroyed by photodissociation.
PS05 give a maximum relative abundance of H_2O of
a few 10-6, quite close to our result.
), water is formed by a chain of ion-neutral reactions
initiated by cosmic ray ionization. Closer to the edges, water is destroyed by photodissociation.
PS05 give a maximum relative abundance of H_2O of
a few 10-6, quite close to our result.
A detailed balance of H_2O is computed using Eq. (19).
Collision rates are taken from Green et al. (1993) for collisions with He
and from Phillips et al. (1996) for collisions with H_2, as found on
http://basecol.obspm.fr/. The explicit inclusion of chemical formation and destruction
terms (D and Fi) leads to a set of equations that does not require the
use of the conservation condition
![]() .
Thus, conservation can be
checked a posteriori as a numerical test. We also computed explicitly the ortho
to para ratio (O/P) of H_2O as a function of position, by taking
all processes into account leading to the formation of one or the other form.
Here, the only term governing that ratio is the balance of chemistry through
a temperature-dependent formation branching ratio Fi. To our knowledge,
there are no reactive collision rates with H or H_2
that have been published and could be used. The resulting O/P ratio is displayed
in Fig. 8. The lowest para-level 000 and ortho-level 101account for most of H_2O and are almost not affected by
the different pumping schemes.
.
Thus, conservation can be
checked a posteriori as a numerical test. We also computed explicitly the ortho
to para ratio (O/P) of H_2O as a function of position, by taking
all processes into account leading to the formation of one or the other form.
Here, the only term governing that ratio is the balance of chemistry through
a temperature-dependent formation branching ratio Fi. To our knowledge,
there are no reactive collision rates with H or H_2
that have been published and could be used. The resulting O/P ratio is displayed
in Fig. 8. The lowest para-level 000 and ortho-level 101account for most of H_2O and are almost not affected by
the different pumping schemes.
This is not true for higher lying levels, as can be seen in Figs. 9 and 10 which show the populations of levels 202 (para) and 212 (ortho). Model PDR-c, with its higher pumping rate, populates upper levels more effectively. Neglecting infrared pumping completely (model PDR-a) may lead to huge differences and will not be considered further. The difference between models PDR-b1 and PDR-b2 shows the importance of using the best possible grain model, although this is still a very uncertain field. The same dust properties are used in models PDR-b2 and PDR-c, and it can be seen that the resulting populations are in fair agreement. However, exact computation of the pumping rate results in central abundances about five times higher, which translates in the line emissivities. The discrepancy increases with level energy as can be seen in Figs. 11.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{figures/9440fi10.eps}\end{figure}](/articles/aa/full/2008/25/aa09440-08/Timg210.gif) |
Figure 9: Relative abundance of para level 202 of H_2O for models PDR-abc (log scale). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{figures/9440fi11.eps}\end{figure}](/articles/aa/full/2008/25/aa09440-08/Timg211.gif) |
Figure 10: Relative abundance of ortho level 212 of H_2O for models PDR-abc (log scale). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{figures/9440fi12.eps}\end{figure}](/articles/aa/full/2008/25/aa09440-08/Timg212.gif) |
Figure 11: Relative abundance of ortho level 220 of H_2O for models PDR-ab (log scale). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{figures/9440fi13.eps}\end{figure}](/articles/aa/full/2008/25/aa09440-08/Timg213.gif) |
Figure 12: Relative level populations of the first six ortho levels of H_2O (log scale). Model PDR-c: exact infrared pumping computation. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{figures/9440fi14.eps}\end{figure}](/articles/aa/full/2008/25/aa09440-08/Timg214.gif) |
Figure 13: Relative level populations of the first five para levels of H_2O (log scale). Model PDR-c: exact infrared pumping computation. |
| Open with DEXTER | |
Figures 12 and 13 show the lowest ortho and para levels, respectively, for model PDR-c, and Table 4 gives the average mean intensities of the first few ortho and para transitions. Agreement is fair with PS05 for the strongest transitions.
We checked that CO is not affected by infrared pumping (variations are less than a few percent), as could be expected from its low permanent dipole moment. In the other hand CS, with a much higher dipole, may be a better target; however, transitions with the right energy are much too high to involve populated levels significantly, so that they are barely modified.
Table 4:
Mean intensities of the first rotational transitions of ortho and para H_2O (in
![]() )
and (last column) optical depth at line centre for model PDR-c.
)
and (last column) optical depth at line centre for model PDR-c.
Cooling is not affected much here, because the main coolants are insensitive to
infrared pumping, as could be guessed from the identical temperature profiles
(see Fig. 14). As explained in Sect. 4.2, cooling
by H_2O (which accounts for less than ![]() of the total) is reduced by
of the total) is reduced by
![]() when infrared pumping is taken into account.
when infrared pumping is taken into account.
The reduced water cooling comes from radiative energy transfer from the warm outer parts of the cloud to the central water-rich core through trapping of the infrared radiation. The higher populated excited levels transfer their energy by collisional deexcitation to the gas, which reduces the amount of kinetic energy removed by collisional excitation.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.9cm,clip]{figures/9440fi15.eps}\end{figure}](/articles/aa/full/2008/25/aa09440-08/Timg289.gif) |
Figure 14: Model PDR-c, cooling rates (log scale). Cooling in the molecular core comes mainly from CO and its isotopes. |
| Open with DEXTER | |
We compared the local cooling rate of water to the empirical proxi found in Pineau des Forêts et al. (1986). We found that, where this term matters (high abundance of H_2O), the formula is within a factor of two from our results, which is a tribute to the physical insight of those authors.
We have also simulated a denser cloud where H_2O
is expected to contribute more to cooling. We choose a symmetric
radiation field of ![]() on both sides, and a lower value for
on both sides, and a lower value for
![]() .
Figure 15 is similar to Fig. 14 and shows
that H_2O now contributes about
.
Figure 15 is similar to Fig. 14 and shows
that H_2O now contributes about ![]()
![]() to the total cooling
at cloud centre.
to the total cooling
at cloud centre.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.85cm,clip]{figures/9440fi16.eps}\end{figure}](/articles/aa/full/2008/25/aa09440-08/Timg292.gif) |
Figure 15:
Cooling rates (log scale) for a cloud illuminated by a field of |
| Open with DEXTER | |
This paper presents a careful analysis of the cooling radiation within a 1D interstellar cloud model containing gas and dust. The various contributions involved in the excitation of atomic and molecular species are discussed, including possible radiative pumping due to internal infrared sources such as dust emission. The main result is that infrared emission coming from hot grains at the edge of the cloud may penetrate deep inside the cloud, providing an efficient radiation source at a location where the cold grains can no longer emit infrared radiation. This procedure is necessary for abundant light species that have their fundamental transitions in the tera-Hertz region, such as H_2O.
We specifically address the emission of H_2O submillimetric transitions, but
the present formalism may be extended to other molecules such as HCN, HNC, floppy carbon
chains that present the appropriate level structure, and the like.
We applied our model to the S 140 PDR region, which may be taken as a benchmark case,
and compared our results with the approach of PS05. We recovered the approximations used by PS05 when we introduced the analytical approximation of the internal mean intensity due to dust, expressed in the escape formalism, and make the additional assumption:
![]() .
.
We have discussed the various modifications in the line intensities with various levels of approximations. Including the exact treatment of the infrared pumping consistently leads to an increase in the line emissivity values, and factors up to two orders of magnitude may result. As shown by PS05 inhomogeneities also impact the integrated line intensities by large factors. It is probable that both effects should be taken into account.
The cooling efficiency does not follow the line emissivities directly. Indeed, adding the infrared pumping contribution implies a higher excitation and also an additional heating contribution. The high excited levels may also be de-excited by collisions, in addition to radiative emission, which reduces the cooling efficiency. The present paper assumes a constant grain size distribution over the whole cloud. This assumption is a shortcoming of the present model and will be removed in subsequent studies.
Despite these inherent model simplifications, including the geometrical assumptions, we think that future observations with Herschel will benefit from this significant improvement in the theoretical treatment of line emissivities. Extension to arbitrary geometry of our semi-analytical computation is not possible since several key equation transformations depend on the 1D assumption. However, other simple geometries are probably tractable. For instance, a spherical cloud with a density profile that depends only on the radial coordinate, but with illumination coming both from an isotropic interstellar radiation field and a close-by star is a good candidate. We expect that the equations are cumbersome, have made no attempt to derive them.
This geometry would lead to smaller optical depths to some cloud boundaries from the bulk of the gas, thus probably further enhancing the line intensities. However, exposure to external ultraviolet photons would also be enhanced, reducing the abundance of molecular species. Thus the overall effect is not easy to anticipate.
Acknowledgements
Part of this work was supported by PCMI national programme of the CNRS. Manuel Gonzalez Garcia acknowledges a grant from the European Marie Curie program ``The Molecular Universe''.
Exponential integrals are defined by
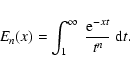
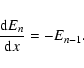
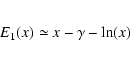
![\begin{figure}
\par\includegraphics[angle=-90,width=7.6cm,clip]{figures/9440fi17.ps}\end{figure}](/articles/aa/full/2008/25/aa09440-08/Timg299.gif) |
Figure A.1: Integral exponentials E1 and E2. |
| Open with DEXTER | |
The total escape probability
![]() from a slab of gas of total optical depth
at line centre
from a slab of gas of total optical depth
at line centre
![]() is
is
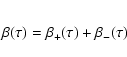
![\begin{figure}
\par\includegraphics[angle=-90,width=7.2cm,clip]{figures/9440fi18.ps}\end{figure}](/articles/aa/full/2008/25/aa09440-08/Timg306.gif) |
Figure A.2:
Escape probability |
| Open with DEXTER | |
The evolution of
![]() as a function of the total optical depth
as a function of the total optical depth
![]() and position into the cloud
and position into the cloud ![]() is displayed in Fig. A.2. Three plateaus
are visible in that plot: for optically thin lines (small (
is displayed in Fig. A.2. Three plateaus
are visible in that plot: for optically thin lines (small (
![]() ), the escape probability
), the escape probability ![]() is close to 1 everywhere. Then, as the line becomes thicker,
is close to 1 everywhere. Then, as the line becomes thicker, ![]() decreases, and two cases exists: either we are close to one edge, and the
escape probability is close to 0.5, or we are deep into the cloud, and
decreases, and two cases exists: either we are close to one edge, and the
escape probability is close to 0.5, or we are deep into the cloud, and ![]() is close to 0. Transitions from one to the other are smooth, but not trivial.
is close to 0. Transitions from one to the other are smooth, but not trivial.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.7cm,clip]{figures/9440fi19.ps}\end{figure}](/articles/aa/full/2008/25/aa09440-08/Timg308.gif) |
Figure A.3:
Escape probability from cloud centre
|
| Open with DEXTER | |
The escape probability from cloud centre as a function of the cloud size
is shown in Fig. A.3. Overplotted is also the function
![]() .
One can see that it is a fair approximation of
.
One can see that it is a fair approximation of
![]() .
However, this is only true at cloud centre! Closer to the edges for
thick lines,
.
However, this is only true at cloud centre! Closer to the edges for
thick lines, ![]() goes to 0.5 when the approximation goes to 1.
goes to 0.5 when the approximation goes to 1.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{figures/9440fi20.ps}\end{figure}](/articles/aa/full/2008/25/aa09440-08/Timg310.gif) |
Figure A.4:
Kernel functions |
| Open with DEXTER | |
Figure A.4 shows the kernel functions ![]() and
and ![]() defined by (see Sect. 3)
defined by (see Sect. 3)
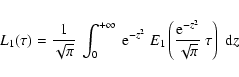
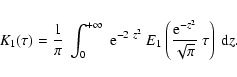
![\begin{eqnarray*}L_{1}(\tau) = \frac{1}{2}~ \left[ \frac{1}{2}-\gamma +\frac{ \t...
...sqrt{2\pi}}
- \ln\left( \frac{\tau}{\sqrt{\pi}}\right) \right]
\end{eqnarray*}](/articles/aa/full/2008/25/aa09440-08/img313.gif)
![\begin{eqnarray*}K_{1}(\tau) = \frac{1}{2\sqrt{2\pi}}
\left[ \frac{1}{4} -\gamma...
...\pi}}~\tau
-\ln\left( \frac{ \tau}{\sqrt{\pi}} \right) \right],
\end{eqnarray*}](/articles/aa/full/2008/25/aa09440-08/img314.gif)
The approximate value of
![]() used in PS05 may be
derived from Eqs. (14) and (15).
First, all quantities dependent on t are taken at their value at
used in PS05 may be
derived from Eqs. (14) and (15).
First, all quantities dependent on t are taken at their value at
![]() and taken out of the integrals.
The sum over t is split at
and taken out of the integrals.
The sum over t is split at
![]() ,
and integration over
,
and integration over ![]() and
t are swapped to give
and
t are swapped to give
We make the change of variable
![]() in the first integral and
in the first integral and
![]() in the second to get
in the second to get