A&A 484, 17-28 (2008)
DOI: 10.1051/0004-6361:20078819
C. Pinto1 - D. Galli2
1 - Dipartimento di Astronomia e Scienza dello Spazio,
Università di Firenze, Largo E. Fermi 5, 50125 Firenze, Italy
2 - INAF - Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
Received 9 October 2007 / Accepted 16 February 2008
Abstract
Context. The charged component of the insterstellar medium consists of atomic and molecular ions, electrons, and charged dust grains, coupled to the local Galactic magnetic field. Collisions between neutral particles (mostly atomic or molecular hydrogen) and charged species, and between the charged species themselves, affect the magnetohydrodynamical behaviour of the medium and the dissipation of electric currents.
Aims. The friction force due to elastic collisions between particles of different species in the multi-component interstellar plasma is a nonlinear function of the temperature of each species and the Mach number of the relative drift velocity. The aim of this paper is to provide an accurate and, as far as possible, complete set of momentum transfer rate coefficients for magnetohydrodynamical studies of the interstellar medium.
Methods. Momentum transfer rates are derived from available experimental data and theoretical calculations of cross sections within the classic approach developed by Boltzmann and Langevin for a wide range of values of the temperature and the drift velocity.
Results. Accurate numerical values for momentum transfer rates are obtained and fitted to simple analytical formulae expressing the dependence of the results on the gas temperature and the relative drift velocity. The often used polarization approximation is in satisfactory agreement with our results only for collisions between H2 and molecular ions (HCO+, H3+). For other kinds of collisions, the polarization approximation fails by large factors, and must be replaced by more accurate expressions.
Key words: atomic processes - molecular processes - plasmas - magnetohydrodynamics (MHD) - ISM: clouds - ISM: jets and outflows
The interstellar medium (ISM) is a multi-component plasma that consists mostly of hydrogen, helium, heavy ions, electrons and charged dust grains. The interaction between these components, and their coupling with the Galactic magnetic field, determine the dynamical properties of the ISM, control its evolution and the nature of the star formation process. In particular, the momentum exchange in collisions between neutral and charged particles is responsible for transfering the effects of electric and magnetic forces to the neutral component, allowing the magnetic field to drift out of weakly-ionized molecular clouds (Mestel & Spitzer 1956), damping the propagation of Alfvèn waves (Zweibel & Josafatsson 1983), and heating the gas by the frictional dissipation of turbulent energy (Scalo 1977).
In a companion paper (Pinto et al. 2008, hereafter Paper I), we have derived the equations governing the dynamics of a three-fluid system, reducing the set of equations to a momentum equation for the mean fluid and an evolution equation for the magnetic field, plus two relations for the drift velocities in terms of the mean fluid velocity and the magnetic field.
In this paper, we report on a detailed analysis of collisional rate coefficients involving the most abundant neutral and charged species in the ISM. The paper is organized as follows: in Sect. 2, we give the general expression for the friction force and the momentum transfer rate coefficient for elastic collisions, and we obtain an analytical solution for a cross section varying as a power of the relative velocity; in Sect. 3, we consider collisions with H2 of HCO+, H3+, H+, and electrons, using available theoretical and/or experimental determination of the collision cross section; similarly, in Sect. 4, we consider collisions with H of C+, H+, and electrons; in Sect. 5, we consider collisions of H+ and electrons with He; in Sects. 6 and 7 we consider collisions between charged dust grains and neutral particles, and between charged particles, respectively; in Sect. 8, we give analytical approximations for our numerical results; finally, in Sect. 9, we summarize our conclusions.
The general expression of the momentum acquired per unit time and unit volume (``friction force'') by a particle of species s with mass ms and initial velocity
![]() (``test particle'') through collisions with particles of species
(``test particle'') through collisions with particles of species ![]() with mass
with mass
![]() and initial velocity
and initial velocity
![]() (``field particles'') was given by Boltzmann (1896),
(``field particles'') was given by Boltzmann (1896),
| (2) |
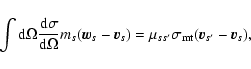 |
(3) |
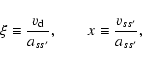 |
(9) |
| (10) |
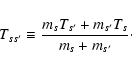 |
(12) |
| (13) |
For a cross section varying as a power-law of the relative velocity,
![]() ,
the integral in
Eq. (8) can be expressed in terms of the confluent
hypergeometric function M(a,b,c) (Abramowitz & Stegun 1965),
,
the integral in
Eq. (8) can be expressed in terms of the confluent
hypergeometric function M(a,b,c) (Abramowitz & Stegun 1965),
Three special cases of Eq. (14) are relevant for collisions between ISM particles:
(a) n=0, with
(b) n=1, with
![]() .
A cross section varying as the inverse of the relative velocity arises
for an induced dipole attraction, where the interaction potential is
proportional to the inverse fourth power of the distance (``polarization
potential''). Particles obeying this particular interaction law are
called ``Maxwell molecules'' (Maxwell 1860a,b), and the corresponding
collisional rate coefficient ``Langevin rate'' (see Appendix). In this
polarization approximation, the momentum transfer rate is independent
of both temperature and drift velocity.
.
A cross section varying as the inverse of the relative velocity arises
for an induced dipole attraction, where the interaction potential is
proportional to the inverse fourth power of the distance (``polarization
potential''). Particles obeying this particular interaction law are
called ``Maxwell molecules'' (Maxwell 1860a,b), and the corresponding
collisional rate coefficient ``Langevin rate'' (see Appendix). In this
polarization approximation, the momentum transfer rate is independent
of both temperature and drift velocity.
(c) n=4, corresponding to a (screened) Coulomb potential, with
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig1.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg80.gif) |
Figure 1:
The normalized function
|
| Open with DEXTER | |
Collisions between H2 molecules and charged particles determine the
rate of diffusion of the interstellar magnetic field through the
dominantly neutral gas of cold molecular clouds (see Paper I). In
applications to molecular clouds (e.g., Nakano 1984; Mouschovias 1996),
the collision rate coefficient
![]() has usually been estimated with the polarization approximation (see
Appendix) for collisions with molecular ions, and, also sometimes, for
collisions with electrons (see discussion in Mouschovias 1996). For
collisions between H2 and dust grains, the hard sphere model
(Sect. 2) has generally been assumed. We review below the validity of
these assumptions and compute accurate values for the collision rate
coefficients using available momentum transfer cross sections.
has usually been estimated with the polarization approximation (see
Appendix) for collisions with molecular ions, and, also sometimes, for
collisions with electrons (see discussion in Mouschovias 1996). For
collisions between H2 and dust grains, the hard sphere model
(Sect. 2) has generally been assumed. We review below the validity of
these assumptions and compute accurate values for the collision rate
coefficients using available momentum transfer cross sections.
Flower (2000) has calculated quantum-mechanically the cross section
between HCO+, a dominant ion in typical molecular cloud conditions,
and H2 molecules in their rotational ground states.
Figure 2 shows the cross section computed by Flower (2000)
compared with the Langevin cross section. As noticed by Flower (2000),
the Langevin value gives a good approximation to the quantal results.
The rate coefficient is, therefore, expected to depend very weakly on
temperature and drift velocity, as shown in Fig. 3![]() . Previous estimates of the molecular ion-H2rate coefficient based on the Langevin formula (see Fig. 3)
have ignored the weak dependence from temperature and drift velocity.
This neglect is, however, of little consequence for models of
magnetically-controlled cloud collapse as long as the temperature of
the infalling gas is in the range 10-20 K and the ion-neutral drift
velocity is a small fraction of the sound speed, as shown e.g., by
Mouschovias & Ciolek (1994).
. Previous estimates of the molecular ion-H2rate coefficient based on the Langevin formula (see Fig. 3)
have ignored the weak dependence from temperature and drift velocity.
This neglect is, however, of little consequence for models of
magnetically-controlled cloud collapse as long as the temperature of
the infalling gas is in the range 10-20 K and the ion-neutral drift
velocity is a small fraction of the sound speed, as shown e.g., by
Mouschovias & Ciolek (1994).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig2.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg82.gif) |
Figure 2:
The momentum transfer cross section for collisions HCO+-H2 as a function of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig3.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg83.gif) |
Figure 3:
The rate coefficient for HCO+-H2 collisions as a function
of the temperature T for
|
| Open with DEXTER | |
Figure 4 shows the momentum transfer cross section for
collisions of H3+ and H2, recommended by Phelps (1990), converted
to energies in the center-of-mass frame. At low energies (
![]() eV), the cross section is obtained from the results of the
mobility experiments of Ellis et al. (1976). At higher energies, the
behavior of the cross section is extrapolated from mobility data at
room temperature. As shown in the figure, the cross section is very
close to the Langevin value up to
eV), the cross section is obtained from the results of the
mobility experiments of Ellis et al. (1976). At higher energies, the
behavior of the cross section is extrapolated from mobility data at
room temperature. As shown in the figure, the cross section is very
close to the Langevin value up to
![]() eV, but
declines steeply (as
eV, but
declines steeply (as
![]() )
above
)
above
![]() eV. Since the cross section tabulated by Phelphs (1990) does not
extend to ion energies below 0.1 eV, we have extrapolated Phelps's
value to lower energies with the asymptotic formula
eV. Since the cross section tabulated by Phelphs (1990) does not
extend to ion energies below 0.1 eV, we have extrapolated Phelps's
value to lower energies with the asymptotic formula
![]() .
Figure 5 shows the corresponding rate coefficient obtained
integrating the cross section, according to Eq. (8) as a
function of the temperature and for various values of the drift
velocity. As in the case of HCO+, given the Langevin behavior of
the cross section at low energies, the dependence of the collisional
rate from temperature and drift velocity is very weak for temperatures
below
.
Figure 5 shows the corresponding rate coefficient obtained
integrating the cross section, according to Eq. (8) as a
function of the temperature and for various values of the drift
velocity. As in the case of HCO+, given the Langevin behavior of
the cross section at low energies, the dependence of the collisional
rate from temperature and drift velocity is very weak for temperatures
below
![]() K.
K.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig4.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg90.gif) |
Figure 4: Momentum transfer cross section for H3+-H2 collisions as a function of the energy in the center-of-mass system according to Phelps (1990) ( solid curve). The dotted line shows our extrapolation at low energies, whereas the dashed line shows the Langevin crosssection. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig5.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg91.gif) |
Figure 5:
The momentum transfer rate coefficient for H3+-H2 collisions as function of the temperature T computed with the cross section shown in Fig. 4 for
|
| Open with DEXTER | |
Figure 6 shows the momentum transfer cross section for
H+-H2 collisions computed by Krstic & Schultz (1999a,c) in the
energy range
![]() (fully-quantal
calculation), by Bachmann & Reiter (1995) in the energy range
(fully-quantal
calculation), by Bachmann & Reiter (1995) in the energy range
![]() (classical calculation)
and the cross section recommended by Phelps (1990) in the energy range
(classical calculation)
and the cross section recommended by Phelps (1990) in the energy range
![]() (obtained interpolating
results from ion mobility experiments for
(obtained interpolating
results from ion mobility experiments for
![]() eV and
theoretical cross sections above 330 eV). As shown in
Fig. 6, the quantal results depart significantly from the
Langevin value at high energies (
eV and
theoretical cross sections above 330 eV). As shown in
Fig. 6, the quantal results depart significantly from the
Langevin value at high energies (
![]() eV), and differ
substancially from the results extrapolated from ion mobility
experiments in the same energy range. Here we adopt the cross section
computed by Krstic & Schultz (1999a,c), extrapolated to energies below
0.1 eV with the asymptotic formula
eV), and differ
substancially from the results extrapolated from ion mobility
experiments in the same energy range. Here we adopt the cross section
computed by Krstic & Schultz (1999a,c), extrapolated to energies below
0.1 eV with the asymptotic formula
![]() .
We show in Fig. 7
the corresponding rate coefficient as a function of the temperature and
the drift velocity. Again, the rate coefficient depends very weakly on
these two quantities for temperatures below
.
We show in Fig. 7
the corresponding rate coefficient as a function of the temperature and
the drift velocity. Again, the rate coefficient depends very weakly on
these two quantities for temperatures below
![]() K.
K.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig6.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg98.gif) |
Figure 6:
The momentum transfer cross section for H+-H2collisions as a function of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig7.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg99.gif) |
Figure 7:
The collision rate coefficient for H+-H2 collisions as a function of the temperature, computed with the momentum transfer cross section of Krstic & Schultz (1999a,c) for
|
| Open with DEXTER | |
The elastic scattering of electrons by H2 has been the subject of
much theoretical and experimental work of the past decades. In
general, it is well established that the momentum transfer cross
section for electron-molecule scattering deviates significantly from
the classical Langevin rate at low energies (below ![]() 1 eV), owing
to the effect of ``electron exchange'', i.e., the exchange of the
incoming electron with one orbital electron in the neutral species (see
e.g., Massey & Ridley 1956; Morrison & Lane 1975). The existence of
this effect has been confirmed experimentally by Ferch et al. (1980) in
the energy range 0.02-2 eV. The net result is a reduction of the
momentum transfer cross section, which compensates the polarization
(Langevin) contribution in such a way that the resulting cross section
is roughly constant at low-collision energies.
1 eV), owing
to the effect of ``electron exchange'', i.e., the exchange of the
incoming electron with one orbital electron in the neutral species (see
e.g., Massey & Ridley 1956; Morrison & Lane 1975). The existence of
this effect has been confirmed experimentally by Ferch et al. (1980) in
the energy range 0.02-2 eV. The net result is a reduction of the
momentum transfer cross section, which compensates the polarization
(Langevin) contribution in such a way that the resulting cross section
is roughly constant at low-collision energies.
We have assembled a compilation of the available measurements of the
e-H2 momentum transfer cross section, for collision energies
ranging from 10-3 eV up to 200 eV. A detailed summary of the
most recent experimental results is given by Brunger & Buckman (2002).
The results are shown in Fig. 8, compared with the
theoretical calculations of Henry & Lane (1969) and the Langevin
value. Clearly, the semi-classical Langevin formula provides a poor
approximation to the actual cross section, especially at energies below
![]() 1 eV, where the effects of ``electron exchange'' are dominant.
The agreement between laboratory measurements and theoretical values of
the scattering cross sections appear to be satisfactory, with the
possible exception of the region of very low electron energies, where
the possible existence of a Ramsauer-Townsend minimum in the momentum
transfer cross section is not completely excluded (Ramanan &
Freeman 1991). The momentum transfer collision rate calculated with
the cross section indicated by the solid line in Fig. 8 is
shown in Fig. 9. At temperatures typical of interstellar
clouds,
1 eV, where the effects of ``electron exchange'' are dominant.
The agreement between laboratory measurements and theoretical values of
the scattering cross sections appear to be satisfactory, with the
possible exception of the region of very low electron energies, where
the possible existence of a Ramsauer-Townsend minimum in the momentum
transfer cross section is not completely excluded (Ramanan &
Freeman 1991). The momentum transfer collision rate calculated with
the cross section indicated by the solid line in Fig. 8 is
shown in Fig. 9. At temperatures typical of interstellar
clouds,
![]() K, the Langevin formula overestimates the actual
value of the momentum transfer rate by about two orders of magnitude.
K, the Langevin formula overestimates the actual
value of the momentum transfer rate by about two orders of magnitude.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig8.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg101.gif) |
Figure 8: The momentum transfer cross section for e-H2 collisions as a function of the electron kinetic energy. Experimental values: England et al. (1988) ( empty triangles), Schmidt et al. (1994) ( empty squares), Shyn & Sharp (1981) ( empty circles), Nishimura et al. (1985) ( filled triangles), Khakoo & Trajmar (1986) ( filled squares), Brunger et al. (1990, 1991) ( filled circles). The dashed and dotted curves show the Langevin cross section and the quantum-mechanical theoretical results of Henry & Lane (1969), respectively. The solid curve shows the cross section adopted in this work. |
| Open with DEXTER | |
The momentum transfer cross section for collisions of C+ ions with H atoms was computed by Flower & Pineau-des-Forêts (1995)
at several values of the collision energy, ranging from
![]() eV to
eV to
![]() eV with the
adiabatic potential of Green et al. (1972) (see Fig. 10).
Figure 11 shows the corresponding rate coefficient computed by
integrating numerically our interpolation of the results of Flower & Pineau-des-Forêts (1995).
eV with the
adiabatic potential of Green et al. (1972) (see Fig. 10).
Figure 11 shows the corresponding rate coefficient computed by
integrating numerically our interpolation of the results of Flower & Pineau-des-Forêts (1995).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig9.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg103.gif) |
Figure 9:
The momentum transfer rate coefficient for e-H2collisions computed with the cross section shown in Fig. 8 as a
function of the temperature T for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig10.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg104.gif) |
Figure 10: The momentum transfer cross section for collisions C+-H computed by Flower & Pineau-des-Fôrets (1995) as a function of the collision energy in the center-of-mass frame (original data, triangles; our interpolation, solid curve). The dashed curve shows the Langevin cross section. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig11.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg105.gif) |
Figure 11:
The collision rate coefficient for collisions C+-H as a
function of the temperature for
|
| Open with DEXTER | |
Being the simplest ion-neutral collision process, the scattering of
H+ by H atoms has been the subject of a large number of theoretical
investigations, from the semiclassical calculations of Dalgarno &
Yadav (1953) to the accurate quantum mechanical calculations of
Krstic & Schultz (1999a,c) and Glassgold et al. (2005,
hereafter GKS). The latter paper, reporting a determination of the
momentum transfer cross section over a range from 10-10 eV to
102 eV (partially shown in Fig. 12), represents the definitive
reference on this elastic process. The only experimental determination
of the H-H+ momentum transfer cross section was obtained by Brennan
& Morrow (1971) at
![]() eV by observing the velocity
and attenuation of compressional Alfven waves propagating in a
partially-ionized hydrogen plasma. The measured value,
eV by observing the velocity
and attenuation of compressional Alfven waves propagating in a
partially-ionized hydrogen plasma. The measured value,
![]() cm2, is in good agreement with
the quantum mechanical results (see Fig. 12). Previous
estimates of the momentum transfer rate coefficient (Geiss &
Bürgi 1986) were based on measurements and calculations of the charge
exchange cross section
cm2, is in good agreement with
the quantum mechanical results (see Fig. 12). Previous
estimates of the momentum transfer rate coefficient (Geiss &
Bürgi 1986) were based on measurements and calculations of the charge
exchange cross section
![]() for the reaction
for the reaction
![]() complemented at low energies with
the polarization cross section computed with the Langevin formula
Eq. (A.4). Since the charge transfer process proceeds with
little momentum transfer between the interacting particles,
Eq. (4) with
complemented at low energies with
the polarization cross section computed with the Langevin formula
Eq. (A.4). Since the charge transfer process proceeds with
little momentum transfer between the interacting particles,
Eq. (4) with
![]() gives
gives
![]() (Dalgarno 1958; Banks & Holzer 1968). As shown by
Fig. 12, a combination of the polarization cross section and
twice the value of the charge exchange cross section roughly reproduces
the accurate results of GKS. However, the momentum transfer rate estimated by Geiss & Bürgi (1986) with this approximation for temperatures between 103 K and
(Dalgarno 1958; Banks & Holzer 1968). As shown by
Fig. 12, a combination of the polarization cross section and
twice the value of the charge exchange cross section roughly reproduces
the accurate results of GKS. However, the momentum transfer rate estimated by Geiss & Bürgi (1986) with this approximation for temperatures between 103 K and
![]() K is about 50% higher than the rate obtained by a numerical integration of the momentum transfer cross section of GKS, shown in Fig. 13 for different values of the drift velocity.
K is about 50% higher than the rate obtained by a numerical integration of the momentum transfer cross section of GKS, shown in Fig. 13 for different values of the drift velocity.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig12.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg112.gif) |
Figure 12:
The momentum transfer cross section for collisions H+-H computed by GKS
as a function of the collision energy in the center-of-mass frame (
solid curve), compared to the Langevin cross section ( dashed
curve). The empty circle is the measurement by Brennan &
Morrow (1971) at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig13.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg113.gif) |
Figure 13:
The collision rate coefficient for collisions H+-H as a function of the temperature for
|
| Open with DEXTER | |
The momentum transfer cross section for e-H collisions has been
computed by Dalgarno, et al. (1999) with the quantal formula of
Dalgarno & Griffing (1958) and the phase shifts of Rudge (1975) and Das & Rudge (1976) at
![]() eV, and by van Wyngaarden & Walters (1986) in the energy range 100-300 eV. Laboratory measurements of the e-H momentum transfer cross sections have been performed by
Williams (1975a,b); Callaway & Williams (1975); Shyn & Cho (1989); Shyn & Grafe (1992) (for a detailed review of the experimental
methods and results, see Bederson & Kieffer 1971; Trajmar & Kanik 1995). Theoretical and experimental results are shown in Fig. 14. The dependence of the cross section on collision
energy is clearly non-Langevin: at low energies the cross section is
approximately constant,
eV, and by van Wyngaarden & Walters (1986) in the energy range 100-300 eV. Laboratory measurements of the e-H momentum transfer cross sections have been performed by
Williams (1975a,b); Callaway & Williams (1975); Shyn & Cho (1989); Shyn & Grafe (1992) (for a detailed review of the experimental
methods and results, see Bederson & Kieffer 1971; Trajmar & Kanik 1995). Theoretical and experimental results are shown in Fig. 14. The dependence of the cross section on collision
energy is clearly non-Langevin: at low energies the cross section is
approximately constant,
![]() cm-2,
whereas at high energies, it decreases with energy as
cm-2,
whereas at high energies, it decreases with energy as
![]() .
As a result, the momentum transfer rate, shown in Fig. 15, is lower by about one order of magnitude than the Langevin value at
.
As a result, the momentum transfer rate, shown in Fig. 15, is lower by about one order of magnitude than the Langevin value at
![]() K, and larger by
K, and larger by
![]() at
at
![]() K, with a weak dependence on the relative drift velocity.
K, with a weak dependence on the relative drift velocity.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig14.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg119.gif) |
Figure 14: Momentum transfer cross section for e-H collisions. Experimental values: Shyn & Cho (1989) ( filled circles); Williams (1975a,b) ( filled triangles); Shyn & Grafe (1992) ( filled squares); Callaway & Williams (1975) ( empty circles). The solid curve is the theoretical calculation of Dalgarno et al. (1999). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig15.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg120.gif) |
Figure 15:
Collision rate coefficient for e-H collisions as a function of temperature, for
|
| Open with DEXTER | |
With the exception of collisions with H+ or electrons, to our knowledge,
there are no experimental or theoretical data available for elastic
collisions between He atoms and charged species. An estimate based on
the Langevin approximation (see Appendix), gives
Collisions with He introduce a small correction to the expression of the friction coefficient
![]() defined by Eq. (7). For a neutral component made of H2 and He, Eq. (20) gives
defined by Eq. (7). For a neutral component made of H2 and He, Eq. (20) gives
| (21) |
![\begin{displaymath}c_i=1+\left[\frac{(m_i+m_{{\rm H}_2})m_{\rm He}p_{\rm He}}
{(...
...ight]^{1/2} \left(\frac{n_{\rm He}}{n_{{\rm H}_2}}\right)\cdot
\end{displaymath}](/articles/aa/full/2008/22/aa8819-07/img124.gif) |
(22) |
Figure 16 shows the momentum transfer cross section for
H+-He collisions computed by Krstic & Schultz (1999a,b) with a semi-classical treatment in the energy range
![]() .
The calculation has been recently extended up
to 104 eV by Krstic & Schultz (2006). The theoretical results are in
good agreement with the Langevin value below
.
The calculation has been recently extended up
to 104 eV by Krstic & Schultz (2006). The theoretical results are in
good agreement with the Langevin value below
![]() eV,
but at larger energies the Langevin formula overestimates the theoretical
results (by one order of magnitude at
eV,
but at larger energies the Langevin formula overestimates the theoretical
results (by one order of magnitude at
![]() eV). To our
knowledge, no experimental results are available for H+-He collisions.
Here we adopt the cross section computed by Krstic & Schultz (1999a,b),
extrapolated to energies below 0.1 eV with the Langevin value. The
resulting collisional rate coefficient is shown in Fig. 17 as a
function of the temperature and the drift velocity. As for H+-H2collisions, the rate coefficient depends very weakly on these two
quantities for temperatures below
eV). To our
knowledge, no experimental results are available for H+-He collisions.
Here we adopt the cross section computed by Krstic & Schultz (1999a,b),
extrapolated to energies below 0.1 eV with the Langevin value. The
resulting collisional rate coefficient is shown in Fig. 17 as a
function of the temperature and the drift velocity. As for H+-H2collisions, the rate coefficient depends very weakly on these two
quantities for temperatures below
![]() K and drift speeds
below
K and drift speeds
below ![]() km s-1. The rate coefficient
km s-1. The rate coefficient
![]() is about 0.9
is about 0.9
![]() ,
whereas Eq. (20) gives a factor
,
whereas Eq. (20) gives a factor ![]() 0.5.
0.5.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig16.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg135.gif) |
Figure 16: The momentum transfer cross section for collisions H+-He, according to the fully-quantal calculations of Krstic & Schultz (1999a,b), as a function of the collision energy in the center-of-mass frame ( solid curve), compared to the Langevin cross section ( dashed line). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig17.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg136.gif) |
Figure 17:
The collisional rate coefficient for H+-He collisions as a
function of the temperature for
|
| Open with DEXTER | |
Accurate values of the momentum transfer cross sections for e-He
collisions have been obtained from mobility experiments (Crompton et al. 1967, 1970; Milloy & Crompton 1977; Ramanan &
Freeman 1990). The agreement between different experimental evaluations
is excellent, at the level of 1-2%. As in the case of
![]() -H2 collisions discussed in Sect. 3, the actual
cross section deviates significantly from the classical Langevin value,
owing to the quantum exchange of the incoming electron with one orbital
electron of He. This is especially evident at low-collision energies,
where the momentum transfer cross section is approximately constant.
The rate coefficient
-H2 collisions discussed in Sect. 3, the actual
cross section deviates significantly from the classical Langevin value,
owing to the quantum exchange of the incoming electron with one orbital
electron of He. This is especially evident at low-collision energies,
where the momentum transfer cross section is approximately constant.
The rate coefficient
![]() is a factor
is a factor ![]() 0.6 of
0.6 of
![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig18.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg140.gif) |
Figure 18:
The momentum transfer cross section for e-He collisions as a
function of the electron kinetic energy. Experimental
values: Crompton et al. (1970) ( filled triangles); Milloy &
Crompton (1977) ( filled squares). The dotted curve shows
the experimental results of Ramanan & Freeman (1990), with uncertainty
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig19.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg141.gif) |
Figure 19:
The momentum transfer rate coefficient for e-He
collisions computed with the cross section shown in Fig. 18 as a
function of the temperature T for
|
| Open with DEXTER | |
For collisions between a spherical grain g of charge
![]() and radius
and radius ![]() with
a neutral particle n of polarizability
with
a neutral particle n of polarizability ![]() ,
the geometrical cross section
,
the geometrical cross section
![]() is larger that the polarization cross section (Eq. (A.4)) when
is larger that the polarization cross section (Eq. (A.4)) when
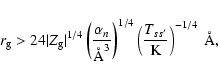 |
(23) |
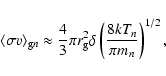 |
(25) |
Figure 20 shows the grain-neutral momentum transfer rate as a
function of the relative drift velocity according to
Eq. (24) with ![]() compared with the
approximations given by Draine & Salpeter (1979), Nakano (1984), and Mouschovias & Ciolek (1999). In this figure, the grain-neutral
momentum transfer rate is normalized to the expression given by
Mouschovias & Ciolek (1999) in the low-drift limit, and the drift
velocity is normalized to the mean thermal speed in the neutrals.
compared with the
approximations given by Draine & Salpeter (1979), Nakano (1984), and Mouschovias & Ciolek (1999). In this figure, the grain-neutral
momentum transfer rate is normalized to the expression given by
Mouschovias & Ciolek (1999) in the low-drift limit, and the drift
velocity is normalized to the mean thermal speed in the neutrals.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig20.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg153.gif) |
Figure 20: Momentum transfer rate coefficient for collisions grain-neutral as a function of the relative drift velocity, from Eq. (15) with n=0 ( solid curve), compared with the expressions from Draine & Salpeter (1979) ( dotted curve); Nakano (1984) ( dashed curve); and Mouschovias & Ciolek ( dot-dashed curve). |
| Open with DEXTER | |
Particles of charge
![]() can exchange momentum with particles of charge Zs e and density ns via long-range Coulomb interactions. In the standard Coulomb scattering theory (see e.g., Chapman & Cowling 1953), the momentum transfer cross section is given by
can exchange momentum with particles of charge Zs e and density ns via long-range Coulomb interactions. In the standard Coulomb scattering theory (see e.g., Chapman & Cowling 1953), the momentum transfer cross section is given by
![\begin{displaymath}\sigma_{\rm mt}=2\pi r_{\rm C}^2(v_{ss^\prime}) \ln\left[\fra...
...{\rm max}^2} {r_{\rm C}^2(v_{{\rm g}s})+r_{\rm min}^2}\right],
\end{displaymath}](/articles/aa/full/2008/22/aa8819-07/img155.gif) |
(26) |
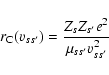 |
(27) |
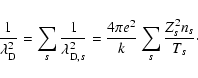 |
(28) |
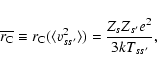 |
(29) |
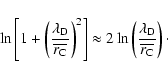 |
(31) |
In astrophysical applications, Eq. (32) has often been adopted
to compute the rate of momentum transfer between grain-ion and
grain-electron collisions (Draine & Salpeter 1979). However, a more
accurate calculation requires a modification of the Coulomb logarithm
to account for the finite size of the grains. Taking
![]() in Eq. (30), and assuming as before
in Eq. (30), and assuming as before
![]() ,
we obtain the modified Coulomb logarithm for
grain-ion (or grain-electron) collisions
,
we obtain the modified Coulomb logarithm for
grain-ion (or grain-electron) collisions
![\begin{displaymath}\ln \Lambda_{\rm gi} = \ln \left[ \frac{\lambda_{\rm D}}{(\overline{r_{\rm C}}^2+r_{\rm g}^2)^{1/2}}\right],
\end{displaymath}](/articles/aa/full/2008/22/aa8819-07/img180.gif) |
(35) |
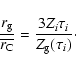 |
(36) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{8819fig21.ps}\end{figure}](/articles/aa/full/2008/22/aa8819-07/Timg189.gif) |
Figure 21:
Argument of the Coulomb logarithm
|
| Open with DEXTER | |
For a more general calculation of the Coulomb logarithm for grain-ion
and grain-electron where
![]() depends on the finite size of
the grain and the relative velocity of the collision, and, in addition,
the approximation
depends on the finite size of
the grain and the relative velocity of the collision, and, in addition,
the approximation
![]() is
removed, see Khrapak & Morfill (2004).
is
removed, see Khrapak & Morfill (2004).
In Table 1 we list analytical fitting formulae for the
momentum transfer rate coefficients computed numerically in
Sects. 3-5. For zero drift velocity, we have approximated the rates
(or their logarithm) with third-order polynomials of the logarithm of
the temperature. The accuracy of these fitting formulae is ![]() %. The dependence on the drift velocity has been approximated,
following GKS and Draine (1980) by power-laws (or modified power-laws)
fits of the numerical results in terms of the rms velocity, defined as
%. The dependence on the drift velocity has been approximated,
following GKS and Draine (1980) by power-laws (or modified power-laws)
fits of the numerical results in terms of the rms velocity, defined as
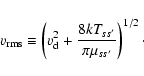 |
(37) |
Table 1:
Fitting formulae for momentum transfer coefficients as a function
of the gas temperature T (in K) and
![]() for
for
![]() .
.
Table 2:
Fitting formulae for momentum transfer coefficients as function of
![]() (in km s-1).
(in km s-1).
We have derived momentum transfer coefficients for collisions between ions, electrons, charged dust grains and atomic/molecular hydrogen from available experimental data and theoretical calculations, within the classic approach developed by Boltzmann (1896) & Langevin (1905). The numerical results have been approximated with simple analytical functions of the temperature and the drift velocity between the colliding species. The main conclusions of our study are the following:
Acknowledgements
We thank A. Glassgold for helpful discussions and for making available to us data on elastic cross sections. The research of D.G. is partially supported by the Marie Curie Research Training networks ``Constellation''.
The cross section for the interaction between an ion i of charge Zi e and a neutral molecule (or atom) n is determined by the attractive polarization potential
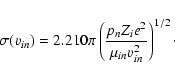 |
(A.2) |
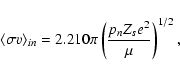 |
(A.3) |
The Langevin cross section for collisions of ions with neutrals, taking
into account Osterbrok's (1961) correction, therefore, results in