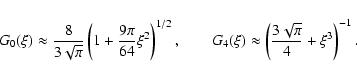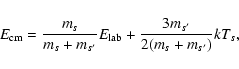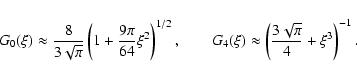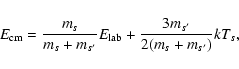- ... gas
![[*]](/icons/foot_motif.gif)
- Draine & Salpeter (1979) give the following accurate approximations for n=0 and
n=4:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...1973)
![[*]](/icons/foot_motif.gif)
- The momentum transfer cross section measured in laboratory experiments is usually given as function of the energy in the
laboratory frame (
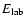 ). Before using Eq. (19),
). Before using Eq. (19),
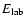 must be converted into the energy in the center-of-mass frame according to the formula
must be converted into the energy in the center-of-mass frame according to the formula
where s and 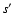 indicate the target and incident particles,
respectively.
indicate the target and incident particles,
respectively.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](/icons/foot_motif.gif)
- Our rate coefficient for zero drift velocity differs by
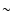 20% from the result by Flower (2000) who adopts an averaging
over the particles kinetic energy slightly different from our
Eq. (19).
20% from the result by Flower (2000) who adopts an averaging
over the particles kinetic energy slightly different from our
Eq. (19).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.