A&A 483, 623-632 (2008)
DOI: 10.1051/0004-6361:20054282
Moments of the latitudinal dependence of the sunspot cycle:
a new diagnostic of dynamo models
S. K. Solanki1 - T. Wenzler1,2 - D. Schmitt1
1 - Max-Planck-Institut für Sonnensystemforschung, 37191 Katlenburg-Lindau, Germany
2 -
Institute of Astronomy, ETH Zentrum, 8092 Zurich, Switzerland
Received 30 September 2005 / Accepted 6 March 2008
Abstract
Aims. The latitude-distribution of solar activity as represented by sunspots is studied.
Methods. We first determined the latitudinal distribution of a sunspot cycle by integrating the butterfly diagram at each latitude over the length of each cycle. We then formed the five lowest moments of the latitudinal distribution of all complete sunspot cycles since 1874 and compared these moments with each other.
Results. The three lowest moments correlate remarkably well with each other. For example, the mean latitude of the sunspots during a cycle and the latitude range are correlated at the 0.96 level. A clear asymmetry is seen between the two hemispheres, with the southern solar hemisphere showing consistently stronger and more positive correlations than the northern hemisphere. When applied to different simple dynamo models, the same analysis reveals significant differences between the models and demonstrates that such moments are a useful diagnostic in distinguishing between dynamo models. Remarkably, dynamos without a meridional flow provide results closer to those of the Sun's northern hemisphere, while a dynamo with a meridional flow produces fields more like those in the Sun's southern hemisphere. This may provide a clue to the cause of the well-known north-south asymmetry of solar activity.
Key words: Sun: activity - methods: data analysis - Sun: sunspots - Sun: magnetic fields
1 Introduction
The cyclic behaviour of solar magnetic activity and its cause, the Sun's
dynamo, are widely studied facets of the Sun (see the volumes edited by
Harvey 1992; Wilson 2002;
Ferriz-Mas & Núñez 2003; and the reviews by Ossendrijver 2003;
Charbonneau 2005). Nonetheless, the origin of the Sun's cyclic
behaviour is not fully understood. One aspect which complicates the study and
analysis of the solar cycle is that the activity cycle is not a periodic
phenomenon, but rather every cycle is different from all others, with its own
amplitude, length and shape. There have been numerous attempts to find
relations between the different parameters of a cycle in order to constrain
various dynamo models of magnetic field generation. Particularly well known
is the strong relation found by Waldmeier (1935) between the amplitude
of a cycle and the length of its rising phase (with weaker relations existing for the length of the descending phase and the whole cycle; cf. Hathaway et al. 2002). Relations have also been found between the
amplitude of a given cycle and the length of an earlier cycle
(e.g. Solanki et al. 2002). Differences in the amplitudes of even and
odd sunspot cycles (Wilson 1988; Mursula et al. 2001; Gnevyshev & Ohl 1948)
and the asymmetry of the rise to maximum and fall to minimum
(Hathaway et al. 1994) are other interesting properties of the sunspot
cycle. An overview of sunspot cycle properties has been given by
Usoskin & Mursula (2003), while the cycle properties deduced from
Zürich sunspot number (Waldmeier 1961) and group sunspot number
(Hoyt & Schatten 1998) records have been compared by
Hathaway et al. (2002).
All of these investigators adopted sunspots as proxies of solar activity,
which is reasonable, given that sunspot observations provide the longest
running direct records of solar activity (Waldmeier 1961; Wolf 1852).
They considered the cycle as a time series and in general neglected the
latitudinal distribution of solar activity (for exceptions see, e.g. Antalova & Gnevyshev 1983; Pelt et al. 2000).
Here we took the opposite approach and considered only the latitudinal
dependence of sunspot areas within a cycle. Sunspot latitudes have been
regularly and reliably measured for less than 2 centuries, so that this
restricts the length of time over which they can be analysed. Since 1874,
measurements of sunspot areas are also available, which have the advantage
that they are proportional to the total magnetic flux contained in the
sunspots (Solanki & Schmidt 1993). In order to be independent of
evolution effects within a cycle we integrated over the life time of a cycle
and thereby distilled the latitudinal dependence of the sunspot area. We then
computed the moments of each such distribution and searched for relations
between them.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{4282fig1}\end{figure}](/articles/aa/full/2008/20/aa4282-05/Timg11.gif) |
Figure 1:
Butterfly diagram from 1874 to 2005 based on data from the Royal
Greenwich Observatory up to 1976, from the former Soviet Union between 1977 and 1985
and from the Mount Wilson Solar Observatory from 1986 onward. The vertical dashed lines
mark the official minima of the sunspot cycle, the inclined solid lines our
estimates of the boundaries between individual cycles. Cycle numbers are
marked at the top of each cycle. |
| Open with DEXTER |
In addition to solar data we also investigated the output of a set of
simple dynamo models in order to judge the diagnostic capabilities of the
relations between moments of the Sun's activity cycle. The motivation
for this work was to develop a new diagnostic of the solar cycle and of models
of the generation of the Sun’s magnetic field. Therefore, the dynamo models
used here are not meant to give a realistic representation of the real Sun,
but rather to test the extent to which the diagnostic found in the observational
data can distinguish between dynamo models with different ingredients. As
causes of variability of the solar cycle we considered stochastic fluctuations
of the 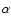 -effect (Ossendrijver et al. 1996), the interplay between
the dynamo at the base of the convection zone and magnetic fields inside it
(Schmitt et al. 1996), and, finally, a variation of the meridional circulation
(Charbonneau & Dikpati 2000).
-effect (Ossendrijver et al. 1996), the interplay between
the dynamo at the base of the convection zone and magnetic fields inside it
(Schmitt et al. 1996), and, finally, a variation of the meridional circulation
(Charbonneau & Dikpati 2000).
Some preliminary results, based on a simpler analysis and a different data
set, were presented by Solanki et al. (2000). A somewhat similar analysis
was also published by Li et al. (2003), who, however, did not use moments
and basically considered only peak sunspot areas, sunspot areas at high
latitudes (>35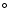 )
and cycle mean latitudes.
)
and cycle mean latitudes.
The paper is structured as follows. In Sect. 2 we describe the
solar data, in Sect. 3 the technique, while in Sect. 4
results obtained from the solar data are presented. In Sect. 5 we
present some simple dynamo calculations which are analysed in the same way as
the historical sunspot data. The results of the analysis of the models are
given in Sect. 6. Finally, we outline our conclusions in
Sect. 7.
2 Sunspot data
The analysed data are the sunspot positions and areas collected by the Royal
Greenwich Observatory (RGO) between 1874 and 1976 and by other observatories
since then. The exact data set used has been described by
Balmaceda et al. (2005). For the period 1977-1985, after the end of the
Greenwich observations up to the official minimum of cycle 21, it is based on
data from the former Soviet Union (called Russian data in the following) and
for the period 1986-2004 on the Mount Wilson Solar Observatory record, which
is composed of a collection of data from different sources. Data from Yunnan,
Catania and Rome were used to fill gaps in the above-mentioned data sets
wherever possible. One problem when combining, in particular, sunspot areas
from different sources is that sunspot areas measured at different
observatories often differ systematically (e.g. Fligge & Solanki 1997; Foster 2004; Hathaway, priv. comm.;
see http://science.nasa.gov/ssl/pad/solar/sunspots.htm).
Balmaceda et al. (2007,2005)
have therefore intercompared the various data
sets and normalized all sunspot areas to the RGO record in order to form a
homogenous data set.
3 Technique
In a first step of the analysis we found the boundary between consecutive
cycles. We considered the latitudes between 4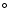 and 24
and 24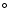 where
there are a sufficient number of sunspots. 2
where
there are a sufficient number of sunspots. 2 wide bins were made over
this range. For each set of these latitude bins we found the boundary between
two cycles by looking for the one year wide interval for which the
number of sunspots in that bin was smallest. In numerous cases the minimum
within a latitude bin was broad and flat. Then the boundary between cycles
was estimated by eye near the middle of this interval. Finally, a straight
line was fit to the minimum times determined for a hemisphere. This line was
subsequently employed as the boundary between cycles. In Fig. 1
we plot the sunspot butterfly diagram for the analysed period. The
identification of cycles and of the boundaries between them (the
inclined straight lines) are indicated. The data from the incompletely
covered cycles 11 and 23 were not analysed, but were used to determine the
boundaries of cycles 12 and 22, respectively. The results of the subsequent
analysis turned out to be unaffected by the exact positions of
these boundaries.
wide bins were made over
this range. For each set of these latitude bins we found the boundary between
two cycles by looking for the one year wide interval for which the
number of sunspots in that bin was smallest. In numerous cases the minimum
within a latitude bin was broad and flat. Then the boundary between cycles
was estimated by eye near the middle of this interval. Finally, a straight
line was fit to the minimum times determined for a hemisphere. This line was
subsequently employed as the boundary between cycles. In Fig. 1
we plot the sunspot butterfly diagram for the analysed period. The
identification of cycles and of the boundaries between them (the
inclined straight lines) are indicated. The data from the incompletely
covered cycles 11 and 23 were not analysed, but were used to determine the
boundaries of cycles 12 and 22, respectively. The results of the subsequent
analysis turned out to be unaffected by the exact positions of
these boundaries.
In a second step, once each sunspot group had been assigned to a given solar
cycle, we added together (over time) the areas of all the sunspots
belonging to that cycle and lying within a given latitude bin (bin width
0.1 ). In this way we obtained for each cycle a two-lobed profile as a
function of latitude, with one lobe each on the southern and the northern
hemisphere of the Sun. The resulting latitude profiles of cycles Nos. 12 and
19, the weakest and strongest of the analysed cycles, respectively, are
illustrated in Fig. 2. These are the data which we analysed
further. Note that in step 3 we considered each hemisphere individually
and compute the 0th to 4th moments, m0 to m4, defined as follows:
). In this way we obtained for each cycle a two-lobed profile as a
function of latitude, with one lobe each on the southern and the northern
hemisphere of the Sun. The resulting latitude profiles of cycles Nos. 12 and
19, the weakest and strongest of the analysed cycles, respectively, are
illustrated in Fig. 2. These are the data which we analysed
further. Note that in step 3 we considered each hemisphere individually
and compute the 0th to 4th moments, m0 to m4, defined as follows:
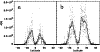 |
Figure 2:
Two examples of the latitude distribution of the cycle-integrated sunspot area.
a) cycle 12, b) cycle 19 (dots). The solid lines represent 5 running means.
running means. |
| Open with DEXTER |
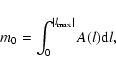 |
(1) |
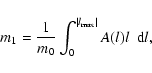 |
(2) |
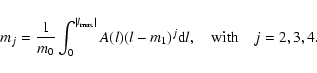 |
(3) |
Here l is the latitude and A(l) is the cycle-integrated sunspot
area as a function of latitude. For
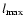 we have chosen
we have chosen
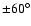 ,
since practically no sunspots have been known to occur at higher
latitudes. The integration was carried out using a five-point
Newton-Cotes integration formula. A small error may be introduced by choosing
the equator to be the boundary of the two wings of the butterfly, since a few
spot groups are known (from their polarity signatures) to lie on the ``wrong
side of the equator''. Spots within
,
since practically no sunspots have been known to occur at higher
latitudes. The integration was carried out using a five-point
Newton-Cotes integration formula. A small error may be introduced by choosing
the equator to be the boundary of the two wings of the butterfly, since a few
spot groups are known (from their polarity signatures) to lie on the ``wrong
side of the equator''. Spots within 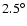 of the equator account for
less than 1.5% of the total area covered by sunspots. Since spots of the
opposite polarity form only a fraction of the spots close to the equator, we
estimated a relatively small error produced by the use of the equator to
demarcate the boundary between the hemispheres. Due to the lack of magnetic
polarity data we could not improve on this in a simple manner.
The moments are related to commonly used
statistical parameters as follows:
of the equator account for
less than 1.5% of the total area covered by sunspots. Since spots of the
opposite polarity form only a fraction of the spots close to the equator, we
estimated a relatively small error produced by the use of the equator to
demarcate the boundary between the hemispheres. Due to the lack of magnetic
polarity data we could not improve on this in a simple manner.
The moments are related to commonly used
statistical parameters as follows:
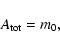 |
(4) |
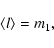 |
(5) |
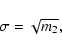 |
(6) |
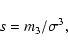 |
(7) |
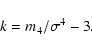 |
(8) |
Here
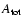 is the total solar surface area covered by
sunspots over the solar cycle and
is the total solar surface area covered by
sunspots over the solar cycle and
 corresponds to the mean
latitude at which sunspots are located during a given cycle. The moment m2represents the variance in latitude of the sunspot distribution, so that
corresponds to the mean
latitude at which sunspots are located during a given cycle. The moment m2represents the variance in latitude of the sunspot distribution, so that
 is the standard deviation, a measure of the width of the latitude
distribution of sunspots, s is the skewness, a measure of the asymmetry in
latitude of the cycle-integrated sunspot distribution. The skewness is zero
for a symmetric profile and positive if the profile is skewed more towards
the equator. The kurtosis k is another parameter describing the shape of a
distribution. As defined in Eq. (8) k is zero for a Gaussian
profile, positive for a sharper (more peaked) profile and negative for
a more box-like profile. It is important to consider s and k instead of
m3 and m4, since these higher order moments are intrinsically
correlated with m2. Dividing by
is the standard deviation, a measure of the width of the latitude
distribution of sunspots, s is the skewness, a measure of the asymmetry in
latitude of the cycle-integrated sunspot distribution. The skewness is zero
for a symmetric profile and positive if the profile is skewed more towards
the equator. The kurtosis k is another parameter describing the shape of a
distribution. As defined in Eq. (8) k is zero for a Gaussian
profile, positive for a sharper (more peaked) profile and negative for
a more box-like profile. It is important to consider s and k instead of
m3 and m4, since these higher order moments are intrinsically
correlated with m2. Dividing by 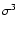 and
and 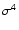 ,
respectively,
removes this artificial correlation, making
,
respectively,
removes this artificial correlation, making  ,
s and k a priori
independent of each other. In principle it is also possible to compute
moments of still higher order, but they are not so directly related as
m0-m4 to intuitively accessible quantities. In addition, the higher order
moments give increasing weight to large
,
s and k a priori
independent of each other. In principle it is also possible to compute
moments of still higher order, but they are not so directly related as
m0-m4 to intuitively accessible quantities. In addition, the higher order
moments give increasing weight to large
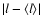 values, i.e.
to high latitudes and the equator (see Eq. (3)). There are few
sunspots at these latitudes and consequently the statistical uncertainties
increase with the order of the moment.
values, i.e.
to high latitudes and the equator (see Eq. (3)). There are few
sunspots at these latitudes and consequently the statistical uncertainties
increase with the order of the moment.
Finally, we compared the different moments of a given cycle with each other.
We did this individually for the two hemispheres, with the ith moment
relating to the northern/southern hemisphere being referred to as
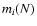 and mi(S), respectively. We also formed the average of the two:
and mi(S), respectively. We also formed the average of the two:
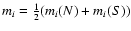 .
Similarly,
.
Similarly,
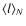 and
and
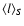 ,
,
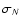 and
and 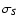 ,
etc. refer to the values obtained in
the northern and southern hemisphere, respectively, of the parameters
introduced in Eqs. (4)-(8).
,
etc. refer to the values obtained in
the northern and southern hemisphere, respectively, of the parameters
introduced in Eqs. (4)-(8).
When analysing the data there are two points that need to be considered
particularly carefully. The first is data gaps. The sunspots present on the
solar disk on days on which no measurements were carried out do not
contribute to the statistics. Two measured parameters of each sunspot enter
into our analysis, its latitude and its area. The error introduced into the
mean latitude, width of the latitude distribution, etc. (i.e. to m1 and
higher moments) due to missing data is a second order effect. E.g. if the
number of data gaps is not too large and reasonably evenly distributed over a
cycle, we expect the effect to be almost negligible, since each integral over
A(l) is normalized by dividing by m0. Hence data gaps increase the
random errors in the m1-m4 values, but do not introduce systematic errors
unless they are concentrated at the beginning or the end of a cycle. This
does preclude the use of incompletely sampled cycles (where, e.g., the
beginning or end is missing). The situation is very different for m0, into
which the actual numerical values of A(l) enter without normalization. Any
missing sunspot data leads to a corresponding decrease in m0. In order to
avoid such systematic errors it is necessary to interpolate the sunspot areas
across data gaps (but not the sunspot latitudes). We have chosen to carry out
a linear interpolation. The other moments m1-m4 are not affected by this
treatment.
The other potential pitfall is produced when data from different sources are
combined (Fligge & Solanki 1997; Balmaceda et al. 2007; Foster 2004). This has
been carefully taken into account by Balmaceda et al. (2007,2005) when
constructing the employed data set (see Sect. 2). Nevertheless,
in order to avoid the remaining uncertainty arising from the combination of
different data sets, we have also carried out the analysis for the Greenwich
data alone. The results in this case are rather similar to those
obtained from the complete data set (see Sect. 4).
4 Results based on observational data
In Fig. 3 we plot the various parameters defined by
Eqs. (4)-(8) against each other, for the northern
hemisphere (left), the southern hemisphere (middle) and the average over both
(right). Each dot represents the values for a given solar cycle. To save
space only a selection of all the possible plots of this type is shown (these
are in general combinations showing high correlations; see below).
![\begin{figure}
\par\includegraphics[width=15cm,clip]{4282fig3}\end{figure}](/articles/aa/full/2008/20/aa4282-05/Timg35.gif) |
Figure 3:
Relationships between parameters describing the latitude dependence
of the sunspot distribution. In the three columns we plot results obtained
for the northern hemisphere (left), the southern hemisphere (middle) and the
parameters averaged over both hemispheres (right). From top to bottom we plot
 vs.
vs.
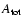 , ,
 vs.
vs.
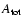 , ,
 vs. vs.
 ,
s vs. ,
s vs.  and k vs. s. Open circles:
cycle 12, filled circles: 13, open triangles: 14, filled triangles: 15, open
squares: 16, filled squares: 17, open diamonds: 18, filled diamonds: 19,
pluses: 20, crosses: 21, crossed squares: 22. The solid lines are least
squares fits. The dashed lines represent fits to cycles 12-20 alone (RGO data).
and k vs. s. Open circles:
cycle 12, filled circles: 13, open triangles: 14, filled triangles: 15, open
squares: 16, filled squares: 17, open diamonds: 18, filled diamonds: 19,
pluses: 20, crosses: 21, crossed squares: 22. The solid lines are least
squares fits. The dashed lines represent fits to cycles 12-20 alone (RGO data). |
| Open with DEXTER |
Figure 3 reveals the range of variation of the different
parameters. Thus, between cycles 12 and 22 the total hemispheric sunspot area varied
between
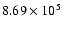 and
and
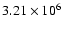 ,
with an average value of
,
with an average value of
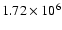 .
In contrast to this factor of 3.7 between the
.
In contrast to this factor of 3.7 between the
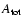 of different cycles,
of different cycles,
 and
and  varied by less
than a factor of 1.5. From Fig. 3 it is also clear that
varied by less
than a factor of 1.5. From Fig. 3 it is also clear that
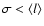 ,
which implies that the N and S sunspot distributions
are distinct, which is also visible from Fig. 2 (cf. Fig. 5). Interesting is that the skewness is almost always
positive, i.e. the profiles are skewed such that they peak closer to the
equator, with a tail towards higher latitudes (the only exception is the
southern part of cycle 14). In contrast, k>0 and k<0 values are equally
common, suggesting that compared to a Gaussian an almost equal number of
cycles is box-shaped as is triangular. The values of these parameters
averaged over all cycles are given in Table 1. The
``uncertainties'' listed in the table reflect the
,
which implies that the N and S sunspot distributions
are distinct, which is also visible from Fig. 2 (cf. Fig. 5). Interesting is that the skewness is almost always
positive, i.e. the profiles are skewed such that they peak closer to the
equator, with a tail towards higher latitudes (the only exception is the
southern part of cycle 14). In contrast, k>0 and k<0 values are equally
common, suggesting that compared to a Gaussian an almost equal number of
cycles is box-shaped as is triangular. The values of these parameters
averaged over all cycles are given in Table 1. The
``uncertainties'' listed in the table reflect the 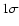 scatter from one
cycle to another.
scatter from one
cycle to another.
Table 1:
Mean values of parameters of the solar
cycles studied in this paper and their 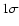 cycle to cycle scatter.
cycle to cycle scatter.
Table 2:
Correlation coefficients, 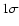 uncertainties of the correlation coefficients and false alarm probability for the combined
data set (1874-2004).
uncertainties of the correlation coefficients and false alarm probability for the combined
data set (1874-2004).
Our main interest lies in the correlations between the different parameters,
which can also be seen in Fig. 3. The linear correlation
coefficient, 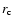 ,
its uncertainty,
,
its uncertainty, 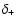 and
and 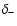
![[*]](/icons/foot_motif.gif) and the probability that this correlation is due to
chance (false alarm probability),
and the probability that this correlation is due to
chance (false alarm probability), 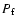 ,
are given in Table 2,
for all combinations of parameters, obtained from the combined data set described in
Sect. 2
,
are given in Table 2,
for all combinations of parameters, obtained from the combined data set described in
Sect. 2![[*]](/icons/foot_motif.gif) .
The comparisons between neighbouring moments are marked
by an X in the last column. The three lowest moments are correlated at a
remarkably high level. The false alarm probability is at or below 1% in all
cases involving just
.
The comparisons between neighbouring moments are marked
by an X in the last column. The three lowest moments are correlated at a
remarkably high level. The false alarm probability is at or below 1% in all
cases involving just
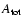 ,
,
 and
and  .
Hence, a
cycle with a large amplitude has sunspots on average at a higher latitude and
distributed over a wider range of latitudes. As
.
Hence, a
cycle with a large amplitude has sunspots on average at a higher latitude and
distributed over a wider range of latitudes. As
 shifts
poleward by 5
shifts
poleward by 5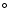 ,
,
 increases by 2
increases by 2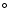 .
This means that the
area covered by sunspots at higher latitudes varies much more strongly from
one cycle to the next than the amplitude of the cycle as a whole, in
agreement with the results of Li et al. (2003).
.
This means that the
area covered by sunspots at higher latitudes varies much more strongly from
one cycle to the next than the amplitude of the cycle as a whole, in
agreement with the results of Li et al. (2003).
Correlations involving k and s are on the whole quite weak. Only a few
individual correlations between k and s and between s and  give
a false alarm probability significantly below 10% in Table 2.
give
a false alarm probability significantly below 10% in Table 2.
Another point that can be gleaned from Table 2 and from
Fig. 3 is that the southern and northern hemispheres behave
rather differently. Thus, the range covered by a given parameter differs,
with
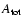 ,
,
 and
and  covering smaller ranges in
the south, while for skewness the situation is reversed. Southern
correlations are always positive (always >0.4 for the combined data set),
while the northern hemisphere gives rise to weak (not significant) negative
correlation coefficients involving s and k. In general, the correlations
are significantly stronger for the south. Only in 2 cases in
Table 2 does the northern hemisphere
exhibit a higher correlation, namely of
covering smaller ranges in
the south, while for skewness the situation is reversed. Southern
correlations are always positive (always >0.4 for the combined data set),
while the northern hemisphere gives rise to weak (not significant) negative
correlation coefficients involving s and k. In general, the correlations
are significantly stronger for the south. Only in 2 cases in
Table 2 does the northern hemisphere
exhibit a higher correlation, namely of  vs.
vs.
 and
for k vs. s. This can also be seen from Fig. 4 in which
differences between
and
for k vs. s. This can also be seen from Fig. 4 in which
differences between 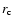 values for N and S are plotted versus the
values for N and S are plotted versus the
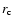 of the averaged moments (note that the symbols have a different meaning
than in Fig. 3; see the figure caption). Obviously, the difference
between high
of the averaged moments (note that the symbols have a different meaning
than in Fig. 3; see the figure caption). Obviously, the difference
between high 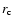 values is small, while for low
values is small, while for low 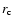 values the
difference is large.
values the
difference is large.
Finally, there is a tendency for a stronger correlation between neighbouring
moments. Thus, the correlation between m0 and m1, (i.e. between
 and
and
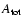 )
and between m1 and m2 (i.e. between
)
and between m1 and m2 (i.e. between
 and
and  )
is stronger than between m0 and
m2 (or
)
is stronger than between m0 and
m2 (or
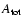 and
and  ). Similarly,
). Similarly,
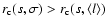
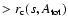 (averaged over both hemispheres). The
effect is weak, however, and not universal, since for the Greenwich data the
kurtosis k is best correlated with m0, at least for the south and when
averaged over both hemispheres. For the northern hemisphere
(averaged over both hemispheres). The
effect is weak, however, and not universal, since for the Greenwich data the
kurtosis k is best correlated with m0, at least for the south and when
averaged over both hemispheres. For the northern hemisphere
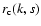 is by
far the highest. It should be recalled, however, that k correlates poorly
with the lower moments, with the probability of a false alarm reaching values
as high as 0.67 (see Table 2).
is by
far the highest. It should be recalled, however, that k correlates poorly
with the lower moments, with the probability of a false alarm reaching values
as high as 0.67 (see Table 2).
It is difficult to determine how the latitudinal shape of the sunspot
distribution over a solar cycle changes from cycle to cycle just from the
data (e.g. Fig. 2) due to the scatter of the data points from
one bin to another. This scatter can be reduced by choosing broader bins
(see Li et al. 2003, who took 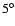 wide bins). An alternative is
to compute the running mean over the data points, as illustrated in
Fig. 2.
wide bins). An alternative is
to compute the running mean over the data points, as illustrated in
Fig. 2.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4282fig4}\end{figure}](/articles/aa/full/2008/20/aa4282-05/Timg58.gif) |
Figure 4:
Difference between correlation coefficients 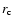 between ``moments'' of latitude distributions
of sunspots in the northern,
between ``moments'' of latitude distributions
of sunspots in the northern,
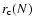 and the southern hemispheres,
and the southern hemispheres,
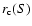 vs.
vs.
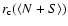 (top panel). In the middle and bottom
panels the difference between
(top panel). In the middle and bottom
panels the difference between
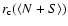 ,
and ,
and
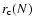 or
or
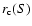 ,
respectively, are plotted. Open circles: ,
respectively, are plotted. Open circles:
 vs.
vs.
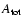 ,
filled circles: ,
filled circles:
 vs.
vs.
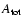 ,
open triangles: s vs. ,
open triangles: s vs.
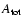 ,
filled triangles:
k vs. ,
filled triangles:
k vs.
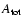 ,
open squares: ,
open squares:  vs.
vs.
 ,
filled squares:
s vs. ,
filled squares:
s vs.
 ,
open diamonds: k vs. ,
open diamonds: k vs.
 ,
filled diamonds:
s vs. ,
filled diamonds:
s vs.  ,
pluses: k vs. ,
pluses: k vs.  ,
crosses: k vs. s. ,
crosses: k vs. s. |
| Open with DEXTER |
In Fig. 5 we display the profiles smoothed by computing
5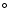 running means of each cycle. The profile shape varies considerably
from one cycle to the next. As in the case of the temporal profiles of
cycles, the latitudinal profiles show one, two or even more humps. Even at
the level of smoothing introduced to make Fig. 5 the shape of
the latitude profile still reflects sub-structure, which could be termed
``active latitudes''. It may well be related to the latitudes of higher
activity seen in 6-month time-averaged sunspot area latitude distributions by
Antalova & Gnevyshev (1983). A more detailed analysis would be needed to ascertain
the reality on any active latitudes, e.g.
running means of each cycle. The profile shape varies considerably
from one cycle to the next. As in the case of the temporal profiles of
cycles, the latitudinal profiles show one, two or even more humps. Even at
the level of smoothing introduced to make Fig. 5 the shape of
the latitude profile still reflects sub-structure, which could be termed
``active latitudes''. It may well be related to the latitudes of higher
activity seen in 6-month time-averaged sunspot area latitude distributions by
Antalova & Gnevyshev (1983). A more detailed analysis would be needed to ascertain
the reality on any active latitudes, e.g. 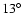 N, at which 5 cycles
display a peak. In particular, it must still be ascertained how robust such
peaks are to different amounts of averaging.
N, at which 5 cycles
display a peak. In particular, it must still be ascertained how robust such
peaks are to different amounts of averaging.
Figure 5 clearly shows that the low latitude part of the cycle
remains relatively unchanged from one cycle to another (the curves
representing the different cycles lie very close together), while the higher
latitude parts of the cycle exhibit a considerable scatter. This agrees well
with the result deduced from the moments: stronger cycles peak at higher
latitudes and are broader, with a (weak) tendency to be more strongly skewed
towards the equator, which also implies that the cycles will be more similar
near the equator than at higher latitudes. Hence, the correlations we find
between the moments suggest that changes at latitudes 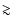 15
15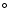 (
(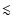
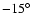 )
are well correlated with the bulk of the cycle. Also
evident from Fig. 5 is the difference in the behaviour of the 2 hemispheres. The northern hemisphere exhibits a larger scatter in amplitude
and width (cf. Fig. 3). There are also more cycles which show
anomalous behaviour immediately to the north of the equator
than to its south. Also plotted in
Fig. 5 is the latitudinal profile averaged over all cycles
(thick black curve). The N and S lobes of this profile are similar in
strength, but differ, e.g., in asymmetry, with the profile in the south being
more symmetric than that in the north.
)
are well correlated with the bulk of the cycle. Also
evident from Fig. 5 is the difference in the behaviour of the 2 hemispheres. The northern hemisphere exhibits a larger scatter in amplitude
and width (cf. Fig. 3). There are also more cycles which show
anomalous behaviour immediately to the north of the equator
than to its south. Also plotted in
Fig. 5 is the latitudinal profile averaged over all cycles
(thick black curve). The N and S lobes of this profile are similar in
strength, but differ, e.g., in asymmetry, with the profile in the south being
more symmetric than that in the north.
5 Dynamo models
In order to test whether the correlations presented in Sect. 4 can be
used as a new diagnostic of the solar dynamo, e.g., to distinguish between
different dynamo models, we have carried out a set of computations with
variants of a simple dynamo model. In order to simulate the irregularity of
the solar cycle we allowed for stochastic fluctuations of the 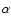 -effect
(models A, B and C), a random source term due to magnetic fields from a
turbulent convection zone dynamo (model D), and a variable meridional flow
(model E).
-effect
(models A, B and C), a random source term due to magnetic fields from a
turbulent convection zone dynamo (model D), and a variable meridional flow
(model E).
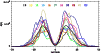 |
Figure 5:
Latitude distributions of the cycle-integrated sunspot area.
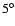 running means are plotted. Colour key is given at the top of the plot.
The thick black line represents the mean cycle distribution.
running means are plotted. Colour key is given at the top of the plot.
The thick black line represents the mean cycle distribution. |
| Open with DEXTER |
We did not aim at a completely realistic and detailed model of the solar cycle
and thus restricted ourselves to the thin shell dynamo of
Schmitt & Schüssler (1989) with prescribed radial dependence in the form
of a spherical wave 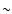
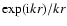 (Hoyng et al. 1994) such
that the axisymmetric magnetic field, described by the toroidal components of
the magnetic field, B, and the vector potential, A,
only depends on the
colatitude
(Hoyng et al. 1994) such
that the axisymmetric magnetic field, described by the toroidal components of
the magnetic field, B, and the vector potential, A,
only depends on the
colatitude 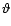 of the spherical shell and on time t. The
dimensionless
of the spherical shell and on time t. The
dimensionless
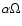 -dynamo equations are written as
-dynamo equations are written as
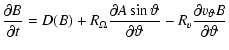 |
|
|
(9) |
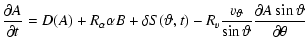 |
|
|
(10) |
with diffusion operator
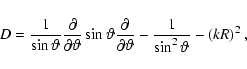 |
(11) |
Reynolds numbers of the 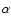 -effect, differential rotation and meridional flow
-effect, differential rotation and meridional flow
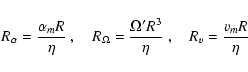 |
(12) |
and a stochastic source term
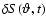 .
The
.
The 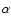 -effect
consists of a regular
-effect
consists of a regular 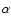 -effect and random fluctuations,
-effect and random fluctuations,
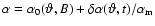 ,
for the
differential rotation we assumed a constant radial gradient
,
for the
differential rotation we assumed a constant radial gradient
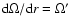 ,
and as part of the meridional circulation a flow in
latitudinal direction
,
and as part of the meridional circulation a flow in
latitudinal direction
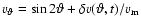 ,
again with regular and fluctuating components.
,
again with regular and fluctuating components.
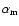 and
and 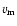 represent the maximum values of the regular parts of the
represent the maximum values of the regular parts of the
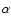 -effect and the meridional flow, respectively. The length scale
-effect and the meridional flow, respectively. The length scale
 was chosen as the radial position of the dynamo
layer at the bottom of the convection zone. We took the diffusion time,
was chosen as the radial position of the dynamo
layer at the bottom of the convection zone. We took the diffusion time,
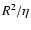 ,
as the time scale, where
,
as the time scale, where 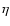 is the turbulent magnetic
diffusivity, and measured B in units of
is the turbulent magnetic
diffusivity, and measured B in units of
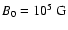 .
Further we
set kR=3. The dynamo equations were solved in the northern hemisphere with
antisymmetric boundary condition for the magnetic field across the equatorial
plane.
.
Further we
set kR=3. The dynamo equations were solved in the northern hemisphere with
antisymmetric boundary condition for the magnetic field across the equatorial
plane.
From the obtained magnetic fields only those above a threshold in field
strength were further analysed. This accounts for the fact that only the
stronger fields become buoyantly unstable, rise to the surface and contribute
to sunspots. In models A, B and D we chose a threshold of 0.3 of the maximum
value of the field strength reached during the whole run, in models C and E
this threshold was set to 0.05. The results do not significantly depend on
the threshold.
![\begin{figure}
\par\includegraphics[angle=90,width=17cm,clip]{4282fig6}\end{figure}](/articles/aa/full/2008/20/aa4282-05/Timg82.gif) |
Figure 6:
Butterfly diagrams for the northern hemisphere produced by 5 simple dynamo models described
in the text. Shown are contours of field strength, with negative fields being indicated by dashed
contours. Time is measured in units of diffusion time. |
| Open with DEXTER |
In models A, B and C we allowed for random fluctuations of the
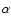 -effect superposed on the regular
-effect superposed on the regular 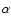 -effect in order to
simulate the irregularity of the solar cycle. While in models A and B the
regular
-effect in order to
simulate the irregularity of the solar cycle. While in models A and B the
regular 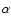 -effect extends from equator to pole as
-effect extends from equator to pole as
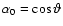 ,
it is confined to latitudes below
,
it is confined to latitudes below 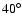 in model C by
taking
in model C by
taking
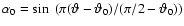 for
for
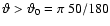 and
and
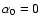 elsewhere, yielding
butterfly wings closer to the equator in the latter case. These models were
run at their corresponding critical excitation, i.e.
elsewhere, yielding
butterfly wings closer to the equator in the latter case. These models were
run at their corresponding critical excitation, i.e.
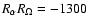 for models A and B and
for models A and B and
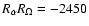 for model C.
The number of fluctuating cells from equator to pole was 50, which were
renewed every 0.001 diffusion time steps, corresponding roughly to 1 month.
The amplitudes
for model C.
The number of fluctuating cells from equator to pole was 50, which were
renewed every 0.001 diffusion time steps, corresponding roughly to 1 month.
The amplitudes
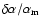 of the fluctuations were random values
from the interval (-3,3), i.e. up to 3 times the regular
of the fluctuations were random values
from the interval (-3,3), i.e. up to 3 times the regular 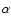 -effect in
models A and C, and from the interval (-4,4) in model B. 33 cycles were
available for analysis of models A and B, and 79 cycles for model C. Note that
only cycles produced after the models reached a statistically steady state
were analysed. For details of the model setup and justification see
Ossendrijver et al. (1996).
-effect in
models A and C, and from the interval (-4,4) in model B. 33 cycles were
available for analysis of models A and B, and 79 cycles for model C. Note that
only cycles produced after the models reached a statistically steady state
were analysed. For details of the model setup and justification see
Ossendrijver et al. (1996).
In model D we describe an overshoot layer dynamo with an 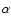 -effect
due to the buoyancy instability of the toroidal magnetic field
(Ferriz-Mas et al. 1994). The regular
-effect
due to the buoyancy instability of the toroidal magnetic field
(Ferriz-Mas et al. 1994). The regular 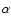 -effect is limited to
-effect is limited to
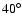 latitude as in model C and, additionally, operates only in a
finite range of field strength,
latitude as in model C and, additionally, operates only in a
finite range of field strength,
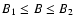 ,
with
,
with
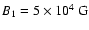 and
and
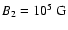 .
Instead of
.
Instead of
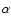 -fluctuations a stochastic source term
-fluctuations a stochastic source term
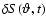 describes poloidal flux loops shed into the overshoot region from magnetic
fields in the convection zone. The latitudinal extension,
describes poloidal flux loops shed into the overshoot region from magnetic
fields in the convection zone. The latitudinal extension,
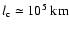 ,
and the duration of such an injection,
,
and the duration of such an injection,
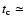 0.001 diffusion times or 1 month, are determined by the length
and time scales of the large-scale convective flows. We chose a random
location
0.001 diffusion times or 1 month, are determined by the length
and time scales of the large-scale convective flows. We chose a random
location
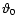 and the amplitude of
and the amplitude of 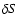 is also a random
number in the interval
is also a random
number in the interval
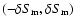 with a dimensionless value
of
with a dimensionless value
of
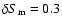 .
After each correlation time
.
After each correlation time 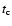 ,
new random values for
,
new random values for
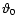 and the amplitude of
and the amplitude of 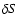 are selected. The dynamo
operated at twice the critical excitation, with
are selected. The dynamo
operated at twice the critical excitation, with
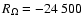 and
and
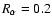 .
Model details are given in Schmitt et al. (1996). The combination
of a threshold in field strength for dynamo action and random fluctuations
due to magnetic fields from a turbulent convection zone dynamo leads to
activity cycles with amplitude variations, interrupted by randomly occurring
grand minima. A time sequence without grand minima was chosen and a total of
33 cycles were available for analysis.
.
Model details are given in Schmitt et al. (1996). The combination
of a threshold in field strength for dynamo action and random fluctuations
due to magnetic fields from a turbulent convection zone dynamo leads to
activity cycles with amplitude variations, interrupted by randomly occurring
grand minima. A time sequence without grand minima was chosen and a total of
33 cycles were available for analysis.
![\begin{figure}
\par\includegraphics[angle=90,width=16cm,clip]{4282fig7}\end{figure}](/articles/aa/full/2008/20/aa4282-05/Timg103.gif) |
Figure 7:
Latitude distribution of cycle-averaged magnetic flux above the threshold for each
of the 5 considered dynamo models. Plotted is the distribution averaged over all cycles (thick
curves), as well as the distributions due to the strongest and weakest analysed
cycles. |
| Open with DEXTER |
Finally in model E we investigated an equatorward flow as part of the
meridional circulation at the location of the dynamo in the overshoot layer
with superposed fluctuations (cf. Charbonneau & Dikpati 2000). The
flow speed was chosen to be rather low in order to keep the
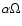 -dynamo mechanism from being quenched by the flow (see
also Petrovay & Kerekes 2004). In particular, for
-dynamo mechanism from being quenched by the flow (see
also Petrovay & Kerekes 2004). In particular, for
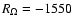 ,
,
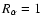 and Rv = 1 the dynamo is critically excited, when a regular
and Rv = 1 the dynamo is critically excited, when a regular
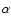 -effect with
-effect with
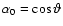 is adopted. The amplitudes of
the fluctuations
is adopted. The amplitudes of
the fluctuations
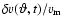 are random numbers in the
interval (-2,2), 5 cells from equator to pole were adopted, and renewed
every 0.1 diffusion times, corresponding roughly to the duration of a
cycle. 31 butterfly wings with amplitudes varying by a factor of about 3 are
analysed.
are random numbers in the
interval (-2,2), 5 cells from equator to pole were adopted, and renewed
every 0.1 diffusion times, corresponding roughly to the duration of a
cycle. 31 butterfly wings with amplitudes varying by a factor of about 3 are
analysed.
In Fig. 6 we plot the analysed butterfly diagrams for each
of the 5 models. The outermost contour in Fig. 6 corresponds to
the relevant threshold level for each model. Solid and dashed contours refer
to opposite polarity fields. Time is given in units of the diffusion time.
Due to the applied boundary condition at the equator the southern hemisphere
is just a mirror image multiplied by -1. The difference between the butterfly diagrams resulting from
the various models is clear already from this figure. Models C and E show
larger variability than the others, which is the reason that a different
threshold was used for these models.
The synthetic butterfly diagrams were analysed in exactly the same manner as
the solar data. The separation between individual cycles is straight forward
for the models, since the sign of the toroidal field alternates between
cycles. After integration over time we obtained latitudinal profiles, plotted
in Fig. 7, similar to those obtained from the data. Shown are
the average distribution of each model (i.e. averaged over all cycles; thick
curves) as well as the distribution due to the weakest and the strongest
cycle. Note that the weakest cycle has the lower m0, but need not have the
lowest magnetic flux at all latitudes. Similarly, the strongest cycle need
not be the strongest at all latitudes.
6 Results obtained with dynamo models
Since the computed dynamos are symmetric around the equator we do not need to
distinguish between the hemispheres as long as we do not directly compare
with solar data. The results are summarised in Table 3.
There are similarities and differences between the models with regard to the
correlations. Some correlation coefficients change comparatively little from
one model to another, e.g.,  vs.
vs.
 or k vs. swhile others are strongly dependent, such as
or k vs. swhile others are strongly dependent, such as
 vs.
vs.
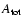 or s vs.
or s vs.
 .
.
These very sensitive parameters, i.e. parameters which change significantly
from one model to another, are of particular interest to distinguish between
the models. Other such parameters include s vs.
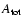 and k vs.
and k vs.
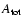 .
.
Model E is the only one for which all 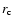 values are positive. It has the
highest
values are positive. It has the
highest
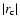 value in 6 out of 10 cases. There is also a tendency for
model C to have more positive
value in 6 out of 10 cases. There is also a tendency for
model C to have more positive 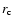 values than models A, B and D. The
highest correlation is reached between
values than models A, B and D. The
highest correlation is reached between  and
and
 ,
between k and s, and to a lesser extent between
,
between k and s, and to a lesser extent between  and
and
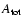 .
Whereas the first and third of these agrees well with the
observations, k and s, although reasonably related in the observational
data
.
Whereas the first and third of these agrees well with the
observations, k and s, although reasonably related in the observational
data
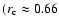 -0.76), is only the fourth highest correlation.
-0.76), is only the fourth highest correlation.
Table 3:
Correlation coefficients, 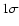 uncertainties of the correlation coefficients
and false alarm probability for dynamo models.
uncertainties of the correlation coefficients
and false alarm probability for dynamo models.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{4282fig8}\end{figure}](/articles/aa/full/2008/20/aa4282-05/Timg127.gif) |
Figure 8:
Difference between correlation coefficients 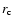 obtained from solar data and from models, plotted vs. the observed obtained from solar data and from models, plotted vs. the observed 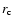 .
The three frames refer from left to right to solar .
The three frames refer from left to right to solar 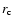 values deduced from the northern
hemisphere, the southern hemisphere and the whole Sun. From top to bottom the frames refer
to models A to E. Open circles:
values deduced from the northern
hemisphere, the southern hemisphere and the whole Sun. From top to bottom the frames refer
to models A to E. Open circles:
 vs.
vs.
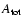 ,
filled circles: ,
filled circles:
 vs.
vs.
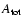 ,
open triangles: s vs. ,
open triangles: s vs.
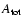 ,
filled triangles:
k vs. ,
filled triangles:
k vs.
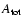 ,
open squares: ,
open squares:  vs.
vs.
 ,
filled squares:
s vs. ,
filled squares:
s vs.
 ,
open diamonds: k vs. ,
open diamonds: k vs.
 ,
filled diamonds:
s vs. ,
filled diamonds:
s vs.  ,
pluses: k vs. ,
pluses: k vs.  ,
crosses: k vs. s. ,
crosses: k vs. s. |
| Open with DEXTER |
Comparing the 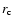 values in Table 3 with the values given in
Table 2 shows some good agreement and some significant
differences. Interestingly, the level of agreement depends strongly on
whether a given model is compared with the northern or the southern solar
hemisphere or with the full Sun.
values in Table 3 with the values given in
Table 2 shows some good agreement and some significant
differences. Interestingly, the level of agreement depends strongly on
whether a given model is compared with the northern or the southern solar
hemisphere or with the full Sun.
To show these similarities and differences more clearly, we plot in
Fig. 8 the difference between the solar and model correlation
coefficients vs. the solar 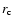 value. It is interesting that models A-D
(in particular C), i.e. models without a meridional flow, reproduce the
behaviour of the northern solar hemisphere, which shows the weaker
correlations between moments. Model E, on the other hand, lies closer to the
behaviour of the whole Sun and the southern hemisphere. Therefore, the
behaviour of the southern hemisphere of the Sun is better described by a
model including a meridional circulation (in a simplified form).
value. It is interesting that models A-D
(in particular C), i.e. models without a meridional flow, reproduce the
behaviour of the northern solar hemisphere, which shows the weaker
correlations between moments. Model E, on the other hand, lies closer to the
behaviour of the whole Sun and the southern hemisphere. Therefore, the
behaviour of the southern hemisphere of the Sun is better described by a
model including a meridional circulation (in a simplified form).
In general, the probabilities that the correlations are due to chance are
much smaller for the models, basically because of the larger number of cycles
that could be calculated compared to the number for which observations are
available.
7 Discussion and conclusions
We have analysed the 5 lowest moments of the latitude dependence of the solar
cycle and have found tight relationships between the total strength of the sunspot
cycle, the mean latitudes of the sunspots and the width of the latitude bands over
which the sunspots are distributed. Correlations involving the skewness and kurtosis
of the latitude distribution of sunspots are weaker, although these two quantities
do correlate significantly with each other. A clear difference between the hemispheres
is evident: The correlations between all these parameters are stronger (and positive) for
the southern hemisphere, while for the northern hemisphere some of the correlations are
weakly negative, although at a level that is not significant. This type of analysis
obviously brings out the differences between the hemispheres particularly clearly.
Since sunspots are formed soon after the emergence of an active region and generally
die long before the active region itself, they can be considered to be tracers of
freshly emerged magnetic flux. Thus our results can be compared directly with models
describing the generation of the Sun's magnetic field (dynamo models). We therefore
tested the usefulness of the relations found here by computing butterfly diagrams for
5 simple dynamo models and analysing these in exactly the same way as the data. The
aim here was not primarily to identify the most appropriate dynamo model, but rather
to use these models to see if moments of cycle-averaged sunspot distributions have the
power to distinguish between models. We found different levels of agreement with the
real Sun from one model to the other. In particular, we could identify correlations
between moments whose diagnostic value is high in that they could clearly distinguish
between models.
The most striking (and surprising) result of our analysis concerns the north-south
asymmetry of solar activity, which has been reported to manifest itself in various
activity indices such as flares, filaments, magnetic flux and sunspot numbers and
areas (e.g. Reid 1968; Temmer et al. 2002; Howard 1974; Verma 1993; Knaack et al. 2004, and references therein).
The models without meridional flow (A-D) reproduce the latitude dependence of the
sunspots in the northern solar hemisphere far better than in the southern hemisphere,
while for the model with meridional flow (E) it is the other way round. This is as yet
no proof that the meridional flow plays different roles in the two solar hemispheres,
but it is intriguing and calls for more work. In particular, an analysis that goes beyond
our exploratory work and involves the comparison with more realistic dynamo models is
needed. In any case our result shows that the north-south asymmetry of solar activity
manifests itself also in rather complex ways.
- Antalova, A., & Gnevyshev,
M. N. 1983, Contributions of the Astronomical Observatory
Skalnate Pleso, 11, 63 [NASA ADS]
- Balmaceda, L., Solanki,
S. K., & Krivova, N. A. 2005, Mem. Soc. Astron. It.,
76, 929 [NASA ADS]
(In the text)
- Balmaceda, L., Solanki,
S. K., Krivova, N. A., & Foster, S. 2007, J. Geophys.
Res., submitted
-
Charbonneau, P. 2005, Living Rev. Sol. Phys., 2, 2 [NASA ADS]
(In the text)
- Charbonneau, P., &
Dikpati, M. 2000, ApJ, 543, 1027 [NASA ADS] [CrossRef]
(In the text)
- Ferriz-Mas, A., &
Núñez, E. 2003, Advances in Nonlinear Dynamos (London and
New York: Taylor & Francis)
(In the text)
- Ferriz-Mas, A., Schmitt, D., &
Schüssler, M. 1994, A&A, 289, 949 [NASA ADS]
(In the text)
- Fligge, M., & Solanki,
S. K. 1997, Sol. Phys., 173, 427 [NASA ADS] [CrossRef]
(In the text)
- Foster,
S. S. 2004, Ph. D. Thesis, University of Southampton
(In the text)
-
Gnevyshev, M. N., & Ohl, A. I. 1948, Astron. Zh., 25,
18
- Harvey,
K. L. 1992, The solar cycle, ASP Conf. Ser., 27, 580
(In the text)
-
Hathaway, D. H., Wilson, R. M., & Reichmann,
E. J. 1994, Sol. Phys., 151, 177 [NASA ADS] [CrossRef]
(In the text)
-
Hathaway, D. H., Wilson, R. M., & Reichmann,
E. J. 2002, Sol. Phys., 211, 357 [NASA ADS] [CrossRef]
(In the text)
- Howard, R.
1974, Sol. Phys., 38, 59 [NASA ADS] [CrossRef]
-
Hoyng, P., Schmitt, D., & Teuben, L. J. W. 1994,
A&A, 289, 265 [NASA ADS]
(In the text)
- Hoyt, D. V., & Schatten,
K. H. 1998, Sol. Phys., 181, 491 [NASA ADS] [CrossRef]
(In the text)
-
Knaack, R., Stenflo, J. O., & Berdyugina, S. V. 2004,
A&A, 418, L17 [NASA ADS] [CrossRef] [EDP Sciences]
- Li,
K. J., Wang, J. X., Zhan, L. S., et al. 2003,
Sol. Phys., 215, 99 [NASA ADS] [CrossRef]
(In the text)
-
Mursula, K., Usoskin, I. G., & Kovaltsov, G. A. 2001,
Sol. Phys., 198, 51 [NASA ADS] [CrossRef]
- Ossendrijver,
A. J. H., Hoyng, P., & Schmitt, D. 1996, A&A,
313, 938 [NASA ADS]
(In the text)
-
Ossendrijver, M. 2003, A&AR, 11, 287 [NASA ADS]
(In the text)
- Pelt,
J., Brooke, J., Pulkkinen, P. J., & Tuominen, I. 2000,
A&A, 362, 1143 [NASA ADS]
- Petrovay, K., & Kerekes, A.
2004, MNRAS, 351, L59 [NASA ADS] [CrossRef]
(In the text)
- Reid, J. H.
1968, Sol. Phys., 5, 207 [NASA ADS] [CrossRef]
- Schmitt, D., &
Schüssler, M. 1989, A&A, 223, 343 [NASA ADS]
(In the text)
-
Schmitt, D., Schüssler, M., & Ferriz-Mas, A. 1996,
A&A, 311, L1 [NASA ADS]
(In the text)
- Solanki, S. K., &
Schmidt, H. U. 1993, A&A, 267, 287 [NASA ADS]
(In the text)
-
Solanki, S. K., Fligge, M., Pulkkinen, P., & Hoyng, P.
2000, JA&A, 21, 163 [NASA ADS]
(In the text)
-
Solanki, S. K., Krivova, N. A., Schüssler, M., &
Fligge, M. 2002, A&A, 396, 1029 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Temmer, M., Veronig, A., & Hanslmeier, A. 2002, A&A, 390,
707 [NASA ADS] [CrossRef] [EDP Sciences]
- Usoskin, I. G., &
Mursula, K. 2003, Sol. Phys., 218, 319 [NASA ADS] [CrossRef]
(In the text)
- Verma,
V. K. 1993, ApJ, 403, 797 [NASA ADS] [CrossRef]
-
Waldmeier, M. 1935, Astron. Mitt. Zürich, 14, 105
(In the text)
-
Waldmeier, M. 1961, The sunspot-activity in the years 1610-1960
(Zurich: Schulthess), 171 [NASA ADS]
(In the text)
- Wilson, A.
2002, From Solar Min to Max: Half a Solar Cycle with SoHO, ESA
SP-508
(In the text)
- Wilson,
R. M. 1988, Sol. Phys., 117, 269 [NASA ADS] [CrossRef]
- Wolf, R. 1852,
Acad. Sci. Compt. Rend., 35, 704
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=16cm,clip]{4282fig1}\end{figure}](/articles/aa/full/2008/20/aa4282-05/Timg11.gif)

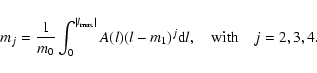
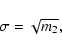
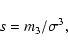
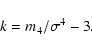
![\begin{figure}
\par\includegraphics[width=15cm,clip]{4282fig3}\end{figure}](/articles/aa/full/2008/20/aa4282-05/Timg35.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4282fig4}\end{figure}](/articles/aa/full/2008/20/aa4282-05/Timg58.gif)

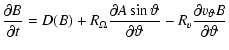
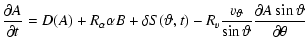
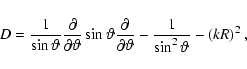
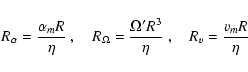
![\begin{figure}
\par\includegraphics[angle=90,width=17cm,clip]{4282fig6}\end{figure}](/articles/aa/full/2008/20/aa4282-05/Timg82.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=16cm,clip]{4282fig7}\end{figure}](/articles/aa/full/2008/20/aa4282-05/Timg103.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{4282fig8}\end{figure}](/articles/aa/full/2008/20/aa4282-05/Timg127.gif)