A&A 480, 45-59 (2008)
DOI: 10.1051/0004-6361:20078678

Magnetic field structures of galaxies derived from analysis of Faraday rotation measures, and perspectives for the SKA

R. Stepanov¹ - T. G. Arshakian^2, - R. Beck² - P. Frick¹ - M. Krause²

1 - Institute of Continuous Media Mechanics, Korolyov str. 1, 614061 Perm, Russia
2 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany

Received 14 September 2007 / Accepted 11 November 2007

Abstract
Context. The forthcoming new-generation radio telescope SKA (Square Kilometre Array) and its precursors will provide a rapidly growing number of polarized radio sources.
Aims. Our analysis looks at what can be learned from these sources concerning the structure and evolution of magnetic fields of external galaxies.
Methods. Recognition of magnetic structures is possible from Faraday rotation measures (${\rm RM}$) towards background sources behind galaxies or a continuous $~{\rm RM}$ map obtained from the diffuse polarized emission from the galaxy itself. We constructed models for the ionized gas and magnetic field patterns of different azimuthal symmetries (axisymmetric, bisymmetric and quadrisymmetric spirals, and superpositions) plus a halo magnetic field. $~{\rm RM}$ fluctuations with a Kolmogorov spectrum due to turbulent fields and/or fluctuations in ionized gas density are superimposed. Assuming extrapolated number density counts of polarized sources, we generated a sample of $~{\rm RM}$ values within the solid angle of the galaxy. Applying various templates, we derived the minimum number of background sources and the minimum quality of the observations. For a large number of sources, reconstruction of the field structure without precognition becomes possible.
Results. Any large-scale regular component of the magnetic field can be clearly recognized from $~{\rm RM}$ data with the help of the $\chi ^2$ criterium. Under favorite conditions, a few dozen polarized sources are enough for a reliable result. A halo field with a vertical component does not affect the results of recognition. The required source number increases for small inclinations of the galaxy's disk and for larger $~{\rm RM}$ turbulence. A flat number density distribution of the sources can be overcome by more sensitive observations. Application of the recognition method to the available $~{\rm RM}$ data in the region around M 31 indicates that there are significant $~{\rm RM}$ contributions intrinsic to the background sources or due to the foreground of the Milky Way. A reliable reconstruction of the field structure needs at least 20 $~{\rm RM}$ values on a cut along the projected minor axis.
Conclusions. Recognition or reconstruction of regular field structures from the $~{\rm RM}$ data of polarized background sources is a powerful tool for future radio telescopes. Measuring $~{\rm RM}$ at frequencies around 1 GHz with the SKA, simple field structures can be recognized in galaxies up to about 100 Mpc distance and will allow to test dynamo against primordial or other models of field origin. The low-frequency SKA array and low-frequency precursor telescopes like LOFAR may also have good $~{\rm RM}$ sensitivity if background sources are still significantly polarized at low frequencies.

Key words: methods: statistical - techniques: polarimetric - galaxies: magnetic fields - galaxies: spiral - galaxies: individual: M 31 - radio continuum: galaxies

   
1 Introduction

Magnetic fields play an important role for the structure and evolution of galaxies. Radio synchrotron emission provides the best tools for measuring the strength and structure of galactic magnetic fields (Beck et al. 1996). However, the sensitivity of present-day radio observations only allows detailed studies for a couple of nearby galaxies (Beck 2005).

Rotation measures ($~{\rm RM}$) towards polarized background sources located behind spiral galaxies can trace regular magnetic fields in these galaxies out to large distances, even where the synchrotron emission of the galaxy itself is too weak to be detected (Han et al. 1998; Gaensler et al. 2005). However, with the sensitivity of present-day radio telescopes, the number density of polarized background sources is only a few sources per solid angle of a square degree, so that only M 31 and the LMC, the two angularly largest galaxies in the sky, could be investigated so far (Han et al. 1998; Gaensler et al. 2005).

Future high-sensitivity radio facilities will be able to resolve the detailed magnetic field structure in galaxies by observing their polarized intensity and $~{\rm RM}$ directly. Furthermore, they will be able to observe a huge number of faint radio sources, thus providing the high density background of polarized point sources. This opens the possibility of mapping the Faraday rotation of polarized background sources towards nearby galaxies and study their magnetic fields. The detection of large-scale field patterns (modes) and their superpositions would strengthen dynamo theory for field amplification and ordering, while the lack of $~{\rm RM}$ patterns would indicate a primordial origin or fields structured by gas flows (Beck 2006). Mapping the $~{\rm RM}$ of the diffuse polarized emission of galaxies at high frequencies is restricted to the star-forming regions where cosmic-ray electrons are produced. At low frequencies the extent of synchrotron emission is larger due to the propagation of cosmic ray electrons, but Faraday depolarization increases much faster with wavelength, so that the diffuse polarized emission is weak. On the other hand, $~{\rm RM}$ towards polarized background sources are generated by regular fields plus ionized gas, which extend to larger galactic radii, as indicated by the existing data sets (Han et al. 1998; Gaensler et al. 2005), and are less affected by Faraday depolarization.

A major step towards a better understanding of galactic magnetism will be achieved by the Square Kilometre Array (SKA, http://www.skatelescope.org) and its pathfinders, the Allen Telescope Array (ATA) in the US, the Low Frequency Array (LOFAR) in Europe, the MeerKAT in South Africa, and the Australia SKA Pathfinder (ASKAP). The SKA will be a new-generation telescope with a square kilometre collecting area, a frequency range of 70 MHz to 25 GHz with continuous frequency coverage, a bandwidth of at least 25%, a field of view of at least 1 square degree at 1.4 GHz, and angular resolution of better than 1 arcsec at 1.4 GHz. The SKA is planned to consist of three separate arrays: a phased array for low frequencies (70-300 MHz), a phased array for medium frequencies (300-1000 MHz), and an array of single-dish antennas for high frequencies (1-25 GHz).

``Cosmic magnetism'' is one of six Key Science Projects for the SKA with the plan to measure a grid of more than 10⁷ $~{\rm RM}$ data towards polarized sources over the whole sky (Gaensler et al. 2004). This will allow measurement of the evolution of magnetic fields in galaxies from the most distant to nearby galaxies and in the Milky Way. Large-scale field structures should be observable via $~{\rm RM}$mapping of the diffuse polarized emission in galaxies (Beck 2006). Even more promising are $~{\rm RM}$ measurements towards polarized background sources, which are discussed in this paper.

   
2 Models of Faraday rotation towards background sources in galaxies

A model for $~{\rm RM}$ towards polarized background sources needs the following ingredients: the distribution and sign of the regular and random field of the galaxy, the distribution of electron density, the density and fluxes of polarized background sources, and their internal RM. The measured $~{\rm RM}$ value towards each background source is the sum of all rotation measure contributions along the line of sight, including the Galactic foreground rotation and any internal $~{\rm RM}$ of the background source itself. The contribution of the Galactic foreground has to be subtracted from the observed $~{\rm RM}$values before any further analysis, but this contribution is presently known only for a coarse grid of background sources on large scales of a few degrees (Johnston-Hollitt et al. 2004; Simard-Normandin et al. 1981). $~{\rm RM}$data of background sources near the plane of the Milky Way reveal fluctuations by several $100~{\rm rad~m^{-2}}$ on scales of a few arcminutes (Brown et al. 2007). The contribution of the Galactic $~{\rm RM}$ can be accounted properly from the density of $~{\rm RM}$ detected with the LOFAR or SKA in a slightly larger region surrounding each galaxy. The internal $~{\rm RM}$ of the background sources will average out if the number of background sources used for the analysis is large enough. Furthermore, a culling algorithm can be used to remove background sources with high internal $~{\rm RM}$ values. Hennessy et al. (1989) and Johnston-Hollitt et al. (2004), for example, removed sources with measured $~{\rm RM}$exceeding n-times the standard deviation from the mean (or median) $~{\rm RM}$.

   
2.1 Models for the regular magnetic field in the disk

The mean-field $\alpha$-$\Omega$ dynamo model is based on differential rotation and the $\alpha$-effect (Beck et al. 1996). Although the physics of dynamo action still faces theoretical problems (e.g. Brandenburg & Subramanian 2005), the dynamo is the only known mechanism able to generate large-scale coherent (regular) magnetic fields of spiral shape. These coherent fields can be represented as a superposition (spectrum) of modes with different azimuthal and vertical symmetries. In a smooth, axisymmetric gas disk the strongest mode is the one with the azimuthal mode number m=0 (axisymmetric spiral field), followed by the weaker m=1 (bisymmetric spiral field), etc. (Elstner et al. 1992). These modes cause typical variations in Faraday rotation along the azimuthal direction in the galaxy disk (Krause 1990). In flat, uniform disks the axisymmetric mode with even vertical symmetry (S0 mode) is excited most easily (Baryshnikova et al. 1987), while the odd symmetry (A0 mode) dominates in spherical objects. The timescale for building up a coherent field from a turbulent one is $\approx$10⁹ yr (Beck et al. 1994).

Most galaxies reveal spiral patterns in their polarization vectors, even flocculent or irregular galaxies. The field observed in polarization can be anisotropic or regular. $~{\rm RM}$ is a signature of regular fields, while anisotropic fields generate polarized emission, but no Faraday rotation. Large-scale $~{\rm RM}$ patterns observed in several galaxies (Beck 2005; Krause 1990) show that at least some fraction of the magnetic field in galaxies is regular. The classical case is the strongly dominating axisymmetric field in the Andromeda galaxy M 31 (Berkhuijsen et al. 2003; Fletcher et al. 2004). A few more cases of dominating axisymmetric fields are known (e.g. the LMC, Gaensler et al. 2005), while dominating bisymmetric fields are rare (Krause et al. 1989). The two magnetic arms in NGC 6946 (Beck & Hoernes 1996), with the field directed towards the galaxy's center in both, are a signature of superposed m=0 and m=2 modes. However, for many of the nearby galaxies for which multi-frequency observations are available, angular resolutions and/or signal-to-noise ratios are still too low to reveal dominating magnetic modes or their superpositions. The regular field of the Milky Way reveals several reversals in the plane, but the global structure is still unclear (Brown et al. 2007; Han et al. 1997; Sun et al., in press). The regular field near the Sun is symmetric with respect to the Galactic plane.

For this paper, we restrict our analysis to the three lowest azimuthal modes of the toroidal regular magnetic field: axisymmetric spiral (ASS, m=0), bisymmetric spiral (BSS, m=1), quadrisymmetric spiral (QSS, m=2), and the superpositions ASS+BSS and ASS+QSS. All modes are assumed to be symmetric with respect to the disk plane (S-modes). The maximum regular field strength is assumed to be $5~\mu$G for all modes, consistent with typical values from observations (Beck 2005).

The radial extent of regular magnetic field is not known yet. In NGC 6946, its scalelength is at least 16 kpc (Beck 2007). $~{\rm RM}$measurements of polarized sources behind M 31 indicate that the regular field strength out to at least 15 kpc radius is similar to that in the inner disk (Han et al. 1998).

   
2.2 Models for the magnetic field in the halo

Galactic dynamos operating in thin disks also generate poloidal fields that extend far into the halo. They are about one order of magnitude weaker than the toroidal fields in the disk (Ruzmaikin et al. 1988) and hence are irrelevant for our models. Polarization observations of nearby galaxies seen edge-on generally show a magnetic field parallel to the disk near the disk plane, but recent high-sensitivity observations of several edge-on galaxies like M104, NGC 891, NGC 253, and NGC 5775 show vertical field components that increase with increasing height z above and below the galactic plane and also with increasing radius, so-called X-shaped magnetic fields (Soida 2005; Krause 2007; Heesen et al. 2005,2007; Krause et al. 2006). Such a vertical field can be due to a galactic wind that may transport the disk field into the halo. Dynamo models including a wind outflow show field structures quite similar to the observed ones (Brandenburg et al. 1993).

The detailed analysis of the highly inclined galaxy NGC 253 allowed a separation of the observed field into an ASS disk field and a vertical field (Heesen et al. 2007). The tilt angle between the vertical field and the disk is about 45$^\circ$. This value corresponds approximately to the tilt angles at large z observed in other edge-on galaxies.

Assuming energy-density equipartition between magnetic fields and cosmic rays, the scale height of the total magnetic field is about 4 times larger than the scale height of synchrotron emission of typically about 1.8 kpc (Krause 2004). As the degree of linear polarization increases with height above the disk midplane, the scale height of the regular field may be even larger.

   
2.3 Thermal electron density models

In this paper we model the ionized gas of the disk by a Gaussian distribution in the radial and vertical (z) directions. A scale height of 1 kpc is adopted from the models of the free electron distribution in the thick disk of the Milky Way fitted to pulsar dispersion measures (Gómez et al. 2001; Cordes & Lazio 2002). The electron density near the galaxy center is assumed to be 0.03 cm^-3, the same as in the Milky Way models.

The radial scalelength of the density $n_{\rm e}$ of free electrons in the Milky Way of $\approx$15 kpc (Gómez et al. 2001) is much larger than the scalelength of radio thermal emission in nearby galaxies, e.g. about 4 kpc in NGC 6946 (Walsh et al. 2002), 3 kpc in M 33 (Tabatabaei et al. 2007), and 5 kpc for the H$\alpha$ disk of the edge-on galaxy NGC 253 (Heesen, priv. comm.). As the thermal emission scales with $n_{\rm e}^2$, the scalelength of $n_{\rm e}$ is twice larger, but still smaller than what is quoted for the Milky Way. As a compromise, we use a Gaussian scalelength of 10 kpc in our model.

The distribution of ionized gas follows that of the optical spiral arms. The arm-interarm-contrast of the H$\alpha$ emission is between 2 and 10 in typical spiral galaxies like NGC 6946 (see the smoothed H$\alpha$ map shown in Frick et al. 2001). On the other hand, regular magnetic fields observed in polarization are strongest in interarm regions (Beck & Hoernes 1996; Frick et al. 2001) with a similar arm-interarm-contrast. As Faraday rotation in NGC 6946 is also highest in the interarm regions (Beck 2007), the azimuthal variation in Faraday rotation, determined by the product of regular field strength and electron density, is mostly determined by the azimuthal variation of the regular field. We conclude that the azimuthal variation in electron density can be neglected in our models.

In summary, we adopt a Gaussian dependence of $n_{\rm e}$ on galactic radius r (in the galactic plane) and on height z above the disk midplane:

$$n_{\rm e}(r,z) = n_0 \exp{\left\{-\left(\frac{z}{h}\right)^2\right\}} \exp{\left\{-\left( \frac{r}{r_0}\right)^2\right\}},$$ (1)

where n₀ =0.03 cm^-3 is the electron density near the galaxy center, r₀=10 kpc is the radial scalelength of the $n_{\rm e}$distribution in the galaxy model, and h=1 kpc is its vertical scalelength.

   
2.4 Faraday rotation models

Two Cartesian coordinate systems are used: the coordinate system l,b,s in the sky plane with the same orientation as the galaxy (l,b are the distances counted from the center of the observed galaxy along the major and minor axes of the projected disk, and scorresponds to the direction of the line of sight) and the system x,y,z attached to the galaxy (x,y are in the galactic midplane and z is perpendicular to it). The coordinates x and l of both systems coincide and i is the angle between coordinates z and s (or y and b, see Fig. 1), called the inclination angle of the galactic plane (where $i=0^{\circ}$ means face-on).

	Figure 1: The two coordinate systems used in this paper: l,b in the sky plane and s along the line of sight, and x,y,z in the model galaxy plane and perpendicular to it. The dashed lines indicate the thickness of the disk.
Open with DEXTER

	Figure 2: Modeled strength of the regular magnetic field multiplied by the thermal electron density in the galactic midplane (i.e. in the plane x,y) for the field modes m=0 (ASS), m=1 (BSS), and m=2 (QSS) for B=1.
Open with DEXTER

The galactic magnetic field is modeled as a superposition of a regular part with a simple azimuthal symmetry B_m and a random part $B_{\rm turb}$, which describes the contribution of large-scale galactic turbulence:

$$\vec B(\vec r) = \vec B_m(\vec r) + \vec B_{\rm turb}(\vec r),$$ (2)

where $\vec r$ is the radius vector in galactic coordinates, which will be written in Cartesian coordinates (x, y, z) or cylindrical ones ( $r=\sqrt{x^2+y^2}$, $\phi=\arctan{y/x}$, z).

First, the regular part of magnetic field is supposed to be purely horizontal (B_z=0), parameterized by the pitch angle p and the intensity B_m of the corresponding azimuthal mode m (we only consider m=0,1,2, using the notation ASS, BSS, and QSS, see Fig. 2). The BSS mode has two reversals along azimuthal angle, the QSS mode has four reversals. All modes are symmetric with respect to the disk plane. The strength of the magnetic field in cylindrical coordinates is defined as

$$B_m (r,\phi,p) = B \cos{\left( m \left(\frac{ \ln{r}}{\tan ... ...phi+\phi_0\right)\right)} \tanh{\left(\frac{5r}{r_0}\right)},$$ (3)

where B is the field amplitude (strength) and $\phi_0$ the azimuthal phase of the mode. The $\tanh$ term is introduced to suppress the field near the center of the galaxy where the spiral field is strongly twisted. Equation (3) does not include any decrease in the field strength with radius r and height z, because the decay in regular field strength is much slower than that of electron density (see Eq. (1)).

The $~{\rm RM}$ is proportional to the product of the density of thermal electrons $n_{\rm e}$ and the component of the regular magnetic field $~B_{\parallel}$ parallel to the line of sight. Note that we cannot separate the contributions of B and $n_{\rm e}$ using the $~{\rm RM}$ data alone and that we can reconstruct only the product ( $\!~B_{\parallel}~ n_{\rm e}$). As we neglect any azimuthal (e.g. spiral) structure in $n_{\rm e}$, the small-scale structure in $~{\rm RM}$ is determined by B, whereas the general radial and vertical decrease in $~{\rm RM}$ is determined by $n_{\rm e}$. The distribution of this field in the galactic midplane for m=0,1,2 (ASS, BSS, and QSS) is shown in Fig. 2.

Second, we consider a model in which a vertical field B_z exists and increases with height z, according to the magnetic field structure observed in the halos of nearby edge-on galaxies (see Sect. 2.2). We suppose that the modulus of the magnetic field follows again Eq. (3), but the field lines are tilted with respect to the plane. The tilt angle $\chi$ is defined as

$$\chi = \chi_0 \tanh{\frac{z}{2h}} \tanh{\frac{3r}{r_0}},$$ (4)

where $\chi_0 = \pi/4$ is the limit of the tilt angle in our model achieved at $r\approx r_0/3$, $z\approx 2h$. The orientations of magnetic field lines for the ASS model are shown in Fig. 3.

	Figure 3: Orientation of the halo magnetic field. The box sketches the region of ionized gas r <r0, -h <z <h.
Open with DEXTER

The magnetic field component $~B_{\parallel}$ parallel to the line of sight includes the turbulent (random) magnetic field as well as the regular one, so that

$$~{\rm RM}(l,b) = 0.81 \int_{-\infty}^{\infty} \left( \vec B_... ...B_{\rm turb}(\vec r) \right) n_{\rm e}(\vec r) {\rm d} \vec s.$$ (5)

The turbulent part of magnetic field $B_{\rm turb}$ should describe the three-dimensional random field with given spectral properties in the whole range of scales. To avoid full 3D simulations of the random vector field and its contribution to $~{\rm RM}$, we prefer to model this contribution of the irregular part of magnetic field directly in the $~{\rm RM}$ maps. Thus we write

$$~{\rm RM}(l,b) = 0.81 \int_{-\infty}^{\infty} \vec B_m(\vec r,p)n_{\rm e}(\vec r) {\rm d} \vec s + ~{\rm RM}_{\rm turb}(l,b),$$ (6)

where we add the random part of the galactic field projected to the sky plane, i.e. integrated along the line of sight.

	Figure 4: Modeled $~{\rm RM}$ maps (in $~{\rm rad~m^{-2}}$) for an inclination angle of $i=10^\circ$ generated for a pure BSS field pattern, for $B=5~\mu$G and n0 =0.03 cm-3 ( left), a random turbulent field $~{\rm RM}_{\rm turb}$for $\Delta\!~{\rm RM}_{\rm turb}=30~~{\rm rad~m^{-2}}$ ( middle), and their superposition ( right).
Open with DEXTER

$~{\rm RM}_{\rm turb}(l,b)$ is produced in a way that allows for the spectral and spatial distribution of galactic turbulent fields. Vogt & Enßlin (2005) show that by observing a turbulent magnetic field with a three-dimensional Fourier power-law spectrum like $\vert\hat{\vec B}(\vec k)\vert^2 \sim k^\alpha$ one obtains an $~{\rm RM}$ map, the two-dimensional spectrum, from which another power law follows $\vert\hat{~{\rm RM}} (\vec{k_\perp})\vert^2 \sim {k_\perp}^\beta$ with the slope $\beta = \alpha$. Here the hat is used for the notation of the Fourier transform of any function $\hat f(\vec k) = \int f(\vec x) {\rm e}^{{\rm i}\vec k \vec x} {\rm d} \vec x$, $\vec k$ is the 3D wave vector and $\vec{k_\perp}$ is the 2D wave vector, defined in the plane of the $~{\rm RM}$ map. It is supposed that the magnetic spectrum is Kolmogorov-like ( $E_B(k) \sim k^2 \vert\hat{\vec B}(\vec k)\vert^2 \sim k^{-5/3}$, hence $\alpha = -11/3$) at large wave numbers (on scales smaller than the thickness of the galactic disk) and is growing at small wave numbers as $E_B(k) \sim k^2$ (then $\alpha=0$). Thus we generate a random map in the Fourier space with the required spectrum of the form:

 

$$\vert\hat{\Phi}(\vec k_\perp)\vert^2 = \left\{ \begin{array}{ll} ... ..._0, & k<k_0 \\ \Phi_0\left( k/k_0 \right)^{-11/3}, & k>k_0. \end{array}\right.$$ (7)

Here $\Phi_0$ defines the amplitude of the turbulent part of the generated map, and k₀ is the wave number corresponding to the turbulence macroscale (k₀=5 is adopted here to reach a realistic spectrum with a maximum on scales corresponding to the typical size of supernova remnants). Hereafter we return to physical space and obtain the map $~{\rm RM}_{\rm turb}(l,b)$ as the product of the random map $\Phi(l,b)$ and the galactic ``electron thickness'':

$$~{\rm RM}_{\rm turb}(l,b) = \Phi(l,b) ~ DM(l,b).$$ (8)

Namely, DM(l,b) is the dispersion measure for the given line of sight:

$$DM(l,b) = \int_{-\infty}^{\infty} n_{\rm e}(\vec r) {\rm d} \vec s.$$ (9)

The amplitude of the signal in this map is normalized by the parameter $\Phi_0$, so that the rms $\Delta\!~{\rm RM}_{\rm turb}$ of the random field  $~{\rm RM}_{\rm turb}$ adopts some given value. We will consider three cases: weak turbulence ( $\Delta\!~{\rm RM}_{\rm turb}=10~~{\rm rad~m^{-2}}$), moderate turbulence ( $\Delta\!~{\rm RM}_{\rm turb}=30~~{\rm rad~m^{-2}}$), and strong turbulence ( $\Delta\!~{\rm RM}_{\rm turb}=50~~{\rm rad~m^{-2}}$). Note that, due to the normalization, $\Delta\!~{\rm RM}_{\rm turb}$ does not depend on the amplitude of DM and hence does not increase with increasing inclination, although such a behavior may occur in real galaxies (see Sect. 6).

Figure 4 shows an example of the $~{\rm RM}$ map calculated for a galactic field observed almost face-on (inclination angle $i=10^\circ$), simulated for a pure BSS field pattern (left), the map of turbulent field $~{\rm RM}_{\rm turb}$, and the resulting $~{\rm RM}$ map for the same BSS model superimposed by a moderate level of turbulence with a ``realistic'' spectrum (right).

   
3 Number density of polarized background sources

Future high-sensitivity radio facilities (LOFAR, SKA) will be able to observe faint radio sources, thus providing a high-density background of polarized sources. This opens a new possibility of mapping the Faraday rotation of polarized background sources towards nearby galaxies and studying their magnetic fields. In this section we estimate the density of the polarized sources towards a typical spiral galaxy placed at different distances from the observer and study the errors associated with rotation measures and their dependence on the telescope specifications.

The differential number counts of polarized sources has been recently studied using the deep polarimetric observations at 1.4 GHz of the European Large Area ISO Survey North 1 region (ELAIS N1) as a part of the DRAO Planck Deep Fields project (Taylor et al. 2007). They show that the observed distribution of number counts in differential representation (i.e. numbers per flux density interval) is almost flat down to polarized flux densities of $\approx$0.5 mJy. They also show that the extrapolated differential number counts of polarized sources decreases down to the 0.01 mJy level. The corresponding cumulative source number counts is shown in Fig. 5, normalized to the solid angle of 1 deg², which roughly corresponds to the area covered by the inner part of the nearest galaxy M 31 (Han et al. 1998).

Observations with the SKA (assuming 10⁶ m² collecting area, 50 K receiver system temperature and $\Delta\nu$/ $\nu = \Delta\lambda$/ $\lambda=0.25$ relative bandwidth) will achieve an rms noise of 0.1 $\mu$Jy/beam area and 0.01 $\mu$Jy/beam area at 1.4 GHz ( $\lambda =21$ cm) within one hour and 100 h integration time, respectively (Carilli & Rawlings 2004).

Figure 5: The dotted line shows the cumulative count N of polarized sources brighter than the polarized flux density P at $\lambda =21$ cm, taken from Taylor et al. (2007), extrapolated to 0.01 mJy polarized flux density and normalized to source numbers per 1 deg2 solid angle on sky. The possible range of extrapolated number counts per galaxy solid angles of 1 deg2 are shown as thick solid lines, 0.013 deg2 as dashed lines, and 0.00013 deg2 as dot-dashed lines. These solid angles correspond to distances of a galaxy (with r0=10 kpc) at 1.15 Mpc, 10 Mpc, and 100 Mpc. The two different lines at each distance refer to slopes $\gamma$ of the extrapolated source numbers of 0.7 ( lower line) and 1.1 ( upper line). The two thin vertical lines represent the $5\sigma _{\rm p}$ detection limit for sources observed at $\lambda =21$ cm with the SKA within 100 h ( left) and 1 h ( right) observation time.

Open with DEXTER

We extrapolate the source counts at $\lambda =21$ cm from P₀=0.5 mJy to the limiting flux density $P_{\rm min}$ of 0.05 $\mu$Jy, assuming a power-law relation between the cumulative number counts per deg² ( $N_{\square}$) and polarized flux density (P):

$$N_{\square}({>}P)= N_0 \left( \frac{P}{P_0}\right)^{-\gamma},$$ (10)

where N₀=16 deg^-2 is the cumulative source number at P=P₀=0.5 mJy. The exponent $\gamma$ is expected in the range between 0.7 and 1.1 (``pessimistic'' and ``optimistic'' number counts). The number count per solid angle of $2 r_0 \times 2 r_0$ around a typical face-on spiral galaxy with a radius of r₀at a distance D is

$$N=N_0\Omega_{\rm g} \left( \frac{P}{P_0}\right)^{-\gamma},$$ (11)

where $\Omega_{\rm g} = (2r_0/D)^2(180/\pi)^2$ is the solid angle of the galaxy, given in square degrees.

In Fig. 5 we show the predicted number counts per typical spiral galaxy (r₀=10 kpc, $20\times20$ kpc² area) observed at a distance of 1.15 Mpc (1 deg² solid angle), 10 Mpc (0.013 deg²) and 100 Mpc (0.00013 deg²). With the ``quick-look'' sensitivity of 0.01 mJy, the SKA will already detect within a few minutes about 1000 polarized sources towards the nearest spiral galaxy M 31. With the best achievable SKA sensitivity of $P\approx0.05~\mu$Jy, about $5\times10^4$ polarized sources behind M 31 and hundreds to tens of polarized background sources will be detected behind a typical galaxy at a distance between 10 and 100 Mpc. Only for the pessimistic case ( $\gamma =0.7$), the source number becomes very small for galaxies near 100 Mpc distance.

The instrumental 1$\sigma$ error in rotation measure $\Delta\! ~{\rm RM}$ of each simulated radio source of polarized flux density (P) in the cumulative number counts is

$$\Delta\! ~{\rm RM}= \frac{\sigma_\phi}{2~\lambda^2 ~ \frac{\Delta\lambda}{\lambda}},$$ (12)

where $\sigma_\phi$ is the 1$\sigma$ error (in rad) of the total difference in polarization angles $\phi$ within the observed wavelength range, $\lambda$ the center wavelength, and $\Delta\lambda/\lambda$ the relative bandwidth of the observations. If the instrumental rms noise in polarized flux density is almost constant across the whole band, $\sigma_\chi$ is determined by the errors of polarization angles in the frequency channels at the smallest and largest wavelength, which for simplicity are assumed to be the same. Then,

$$\sigma_\phi = \sqrt{2}~\frac{\sigma_{\rm p}}{2~P},$$ (13)

where $\sigma_{\rm p}$ is the instrumental rms noise in polarized flux density per frequency channel and P is the polarized flux density of the source. Hence,

$$\Delta\! ~{\rm RM}= \frac{A}{P},$$ (14)

where

$$A = \frac{\sigma_{\rm p}}{2~\sqrt{2}~\lambda^2 ~ \frac{\Delta\lambda}{\lambda}}\cdot$$ (15)

The ``sensitivity parameter'' A only depends on instrumental specifications. It becomes smaller for lower noise $\sigma_{\rm p}$(larger integration time of the telescope), larger relative bandwidth, and longer observation wavelength. For the expected performance of the SKA at $\lambda =21$ cm (see above), $A \approx 3~\mu$Jy rad m $^{-2}/\!\sqrt{t}$ where t is the observation time in hours. For a more general discussion of $~{\rm RM}$ errors, see Appendix A of Brentjens & de Bruyn (2005).

The maximum error of $~{\rm RM}$ is reached at the limiting flux density $P_{\rm min}$ of the survey. For $P_{\rm min}\approx 5 \sigma_{\rm p}$ one derives

$$\Delta\! ~{\rm RM}_{\rm max}(P_{\rm min}) = \frac{A}{P_{\rm... ...prox \frac{1}{14 \lambda^2 ~ \frac{\Delta \lambda}{\lambda}},$$ (16)

which is independent of noise $\sigma_{\rm p}$ and of observation time. For the SKA $\Delta\! ~{\rm RM}_{\rm max}$ is $\approx$6 rad m^-2. For comparison, the VLA (using two bands centered at $\lambda=22$ cm and 18 cm, see Sect. 4.5) gives $\Delta\! ~{\rm RM}_{\rm max} \approx 10$ rad m^-2.

Typical maximum values of $~{\rm RM}$ are $~{\rm RM}~\approx$ 40 rad m^-2for a galaxy inclined by $i=10^\circ$ (almost face-on) and $~{\rm RM}\approx 200$ rad m^-2 for $i=90^\circ$ inclination (edge-on). With the SKA centered at $\lambda =21$ cm, the maximum error $\Delta\! ~{\rm RM}_{\rm max}$ is significantly smaller than the typical maximum values of $~{\rm RM}$ for edge-on and face-on nearby galaxies.

Figure 6: Relation between instrumental noise and distance to the galaxy (see Eq. (18)) for different values of the ``observation parameter'' Q=0.001, 0.01, 0.1, 1, 10 rad m-2 ( from left to right) drawn for pessimistic and optimistic slopes, $\gamma =0.7$ (dashed line) and $\gamma =1.1$ (solid line) for $\lambda =21$ cm, $\delta \lambda /\lambda = 0.25$. The dotted line corresponds to the observed slope $\gamma \approx 1$ (see Fig. 5). The numbers of sources per solid angle of the galaxy corresponding to the above Q values are $N_{\rm max}=462, 92, 18, 4, 1$ for $\gamma =0.7$ and $N_{\rm max}=15~411, 1224, 97, 8, 1$ for $\gamma =1.1$ (Eq. (19)).

Open with DEXTER

From Eqs. (14) and (10-11) one may recover

$$\Delta\!~{\rm RM}= Q~N^{1/\gamma},$$ (17)

where

$$Q = A~(N_0\Omega_{\rm g})^{-1/\gamma} P_0^{-1}.$$ (18)

The ``observation parameter'' Q only depends on observational characteristics. It defines $\Delta\! ~{\rm RM}$ for the brightest source statistically expected within the solid angle of a given galaxy by a given telescope (i.e. for N=1 in Eq. (17)). It varies with noise $\sigma_{\rm p}$ and with distance D as $\sigma_{\rm p} D^{2/\gamma}$. The value of Q lies in the range between $\approx$0.001 rad m^-2 and $\approx$10 rad m^-2for $\sigma_{\rm p}$ between $0.01~\mu$Jy and 0.03 mJy and the range of distances from 1 Mpc to 100 Mpc (Fig. 6). From Eqs. (11) and (18), the parameter Q directly relates to the maximum number of sources $N_{\rm max}$ (above the $5\sigma _{\rm p}$ detection limit $P_{\rm min}$) per solid angle of the galaxy:

$$N_{\rm max}(P_{\rm min}) = \left(10 \sqrt{2}~ \lambda^2 \frac{\Delta\lambda}{\lambda}\right)^{-\gamma} Q^{-\gamma}.$$ (19)

   
4 Recognition of regular galactic field structures from a limited sample of background sources

In this section we describe and use the $\chi ^2$ minimization method to test the magnetic field models in the disk and halo of a galaxy. Application of this method to recognize the magnetic field structure in M 31 is also presented.

4.1 Method

Suppose that N polarized background sources are observed with an ``observation parameter'' Q towards a galaxy with radius r₀ at distance D. Given the Faraday rotation values of the model ( ${\rm {RM}}_{\rm mod}$) caused by the regular field ( ${\rm {RM}}_{\rm reg}$) and the turbulent field in the galaxy, we want to recognize the structure of the regular magnetic field, such as ASS, BSS, QSS, or their combinations, and determine the best-fit parameters of the model (amplitude, spiral pitch angle, and azimuthal phase) and their standard deviations.

For a fixed inclination angle of the galaxy, we simulate a ``template'' of Faraday rotation values $~{\rm RM}_{{\rm reg},~n}(\xi_1,...,\xi_d)$ of N points (with coordinates (l<sub>n</sub>,b<sub>n</sub>)) for the regular field only where $\xi_j$ are the free parameters of the magnetic field model: the amplitude and spiral pitch angle of the magnetic field (number of free parameters d=2for ASS), the azimuthal phase (d=3 for BSS and QSS), and the relative amplitude q for the ASS field in combination with the BSS or QSS field where the BSS or QSS field has the amplitude of 1-q(d=4 for the combination). For the same set of points we simulate the ``observed'' $~{\rm RM}_{{\rm mod},~n}$ (Eq. (5)) which takes both the regular and turbulent magnetic fields into account. By varying the free parameters we minimize the normalized $\chi ^2$ value between the ``observed'' and ``template'' $~{\rm RM}$ maps,

$$\chi^2 = \frac{1}{N_{\rm w}-d} \sum_{n=1}^N \frac{(~{\rm RM}_... ...M}_{{\rm noise},n}^2 + \Delta\!~{\rm RM}_{\rm turb}^2w_n^2)} ,$$ (20)

and estimate the best-fit parameters for each model. ( $\Delta\!~{\rm RM}_{{\rm noise}}$ and $\Delta\!~{\rm RM}_{\rm turb}$ are the instrumental noise (Eq. (17)) and the noise of the random field, respectively.) The coefficients w_n define the weight of each point w_n = DM(l_n,b_n)/DM(0,0), hence the contribution of each point to the minimization procedure. The weight of the point w_n is defined by the dispersion measure DM(l_n,b_n) (Eq. (9)) along the line of the sight. Introducing this weight is needed to balance the contribution of strong $~{\rm RM}$ sources with small error, which are located at the galactic periphery, where the low thermal electron density does not allow to obtain reliable information about the galactic magnetic field. The total value of w_n gives the weighted (effective) number of points $N_{\rm w}=\sum_n w_n$. This number is different from the real number of points N taken per $2 r_0 \times 2 r_0$ area. It also depends on the inclination angle i (see Fig. 7). This dependence is similar to $\cos i$, but it is not equal to 1 at $i=0^{\circ}$ because of the Gaussian distribution of the thermal electrons and not equal to 0 at $i=90^\circ$ due to the finite thickness of the disk. The inclination angle $45^{\circ }$ yields $N_{\rm w}=0.44 N$. This means that in order to obtain at least $N_{\rm w}=4$ we need a minimum of N=10.

	Figure 7: Factor of effective points vs. inclination angle i due to geometry of the disk of thermal electrons.
Open with DEXTER

This method is suited for simple field structures and a relatively small number of $~{\rm RM}$ points allowing the limited number of parameters to be fitted. In the case of complicated field structures and/or a large number of $~{\rm RM}$ points, a full reconstruction should be attempted (Sect. 5).

   
4.2 Fitting the simulated data

Throughout this paper we use typical values of r₀=10 kpc, $h=1~{\rm kpc}$, $p=20^{\circ }$, $~n_{\rm e}=0.03~{\rm cm^{-3}}$ in Eq. (1) and $B=5~\mu$G in Eq. (3). We start with recognition of an ASS field as the simplest model. For a fixed $i=45^{\circ }$, we simulate the $~{\rm RM}$ values, noise distribution $\Delta\! ~{\rm RM}$, and turbulent components of N uniformly distributed background sources. We determine the best-fit parameters p' and B' by applying the $\chi ^2$ minimization technique (Eq. (20)). Repeating this procedure for several thousand realizations we calculate the mean pitch angle ($\bar{p}'$), amplitude ($\bar{B'}$), and their standard deviations ($\delta p'$ and $\delta B'$). The dependence of the statistical properties of the fitted parameters on the number N of sources per solid angle of the galaxy and on Qare shown in Fig. 8.

Figure 8: ASS field model: mean values (figures in left column) and standard deviations (figures in right column) of pitch angles $\bar{p}'$ and amplitudes $\bar{B'}$ (given in $\mu$G) for fixed values of $h=1~{\rm kpc}$, $p=20^{\circ }$, $B=5~\mu$G, $i=45^{\circ }$ and assuming the pessimistic case of number counts ( $\gamma =0.7$). N is the real number of points observed within the solid angle of the galaxy and Q is the observation parameter (Eq. (18)).

Open with DEXTER

The simulated value of $\bar{p}'$ is in good agreement with the value $p=20^{\circ }$ used for the model calculation over a wide range of N and Q. However, the standard deviation of $\delta p'$is quite small only for low values of Q and for large numbers N. The amplitude $\bar{B'}$ is well defined, too. The behaviour of $\delta B'$ is the same as for $\delta p'$. The standard deviation diagrams show that there is a certain value of Q below which better observations do not improve the result of fitting. The same is valid beyond a certain value of N. For example, for the level of $\delta p'=3^{\circ }$ no more than 36 sources observed with Q=0.2 are needed, or no better values than Q=0.05 when observing 21 sources. Hence, the fitting problem can be characterized by two asymptotic values N^* and Q^*, provided that the accuracy of the fitting is fixed. (For the given example one obtains N^*=21 and Q^*=0.2.) These two parameters define the required quality of observations.

In Fig. 9 we show the dependence of asymptotic parameters N^* and Q^* on the level of turbulence and pitch angle of the observed galaxy for optimistic and pessimistic values of $\gamma$. The required level of accuracy is fixed at $\delta p'=3^{\circ }$.

Figure 9: Required asymptotic values N* and Q* to recognize an ASS-type field. The points correspond to $\delta p'=3^{\circ }$ for three different levels of turbulence (from bottom to top in each triplet: 10  $~{\rm rad~m^{-2}}$, 30  $~{\rm rad~m^{-2}}$ and 50  $~{\rm rad~m^{-2}}$) and for different inclination angles ( $15^{\circ }$, $45^{\circ }$, $75^{\circ }$) for fixed $h=1~{\rm kpc}$, $p=20^{\circ }$. Filled symbols correspond to the optimistic case ( $\gamma =1.1$), open symbols to the pessimistic one ( $\gamma =0.7$).

Open with DEXTER

We conclude that, in the case of the pessimistic slope, one needs observations with smaller Q, hence smaller noise $\sigma_{\rm p}$, which requires a longer integration time. An increase in the number of sources (for a fixed noise value  $\sigma_{\rm p}$) does not help. This can be explained by the fact that for low values of $\gamma$ additional sources are fainter, have higher errors, and do not improve the result. The optimistic evaluation of $\gamma$ essentially increases the values of Q^*, but slightly affects the values of N^*. As expected, the result of fitting strongly depends on the level of turbulence of the galactic field: in the case of intense turbulence one needs more points and smaller Q (longer observations or a more sensitive instrument). The dependence on turbulence becomes dramatic for weakly inclined (face-on) galaxies - the reliable fitting requires a huge number of sources under any value of $\gamma$.

Figure 10: BSS field model: mean values (figures in left column) and standard deviations (figures in right column) of fitted pitch angles $\bar{p}'$, amplitudes $\bar{B'}$, and azimuthal phases $\bar{\phi_0}'$ for fixed $h=1~{\rm kpc}$, $p=20^{\circ }$, $\phi _0=0^\circ$, and $i=45^{\circ }$, and assuming the pessimistic case of number counts ( $\gamma =0.7$). N is the real number of points observed within the solid angle of the galaxy and Q the observation parameter.

Open with DEXTER

Figure 11: Required asymptotical values N* and Q* to recognize a BSS-type field. The points correspond to $\delta p'=3^{\circ }$ for three different levels of turbulence (from bottom to top in each triplet: 10  $~{\rm rad~m^{-2}}$, 30  $~{\rm rad~m^{-2}}$ and 50  $~{\rm rad~m^{-2}}$) and different inclination angles ( $15^{\circ }$, $45^{\circ }$, $75^{\circ }$) for fixed $h=1~{\rm kpc}$, $p=20^{\circ }$. Filled symbols correspond to optimistic case ( $\gamma =1.1$), open symbols to the pessimistic one ( $\gamma =0.7$).

Open with DEXTER

	Figure 12: Probabilities calculated from $\chi ^2$ for ASS ( left) and BSS ( right).
Open with DEXTER

The same simulations are performed for the BSS and QSS models. An additional free parameter (the phase $\phi$) is accounted for, but, in general, the results are similar to those obtained for the ASS model (see Figs. 10 and 11). Comparing Figs. 9 and 11 (or Figs. 8 and 10), we conclude that the bisymmetric field can be easier recognized (it requires fewer points and higher Q for the same accuracy of pitch angle definition) and weakly depends on the turbulent component of magnetic field. The BSS field has better chances of being recognized in slightly inclined galaxies. However, with values of N, the BSS model has a higher probability of being false than the ASS model (see Fig. 12).

The dependence of the fitting accuracy on the inclination angle is shown in Fig. 13. We learn that face-on galaxies always pose more problems for recognition of the field structure. The accuracy of the ASS or BSS recognition increases monotonically with inclination angle due to stronger line-of-sight components of the regular field. For inclination angles $\ge$ $70\hbox{$^\circ$ }$, the number of effective points decreases. Furthermore, $~{\rm RM}$ becomes sensitive to fluctuations of the regular field, e.g. due to spiral arms (see Sect. 6), so that the reconstruction method (Sect. 5) is recommended for strongly inclined galaxies.

Figure 13: Accuracy (standard deviation) of the fitted pitch angle ( upper panel) and the magnetic field amplitude ( lower panel) for the ASS model (open circles, black lines) and the BSS model (triangles, red lines) vs. inclination angle i. Weak turbulence - dashed lines, strong turbulence - solid lines. Fixed parameters of the model are the pitch angle $p=20^{\circ }$ and the field amplitude $B=5~\mu$G. Each template is based on 35 $~{\rm RM}$ points.

Open with DEXTER

To illustrate the potential of identification of different models of the regular magnetic field, using a set of templates, we present in Table 1 the results of recognition under a moderate level of galactic turbulence ( $\Delta\! ~{\rm RM}_{\rm turb}=30~{\rm rad~m^{-2}}$) for a sample of 35 sources. The models of magnetic field structures with fixed parameters of $p=20^{\circ }$, $\phi _0=0^\circ$, and $B=5~\mu$G are used. The assumed level of galactic turbulence is $\Delta\! ~{\rm RM}_{\rm turb}=30~{\rm rad~m^{-2}}$, the inclination of the galaxy's disk is  $45^{\circ }$, the slope of the source counts $\gamma =0.7$(``pessimistic case''), and the ``observation parameter'' is Q=0.04. The statistics for each case has been done over 220 random distributions of 35 points within the solid angle of the galaxy and 30 different turbulent fields for each distribution (in total $220\times 30=6600$ realizations). We adopt a significance level of 98% for the rejection of a model, corresponding to the $\chi ^2$ probability function Q $(\nu/2,\chi^2\nu/2)<0.02$ where $\nu= N_{\rm w} - d$ is the weighted number of degrees of freedom (Eq. (20)) and $N_{\rm w} \simeq 27$ for $i=45^{\circ }$ (Fig. 7). A model is rejected at the 98% confidence limit if $\chi^2>1.7$ (see Table 1).

In all cases the model is clearly identified as the template with the lowest value of $\chi ^2$, almost reaching the limit of 1.0 for a perfect fit. The pitch angle is reproduced almost precisely, with an uncertainty that decreases from $\pm$$2^{\circ}$ for the ASS field to $\pm$$1^{\circ}$ for the QSS field. The accuracy of the field amplitude is about 10% for all field modes.

Table 1: The ``$\chi ^2$ Championship''.

4.3 Influence of vertical magnetic field

We also tested models including a vertical magnetic field in the halo, as described in Sect. 2.4 and shown in Fig. 3. We find that such a vertical magnetic field in the halo only slightly changes the $~{\rm RM}$ map even at small inclination angles.

The influence of the vertical component of magnetic field on the recognition procedure is studied by the following test. We calculate the $~{\rm RM}$ map for a model with a vertical magnetic field and try to recognize it by a template having only horizontal magnetic fields. As shown in Fig. 14, the fitted pitch angles and amplitudes of the magnetic field are in the same range as without a vertical magnetic field for galaxies with inclination angles $i \ga 15 \hbox{$^\circ$ }$, but large deviations occur for smaller inclinations. The reason becomes clear from Fig. 3: for small inclinations the line-of-sight components of the vertical field are larger than those of the field in the plane and hence distort the results, while at larger inclinations the vertical field becomes unimportant. We conclude that the regular magnetic field structure of spiral galaxies (at least for inclinations of $i > 15\hbox{$^\circ$ }$) can be recognized well by a magnetic field template without a vertical field, even if the galaxy has such a vertical magnetic field.

Figure 14: Fitted pitch angle ( upper panel) and the magnetic field amplitude ( lower panel) for the ASS model (open circles, black lines) and the BSS model (triangles, red lines), both including a vertical field, recognized with templates without a vertical field, plotted vs. inclination angle i. Weak turbulence - dashed lines, strong turbulence - solid lines. Fixed parameters of the model are the pitch angle $p=20^{\circ }$ and the field amplitude $B=5~\mu$G. Each template is based on 35 $~{\rm RM}$ points.

Open with DEXTER

4.4 Effect of position uncertainty

Our method assumes that the position of the galaxy center known is precisely. However, this may not be the case for distant galaxies for which only low-resolution optical images from surveys are available. A 2 $^{\prime\prime}$ uncertainty corresponds to 0.5 kpc at 50 Mpc and 1 kpc at 100 Mpc distance.

To test the effect of position uncertainties, we shifted the templates by 0.5 kpc and 1 kpc with respect to the models of type ASS, BSS, and QSS. The best fits have the same parameters of the field structures as in Table 1, but the $\chi ^2$ values for the ASS field increase to 1.3 and 1.8 for 0.5 kpc and 1 kpc shifts, respectively, to 1.5 and 2.4 for the BSS field, and to 2.2 and 4.3 for the QSS field. This tells us that the disturbing effect of a position uncertainty increases with mode number. A typical 2 $^{\prime\prime}$ uncertainty is uncritical for ASS-type fields even at 100 Mpc distance, while QSS-type fields can no longer be recognized at distances greater than about 50 Mpc.

   
4.5 Application of the recognition method to M 31

	Figure 15: $~{\rm RM}$ source sample of M 31 (from Han et al. 1998). Numbers give $~{\rm RM}$ (in $~{\rm rad~m^{-2}}$), after subtraction of the mean $~{\rm RM}$ from the Galactic foreground. Isolines show the weight function used for $\chi ^2$. Coordinates are given in kpc.
Open with DEXTER

Table 2: The ``$\chi ^2$ Championship'' for M 31.

Han et al. (1998) measured 22 $~{\rm RM}$ values from polarized background sources within a solid angle of about 1 deg² in the inner part of M 31 (Fig. 15). Their VLA observations at $\lambda=22$ cm and at $\lambda=18$ cm ( $\Delta \lambda / \lambda \approx 0.015$) reached a sensitivity limit of 0.3 mJy/beam area. The source number agrees well with the source counts from Fig. 5. Han et al. (1998) claimed that their $~{\rm RM}$ values are consistent with an ASS field in M 31, but did not include a statistical test.

Observations of the diffuse polarized emission and its $~{\rm RM}$ from M 31 has been described by an ASS field with $8^{\circ}{-}19^{\circ}$pitch angle, $4~\mu$G amplitude (assuming $~n_{\rm e}=0.03~{\rm cm^{-3}}$ and 1 kpc pathlength), with a weaker QSS field superimposed in the inner part of the galaxy (Fletcher et al. 2004), while earlier results indicated a superimposed weaker BSS field (Sofue & Beck 1987).

Firstly, we estimate how representative the sample of Han et al. (1998) is. We use the same models with fixed parameters and assumptions as described in Sect. 4.2 and repeat the same test as described above (see Table 1) for different model fields, but using for the recognition only the coordinates of the 22 sources (shown in Fig. 15) and the observed instrumental errors $\Delta\!~{\rm RM}_{{\rm noise}}$ for each source, but we used the $~{\rm RM}$ values obtained from the field models. The results in Table 2 show that the sample of 22 sources is large enough to clearly recognize the field structure with simple symmetry (if it exists). Models with $\chi^2>2.7$ are rejected at the 98% significance level, which corresponds to a weighted number of degrees of freedom of $\nu=N_{\rm w}-d \simeq 5$, where $N_{\rm w} \simeq 8$(for the inclination of M 31 of $i=75^{\circ}$) and the number of free parameters is d=2, 3, or 4.

Secondly, we use the observed data to apply our recognition model. The analysis was performed in a first run for all 22 points. In a second run we exclude the two sources with the highest $~{\rm RM}$deviations from the template model field (those with +57 rad m^-2 and -17 rad m^-2), following the culling algorithm as described in Sect. 2 in order to reduce the influence of strong internal $~{\rm RM}$ of the background sources. As shown in Table 3 none of the two runs give a clear result. Using all 22 sources, all templates give a similar value of $\chi ^2$. Taking only 20 sources (middle part of Table 3), a small preference for the ASS model is indicated. However, all models are rejected at the 98% significance level ( $\chi^2>2.7$). As the simple field structures could be clearly identified in our test using the same set of sources (Table 2), the results of Table 3 seem to indicate that the structure of the regular magnetic field of M 31 is more complicated than suggested by our templates. However, the analysis of the diffuse emission by (Fletcher et al. 2004) is statistically reliable and does not require higher modes with significant amplitudes. We conclude that the measured $~{\rm RM}$ values towards the background sources contain a significant, intrinsic contribution or a fluctuating contribution of the Milky Way foreground, which can be subtracted only if a larger number of background sources becomes available.

Thirdly, to account for the $~{\rm RM}$ intrinsic to the sources or from the Galactic foreground, we increase all $~{\rm RM}$ errors by an arbitrary factor of three. The $\chi ^2$ values of the best fit decrease and the ASS model becomes slightly preferred statistically (see bottom part of Table 3), in agreement with the results from diffuse $~{\rm RM}$.

Table 3: The field recognition for M 31.

   
5 Magnetic field reconstruction from RM grids of inclined galaxies

In the previous section the possibility of recognizing the large-scale structure of the regular magnetic field using a small number of sources has been discussed. In this one we switch to the case of a large number of sources, which allows us to reconstruct the structure of the galactic field, without precognition of a given set of simple models. The method discussed below is especially powerful for resolving the detailed structure of the magnetic field of a strongly inclined galaxy, provided an $~{\rm RM}$ grid with strong enough resolution is available.

Observations reveal a grid of $~{\rm RM}(l,b)\pm\Delta\!~{\rm RM}(l,b)$ where the standard deviation $\Delta\!~{\rm RM}(l,b)$ characterizes the observational noise. Note again that here, in contrast to the recognition method discussed in the previous section, we do not separate $~{\rm RM}(l,b)$into its regular and turbulent parts, but instead merely reconstruct the existing field structure, trying to suppress the influence of random signals (instrumental or generated in the galaxy). The Faraday rotation measure is proportional to the product $\left(B_{\parallel}~ n_{\rm e} \right)$. Ignoring the problem of the $~B_{\parallel}$and $n_{\rm e}$ separation, we consider the problem of reconstructing the magnetic field $\left(B_{\parallel}~ n_{\rm e} \right)$ from the observed $~{\rm RM}$grid. We suppose that $\left(B_{\parallel}~ n_{\rm e} \right)$ can be written in the form:

$$\left(\!~B_{\parallel}~ n_{\rm e} \right) = f(x,y) ~ ~ \eta(z).$$ (21)

This allows us to describe the decrease in $\vert{\rm RM}\vert$ in the z-direction by one term $\eta(z)$ and to state the problem as the reconstruction of the 2D scalar function f(x,y) (see Fig. 1 for the coordinate system).

The aim is to reconstruct the field f(x,y) from the $~{\rm RM}$ grid. The rotation measure grid, even in the case of noiseless measurements, is a convolution of the required field f(x,y) with some function g(y), defined by the vertical structure of the galactic field. For the case B_z=0, the function g(y) is defined only by the function $\eta(z)$. Hence,

 

$$~{\rm RM}(l,b) C \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x,y) ~ \eta(z) ~ \delta \left(z-\frac{y\cos i -b}{\sin i}\right) {\rm d}y {\rm d}z$$ =

$$C \int_{-\infty}^{\infty} f(x,y) ~ g(b/\!\sin i -y) ~ {\rm d}y,$$ = (22)

where

$$g(y)= \int_{-\infty}^{\infty}\eta\left(y\cos i\right) ~ {\rm d}z,$$

where i is the inclination angle and C a constant.

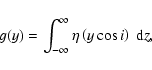
The standard solution for a problem like Eq. (22) is based on the Fourier deconvolution. Actually,

$$\hat f(x, k) = \frac{\hat{~{\rm RM}}(l, k)}{\hat g(k)}$$ (23)

where k is the wave number. The hat denotes the Fourier transform of the corresponding function. The Fourier deconvolution gives the exact solution of Eq. (22), but requires some regularization procedure (Heinz & Martin 1996) to avoid the amplification of high spatial frequency noise, especially if the spectrum of the kernel function g decreases rapidly with k. The often-suggested Gaussian form of the galactic profile $\eta(z)$ leads to a kernel that is ``bad'' in this sense. We do not discuss the regularization problem here in detail. The simplest algorithms use some kind of high-frequency cut-off in the Fourier space, while more sophisticated ones introduce subtle filtration, based for example on wavelet algorithms (Johnstone et al. 2004).

The main problems of using Eq. (23) arise from the limited resolution of the $~{\rm RM}$ grid (small number of points), noise, and unknown kernel function g (namely, one does not know the vertical distribution function $\eta(z)$).

	Figure 16: The function f(x,y) ( left) and the $~{\rm RM}$ grid ( right) for a BSS galaxy model (pitch angle $p=20^{\circ }$) inclined at $i=70^{\circ }$.
Open with DEXTER

As an example let us consider a strongly inclined galaxy with a pure BSS-type magnetic field. The required function f(x,y) for this case and the simulated $~{\rm RM}$ grid for the inclination angle $i=70^{\circ }$ are shown in Fig. 16. The problem can be illustrated by reconstructing the one-dimensional profiles f(y) for given cross-sections $x=\rm const$. Figure 17 shows the profiles of f(y) for three different values of x and the corresponding three profiles of $~{\rm RM}(b)$ at the inclination $i=70^{\circ }$. To use the deconvolution (23) one needs the function $\eta(z)$. Even if a Gaussian shape is adopted, one free parameter (the half-thickness of the ionized gas disk h) remains. We denote by h' the supposed value of h used for the deconvolution.

	Figure 17: The profiles f(y) along or parallel to the minor axis of the projected galaxy disk in the sky plane and the corresponding profiles of $~{\rm RM}(b)$ for a BSS-type galaxy, inclined at $i=70^{\circ }$: x=0 (thick curve), x=3 kpc (dashed), and x=7.5 kpc (thin).
Open with DEXTER

Figure 18 shows the profiles f(y) reconstructed from $~{\rm RM}(b)$ by deconvolution with different assumed values for the half thickness h'. The simulation is done for a set of points corresponding to 20 sources across the galaxy (which seems to be quite realistic in the frame of the SKA project). This figure illustrates that the result of reconstruction strongly depends on the choice of h'. An underestimated value of the thickness of the ionized disk leads to insufficient reinforcement of small-scale structures - the deconvolution merely stretches the $~{\rm RM}$projection. In contrast, an overestimation of h' implies an overrated smoothing and results in a disproportional amplification of high spatial frequencies (small scales). According to the last panel of Fig. 18, the oscillations of f(y)essentially exceed the real solid angle of the galaxy. The correct value h'=h allows restoration of two positive maxima in the central part of the minor axis profile x=0, which were completely hidden in the $~{\rm RM}$ projection. This example tells us that a slight underestimate of h' is more acceptable than an overestimate. Figure 18 also shows that the central profile at x=0 is the most informative one for the reconstruction, while the outer profiles are more similar.

	Figure 18: The profiles f(y) reconstructed using three different values of the supposed galactic thickness: h'=0.75 kpc ( top), h'=1 kpc ( middle), h'=1.25 kpc ( bottom). The correct value is h=1 kpc. The profiles are given for x=0 (thick curve), x=3 kpc (dashed), and x=7.5 kpc (thin).
Open with DEXTER

   
6 Discussion

Up to now the analysis of the magnetic field structure in external galaxies from $~{\rm RM}$ observations is still in a rudimentary state. There are only two nearby galaxies behind which a limited sample of polarized background sources were observed (M 31 and LMC). The impressive projects of large radio telescope arrays (LOFAR and SKA) promote the investigations of future possibilities. We considered two kinds of analyzes that may become possible: the detailed reconstruction of the structure of the regular magnetic field in a number of nearby galaxies from a dense grid of $~{\rm RM}$ values from background sources in the galaxy field, and the recognition of the main symmetry of the large-scale regular magnetic field from the $~{\rm RM}$ of a number of background sources. We studied this problem based on current estimates of the increasing number density of polarized sources with improving telescope sensitivity. We took an optimistic and a pessimistic extrapolation of the existing cumulative number counts into account.

In the first part of the paper, we studied the possibility of recognizing the large-scale regular component of the magnetic field with a simple symmetry using a straightforward testing by templates, which correspond to axisymmetric, bisymmetric, and quadrisymmetric modes, or their superpositions, and applying the $\chi ^2$ criterium for evaluating the reliability of the different modes. We showed that, if a symmetric part indeed exists in the analyzed field (even mixed with a relatively strong turbulent field), dozens of sources provide a good chance of a reliable recognition. These templates can be even successfully applied if the disk field is accompanied by an X-shaped vertical field as found in nearby galaxies observed almost edge-on. The result strongly depends on the quality of the observations, the flux density of the sources, and their number density distribution.

Our results show that regular magnetic fields of simple azimuthal symmetry (modes), like axisymmetric (ASS), bisymmetric (BSS), and quadrisymmetric spiral fields (QSS), and superpositions of these, can be recognized with $~{\rm RM}$ values from a number of background sources depending on the inclination of the galaxy's disk, the level of $~{\rm RM}$ turbulence in the galaxy, and the slope of the number density distribution of the polarized sources. The fitted parameters are the spiral pitch angle, the amplitude of the regular field strength, and the phase (for non-axisymmetric fields). The typical accuracies achieved for the fitted parameters are $\pm$ $(1^{\circ}{-}4^{\circ})$ for the pitch angle and $\pm$$10\%$ for the field amplitude. Under the favorite conditions, 10-30 sources are already reliable enough to recognize the field structure. However, the unknown internal $~{\rm RM}$ of the background sources themselves may require a larger number of measured sources in order to statistically average out the contribution of internal RM, or to be able to apply a culling algorithm, as mentioned in Sect. 2.

The regular field of a higher order of symmetry can be easier recognized; i.e. it requires fewer points and shorter observation time for the same accuracy of the fitted pitch angle definition and is less affected by the turbulent component of $~{\rm RM}$. The BSS and QSS fields seem to have better chances of being recognized in slightly inclined galaxies. However, the smaller required N^* and the larger number of parameters for the higher mode decreases the reliability of the recognition.

The dependence on turbulence becomes dramatic for weakly inclined (almost face-on) galaxies - a reliable fitting requires a huge number of sources. This problem may occur especially for small, slowly rotating galaxies with a high rate of star formation, where the large-scale regular field is expected to be weaker than the turbulent field (Beck et al. 1996). Interactions or ram pressure may also enhance the turbulent field and mask any large-scale pattern in the $~{\rm RM}$ distribution.

In our models we did not consider deviations of the regular field structure from simple azimuthal modes, e.g. due to spiral arms or additional field reversals. These would lead to further $~{\rm RM}$fluctuations that may become large for strongly inclined galaxies and hence decrease the accuracy of the fits. Strong $~{\rm RM}$fluctuations have been observed near the plane of the Milky Way (Brown et al. 2007).

For our test case M 31, the best case of a dominating field mode (ASS) so far, the available $~{\rm RM}$ data from polarized background sources confirm the results from the analysis of $~{\rm RM}$ data from the diffuse emission of M 31 (Sect. 4.5) if the $~{\rm RM}$ errors are increased to account for the $~{\rm RM}$ contributions intrinsic to the sources or from the foreground in the Milky Way. A larger number of sources is needed for proper subtraction of these effects. However, it is possible that higher field modes exist and will prevent a clear result even in case of a greater source number.

The detection of the ASS mode in M 31 from $~{\rm RM}$ of background sources also indicates that this mode is symmetric with respect to the plane (mode S0) because $~{\rm RM}$ in a strongly inclined galaxy hosting an A0 mode should reverse above and below the plane. The $~{\rm RM}$ amplitude of polarized sources behind a S0-type field should be twice larger than that from the $~{\rm RM}$ map of the diffuse polarized emission from the galaxy itself, which has to be confirmed with more sensitive data.

For many galaxies no strongly dominating field mode can be expected. A high $\chi ^2$ value, which does not decrease with increasing source number, would indicate that the field structure is more complicated than a superposition of a few simple modes or that the turbulent field is stronger than the regular field. In this case, our reconstruction method should be applied, because it does not need a ``precognition'' template but needs a higher density of $~{\rm RM}$ sources and hence deeper observations.

Observations provide the 2D projection of the product $(B_{\vert\vert}~n_{\rm e})$. Interpretation of this projection can by impeded by a vertical magnetic field B_z, but the contribution of this field is not crucial in the case of symmetrically tilted fields. If the inclination angle increases, the $~{\rm RM}$ grid is entirely dominated by the horizontal field, but another problem arises: the smoothing of detailed structures (of the size of a spiral arm) due to their superposition in a highly inclined projection. In other words, the function f(x,y) describing the field structure in the galaxy's plane is convolved by a smoothing function, defined by the vertical profile of the galaxy. Provided a universal shape of the profile exists, one can apply the deconvolution technique to restore the structure of the magnetic field in the galaxy's plane. In principle, this method works for any field structure.

The reconstruction method is superior for strongly inclined galaxies (about $70^{\circ}$ and more) and is successful if a large sample of sources is available. At least about 20 sources are required for one cut along the minor galactic axis (or $\sim$1200 sources within the solid angle covered by the galaxy) to reconstruct the spiral arms in a spiral galaxy. The number of points increases if the scale of reconstructed details decreases, following the well-known Kotelnikov-Nyquist relation.

Note that the reconstruction procedure can be applied to the $~{\rm RM}$obtained from the diffusive polarized emission of the galaxy itself, but this would require the deconvolution of a more complicated integral equation than Eq. (22). On the other hand, the recognition method also works for a continuous $~{\rm RM}$ map obtained from the diffuse polarized emission.

Finally, we wish to point out that little is known about the statistical properties of the $~{\rm RM}$ contributions intrinsic to the background sources and of the contribution of small-scale $~{\rm RM}$inhomogeneities in the foreground of the Milky Way. Large, nearby galaxies will suffer most from fluctuations in the foreground. Another uncertainty are depolarization effects within the background sources, or in the foreground of the galaxy or the Milky Way, if the angular extent of a source is greater than the angular turbulence scale in the foreground medium. Depolarization of background sources in the LMC were detected by Gaensler et al. (2005). The latter depolarization effect increases with distance because larger turbulence scales can contribute. Both depolarization effects, internal and external, depend on angular resolution and on observation frequency. No statistical data are available yet. Further investigations in this direction may modify the number of sources required for a reliable recognition.

   
7 Application to LOFAR and SKA

The reconstruction of magnetic field structures of strongly inclined spiral galaxies is possible for a sample of $\geq$1200$~{\rm RM}$ sources. This would require a sensitivity of the SKA at 1.4 GHz of $\approx$ $0.5{-}5~\mu$Jy (or integration time less than one hour) for galaxies at distances of about one Mpc. The field structures of galaxies at about 10 Mpc distance can be reconstructed with tens to a hundred hours of integration time.

The results for the recognition method presented in this paper are very promising for future observations with the SKA of background sources behind galaxies that are too faint to be observed directly by their extended polarized emission. Simple field structures can be recognized with the SKA at 1.4 GHz (21 cm) with an ``observation parameter'' $Q\approx 1$. This needs a $\sigma_{\rm p} \approx 0.2~\mu$Jy for galaxies at 30 Mpc distance and $\sigma_{\rm p} \approx 0.015~\mu$Jy for galaxies at 100 Mpc distance. These sensitivities can be achieved within 15 min and 100 h observation time, respectively, assuming that polarization calibration of the SKA is possible down to such low flux-density levels.

Let us estimate the number of spiral galaxies for which one can reconstruct or recognize the magnetic fields. Marinoni et al. (1999) estimate the mean number of galaxies ($\simeq$0.032 Mpc^-3; the multi-attractor model was used to predict the distances to the galaxies) for a magnitude-limited all-sky optical sample of nearby $\simeq$5300 galaxies with recession velocities of cz<5500 km s^-1. The mean density of 2240 Sbc-Sd spirals is about 0.013 Mpc^-3, which counts for about 60 spirals within a distance of 10 Mpc and $\approx$60 000 spirals within 100 Mpc.

The recognition method raises requirements for the dynamic range of the telescope for polarization measurements (polarization purity), which can be directly taken from Fig. 5. The detection of about 100 polarized sources in the solid angle of a galaxy at about 1 Mpc distance needs a dynamic range of about 20 dB, while at 10 Mpc distance 30 dB may already be needed for a pessimistic value of $\gamma$, and even 40 dB at 100 Mpc distance. Hence, reliable estimates of $\gamma$ are essential to compute the required polarization purity.

Observing at longer distances D requires increasing the observation time T according to $T\propto D^{4/\gamma}$ to obtain the same number N of sources per solid angle of the galaxy and the same observation parameter Q. Better knowledge of the slope $\gamma$ of cumulative number counts in the flux range accessible to the SKA is crucial for observations of distant galaxies.

The existence of simple field modes in a majority of galaxies would give strong evidence of dynamo action. Failure to detect simple field structures would suggest that large-scale dynamos are unimportant in galaxies or that other processes like shearing or compressing gas flows deform the field lines (Beck 2006). Complicated field structures require application of the reconstruction method, which will become possible for a large number of relatively nearby galaxies with the SKA, hereby offering the chance to get good statistics about the magnetic field modes and their superpositions that may exist in nearby galaxies.

Field recognition may turn out to be also useful at low frequencies. Equations (16) and (18) illustrate the advantage of radio telescopes operating at long wavelengths. For example, LOFAR will provide a maximum bandwidth of 32 MHz in its lowband (30-80 MHz) and highband (110-240 MHz). With the large number of spectral channels available for LOFAR, bandwidth depolarization will be negligible. The channel width determines the maximum detectable $~{\rm RM}$. More severe is the maximum scale in Faraday depth beyond which an extended source with internal Faraday rotation (i.e. emission and rotation occur in the same volume) becomes depolarized (Brentjens & de Bruyn 2005); it varies with $\lambda_{\rm min}^{-2}$, is below 1 rad m^-2 in the LOFAR bands and will limit low-frequency $~{\rm RM}$measurements of extended sources.

LOFAR is planned to reach an rms noise (within one hour of observation time and with 4 MHz bandwidth) of 1-2 mJy/beam area in the lowband and better than 0.1 mJy/beam area in the highband. This gives a sensitivity parameter for $~{\rm RM}$ measurements of (Eq. (15)) of $A\approx30{-}50~\mu$Jy rad m^-2 in both bands, compared to $A \approx 3~\mu$Jy rad m^-2 with the SKA at 1 GHz. LOFAR will allow RM to be measured from sources at the detection limit with errors of $\Delta\! ~{\rm RM}_{\rm max} \approx 0.005$ rad m^-2 in the lowband and $\Delta\! ~{\rm RM}_{\rm max} \approx 0.1$ rad m^-2 in the highband. However, the RM errors will be much greater under realistic conditions due to the limitations of correcting for ionospheric Faraday rotation.

The low-frequency array of the SKA should reach an rms noise of $1.4~\mu$Jy/beam area within one hour at 200 MHz (Carilli & Rawlings 2004), hence $A\approx1~\mu$Jy rad m^-2, much better than with the SKA at higher frequencies and better than with LOFAR, while the maximum $~{\rm RM}$ error of $\Delta\! ~{\rm RM}_{\rm max} \approx 0.1$ rad m^-2 is similar to that using the LOFAR highband.

However, the number density of polarized sources at low frequencies may be much lower than at high frequencies that would increase the observation parameter Q (Eq. (18)) and hence reduce the number of $~{\rm RM}$ points per solid angle of the galaxy. First, the overall degree of polarization is most probably lower due to Faraday depolarization effects. Second, the typical degree of polarization may decrease for more distant sources. Star formation was stronger in young spiral galaxies, and lobes of radio galaxies were smaller. Third, internal and external depolarization may significantly reduce the number of polarized sources (Sect. 6). For planning $~{\rm RM}$ surveys at frequencies of 300 MHz and lower, much more needs to be known about the statistics of polarized sources at low frequencies.

Another problem at low frequencies is thermal absorption that may reduce the radio fluxes at frequencies below about 100 MHz for strongly inclined galaxies with high densities of the ionized gas.

   
8 Conclusions

Recognition of simple structures of regular magnetic fields in galaxies, characterized by spiral pitch angle, amplitude of regular field strength, and azimuthal phase, can be reliably performed from a limited sample of $~{\rm RM}$ measurements towards polarized background sources. Applying templates to the field models, we could show that single and mixed modes can be clearly recognized based on the $\chi ^2$ criterium. The quality of $~{\rm RM}$ observations can be characterized by the number N of detected polarized sources within the solid angle of the galaxy, varying with distance D and instrumental noise in polarization  $\sigma_{\rm p}$ as $N \propto \sigma_{\rm p}^{-\gamma} D^{-2}$, and the ``observation parameter'' Q, which varies as $Q \propto \sigma_{\rm p} D^{2/\gamma}$ and also depends on wavelength and bandwidth of the observations. Field recognition is successful beyond a minimum source number N^* and below a maximum observation parameter Q^*.

The slope $\gamma$ of the cumulative number density counts of polarized sources with flux densities P ( $N \propto P^{-\gamma}$) is actually known beyond P=0.5 mJy from available source counts at 1.4 GHz. Extrapolation to smaller P yields $0.7 \le \gamma \le 1.1$. $\gamma$ still needs to be determined, also at lower and higher frequencies. For the optimistic case of $\gamma =1.1$, significant inclination of the galaxy's disk ( $i > 25^{\circ}$) and weak $~{\rm RM}$ turbulence (due to turbulent magnetic fields and/or fluctuations of the ionized gas density), a few dozen polarized sources are already sufficient to reliably recognize a simple field structure of type ASS, BSS, or QSS. Higher modes (BSS and QSS) are easier to recognize; i.e., they need less sources or yield smaller errors of the pitch angle for the same source number compared to the basic ASS mode. The requirement for a telescope's dynamic range in polarization (polarization purity) may exceed 30 dB in case of a flat slope $\gamma$ of the cumulative number density counts of polarized sources.

Vertical fields do not affect the results of the reconstruction for galaxies with inclinations $i>15^{\circ}$. The method should not be applied for galaxies at smaller inclinations where $~{\rm RM}$ from the disk field is small and a vertical field may dominate $~{\rm RM}$.

Strong turbulence or small inclination need more polarized sources for a statistically reliable recognition. In the case of small inclination angles, $~{\rm RM}$ turbulence can get comparable to the $~{\rm RM}$amplitude of the regular field and the required number of polarized sources may become unreasonably large. As the required number of polarized sources per solid angle also increases for large inclination angles due to geometry, the recognition method works best for intermediate inclination angles.

Uncertainties in the position of the galaxy's center of a few arcseconds are even acceptable for galaxies at 100 Mpc distance if the field pattern is type ASS. For BSS-type fields accuracies of better than 2 $^{\prime\prime}$ are needed beyond 50 Mpc distance, and better than 1 $^{\prime\prime}$ beyond 50 Mpc distance for QSS-type fields.

The application of the recognition method to the available $~{\rm RM}$values within the solid angle of the galaxy M 31 is consistent with the analysis of the diffuse polarized emission if significant $~{\rm RM}$contributions intrinsic to the background sources or fluctuating $~{\rm RM}$ in the Milky Way foreground are assumed. The regular field of M 31 is type S0, i.e. axisymmetric spiral in the plane and symmetric with respect to the plane.

Reconstruction of the field structure without precognition needs a large number of sources. A reliable reconstruction of the field structure is possible for at least 20 $~{\rm RM}$ values on a cut along the projected minor axis.

Future RM observations with the SKA at about 1 GHz will extend the possible targets for field recognition to about 100 Mpc distance, allow detailed statistical studies of the frequency of field structures, dependencies on galaxy properties, and test dynamo against primordial models or other models of field generation. About 60 spiral galaxies can be observed within a distance of 10 Mpc and $\approx$60 000 spirals within 100 Mpc.

Radio telescopes operating at low frequencies (LOFAR, ASKAP, and the low-frequency SKA array) may also be useful instruments for field recognition or reconstruction with the help of $~{\rm RM}$, if background sources are still significantly polarized at low frequencies.

Acknowledgements

This work is supported by the European Community Framework Programme 6, Square Kilometre Array Design Study (SKADS),contract No. 011938, by DAAD No. A/07/09440 (RS), RFBR No. 06-01-00234, and grant MK-4338.2007.1 (P.F. and R.S.). P.F. and R.S. are grateful for financial support from Prof. Anton Zensus, MPIfR Bonn. We thank Dr. Wolfgang Reich for careful reading of the manuscript, and thank Prof. Bryan Gaensler and the anonymous referee for valuable comments. The simulations were performed on the computer cluster of the IMM (Ekaterinburg, Russia).

References

• Baryshnikova, I., Shukurov, A., Ruzmaikin, A., & Sokoloff, D. D. 1987, A&A, 177, 27 [NASA ADS] (In the text)
• Beck, R. 2005, in Cosmic Magnetic Fields, ed. R. Wielebinski, & R. Beck, Lecture Notes in Physics (Berlin: Springer Verlag), 664, 41 (In the text)
• Beck, R. 2006, Astron. Nachr., 327, 512 [NASA ADS] [CrossRef] (In the text)
• Beck, R. 2007, A&A, 470, 539 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Beck, R., & Hoernes, P. 1996, Nature, 379, 47 [NASA ADS] [CrossRef] (In the text)
• Beck, R., Brandenburg, A., Moss, D., Shukurov, A., & Sokoloff, D. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] (In the text)
• Beck, R., Poezd, A. D., Shukurov, A., & Sokoloff, D. D. 1994, A&A, 289, 94 [NASA ADS] (In the text)
• Berkhuijsen, E. M., Beck, R., & Hoernes, P. 2003, A&A, 398, 937 [NASA ADS] [CrossRef] [EDP Sciences]
• Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] (In the text)
• Brandenburg, A., Donner, K. J., Moss, D., et al. 1993, A&A, 271, 36 [NASA ADS] (In the text)
• Brentjens, M. A., & de Bruyn, A. G. 2005, A&A, 441, 1217 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Brown, J. C., Haverkorn, M., Gaensler, B. M., et al. 2007, ApJ, 663, 258 [NASA ADS] [CrossRef] (In the text)
• Carilli, C. L., & Rawlings, S. 2004, New Astron. Rev., 48, 979 [NASA ADS] [CrossRef] (In the text)
• Cordes, J. M., & Lazio, T. J. W. 2002, [arXiv:astro-ph/0207156]
• Elstner, D., Meinel, R., & Beck, R. 1992, A&AS, 94, 587 [NASA ADS] (In the text)
• Fletcher, A., Berkhuijsen, E. M., Beck, R., & Shukurov, A. 2004, A&A, 414, 53 [NASA ADS] [CrossRef] [EDP Sciences]
• Frick, P., Beck, R., Berkhuijsen, E. M., & Patrickeyev, I. 2001, MNRAS, 327, 1145 [NASA ADS] [CrossRef] (In the text)
• Gaensler, B. M., Beck, R., & Feretti, L. 2004, New Astron. Rev., 48, 1003 [NASA ADS] [CrossRef] (In the text)
• Gaensler, B. M., Haverkorn, M., Staveley-Smith, L., et al. 2005, Science, 307, 1610 [NASA ADS] [CrossRef]
• Gómez, G. C., Benjamin, R. A., & Cox, D. P. 2001, AJ, 122, 908 [NASA ADS]
• Han, J. L., Manchester, R. N., Berkhuijsen, E. M., & Beck, R. 1997, A&A, 322, 98 [NASA ADS]
• Han, J. L., Beck, R., & Berkhuijsen, E. M. 1998, A&A, 335, 1117 [NASA ADS]
• Heesen, V., Krause, M., Beck, R., & Dettmar, R.-J. 2005, in The Magnetized Plasma in Galaxy Evolution, ed. K. T. Chyzy, K. Otmianowska-Mazur, M. Soida, & R.-J. Dettmar, 156
• Heesen, V., Krause, M., Beck, R., & Dettmar, R.-J. 2007, Astron. Nachr., 328, 637 [NASA ADS]
• Heinz, W. E., & Martin, H. 1996, Regularization of Inverse Problems (Dordrecht: Kluwer) (In the text)
• Hennessy, G. S., Owen, F. N., & Eilek, J. A. 1989, ApJ, 347, 144 [NASA ADS] [CrossRef] (In the text)
• Johnston-Hollitt, M., Hollitt, C. P., & Ekers, R. D. 2004, in The Magnetized Interstellar Medium, ed. B. Uyaniker, W. Reich, & R. Wielebinski, 13
• Johnstone, I. M., Kerkyacharian, G., Picard, D., & Raimondo, M. 2004, Journal Of The Royal Statistical Society Series B, 66, 547 [CrossRef], available at http://ideas.repec.org/a/bla/jorssb/v66y2004i3p547-573.html (In the text)
• Krause, M. 1990, in Galactic and Intergalactic Magnetic Fields, ed. R. Beck, R. Wielebinski, & P. P. Kronberg, IAU Symp., 140, 187 (In the text)
• Krause, M. 2004, in The Magnetized Interstellar Medium, ed. B. Uyaniker, W. Reich, & R. Wielebinski, 173 (In the text)
• Krause, M. 2007, Mem. Soc. Astron. It., 78, 314 [NASA ADS]
• Krause, M., Beck, R., & Hummel, E. 1989, A&A, 217, 17 [NASA ADS] (In the text)
• Krause, M., Wielebinski, R., & Dumke, M. 2006, A&A, 448, 133 [NASA ADS] [CrossRef] [EDP Sciences]
• Marinoni, C., Monaco, P., Giuricin, G., & Costantini, B. 1999, ApJ, 521, 50 [NASA ADS] [CrossRef] (In the text)
• Ruzmaikin, A., Sokolov, D., & Shukurov, A. 1988, Nature, 336, 341 [NASA ADS] [CrossRef] (In the text)
• Simard-Normandin, M., Kronberg, P. P., & Button, S. 1981, ApJS, 45, 97 [NASA ADS] [CrossRef]
• Sofue, Y., & Beck, R. 1987, PASJ, 39, 541 [NASA ADS] (In the text)
• Soida, M. 2005, in The Magnetized Plasma in Galaxy Evolution, ed. K. T. Chyzy, K. Otmianowska-Mazur, M. Soida, & R.-J. Dettmar, 185
• Tabatabaei, F. S., Beck, R., Krause, M., et al. 2007, A&A, 466, 509 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Taylor, A. R., Stil, J. M., Grant, J. K., et al. 2007, ApJ, 666, 201 [NASA ADS] [CrossRef] (In the text)
• Vogt, C., & Enßlin, T. A. 2005, A&A, 434, 67 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Walsh, W., Beck, R., Thuma, G., et al. 2002, A&A, 388, 7 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)