A&A 479, 427-452 (2008)
DOI: 10.1051/0004-6361:20078723
J. Lavalle1 - Q. Yuan2 - D. Maurin3 - X.-J. Bi2
1 - Centre de Physique des Particules (CPPM),
CNRS-IN2P3, Université de la Méditerranée, 163 avenue de Luminy,
case 902, 13288 Marseille Cedex 09, France
2 - Key Laboratory of Particle Astrophysics,
Institute of High Energy Physics, Chinese Academy of Sciences,
PO Box 918-3, Beijing 100049, PR China
3 - Laboratoire de Physique Nucléaire et Hautes Énergies
( LPNHE),
CNRS-IN2P3, Universités Paris VI et Paris VII,
4 place Jussieu, Tour 33,
75252 Paris Cedex 05, France
Received 23 September 2007 / Accepted 27 November 2007
Abstract
Context. Anti-proton and positron Galactic cosmic ray spectra are among the key targets for indirect detection of dark matter. The boost factors, corresponding to an enhancement of the signal, and linked to the clumpiness properties of the dark matter distribution, have been taken as high as thousands in the past. The dramatic impact of these boost factors for indirect detection of antiparticles, for instance with the PAMELA satellite or the coming AMS-02 experiment, asks for their detailed calculation.
Aims. We take into account the state-of-the-art results of high resolution N-body dark matter simulations to calculate the most likely energy dependent boost factors, which are linked to the cosmic ray propagation properties, for anti-protons and positrons. The results from extreme, but still possible, configurations of the clumpy dark matter component are also discussed.
Methods. Starting from the mass and space distributions of sub-halos, the anti-proton and positron propagators are used to calculate the mean value and the variance of the boost factor for the primary fluxes. We take advantage of the statistical method introduced in Lavalle et al. (2007) and cross-check the results with Monte Carlo computations.
Results. By spanning some extreme configurations of sub-halo and propagation properties, we find that the average contribution of the clumps is negligible compared to that of the smooth dark matter component. Dark matter clumps do not lead to enhancement of the signals, unless they are taken with some extreme (unexpected) properties. This result is independent of the nature of the self-annihilating dark matter candidate considered, and provides precise estimates of the theoretical and the statistical uncertainties of the antimatter flux from sub-halos.
Conclusions. Spectral distortions can still be expected in antimatter flux measurements, but scenarios invoking large and even mild clumpiness boost factors are strongly disfavoured by our analysis. Some very extreme configurations could still lead to large enhancements, e.g. (i) very small clumps with masses ![]()
![]() following a
following a
![]() mass distribution with
mass distribution with
![]() ,
highly concentrated with internal
,
highly concentrated with internal
![]() profiles with
profiles with
![]() ,
and spatially distributed according to the smooth component; or (ii) a big sub-halo of mass
,
and spatially distributed according to the smooth component; or (ii) a big sub-halo of mass ![]()
![]() within a distance of
within a distance of ![]() 1 kpc from the Earth. However, they are very unlikely from either theoretical or statistical arguments.
1 kpc from the Earth. However, they are very unlikely from either theoretical or statistical arguments.
Key words: cosmology: dark matter
The existence of dark matter (DM) has been established by various astronomical observations, from galactic to cosmological scales. The evidence come from gravitational effects, such as the observation of the rotation curves in spiral galaxies and velocity dispersion in elliptical galaxies, the X-ray emission and peculiar velocity dispersion of galaxies in the clusters of galaxies and the weak lensing effects, all indicating much steeper gravitational potentials than those inferred from the luminous matter. Recently, there have been two strong smoking guns from the Bullet cluster system 1E0561 (Clowe et al. 2006; Bradac et al. 2006; Clowe et al. 2004) and a DM ring discovered around the cluster CL0024+17 (Jee et al. 2007), which may indicate the existence of DM in the sense that it has first provided means to study the dynamics of DM itself. Note, however, that modified gravity models might still offer a viable alternative (Famaey et al. 2007; Angus & McGaugh 2007; Angus et al. 2007,2006).
The nature of DM is still unknown, remains one of the most outstanding puzzles
in astrophysics and cosmology, and is challenging from the particle physics
view point. Nevertheless, the unprecedented precision reached in observational
cosmology in the last decade, thanks to the combined use of different probes
(CMB, type 1A supernovae, large scale structures, deep surveys, primordial
abundances, etc.), yields a rather precise estimate of the total amount of
non-relativistic matter in the Universe, encompassing the standard baryonic
matter, of which density can be predicted and measured independently
(for reviews, see e.g. Tytler et al. 2000; Yao & et al. 2006; Lesgourgues 2004). The overall contribution
of matter to the (critical) energy density of the Universe is ![]() 30%,
while the baryonic component accounts for 4% only. Hence most of the
matter should be dark and of non-baryonic origin, requiring
physics beyond the standard model of particle physics. The most attractive
scenario involves weakly interacting massive particles (WIMPs). An appealing
idea is that WIMPs could be thermal relics of the early Universe, which
naturally give rise to a cosmological abundance in the range of the observed
value if both the interaction strength and the masses are taken at the weak
scale. Indeed, because of their thermal origin, WIMPs should still (weakly)
interact with ordinary matter, and even annihilate if they are preserved from
matter-antimatter asymmetry. Such particles can originate naturally in the
context of supersymmetric (SUSY) or extra-dimensional (ED) extensions
of the standard model, independently developed to tackle the issues of
the unification of interactions and energy scale hierarchical problems.
Indeed, in such theories, the stability of the proton is very often ensured
by the conservation of some new discrete symmetry that guaranties the
lightest exotic particle to be stable. Such
paradigms provide very good candidates for DM
(for reviews, see e.g. Bertone et al. 2005a; Jungman et al. 1996; Bergström 2000). In particular, the minimal
SUSY extension of the standard model (MSSM) can yield DM particles,
the most famous being the neutralino, a Majorana fermion. The
cosmological constraints on the SUSY parameter space have
been extensively studied in the literature (Ellis et al. 2003; Bélanger et al. 2006; Baer et al. 2005; Djouadi et al. 2006):
WIMPs could be detected on the present running or proposed experiments,
either directly by measuring the recoil energy when they scatter off a
detector nuclei (Muñoz 2004), or indirectly by observing their
annihilation products, such as anti-protons, positrons,
30%,
while the baryonic component accounts for 4% only. Hence most of the
matter should be dark and of non-baryonic origin, requiring
physics beyond the standard model of particle physics. The most attractive
scenario involves weakly interacting massive particles (WIMPs). An appealing
idea is that WIMPs could be thermal relics of the early Universe, which
naturally give rise to a cosmological abundance in the range of the observed
value if both the interaction strength and the masses are taken at the weak
scale. Indeed, because of their thermal origin, WIMPs should still (weakly)
interact with ordinary matter, and even annihilate if they are preserved from
matter-antimatter asymmetry. Such particles can originate naturally in the
context of supersymmetric (SUSY) or extra-dimensional (ED) extensions
of the standard model, independently developed to tackle the issues of
the unification of interactions and energy scale hierarchical problems.
Indeed, in such theories, the stability of the proton is very often ensured
by the conservation of some new discrete symmetry that guaranties the
lightest exotic particle to be stable. Such
paradigms provide very good candidates for DM
(for reviews, see e.g. Bertone et al. 2005a; Jungman et al. 1996; Bergström 2000). In particular, the minimal
SUSY extension of the standard model (MSSM) can yield DM particles,
the most famous being the neutralino, a Majorana fermion. The
cosmological constraints on the SUSY parameter space have
been extensively studied in the literature (Ellis et al. 2003; Bélanger et al. 2006; Baer et al. 2005; Djouadi et al. 2006):
WIMPs could be detected on the present running or proposed experiments,
either directly by measuring the recoil energy when they scatter off a
detector nuclei (Muñoz 2004), or indirectly by observing their
annihilation products, such as anti-protons, positrons, ![]() -rays or
neutrinos (Bertone et al. 2005a; Carr et al. 2006).
They may also be generated in the next generation colliders, which is the
most direct way to probe the existence of new particles. The direct and
indirect detection methods are viable and complementary to collider
studies in order to further constrain the nature of DM.
-rays or
neutrinos (Bertone et al. 2005a; Carr et al. 2006).
They may also be generated in the next generation colliders, which is the
most direct way to probe the existence of new particles. The direct and
indirect detection methods are viable and complementary to collider
studies in order to further constrain the nature of DM.
For indirect detection in the Milky Way, since the annihilation rate
is proportional to the square of the DM density,
the Galactic Centre is believed to be a promising source of DM annihilation (Bergström et al. 1998). However, the existence of the
central super-massive black hole and the supernova remnant Sgr A* are
likely to heavily contaminate the DM signals with high-energy
standard astrophysical processes (Aharonian et al. 2006). Alternative
sites, such as the DM dominated dwarf spheroidal galaxies (dSph)
orbiting close around the Milky Way, or even DM substructures inside
the Milky Way, could be more favourable.
Indeed, the existence of a myriad of sub-halos throughout galactic-scale host
halos is a generic prediction of the cold dark matter (CDM) paradigm of
structure formation in the Universe. High resolution simulations
(e.g. Diemand et al. 2006,2007a,b)
show that for the
![]() scenario, the large scale structures form
hierarchically by continuous merging of smaller halos. As remnants of the
merging process, about 10% to 50% of the total mass of the halo could be in
the form of sub-halos. Moreover, the centres of sub-halos, like their hosts,
are found to have high mass densities and therefore, could be ideal targets
for
scenario, the large scale structures form
hierarchically by continuous merging of smaller halos. As remnants of the
merging process, about 10% to 50% of the total mass of the halo could be in
the form of sub-halos. Moreover, the centres of sub-halos, like their hosts,
are found to have high mass densities and therefore, could be ideal targets
for ![]() -rays searches of WIMP annihilation products (e.g. Koushiappas et al. 2004; Bi 2006; Bi et al. 2007, and
references therein). A
long-standing issue is the possible overall enhancement - boost
factor - of the signals from the smooth component, due to the presence of
such inhomogeneities (Silk & Stebbins 1993). The first studies dedicated
to indirect detection of DM focused essentially on
-rays searches of WIMP annihilation products (e.g. Koushiappas et al. 2004; Bi 2006; Bi et al. 2007, and
references therein). A
long-standing issue is the possible overall enhancement - boost
factor - of the signals from the smooth component, due to the presence of
such inhomogeneities (Silk & Stebbins 1993). The first studies dedicated
to indirect detection of DM focused essentially on ![]() -rays, and more
marginally on anti-protons, but suffered from the lack of information on DM
substructures (see e.g. Bergström et al. 1999).
More recently, Berezinsky et al. (2003) discussed in more details
the
-rays, and more
marginally on anti-protons, but suffered from the lack of information on DM
substructures (see e.g. Bergström et al. 1999).
More recently, Berezinsky et al. (2003) discussed in more details
the ![]() -rays case, finding boost factors no larger than a few.
Furthermore, a recent study by Diemand et al. (2005a) reheated the debate
on clumpiness, because the authors, by means of a very high resolution
N-body experiment (but stopping at z=26), found that the Galaxy could be
populated by a huge number density of sub-halos as light as the Earth. While
the survival of such light clumps against tidal effects is still questionable,
they could yield a significant contribution to the Galactic diffuse
-rays case, finding boost factors no larger than a few.
Furthermore, a recent study by Diemand et al. (2005a) reheated the debate
on clumpiness, because the authors, by means of a very high resolution
N-body experiment (but stopping at z=26), found that the Galaxy could be
populated by a huge number density of sub-halos as light as the Earth. While
the survival of such light clumps against tidal effects is still questionable,
they could yield a significant contribution to the Galactic diffuse
![]() -ray flux by assuming a very cuspy sub-halo profile (Bi et al. 2006).
Nevertheless, some recent works also indicate that the current parameter range
for clumpiness may provide only marginal global effects
(Diemand et al. 2007a; Pieri et al. 2007).
The aim of the present paper is to provide a detailed study of the impact of
cosmological sub-halos on the primary antimatter Galactic cosmic ray (GCR)
flux, as elaborate as that already performed for
-ray flux by assuming a very cuspy sub-halo profile (Bi et al. 2006).
Nevertheless, some recent works also indicate that the current parameter range
for clumpiness may provide only marginal global effects
(Diemand et al. 2007a; Pieri et al. 2007).
The aim of the present paper is to provide a detailed study of the impact of
cosmological sub-halos on the primary antimatter Galactic cosmic ray (GCR)
flux, as elaborate as that already performed for ![]() -rays.
-rays.
In Maurin & Taillet (2003), the authors noted that the
difference in propagation properties for
![]() and
and ![]() was likely to
translate into different boost factors for these species. More recently,
Lavalle et al. (2007) provided a detailed formalism to
tackle the calculation of antimatter CR fluxes, when boosted by DM clumpiness.
They showed how the uncertainty on the spatial distribution of clumps
transfers to an uncertainty to the predicted boosted cosmic ray positron
flux, an effect that depends on energy. More generally, this effect depends
on the clump number density in a volume bounded by the characteristic
diffusion length of the involved species. For the sake of clarity,
these authors have used a very simple model, in which all clumps have the
same internal properties (masses and intrinsic luminosities), and mainly
stressed the effects coming from their space distribution.
Using this method, Brun et al. (2007) fully treated a particular
class of DM inhomogeneities - the intermediate mass black
holes (Bertone et al. 2005b) - finding large boosts with huge
variances for the signals: such large variances tag unpredictive scenarios.
This means that in the case of a positive detection, such scenarios can
certainly be tuned to reproduce the data, but generally at the cost
of a vanishingly small associated likelihood for this configuration.
was likely to
translate into different boost factors for these species. More recently,
Lavalle et al. (2007) provided a detailed formalism to
tackle the calculation of antimatter CR fluxes, when boosted by DM clumpiness.
They showed how the uncertainty on the spatial distribution of clumps
transfers to an uncertainty to the predicted boosted cosmic ray positron
flux, an effect that depends on energy. More generally, this effect depends
on the clump number density in a volume bounded by the characteristic
diffusion length of the involved species. For the sake of clarity,
these authors have used a very simple model, in which all clumps have the
same internal properties (masses and intrinsic luminosities), and mainly
stressed the effects coming from their space distribution.
Using this method, Brun et al. (2007) fully treated a particular
class of DM inhomogeneities - the intermediate mass black
holes (Bertone et al. 2005b) - finding large boosts with huge
variances for the signals: such large variances tag unpredictive scenarios.
This means that in the case of a positive detection, such scenarios can
certainly be tuned to reproduce the data, but generally at the cost
of a vanishingly small associated likelihood for this configuration.
In this paper, we study a more natural DM scenario
(e.g. Diemand et al. 2005a), in which substructures fill
the whole Galaxy down to a minimal mass
![]() ,
with a mass distribution
,
with a mass distribution
![]() (
(
![]() ), and a cored spatial distribution. We survey different DM
configurations in great details by using different sub-halo inner profiles,
different mass distributions or different concentration models (this has
already been well studied in the context of gamma-rays, see e.g.
Ullio et al. 2002). It is important to better quantify the boost
and variance of antimatter signals since the satellite PAMELA
(Casolino et al. 2007; Picozza et al. 2006), successfully launched in June
2006, will soon provide new results on antimatter fluxes. The DM
description suffers uncertainties, and its impact on the calculated fluxes
adds up to the existing uncertainties from the propagation parameters
(Lionetto et al. 2005; Donato et al. 2001,2004).
Regarding this latter issue, PAMELA should also update our current
knowledge of the particles transport in the Galaxy, thanks to
secondary-to-primary ratio measurements (e.g. B/C). This is crucial for
the background calculation (standard antimatter production) in order to
confirm/support any claim of an excess. Besides, AMS-02 should be
launched in the coming years, and provide additional crucial information
on GCR propagation by measuring the radioactive species
(Battiston 2007).
), and a cored spatial distribution. We survey different DM
configurations in great details by using different sub-halo inner profiles,
different mass distributions or different concentration models (this has
already been well studied in the context of gamma-rays, see e.g.
Ullio et al. 2002). It is important to better quantify the boost
and variance of antimatter signals since the satellite PAMELA
(Casolino et al. 2007; Picozza et al. 2006), successfully launched in June
2006, will soon provide new results on antimatter fluxes. The DM
description suffers uncertainties, and its impact on the calculated fluxes
adds up to the existing uncertainties from the propagation parameters
(Lionetto et al. 2005; Donato et al. 2001,2004).
Regarding this latter issue, PAMELA should also update our current
knowledge of the particles transport in the Galaxy, thanks to
secondary-to-primary ratio measurements (e.g. B/C). This is crucial for
the background calculation (standard antimatter production) in order to
confirm/support any claim of an excess. Besides, AMS-02 should be
launched in the coming years, and provide additional crucial information
on GCR propagation by measuring the radioactive species
(Battiston 2007).
Below, we take advantage of simplified
formulations for the
![]() (e.g. Maurin et al. 2006a) and
(e.g. Maurin et al. 2006a) and ![]() (e.g. Lavalle et al. 2007) propagators. Using the information
of the mass and space distributions of sub-halos from N-body numerical
simulations (see e.g. the recent Via Lactea simulation,
Diemand et al. 2006,2007a,b),
we calculate the boost and the variance of the fluxes.
We find that for all plausible choices of the clump properties and
propagation parameters, boost factors for anti-protons and positrons
are close to unity, with small systematic and statistical uncertainties.
(e.g. Lavalle et al. 2007) propagators. Using the information
of the mass and space distributions of sub-halos from N-body numerical
simulations (see e.g. the recent Via Lactea simulation,
Diemand et al. 2006,2007a,b),
we calculate the boost and the variance of the fluxes.
We find that for all plausible choices of the clump properties and
propagation parameters, boost factors for anti-protons and positrons
are close to unity, with small systematic and statistical uncertainties.
The paper is organised as follows. All relevant aspects (for this study) of the DM distributions in the Galaxy, including N-body simulation results are discussed in Sect. 2. The configurations retained are given in Sect. 3, where the key parameters entering the calculation of the clumpy flux (and its variance) are underlined. The propagation aspects are treated in Sect. 4. The methodology to calculate the antimatter flux, its variance and the corresponding boost factors is given in Sect. 5, either by means of a semi-analytical approach (Sect. 5.2) or by Monte Carlo (MC) simulations (Sect. 5.3). The reader not interested in the technical details can directly jump to Sect. 6, where the results for positrons (Sect. 6.2) and anti-protons (Sect. 6.3) are presented, highlighting the physical effects coming from clump properties, space distribution, mass distribution and GCR propagation. Because of the complex origins and the mixing of the relevant physical quantities, such details really help to fully understand what kind of information boost factors actually encodes. We summarise and conclude in Sect. 7.
In the last few years, the advent of high resolution N-body simulations have increased the number of studies in this field, allowing for a better understanding and description of the DM dynamics. Even if many issues remain unclear, when comparing simulation results to the current observations, collisionless codes now agree at the 10% level over wide dynamic ranges, providing a robust framework for DM studies (Heitmann et al. 2007).
Throughout this paper, we will separate the WIMP annihilation contribution
associated with sub-halos from that associated with a smooth
component. The former will be related to any DM inhomogeneity
in the Galactic halo, independently of its physical scale - resolved or not
in N-body simulations - while the latter will refer to the Galactic DM
host halo itself, which will be considered as a continuous fluid (again
independently of the current resolution of N-body simulations). Although the
Vlasov (or fluid) limit is likely to be reached when the number of
particles involved in N-body experiments is huge, one should still be aware
that such a statement is not trivial at all when dealing with the cosmological
evolution of structures, and that discreteness might induce important biases
(Joyce & Marcos 2007). Furthermore, one should also keep in mind that
our DM modelling will rest on (or be extrapolated from)
N-body experiment results, in the most precise of which the test particle mass
is not lighter than ![]()
![]() (cf. the Via Lactea simulation, Diemand et al. 2006),
and for which the Vlasov limit is not reached at small scales. Nevertheless,
we will assume throughout this study that the host halo profiles of
Milky-Way-like galaxies provided by N-body simulations describe a smooth fluid
(WIMP gas), on top of which some sub-halos may be wandering.
(cf. the Via Lactea simulation, Diemand et al. 2006),
and for which the Vlasov limit is not reached at small scales. Nevertheless,
we will assume throughout this study that the host halo profiles of
Milky-Way-like galaxies provided by N-body simulations describe a smooth fluid
(WIMP gas), on top of which some sub-halos may be wandering.
In the following subsections, we summarise the recent results concerning (i) generalities about DM distribution in halos of galaxies (Sect. 2.1) and (ii) some specific considerations about sub-halo description (Sects. 2.2 and 2.3).
Given the scope of this work, we will merely consider spherical profiles. For sub-halos, several cases will be chosen to encompass some extreme (but still plausible) scenarios. This aims at providing realistic estimates of the boost factor uncertainties related to the clumpy DM component.
A scale-invariant DM distribution based on N-body numerical simulation
results can be written in a general form as (Zhao 1996)
Navarro, Frenk and White (Navarro et al. 1997) worked out the following
set of parameters
![]() ,
which define the
NFW profile, with a cusp scaling like r-1 at radii smaller than
,
which define the
NFW profile, with a cusp scaling like r-1 at radii smaller than ![]() .
Moore et al. (1998) found another set with
.
Moore et al. (1998) found another set with
![]() to fit their simulation results,
which is steeper than NFW at small radii, scaling like r-1.5. More recent
high resolution N-body simulations found that an NFW profile seems to
underestimate the DM density in the central regions, while a Moore
profile
to fit their simulation results,
which is steeper than NFW at small radii, scaling like r-1.5. More recent
high resolution N-body simulations found that an NFW profile seems to
underestimate the DM density in the central regions, while a Moore
profile![]() probably overestimates it (Diemand et al. 2005b; Navarro et al. 2004; Diemand et al. 2004a, and references therein). The mean
slope of the cusp obtained from various codes is well fitted by a
probably overestimates it (Diemand et al. 2005b; Navarro et al. 2004; Diemand et al. 2004a, and references therein). The mean
slope of the cusp obtained from various codes is well fitted by a
![]() profile, with
profile, with
![]() (Diemand et al. 2004a),
still in agreement with (
(Diemand et al. 2004a),
still in agreement with (
![]() )
analytical similarity solutions
(Ahn & Shapiro 2005). However, profiles may not have a universal shape
(e.g. Navarro et al. 2004; Stoehr 2006). First,
from the observational point of view, the relative scatter observed for the
slope for four nearby low-mass spiral galaxies is 0.44 (Simon et al. 2005), three times larger than in simulations.
Second, it was also recently stressed that asymptotic slopes may not be
reached at all (Navarro et al. 2004; Merritt et al. 2006; Graham et al. 2006; Stoehr 2006; Ricotti et al. 2007): according to
Graham et al. (2006), the Einasto function describes a simulated DM
halo better than a NFW-like model.
)
analytical similarity solutions
(Ahn & Shapiro 2005). However, profiles may not have a universal shape
(e.g. Navarro et al. 2004; Stoehr 2006). First,
from the observational point of view, the relative scatter observed for the
slope for four nearby low-mass spiral galaxies is 0.44 (Simon et al. 2005), three times larger than in simulations.
Second, it was also recently stressed that asymptotic slopes may not be
reached at all (Navarro et al. 2004; Merritt et al. 2006; Graham et al. 2006; Stoehr 2006; Ricotti et al. 2007): according to
Graham et al. (2006), the Einasto function describes a simulated DM
halo better than a NFW-like model.
Closer to the Galactic centre, the super-massive black hole dominates the
mass (
![]() pc). The adiabatic growth of the black hole,
if taking place in the centre of the DM gravitational potential and
without any merger, could lead to an enhanced DM density in this
region (slope as steep as
pc). The adiabatic growth of the black hole,
if taking place in the centre of the DM gravitational potential and
without any merger, could lead to an enhanced DM density in this
region (slope as steep as ![]() 2.3-2.4, dubbed spike). Nonetheless,
recent works seem to prefer a final r-1.5 behaviour for the DM
density in the inner regions (see Merritt 2004; Gnedin & Primack 2004, and references therein).
2.3-2.4, dubbed spike). Nonetheless,
recent works seem to prefer a final r-1.5 behaviour for the DM
density in the inner regions (see Merritt 2004; Gnedin & Primack 2004, and references therein).
Finally, the luminosity of cuspy or spiky halos is singular at the centre of
the halo. However, a cut-off radius
![]() naturally appears, within
which the DM density saturates due to the balance between the annihilation
rate
naturally appears, within
which the DM density saturates due to the balance between the annihilation
rate
![]() and the
gravitational infalling rate of DM particles
and the
gravitational infalling rate of DM particles
![]() (Berezinsky et al. 1992). Taking
(Berezinsky et al. 1992). Taking
![]() about 200 times
the critical density, we get
about 200 times
the critical density, we get
During their history, structures undergo several mergers. The survival of the
inner cusp of DM in these events has been investigated. The inner
profile was found to be exceptionally robust, despite the relaxation that
follows merging processes (Valluri et al. 2007; Kazantzidis et al. 2006; McMillan et al. 2007; Aceves & Velázquez 2006; Boylan-Kolchin & Ma 2004). The
implications are deep: the characteristic universal shape of the DM
density profile may be set early in the evolution of halos
(Kazantzidis et al. 2006). However, it is still not clear whether the
central cusp is steepened or flattened when the baryonic distribution is
taken into account. Using N-body hydrodynamical simulations,
Gnedin et al. (2004), Gustafsson et al. (2006) and
Macciò et al. (2006) find that the effect of gas cooling steepens the
inner density profile to ![]() ,
while Mashchenko et al. (2006) claim that the random bulk motion of gas in
small primordial galaxies (driven by supernovae explosions) removes the cusp,
leaving only cored profiles for both small and large galaxies in the present
Universe.
,
while Mashchenko et al. (2006) claim that the random bulk motion of gas in
small primordial galaxies (driven by supernovae explosions) removes the cusp,
leaving only cored profiles for both small and large galaxies in the present
Universe.
Several other controversial issues remain and we only briefly quote
them. The first one is the question of the halo evolution in the presence of a
rotating stellar bar, leading to either a destruction of the cusp
(see Sellwood 2006; McMillan & Dehnen 2005, and
references therein) or a steepening of the cusp (Colín et al. 2006; Gnedin et al. 2004). Some recent simulations including a stellar bar also
hint at the emergence of a bar-like structure for the DM (DM bar) in the
central region in the case of a strong stellar bar
(Athanassoula 2007; Colín et al. 2006): this is the second issue,
namely departure from sphericity. Direct observations either favour
prolatness (Helmi 2004b; Libeskind et al. 2005; Helmi 2004a)
or oblateness (Ruzicka et al. 2007; Johnston et al. 2005; Metz et al. 2007), whereas for pure collisionless simulations, prolatness
is generally preferred (see also
Kuhlen et al. 2007; Bett et al. 2007; Romano-Díaz et al. 2007)![]() . Prolatness for sub-halos is
likely to depend on the position in the galaxy, halos being
more spherical in the outer regions (Hayashi et al. 2007).
Then, more generally, there is some evidence that halos become more spherical
when the baryonic cooling is taken into account (Berentzen & Shlosman 2006; Macciò et al. 2007b; Novak et al. 2006; Debattista et al. 2007; Kazantzidis et al. 2004a), or when a stellar bar is taken
into account (Berentzen et al. 2006), or even during mergers
(Novak et al. 2006).
. Prolatness for sub-halos is
likely to depend on the position in the galaxy, halos being
more spherical in the outer regions (Hayashi et al. 2007).
Then, more generally, there is some evidence that halos become more spherical
when the baryonic cooling is taken into account (Berentzen & Shlosman 2006; Macciò et al. 2007b; Novak et al. 2006; Debattista et al. 2007; Kazantzidis et al. 2004a), or when a stellar bar is taken
into account (Berentzen et al. 2006), or even during mergers
(Novak et al. 2006).
It was shown that the choice of one or another DM profile for the
smooth component (Donato et al. 2004; Maurin & Taillet 2003) is not crucial
for the calculated flux of anti-protons and positrons. Indeed, charged
particles diffuse on magnetic inhomogeneities and fluxes are heavily suppressed
(escape from the Galaxy) when originating far away from us, i.e. those from
the Galactic centre. For cuspy profiles, the maximal difference is obtained
between cored isothermal and Moore profiles (a factor ![]() 2, see e.g.
Fig. 2 of Barrau et al. 2005), the difference between
isothermal and NFW profiles being even smaller (
2, see e.g.
Fig. 2 of Barrau et al. 2005), the difference between
isothermal and NFW profiles being even smaller (![]()
![]() ,
see
Table II in Donato et al. 2004). Due to the lack of a definitive
answer for the DM profile in the Galaxy (see the above-discussion), we will
restrict ourselves in this paper to a spherically symmetric NFW profile
,
see
Table II in Donato et al. 2004). Due to the lack of a definitive
answer for the DM profile in the Galaxy (see the above-discussion), we will
restrict ourselves in this paper to a spherically symmetric NFW profile
![]() for the galactic smooth distributions. Using
triaxial halos or different profiles (e.g.
for the galactic smooth distributions. Using
triaxial halos or different profiles (e.g.
![]() or any other profile)
is expected to leave the main conclusions of the paper concerning the effects
of clump granularity in the Galactic halo unchanged. Sphericity is also
assumed for the substructures
or any other profile)
is expected to leave the main conclusions of the paper concerning the effects
of clump granularity in the Galactic halo unchanged. Sphericity is also
assumed for the substructures![]() . Departure from spherical symmetry is left to a
forthcoming study.
. Departure from spherical symmetry is left to a
forthcoming study.
Finally, we stress that although the existence of a DM spike in the Galactic
centre is crucial in the context of ![]() -ray/neutrino indirect detection
(Bertone & Merritt 2005), its effect is merely not relevant in this
study. This is due to the depletion of the signal through the diffusive
transport of antiparticles, and also to the fact that GCRs originating from
annihilations in the very tiny extent of this region are only a small
fraction of the total yield that can reach the Earth (the DM annihilation
contribution to the GCR flux is integrated over a diffusion volume instead of
a line of sight for
-ray/neutrino indirect detection
(Bertone & Merritt 2005), its effect is merely not relevant in this
study. This is due to the depletion of the signal through the diffusive
transport of antiparticles, and also to the fact that GCRs originating from
annihilations in the very tiny extent of this region are only a small
fraction of the total yield that can reach the Earth (the DM annihilation
contribution to the GCR flux is integrated over a diffusion volume instead of
a line of sight for ![]() -rays).
-rays).
The concentration parameter is a crucial quantity for computing the annihilation rates in (sub)structures. In this section, we actually present all relevant parameters that define a sub-halo. We will come back to the concentration (and the scale radius) associated with the host smooth halo just at the end (Sect. 2.2.2).
In the
![]() cosmology, the structures form hierarchically bottom-up via
gravitational amplification of initial density fluctuations. The properties of
the emerging structures and their subsequent evolution
may be described by using the virial quantities. Following the approach
and definitions of Bullock et al. (2001), the two parameters
cosmology, the structures form hierarchically bottom-up via
gravitational amplification of initial density fluctuations. The properties of
the emerging structures and their subsequent evolution
may be described by using the virial quantities. Following the approach
and definitions of Bullock et al. (2001), the two parameters
![]() and
and ![]() ,
defined in Eq. (1), of a structure of mass
,
defined in Eq. (1), of a structure of mass
![]() are expressed in terms of the concentration
are expressed in terms of the concentration
![]() and
the virial radius
and
the virial radius
![]() .
This outer radius is defined as the radius within
which the mean density is
.
This outer radius is defined as the radius within
which the mean density is
![]() times the matter density
times the matter density
![]() at redshift z. At z=0,
at redshift z. At z=0,
The concentration parameter is defined as (Bullock et al. 2001)
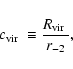 |
(4) |
The last relation links
![]() to
to
![]() .
Rewriting
the profile
.
Rewriting
the profile
![]() ,
we get
,
we get
Hence, in these models, once the
![]() relation is specified, the
profile of a clump is fully determined by its virial mass
relation is specified, the
profile of a clump is fully determined by its virial mass
![]() .
The
behaviour of
.
The
behaviour of
![]() ,
,
![]() ,
as well as
,
as well as
![]() and other related quantities, are illustrated in
Fig. 2.
and other related quantities, are illustrated in
Fig. 2.
We will use the two toy models B01 (Bullock et al. 2001) and ENS01 (Eke et al. 2001), which are based on N-body simulations; we refer the reader to these two papers for a detailed description.
These models predict that the halo concentration decreases with the halo
mass (see also Navarro et al. 1997). Note that this behaviour has
been observationally confirmed recently at the cluster scale
(Comerford & Natarajan 2007; Buote et al. 2007), albeit with a slightly
higher
![]() normalisation than predicted (Comerford & Natarajan 2007).
In subsequent N-body simulations (Kuhlen et al. 2005; Macciò et al. 2007a; Wechsler et al. 2002,2006), a good
agreement was found with the B01 model, adjusted to a slightly lower
normalisation
normalisation than predicted (Comerford & Natarajan 2007).
In subsequent N-body simulations (Kuhlen et al. 2005; Macciò et al. 2007a; Wechsler et al. 2002,2006), a good
agreement was found with the B01 model, adjusted to a slightly lower
normalisation ![]()
![]()
![]() . On the
other hand, the ENS01 model is excluded in Macciò et al. (2007a)
(because of a too shallow slope), but preferred from the analysis of
analytic lens models in Fedeli et al. (2007). The state-of-the-art
results for halo concentrations come from the recent Millennium
Simulation (Neto et al. 2007). The analysis at z=0 shows a clear
disagreement with B01 for high halo masses
. On the
other hand, the ENS01 model is excluded in Macciò et al. (2007a)
(because of a too shallow slope), but preferred from the analysis of
analytic lens models in Fedeli et al. (2007). The state-of-the-art
results for halo concentrations come from the recent Millennium
Simulation (Neto et al. 2007). The analysis at z=0 shows a clear
disagreement with B01 for high halo masses
![]() with a better match with ENS01. Still, no conclusion can be drawn to favour
one model or another at the low mass end (Neto et al. 2007).
with a better match with ENS01. Still, no conclusion can be drawn to favour
one model or another at the low mass end (Neto et al. 2007).
In any case, both toy models are likely to be not realistic enough. For
example, Romano-Díaz et al. (2007) showed that, to some extent, the
evolution of
![]() could forget the initial conditions depending on the
degree of violence in its merger events. The dependence of dark halo
clustering on the concentration parameter also affects the relation
(Sheth & Tormen 2004; Wechsler et al. 2006; Diemand et al. 2007b; Gao & White 2007; Jing et al. 2007), but this is sub-dominant compared to the observed
dispersion of
could forget the initial conditions depending on the
degree of violence in its merger events. The dependence of dark halo
clustering on the concentration parameter also affects the relation
(Sheth & Tormen 2004; Wechsler et al. 2006; Diemand et al. 2007b; Gao & White 2007; Jing et al. 2007), but this is sub-dominant compared to the observed
dispersion of
![]() (Macciò et al. 2007a; Ragone-Figueroa & Plionis 2007, and
references therein).
(Macciò et al. 2007a; Ragone-Figueroa & Plionis 2007, and
references therein).
However, as our goal is to bracket the uncertainties due to the clumpy
contribution, we will stick to the simple descriptions of B01 and ENS01,
which give respectively an upper limit and a lower limit
on the concentration for the lower masses (see also Fig. 1 in
Colafrancesco et al. 2006)![]() .
For our purpose, it is sufficient (and convenient) to use a fitted polynomial
form at z=0, to encompass the two extreme cases (see
Fig. 2 for an illustration of the B01 relation):
.
For our purpose, it is sufficient (and convenient) to use a fitted polynomial
form at z=0, to encompass the two extreme cases (see
Fig. 2 for an illustration of the B01 relation):
The DM smooth halo of the Galaxy also follows the previous relation, but a more precise description of the halo properties is in principle possible from in-situ observations. However, the determination of the mass distributions in the Galaxy remains challenging, especially if no assumption is made on the DM profile.
In Dehnen & Binney (1998), the authors fitted a
multi-parameter mass model to the available kinematic data for the Galaxy.
They found a wide variety of models surviving the fitting process,
showing that the mass distribution within the Milky Way is still ill-defined.
The case of the NFW profile, which performs as good as any other profile
(see Model 2c in their Table 4), was best fitted with a scale radius
![]() kpc and
kpc and
![]() GeV cm-3.
A more recent analysis (Battaglia et al. 2005)
using a new sample of 240 halo objects (including globular clusters,
satellite galaxies and stars) found that the isothermal profile
was ruled out for a constant velocity anisotropy of DM.
This conclusion is disputed by Dehnen et al. (2006).
Nevertheless, both analyses come to similar conclusions concerning
the best fit profiles. For example, for the NFW profile,
Battaglia et al. (2006) find
GeV cm-3.
A more recent analysis (Battaglia et al. 2005)
using a new sample of 240 halo objects (including globular clusters,
satellite galaxies and stars) found that the isothermal profile
was ruled out for a constant velocity anisotropy of DM.
This conclusion is disputed by Dehnen et al. (2006).
Nevertheless, both analyses come to similar conclusions concerning
the best fit profiles. For example, for the NFW profile,
Battaglia et al. (2006) find
![]() kpc,
kpc,
![]() GeV cm-3 (corresponding to
GeV cm-3 (corresponding to
![]() for
for
![]() kpc). These values are in agreement with those found for
simulated halos with similar mass ranges (see e.g.
Diemand et al. 2007a; Navarro et al. 2004):
in the Via Lactea run,
kpc). These values are in agreement with those found for
simulated halos with similar mass ranges (see e.g.
Diemand et al. 2007a; Navarro et al. 2004):
in the Via Lactea run,
![]() kpc,
kpc,
![]() GeV cm-3 (corresponding to
GeV cm-3 (corresponding to
![]() for
for
![]() kpc). Finally note that a recent analysis
(Cowsik et al. 2007) based on the dynamics of dwarf-spheroidals derives
kpc). Finally note that a recent analysis
(Cowsik et al. 2007) based on the dynamics of dwarf-spheroidals derives
![]() GeV cm-3.
GeV cm-3.
We shall fix the parameters of the Milky Way smooth DM distribution.
In agreement with the previous values, we define our reference model
with
![]() kpc and normalise it to the local density
kpc and normalise it to the local density
![]() GeV cm-3 at
GeV cm-3 at
![]() kpc.
This allows the calculation of the mass within any radius r,
which gives the virial halo radius
kpc.
This allows the calculation of the mass within any radius r,
which gives the virial halo radius
![]() when combined with
Eq. (3):
when combined with
Eq. (3):
![]() kpc (so that
kpc (so that
![]() ),
),
![]() .
Varying
.
Varying
![]() only changes the overall normalisation of all fluxes,
whereas modifying
only changes the overall normalisation of all fluxes,
whereas modifying ![]() would slightly change the spatial distribution,
which does not affect the conclusions of this paper.
would slightly change the spatial distribution,
which does not affect the conclusions of this paper.
High resolution simulations have revealed that a large number of self-bound substructures survived in the Galactic halo (Springel et al. 2001; Kravtsov et al. 2004; Diemand et al. 2007a; Klypin et al. 1999; Tormen et al. 1998; Weinberg et al. 2006; Moore et al. 1999; De Lucia et al. 2004; Zentner & Bullock 2003; Macciò et al. 2007a).
The mass and spatial distribution of sub-halos shown by these simulations
can be approximated as (e.g. Diemand et al. 2004b)
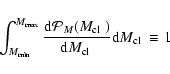 |
(12) |
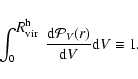 |
(13) |
For the mass distribution, the following power-law dependence is observed:
The mass distribution covers a wide range, from the heaviest sub-halo mass
in the Galaxy,
![]() (e.g. Moore et al. 1999; Diemand et al. 2005a),
down to a mass
(e.g. Moore et al. 1999; Diemand et al. 2005a),
down to a mass
![]() ,
of which the value is still debated.
At an early stage of structure formation, a cut-offs on the lower masses
appears due to (i) the diffusion of the DM particles
(collisional damping) out of a fluctuation and (ii) free streaming
(Hofmann et al. 2001; Bringmann & Hofmann 2007; Berezinsky et al. 2003,
and references therein). The first process occurs after freeze-out of the
DM particles, when it is still in kinetic equilibrium for some time
with the thermal bath (leptons, quarks, gauge bosons). Elastic and inelastic
scattering on fast particles results in momentum exchange such that DM
particles diffuse in space, leading to a cut-off mass
,
of which the value is still debated.
At an early stage of structure formation, a cut-offs on the lower masses
appears due to (i) the diffusion of the DM particles
(collisional damping) out of a fluctuation and (ii) free streaming
(Hofmann et al. 2001; Bringmann & Hofmann 2007; Berezinsky et al. 2003,
and references therein). The first process occurs after freeze-out of the
DM particles, when it is still in kinetic equilibrium for some time
with the thermal bath (leptons, quarks, gauge bosons). Elastic and inelastic
scattering on fast particles results in momentum exchange such that DM
particles diffuse in space, leading to a cut-off mass ![]() for the
structures. After kinetic decoupling, the particles move freely
in the expanding Universe background and the temperature
of this decoupling sets the free streaming
cut-off
for the
structures. After kinetic decoupling, the particles move freely
in the expanding Universe background and the temperature
of this decoupling sets the free streaming
cut-off
![]() of the mass spectrum. Both cut-off depend
on the DM candidate properties. For neutralinos,
Green et al. (2005,2004); Berezinsky et al. (2003)
find
of the mass spectrum. Both cut-off depend
on the DM candidate properties. For neutralinos,
Green et al. (2005,2004); Berezinsky et al. (2003)
find
![]() and
and
![]() .
This lower mass is slightly increased when taking into account
acoustic oscillations owing to the initial coupling between
the CDM and the radiation field
(Bertschinger 2006; Loeb & Zaldarriaga 2005).
A more careful analysis of the temperature of kinetic decoupling taking into
account a more realistic range of variations of the particle-physics models
consistent with cosmological data was recently done in
Profumo et al. (2006). Considering SUSY models (MSSM and mSUGRA) as well as models with universal extra dimensions (UED), these authors
found the range
.
This lower mass is slightly increased when taking into account
acoustic oscillations owing to the initial coupling between
the CDM and the radiation field
(Bertschinger 2006; Loeb & Zaldarriaga 2005).
A more careful analysis of the temperature of kinetic decoupling taking into
account a more realistic range of variations of the particle-physics models
consistent with cosmological data was recently done in
Profumo et al. (2006). Considering SUSY models (MSSM and mSUGRA) as well as models with universal extra dimensions (UED), these authors
found the range
![]() .
.
To follow the history of these tiny substructures,
Diemand et al. (2005a) performed a high resolution N-body simulation.
The authors were able, for the first time, to
resolve a Milky-Way size dark halo down to the free-streaming
stage. They report survival from the smallest structures
(injected down to
![]() ,
size
,
size ![]() 0.01 pc)
at z=26.
However, tidal destruction of the lightest clumps and encounters with
stars are still possible at late stages. In an analytical model,
Berezinsky et al. (2006) compared the strength of tidal stripping (i) during the hierarchical clustering, (ii) by stars from the stellar bulge,
(iii) by stars from the halo and (iv) by the Galactic disk. They found that
the last of these processes was the most effective, predicting that only 17%
of the Earth-mass clumps survived the tidal destruction. Note that the
efficiency of tidal disruption depends on the mass of the clump but also on
its environment (position in the Galaxy) so that, in principle,
Eq. (11) cannot be used. Indeed, tidal stripping is more
efficient towards the Galactic centre: for example,
Berezinsky et al. (2006) predict no light clumps at the radial
distance
0.01 pc)
at z=26.
However, tidal destruction of the lightest clumps and encounters with
stars are still possible at late stages. In an analytical model,
Berezinsky et al. (2006) compared the strength of tidal stripping (i) during the hierarchical clustering, (ii) by stars from the stellar bulge,
(iii) by stars from the halo and (iv) by the Galactic disk. They found that
the last of these processes was the most effective, predicting that only 17%
of the Earth-mass clumps survived the tidal destruction. Note that the
efficiency of tidal disruption depends on the mass of the clump but also on
its environment (position in the Galaxy) so that, in principle,
Eq. (11) cannot be used. Indeed, tidal stripping is more
efficient towards the Galactic centre: for example,
Berezinsky et al. (2006) predict no light clumps at the radial
distance ![]() kpc. However, the fraction of surviving clumps is still
controversial. Several recent studies have focused on the fate of these
Earth-mass clumps. Although some of them conclude to near-complete destruction
(Zhao et al. 2007; Angus & Zhao 2007), some others
underlined their resilience (Goerdt et al. 2007; Hayashi et al. 2003; Green & Goodwin 2007) in the Galactic potential. In the latter case, it is
likely that the inner density slope of cuspy satellite halos remains unchanged,
even if the halo loses a lot of its mass (Kazantzidis et al. 2004b).
kpc. However, the fraction of surviving clumps is still
controversial. Several recent studies have focused on the fate of these
Earth-mass clumps. Although some of them conclude to near-complete destruction
(Zhao et al. 2007; Angus & Zhao 2007), some others
underlined their resilience (Goerdt et al. 2007; Hayashi et al. 2003; Green & Goodwin 2007) in the Galactic potential. In the latter case, it is
likely that the inner density slope of cuspy satellite halos remains unchanged,
even if the halo loses a lot of its mass (Kazantzidis et al. 2004b).
In any case, as we have already emphasised, the contribution of
the central regions of the Galaxy is suppressed by the diffusive
transport (for charged particles), therefore it is expected to
be unimportant. This assumption is reinforced by the fact that,
compared to the smooth distribution that is cuspy, the clump distribution
might be cored (see Sect. 2.3.2 below). We checked that
taking or not taking into account a significant destruction of low mass
clumps - as modelled and described, in e.g.
Bi (2006) - left the results unchanged.
Thus, for our purpose, Eq. (16)
is a good enough description of the clump distribution.
The mass distribution is then fully characterised by its slope
![]() and its minimal mass cut-off
and its minimal mass cut-off
![]() .
.
In most N-body experiments, the spatial distribution of clumps is found
to be anti-biased with respect to the DM density, at least down
to the smallest clumps resolved (![]()
![]() )
at the moment
(Gill et al. 2004; Ghigna et al. 2000; De Lucia et al. 2004; Diemand et al. 2004b; Gao et al. 2004, and references therein). It is
parametrised as (spherical symmetry is assumed)
)
at the moment
(Gill et al. 2004; Ghigna et al. 2000; De Lucia et al. 2004; Diemand et al. 2004b; Gao et al. 2004, and references therein). It is
parametrised as (spherical symmetry is assumed)
![\begin{displaymath}K_V \equiv
\left\{
4\pi r_{\rm H}^3 \times \left[ \frac{{\...
...}^{\rm h}$ }}}
{r_{\rm H}}\right) \right]
\right\}^{-1}\cdot
\end{displaymath}](/articles/aa/full/2008/08/aa8723-07/img162.gif)
However, some recent studies
argue that this cored distribution could be a selection bias
(Kuhlen et al. 2007) or a limitation of collisionless simulations
(Macciò et al. 2006; Shaw et al. 2007). For example,
Kuhlen et al. (2007) find in their Via Lactea run a spatial
distribution that matches the prolate shape of the host halo. The same trend
is observed in Macciò et al. (2006), where the dissipation of the
baryons greatly enhances the survival of the sub-halos. These authors
(see also Nagai & Kravtsov 2005)
find that the clumps profile is well fitted by a NFW, even if the latter is
still less concentrated (
![]() )
than their simulated
overall mass distribution (
)
than their simulated
overall mass distribution (
![]() ).
Indeed, the smallest clumps are likely to follow the smooth DM spatial
distribution, and such an assumption has very often been used in analytical
studies of DM clumpiness effects on gamma-ray production (e.g.
Berezinsky et al. 2003). For the sake of completeness,
such a configuration will also be used later for the calculations, and
to be conservative, the space distribution of clumps will be taken to be
exactly that of the smooth component (same global concentration relation).
).
Indeed, the smallest clumps are likely to follow the smooth DM spatial
distribution, and such an assumption has very often been used in analytical
studies of DM clumpiness effects on gamma-ray production (e.g.
Berezinsky et al. 2003). For the sake of completeness,
such a configuration will also be used later for the calculations, and
to be conservative, the space distribution of clumps will be taken to be
exactly that of the smooth component (same global concentration relation).
The parameter
![]() is often determined by adopting the number of sub-halos
within a mass range. For example, Moore et al. (1999)
found 500 sub-halos with bound masses
is often determined by adopting the number of sub-halos
within a mass range. For example, Moore et al. (1999)
found 500 sub-halos with bound masses ![]()
![]() .
The recent Via Lactea simulation of Diemand et al. (2006) gives
.
The recent Via Lactea simulation of Diemand et al. (2006) gives
![]() ,
which corresponds to
,
which corresponds to
![]() .
.
In a more general context of various masses of host halos, several
simulations (van den Bosch et al. 2005, and references therein) are
compatible with the value
![]() .
Taking a mass
.
Taking a mass
![]() for the Galaxy leads to
for the Galaxy leads to
![]() .
.
For definitiveness, we choose to set the normalisation
![]() such as
such as
![]() .
Taking an upper bound of
.
Taking an upper bound of
![]() ,
we get for
,
we get for
![]() :
:
Having discussed in detail the values, uncertainties and
relevance of various parameters entering the DM distributions (both smooth
and clumpy), we now summarise the reference configurations
used as inputs of this paper (Sect. 3.1). Two main
consequences are observed:
the index of the mass distribution strongly affects the mass
fraction of DM in clumps (Sect. 3.2), whereas
the
![]() relation impacts on the luminosity profile
(Sect. 3.3).
relation impacts on the luminosity profile
(Sect. 3.3).
The distance of the Sun to the Galactic centre is fixed
to
![]() kpc.
Whatever the clump configuration, the virial radius of the dark halo
in the Galaxy is set to
kpc.
Whatever the clump configuration, the virial radius of the dark halo
in the Galaxy is set to
![]() kpc, and the local
DM density (smooth and clump altogether) to
kpc, and the local
DM density (smooth and clump altogether) to
![]() GeV cm-3 (Sect. 2.2.2).
GeV cm-3 (Sect. 2.2.2).
| Cosmology | DM (Milky Way) | Clumps | Smooth DM halo |
|
|
|
Global |
NFW (1,3,1) |
|
|
|
Inner profile: NFW, B01 |
|
|
|
|
|
|
|
|
It is chosen as a NFW (see discussion in Sect. 2.1.3)
with an inner radius
![]() kpc (
kpc (
![]() ).
In the absence of any clump - we denote
).
In the absence of any clump - we denote
![]() the corresponding smooth distribution - and with the above values for
the corresponding smooth distribution - and with the above values for
![]() ,
,
![]() and
and ![]() ,
we recover
,
we recover
![]() .
The fraction f is usually defined as the fraction
of DM taken from the smooth profile and redistributed into the clumps.
The smooth contribution in this configuration is then
.
The fraction f is usually defined as the fraction
of DM taken from the smooth profile and redistributed into the clumps.
The smooth contribution in this configuration is then
![]() ,
such that
,
such that
![]() .
.
If the spatial density of clumps is ![]()
![]() ,
the redistribution of the fraction f of the DM into clumps is
straightforwardly written as
,
the redistribution of the fraction f of the DM into clumps is
straightforwardly written as
![]() .
Note that in this case, we have a local density of clumps
.
Note that in this case, we have a local density of clumps
![]() and
and
![]() (such that
(such that
![]() ).
We elaborate on the important case when the two distributions
are different in the next Sect. 3.1.3. Otherwise,
the clumps parameters are as follows:
).
We elaborate on the important case when the two distributions
are different in the next Sect. 3.1.3. Otherwise,
the clumps parameters are as follows:
| Clump description | Values |
|
|
Cored |
| Inner profile | NFW |
|
|
|
|
|
|
|
|
B01 |
If the smooth (e.g. NFW) and the sub-halos (e.g. cored) spatial distributions
are different, the mass fraction of DM in sub-halos within
![]() is not
constant, but depends on the galactocentric radius r. The point is that in
order to compute boost factors, one would naively want to subtract any
fraction of DM added in the form of clumps to the smooth component, and
compare this new setup to the case in which DM is only smooth. A
clear definition of that fraction is crucial before going further. Indeed, we
show hereafter that if not treated carefully, there is a source of ambiguity
in the interpretation of the resulting boost factor.
is not
constant, but depends on the galactocentric radius r. The point is that in
order to compute boost factors, one would naively want to subtract any
fraction of DM added in the form of clumps to the smooth component, and
compare this new setup to the case in which DM is only smooth. A
clear definition of that fraction is crucial before going further. Indeed, we
show hereafter that if not treated carefully, there is a source of ambiguity
in the interpretation of the resulting boost factor.
Let us first introduce the total mass carried by the clumps within
![]() ,
defined as
,
defined as
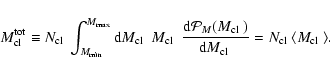 |
(19) |
Two observational constraints can help to define what kind of fraction f
is needed for consistency: the total mass of the Galaxy
![]() ,
and the local
density
,
and the local
density
![]() .
If one wants to ensure that the total mass is left
unchanged when adding clumps, then f is the mass fraction fM
given by:
.
If one wants to ensure that the total mass is left
unchanged when adding clumps, then f is the mass fraction fM
given by:
Now, if the two distributions spatially differ, it is no longer possible to fulfil both constraints. We have no choice but to abandon either the halo mass to be constant, or the local density to be constant. Let us see what happens when one of the two above conditions, Eqs. (21) or (22), is plugged in Eq. (20).
![\begin{displaymath}\rho_{\rm tot}({\mbox{$R_{\odot}$ }}) = \left[ 1 - f_M \left(...
...}})}{{\rm d}V}\right)\right]
\times {\mbox{$\rho_{\odot}$ }}.
\end{displaymath}](/articles/aa/full/2008/08/aa8723-07/img231.gif) |
(23) |
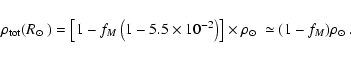 |
(24) |
However, this choice is not judicious in our study. Doing so would
even bring additional confusion to the issue of boost factors. Indeed,
unlike ![]() -rays, we remind that for primary cosmic antimatter, the flux
is very sensitive to the local density (see Appendix A). Assuming
for a while that the smooth component locally dominates the clumpy one (it
will actually be shown later to be the case, see e.g.
Fig. 5), the calculated mean boost factor would
be
-rays, we remind that for primary cosmic antimatter, the flux
is very sensitive to the local density (see Appendix A). Assuming
for a while that the smooth component locally dominates the clumpy one (it
will actually be shown later to be the case, see e.g.
Fig. 5), the calculated mean boost factor would
be
![]() (see Eqs. (67) and (68)),
which would result in a number significantly less than unity. This would
consequently lead to a damping factor instead of a an enhancement,
which would bring about misleading interpretations.
(see Eqs. (67) and (68)),
which would result in a number significantly less than unity. This would
consequently lead to a damping factor instead of a an enhancement,
which would bring about misleading interpretations.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{FigAA/8723fig1.eps}\end{figure}](/articles/aa/full/2008/08/aa8723-07/Timg239.gif) |
Figure 1:
Mass fraction fM as a function of
|
Finally, before closing the DM section, let us discuss how the various configurations gathered in Table 2 impact on some generic properties for the clumps (mass fraction fM and luminosities).
The minimal mass
![]() of the clumps able to form - and to survive
tidal disruption - is a crucial parameter (see also next subsection). Along
with the slope
of the clumps able to form - and to survive
tidal disruption - is a crucial parameter (see also next subsection). Along
with the slope
![]() appearing in the mass distribution
Eq. (14), it sets the
fraction of DM in clumps,
appearing in the mass distribution
Eq. (14), it sets the
fraction of DM in clumps,
![]() .
.
The evolution of fM with
![]() and
and
![]() is shown in Fig. 1.
The behaviours are in agreement with the figures discussed in several
simulations. For example, taking a resolved mass
is shown in Fig. 1.
The behaviours are in agreement with the figures discussed in several
simulations. For example, taking a resolved mass
![]() ,
Shaw et al. (2007, and references therein) found
,
Shaw et al. (2007, and references therein) found
![]() for
for
![]() .
As argued in Diemand et al. (2007a),
where a larger value of
.
As argued in Diemand et al. (2007a),
where a larger value of
![]() is preferred, 10% might be only a
lower limit and this fraction could reach
is preferred, 10% might be only a
lower limit and this fraction could reach
![]() .
In the extreme
case of a slope
.
In the extreme
case of a slope
![]() ,
all the DM could be distributed in clumps,
even forbidding the existence of clumps of mass smaller than
,
all the DM could be distributed in clumps,
even forbidding the existence of clumps of mass smaller than ![]()
![]() .
This latter configuration is probably not realistic, so we
choose to limit the study to the range
.
This latter configuration is probably not realistic, so we
choose to limit the study to the range
![]() .
Consequently,
as observed from Fig. 1, the fraction of mass in clumps
.
Consequently,
as observed from Fig. 1, the fraction of mass in clumps
![]() ,
corresponding also to the additional mass added to
,
corresponding also to the additional mass added to
![]() (see Eq. (25)), will lie in the range
(see Eq. (25)), will lie in the range ![]() 10-40%.
10-40%.
Before plugging the propagation, it is interesting to have a look at the
luminosity of the source terms in the various configurations. The total
luminosity of DM sources can be separated into a particle physics
term times an astrophysical term:
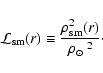 |
(26) |
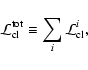 |
(27) |
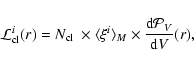 |
(31) |
Before concluding on resulting luminosities
![]() and
and
![]() ,
let us further detail
the various terms appearing in the clump luminosity term.
,
let us further detail
the various terms appearing in the clump luminosity term.
This quantity is a function of the mass clump M, and it depends
on the inner profile (NFW or Moore), the
![]() relation (B01 or ENS01)
and the saturation density
relation (B01 or ENS01)
and the saturation density
![]() .
.
![\begin{displaymath}\eta^{\rm nfw}(r)\equiv \left[ 1+\frac{r}{r_{\rm s}^{\rm nfw}(M)} \right]^{-3},
\end{displaymath}](/articles/aa/full/2008/08/aa8723-07/img269.gif) |
(35) |
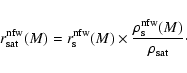 |
(36) |
The local intrinsic boost factor
![]() can also be
analytically expressed in terms of the virial parameters:
can also be
analytically expressed in terms of the virial parameters:
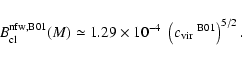 |
(38) |
|
|
|
|
|
|
|
|
| ( |
(kpc) | (kpc) | (
|
(kpc3) | ||
| 10-6 |
|
|
|
119 |
|
20 |
| 10-3 |
|
|
|
98 |
|
12 |
| 1 |
|
|
|
77 |
|
6.8 |
| 103 | 0.27 |
|
|
58 |
|
3.4 |
| 106 | 2.7 |
|
|
41 | 0.19 | 1.5 |
| 109 | 27 | 1 |
|
26 | 69 | 0.5 |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{FigAA/8723fig2.eps}\end{figure}](/articles/aa/full/2008/08/aa8723-07/Timg303.gif) |
Figure 2: Same as in Table 3. Each parameter is normalised with respect to its maximum value (in the mass range displayed). |
The differential luminosity Eq. (29) is evaluated taking into
account the mass distribution of clumps Eq. (14). The result
is shown in Fig. 4 for different values of the slope
![]() .
We recover the various trends seen in the literature (see, e.g. Fig. 8 of
Diemand et al. 2007a; Berezinsky et al. 2003). In particular,
the value
.
We recover the various trends seen in the literature (see, e.g. Fig. 8 of
Diemand et al. 2007a; Berezinsky et al. 2003). In particular,
the value
![]() ,
favoured in simulations, shows a roughly constant
luminosity per decade. For smaller (respectively greater) value of
,
favoured in simulations, shows a roughly constant
luminosity per decade. For smaller (respectively greater) value of
![]() ,
the luminosity will be dominated by the heaviest (lightest) clumps.
In that case, based upon the understanding gained from the previous
discussions, the boost is expected to be small (close to unity, from the
intrinsic boost factor).
At the same time, the variance of the clumpy signal is expected to be large
(light clumps add no contribution and heavy clumps are scarce).
For larger
,
the luminosity will be dominated by the heaviest (lightest) clumps.
In that case, based upon the understanding gained from the previous
discussions, the boost is expected to be small (close to unity, from the
intrinsic boost factor).
At the same time, the variance of the clumpy signal is expected to be large
(light clumps add no contribution and heavy clumps are scarce).
For larger
![]() ,
the mass
,
the mass
![]() of the lightest clump is crucial,
because the latter drives the total luminosity. These large
of the lightest clump is crucial,
because the latter drives the total luminosity. These large
![]() configurations are expected to give the largest boost factors. The last step
is to put together the smooth and clumpy luminosities.
configurations are expected to give the largest boost factors. The last step
is to put together the smooth and clumpy luminosities.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{FigAA/8723fig4.eps}\end{figure}](/articles/aa/full/2008/08/aa8723-07/Timg310.gif) |
Figure 4:
Differential luminosity (true units in kpc3) of the
population of clumps
|
The last hint at small boost factors for the case of antimatter DM
is given when comparing the smooth and clump luminosities.
This is first shown for the reference configuration
in Fig. 5 (top left panel).
As already emphasised (see also Diemand et al. 2007a), for the
reference configuration
![]() ,
the contributions to the average
annihilation fluxes of any decade mass range will be almost the same on the
whole range of mass clumps (see also Fig. 1 of Yuan & Bi 2007).
Around
,
the contributions to the average
annihilation fluxes of any decade mass range will be almost the same on the
whole range of mass clumps (see also Fig. 1 of Yuan & Bi 2007).
Around
![]() ,
the luminosity is completely dominated
by the smooth contribution (
,
the luminosity is completely dominated
by the smooth contribution (![]() 100 times more than the total clump
luminosity), so that for this configuration, we may predict beforehand (i)
no boost factor and (ii) a small variance on this boost factor.
100 times more than the total clump
luminosity), so that for this configuration, we may predict beforehand (i)
no boost factor and (ii) a small variance on this boost factor.
The logarithmic slope of the mass distribution
![]() reverses
hierarchy in the mass contribution: for
reverses
hierarchy in the mass contribution: for
![]() (see
Fig. 5, top right),
the more massive the population of clump the more luminous it is, whereas
for
(see
Fig. 5, top right),
the more massive the population of clump the more luminous it is, whereas
for
![]() (see Fig. 5, bottom left), the
less massive, the more luminous. The trade off is reached close to
(see Fig. 5, bottom left), the
less massive, the more luminous. The trade off is reached close to
![]() .
However, the total clump luminosity never reaches the level
of the smooth one! In the best case (
.
However, the total clump luminosity never reaches the level
of the smooth one! In the best case (
![]() ), it is 10 times smaller.
Nevertheless, taking larger
), it is 10 times smaller.
Nevertheless, taking larger
![]() values naturally leads to larger boost, in
a more general context.
values naturally leads to larger boost, in
a more general context.
Now, if we now assume that, instead of having a cored profile, the spatial distribution follows the parent one (NFW), we see in Fig. 5 (bottom right) that the situation is more favourable for the boost factors. Keep in mind that this is an upper limit since the the averaged radial mass density profile of clumps is believed to be a flatter distribution than the smooth one (see Sect. 2.3.2).
Anticipating the results of using ENS01 instead of B01, or using a Moore inner profile instead of a NFW, especially from Fig. 3, we already know that ENS01 will only further decrease the total clump luminosity (roughly by a factor of 10 compared to B01), whereas Moore will increase the total clump luminosity (roughly by a factor of 10 compared to NFW).
To summarise, from the general study of the luminosity, we might already
conclude that no configuration of DM will lead to huge boost factors.
Pushing all the parameters for the maximum effect, i.e. Moore inner profile,
NFW spatial distribution, B01 and
![]() ,
would possibly lead to a
boost factor of a few, but certainly not a hundred. We can expect all other
configurations to end up with a boost factor close to unity. The rest of the
paper is devoted to the full calculations to confirm these expectations.
,
would possibly lead to a
boost factor of a few, but certainly not a hundred. We can expect all other
configurations to end up with a boost factor close to unity. The rest of the
paper is devoted to the full calculations to confirm these expectations.
In the Galaxy, a charged particle travelling from its source to the solar neighbourhood is affected by several processes. The scattering off random magnetic fields leads to spatial and energy diffusion (reacceleration) and particles may also be spatially convected away by the galactic wind (which induces adiabatic losses).
In this paper, the framework used is the following
(e.g. Berezinskii et al. 1990): for the transport processes
we take a spatial independent diffusion coefficient
![]() (where
(where
![]() is the rigidity) and a constant wind
is the rigidity) and a constant wind ![]() directed
outwards along z. Cosmic rays are confined within a diffusive halo L,
such as the differential density,
directed
outwards along z. Cosmic rays are confined within a diffusive halo L,
such as the differential density,
![]() ,
is bound by
N(z=L,r)=0.
The free parameters of the model are the halo size
L of the Galaxy, the normalisation of the diffusion coefficient K0and its slope
,
is bound by
N(z=L,r)=0.
The free parameters of the model are the halo size
L of the Galaxy, the normalisation of the diffusion coefficient K0and its slope ![]() ,
and the constant galactic wind
,
and the constant galactic wind ![]() (see Sect. 4.3).
Other processes (such as continuous and catastrophic gain/losses)
are more species-dependent. Hence,
although all charged particles are propagated in the same framework,
due to this dependence, the phenomenology of propagation is completely
different for
(see Sect. 4.3).
Other processes (such as continuous and catastrophic gain/losses)
are more species-dependent. Hence,
although all charged particles are propagated in the same framework,
due to this dependence, the phenomenology of propagation is completely
different for
![]() and positrons.
and positrons.
The reader is referred to Maurin et al. (2001) for
a more detailed presentation and motivation of the framework.
Note that this model has been repeatedly and consistently used in several
studies to constrain the propagation parameters
(Maurin et al. 2001,2002; Donato et al. 2002)
and examine the consequences (Taillet & Maurin 2003; Maurin & Taillet 2003)
for the standard
![]() flux (Donato et al. 2001),
the exotic
flux (Donato et al. 2001),
the exotic
![]() and
and
![]() fluxes (Maurin et al. 2006a,2004; Barrau et al. 2005; Bringmann & Salati 2007; Barrau et al. 2002; Donato et al. 2004),
but also for positrons (Brun et al. 2007; Lavalle et al. 2007).
fluxes (Maurin et al. 2006a,2004; Barrau et al. 2005; Bringmann & Salati 2007; Barrau et al. 2002; Donato et al. 2004),
but also for positrons (Brun et al. 2007; Lavalle et al. 2007).
It was shown in Maurin et al. (2006a) that neglecting all energy
redistribution terms (energy losses, reacceleration and tertiary source term)
provides a correct description at sufficiently high energy, while remaining
good enough down to ![]() GeV IS energies (better than 50% depending on the
propagation parameters considered). This approximation is retained here.
The only catastrophic losses for anti-protons are spallations - the particle
does not survive the interaction.
GeV IS energies (better than 50% depending on the
propagation parameters considered). This approximation is retained here.
The only catastrophic losses for anti-protons are spallations - the particle
does not survive the interaction.
Denoting
![]() the destruction rate of
the destruction rate of
![]() in
the thin gaseous disk (
in
the thin gaseous disk (
![]() ,
He), the transport equation for a
point source, defining the propagator, reads (Maurin et al. 2006a):
,
He), the transport equation for a
point source, defining the propagator, reads (Maurin et al. 2006a):
 |
(40) |
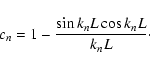 |
(42) |
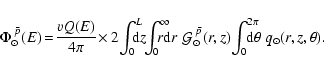 |
(43) |
Contrarily to nuclear species, there are no catastrophic losses for positrons.
A more crucial point is that propagation of positrons is dominated by energy
losses (e.g. Moskalenko & Strong 1998). In that case, a monochromatic
line at the source leads to a spectrum once propagated. This is at variance to
![]() whose propagator for exotic sources is at constant energy.
whose propagator for exotic sources is at constant energy.
The diffusion equation that characterises the evolution of the positron number
density N per unit energy, with a source term
![]() ,
reads
,
reads
We proceed as in Lavalle et al. (2007, and see references therein).
The synchrotron and inverse Compton losses can be written as
![]() ,
with E0=1 GeV and
,
with E0=1 GeV and
![]() .
Defining a pseudo-time
.
Defining a pseudo-time
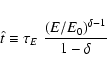
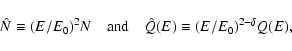
It proves convenient to separate diffusion along the radial and vertical
direction. Considering a source located at
![]() detected at
detected at
![]() ,
the corresponding flux depends only on the radial
relative distance
,
the corresponding flux depends only on the radial
relative distance
![]() ,
the distance of the source
from the plane z=zS and the relative pseudo-time
,
the distance of the source
from the plane z=zS and the relative pseudo-time
![]() .
The Green function
.
The Green function
![]() of
Eq. (45) is then given by:
of
Eq. (45) is then given by:
![$\displaystyle \phi_n(z) = \sin \left[ k_n (L-\vert z\vert) \right] ; \; k_n =
\left( n - \frac{1}{2} \right)\frac{\pi}{L}\;\; {\rm (even)}$](/articles/aa/full/2008/08/aa8723-07/img352.gif) |
|||
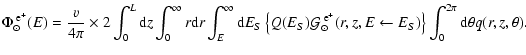 |
(50) |
The halo height L determines the total number of sources inside
the diffusive region and the typical distance a GCR can travel before escaping
from the Galaxy (see also Appendix A). The galactic wind wipes the
particles away from the disk, and a similar effect occurs if ![]() is large
enough. The parameters L,
is large
enough. The parameters L, ![]() and K0 are correlated.
In the subset of parameters giving the observed B/C ratio
(Maurin et al. 2001,2002), low values of K0 generally correspond to low L and
and K0 are correlated.
In the subset of parameters giving the observed B/C ratio
(Maurin et al. 2001,2002), low values of K0 generally correspond to low L and ![]() ,
so that the DM signal is
expected to decrease with decreasing K0. On that basis,
extreme and median parameters can be extracted, in the sense
that these parameters lead to the minimal and maximum expected flux,
while the median parameters (best fit to B/C data) provide the most
likely flux. These parameters are recalled in Table 4.
,
so that the DM signal is
expected to decrease with decreasing K0. On that basis,
extreme and median parameters can be extracted, in the sense
that these parameters lead to the minimal and maximum expected flux,
while the median parameters (best fit to B/C data) provide the most
likely flux. These parameters are recalled in Table 4.
| K0 (kpc2 Myr-1) | L (kpc) | |||
| max | 0.46 | 0.0765 | 15 | 5.0 |
| med | 0.70 | 0.0112 | 4 | 12.0 |
| min | 0.85 | 0.0016 | 1 | 13.5 |
Having in mind the connection between the propagation parameters and the
fluxes, we can now justify discarding, for our calculations,
the effects of the wind and reacceleration for the positrons. For example,
for configurations with small ![]() ,
as the effect of the wind is always
negligible for anti-protons, it is also the case for positrons (their travel
time in the Galaxy is less or at most that of the anti-protons).
For the sets of parameters with larger
,
as the effect of the wind is always
negligible for anti-protons, it is also the case for positrons (their travel
time in the Galaxy is less or at most that of the anti-protons).
For the sets of parameters with larger ![]() ,
the effect of the
wind becomes dominant below
,
the effect of the
wind becomes dominant below ![]() 1 GeV. However, we are mainly
interested in the high energy regime for positrons. Furthermore, if the
low-energy behaviour is strongly dominated by convection (as is the case for
anti-protons when
1 GeV. However, we are mainly
interested in the high energy regime for positrons. Furthermore, if the
low-energy behaviour is strongly dominated by convection (as is the case for
anti-protons when
![]() ), then it superseeds energy loss effects for
positrons: in that case, all the conclusion about
), then it superseeds energy loss effects for
positrons: in that case, all the conclusion about
![]() would also hold for
would also hold for ![]() .
.
The smooth contribution is straightforwardly calculated, contrarily to the clumpy contribution that is plagued by statistical uncertainties (in the sense that the position of clumps is a random variable, see Sect. 5.2). The latter issue is the primary concern of this section.
Two complementary approaches are followed to calculate the Galactic variance of the clumpy contribution. The first one (Lavalle et al. 2007) is a semi-analytical calculation of the mean and variance from the generic statistical properties of the clumps (spatial and mass distributions), using the particle propagators that we recalled. The second one uses the same ingredients, but quantities under scrutiny (mean and variance) are obtained by accumulating realisations of a clumpy galactic halo. Due to the lack of any clue about the precise location and intrinsic properties of each individual DM clump, working with statistical tools is well motivated. The numerous clumps can be treated as random objects, which average properties are taken here from N-body simulations.
Note that both methods rest on the assumption that clumps are considered as point-like sources. This is correct while the distance of a clump to the Earth is greater than its spatial extension, and if the GCR propagation properties do not change within the spatial extension of a clump (see Table 3). As the flux, on average, is not dominated by nearby substructures, and since for those far away clumps the spatial dependence of the propagator is smooth enough (diffusive process), the point-like source assumption holds. Would a nearby clump dominate the positron or anti-proton flux - which is very unlikely according to our calculation - a single source computation would be enough to deal with the clumpiness issue. Nevertheless, such a case, while easier to calculate, would make the clumpiness itself an absolutely unpredictive scenario for the indirect search for DM using antimatter GCRs, and is beyond the scope of this paper.
Before exposing the methods, it is convenient to define a pseudo-Green
function, denoted
![]() ,
by absorbing the energy dependence of the
GCR propagators. To this aim, we define the quantity
,
by absorbing the energy dependence of the
GCR propagators. To this aim, we define the quantity
![]() to be the
antimatter species spectrum at the source, which is defined here as the number
of antimatter particles injected per annihilation and per energy unit.
to be the
antimatter species spectrum at the source, which is defined here as the number
of antimatter particles injected per annihilation and per energy unit.
For anti-protons, the pseudo-Green function reads:
In the following, we will make use of
![]() ,
where the energy
dependence is implicit for any species.
,
where the energy
dependence is implicit for any species.
The total GCR flux
![]() originating from DM annihilations may be
separated into two contributions, for the smooth component and for clumps:
originating from DM annihilations may be
separated into two contributions, for the smooth component and for clumps:
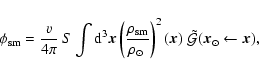 |
(54) |
In this section, we apply the formalism developed in Lavalle et al. (2007) in order to predict how boosted the antimatter cosmic ray fluxes should be when adding sub-halos.
As the intrinsic luminosity of a clump is entirely set once its mass is known,
the effective volume ![]() can be expressed as
can be expressed as
![]() .
Thus, given Eq. (57), the flux associated with a single
clump is a stochastic variable that depends on two probability
distributions: the space and the mass distributions
(Sect. 2.3). This is summarised in the following
equation:
.
Thus, given Eq. (57), the flux associated with a single
clump is a stochastic variable that depends on two probability
distributions: the space and the mass distributions
(Sect. 2.3). This is summarised in the following
equation:
The halo is populated by a constellation of many clumps whose total
contribution to the GCR flux is given by
The fact that we do not know how clumps are actually distributed, in the phase
space defined by their locations and masses, can be expressed in terms of a
variance
![]() associated with their total mean flux
associated with their total mean flux
![]() .
For a single clump, the relative
flux variance is given by:
.
For a single clump, the relative
flux variance is given by:
The resulting relative flux variance for the whole population of sub-halos is
then merely:
Once the contribution of sub-halos to the flux is fully determined, the boost factor is easily computed for any species. As cosmic ray propagation has an explicit energy dependence, the boost factor is also energy-dependent (Lavalle et al. 2007), and, of course, also depends on the cosmic ray species (Maurin & Taillet 2003).
The energy-dependent mean effective boost factor is given by the sum of the
clumpy and the smooth contribution divided by the flux that would provide the
only smooth reference halo
![]() (see Sect. 3.1.1):
(see Sect. 3.1.1):
It may be useful to determine the limit for which only an infinitely small
volume around the Earth
![]() is taken into
account. Actually, this will give a rough estimate of the asymptotic
(maximum) value of the boost factor for both positrons (at detected
energies very close to injected energies) and anti-protons (at low
energies), because we are blind to contributions from regions close to the
Galactic centre - where the smooth DM density dominates - in this case. This
local asymptotic value is given by:
is taken into
account. Actually, this will give a rough estimate of the asymptotic
(maximum) value of the boost factor for both positrons (at detected
energies very close to injected energies) and anti-protons (at low
energies), because we are blind to contributions from regions close to the
Galactic centre - where the smooth DM density dominates - in this case. This
local asymptotic value is given by:
The above value of the boost factor fluctuates up to a variance
![]() ,
which reads
,
which reads
A complementary approach is to calculate and add explicitly the contribution
of each clump by MC drawing. Simulating many realisations of the DM
sub-halos is another way to extract the mean flux as well as the variance
of the clump contribution. The ensuing calculation of boost factors
is as before, but in addition, MC provides the law of probability for the
stochastic variable
![]() that describes the single clump flux, which
is hardly inferred from the clump phase space distribution itself due
to the needed convolution with propagation.
that describes the single clump flux, which
is hardly inferred from the clump phase space distribution itself due
to the needed convolution with propagation.
From a technical point of view, it is very inefficient to calculate
contributions from so many sub-halos (e.g. ![]() 1015 for the lightest
ones) one at a time. Indeed, for the clumps in a given mass range, two types
of contributions exist. For low mass clumps, which are numerous, the variance
associated with the flux is expected to be small (i.e.
1015 for the lightest
ones) one at a time. Indeed, for the clumps in a given mass range, two types
of contributions exist. For low mass clumps, which are numerous, the variance
associated with the flux is expected to be small (i.e.
![]() ). In this case, we can spare the effort of averaging many
configurations and directly compute the flux from a single realisation.
Conversely, as the mass of the sub-halos increases, the associated number of
clumps decreases, so that the variance finally become sizable. A threshold
mass
). In this case, we can spare the effort of averaging many
configurations and directly compute the flux from a single realisation.
Conversely, as the mass of the sub-halos increases, the associated number of
clumps decreases, so that the variance finally become sizable. A threshold
mass
![]() needs to be specified, below which the contribution to the
total variance
needs to be specified, below which the contribution to the
total variance
![]() can be neglected: only sub-halos
that have masses
can be neglected: only sub-halos
that have masses
![]() need to be calculated for all samplings.
The value of
need to be calculated for all samplings.
The value of
![]() is discussed in Appendix A.
is discussed in Appendix A.
For one sample, the total annihilation flux observed in the solar
neighbourhood may be rewritten as
When taking into account all realisations:
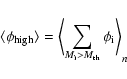
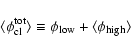 |
(75) |
The total flux and variance are now given by
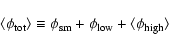 |
(77) |
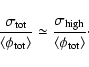 |
(78) |
Fluxes, boost factors and associated variances have been calculated for both positrons and anti-protons using a semi-analytical approach (Sect. 5.2) and, for the sake of comparison, MC simulations (Sect. 5.3).
The coming results are based on a fiducial model for the injection of
antimatter in the Galaxy, which allows a WIMP-model-independent analysis. In
practise, for positrons, a monochromatic line of 200 GeV is injected at a rate
assumed to be proportional to the squared density of DM in
sources. In order to recover realistic orders of magnitude, especially for
fluxes, we will also suppose that those positrons originate from, e.g.
not-s-wave-suppressed annihilations of WIMPs at rest, with masses of 200 GeV
and annihilation cross-section
![]() cm3 s-1 (for instance, Dirac fermions/anti-fermions with only
trilinear couplings to
cm3 s-1 (for instance, Dirac fermions/anti-fermions with only
trilinear couplings to
![]() ,
where
,
where
![]() would be some
exotic - conjugate - charged scalar fields). Besides, because anti-protons do not
loose energy, we took their injection spectrum to be constant
would be some
exotic - conjugate - charged scalar fields). Besides, because anti-protons do not
loose energy, we took their injection spectrum to be constant
![]() between kinetic energies 0.1-200 GeV (any spectrum
could have been taken, as it can be factorised out). One can easily guess what
the results for any injection spectrum would be (originating from
hadronisation or fragmentation processes for instance) by a mere rescaling. In
this case, the WIMP properties can be almost the same as for positrons: fluxes
have been computed using a Majorana WIMP with a mass of 200 GeV, and an
annihilation cross-section of
between kinetic energies 0.1-200 GeV (any spectrum
could have been taken, as it can be factorised out). One can easily guess what
the results for any injection spectrum would be (originating from
hadronisation or fragmentation processes for instance) by a mere rescaling. In
this case, the WIMP properties can be almost the same as for positrons: fluxes
have been computed using a Majorana WIMP with a mass of 200 GeV, and an
annihilation cross-section of
![]() .
.
Before going into the details of the studied configurations, we show in
Fig. 6 the extreme cases that we obtained for both
species (with the medium set of propagation parameters). The first line panels
are plots of the smooth and sub-halo fluxes and the resulting effective
boosts, with associated ![]() statistical contours. The second line
panels are the same plots, but for anti-protons. The maximal
configuration is given by: largest
statistical contours. The second line
panels are the same plots, but for anti-protons. The maximal
configuration is given by: largest
![]() (2), cuspiest sub-halo
inner profile (Moore), smallest
(2), cuspiest sub-halo
inner profile (Moore), smallest
![]() (
(
![]() ), spatial distribution
according to the smooth NFW profile, and the B01 concentration model. The
minimal configuration is the reverse: smallest
), spatial distribution
according to the smooth NFW profile, and the B01 concentration model. The
minimal configuration is the reverse: smallest
![]() (1.8), flattest
inner profile (NFW), greatest
(1.8), flattest
inner profile (NFW), greatest
![]() (
(
![]() ), and smallest local
number density (cored isothermal profile). The intermediate is close to
the reference configuration, given in Sect. 3.1.2, and takes
the most likely values of parameters according to N-body simulations (except
for
), and smallest local
number density (cored isothermal profile). The intermediate is close to
the reference configuration, given in Sect. 3.1.2, and takes
the most likely values of parameters according to N-body simulations (except
for
![]() ,
of which the used reference value is
,
of which the used reference value is
![]() ;
and for the
spatial distribution of sub-halos which tracks the smooth NFW profile).
;
and for the
spatial distribution of sub-halos which tracks the smooth NFW profile).
From this figure, we see that the boost factors obtained are functions of the
energy and lie between 1 and 20, with small statistical uncertainties. Such
a range has to be taken as that of theoretical uncertainties affecting
the DM distribution in the Galaxy. From the approximate
Eq. (68), the asymptotic values obtained are also 1 and 20
(neglecting the density fraction
![]() ), which are in excellent agreement
with our full results. Before going into deeper details, it is worth
emphasising that the maximal value of
), which are in excellent agreement
with our full results. Before going into deeper details, it is worth
emphasising that the maximal value of ![]() 20 is as large as unlikely, as
already discussed in Sect. 2. For completeness, we have checked our
results with MC simulations (see Sect. 5.3). In
Fig. 7, we
show that the agreement between the MC and the semi-analytic calculation
is excellent for anti-protons, up to a few percents. It is the same for
positrons, as already demonstrated in Brun et al. (2007); Lavalle et al. (2007).
20 is as large as unlikely, as
already discussed in Sect. 2. For completeness, we have checked our
results with MC simulations (see Sect. 5.3). In
Fig. 7, we
show that the agreement between the MC and the semi-analytic calculation
is excellent for anti-protons, up to a few percents. It is the same for
positrons, as already demonstrated in Brun et al. (2007); Lavalle et al. (2007).
Remembering that the whole sub-halo flux reads
![]() ,
it makes sense to
gather
the impact of the various ingredients into two main physical classes.
,
it makes sense to
gather
the impact of the various ingredients into two main physical classes.
Once the space distribution of sub-halos and the propagation model are fixed,
the propagator mean value
![]() of the sub-halo
flux Eq. (60) is fully determined, as well as its
statistical fluctuation
of the sub-halo
flux Eq. (60) is fully determined, as well as its
statistical fluctuation ![]() .
Hence, provided the WIMP model
is also fixed, the only differences from one sub-halo configuration to another
will be the averaged total amount of antimatter yielded by clumps, given by
the integrated clump luminosity
.
Hence, provided the WIMP model
is also fixed, the only differences from one sub-halo configuration to another
will be the averaged total amount of antimatter yielded by clumps, given by
the integrated clump luminosity
![]() ,
and its associated fluctuations. Such a quantity depends on two
parameters only:
,
and its associated fluctuations. Such a quantity depends on two
parameters only:
![]() and
and
![]() (plus the concentration-mass relation,
plus the choice of the inner sub-halo profile). A decrease of
(plus the concentration-mass relation,
plus the choice of the inner sub-halo profile). A decrease of
![]() enhances
the total number of clumps in the Galaxy, and an increase of
enhances
the total number of clumps in the Galaxy, and an increase of
![]() raises
the relative density of light compared to heavy objects (and the total
luminosity accordingly because the clump number density is normalised with
respect to the heaviest clumps, as given in Eq. (17)). More precisely,
we find the luminosity to approximately scale with
raises
the relative density of light compared to heavy objects (and the total
luminosity accordingly because the clump number density is normalised with
respect to the heaviest clumps, as given in Eq. (17)). More precisely,
we find the luminosity to approximately scale with
![]() only logarithmically
(see the details in Appendix B.1) like:
only logarithmically
(see the details in Appendix B.1) like:
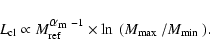 |
(79) |
Regarding the pure mass-related relative fluctuations, given by
![]() (see Eq. (63)), we
would naively expect them to significantly deplete when decreasing
(see Eq. (63)), we
would naively expect them to significantly deplete when decreasing
![]() ,
which enhances the total number of clumps. Furthermore, since the relative
luminosity of light clumps is raised by increasing
,
which enhances the total number of clumps. Furthermore, since the relative
luminosity of light clumps is raised by increasing
![]() ,
the relative
variance should be significantly reduced accordingly. Nevertheless,
interestingly, we find the mass-related relative fluctuations to roughly scale
like
,
the relative
variance should be significantly reduced accordingly. Nevertheless,
interestingly, we find the mass-related relative fluctuations to roughly scale
like
![]() ,
and to vary only in the range 0.1-10% when
spanning over (
,
and to vary only in the range 0.1-10% when
spanning over (
![]() ,
,
![]() )
from minimal to maximal parameter sets (see
above). The physical interpretation is the following: as
)
from minimal to maximal parameter sets (see
above). The physical interpretation is the following: as
![]() goes up, the
number of clumps decreases accordingly, but in the meantime, the intrinsic
clump luminosity (
goes up, the
number of clumps decreases accordingly, but in the meantime, the intrinsic
clump luminosity (![]()
![]() ), which is fixed by the mass, fluctuates much
less from clump to clump; there is a trade-off between shrinking the
statistical sample and reducing the phase space, so that the relative
mass-related variance remains almost constant. Taking a Moore inner profile
does not affect the relative mass-related variance, while adopting the ENS01
mass-concentration relation increases it by a few (see the third line panels
of Fig. 8).
), which is fixed by the mass, fluctuates much
less from clump to clump; there is a trade-off between shrinking the
statistical sample and reducing the phase space, so that the relative
mass-related variance remains almost constant. Taking a Moore inner profile
does not affect the relative mass-related variance, while adopting the ENS01
mass-concentration relation increases it by a few (see the third line panels
of Fig. 8).
As a consequence, the global flux relative variance given in
Eqs. (63) and (66), should vary over two
orders of magnitude at most, once the GCR propagation is fixed and at a given
energy. Indeed, as mass-related uncertainties are almost always greater than
space-related ones (see Appendix B.1), the dominant
contribution is the space-mass crossing term
![]() ,
so
that the global relative variance encompasses values in the range
,
so
that the global relative variance encompasses values in the range
![]() when varying
when varying
![]() and
and
![]() from extreme configurations.
from extreme configurations.
From the previous statements together with the luminosity profiles already
discussed and shown in Fig. 5, scanning over
the most likely mass-related parameters is unlikely to make the sub-halo
contribution dominate over the smooth flux, except for extreme configurations
combining the B01 concentration model, Moore inner profiles, large
![]() and very small
and very small
![]() .
.
![\begin{figure}
\par\includegraphics[width=3.8cm,clip]{FigAA/8723fig9a.eps}\hspac...
...hspace*{4mm}
\includegraphics[width=3.8cm,clip]{FigAA/8723fig9h.eps}\end{figure}](/articles/aa/full/2008/08/aa8723-07/Timg447.gif) |
Figure 9: Space-related effects on positrons, with the same panel organisation as in Fig. 8. First row: effects of varying the GCR propagation modelling, by using the three propagation sets of parameters of Table 4. Second row: effect of varying the space distribution of sub-halos, going from the cored isothermal space distribution to a case in which sub-halos track the smooth NFW component (for completeness, we also take an example where we also modify the inner sub-halo profile by taking a Moore instead of an NFW). |
The space-related effects for positrons come through the averaging of the
propagator
![]() over the sub-halo spatial
distribution. We summarise here a more detailed discussion that will be found
in the appendix (see Appendix B.2). The relevant
scale is the propagation scale
over the sub-halo spatial
distribution. We summarise here a more detailed discussion that will be found
in the appendix (see Appendix B.2). The relevant
scale is the propagation scale
![]() that depends on both diffusion and
energy loss processes for positrons.
that depends on both diffusion and
energy loss processes for positrons.
![]() is obviously larger for
larger diffusion coefficients, and smaller when the detected energy gets
closer to the injected energy. Since it is of the order of kpc, we can safely
focus on local quantities. Actually,
is obviously larger for
larger diffusion coefficients, and smaller when the detected energy gets
closer to the injected energy. Since it is of the order of kpc, we can safely
focus on local quantities. Actually,
![]() encodes an
effective detection volume bound by
encodes an
effective detection volume bound by
![]() and weighted by the clump
spatial probability function
and weighted by the clump
spatial probability function
![]() in the solar neighbourhood. In
the limit of infinite 3D diffusion, and when the propagation length is small
enough, we find in Appendix B.2 that
in the solar neighbourhood. In
the limit of infinite 3D diffusion, and when the propagation length is small
enough, we find in Appendix B.2 that
![]() .
Hence, the averaged propagator increases linearly with the local value of the
clump spatial probability function. As
.
Hence, the averaged propagator increases linearly with the local value of the
clump spatial probability function. As
![]() for the reference case (clumps are spatially
distributed according to a cored isothermal profile), we see that given
mass-related parameters, a configuration in which the clumps track the smooth
profile will give a higher flux.
for the reference case (clumps are spatially
distributed according to a cored isothermal profile), we see that given
mass-related parameters, a configuration in which the clumps track the smooth
profile will give a higher flux.
Regarding the pure space-related relative variance for a single object
![]() ,
we find it to scale like
,
we find it to scale like
![]() ,
thus, decreasing when the
effective detection volume or the clump local spatial probability increase
(detected energies much lower than injected ones). When
taking the whole contribution, an additional factor of
,
thus, decreasing when the
effective detection volume or the clump local spatial probability increase
(detected energies much lower than injected ones). When
taking the whole contribution, an additional factor of
![]() reduces the global variance, and the picture becomes very simple: the
relative space-related variance scales like
reduces the global variance, and the picture becomes very simple: the
relative space-related variance scales like
![]() ,
one over
the square root of the number of clumps contributing to the signal at the
Earth. It is maximal at high energy for positrons.
,
one over
the square root of the number of clumps contributing to the signal at the
Earth. It is maximal at high energy for positrons.
To summarise, the space-related contribution for positrons increases with the diffusion coefficient, and with the clump local space probability function. The relative space-related variance decreases when the propagation length raises (at low energy for positrons), because a larger number of sub-halos can contribute to the signal at the Earth.
Taking this fiducial injection model, we assess the different effects and draw four typical plots, which will compose four specific panels in the next figures, from left to right: positron flux, relative flux variance, boost factor, relative boost variance (as functions of the positron detected energy).
Figure 8 illustrates the mass-like effects, whereas Fig. 9 show the space-like ones.
In the second line panels of Fig. 8,
![]() is varied, giving three different mass configurations: 1.8, 1.9 and 2.0. As expected, the flux due to sub-halos is affected, and predictions
slightly spread within one order of magnitude (a factor of
is varied, giving three different mass configurations: 1.8, 1.9 and 2.0. As expected, the flux due to sub-halos is affected, and predictions
slightly spread within one order of magnitude (a factor of ![]() 30 between 1.8 and 2.0). The relative flux variance is lower for large values of
30 between 1.8 and 2.0). The relative flux variance is lower for large values of
![]() ,
as expected, because this
increases the total number of sub-halos, more precisely the lighter ones.
Nevertheless, varying
,
as expected, because this
increases the total number of sub-halos, more precisely the lighter ones.
Nevertheless, varying
![]() within the reference configuration is not
enough for sub-halos to strongly dominate over the smooth contribution: the
averaged boost factors associated with the three examples lie around unity,
even when getting closer to the injected energy (the maximum value is 1.08
for
within the reference configuration is not
enough for sub-halos to strongly dominate over the smooth contribution: the
averaged boost factors associated with the three examples lie around unity,
even when getting closer to the injected energy (the maximum value is 1.08
for
![]() ), with small statistical uncertainties.
), with small statistical uncertainties.
The third line of Fig. 8 shows the consequences
of varying the mass-concentration relation and the inner sub-halo profile. The
reference model, which is inner NFW + B01, is compared with NFW+ENS01 (less
concentrated sub-halos) and with Moore+B01 (more cuspy sub-halos). As
expected, the flux obtained with the ENS01 concentration model is far below
the reference one, by a factor of ![]() 20, whereas the Moore sub-halos gives
ten times more
signal (this can also be seen from Fig. 3). These
ratios are constant with the detected energy, as they are characterised by the
ratios of
20, whereas the Moore sub-halos gives
ten times more
signal (this can also be seen from Fig. 3). These
ratios are constant with the detected energy, as they are characterised by the
ratios of
![]() 's. Again, we see that the expected boost
factor is again negligible in all cases, around unity (
's. Again, we see that the expected boost
factor is again negligible in all cases, around unity (![]() 1.13 for the
best case, i.e. Moore inner profile + B01). Nevertheless, the increase of the
variance associated with the latter happens at lower energies than previously,
because the probability for a single clump to contribute more than the smooth
component becomes sizable at farther distances.
1.13 for the
best case, i.e. Moore inner profile + B01). Nevertheless, the increase of the
variance associated with the latter happens at lower energies than previously,
because the probability for a single clump to contribute more than the smooth
component becomes sizable at farther distances.
Finally, the second line panels of Fig. 9
show the effect of changing the spatial distribution of clumps, from the
reference cored isothermal to a situation in which they track the smooth NFW
profile. For completeness, we do the exercise for both inner NFW and Moore
profiles. In the left panels, we see that the sub-halo flux is enhanced when
they track the smooth profile, of about one order of magnitude in this case.
The effect is obviously stronger when an inner Moore density is taken, for
which another order of magnitude arises. Nevertheless, the boost factors do
not obey the same hierarchy. This is due to the way the smooth component is
normalised when clumps are added. Indeed, we chose to readjust the smooth
density by a factor
![]() ,
where the fraction density
,
where the fraction density ![]() is defined
in Eq. (22), in order to get a constant local density
is defined
in Eq. (22), in order to get a constant local density
![]() .
When clumps track the smooth component, their number density is
enhanced in the local neighbourhood, so that
.
When clumps track the smooth component, their number density is
enhanced in the local neighbourhood, so that ![]() is enhanced accordingly.
As the boost factor remains around
is enhanced accordingly.
As the boost factor remains around
![]() (the sub-halo contribution
is negligible), except when considering inner Moore profiles, the case for
which clumps track the smooth component is worse. However, taking an inner
Moore profile for clumps gives a higher flux than the smooth alone, and
the mean boost factor can reach an asymptotic value of
(the sub-halo contribution
is negligible), except when considering inner Moore profiles, the case for
which clumps track the smooth component is worse. However, taking an inner
Moore profile for clumps gives a higher flux than the smooth alone, and
the mean boost factor can reach an asymptotic value of ![]() 2-3.
2-3.
In summary, we have shown, by extensively playing with the maximum number of
available parameters, that sizable boost factors to the positron flux are
unlikely to arise from clumpiness. There could be situations in which a
single sub-halo would be close enough to the Earth to dominate over the smooth
component, but within the most reasonable modellings, the probability for
this to happen is vanishingly small. Nevertheless, in order to provide more
optimistic scenarios, even if less realistic according to the standard
values of the parameters, a model characterised by
![]() sub-halos
with inner Moore profiles, with concentrations described by the B01 relation,
spatially tracking the smooth DM density, would yield a mean boost factor
whose asymptotic value would be around 3 for a logarithmic slope
sub-halos
with inner Moore profiles, with concentrations described by the B01 relation,
spatially tracking the smooth DM density, would yield a mean boost factor
whose asymptotic value would be around 3 for a logarithmic slope
![]() = 1.9
(see lower panels of Fig. 8). Taking
= 1.9
(see lower panels of Fig. 8). Taking
![]() = 2 leads to a boost of
= 2 leads to a boost of ![]() 20 (see Fig. 6). This is
the most optimistic estimate that we can provide so far, but also the most
unrealistic. Note finally that although the primary fluxes may vary by 2 orders of magnitude due to uncertainties in the propagation parameters
(see Table 4 and upper panels
of Fig. 9),
the resulting average boost factors are unaffected because they are defined
as flux ratios; the variance is nevertheless larger when the GCR horizon is
reduced (min configuration).
20 (see Fig. 6). This is
the most optimistic estimate that we can provide so far, but also the most
unrealistic. Note finally that although the primary fluxes may vary by 2 orders of magnitude due to uncertainties in the propagation parameters
(see Table 4 and upper panels
of Fig. 9),
the resulting average boost factors are unaffected because they are defined
as flux ratios; the variance is nevertheless larger when the GCR horizon is
reduced (min configuration).
The HEAT experiment results for the 1994 flight hinted at the possibility of
an excess of positrons near 8 GeV (Barwick et al. 1997), which could not
be explained by a purely secondary production
mechanism (Coutu et al. 1999). Baltz & Edsjö (1999) then found
that neutralino annihilation could account for the missing flux providing that
boost factors are larger than six; at that time, these authors estimate
realistic boost factors to fall in the range
![]() .
Note that such high boost factors would be ruled out in the present study.
However, later on, combining both 1994 and 1995 HEAT balloon flights,
DuVernois et al. (2001) concluded that the positrons flux
was consistent with a secondary origin. Results
from the MASS91 balloon-borne magnetic spectrometer above 7 GeV
(Grimani et al. 2002) do not provide a definitive answer either.
As emphasised by these authors, very high energy
.
Note that such high boost factors would be ruled out in the present study.
However, later on, combining both 1994 and 1995 HEAT balloon flights,
DuVernois et al. (2001) concluded that the positrons flux
was consistent with a secondary origin. Results
from the MASS91 balloon-borne magnetic spectrometer above 7 GeV
(Grimani et al. 2002) do not provide a definitive answer either.
As emphasised by these authors, very high energy ![]() 100 GeV
measurements are probably necessary to positively conclude for
standard or exotic mechanisms. Finally, from the most recent data
coming from the HEAT 2000 flight, Beatty et al. (2004) cautiously
conclude that a primary contribution above a few GeV can still not
be ruled out.
100 GeV
measurements are probably necessary to positively conclude for
standard or exotic mechanisms. Finally, from the most recent data
coming from the HEAT 2000 flight, Beatty et al. (2004) cautiously
conclude that a primary contribution above a few GeV can still not
be ruled out.
Given these observations, several subsequent studies have focused on finding a good DM candidate to explain this possible excess. We do not wish to comment here on the best candidate, but rather survey the boost factors used in the studies. For example, for SUSY candidates, boost factors of 2.7 and 3.9 were used in Kane et al. (2002b), values in the range 30-100 in Baltz et al. (2002), from small to large boost factors in Kane et al. (2002a), in the range 1-5 in Hisano et al. (2006), and around 100 in Cumberbatch & Silk (2007). Mambrini et al. (2006) favoured boosts of 5-10 to accommodate the expected measurements of PAMELA, for SUSY models with non-universal scalar and gaugino masses. For KK DM, Hooper & Kribs (2004) found a range of 10-30. The boost factor used to fit the data depends of course on the WIMP candidate considered and its mass.
It appears that most of the models found so far to match the positron data
require mild to significant boost factors. Such boost factors are disfavoured
by our results if the clump parameters fall in the large ranges taken in this
study. A high energy feature in the positrons data could still be an important
clue to DM indirect detection, and it would be interesting in forthcoming
studies to scan, e.g. the SUSY parameter space looking for models matching
the data without boost factors. According to Asano et al. (2007),
the little Higgs model provides good options for detectability by the AMS-02
experiment, but could be short for PAMELA. In addition, it is worth noting
that if some ![]() -like searches for clump signatures are performed in the
coming positron data, it will be very important to take the energy dependence
of any boost factor into account, as soon as it is invoked.
-like searches for clump signatures are performed in the
coming positron data, it will be very important to take the energy dependence
of any boost factor into account, as soon as it is invoked.
To conclude, although having no boost factors may be less interesting
for SUSY theories to explain the data, any result that will be obtained
when comparing to forthcoming data, if an excess is confirmed, will be more
robust if no boost factor (an additional unknown parameter till now) is
invoked. We recall that the two main uncertainties for WIMP annihilation
induced antimatter signals are the propagation parameters in the Galaxy
(a factor ![]() 100) and the local DM density
(a factor
100) and the local DM density
(a factor ![]() 2, that shifts to 4 in terms of annihilation rate).
2, that shifts to 4 in terms of annihilation rate).
First of all, it is worth quoting that contrary to positrons, for which an excess is still not understood, anti-proton present measurements are now well accounted for by purely standard secondary production (e.g. Donato et al. 2001). This means that there is no need of DM, and obviously of any clump to fit the data: the present data has to be consider as an upper limit for the DM contribution. Things could change with the future results of PAMELA and AMS-02 at higher energies.
The flux enhancement for anti-protons has features different from positrons, as already stressed by Bringmann & Salati (2007) and Brun et al. (2007). This is mainly due to propagation, which is quite different from the positron case. Indeed, anti-protons do not lose energy, and can experience spallation processes and wind convection along their travel to the Earth, which occurs to be dominant at low energy. Nevertheless, as for positrons, the same classes of physical effects can be discussed.
Regarding the space-related effects, the comments are the same as for positrons but with a reversal energy point of view (see Appendix B.3). The relative variance is then maximal at low anti-proton energy. Note, however, that the three sets of propagation parameters give separate absolute fluxes (decreasingly according to max, med and min), whereas max and med configurations give about the same fluxes for positrons.
We now discuss the origin of systematic differences when varying the DM configuration as well as the propagation modelling. Figure 10 illustrates effects that are of mass type, while Fig. 11 shows the space-related ones. They are presented the same way as for positrons.
For the mass-type category, the comments are exactly the same as those for positrons, and are already discussed in Sect. 6.2.2.
Regarding space-related consequences, the picture is the reversal from that of positrons, and the conclusion are the same as for positron, given the energy axis is read inversely.
In summary, the maximum boost factor occurs at low anti-proton energies
when clumps are spatially distributed according to the smooth profile, and
when they have an inner Moore profile. But even in this (disfavoured)
configuration, the asymptotic mean value of the enhancement factor is ![]() 3.
3.
![\begin{figure}
\par\includegraphics[width=3.8cm,clip]{FigAA/8723fig10a.eps}\hspa...
...space*{4mm}
\includegraphics[width=3.8cm,clip]{FigAA/8723fig10l.eps}\end{figure}](/articles/aa/full/2008/08/aa8723-07/Timg468.gif) |
Figure 10:
Mass-related effects for anti-protons; a toy flat
spectrum is injected at the sources, at a rate corresponding to
standard values of WIMP annihilation - same panel organisation
as for positrons (see Fig. 8). First
row: varying
|
![\begin{figure}
\par\includegraphics[width=3.8cm,clip]{FigAA/8723fig11a.eps}\hspa...
...space*{4mm}
\includegraphics[width=3.8cm,clip]{FigAA/8723fig11h.eps}\end{figure}](/articles/aa/full/2008/08/aa8723-07/Timg469.gif) |
Figure 11: Same than Fig. 9, but focusing on space-related effects for anti-protons. First row: varying the propagation modelling. Second row: varying the space distribution (and the sub-halo inner profile). |
Clumpiness is a robust prediction of hierarchical structure formation, where
the bottom-up growth of structures is a consequence of the
![]() cosmology.
Many issues remain about clumps, beside their survival, such as their number
density, their mass and spatial distribution, as well as their intrinsic
properties. In recent years, high resolution N-body simulations succeeded
in tracing their gross features, although we are still far from a definite
answer for several key parameters. Indeed, whereas numerical experiments
now converge to a level better than 10% over wide dynamic ranges
(Heitmann et al. 2007), the inclusion of baryons in hydrodynamical
simulations, which could strongly modify the inner properties of sub-halos,
remains a very difficult task.
cosmology.
Many issues remain about clumps, beside their survival, such as their number
density, their mass and spatial distribution, as well as their intrinsic
properties. In recent years, high resolution N-body simulations succeeded
in tracing their gross features, although we are still far from a definite
answer for several key parameters. Indeed, whereas numerical experiments
now converge to a level better than 10% over wide dynamic ranges
(Heitmann et al. 2007), the inclusion of baryons in hydrodynamical
simulations, which could strongly modify the inner properties of sub-halos,
remains a very difficult task.
The impact of the DM inhomogeneities on DM annihilation
in the Galaxy was first underlined in Silk & Stebbins (1993).
With the achievement of cosmological N-body simulations in the last decade,
and due to their positive results on clumpiness, many papers have
subsequently focused on the consequences for the phenomenology of SUSY
indirect detection in several channels, involving ![]() -rays and antimatter
GCRs (e.g. Bergström et al. 1999). The effects for
-rays and antimatter
GCRs (e.g. Bergström et al. 1999). The effects for ![]() -rays
have been extensively studied, whereas diffusion processes make the study
much more difficult for antimatter GCRs. Berezinsky et al. (2003) carried
out a detailed study of boost factors for
-rays
have been extensively studied, whereas diffusion processes make the study
much more difficult for antimatter GCRs. Berezinsky et al. (2003) carried
out a detailed study of boost factors for ![]() -ray signal (so the
conclusions also hold for neutrinos), and concluded to a factor of 2 to 5 for
different density profiles in a clump. However, whether or not primary
antimatter fluxes may be boosted by clumpiness is an important issue for the
interpretation of forthcoming data, especially for positrons (see the
discussion below), and for putting more robust constraints on new physics.
-ray signal (so the
conclusions also hold for neutrinos), and concluded to a factor of 2 to 5 for
different density profiles in a clump. However, whether or not primary
antimatter fluxes may be boosted by clumpiness is an important issue for the
interpretation of forthcoming data, especially for positrons (see the
discussion below), and for putting more robust constraints on new physics.
In this paper, we have inspected the boost factors for antimatter GCRs as deeply as possible and the results are mostly independent from any WIMP model, in the context of cosmological substructures. To this aim, we have followed the semi-analytical method proposed in Lavalle et al. (2007), already used by Bringmann & Salati (2007) and Brun et al. (2007) to compute the boost factors for positrons and anti-protons, but in a scenario in which DM inhomogeneities are due to the presence of intermediate mass black holes. We have also cross-checked our results with a more time-consuming MC simulation.
A full DM model was defined with (i) the host halo smooth DM profile,
(ii) inner properties, minimal mass, space and mass distributions of
sub-halos, and (iii) the mass-concentration relation. The reference set was
chosen accordingly, with (i) NFW (kept fixed throughout the paper, see
Table 1), (ii) inner-NFW + 10-6 ![]() + cored
isothermal +
+ cored
isothermal +
![]() ,
and (iii) B01 concentration. We then
extensively spanned over some extreme values of each parameter. We normalised
all configurations so that the average local DM density was kept constant
,
and (iii) B01 concentration. We then
extensively spanned over some extreme values of each parameter. We normalised
all configurations so that the average local DM density was kept constant
![]() GeV cm-3. For completeness, we
also considered three sets of GCR propagation modelling, mainly characterised
by the size of the diffusive halo, and by the amplitudes of diffusion and
convection processes; all of them decrease from
max to min settings (med being the reference).
GeV cm-3. For completeness, we
also considered three sets of GCR propagation modelling, mainly characterised
by the size of the diffusive halo, and by the amplitudes of diffusion and
convection processes; all of them decrease from
max to min settings (med being the reference).
We found our results to depend on two main classes of effects, namely
mass- and space-related. The mass-type effects characterise the full
amount of antimatter produced in clumps through WIMP annihilations, given by
the product
![]() (see Sect. 6.1),
and its variance; they depend on the number of clumps (fixed by
(see Sect. 6.1),
and its variance; they depend on the number of clumps (fixed by
![]() at a
given
at a
given
![]() ), their inner profiles (NFW or Moore) and mass distribution
(
), their inner profiles (NFW or Moore) and mass distribution
(
![]() ). The space-related effects describe the average probability for the
produced antimatter to reach the Earth, and is determined by
). The space-related effects describe the average probability for the
produced antimatter to reach the Earth, and is determined by
![]() ,
and the associated variance; they therefore encode the whole
spatial information, i.e. the propagation averaged on the clump space
distribution, as well as the energy dependency. Our results are the following,
some trends being consistent with some found in previous studies:
,
and the associated variance; they therefore encode the whole
spatial information, i.e. the propagation averaged on the clump space
distribution, as well as the energy dependency. Our results are the following,
some trends being consistent with some found in previous studies:
Furthermore, note that the only relevant parameters for estimating the variance on the sub-halo flux are the minimal mass of clumps, their mass distribution and their local number density, beside the propagation length of the GCR species that defines an effective detection volume.
These results are in agreement with those of Hooper et al. (2004),
who concluded, though mostly qualitatively, that it is very unlikely that
significant boost factors occur for positrons. Our results, however, are more
quantitative and detailed, apply to both anti-protons and positrons for any
set of propagation parameters, and encompass the single configuration
(NFW-ENS01) used in the above paper for clumps. This is also consistent with
the results of Berezinsky et al. (2003) for ![]() -rays, where slightly
larger boost factors were found: such a difference is expected because, as
already underlined,
-rays, where slightly
larger boost factors were found: such a difference is expected because, as
already underlined, ![]() -rays are integrated along the line of sight (we
remind that the luminosity of clumps dominates over the smooth distribution
one beyond a few tens of kpc from the Galactic centre), instead of integrated
inside a more local volume like for GCRs.
-rays are integrated along the line of sight (we
remind that the luminosity of clumps dominates over the smooth distribution
one beyond a few tens of kpc from the Galactic centre), instead of integrated
inside a more local volume like for GCRs.
It is interesting to ask the dependence of our calculation on the
mass resolution achieved so far in N-body simulations, which we have
referred to in defining our parameter sets. Indeed, the N-body numerical
results are only valid at the spatial scale associated with the test particle
mass, so that the Vlasov limit may not be reached at the smallest scales
considered here (see discussion in Sect. 2). Therefore,
extrapolations of the physical properties of sub-halos down to
![]() should always be taken cautiously, even if some numerical studies were able to
survey such small systems at high redshifts (Diemand et al. 2005a).
Besides, even if DM sub-halos of
should always be taken cautiously, even if some numerical studies were able to
survey such small systems at high redshifts (Diemand et al. 2005a).
Besides, even if DM sub-halos of
![]() wander in the Galaxy, we can
actually not know anything about their characteristics. Nevertheless,
theoretical arguments based on the (inflation-motivated) scale invariance of
the DM power spectrum down to the free streaming scale set by particle
physics, the theoretical understanding of the DM mass function, the current
knowledge, would it be far from complete, of hierarchical structure formation,
and some numerical studies on the survival of very small sub-halos, somehow
guarantee that our choice of parameter ranges is rather reasonable and
sufficiently large to encompass a wide field of possibilities. Therefore,
while this strongly asks for more detailed studies of the smallest DM structures, our results should also be taken as general statements that
describe the effect of each considered parameter on boost factor predictions.
wander in the Galaxy, we can
actually not know anything about their characteristics. Nevertheless,
theoretical arguments based on the (inflation-motivated) scale invariance of
the DM power spectrum down to the free streaming scale set by particle
physics, the theoretical understanding of the DM mass function, the current
knowledge, would it be far from complete, of hierarchical structure formation,
and some numerical studies on the survival of very small sub-halos, somehow
guarantee that our choice of parameter ranges is rather reasonable and
sufficiently large to encompass a wide field of possibilities. Therefore,
while this strongly asks for more detailed studies of the smallest DM structures, our results should also be taken as general statements that
describe the effect of each considered parameter on boost factor predictions.
One could recover a sizable (energy dependent) boost factor by considering
either a sub-halo which would be very massive (![]()
![]() )
as well
as very close to the Earth (
)
as well
as very close to the Earth (![]() 1 kpc, see e.g.
Sect. 6.2.1), or very cuspy inner profiles combined
with a significant local abundance of sub-halos. The latter case would
correspond to a clump configuration given by a smooth-tracking spatial
distribution,
1 kpc, see e.g.
Sect. 6.2.1), or very cuspy inner profiles combined
with a significant local abundance of sub-halos. The latter case would
correspond to a clump configuration given by a smooth-tracking spatial
distribution,
![]() ,
,
![]() ,
concentration
,
concentration ![]() B01, and
B01, and
![]() inner profiles with
inner profiles with
![]() .
Such
a situation is very improbable given the current theoretical results of
gravitational collapse or mass function studies, and also considering the most
likely configurations of clumpiness found among N-body results. Thus, it may
not be taken as a natural prediction of structure formation. Regarding
the former case, we stress that the statistical probability to find such a
massive object in the solar neighbourhood is vanishingly small (such masses
are now well resolved in numerical simulations, and are not expected to be
numerous). Moreover, some observational constraints might exist on the
presence of such a massive and close object. Anyway, the calculation of
fluxes originating from a single nearby source is straightforward, and one can
very easily model its required features. The price to pay would be to invoke
some kind of Galactic lottery in order to explain why a single
clump would wander here and now.
.
Such
a situation is very improbable given the current theoretical results of
gravitational collapse or mass function studies, and also considering the most
likely configurations of clumpiness found among N-body results. Thus, it may
not be taken as a natural prediction of structure formation. Regarding
the former case, we stress that the statistical probability to find such a
massive object in the solar neighbourhood is vanishingly small (such masses
are now well resolved in numerical simulations, and are not expected to be
numerous). Moreover, some observational constraints might exist on the
presence of such a massive and close object. Anyway, the calculation of
fluxes originating from a single nearby source is straightforward, and one can
very easily model its required features. The price to pay would be to invoke
some kind of Galactic lottery in order to explain why a single
clump would wander here and now.
Acknowledgements
We warmly thank C. Tao and all the organisers of the 2nd Sino-French Workshop on the Dark Universe, during which this work has been initiated. We are grateful to J. Diemand, P. Salati and R. Taillet for enlightening exchanges and comments, and to V. Eke for providing us with his concentration code. J.L. and D.M. acknowledge the support from the French GDR-SUSY, as well as the incentive of its current headmaster J. Orloff. D.M. thanks all people at IHEP for warm hospitality during his stay. X.-J.B. is supported by the NSF of China under the grant Nos. 10575111, 10773011 and also in part by the Chinese Academy of Sciences under the grant No. KJCX3-SYW-N2.
On the one hand, the spatial distribution and the number of clumps
in each mass decade is known. On the other hand, the propagation
properties define effective volumes
![]() (Taillet & Maurin 2003; Maurin & Taillet 2003),
which enclose and pre-select the sources contributing to the flux.
This is all we need for a quick estimate of the variance on the fluxes
(for the clumps in that given mass range), hence
the estimate of the threshold mass
(Taillet & Maurin 2003; Maurin & Taillet 2003),
which enclose and pre-select the sources contributing to the flux.
This is all we need for a quick estimate of the variance on the fluxes
(for the clumps in that given mass range), hence
the estimate of the threshold mass
![]() .
Effective volumes
.
Effective volumes
![]() are reminded in Appendix A.1 and
are reminded in Appendix A.1 and
![]() is given in Appendix A.2. In Appendix A.3,
we show that
is given in Appendix A.2. In Appendix A.3,
we show that
![]() can be set to a higher value than that derived
from the effective volumes.
can be set to a higher value than that derived
from the effective volumes.
The method is general, and is discussed below for
![]() (Sect. 2.3.1, Eq. (14))
and the cored distribution of clumps (Sect. 2.3.2,
Eq. (16)).
(Sect. 2.3.1, Eq. (14))
and the cored distribution of clumps (Sect. 2.3.2,
Eq. (16)).
All DM sources beyond the boundary z=L (size of the diffusive halo of the
Galaxy) can be safely discarded (Barrau et al. 2002). Furthermore,
in a diffusive process, a source located at a radial distance r gives
a negligible contribution if
![]() is larger than a few
(Taillet & Maurin 2003; Maurin & Taillet 2003). These two boundaries
generate a cylinder
is larger than a few
(Taillet & Maurin 2003; Maurin & Taillet 2003). These two boundaries
generate a cylinder
![]() ;
sources out of it
may be considered to add negligible contribution to the total
flux
;
sources out of it
may be considered to add negligible contribution to the total
flux![]() .
.
In addition to the parameter L, effective volumes may be further decreased
depending on the value of the galactic convecting wind ![]() :
the effective
halo size
:
the effective
halo size
![]() plays a similar role as L (exponential cut-off
of the contributions, Taillet & Maurin 2003). At low energy,
plays a similar role as L (exponential cut-off
of the contributions, Taillet & Maurin 2003). At low energy,
![]() ,
decreasing
,
decreasing
![]() .
This set the effective volume for
.
This set the effective volume for
![]() ,
,
In Eqs. (A.1) and (A.2), we set ![]() .
We remind that this parameter sets the distance beyond which sources can
be discarded. Taking a high value for
.
We remind that this parameter sets the distance beyond which sources can
be discarded. Taking a high value for ![]() gives a conservative estimate of
gives a conservative estimate of
![]() .
The effective volumes, which do depend on energy, completely
determine the number of clumps
.
The effective volumes, which do depend on energy, completely
determine the number of clumps
![]() contributing to the flux. As
fluctuations in
contributing to the flux. As
fluctuations in
![]() generate fluctuations in the signal, the mass
threshold
generate fluctuations in the signal, the mass
threshold
![]() is obtained demanding that
is obtained demanding that
![]() .
We recall that for antimatter primaries, the most
relevant contribution comes from the local neighbourhood, so that the local
number density of sub-halos
.
We recall that for antimatter primaries, the most
relevant contribution comes from the local neighbourhood, so that the local
number density of sub-halos
![]() can be used in the next
approximations.
can be used in the next
approximations.
| |
|||
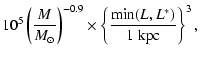 |
![\begin{displaymath}N^{{\rm e}^+}_{\rm eff}[M-10M]\approx 10^9\left (\frac{M}{M_{...
...mes E^{\delta-1}}
{1~{\rm kpc}^2~{\rm Myr}^{-1}}\right)^{3/2}
\end{displaymath}](/articles/aa/full/2008/08/aa8723-07/img507.gif)
| Ek | 0.5 GeV | 1 GeV | 10 GeV | 100 GeV |
|
|
|
|
|
|
| max | 340./37. | 340./21. | 340./3.3 | 340./0.51 |
| med | 0.32/1.6 | 1.2/1.2 | 6.4/0.42 | 6.4/0.15 |
| min | 0.0007/0.08 | 0.003/0.06 | 0.1/0.04 | 0.1/0.02 |
From these numbers, we may already predict that propagation parameters
corresponding to small
![]() will lead to smaller fluxes
(Maurin et al. 2006b; Barrau et al. 2005,2002; Donato et al. 2004), but also a larger associated variance than the
configurations with large
will lead to smaller fluxes
(Maurin et al. 2006b; Barrau et al. 2005,2002; Donato et al. 2004), but also a larger associated variance than the
configurations with large
![]() .
.
In principle, in the MC realisations (Sect. 5.3),
all sub-halos with a mass larger than
![]() need to be generated.
We just provided an absolute criterion in Appendix A.2.
Using a relative criterion, a higher
need to be generated.
We just provided an absolute criterion in Appendix A.2.
Using a relative criterion, a higher
![]() (useful
for reducing the computational time) can be found.
(useful
for reducing the computational time) can be found.
The mean flux from clumps in the mass range
![]() is given by the number
of clumps N(M) in the diffusive volume, and the variance of the signal is
just proportional to
is given by the number
of clumps N(M) in the diffusive volume, and the variance of the signal is
just proportional to ![]() ,
so that the variance-flux-ratio is
(see also Lavalle et al. 2007)
,
so that the variance-flux-ratio is
(see also Lavalle et al. 2007)
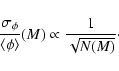 |
(A.5) |
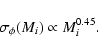 |
(A.7) |
As an illustration, Eq. (A.6) is shown to be in full
agreement with the result of the MC simulation
in Fig. A.1 (for anti-protons and
![]() ).
The latter graphs are independent of the intrinsic profile of the clumps
and of the propagation parameters. In Sect. 5.3, we take
advantage of this higher value to speed up the MC calculations.
).
The latter graphs are independent of the intrinsic profile of the clumps
and of the propagation parameters. In Sect. 5.3, we take
advantage of this higher value to speed up the MC calculations.
We recall that the total contribution of sub-halos to the antimatter flux has
a mean value given by:
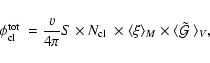 |
(B.1) |
| (B.2) |
The pure mass-induced relative fluctuations of the sub-halo flux are given by
![]() (see Eq. (63)). As
(see Eq. (63)). As
![]() from the same arguments as above,
those relative uncertainties approximately scale like
from the same arguments as above,
those relative uncertainties approximately scale like
![]() ,
and are thus expected to only slightly
(logarithmically) decrease when
,
and are thus expected to only slightly
(logarithmically) decrease when
![]() increases. They are actually found to
lie in the range 10-0.1% for (
increases. They are actually found to
lie in the range 10-0.1% for (
![]() ,
,
![]() )
going respectively from
(
)
going respectively from
(
![]() )
to (
)
to (
![]() )
(see
Table B.1). This may appear surprising because we
would naively expect the relative variance to scale like
)
(see
Table B.1). This may appear surprising because we
would naively expect the relative variance to scale like
![]() ,
and then to depend much more
strongly on
,
and then to depend much more
strongly on
![]() .
To summarise, the dropping of the total number of
clumps, which reduces the statistical sample, is compensated by smaller
fluctuations around the mean luminosity
.
To summarise, the dropping of the total number of
clumps, which reduces the statistical sample, is compensated by smaller
fluctuations around the mean luminosity
![]() from clump to
clump (the range
from clump to
clump (the range
![]() -
-
![]() gets thinner), so that the mass-induced relative
uncertainties remain roughly constant.
gets thinner), so that the mass-induced relative
uncertainties remain roughly constant.
|
|
|
|
|
|
|
|
(kpc3) | (kpc3) | ||
| 10-6 |
|
|
|
|
| 1 |
|
|
|
|
| 106 |
|
( 1.8 | 1.3 | 1.0 ) | 6.0 | 6.0 | 5.7 |
|
| Propagation |
|
|
|
|
| (s kpc-3 GeV-1) | (s kpc-3 GeV-1) | |||
| Min |
|
287.1 | 1089 |
|
829.2 | 622.2 |
| Med |
|
67.95 | 446.6 |
|
106.2 | 84.6 |
| Max |
|
25.84 | 267.3 |
|
18.42 | 15.22 |
| Med |
|
15.02 | 104.3 |
|
23.34 | 18.53 |
The space-related effects for positrons are characterised by the mean value
and the variance of
![]() over the spatial sub-halo distribution. For
positrons, the relevant scale is the energy loss scale, which sets the
characteristic propagation length, as stressed in Lavalle et al. (2007).
This propagation length is given by the following equation:
over the spatial sub-halo distribution. For
positrons, the relevant scale is the energy loss scale, which sets the
characteristic propagation length, as stressed in Lavalle et al. (2007).
This propagation length is given by the following equation:
Assuming now that all relevant contributions are those inside a volume ![]() around the Earth bounded by
around the Earth bounded by
![]() (L is half the vertical
extension of the diffusive halo), and that the propagation is roughly constant
over this small volume, we can simplify the propagator
(L is half the vertical
extension of the diffusive halo), and that the propagation is roughly constant
over this small volume, we can simplify the propagator
![]() in the
limit of infinite 3D diffusion:
in the
limit of infinite 3D diffusion:
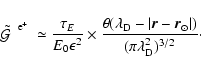 |
(B.4) |
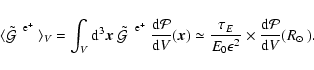 |
(B.5) |
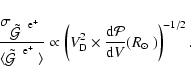 |
(B.6) |
A more quantitative information is given in Table B.2. In
this table, we calculate the mean value and the variance of
![]() as defined by Eqs. (61) and (64), respectively, for
the three propagation models detailed in Table 4. We consider
the injection of 200 GeV positrons in sources, (
as defined by Eqs. (61) and (64), respectively, for
the three propagation models detailed in Table 4. We consider
the injection of 200 GeV positrons in sources, (
![]() ), and compute the propagator averaged on the spatial
distribution of sub-halos together with the associated statistical variance.
We show the results obtained for detected energies of 150 and 10 GeV, which
correspond to diffusion lengths
), and compute the propagator averaged on the spatial
distribution of sub-halos together with the associated statistical variance.
We show the results obtained for detected energies of 150 and 10 GeV, which
correspond to diffusion lengths
![]() of
of ![]() 0.9 and 3.8 kpc,
respectively. Such quantities are parts of the flux probability function
related to a single clump, but encoding only the spatial and propagation
information.
0.9 and 3.8 kpc,
respectively. Such quantities are parts of the flux probability function
related to a single clump, but encoding only the spatial and propagation
information.
We see from this table the expected behaviour when varying the propagation
model: at a given detected energy,
![]() increases from
the minimal to the maximal propagation configuration, and also increases when
the positron is detected at a lower energy (its mean free path is somehow
longer). There is a factor of
increases from
the minimal to the maximal propagation configuration, and also increases when
the positron is detected at a lower energy (its mean free path is somehow
longer). There is a factor of ![]() 20 between the minimum (min model,
high Ed) and maximum values (max model, low Ed). The
space-associated contribution to the relative variance affecting the single
clump flux is also given in Table B.2, and is in the
range 10-1000. It has to be compared with the relative mass-induced variance
of Table B.1, i.e. that on
20 between the minimum (min model,
high Ed) and maximum values (max model, low Ed). The
space-associated contribution to the relative variance affecting the single
clump flux is also given in Table B.2, and is in the
range 10-1000. It has to be compared with the relative mass-induced variance
of Table B.1, i.e. that on ![]() .
We see that while
the relative variance on
.
We see that while
the relative variance on
![]() is large, the one affecting
is large, the one affecting ![]() almost
always dominates, unless the minimal mass of clumps is
almost
always dominates, unless the minimal mass of clumps is ![]()
![]() .
Thus, though propagation uncertainties are important, the mass-induced effects
are likely to outclass the systematic uncertainties over a large energy range.
Nevertheless, they re-enter the game as soon as the propagation scale gets
very short (detected energies very close to the injected energy). As the
crossing space-mass term dominates the global relative variance, we can
determine the systematic errors affecting the global flux predictions, taking
the previous ranges obtained for mass-like contributions. For the average
clumpy contribution to the flux, we get
.
Thus, though propagation uncertainties are important, the mass-induced effects
are likely to outclass the systematic uncertainties over a large energy range.
Nevertheless, they re-enter the game as soon as the propagation scale gets
very short (detected energies very close to the injected energy). As the
crossing space-mass term dominates the global relative variance, we can
determine the systematic errors affecting the global flux predictions, taking
the previous ranges obtained for mass-like contributions. For the average
clumpy contribution to the flux, we get ![]()
![]() ,
which are three
orders of magnitude. For the associated relative variance, we find ranges
,
which are three
orders of magnitude. For the associated relative variance, we find ranges
![]() (clump mass and number) and 10-1000 (space-induced), which yield
a total of four orders of magnitude. This provides the systematic
uncertainties on the flux and its variance. Nevertheless, such uncertainties
are diluted for the boost factor estimate, as only a small part of the
parameter space gives a sub-halo contribution greater than that of the smooth.
(clump mass and number) and 10-1000 (space-induced), which yield
a total of four orders of magnitude. This provides the systematic
uncertainties on the flux and its variance. Nevertheless, such uncertainties
are diluted for the boost factor estimate, as only a small part of the
parameter space gives a sub-halo contribution greater than that of the smooth.
The same reasoning used for positrons can apply to anti-protons, that is the use of the propagation effective volume. Therefore, complementary to the following discussion, we refer the reader to the arguments and conclusion of the previous paragraph.
The typical diffusion length for anti-protons depends mainly on the convective
wind, and can be expressed as:
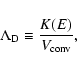 |
(B.7) |
Numerical values for the mean value and variance of
![]() are given in
Table B.2, where we have taken a flat injection
spectrum for anti-protons,
are given in
Table B.2, where we have taken a flat injection
spectrum for anti-protons,
![]() ,
and we have considered
two detected kinetic energies of 10 and 150 GeV (no energy losses for
anti-protons). We recover the same range for systematic uncertainties as for
positrons (see Appendix B.2).
,
and we have considered
two detected kinetic energies of 10 and 150 GeV (no energy losses for
anti-protons). We recover the same range for systematic uncertainties as for
positrons (see Appendix B.2).