A&A 478, 701-715 (2008)
DOI: 10.1051/0004-6361:20078480
G. Vladilo1 - J. X. Prochaska2 - A. M. Wolfe3
1 - Osservatorio Astronomico di Trieste, Istituto Nazionale di Astrofisica, Trieste, Italy
2 -
Department of Astronomy and Astrophysics, UCO/Lick Observatory, University of California, Santa Cruz, CA, USA
3 -
Department of Physics, and Center for Astrophysics and Space Sciences,
University of California at San Diego, La Jolla, CA, USA
Received 14 August 2007 / Accepted 3 December 2007
Abstract
We analyzed the spectroscopic and photometric database
of the 5th data release of the Sloan Digital Sky Survey (SDSS)
to search for evidence of the quasar reddening produced
by dust embedded in intervening damped Ly ![]() (DLA) systems.
From a list of 5164 quasars in the interval of emission redshift
(DLA) systems.
From a list of 5164 quasars in the interval of emission redshift
![]() and SDSS spectra with signal-to-noise ratio SNR
and SDSS spectra with signal-to-noise ratio SNR ![]() 4,
we built up an ``absorption sample'' of 248 QSOs with a single
DLA system in the interval of absorption redshift
4,
we built up an ``absorption sample'' of 248 QSOs with a single
DLA system in the interval of absorption redshift
![]() and a ``pool'' of 1959 control QSOs without DLA systems or strong metal systems. For each QSO of the absorption sample we extracted from the pool
a subset of control QSOs that are closest in redshift and magnitude.
The mean color of this subset was used as a zero point to measure the ``deviation
from the mean color'' of individual DLA-QSOs,
and a ``pool'' of 1959 control QSOs without DLA systems or strong metal systems. For each QSO of the absorption sample we extracted from the pool
a subset of control QSOs that are closest in redshift and magnitude.
The mean color of this subset was used as a zero point to measure the ``deviation
from the mean color'' of individual DLA-QSOs, ![]() .
The colors were measured using ``BEST'' ugriz SDSS imaging data.
The mean color excess of the absorption sample,
.
The colors were measured using ``BEST'' ugriz SDSS imaging data.
The mean color excess of the absorption sample,
![]() ,
was estimated
by averaging the individual color deviations
,
was estimated
by averaging the individual color deviations ![]() .
We find
.
We find
![]() mag
and
mag
and
![]() mag. These values are
representative of the reddening of DLA systems at
mag. These values are
representative of the reddening of DLA systems at
![]() in SDSS QSOs with limiting magnitude
in SDSS QSOs with limiting magnitude
![]() .
The detection of the mean reddening is confirmed by several statistical tests.
Analysis of the results suggests an origin of the reddening
in dust embedded in the DLA systems, with an SMC-type extinction curve.
By converting the reddening into rest-frame extinction, we derive a mean dust-to-gas ratio
.
The detection of the mean reddening is confirmed by several statistical tests.
Analysis of the results suggests an origin of the reddening
in dust embedded in the DLA systems, with an SMC-type extinction curve.
By converting the reddening into rest-frame extinction, we derive a mean dust-to-gas ratio
![]() to 4
to 4 ![]() 10-23 mag cm2.
This value is
10-23 mag cm2.
This value is ![]() -1.25 dex lower than the mean dust-to-gas ratio of the Milky Way,
in line with the lower level of metallicity in the present DLA sample.
-1.25 dex lower than the mean dust-to-gas ratio of the Milky Way,
in line with the lower level of metallicity in the present DLA sample.
Key words: ISM: dust, extinction - galaxies: ISM - galaxies: high-redshift - quasars: absorption lines
Quasar absorption-line systems allow us to probe the physical properties
of intergalactic/interstellar gas over a large fraction
of the Hubble time, back to the epoch of quasar formation.
The quasar absorbers with neutral hydrogen column density
![]() atoms cm-2 are believed to originate in the interstellar gas of intervening galaxies
(Wolfe et al. 2005), rather than in the intergalactic medium.
The presence of a strong Ly
atoms cm-2 are believed to originate in the interstellar gas of intervening galaxies
(Wolfe et al. 2005), rather than in the intergalactic medium.
The presence of a strong Ly ![]() profile with ``damping'' wings extending well beyond
the Doppler core of the line is a distinctive feature that gives the
name to this class of absorbers (Wolfe et al. 1986).
Spectroscopic studies of ``damped Ly
profile with ``damping'' wings extending well beyond
the Doppler core of the line is a distinctive feature that gives the
name to this class of absorbers (Wolfe et al. 1986).
Spectroscopic studies of ``damped Ly ![]() '' (DLA) systems
yield unique and accurate information on gas-rich, high-redshift galaxies observed in absorption
(hereafter ``DLA galaxies'').
'' (DLA) systems
yield unique and accurate information on gas-rich, high-redshift galaxies observed in absorption
(hereafter ``DLA galaxies'').
At redshift ![]() about 20 DLA host galaxies have been imaged in the quasar field,
showing a variety of morphological types
(Le Brun et al. 1997; Rao et al. 2003; Chen et al. 2004).
At higher redshift, where the bulk of known DLA systems are located,
the imaging identification of the galaxy is quite difficult and
most of the studies on the nature of DLA galaxies are based on spectroscopic observations.
In spite of a long series of studies on their kinematics
(Prochaska & Wolfe 1997, 1998), chemical abundances (Pettini et al. 1994; Lu et al. 1996; Prochaska & Wolfe 1999; Molaro et al. 2000; Dessauges-Zavadsky et al. 2006), and physical properties (Petitjean et al. 2000; Wolfe et al. 2003),
the exact nature of DLA galaxies is still open to debate (Wolfe & Chen 2006).
Studies of DLA systems allow us to probe faint galaxies that happen to lie
in the direction of the quasar.
It is not clear whether there is a continuity or not between the
properties of absorption-selected DLA galaxies and
photometrically selected Ly-break galaxies, which are biased in luminosity
(e.g. Møller et al. 2004).
about 20 DLA host galaxies have been imaged in the quasar field,
showing a variety of morphological types
(Le Brun et al. 1997; Rao et al. 2003; Chen et al. 2004).
At higher redshift, where the bulk of known DLA systems are located,
the imaging identification of the galaxy is quite difficult and
most of the studies on the nature of DLA galaxies are based on spectroscopic observations.
In spite of a long series of studies on their kinematics
(Prochaska & Wolfe 1997, 1998), chemical abundances (Pettini et al. 1994; Lu et al. 1996; Prochaska & Wolfe 1999; Molaro et al. 2000; Dessauges-Zavadsky et al. 2006), and physical properties (Petitjean et al. 2000; Wolfe et al. 2003),
the exact nature of DLA galaxies is still open to debate (Wolfe & Chen 2006).
Studies of DLA systems allow us to probe faint galaxies that happen to lie
in the direction of the quasar.
It is not clear whether there is a continuity or not between the
properties of absorption-selected DLA galaxies and
photometrically selected Ly-break galaxies, which are biased in luminosity
(e.g. Møller et al. 2004).
In the present work we focus our attention on the dust component of DLA systems. By analogy with studies of local galaxies, we expect interstellar dust to be a pervasive component of DLA galaxies. The properties of dust are poorly understood, but may play a critical role in several investigations aimed at understanding the nature of DLA galaxies. In fact, dust is expected to play a major role in a variety of physical processes and to affect the measurement of observational quantities.
An example of the importance of dust in governing the physical processes at work
in DLA galaxies comes from the study of the C II![]() 1335.7 Å line,
which can be used to estimate the star formation rate assuming that the heating is dominated
by photoelectric emission from dust grains (Wolfe et al. 2003).
The efficiency of the heating mechanism and the accuracy
of the SFR determined in this way depend on the dust-to-gas ratio,
which is poorly constrained.
Also the production of molecular gas is believed to be influenced
by the presence of dust, which acts as a catalyst of H2 formation.
1335.7 Å line,
which can be used to estimate the star formation rate assuming that the heating is dominated
by photoelectric emission from dust grains (Wolfe et al. 2003).
The efficiency of the heating mechanism and the accuracy
of the SFR determined in this way depend on the dust-to-gas ratio,
which is poorly constrained.
Also the production of molecular gas is believed to be influenced
by the presence of dust, which acts as a catalyst of H2 formation.
An example of the impact of dust on the observations of DLA systems comes from the different estimates of chemical abundances obtained from refractory and volatile elements (Pettini et al. 1994; Vladilo 1998, 2002; Centurión et al. 2000; Hou et al. 2001; Prochaska & Wolfe 2002). A significant fraction of refractory elements is depleted from the gas phase, where they can be detected via absorption line spectroscopy, to the dust component, where they escape detection with this technique. Studies of galactic chemical evolution are based on measurements of abundance ratios which may be affected by differential dust depletion. The inferences of galactic chemical evolution models on the nature of DLA galaxies depend on the exact amount of dust depletion in these systems (e.g. Calura et al. 2003; Dessauges-Zavadsky et al. 2006).
Another observational effect that we expect to occur is the absorption and scattering of the photons of the quasar continuum by dust embedded in the intervening DLA system. This extinction process is more efficient at shorter wavelengths and is expected to redden the quasar colors. In the most extreme cases the extinction could lead to the obscuration of the background quasars (Ostriker & Heisler 1984; Fall & Pei 1989, 1993). In the more general case, the extinction may induce a selection bias acting against the detection of metal-rich galactic regions in magnitude-limited surveys of quasars (Prantzos & Boissier 2000; Vladilo & Péroux 2005). Studies of radio-selected quasars surveys suggest that the impact of this effect on the statistical properties of DLA systems is modest (Ellison et al. 2001; Akerman et al. 2005; Jorgenson et al. 2006), but the size of these surveys is not sufficiently large to reach firm conclusions. The existence of empty fields without optical identifications in the radio-selected survey of Jorgenson et al. (2006) suggests that a fraction of quasars may indeed be obscured. A better understanding of the amount and type of dust present in DLA systems is fundamental to assess the importance of the dust extinction effect.
Because of the potential impact of dust in studies of DLA systems,
a significant observational effort has been dedicated to
prove its existence and to understand its properties.
At redshift ![]() definitive evidence for DLA dust
has been found in one line of sight where the dust extinction bump at 2175 Å and the silicate absorption at 9.7
definitive evidence for DLA dust
has been found in one line of sight where the dust extinction bump at 2175 Å and the silicate absorption at 9.7 ![]() have been detected
(Junkkarinen et al. 2004; Kulkarni et al. 2007).
Evidence for reddening due to DLA absorbers at redshift
have been detected
(Junkkarinen et al. 2004; Kulkarni et al. 2007).
Evidence for reddening due to DLA absorbers at redshift ![]() has been found in a few quasars with metal rich DLA systems (Vladilo et al. 2006).
At
has been found in a few quasars with metal rich DLA systems (Vladilo et al. 2006).
At ![]() the evidence for dust in DLA systems
is mostly based on studies of elemental depletions
(Pettini et al. 1997, 2000; Hou et al. 2001; Prochaska & Wolfe 2002; Vladilo 1998, 2004;
Dessauges-Zavadsky et al. 2006) and on the existence of general
trends between depletion, metallicity and H2 molecular fraction
(Ledoux et al. 2003; Petitjean et al. 2006). In order to establish more firmly the presence of dust at
the evidence for dust in DLA systems
is mostly based on studies of elemental depletions
(Pettini et al. 1997, 2000; Hou et al. 2001; Prochaska & Wolfe 2002; Vladilo 1998, 2004;
Dessauges-Zavadsky et al. 2006) and on the existence of general
trends between depletion, metallicity and H2 molecular fraction
(Ledoux et al. 2003; Petitjean et al. 2006). In order to establish more firmly the presence of dust at ![]() and to understand its properties, it is fundamental to complement the
studies of depletion with measurements of quasar reddening.
A claim of reddening detection was reported by Pei et al. (1991),
based on the analysis of a sample of 13 DLA-quasars. This claim was not confirmed by subsequent work, including a photometric study of the colors of radio-selected quasars with and
without DLA systems (Ellison et al. 2005) and a study of quasar spectra of the 2nd data release of the Sloan Digital Sky Survey (SDSS) (Murphy & Liske 2004). The remarkably low upper limit of reddening found by Murphy & Liske,
and to understand its properties, it is fundamental to complement the
studies of depletion with measurements of quasar reddening.
A claim of reddening detection was reported by Pei et al. (1991),
based on the analysis of a sample of 13 DLA-quasars. This claim was not confirmed by subsequent work, including a photometric study of the colors of radio-selected quasars with and
without DLA systems (Ellison et al. 2005) and a study of quasar spectra of the 2nd data release of the Sloan Digital Sky Survey (SDSS) (Murphy & Liske 2004). The remarkably low upper limit of reddening found by Murphy & Liske,
![]() mag
in the absorber frame, indicates how challeging this type of measurement is.
On the other hand, the detection of quasar reddening due to Ca II systems
(Wild & Hewett 2005; Wild et al. 2006) and Mg II systems
(York et al. 2006; Menard et al. 2007) suggests that also DLA systems should produce a reddening signal.
mag
in the absorber frame, indicates how challeging this type of measurement is.
On the other hand, the detection of quasar reddening due to Ca II systems
(Wild & Hewett 2005; Wild et al. 2006) and Mg II systems
(York et al. 2006; Menard et al. 2007) suggests that also DLA systems should produce a reddening signal.
The aim of the present work is to exploit the large database of the 5th SDSS Data Release, in conjunction with novel features in the analysis, to detect the mean reddening of DLA-QSOs at z > 2. As in previous work we use the spectroscopic database in the process of selection of the quasars of the absorption and control samples. At variance with previous work on DLA reddening, the quasar colors are measured making use of the photometric database. The photometric measurement of the reddening avoids some critical steps inherent to the spectroscopic method, such as the photometric calibration of the spectra and the tracing of the quasar continuum. Uncertainties in the photometric calibration, even if small (Adelman-McCarthy et al. 2007), translate into uncertainties in the slope of the continuum.
In Sect. 2 we describe the process of selection of the quasar samples. Novel features of our approach include (i) the use of spectra with the same signal-to-noise ratio for the selection of DLA quasars and control quasars, (ii) the rejection of low-redshift absorption systems that may affect the measurement of the reddening at high-redshift, and (iii) the rejection of quasars with multiple DLA systems. Thanks to these last criteria we are in the position to search for correlations between the color excess and the properties of individual DLA systems. In Sect. 3 we explain the method adopted to measure the mean reddening of the absorption sample. The measurement is presented in Sect. 4 and its interpretation is discussed in Sect. 5.
The starting list of quasars was extracted with the SDSS DR5 spectroscopic query format.
A total of 7294 objects with spectroscopic constraints ``QSO'' or ``HiZ_QSO'',
emission redshift
![]() and imaging constraints
``Point Sources'' were extracted from the query.
Quasars at lower redshift do not yield sufficient redshift path
to search for DLA absorptions. The upper limit on
and imaging constraints
``Point Sources'' were extracted from the query.
Quasars at lower redshift do not yield sufficient redshift path
to search for DLA absorptions. The upper limit on ![]() comes from the requirement
that the photometric band r
falls redwards of the quasar Ly
comes from the requirement
that the photometric band r
falls redwards of the quasar Ly ![]() emission (see Sect. 3.2).
emission (see Sect. 3.2).
The detectability of the spectral signatures suggestive of reddening
depends on the signal-to-noise ratio (SNR) of their SDSS spectra.
In order to perform a homogeneous comparison between absorption and control samples
we defined a common threshold value of SNR. In practice, we adopted the criterion
SNR ![]() 4, where SNR is the mean signal-to-noise ratio per pixel calculated in the spectral window 1440-1490 Å in the rest frame of the quasar.
We found 5164 quasars with
4, where SNR is the mean signal-to-noise ratio per pixel calculated in the spectral window 1440-1490 Å in the rest frame of the quasar.
We found 5164 quasars with
![]() and
SNR
and
SNR ![]() 4 in the adopted spectral window.
4 in the adopted spectral window.
Table 1:
Data for the quasars of the absorption sample and measurements of the deviations from the mean color
![]() and
and
![]() .
Measurements in the (g-z) color index are only given for quasars with
.
Measurements in the (g-z) color index are only given for quasars with
![]() (see Sect. 3.2.2). The first 20 DLA-quasars are shown.
The full table is available in electronic form at the CDS
(see also web page http://adlibitum.oats.inaf.it/vladilo/tables.html).
(see Sect. 3.2.2). The first 20 DLA-quasars are shown.
The full table is available in electronic form at the CDS
(see also web page http://adlibitum.oats.inaf.it/vladilo/tables.html).
From this list of quasars we extracted the ``absorption sample'' and the ``control sample''. The absorption sample is the subset of quasars with a single DLA system and without any other potential sources of foreground reddening. The control sample is the subset of quasars without DLA systems or any other potential sources of foreground reddening.
The identification of DLA systems and potential sources of reddening is based on the analysis of the quasar spectra, as explained below. Concerning the DLA identification, we adopt tight criteria in order to select only genuine DLA systems. Concerning the other sources of reddening, we instead adopt broader criteria since we want to be sure to reject any potential source that may affect the reddening measurement.
The list of signatures of potential sources of reddening that we considered includes:
strong H I absorptions at redshift
![]() ,
strong, low-ionization metal systems at
,
strong, low-ionization metal systems at
![]() ,
Broad Absorption Line (BAL) features,
and strong self-absorptions in the quasar Ly
,
Broad Absorption Line (BAL) features,
and strong self-absorptions in the quasar Ly ![]() emission.
Strong metal lines of low ionization allow us to search for
low-redshift intervening systems not directly detectable as a Ly
emission.
Strong metal lines of low ionization allow us to search for
low-redshift intervening systems not directly detectable as a Ly ![]() line
because of the limited spectral coverage of SDSS spectra. For instance,
Mg II absorbers are detectable down to redshift z=0.95 in quasars at
line
because of the limited spectral coverage of SDSS spectra. For instance,
Mg II absorbers are detectable down to redshift z=0.95 in quasars at
![]() ,
and down to z=0.4 in quasar at
,
and down to z=0.4 in quasar at
![]() .
Other low-ionization metal lines redwards of the Ly
.
Other low-ionization metal lines redwards of the Ly ![]() emission
(e.g. Si II 1526 Å, Fe II 2600 Å)
can trace potential sources of reddening at low redshift.
BAL features and strong Ly
emission
(e.g. Si II 1526 Å, Fe II 2600 Å)
can trace potential sources of reddening at low redshift.
BAL features and strong Ly ![]() self-absorptions
arise in the quasar environment and represent
a reason of concern in the present analysis since they may be associated with dust. In fact,
BAL quasars tend to show peculiar colors relative to non-BAL ones (see e.g. Trump et al. 2006), possibly as the result of dust present in the broad line region.
Strong H I self-absorptions at
self-absorptions
arise in the quasar environment and represent
a reason of concern in the present analysis since they may be associated with dust. In fact,
BAL quasars tend to show peculiar colors relative to non-BAL ones (see e.g. Trump et al. 2006), possibly as the result of dust present in the broad line region.
Strong H I self-absorptions at
![]() are suggestive of large amount of neutral gas, potentially associated with dust.
are suggestive of large amount of neutral gas, potentially associated with dust.
To build up the absorption sample we started by identifying
damped Ly ![]() systems with the automated algorithm described by Prochaska et al. (2005, hereafter PHW05) applied here to the DR5.
Only systems with Ly
systems with the automated algorithm described by Prochaska et al. (2005, hereafter PHW05) applied here to the DR5.
Only systems with Ly ![]() absorption blueshifted by at least 3000 km s-1 relative to the quasar Ly
absorption blueshifted by at least 3000 km s-1 relative to the quasar Ly ![]() emission
emission![]() were considered. Quasars with BAL flags = 1 and 2 according to the criteria explained in PHW05
were rejected. In this way we obtained a list
were considered. Quasars with BAL flags = 1 and 2 according to the criteria explained in PHW05
were rejected. In this way we obtained a list![]() of 422 DLA systems in quasars with
of 422 DLA systems in quasars with
![]() and SNR
and SNR ![]() 4 in the rest-frame window 1440-1490 Å.
4 in the rest-frame window 1440-1490 Å.
Starting from this list the final absorption sample was built up
in the following way. We first discarded 69 quasars with strong Mg II absorbers
at redshift
![]() .
In practice,
due to the limitation of the SDSS wavelength coverage, we were able to search
for absorbers with
.
In practice,
due to the limitation of the SDSS wavelength coverage, we were able to search
for absorbers with
![]() .
To implement this rejection process we used the SDSS catalog of
strong Mg II absorbers with rest-frame equivalent width
.
To implement this rejection process we used the SDSS catalog of
strong Mg II absorbers with rest-frame equivalent width ![]() 1 Å (Prochter et al. 2006) updated to DR5 (Prochter 2007, priv. comm.).
We then discarded 54 quasars with multiple DLA systems.
Finally we rejected 30 quasars with a strong H I absorption at
1 Å (Prochter et al. 2006) updated to DR5 (Prochter 2007, priv. comm.).
We then discarded 54 quasars with multiple DLA systems.
Finally we rejected 30 quasars with a strong H I absorption at
![]() .
For this purpouse we used a list of candidate H I absorptions
automatically generated. We rejected cases with
.
For this purpouse we used a list of candidate H I absorptions
automatically generated. We rejected cases with
![]() atoms cm-2 within the errors.
atoms cm-2 within the errors.
After this automatic process we visually inspected the remaining 269 quasar spectra to search for spectroscopic features undetected by the automated algorithms.
A dozen of quasars with strong Mg II absorption not associated with the DLA systems
were discarded in this way, as well as a few cases with anomalous spectra
(e.g. extremely narrow Ly ![]() emission). Other unidentified weak features were tentatively attributed to metal lines associated with the DLA system.
emission). Other unidentified weak features were tentatively attributed to metal lines associated with the DLA system.
At the end of the rejection process we obtained a list of 248 DLA-quasar pairs
representing our absorption sample, listed in Table 1.
At the mean emission redshift of this sample,
![]() ,
the quasars are free of foreground (Mg II) systems
down to absorption redshift
,
the quasars are free of foreground (Mg II) systems
down to absorption redshift
![]() .
The chance of intersecting an additional DLA system at lower redshifts
is low, so that the resulting DLA-quasar list is a good approximation of
an ideal sample of quasars with a single intervening DLA system at
high redshift (
.
The chance of intersecting an additional DLA system at lower redshifts
is low, so that the resulting DLA-quasar list is a good approximation of
an ideal sample of quasars with a single intervening DLA system at
high redshift (
![]() ).
).
To construct the control sample we started again from the list of 5164 DR5 quasars
with
![]() and
SNR
and
SNR ![]() 4 in the spectral window 1440-1490 Å.
We then rejected quasars with spectral signatures of potential sources of reddening,
using the same automated algorithms adopted for the absorption sample.
In this way we discarded 270 BAL quasars (BAL flag = 1 or 2),
997 quasars with strong Mg II lines
(rest frame equivalent width
4 in the spectral window 1440-1490 Å.
We then rejected quasars with spectral signatures of potential sources of reddening,
using the same automated algorithms adopted for the absorption sample.
In this way we discarded 270 BAL quasars (BAL flag = 1 or 2),
997 quasars with strong Mg II lines
(rest frame equivalent width ![]() 1 Å), and 669 quasars with strong H I systems
(including DLA systems closer than 3000 km s-1 to the Ly
1 Å), and 669 quasars with strong H I systems
(including DLA systems closer than 3000 km s-1 to the Ly ![]() emission).
emission).
The remaining 3228 quasars show, in many cases, absorption systems
undetected by the automated algorithms.
This is due to the fact that the algorithms do not search for absorption lines
in spectral regions with insufficient SNR (e.g.
portions of the Lyman ![]() forest particularly crowded)
or close to strong quasar emissions (e.g. the O VI emission).
While this limitation is not critical for the selection of the absorption sample
(only bona fide damped systems are
automatically identified), it is a reason of concern for the selection of control quasars
free of any potential source of reddening.
We therefore proceeded to a visual classification of the quasar spectra
in a search for intervening absorbers
not detected automatically. Metal lines and strong H I systems
were tentatively identified by visual inspection with the following criteria.
forest particularly crowded)
or close to strong quasar emissions (e.g. the O VI emission).
While this limitation is not critical for the selection of the absorption sample
(only bona fide damped systems are
automatically identified), it is a reason of concern for the selection of control quasars
free of any potential source of reddening.
We therefore proceeded to a visual classification of the quasar spectra
in a search for intervening absorbers
not detected automatically. Metal lines and strong H I systems
were tentatively identified by visual inspection with the following criteria.
Narrow absorption lines redward of the QSO Ly![]() emission
with central depth
emission
with central depth ![]() 0.2 relative to the adjacent continuum
and located away from the C IV/Si IV quasar profiles
were tentatively attributed to low-ionization metal absorptions.
The SNR preselection was in general sufficient to identify
features with central depth
0.2 relative to the adjacent continuum
and located away from the C IV/Si IV quasar profiles
were tentatively attributed to low-ionization metal absorptions.
The SNR preselection was in general sufficient to identify
features with central depth ![]() 0.2 in the full spectral range.
For the typical FWHM that can be appreciated by eye in the SDSS spectra (
0.2 in the full spectral range.
For the typical FWHM that can be appreciated by eye in the SDSS spectra (![]() 20 Å)
a central depth of 0.2 corresponds to an equivalent width of
20 Å)
a central depth of 0.2 corresponds to an equivalent width of ![]() 4 Å in the observer
rest frame. This corresponds to a rest-frame equivalent width of
4 Å in the observer
rest frame. This corresponds to a rest-frame equivalent width of ![]() 1 Å
(
1 Å
(![]() 2 Å) for absorbers at redshift
2 Å) for absorbers at redshift
![]() (
(
![]() ). Metal lines with equivalent widths of this magnitude are generally saturated and suggestive of strong metal absorptions potentially associated with DLA systems.
). Metal lines with equivalent widths of this magnitude are generally saturated and suggestive of strong metal absorptions potentially associated with DLA systems.
Saturated absorptions in the Ly ![]() forest
with FWHM
forest
with FWHM ![]() 40 Å and zero residual intensity
were attributed to strong H I systems. For the typical absorption redshift
detectable in our spectra, this threshold roughly
corresponds to an equivalent width of
40 Å and zero residual intensity
were attributed to strong H I systems. For the typical absorption redshift
detectable in our spectra, this threshold roughly
corresponds to an equivalent width of ![]() 10 Å in the rest frame of the QSO.
This value is traditionally used to identify candidate damped Ly
10 Å in the rest frame of the QSO.
This value is traditionally used to identify candidate damped Ly![]() absorptions
in low resolution spectra (Wolfe et al. 1986). For features lying on the wings of strong quasar emissions the criterion was relaxed to FWHM
absorptions
in low resolution spectra (Wolfe et al. 1986). For features lying on the wings of strong quasar emissions the criterion was relaxed to FWHM ![]() 20 Å,
given the fact that part of the absorption is probably washed out by the emission itself.
20 Å,
given the fact that part of the absorption is probably washed out by the emission itself.
In the course of the visual inspection process we also searched for
quasars with strong Ly ![]() self-absorption
and BAL quasars not identified automatically.
self-absorption
and BAL quasars not identified automatically.
As a result of the visual inspection process we rejected 37 quasars with BAL features,
1074 suspect metal systems![]() ,
141 potential DLA systems (including absorptions in the proximity of the Ly
,
141 potential DLA systems (including absorptions in the proximity of the Ly ![]() emission),
and 17 cases with a strong Ly
emission),
and 17 cases with a strong Ly ![]() self-absorption. In this way
we were left with a sample of 1959 control quasars
listed in Table 2. This is a reasonable approximation of an ideal sample of quasars
without intervening sources of reddening.
As we explain in the next section, this sample is used as a ``pool''
from which we extract subsets of control quasars specifically designed
for each quasar of the absorption sample.
self-absorption. In this way
we were left with a sample of 1959 control quasars
listed in Table 2. This is a reasonable approximation of an ideal sample of quasars
without intervening sources of reddening.
As we explain in the next section, this sample is used as a ``pool''
from which we extract subsets of control quasars specifically designed
for each quasar of the absorption sample.
Table 2: Pool of control quasars used in the present investigation (see Sect. 2). The first 20 quasars are shown. The full table is available in electronic form at the CDS (see also http://adlibitum.oats.inaf.it/vladilo/tables.html).
Given two measurements mx and my of the apparent magnitude of a quasar
in two photometric bands x and y, we call
C(y-x)=my-mx the quasar color.
If dust is present in a foreground absorption system, the observed color will be different from the intrinsic, unreddened color C0(y-x), yielding a color excess
E(y-x)=C(y-x)-C0(y-x). This cannot be measured directly since the unreddened color of the individual quasar is unknown. We can however measure the mean color excess of a sample
of DLA-quasars in the following way. For each DLA-quasar we build a set of nj unreddened control quasars with same redshift and magnitude. We then estimate the mean color of these unreddened quasars,
![]() ,
and hence the deviation from the mean color
,
and hence the deviation from the mean color
Since our ideal goal is to measure the color of the quasar continuum,
we excluded photometric bands contaminated by the absorptions in the Ly ![]() forest
or the Ly
forest
or the Ly ![]() emission of the quasar.
Taking into account the average wavelengths
emission of the quasar.
Taking into account the average wavelengths
![]() and the FWHMs of the
SDSS photometric bands (Fukugita et al. 1996; see also SDSS web page
http://www.sdss.org/dr5/instruments/imager)
this condition constrains the maximum quasar redshift to
and the FWHMs of the
SDSS photometric bands (Fukugita et al. 1996; see also SDSS web page
http://www.sdss.org/dr5/instruments/imager)
this condition constrains the maximum quasar redshift to
![]() ,
and 5.78
for the u, g, r, i, and z bands, respectively.
Since the wavelength coverage of SDSS spectra prevents detection of DLA systems
at
,
and 5.78
for the u, g, r, i, and z bands, respectively.
Since the wavelength coverage of SDSS spectra prevents detection of DLA systems
at
![]() ,
only the r, i and z bands provide quasars with
uncontaminated photometry (in the sense specified above)
and sufficient redshift coverage for detection of DLA systems.
The maximum leverage for reddening detection with these bands is given by the (r-z) color.
,
only the r, i and z bands provide quasars with
uncontaminated photometry (in the sense specified above)
and sufficient redshift coverage for detection of DLA systems.
The maximum leverage for reddening detection with these bands is given by the (r-z) color.
In Fig. 1 we plot the color excess E(r-z) in the observer's frame
that we expect to measure for an absorber at redshift ![]() with rest-frame extinction
with rest-frame extinction
![]() mag. To estimate E(r-z) we considered different possible
types of extinction curves for the dust in the DLA systems, such as
the Milky-Way curves by Cardelli et al. (1998), with the characteristic extinction bump at 2175 Å, and the SMC curves (Pei 1992; Gordon et al. 2003), characterized by a more regular UV rise. The extinction curves are normalized in the V band,
mag. To estimate E(r-z) we considered different possible
types of extinction curves for the dust in the DLA systems, such as
the Milky-Way curves by Cardelli et al. (1998), with the characteristic extinction bump at 2175 Å, and the SMC curves (Pei 1992; Gordon et al. 2003), characterized by a more regular UV rise. The extinction curves are normalized in the V band,
![]() ,
all the quantities in this definition
being in the rest frame of the absorber.
For an absorber at redshift
,
all the quantities in this definition
being in the rest frame of the absorber.
For an absorber at redshift ![]() the extinction measured at wavelength
the extinction measured at wavelength
![]() in the observer's frame is
in the observer's frame is
![]() .
The color excess in the observer's frame per unit extinction in the rest frame
is therefore
.
The color excess in the observer's frame per unit extinction in the rest frame
is therefore
For an SMC-type extinction curve we expect a smooth variation of the predicted color excess in the redshift interval of interest, with a typical value
![]() mag
for absorbers with rest-frame
mag
for absorbers with rest-frame
![]() mag. For a MW-type curve we expect a small (or even negative) reddening in the interval of absorption redshift of our sample.
The minimum in the MW lines of Fig. 1 corresponds
to minimum between the end of the extinction bump at 2175 Å and the UV rise. The implications of these different behaviours
of the SMC-type and MW-type extinction curves are discussed in Sect. 5.1.
mag. For a MW-type curve we expect a small (or even negative) reddening in the interval of absorption redshift of our sample.
The minimum in the MW lines of Fig. 1 corresponds
to minimum between the end of the extinction bump at 2175 Å and the UV rise. The implications of these different behaviours
of the SMC-type and MW-type extinction curves are discussed in Sect. 5.1.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8480fg1.eps}\end{figure}](/articles/aa/full/2008/06/aa8480-07/Timg158.gif) |
Figure 1:
Color excess E(r-z) in the observer frame calculated for an absorber at redshift |
| Open with DEXTER | |
The measurement of the (g-z) color is challenging
because the g band is generally contaminated by the
Ly ![]() forest, or even the QSO Lyman break,
in the interval of emission redshift considered.
However, measuring the reddening in the (g-z) color,
in addition of the (r-z) color, offers several advantages.
One is the higher leverage for reddening detection: we expect a gain of
a factor of
forest, or even the QSO Lyman break,
in the interval of emission redshift considered.
However, measuring the reddening in the (g-z) color,
in addition of the (r-z) color, offers several advantages.
One is the higher leverage for reddening detection: we expect a gain of
a factor of ![]() 2.2 in the ratio
E(g-z)/E(r-z)at the redshift of our sample if the extinction curve is of SMC type.
Another advantage is the possibility of probing the
wavelength dependence of the reddening, i.e. the extinction curve of the dust,
by comparing the (g-z) and (r-z) color excesses.
We decided therefore to perform the measurements also in the (g-z) color index
taking care of the contaminations present in the g bandpass.
2.2 in the ratio
E(g-z)/E(r-z)at the redshift of our sample if the extinction curve is of SMC type.
Another advantage is the possibility of probing the
wavelength dependence of the reddening, i.e. the extinction curve of the dust,
by comparing the (g-z) and (r-z) color excesses.
We decided therefore to perform the measurements also in the (g-z) color index
taking care of the contaminations present in the g bandpass.
To avoid overlap of the g band with the QSO Lyman break, we restricted the analysis
of the (g-z) colors to the QSOs with
![]() in our sample.
We then took care of the contamination due to Ly
in our sample.
We then took care of the contamination due to Ly ![]() absorptions.
The contamination due to the forest is present both in the
quasars of the absorption sample and of the control sample.
Line-to-line variations of the forest absorption will
contribute to the dispersion of the quasar colors, making
the measurement of the color excess more difficult.
If such variations are randomly distributed,
we still can measure the difference between the quasar colors
of the absorption and control samples.
In doing this, however, we must take into
account the fact that the g band of the absorption sample
is generally contaminated by the damped Ly
absorptions.
The contamination due to the forest is present both in the
quasars of the absorption sample and of the control sample.
Line-to-line variations of the forest absorption will
contribute to the dispersion of the quasar colors, making
the measurement of the color excess more difficult.
If such variations are randomly distributed,
we still can measure the difference between the quasar colors
of the absorption and control samples.
In doing this, however, we must take into
account the fact that the g band of the absorption sample
is generally contaminated by the damped Ly ![]() profile, which is absent in the control quasars. To cope with this problem we correct the g magnitude by taking into account
the effect of the damped Ly
profile, which is absent in the control quasars. To cope with this problem we correct the g magnitude by taking into account
the effect of the damped Ly ![]() absorption
absorption![]() in the filter bandbass.
The magnitudes in the SDSS photometric system are defined as
in the filter bandbass.
The magnitudes in the SDSS photometric system are defined as
![]() (Fukugita et al. 1996), where
(Fukugita et al. 1996), where ![]() is the quasar spectral distribution and
is the quasar spectral distribution and ![]() the response function
of the filter. We define the correction for the DLA absorption in the g band as
the response function
of the filter. We define the correction for the DLA absorption in the g band as
The ``BEST'' ugriz imaging data were recovered for all quasars of the absorption and control samples. These photometric data were corrected for the effects of the Galactic extinction according to the prescriptions given by Schneider et al. (2005).
For each quasar of the absorption sample we calculate the colors (r-z)i and (g-z)i and then
select a taylored subset of control quasars closest in redshift and magnitude
in the following way. We first select the
![]() control quasars closest to the redshift
control quasars closest to the redshift ![]() of the DLA quasar. From this subset we then select the nm control quasars
closest to the z-band magnitude mz (the least affected by extinction)
of the DLA quasar. This last subset is used to estimate the mean
unreddened colors
of the DLA quasar. From this subset we then select the nm control quasars
closest to the z-band magnitude mz (the least affected by extinction)
of the DLA quasar. This last subset is used to estimate the mean
unreddened colors
![]() and
and
![]() .
The deviations from the mean color are finally calculated as
.
The deviations from the mean color are finally calculated as
![]() and
and
![]() .
.
With this procedure each subset of control quasars has
the same size nm for all DLA-QSOs and we have
a comparable statistics for all the measurements.
The choice of
![]() and nm is determined by the requirement
that the total intervals in emission redshift,
and nm is determined by the requirement
that the total intervals in emission redshift,
![]() ,
and z magnitude,
,
and z magnitude,
![]() ,
spanned by each subset are
sufficiently small to guarantee a good degree of homogeneity of
the control samples.
In practice, this gives the contraints
,
spanned by each subset are
sufficiently small to guarantee a good degree of homogeneity of
the control samples.
In practice, this gives the contraints
![]() and
and
![]() in order to
have typical (median) values
in order to
have typical (median) values
![]() and
and
![]() mag.
The redshift interval is similar to the redshift bins
commonly adopted in studies of the mean quasar color
as a function of
mag.
The redshift interval is similar to the redshift bins
commonly adopted in studies of the mean quasar color
as a function of ![]() (e.g. Richards et al. 2001).
Changes of the intrinsic slopes of the quasar continua over
the above magnitude interval are expected to be modest
(Yip et al. 2004).
(e.g. Richards et al. 2001).
Changes of the intrinsic slopes of the quasar continua over
the above magnitude interval are expected to be modest
(Yip et al. 2004).
In Table 1 we report the measurements of
![]() and
and
![]() for the DLA-QSOs of the absorption sample. In Cols. 6 and 7 of the table we give
the intervals in emission redshift,
for the DLA-QSOs of the absorption sample. In Cols. 6 and 7 of the table we give
the intervals in emission redshift,
![]() ,
and z magnitude,
,
and z magnitude,
![]() ,
spanned by each subset of control quasars obtained by adopting
,
spanned by each subset of control quasars obtained by adopting
![]() and nm=25.
In Cols. 8 and 9 we list the mean colors
and nm=25.
In Cols. 8 and 9 we list the mean colors
![]() and
and
![]() ,
obtained from the weighted mean of the colors of each control subset.
The weights are taken to be proportional to the inverse squares of the errors
of individual colors.
,
obtained from the weighted mean of the colors of each control subset.
The weights are taken to be proportional to the inverse squares of the errors
of individual colors.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8480fg2.eps} \end{figure}](/articles/aa/full/2008/06/aa8480-07/Timg185.gif) |
Figure 2:
Mean color
|
| Open with DEXTER | |
The errors of individual colors of DLA quasars and control quasars
are obtained by propagation of the
photometric errors and of the errors of the Galactic extinction correction.
For the latter we adopted an uncertainty of ![]()
![]() of the correction itself.
The (g-z) data include the correction for damped Ly
of the correction itself.
The (g-z) data include the correction for damped Ly ![]() absorption in
the g band, when approprite. An uncertainty of
absorption in
the g band, when approprite. An uncertainty of ![]()
![]() of this correction is propagated
in the error budget.
of this correction is propagated
in the error budget.
The errors of the mean colors
![]() and
and
![]() quoted in Table 1
are the standard deviation of the colors of each subset.
These errors dominate the budget of the errors of the color deviations
quoted in Table 1
are the standard deviation of the colors of each subset.
These errors dominate the budget of the errors of the color deviations
![]() and
and
![]() .
.
In Fig. 2 we plot the mean colors
![]() of the subsets of unreddened quasars versus
of the subsets of unreddened quasars versus ![]() .
Each data point corresponds to the subset of an individual DLA-quasar of Table 1.
We use different symbols for quasars brighter and fainter than the median
magnitude of the absorption sample,
.
Each data point corresponds to the subset of an individual DLA-quasar of Table 1.
We use different symbols for quasars brighter and fainter than the median
magnitude of the absorption sample,
![]() .
In addition to a trend with
.
In addition to a trend with ![]() ,
known from previous studies, the figure shows
a dependence on the quasar magnitude.
For instance, at
,
known from previous studies, the figure shows
a dependence on the quasar magnitude.
For instance, at
![]() ,
where many quasars
both fainter and brighter than
,
where many quasars
both fainter and brighter than
![]() are present,
the fainter quasars (red circles) lie systematically below the brighter
ones (blue crosses). This result justifies our choice of grouping the control quasars
not only in redshift, but also in magnitude.
are present,
the fainter quasars (red circles) lie systematically below the brighter
ones (blue crosses). This result justifies our choice of grouping the control quasars
not only in redshift, but also in magnitude.
Table 3:
Mean reddening in the observer's frame,
![]() ,
and mean extinction in the rest frame,
,
and mean extinction in the rest frame,
![]() ,
for different colors and DLA/QSO samples.
,
for different colors and DLA/QSO samples.
In Table 3 we give the weighted means
![]() and
and
![]() estimated with the expression
estimated with the expression
![]() ,
where
,
where
![]() ,
and
,
and ![]() are the errors of individual measurements. The use of the weighted mean allows us to minimize the
contribution of the QSOs with largest uncertainty
of their intrinsic colors, the dominant source of the error budget.
are the errors of individual measurements. The use of the weighted mean allows us to minimize the
contribution of the QSOs with largest uncertainty
of their intrinsic colors, the dominant source of the error budget.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8480fg3a.eps}\hspace*{0.8cm}
\includegraphics[width=7.5cm,clip]{8480fg3b.eps} \end{figure}](/articles/aa/full/2008/06/aa8480-07/Timg203.gif) |
Figure 3:
Frequency distribution of the mean color excess
|
| Open with DEXTER | |
For the error of the mean we adopted the unbiased estimate
From the results shown in Table 3 one can see that the mean (r-z) reddening is detected at ![]()
![]() confidence level (statistical error) in the complete sample of 248 DLA/QSO pairs for which the r band is uncontaminated by Ly
confidence level (statistical error) in the complete sample of 248 DLA/QSO pairs for which the r band is uncontaminated by Ly ![]() forest (
forest (
![]() ).
The mean (g-z) reddening is detected at
).
The mean (g-z) reddening is detected at ![]()
![]() confidence level
in the sample of 232 DLA/QSO pairs with g magnitude uncontaminated by the QSO Lyman break (
confidence level
in the sample of 232 DLA/QSO pairs with g magnitude uncontaminated by the QSO Lyman break (
![]() )
and corrected for DLA flux suppression (Sect. 3.2.2).
)
and corrected for DLA flux suppression (Sect. 3.2.2).
To estimate the confidence level of the detection other than in terms of ![]() we applied the method of bootstrap resampling (Efron 1979).
A bootstrap sample is obtained by extracting n data at random with repetition
from the original sample of n measurements. This type of extraction is, in practice,
an extraction with replacement because
part of the original measurements is replaced by repeated data.
By iterating this extraction process many times it is possible to build a
large number
we applied the method of bootstrap resampling (Efron 1979).
A bootstrap sample is obtained by extracting n data at random with repetition
from the original sample of n measurements. This type of extraction is, in practice,
an extraction with replacement because
part of the original measurements is replaced by repeated data.
By iterating this extraction process many times it is possible to build a
large number ![]() of bootstrap samples from the original set of n data.
For each of the
of bootstrap samples from the original set of n data.
For each of the ![]() samples one can compute a statistical estimator of interest
(e.g. the weighted mean) and study the distribution of such estimator,
without making any assumption on the parent distribution.
We applied this method to the original sample of n measurements
samples one can compute a statistical estimator of interest
(e.g. the weighted mean) and study the distribution of such estimator,
without making any assumption on the parent distribution.
We applied this method to the original sample of n measurements ![]() ,
from which
we built up
,
from which
we built up
![]() bootstrap samples.
The weighted mean
bootstrap samples.
The weighted mean
![]() was recomputed in each case.
We analyzed the resulting distribution of
was recomputed in each case.
We analyzed the resulting distribution of
![]() values
(Fig. 3) to estimate the fraction of cases in which the mean value is positive.
We find
values
(Fig. 3) to estimate the fraction of cases in which the mean value is positive.
We find
![]() in
in ![]()
![]() of the
of the
![]() bootstrap samples and
bootstrap samples and
![]() in
in ![]()
![]() of the
of the
![]() bootstrap samples. These percent figures indicate the probability that a positive
color excess has been detected.
bootstrap samples. These percent figures indicate the probability that a positive
color excess has been detected.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8480fg4a.eps}\hspace*{0.8cm}
\includegraphics[width=7.5cm,clip]{8480fg4b.eps} \end{figure}](/articles/aa/full/2008/06/aa8480-07/Timg215.gif) |
Figure 4:
Frequency distribution of the mean deviations
|
| Open with DEXTER | |
A reason of concern in the present analysis is the possibility that
the mean color excess that we detect is due to sources of reddening other than the DLA systems
(e.g. dust in the quasar environment or in unidentified absorbers).
If present, these reddening contribution would also affect the quasars of the control sample.
To understand if these effects may accidentally yield
a mean color excess comparable to that measured in the DLA sample,
we applied our procedure to a large number of ``twin control samples''
with same size, redshift distribution and magnitude distribution
as the DLA sample. We then analyzed the values of
![]() obtained from these twin control samples in a search for
cases with a value equal to those reported in Table 3. In practice,
each twin control sample was created by extracting at random,
for each DLA-QSO of Table 1, a control QSO at the same redshift and magnitude.
The control QSOs extracted in this way were treated as DLA-QSOs and temporarily
excluded from the estimate of the mean unreddened colors
obtained from these twin control samples in a search for
cases with a value equal to those reported in Table 3. In practice,
each twin control sample was created by extracting at random,
for each DLA-QSO of Table 1, a control QSO at the same redshift and magnitude.
The control QSOs extracted in this way were treated as DLA-QSOs and temporarily
excluded from the estimate of the mean unreddened colors
![]() (Sect. 3.1).
As a consequence, the estimates of
(Sect. 3.1).
As a consequence, the estimates of
![]() were different for each realization of the twin control sample.
We built up 10 000 twin control samples and
computed the weighted mean
were different for each realization of the twin control sample.
We built up 10 000 twin control samples and
computed the weighted mean
![]() for each of them.
The resulting frequency distribution of
for each of them.
The resulting frequency distribution of
![]() values
is shown in Fig. 4 for both color indices of interest.
For comparison we show the mean color excess of the absorption sample (dotted lines).
The probability for a twin control sample to attain a value
values
is shown in Fig. 4 for both color indices of interest.
For comparison we show the mean color excess of the absorption sample (dotted lines).
The probability for a twin control sample to attain a value
![]() as high as the mean color excess of the absorption sample is <
as high as the mean color excess of the absorption sample is <![]() in (g-z)
and
in (g-z)
and ![]()
![]() in (r-z). We conclude that the mean color excess detected in the absorption sample cannot be ascribed to dust in the quasar environment or in unidentified low-redshift absorbers. The same low probability applies to any sort of systematic effect that
might accidentally conspire to yield a mean color excess as a consequence of the application of our procedure to a quasar sample with same size, redshift distribution and magnitude distribution
as the DLA sample.
in (r-z). We conclude that the mean color excess detected in the absorption sample cannot be ascribed to dust in the quasar environment or in unidentified low-redshift absorbers. The same low probability applies to any sort of systematic effect that
might accidentally conspire to yield a mean color excess as a consequence of the application of our procedure to a quasar sample with same size, redshift distribution and magnitude distribution
as the DLA sample.
For a correct interpretation of the present results
it is important to understand whether the mean reddening that we detect
is a signature of the bulk of the DLA population or is just due
to the presence of a few reddened quasars.
To clarify this point we rejected the most reddened DLA-QSOs
from the original sample of Table 1 and repeated the computation of the mean reddening.
In practice, we discarded the cases with individual color deviation ![]() larger than the mean color deviation
larger than the mean color deviation
![]() at
at ![]() level
(``absorption sample 2'') and at
level
(``absorption sample 2'') and at ![]() level (``absorption sample 3'').
In the second and third row of Table 3 we show the mean color excess recomputed
after rejecting the most reddened cases in this way.
One can see that the mean color excess is still detected at
level (``absorption sample 3'').
In the second and third row of Table 3 we show the mean color excess recomputed
after rejecting the most reddened cases in this way.
One can see that the mean color excess is still detected at ![]() 2.8
2.8![]() level in (r-z) and at 3.5
level in (r-z) and at 3.5![]() level in (g-z)for the absorption sample 3. The detection is firmer for the absorption sample 2.
level in (g-z)for the absorption sample 3. The detection is firmer for the absorption sample 2.
As an final test we checked the stability of the results
for the adoption of different values of
![]() and nm
(Sect. 3.3). We tested this effect by varying these
parameters around their optimal values
and nm
(Sect. 3.3). We tested this effect by varying these
parameters around their optimal values
![]() and
and
![]() .
The resulting changes of the mean reddening are significantly
smaller than the statistical error discussed above.
.
The resulting changes of the mean reddening are significantly
smaller than the statistical error discussed above.
The analysis presented in the previous section indicates that
high-redshift quasars with intervening DLA systems
at
![]() have redder colors than quasars
at the same redshift without foreground absorption systems.
have redder colors than quasars
at the same redshift without foreground absorption systems.
The most natural process to explain the origin of this reddening is dust extinction, with its characteristic rise at shorter wavelengths. If this is the case, we expect the measured reddening to show similarities with that predicted for typical interstellar dust extinction curves. We also expect the most reddened quasars to be dimmed by dust extinction and therefore to be statistically fainter than unreddened quasars. In Sects. 5.1 and 5.2 below we present observational evidence consistent with these expectations.
The location of the dust is of special interest in the present work. Reddening sources in the quasar environment cannot explain the difference in color between the quasars of the absorption and control samples since this type of reddening would affect in the same way, on the average, the quasars of both samples. Dust embedded in the DLA systems is the most natural hypothesis to explain the measured color excess. This hypothesis bears some predictions that can be tested empirically.
One is that the reddening should increase with the column density of the metals embedded in the DLA systems. Another is that the dust-to-gas ratio should approximately scale with the level of metallicity of DLA systems. In Sects. 5.3 and 5.4 below we present observational evidence consistent with these expectations. In Sects. 5.5 and 5.6 we discuss the reddening versus H I column density and versus absorption redshift.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8480fg5a.eps}\hspace*{0.8cm}
\includegraphics[width=7.5cm,clip]{8480fg5b.eps} \end{figure}](/articles/aa/full/2008/06/aa8480-07/Timg224.gif) |
Figure 5:
Deviation from the mean color,
|
| Open with DEXTER | |
One of the properties used to characterize
the interstellar dust is its extinction curve,
![]() .
In spite of strong spatial variability, interstellar extinction curves
can be classified in two types:
Milky-Way type curves, with the characteristic extinction bump at 2175 Å (e.g. Cardelli et al. 1998),
and SMC-type curves, characterized by a more regular UV rise
(e.g. Pei 1992; Gordon et al. 2003).
The different slopes of these curves can be used to distinguish between them.
.
In spite of strong spatial variability, interstellar extinction curves
can be classified in two types:
Milky-Way type curves, with the characteristic extinction bump at 2175 Å (e.g. Cardelli et al. 1998),
and SMC-type curves, characterized by a more regular UV rise
(e.g. Pei 1992; Gordon et al. 2003).
The different slopes of these curves can be used to distinguish between them.
If the reddening originates in the DLA systems, we can measure the slope of the DLA dust extinction curve by comparing the mean reddening in the (g-z) and (r-z) colors.
We use the restricted sample of 232 DLA-QSOs with
![]() ,
for which both (g-z) and (r-z) can be derived.
For this sub-sample we measure
,
for which both (g-z) and (r-z) can be derived.
For this sub-sample we measure
![]()
![]() 10-3 mag
and we obtain
10-3 mag
and we obtain
![]() = 2.2
= 2.2 ![]() 0.9.
This measurement is in good agreement with the ratio
predicted for absorbers with SMC-type extinction curve at
0.9.
This measurement is in good agreement with the ratio
predicted for absorbers with SMC-type extinction curve at
![]() ,
,
![]() .
.
The fact that we detect reddening in the (r-z) color argues againts a MW-type extinction curve. In fact, this type of curve is expected to give a negligible or even negative reddening in the interval of absorption redshift spanned by of our sample (Fig. 1). This is due to the fact that in this interval the (r-z) color probes a part of the MW extinction curve with negative slope, namely the end of the 2175 Å extinction bump. The fact that we detect reddening in the (r-z) color indicates that extinction curve of MW type must be uncommon in the sample.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8480fg6a.eps}\hspace*{0.7cm}
\includegraphics[width=7.5cm,clip]{8480fg6b.eps} \end{figure}](/articles/aa/full/2008/06/aa8480-07/Timg229.gif) |
Figure 6:
Deviations from the mean color,
|
| Open with DEXTER | |
If DLAs with MW-type curves exist, a broad absorption
centered at
![]()
![]()
![]() should affect the quasar continuum. We searched for
this feature in all the spectra of the absorption sample, and in particular
of the quasars with anomalous colors, but without success
(see e.g. Fig. 8).
should affect the quasar continuum. We searched for
this feature in all the spectra of the absorption sample, and in particular
of the quasars with anomalous colors, but without success
(see e.g. Fig. 8).
The above results are in line with the general finding that MW-type extinction
curves are rare among quasar absorbers (Junkkarinen et al. 2004; Wang et al. 2004),
while SMC-type are common (Wild & Hewett 2005; York et al. 2006).
By adopting an SMC extinction curve, our results imply a rest-frame extinction
![]() mag (Table 3),
corresponding to
mag (Table 3),
corresponding to
![]() mag.
mag.
As we mentioned above, we expect the most reddened quasars to be statistically fainter than unreddened quasars if the reddening originates in dust.
In Fig. 5 we plot
![]() and
and
![]() versus the r magnitude.
The largests values of color excess lie at faint magnitudes (
versus the r magnitude.
The largests values of color excess lie at faint magnitudes (![]() mag),
in broad agreement with this expectation. To quantify the effect we compared
the mean magnitude of the 30 DLA-QSOS with highest
mag),
in broad agreement with this expectation. To quantify the effect we compared
the mean magnitude of the 30 DLA-QSOS with highest
![]() with the mean magnitude of the remaining DLA-QSOs
with lower
with the mean magnitude of the remaining DLA-QSOs
with lower
![]() .
The most reddened cases are slightly fainter
on the average,
.
The most reddened cases are slightly fainter
on the average,
![]()
![]() 0.08,
than the remaining cases,
0.08,
than the remaining cases,
![]()
![]() 0.04.
A similar computation for the (g-z) color yields
0.04.
A similar computation for the (g-z) color yields
![]()
![]() 0.09 for the 30 most reddened cases
and
0.09 for the 30 most reddened cases
and
![]()
![]() 0.05 for the remaining cases.
The effect is modest, but is in line with the prediction that
quasars with higher reddening should be statistically fainter.
0.05 for the remaining cases.
The effect is modest, but is in line with the prediction that
quasars with higher reddening should be statistically fainter.
If the reddening originates in dust embedded in the DLA system we expect
a trend between the color excess and the total column density of metals
in the absorber.
The limited spectral resolution of SDSS spectra prevents the accurate measurement
of metal column densities, but is sufficient to measure the equivalent width of strong metal lines.
To search for a possible trend between color excess and metals
we performed a study of the Si II line at 1526 Å, which is
sufficiently strong to be detected in SDSS spectra
and lies redwards of the Ly ![]() forest in most of the redshift range of interest.
Since the 1526 Å line is saturated, its rest-frame equivalent width,
forest in most of the redshift range of interest.
Since the 1526 Å line is saturated, its rest-frame equivalent width,
![]() ,
is not a good tracer of the metal column density. Nevertheless, an empirical correlation between
,
is not a good tracer of the metal column density. Nevertheless, an empirical correlation between
![]() and metallicity has been recently found for DLA-QSOs, in the form
[M/H]
and metallicity has been recently found for DLA-QSOs, in the form
[M/H] ![]()
![]() (Prochaska et al. 2007b).
This correlation is probably the consequence of the mass-metallicity and mass-kinematics relations in galaxies. Galaxies with higher masses (and metallicities) have larger kinematical motions, which result in larger spread (and equivalent width) of saturated metal lines such as the Si II line at 1526 Å.
(Prochaska et al. 2007b).
This correlation is probably the consequence of the mass-metallicity and mass-kinematics relations in galaxies. Galaxies with higher masses (and metallicities) have larger kinematical motions, which result in larger spread (and equivalent width) of saturated metal lines such as the Si II line at 1526 Å.
To estimate
![]() we used an automated algorithm
which fits a Gaussian profile to the strongest absorption feature (if any)
at the predicted wavelength,
we used an automated algorithm
which fits a Gaussian profile to the strongest absorption feature (if any)
at the predicted wavelength,
![]() Å,
provided this line occurs redwards of the Ly
Å,
provided this line occurs redwards of the Ly ![]() forest.
Each fit was visually inspected and the line-strength of Si II 1526
was compared against other metal-lines observed redwards of the Ly
forest.
Each fit was visually inspected and the line-strength of Si II 1526
was compared against other metal-lines observed redwards of the Ly![]() forest. In a few cases, we rejected lines because of obvious blends with
coincident absorption lines from systems at unrelated redshifts. As a result
of this analysis, we measured an equivalent width
in 180 DLA-QSOs of our sample. In Fig. 6 we plot
the deviations from the mean colors
forest. In a few cases, we rejected lines because of obvious blends with
coincident absorption lines from systems at unrelated redshifts. As a result
of this analysis, we measured an equivalent width
in 180 DLA-QSOs of our sample. In Fig. 6 we plot
the deviations from the mean colors
![]() and
and
![]() versus the rest-frame equivalent width
versus the rest-frame equivalent width
![]() measured by the automated algorithm. No clear trend is present, possibly because
most of the data are clumped at low values of equivalent width,
where we expect a modest reddening. The interval
measured by the automated algorithm. No clear trend is present, possibly because
most of the data are clumped at low values of equivalent width,
where we expect a modest reddening. The interval
![]() ,
where the reddening is expected
to be stronger, is much less populated, but its size is sufficiently
large to compute the mean value.
We therefore splitted the data in two subsets of
``weak'' and ``strong'' Si II absorbers by using
,
where the reddening is expected
to be stronger, is much less populated, but its size is sufficiently
large to compute the mean value.
We therefore splitted the data in two subsets of
``weak'' and ``strong'' Si II absorbers by using
![]() as a threshold value.
The mean values of reddening derived for these subsets are shown in Table 4
for the three absorption samples defined in Table 3.
One can see that the mean reddening tends to be higher
in strong Si II absorbers than in weak Si II absorbers, as expected
if the dust is embedded in DLA systems.
The difference in mean reddening between the two sub-samples is
marginal in the (r-z) color, but more evident in the (g-z) color.
as a threshold value.
The mean values of reddening derived for these subsets are shown in Table 4
for the three absorption samples defined in Table 3.
One can see that the mean reddening tends to be higher
in strong Si II absorbers than in weak Si II absorbers, as expected
if the dust is embedded in DLA systems.
The difference in mean reddening between the two sub-samples is
marginal in the (r-z) color, but more evident in the (g-z) color.
Table 4: Mean reddening of sub-samples with different strengths of the Si II 1526 line detected at the redshift of the DLA system.
To investigate the physical relation between dust and metals
we converted the color deviations ![]() into a mean extinction
and the Si II equivalent widths into a metallicity.
The rest-frame extinction,
into a mean extinction
and the Si II equivalent widths into a metallicity.
The rest-frame extinction, ![]() ,
is expected to scale with the metal column density
,
is expected to scale with the metal column density
![]() ,
where (M/H) is the total abundance by number
(gas plus dust) of the reference element M (e.g. Vladilo et al. 2006).
,
where (M/H) is the total abundance by number
(gas plus dust) of the reference element M (e.g. Vladilo et al. 2006).
To derive the extinction we used the expression
![]() ,
obtained from Eq. (3). The true color excess Ei of the individual quasar is unknown,
but we can take
,
obtained from Eq. (3). The true color excess Ei of the individual quasar is unknown,
but we can take
![]() since we average the above expression for a large sample
to obtain
since we average the above expression for a large sample
to obtain
![]() (see Sect. 3.1).
An SMC extinction curve
(see Sect. 3.1).
An SMC extinction curve
![]() was adopted in this conversion.
was adopted in this conversion.
To derive the metal column density we used the empirical relation
[M/H] ![]()
![]() (Prochaska et al. 2007c) and
then averaged the individual values of metal column density
(Prochaska et al. 2007c) and
then averaged the individual values of metal column density
![]() .
.
In Fig. 7 we plot the results of these computations obtained for the subsets of weak and strong Si II absorbers of Table 4 (sample 2). The data are consistent with the existence of the trend between metal column density and extinction expected if the reddening and metals originate in the same medium. Again, the evidence for this trend is very weak in (r-z) and firmer in (g-z). Given the uncertainties in the above conversions and the limited statistics it is not possible to reach firmer conclusions.
The quasars of the absorption sample with high color deviations
and strong Si II absorptions are excellent candidates for detailed
follow up studies of dusty DLA systems based on high resolution spectroscopy.
In Fig. 8 we show, as an example,
the spectra of the DLA-quasars with
![]() and
and
![]() .
The typical metallicity of these systems is a factor 3 larger than the average metallicity of the absorption sample.
.
The typical metallicity of these systems is a factor 3 larger than the average metallicity of the absorption sample.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8480fg7.eps} \end{figure}](/articles/aa/full/2008/06/aa8480-07/Timg258.gif) |
Figure 7: Mean values of rest-frame extinction and metal column density of the two subsets of DLA-QSOs with different strengths of the Si II line 1526 Å shown in Table 4 (absorption sample 2). The extinction values derived from the (g-z) and (r-z) color deviations are plotted with diamonds and circles, respectively. The mean values of metal column density of the two subsets are the same and have been slightly shifted along the horizontal direction for clarity. See Sect. 5.3. |
| Open with DEXTER | |
By adopting an extinction curve
![]() of SMC-type
we can convert the reddening measured in the observer's frame into
an extinction in the rest frame.
From this in turn we can measure, for the first time in studies of DLA systems,
the dust-to-gas ratio in the same units used in local
interstellar studies, namely the ratio
of SMC-type
we can convert the reddening measured in the observer's frame into
an extinction in the rest frame.
From this in turn we can measure, for the first time in studies of DLA systems,
the dust-to-gas ratio in the same units used in local
interstellar studies, namely the ratio
![]() between the extinction in the V band and the H I column density.
From Eq. (3) the individual dust-to-gas ratio is given by
between the extinction in the V band and the H I column density.
From Eq. (3) the individual dust-to-gas ratio is given by
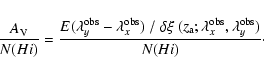 |
(6) |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{8480fg8a.eps}\hspace*{0.4cm}...
...eps}\hspace*{0.4cm}
\includegraphics[width=5cm,clip]{8480fg8c.eps} \end{figure}](/articles/aa/full/2008/06/aa8480-07/Timg264.gif) |
Figure 8:
Quasars of the absorption sample with color deviations
|
| Open with DEXTER | |
Table 5: Mean metallicity and extinction per unit metal column density for the DLA-QSOs with Si II measurements.
The present measurements of reddening and metallicity can be combined to
estimate the mean extinction per unit metal column density in the DLA systems of our sample.
We start from the relation
By combining the Eqs. (7) and (3) we obtain
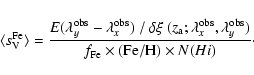 |
(8) |
In Fig. 9 we plot the color deviations
![]() and
and
![]() versus H I column density. A linear correlation analysis of
versus H I column density. A linear correlation analysis of
![]() and
and
![]() versus
versus ![]() (H I)
for the complete absorption sample yields correlation coefficients r=-0.01 and r=+0.01, respectively. The comparison of sub-samples with low and high values of N(H I)
does not indicate the existence of a trend with reddening.
Most DLA-QSOs are concentrated at low H I column densities as a consequence of the
well-known decrease of the number of DLA systems
with increasing
(H I)
for the complete absorption sample yields correlation coefficients r=-0.01 and r=+0.01, respectively. The comparison of sub-samples with low and high values of N(H I)
does not indicate the existence of a trend with reddening.
Most DLA-QSOs are concentrated at low H I column densities as a consequence of the
well-known decrease of the number of DLA systems
with increasing
![]() (Wolfe et al. 2005; Prochaska et al. 2005).
Some of the most reddened quasars are concentrated
at low H I column densities, at odd with
the expectation that large reddening is associated with
large column density of neutral gas.
The paucity of highly reddened cases at
(Wolfe et al. 2005; Prochaska et al. 2005).
Some of the most reddened quasars are concentrated
at low H I column densities, at odd with
the expectation that large reddening is associated with
large column density of neutral gas.
The paucity of highly reddened cases at
![]() atoms cm-2could be the consequence of low-number statistics: systems with high H I column density are rare and the present statistics might be insufficient to detect cases of high reddening.
It is worth noticing that lines of sight of high metallicity are
generally not observed in DLA systems with
atoms cm-2could be the consequence of low-number statistics: systems with high H I column density are rare and the present statistics might be insufficient to detect cases of high reddening.
It is worth noticing that lines of sight of high metallicity are
generally not observed in DLA systems with
![]() atoms cm-2 (Boissé et al. 1998).
If this is the case also for the present sample,
this fact could conspire to make rare the systems of high reddening
at
atoms cm-2 (Boissé et al. 1998).
If this is the case also for the present sample,
this fact could conspire to make rare the systems of high reddening
at
![]() atoms cm-2.
atoms cm-2.
The metal abundances of DLA systems are often used to estimate
the mean cosmic metallicity of the neutral gas at high redshift.
In this type of estimate the metallicity of each system
must be weighted by its H I column density to estimate
a mean cosmic value
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8480fg9a.eps}\hspace*{0.8cm}
\includegraphics[width=7.5cm,clip]{8480fg9b.eps} \end{figure}](/articles/aa/full/2008/06/aa8480-07/Timg290.gif) |
Figure 9:
Deviations from the mean color,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{8480fg10a.eps}\hspace*{0.6cm}
\includegraphics[width=7.7cm,clip]{8480fg10b.eps} \end{figure}](/articles/aa/full/2008/06/aa8480-07/Timg291.gif) |
Figure 10:
Deviations from the mean color,
|
| Open with DEXTER | |
In Fig. 10 we plot the color deviations
![]() and
and
![]() versus absorption redshift
versus absorption redshift ![]() .
The data
are spread more or less uniformly in the interval of absorption redshift considered.
A linear correlation analysis of
.
The data
are spread more or less uniformly in the interval of absorption redshift considered.
A linear correlation analysis of
![]() and
and
![]() versus
versus ![]() for the complete absorption sample yields
correlation coefficients r=+0.13 and r=+0.06, respectively.
The lack of a trend with redshift implies
that the color excess that we derive is sufficiently
representative of the mean reddening of
DLA systems over the full interval
for the complete absorption sample yields
correlation coefficients r=+0.13 and r=+0.06, respectively.
The lack of a trend with redshift implies
that the color excess that we derive is sufficiently
representative of the mean reddening of
DLA systems over the full interval
![]() covered by our sample.
The lack of redshift evolution is, to some extent, surprising.
Two types of evolutionary effects
are expected to occur if the reddening originates in DLA dust.
On the one hand, a rise of the reddening
with increasing
covered by our sample.
The lack of redshift evolution is, to some extent, surprising.
Two types of evolutionary effects
are expected to occur if the reddening originates in DLA dust.
On the one hand, a rise of the reddening
with increasing ![]() is expected due the UV rise of the extinction curve.
For an SMC extinction curve this effect is roughly a factor of 2 in E(r-z)in the redshift range of interest, as shown in Fig. 1.
On the other hand, a decrease of the reddening
with increasing
is expected due the UV rise of the extinction curve.
For an SMC extinction curve this effect is roughly a factor of 2 in E(r-z)in the redshift range of interest, as shown in Fig. 1.
On the other hand, a decrease of the reddening
with increasing ![]() is expected as a consequence of cosmic chemical evolution
if the dust scales with the metals. Also this effect is expected to be approximately a factor of 2
in the redshift interval of interest, where the mean metallicity decreases by
is expected as a consequence of cosmic chemical evolution
if the dust scales with the metals. Also this effect is expected to be approximately a factor of 2
in the redshift interval of interest, where the mean metallicity decreases by
![]() 0.3 dex per unit redshift interval (Prochaska et al. 2000).
The lack of a trend could be the consequence of the opposite behaviour
of two evolutionary effects, which tend to cancel each other.
0.3 dex per unit redshift interval (Prochaska et al. 2000).
The lack of a trend could be the consequence of the opposite behaviour
of two evolutionary effects, which tend to cancel each other.
To perform a homogeneous comparison with the work of Murphy & Liske (2004, ML04) we applied our procedure to their original list of quasars![]() extracted from the second data release (DR2).
The list includes 70 DLA-quasars and 1396 non-DLA quasars
in spectra with SNR
extracted from the second data release (DR2).
The list includes 70 DLA-quasars and 1396 non-DLA quasars
in spectra with SNR ![]() 3 as defined in ML04.
To apply our procedure we selected
the 56 DLA-quasars and 1074 non-DLA quasars with
3 as defined in ML04.
To apply our procedure we selected
the 56 DLA-quasars and 1074 non-DLA quasars with
![]() .
The non-DLA quasars were used to build the control pool.
From the application of our method to these lists we obtain
the weighted mean values
.
The non-DLA quasars were used to build the control pool.
From the application of our method to these lists we obtain
the weighted mean values
![]()
![]() 10-3 mag and,
for the subset of 52 quasars with
10-3 mag and,
for the subset of 52 quasars with
![]() ,
,
![]()
![]() 10-3 mag.
The lack of detection of the reddening is due to the small size of the sample.
By converting these results to rest-frame color excess with an SMC extinction curve we obtain a
10-3 mag.
The lack of detection of the reddening is due to the small size of the sample.
By converting these results to rest-frame color excess with an SMC extinction curve we obtain a ![]() upper limit
E(B-V) < 0.02 mag from both color indices.
This limit is equal to that obtained by ML04 from their analysis
of the spectral index distribution of the quasar spectra.
The photometric method presented here
and the spectral index method adopted by ML04 yield therefore consistent results.
upper limit
E(B-V) < 0.02 mag from both color indices.
This limit is equal to that obtained by ML04 from their analysis
of the spectral index distribution of the quasar spectra.
The photometric method presented here
and the spectral index method adopted by ML04 yield therefore consistent results.
We have used the spectroscopic and photometric database of the 5th data release of the SDSS
to measure the reddening of quasars with intervening damped Ly ![]() systems at
high redshift (
systems at
high redshift (
![]() ). The spectroscopic database was used
to distinguish quasars with and without intervening absorption systems.
Only good quality spectra, with typical
signal-to-noise ratio SNR
). The spectroscopic database was used
to distinguish quasars with and without intervening absorption systems.
Only good quality spectra, with typical
signal-to-noise ratio SNR ![]() 4 in the spectral regions of interest,
were considered in the analysis.
We built up an ``absorption sample'' of 248 quasars with a single DLA system
in the redshift interval
4 in the spectral regions of interest,
were considered in the analysis.
We built up an ``absorption sample'' of 248 quasars with a single DLA system
in the redshift interval
![]() and without metal systems
at
and without metal systems
at
![]() .
We then selected about 2 thousand control quasars without DLA systems
or metal systems.
The large SDSS photometric database, employed
for the first time in the DLA reddening analysis,
was used to measure the colors
of individual quasars of the absorption and control samples.
.
We then selected about 2 thousand control quasars without DLA systems
or metal systems.
The large SDSS photometric database, employed
for the first time in the DLA reddening analysis,
was used to measure the colors
of individual quasars of the absorption and control samples.
The analysis was performed on the (r-z) and (g-z) color indices.
The color index (r-z) is uncontaminated by Ly ![]() absorption
in the redshift interval considered.
The color (g-z) offers a higher leverage for reddening detection,
but the g bandpass is contaminated by Ly
absorption
in the redshift interval considered.
The color (g-z) offers a higher leverage for reddening detection,
but the g bandpass is contaminated by Ly ![]() absorption.
To derive the (g-z) colors we corrected the g magnitude
for flux suppresion due to the presence of the damped Ly
absorption.
To derive the (g-z) colors we corrected the g magnitude
for flux suppresion due to the presence of the damped Ly ![]() absorption
in the spectra. We obtain a mean color excess
absorption
in the spectra. We obtain a mean color excess
![]()
![]() 10-3 mag and
10-3 mag and
![]()
![]() 10-3 mag.
The quoted statistical error is not significantly affected by the presence
correlated errors. The detection is confirmed by the analysis of 10 000 bootstrap
samples originated from the absorption sample.
The reddening is detected at
10-3 mag.
The quoted statistical error is not significantly affected by the presence
correlated errors. The detection is confirmed by the analysis of 10 000 bootstrap
samples originated from the absorption sample.
The reddening is detected at ![]()
![]() c.l. also when
the most reddened DLA-QSOs of the sample are rejected,
assuming that they are spurious.
c.l. also when
the most reddened DLA-QSOs of the sample are rejected,
assuming that they are spurious.
The most natural hypothesis to explain the observed reddening
is dust along the line of sight.
The ratio
![]()
![]() 0.9
that we measure lends support to this hypothesis, since this
value is in agreement with that predicted
for dust with SMC-type extinction curve at the absorption redshift of our sample.
Also the study of the reddening versus quasars magnitude
is consistent with the dust hypothesis: the most reddened quasars
are, on the average, slightly fainter than the others, in line with the expectation that
extinction and reddening should increase together if the reddening is due to dust.
0.9
that we measure lends support to this hypothesis, since this
value is in agreement with that predicted
for dust with SMC-type extinction curve at the absorption redshift of our sample.
Also the study of the reddening versus quasars magnitude
is consistent with the dust hypothesis: the most reddened quasars
are, on the average, slightly fainter than the others, in line with the expectation that
extinction and reddening should increase together if the reddening is due to dust.
Dust in the quasar environment or in low-redshift interlopers is not a viable explanation for the observed reddening since it would affect in the same way, on the average, the quasars of the absorption sample and those of the control sample. Quasars with anomalous colors would not be able to produce accidentally the measured reddening (Sect. 4.1).
The above arguments indicate that the reddening is due to
dust embedded in the intervening DLA systems. This conclusion is consistent with two other
studies performed in the present work.
One is the comparison of the color excess with the equivalent width
of the Si II 1526 Å line at the redshift of the DLA system:
strong Si II absorbers (
![]() )
show
a slightly higher reddening, on the average,
than weak Si II absorbers (
)
show
a slightly higher reddening, on the average,
than weak Si II absorbers (
![]() ),
in line with the expectation that the amount of dust and metals
should increase together inside the DLA systems.
Also the study of the mean dust-to-gas ratio, obtained by converting the observed
reddening into rest-frame extinction, yields a similar conclusion.
We find
),
in line with the expectation that the amount of dust and metals
should increase together inside the DLA systems.
Also the study of the mean dust-to-gas ratio, obtained by converting the observed
reddening into rest-frame extinction, yields a similar conclusion.
We find
![]() 2 to 4
2 to 4 ![]() 10-23 mag cm2,
a value
10-23 mag cm2,
a value ![]() -1.25 lower than that of the Milky Way,
consistent with the lower level of metallicity
of DLA systems of our sample estimated indirectly from
-1.25 lower than that of the Milky Way,
consistent with the lower level of metallicity
of DLA systems of our sample estimated indirectly from
![]() .
Also this result is in line with
the expectation that metals and dust should increase together.
.
Also this result is in line with
the expectation that metals and dust should increase together.
The conversion of our reddening measurement to rest-frame color excess
by means of an SMC extinction curve yields
![]()
![]() 0.005/0.007 mag.
This value fits the trend of
0.005/0.007 mag.
This value fits the trend of
![]() versus redshift in quasar absorbers extrapolated
from measurements of Mg II systems at lower redshift (Menard et al. 2007, Fig. 10).
versus redshift in quasar absorbers extrapolated
from measurements of Mg II systems at lower redshift (Menard et al. 2007, Fig. 10).
The mean color excess that we have derived is
representative of the mean reddening of DLA systems at
![]() in SDSS QSOs with limiting magnitude
in SDSS QSOs with limiting magnitude
![]() .
The magnitude limit results from the
condition SNR
.
The magnitude limit results from the
condition SNR ![]() 4, required to distinguish the presence of
absorption systems in the quasar spectra.
Since highly reddened quasars are more likely to be found at
fainter magnitudes, a larger reddening could be obtained from deeper surveys.
4, required to distinguish the presence of
absorption systems in the quasar spectra.
Since highly reddened quasars are more likely to be found at
fainter magnitudes, a larger reddening could be obtained from deeper surveys.
Follow-up, direct measurements of metallicity of the DLA systems of the present sample
are required to test the indirect estimates based on
![]() ,
to obtain an accurate measurement of the extinction per unit metal column density,
which seems to be similar to that found at lower redshift,
and to assess the importance of the extinction bias in studies of DLA-QSOs.
,
to obtain an accurate measurement of the extinction per unit metal column density,
which seems to be similar to that found at lower redshift,
and to assess the importance of the extinction bias in studies of DLA-QSOs.
Acknowledgements
We thank Gabriel Prochter for providing an updated list of Mg II absorptions in SDSS DR5 quasar spectra. G.V. thanks Matteo Viel, Sergei Levshakov and Carlo Morossi for helpful discussions on the analysis of the data. J.X.P. is partially supported by an NSF CAREER grant (AST-0548180). We thank an anonymous referee for comments that improved this paper.
By comparing the definitions E=C-C0 and
![]() given in Sect. 3.1, we have
given in Sect. 3.1, we have
If we have a large sample of reddened quasars with varying properties pi, then the condition
![]() is still satisfied provided the distributions of
unreddened colors around their mean value
are the same for different subsets of control quasars.
The validity of the condition
is still satisfied provided the distributions of
unreddened colors around their mean value
are the same for different subsets of control quasars.
The validity of the condition
![]() can be tested from
the analysis of quasars of the twin control samples (Sect. 4.1).
Each control sample is built with unreddened QSOs and therefore its color deviations
are
can be tested from
the analysis of quasars of the twin control samples (Sect. 4.1).
Each control sample is built with unreddened QSOs and therefore its color deviations
are
![]() .
By measuring the mean value of these deviations
we can test if
.
By measuring the mean value of these deviations
we can test if
![]() .
From Fig. 4 one can see that
the mean values of the color excess of the control samples are peaked at zero,
implying that the above condition is generally satisfied.
.
From Fig. 4 one can see that
the mean values of the color excess of the control samples are peaked at zero,
implying that the above condition is generally satisfied.