A&A 477, 967-977 (2008)
DOI: 10.1051/0004-6361:20065969
Advanced fit technique for astrophysical spectra
Approach insensitive to a large fraction of outliers
S. Bukvic1 -
Dj. Spasojevic1 -
V. Zigman2
1 - Faculty of Physics, University of Belgrade, Studentski Trg 12-16, Belgrade, Serbia
2 -
University of Nova Gorica, Vipavska cesta 13, Nova Gorica, Slovenia
Received 4 July 2006 / Accepted 23 September 2007
Abstract
Aims. The purpose of this paper is to introduce a robust method of data fitting convenient for dealing with astrophysical spectra contaminated by a large fraction of outliers.
Methods. We base our approach on the suitable defined measure: the density of the least squares (DLS) that characterizes subsets of the whole data set. The best-fit parameters are obtained by the least-square method on a subset having the maximum value of DLS or, less formally, on the largest subset free of outliers.
Results. We give the FORTRAN90 source code![[*]](/icons/foot_motif.gif) of the subroutine that implements the DLS method. The efficiency of the DLS method is demonstrated on a few examples: estimation of continuum in the presence of spectral lines, estimation of spectral line parameters in the presence of outliers, and estimation of the thermodynamic temperature from the spectrum that is rich in spectral lines.
of the subroutine that implements the DLS method. The efficiency of the DLS method is demonstrated on a few examples: estimation of continuum in the presence of spectral lines, estimation of spectral line parameters in the presence of outliers, and estimation of the thermodynamic temperature from the spectrum that is rich in spectral lines.
Conclusions. Comparison of the present results with the ones obtained with the widely used comprehensive multi-component fit yields agreement within error margins. Due to simplicity and robustness, the proposed approach could be the method of choice whenever outliers are present, or whenever unwelcome features of the spectrum are to be considered as formal outliers (e.g. spectral lines while estimating continuum).
Key words: methods: data analysis - methods: numerical - techniques:
spectroscopic - line: profiles
1 Introduction
The task often met in data processing is to find the best
parameters of some model function that would represent a
particular set of data in the best-fit sense. For this purpose it
is a common practice to use the least squares as a merit function
for various data fittings. Unfortunately, measurements are not
free of errors, which occasionally cause some experimental points
to simply be way off. Also, data of interest are frequently
spoiled by the irregular deviation of a certain number of data
points due to some undesirable process that cannot be avoided.
This can easily turn the results obtained with the least-square
method into nonsense.
The reliability of the best-fit could be significantly enhanced if
outliers could be successfully recognized and subsequently
removed. A variety of statistical tests, reviewed in
(Barnett & Lewis 1994), have been developed to decide whether
a data point is an outlier or not. If there is a sufficient number
of replicate points at each value of x, these tests could be
useful for determining whether a single value is a significant
outlier. Unfortunately, each point is measured only once in
typical experiments. In such a case, one can choose to perform an
outlier test on the entire set of residuals of the least-square
fit. The problem arises if outliers are allocated asymmetrically.
In this case the best-fit curve tends to be inclined towards the
outliers, so that outlying points might not be recognized.
In order to minimize the impact of outliers, a multitude of robust
approaches has been proposed (Hoaglin et al. 1983; Hampel et al. 1986). While efficient in the case of symmetrically allocated outliers, most of the robust fit approaches are
scale-dependent and ineffective if a large fraction of outlying
points lie on the same side of the best-fit curve. Some relevant
ideas for how to deal with outliers in case of a linear, as well
as nonlinear, fit are presented in (Marx 1996; Motulsky & Brown 2006; Liu et al. 2005).
Well-known tasks to which the least-square method is not directly
applicable include determining the spectrum base line and spectrum
continuum. Both issues often arise in spectroscopy, since for many
applications in astrophysics (Peterson et al. 2002; Freudling et al. 2003; Gilbert & Peterson 2003; Contini & Viegas 2000; Rossa et al. 2000; Gabel et al. 2005) and
in physics (Meisel & Cote 1992; Spasojevic et al. 1996), accurate knowledge
of both the local continuum value and signal base line is
essential. To overcome the drawbacks of the least squares, a few
specific, non robust approaches have been proposed. One of them is
to estimate the continuum and power-law exponents from the
spectral regions uncontaminated by emission or absorption lines
(Liu & Yan 2005; Wang et al. 2005; Gabel et al. 2005). Within this approach, the
spectral lines are unwelcome features - formal outliers, which can
produce spurious results. Another approach is to apply a complex
multi-component fit (Dietrich et al. 2002; Freudling et al. 2003; Dietrich et al. 2005; Gabel et al. 2005), which takes all known features of the spectrum into account. However, some unknown, non-implied
features, or true outlying points can still induce inaccurate
estimates of the fit coefficients.
In a recent paper (Bukvic & Spasojevic 2005), a robust method for
estimating of the spectrum base line and continuum from large data
sets has been proposed. The method was based on the close
points concept (CPC), capable to distinguish outliers from
close points, with the resulting best-fit parameters
obtained only on the set of close points.
In this paper we develop this technique further by applying the
least-square approach in accordance with CPC. The proposed method
is insensitive to the presence of a large number of outlying
points, which makes it appropriate for various purposes. For
example, in spectrum analysis, it can be used to fit the full
spectrum (base line/continuum + all spectral lines), to fit only
selected spectrum characteristics (base line/continuum + selected
spectral lines, while all other spectral lines are treated as
outliers), or to fit the base line/continuum only (with all
spectral lines being treated as outliers).
2 Merit function
Consider a data set
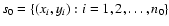 consisting of n0 experimental points and a family of model
functions
consisting of n0 experimental points and a family of model
functions
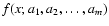 depending on x and on the
parameters
depending on x and on the
parameters
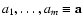 ,
specifying a model
function from the family. In the least-square approach, the best
model function is usually found by applying the method to the
whole data set s0. However, the set s0 may be contaminated
by various types of unwelcome data. Therefore, it could happen
that the model function that optimally reflects the features of
interest actually corresponds not to the initial data set s0,
but rather to some of its subsets, sb - the "best'' one - not
known in advance.
,
specifying a model
function from the family. In the least-square approach, the best
model function is usually found by applying the method to the
whole data set s0. However, the set s0 may be contaminated
by various types of unwelcome data. Therefore, it could happen
that the model function that optimally reflects the features of
interest actually corresponds not to the initial data set s0,
but rather to some of its subsets, sb - the "best'' one - not
known in advance.
In order to identify it, we introduce the density of least
squares - the quantity suitable for characterizing the initial
data set s0 and any particular subset s, in the following
way:
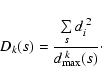 |
(1) |
Here, symbol 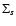 denotes summation over all data points of
subset s, and
di=|yi-f(xi;a(s))| is the absolute
value of the deviation of yi from the model function
f(xi;a(s)), defined here as distance of data
point
denotes summation over all data points of
subset s, and
di=|yi-f(xi;a(s))| is the absolute
value of the deviation of yi from the model function
f(xi;a(s)), defined here as distance of data
point
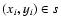 from
f(xi;a(s)), as specified
by
a(s). The parameters
a(s) are the
best-fit parameters, obtained by applying the ordinary
least-square (OLS) method to the subset s, so that
from
f(xi;a(s)), as specified
by
a(s). The parameters
a(s) are the
best-fit parameters, obtained by applying the ordinary
least-square (OLS) method to the subset s, so that
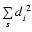 is the corresponding OLS sum for
that subset. Analogously,
is the corresponding OLS sum for
that subset. Analogously,
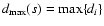 is the maximal
distance, which specifies the width of subset s, relative
to the model function
f(xi;a(s)). The exponent k is
a real number, whose value is yet to be determined. It will be
shown in Sect. 3 that
is the maximal
distance, which specifies the width of subset s, relative
to the model function
f(xi;a(s)). The exponent k is
a real number, whose value is yet to be determined. It will be
shown in Sect. 3 that
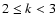 ,
and that the choice k=2 additionally simplifies our method.
,
and that the choice k=2 additionally simplifies our method.
The subset sb, singled out by having maximum density of the
least squares, is taken as the best subset; its OLS best-fit
parameters
a(sb) are considered to yield the most
reliable estimate of the features of interest, hence, are accepted
as the final outcome of the proposed method. The estimation of
uncertainties
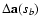 of the OLS best-fit
parameters
a(sb) is explained in
Sect. 4. To conform to standard
terminology, we introduce the merit function
of the OLS best-fit
parameters
a(sb) is explained in
Sect. 4. To conform to standard
terminology, we introduce the merit function
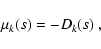 |
(2) |
which is a function of subset s of the data set s0.
Obviously, on subset sb, merit function (2)
attains its minimum value, whereas Dk(s) attains its maximum value.
We call the foregoing approach the density of least-square
(DLS) method. We call the points from subset sb close
points, while all other points we call distant points or
outliers with respect to the model function
f(xi;a(s)). In the same sense, the width of the best subset
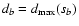 can be conveniently used to set a
discrimination level between distant and close points.
can be conveniently used to set a
discrimination level between distant and close points.
So far, we have considered data sets with unspecified errors of
ordinates yi,
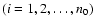 .
If individual errors
.
If individual errors 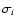 are, on the other hand, assigned to corresponding yi then,
instead of geometrical distances di, relative distances
are, on the other hand, assigned to corresponding yi then,
instead of geometrical distances di, relative distances
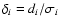 should be used. Accordingly, the density
of weighted least squares is defined by an appropriate
extension of Eq. (1):
should be used. Accordingly, the density
of weighted least squares is defined by an appropriate
extension of Eq. (1):
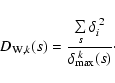 |
(3) |
The geometrical interpretation of Eq. (3) is,
however, less obvious. In what follows we will, therefore, refer
mostly to Eq. (1).
As shown in the Appendix, the best-fit parameters
a(sb) found by the DLS method are, actually, the maximum likelihood parameters, obtained by a specific Local
maximum-likelihood estimator. This evidence, together with the
calibration procedure put forward in Sect. 3.1, forms the formal basis of the DLS method.
Now we proceed to intuitive considerations, illustrating how DLS works in the case k=2. Let s0 be a data set containing one outlying point with respect to a model function, and
let s be its subset that contains all points from s0, except
the outlying point. Although both the numerator
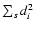 and
denominator
and
denominator
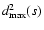 in Eq. (1) are smaller
on s than on s0, the effect of the decrease in
in Eq. (1) are smaller
on s than on s0, the effect of the decrease in
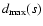 in
in
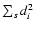 is lessened by the contribution of other points,
so that the denominator decrease becomes dominant. It follows that
the density Dk(s) of the subset s will typically be higher
than Dk(s0). More generally, if the data set s0contains outlying points, then the density of least squares
typically attains its maximum value on some subset that is free of
outliers, but still contains a large percentage of data.
is lessened by the contribution of other points,
so that the denominator decrease becomes dominant. It follows that
the density Dk(s) of the subset s will typically be higher
than Dk(s0). More generally, if the data set s0contains outlying points, then the density of least squares
typically attains its maximum value on some subset that is free of
outliers, but still contains a large percentage of data.
With respect to definition (2), we would like to
emphasize that we do not simply seek for parameters that
minimize the value of merit function 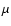 on the initial data
set. Instead, we are presently concerned with finding the
best subset sb for which the density of least squares
exhibits its maximum. This task cannot be reduced to the standard
minimization problem.
on the initial data
set. Instead, we are presently concerned with finding the
best subset sb for which the density of least squares
exhibits its maximum. This task cannot be reduced to the standard
minimization problem.
Indeed, the standard minimization problem takes place in a
multidimensional space of model function parameters. Provided the
initial guess is given, the standard minimization algorithms
follow the gradient direction, assuring rapid approach to some
local minimum. For functions that, like merit function (2), have data subset as an argument some appropriate substitute for the gradient minimization algorithm is to be
sought; see the discussion for details. To this end we establish
an ordered collection of data subsets in agreement with our main
intention of removing outlying points, so as to obtain the subset
with the maximum density of least squares.
We define the ordered collection of data subsets by iterating the
following two-stage procedure. We first calculate the OLS best-fit
model function for the given subset s and then remove from sthe point with the greatest distance
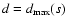 with respect
to the best-fit curve. In the second stage, we apply OLS only to
the retained data points and recalculate distances di of the
remaining data points from the new best-fit model function. If
there are points with distances larger than the starting
with respect
to the best-fit curve. In the second stage, we apply OLS only to
the retained data points and recalculate distances di of the
remaining data points from the new best-fit model function. If
there are points with distances larger than the starting
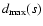 ,
we remove them as well.
We repeat these steps until all points with distances
,
we remove them as well.
We repeat these steps until all points with distances
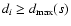 are removed. The smaller subset of retained points,
with new
are removed. The smaller subset of retained points,
with new
 ,
is now ready for the next iteration cycle.
Points eliminated from s by this procedure, see Fig. 1, constitute a
layer of outer points for subset s or, simply,
layer
,
is now ready for the next iteration cycle.
Points eliminated from s by this procedure, see Fig. 1, constitute a
layer of outer points for subset s or, simply,
layer![[*]](/icons/foot_motif.gif) .
.
![\begin{figure}
\par\includegraphics[height=8.85cm,width=7.15cm,clip]{5969f1.eps}\end{figure}](/articles/aa/full/2008/03/aa5969-06/Timg45.gif) |
Figure 1:
Flowchart of the procedure used to obtain the ordered
collection
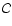 .
Index j=n-l denotes the number of
points in the subset s(j). Yellow and blue colors indicate
algorithm steps of the first and of the second stages,
respectively. The algorithm step painted in both colors is invoked
only once within the first stage, at the very beginning; all its
subsequent calls are within the second stage. .
Index j=n-l denotes the number of
points in the subset s(j). Yellow and blue colors indicate
algorithm steps of the first and of the second stages,
respectively. The algorithm step painted in both colors is invoked
only once within the first stage, at the very beginning; all its
subsequent calls are within the second stage. |
By using the foregoing procedure, we iteratively remove
layer-by-layer from the initial data set s0, and we eventually
obtain an ordered collection of data subsets
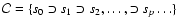 where index pcounts the subsets in the collection. After each iteration, we
calculate Dk(sp). Although one can fit the subset of n data
points to a m-parameter model function technically whenever
where index pcounts the subsets in the collection. After each iteration, we
calculate Dk(sp). Although one can fit the subset of n data
points to a m-parameter model function technically whenever
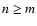 ,
we terminate the build-up of collection
,
we terminate the build-up of collection
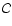 whenever a more conservative condition n< m+3 is met, or after
Dk(sp) becomes indefinite - see Sect. 3.2. As the best subset sb, we accept the subset from collection
whenever a more conservative condition n< m+3 is met, or after
Dk(sp) becomes indefinite - see Sect. 3.2. As the best subset sb, we accept the subset from collection
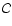 having a maximum value of
DLS. For the users' convenience, a FORTRAN code of the DLS data-fitting method is given in Sect. 8.2.
having a maximum value of
DLS. For the users' convenience, a FORTRAN code of the DLS data-fitting method is given in Sect. 8.2.
3 Calibration procedure
3.1 Normal distribution case
Let the data set
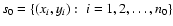 contain n0normally distributed points around the value y=0. We assume that
the number n0 is large enough for the statistical parameters
related to s0 to be indistinguishable from their corresponding
limits, when
contain n0normally distributed points around the value y=0. We assume that
the number n0 is large enough for the statistical parameters
related to s0 to be indistinguishable from their corresponding
limits, when
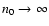 .
.
Then, the number dn of yi's in the interval
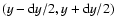 is
is
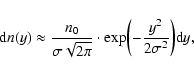 |
(4) |
where 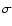 is the corresponding standard deviation. In this
particular case, we take the horizontal lines
is the corresponding standard deviation. In this
particular case, we take the horizontal lines
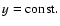 for the
family of model functions. Let sd be a d-stripe, i.e. the
subset consisting of all points from s0 located between the two
horizontal lines: y=-d and y=d. For sd we see that
for the
family of model functions. Let sd be a d-stripe, i.e. the
subset consisting of all points from s0 located between the two
horizontal lines: y=-d and y=d. For sd we see that
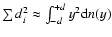 ,
so that
,
so that
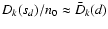 ,
where
,
where
is the DLS per one data point for d-stripes, in the case of
Gaussian distribution.
On the other hand, one can show that inequality
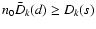 holds
holds![[*]](/icons/foot_motif.gif) for any subset s with
for any subset s with
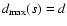 ,
implying that the maximum of
,
implying that the maximum of
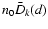 is
equal to the DLS maximum
is
equal to the DLS maximum![[*]](/icons/foot_motif.gif) . The same maximum is found in the ordered
collection
. The same maximum is found in the ordered
collection
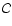 ,
since
,
since
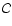 consists of
d-stripes. In the top panel of Fig. 2 we present
plots of
consists of
d-stripes. In the top panel of Fig. 2 we present
plots of
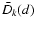 scaled by
scaled by
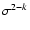 for three
characteristic values of parameter k; each curve manifests
distinct maximum.
for three
characteristic values of parameter k; each curve manifests
distinct maximum.
![\begin{figure}
\par\includegraphics[width=7.85cm,clip]{5969f2.eps}\end{figure}](/articles/aa/full/2008/03/aa5969-06/Timg73.gif) |
Figure 2:
Top panel:
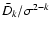 versus
relative width
versus
relative width 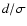 of d-stripes for Gaussian
distribution. Presented curves correspond to three characteristic
values of k, as given in the legend, together with abscissae
of d-stripes for Gaussian
distribution. Presented curves correspond to three characteristic
values of k, as given in the legend, together with abscissae
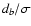 of the corresponding maxima;
of the corresponding maxima; 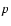 is the
percentage of points contained in the corresponding
db-stripes. Bottom panel: exponent k versus
is the
percentage of points contained in the corresponding
db-stripes. Bottom panel: exponent k versus
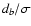 ,
according to Eq. (6) for Gaussian
distribution - bold curve. As indicated, analogous curves for
Lorentzian and for double-exponential distribution are also given.
In DLS method we only use the values ,
according to Eq. (6) for Gaussian
distribution - bold curve. As indicated, analogous curves for
Lorentzian and for double-exponential distribution are also given.
In DLS method we only use the values 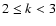 . . |
The condition for the maximum of (5), i.e.
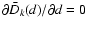 ,
leads to a scale-independent
equation,
,
leads to a scale-independent
equation,
![\begin{displaymath}%
\biggl(\frac{d_b}{\sigma}\biggr)^3\exp\biggl[-
\frac{d_b^{\...
...ma^2}\biggr]-k\int^{d_b/\sigma}_{0}
t^2\exp(-t^2/2){\rm d}t=0,
\end{displaymath}](/articles/aa/full/2008/03/aa5969-06/img75.gif) |
(6) |
which relates exponent k to the ratio
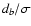 .
In other
words, if we choose one of them, e.g.
.
In other
words, if we choose one of them, e.g.
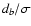 ,
then the other
one (k) will follow from (6). Thus, for
,
then the other
one (k) will follow from (6). Thus, for
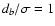 we find
we find
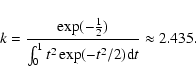 |
(7) |
Alternatively, if we specify the value of exponent k, then the
value db for which
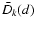 attains a maximum follows
from Eq. (6). Thus, for k=2 we obtain
attains a maximum follows
from Eq. (6). Thus, for k=2 we obtain
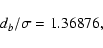 |
(8) |
implying that the best subset sb consists of all data points
between horizontal lines y=-db and y=db, containing
approximately 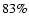 of normally distributed data points.
of normally distributed data points.
The bottom panel of Fig. 2 presents k versus
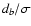 ,
for a Gaussian distribution (bold line), according
to (6). For comparison, analogous curves
,
for a Gaussian distribution (bold line), according
to (6). For comparison, analogous curves
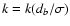 are shown for Lorentzian and for
double-exponential distribution.
are shown for Lorentzian and for
double-exponential distribution.
It should be noted that exponent k is not completely free of
constraints. The upper limit is strict and amounts to k<3.
Namely, from Eq. (6), it follows that
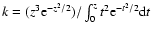 ,
where
,
where
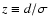 .
For
.
For 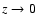 ,
we also have
,
we also have 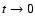 ,
so that
,
so that
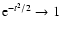 .
Therefore, the upper limit is evaluated as
.
Therefore, the upper limit is evaluated as
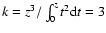 .
.
The lower limit is not as strict and cannot be deduced from Eq. (6), which holds in the case of pure Gaussian scatter around a y=0 value. Apart from defining the width of the
best subset, exponent k has a significant impact on the ability
of the DLS method to resolve outliers. When outliers actually do
occur, details of bulk data distribution become of secondary
importance. The following example illustrates the effect of the
exponent k on the order-of-magnitude scale. Consider a set s0containing an odd number n0=2m+1 of points, such that
xi=i,
(i=1, n0),
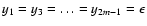 ,
,
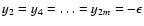 ,
and
y2m+1=1. For small
,
and
y2m+1=1. For small
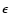 ,
the last point is a typical outlier. Let us choose the
horizontal lines y(x)=a as model functions. Considering that the
best horizontal line level ab is equal to the mean value of
,
the last point is a typical outlier. Let us choose the
horizontal lines y(x)=a as model functions. Considering that the
best horizontal line level ab is equal to the mean value of
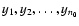 ,
we find
,
we find
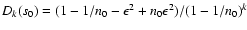 for the whole data set, and
for the whole data set, and
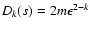 for the set s, obtained by removing
the outlying point from s0. For sufficiently small
for the set s, obtained by removing
the outlying point from s0. For sufficiently small 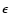 and k<2, it follows that
Dk(s0)>Dk(s), which implies that
the outlier could not be removed if k<2. Therefore, we accept
the constraint
and k<2, it follows that
Dk(s0)>Dk(s), which implies that
the outlier could not be removed if k<2. Therefore, we accept
the constraint 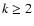 as the lower limit for the exponent k,
with the remark that in the case of well-behaved data
distributions, with soft outliers, DLS will work even if k<2,
though its ability to resolve outliers will be reduced.
as the lower limit for the exponent k,
with the remark that in the case of well-behaved data
distributions, with soft outliers, DLS will work even if k<2,
though its ability to resolve outliers will be reduced.
3.2 Indefinite case
By removing layer-by-layer from the initial data set, the
successive data subsets contain a smaller and smaller number of
points. It may happen, eventually, that we have to deal with a
subset s, such that each of its n data points lies on the
corresponding OLS best-fit curve y=ys(x). Then, both
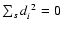 and
and
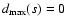 ,
so that the density of least
squares
,
so that the density of least
squares
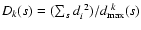 apparently
becomes indefinite.
apparently
becomes indefinite.
This difficulty can be resolved by taking into account that the
measured data are subject to a limited resolution of measurement.
Therefore, although all data points lie on the best-fit curve at
the current resolution, it is more likely that their actual
values are scattered around it according to some "unknown''
sub-distribution that is beyond measurement resolution. In other
words, a quantity
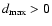 ,
assigned to this sub-distribution
exists, though not accessible by the measurement technique,
characterizes the data set. That being the case, one can rewrite
the expression for Dk(s) in the form
,
assigned to this sub-distribution
exists, though not accessible by the measurement technique,
characterizes the data set. That being the case, one can rewrite
the expression for Dk(s) in the form
where di
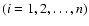 are actual distances, inherent
in the unknown sub-distribution
are actual distances, inherent
in the unknown sub-distribution![[*]](/icons/foot_motif.gif) . Hence, it is
convenient to introduce the quotient q of the
mean-squared distance
. Hence, it is
convenient to introduce the quotient q of the
mean-squared distance
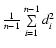 and
and
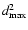 ,
i.e.,
,
i.e.,
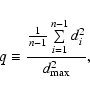 |
(9) |
as a characteristic parameter of the assumed sub-distribution,
such that Dk (s) takes the form
![\begin{displaymath}%
D_k(s)=d^{2-k}_{\rm max}\biggl[1+(n-1)q\biggr ].
\end{displaymath}](/articles/aa/full/2008/03/aa5969-06/img105.gif) |
(10) |
According to (10), the density of least squares Dk(s) is determined by the parameters:
 and q(0<q<1). Since not accessible to measurements, one may treat
both parameters as subject to choice. The exception arises for
k=2, when (10) simplifies to
and q(0<q<1). Since not accessible to measurements, one may treat
both parameters as subject to choice. The exception arises for
k=2, when (10) simplifies to
with q as a single parameter required to specify D2 (s).
One can try to elaborate the choice of q by arguing that any
distribution, taken in narrow limits of stochastic variable,
should be nearly uniform. Consequently, in the narrow limits set
by the resolution of measurement, the presently assumed
sub-distribution should be uniform as well. Therefore, the
expected value of quantity q, given by Eq. (9), is
which evaluates to
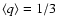 in the case of uniform distribution
in the case of uniform distribution
 .
Hence,
.
Hence,
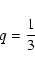 |
(12) |
is an appropriate choice according to our experience. In this
case, the density of least squares, Eq. (11),
amounts to
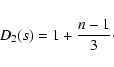 |
(13) |
However, if k>2 is adopted, an independent estimate of
 is to be supplied to evaluate Dk(s), see Eq. (10). A reasonable choice is to assume that
is to be supplied to evaluate Dk(s), see Eq. (10). A reasonable choice is to assume that
 has the same order of magnitude as dr, the original
resolution of measurement.
has the same order of magnitude as dr, the original
resolution of measurement.
If the data set is accompanied by measurement errors 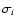 ,
then the density of weighted least squares is given by Eq. (3). Technically, the foregoing analysis holds,
but when applied to relative distances
,
then the density of weighted least squares is given by Eq. (3). Technically, the foregoing analysis holds,
but when applied to relative distances
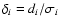 ,
rather than to geometrical distances di. The density of
weighted least squares in the indefinite case is given analogously
to Eq. (11) by
,
rather than to geometrical distances di. The density of
weighted least squares in the indefinite case is given analogously
to Eq. (11) by
![\begin{displaymath}%
D_{w,k}(s)=\delta^{2-k}_{\rm max}\biggl [1+(n-1)q\biggr ],
\end{displaymath}](/articles/aa/full/2008/03/aa5969-06/img111.gif) |
(14) |
which yields
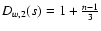 ,
for k=2 and
q=1/3. If
,
for k=2 and
q=1/3. If 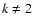 we also need an independent estimate of
measurement resolution, dr, to evaluate
we also need an independent estimate of
measurement resolution, dr, to evaluate
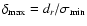 .
Here
.
Here
 denotes the
minimal error pertaining to the subset of points that lie on the
weighted least-square best-fit curve.
denotes the
minimal error pertaining to the subset of points that lie on the
weighted least-square best-fit curve.
4 Error estimation in the best-fit parameters
We propose a procedure for rough estimation of the
uncertainties of DLS best-fit parameters based on parameter db - the width of DLS best subset. The benefit is most evident when
the data set is not accompanied by measurement errors. For the
sake of simplicity, we assume that the DLS exponent k is set to 2,
therefore
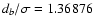 .
.
(i) Measurement errors are not available in the original
data set. After running DLS, we assign
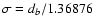 to
all close points and use these estimated errors in a WLS fitting
algorithm. The reported uncertainties we accept as the errors of
the DLS best-fit parameters. For data sets containing a small
number of points, it may happen that all close points lie on the
OLS best-fit curve; i.e. we have to deal with the indefinite case.
Since experimental errors are not given, there is no way to
estimate uncertainties of the best-fit parameters even for k=2,
unless the resolution of measurement dr is known. In this case,
one can accept
to
all close points and use these estimated errors in a WLS fitting
algorithm. The reported uncertainties we accept as the errors of
the DLS best-fit parameters. For data sets containing a small
number of points, it may happen that all close points lie on the
OLS best-fit curve; i.e. we have to deal with the indefinite case.
Since experimental errors are not given, there is no way to
estimate uncertainties of the best-fit parameters even for k=2,
unless the resolution of measurement dr is known. In this case,
one can accept
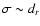 as a surrogate for missing
experimental variances and proceed with WLS to estimate
uncertainties of the best-fit parameters.
as a surrogate for missing
experimental variances and proceed with WLS to estimate
uncertainties of the best-fit parameters.
(ii) Measurement errors 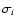 are available in the
original data set. Instead of db, DLS will give
are available in the
original data set. Instead of db, DLS will give 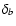 which is related to the standard deviation
which is related to the standard deviation 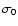 of the
relative residuals
of the
relative residuals
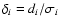 - therefore:
- therefore:
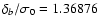 .
Note that, if the individual errors
.
Note that, if the individual errors
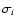 are correctly estimated, then
are correctly estimated, then
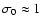 or
or
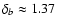 .
If so, after running the WLS algorithm on
the set of close points (with original
.
If so, after running the WLS algorithm on
the set of close points (with original 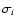 ), the returned
uncertainties are accepted. However, if
), the returned
uncertainties are accepted. However, if 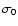 is notably
different from 1, it signifies that original measurement errors
were badly estimated. In this case, the best one can do is to go
back to the experiment, if possible. If not, it is safer to
correct original errors than to proceed with wrong ones,
especially if
is notably
different from 1, it signifies that original measurement errors
were badly estimated. In this case, the best one can do is to go
back to the experiment, if possible. If not, it is safer to
correct original errors than to proceed with wrong ones,
especially if
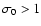 .
The correction is quite simple:
.
The correction is quite simple:
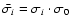 .
If we run the WLS algorithm on the set of close points with corrected errors
.
If we run the WLS algorithm on the set of close points with corrected errors
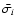 ,
the reported uncertainties will suit the data
scatter. Finally, if the indefinite case occurs while processing a
data set with known
,
the reported uncertainties will suit the data
scatter. Finally, if the indefinite case occurs while processing a
data set with known 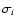 ,
it is enough to apply WLS fit on
the subset of close points retaining original errors.
,
it is enough to apply WLS fit on
the subset of close points retaining original errors.
5 Examples
For the sake of simplicity, in all our
examples we have taken k=2 and assumed that no experimental
errors have been assigned to data points. The uncertainties are
estimated from the data scattering, as discussed above.
In Fig. 3, we present a data set consisting of 11
moderately scattered points. By applying the DLS method to the
family of straight-line model functions, we found 3 outlying
points, while 8 points were recognized as close points. In order
to find the best-fit parameters and the corresponding
uncertainties, one can simply run WLS for the close points only.
In the inset, we present the density of least squares versus width
of the consecutive data subsets. The rightmost point represents
the density of least squares for the whole data set. The next
point represents the density of least squares after the first
layer is removed, and so on. The density of least squares attains
its maximum after removal of three layers, each containing one
point. Therefore, the best subset contains 8 points, recognized as
close points.
![\begin{figure}
\par\includegraphics[height=6.25cm,width=7.3cm,clip]{5969f3.eps}\end{figure}](/articles/aa/full/2008/03/aa5969-06/Timg127.gif) |
Figure 3:
Eleven moderately scattered points and the best-fit
straight line according to the DLS method. Three points are
recognized as distant points, i.e. outliers. The remaining eight
points are close points. The best-fit parameters are only obtained
on the subset of close points only. The inset displays the density
of least squares, DLS, versus subset width. The maximum of DLS is
clearly noticeable. The density of least squares for the whole
data set is shown by the rightmost point. The density of least
squares of the subset obtained after the first layer has been
removed is presented by the next point and so on. We removed 6 layers, each containing 1 point. The width of the last set analyzed, containing n=5 points, is 0.03106. |
An artificially generated spectrum with three spectral lines is
shown in Fig. 4. The magnitude of applied Gaussian
noise is
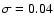 .
To demonstrate stability and robustness of
the DLS method, we fitted the horizontal base line with the
fourth-order polynomials. Note the pronounced stability of DLS best-fit: though determined by five coefficients, the best-fit
polynomial has the appearance of a horizontal line. For the sake
of comparison, we also present the best-fit polynomial according
to the OLS method and the best-fit polynomial obtained by the
robust approach with a Lorentzian probability distribution. The
difference is self-evident. The width of the best subset
db=0.038 is quite close to the magnitude of the applied
Gaussian noise, and it can serve as a distinguishing parameter:
points that satisfy di>db belong to spectral lines and are
treated as formal outliers, while data points satisfying di<dbare associated to the feature of interest, the base line in our
example. The scattering of the data points di<db around the
best-fit curve can be attributed to noise.
.
To demonstrate stability and robustness of
the DLS method, we fitted the horizontal base line with the
fourth-order polynomials. Note the pronounced stability of DLS best-fit: though determined by five coefficients, the best-fit
polynomial has the appearance of a horizontal line. For the sake
of comparison, we also present the best-fit polynomial according
to the OLS method and the best-fit polynomial obtained by the
robust approach with a Lorentzian probability distribution. The
difference is self-evident. The width of the best subset
db=0.038 is quite close to the magnitude of the applied
Gaussian noise, and it can serve as a distinguishing parameter:
points that satisfy di>db belong to spectral lines and are
treated as formal outliers, while data points satisfying di<dbare associated to the feature of interest, the base line in our
example. The scattering of the data points di<db around the
best-fit curve can be attributed to noise.
![\begin{figure}
\par\includegraphics[height=6.25cm,width=7.3cm,clip]{5969f4.eps}\end{figure}](/articles/aa/full/2008/03/aa5969-06/Timg128.gif) |
Figure 4:
Artificially generated spectrum with three spectral
lines superimposed on line y(x)=0. The magnitude of the applied
Gaussian noise is
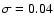 .
Fourth-order polynomials are
employed as base-line model functions. The solid gray line
represents the DLS best-fit polynomial, with respective parameters
given in the legend. The dashed line represents the OLS best-fit
polynomial, while the solid black line represents the best-fit
polynomial obtained by the robust approach with a Lorentzian
probability distribution. The inset shows the density of least
squares, DLS, versus subset width. The width of the best subset is
db=0.038, which is almost the same as the magnitude of the
applied noise. In DLS method, db determines the discrimination
level; accordingly, spectral lines are recognized as (formal)
outliers. .
Fourth-order polynomials are
employed as base-line model functions. The solid gray line
represents the DLS best-fit polynomial, with respective parameters
given in the legend. The dashed line represents the OLS best-fit
polynomial, while the solid black line represents the best-fit
polynomial obtained by the robust approach with a Lorentzian
probability distribution. The inset shows the density of least
squares, DLS, versus subset width. The width of the best subset is
db=0.038, which is almost the same as the magnitude of the
applied noise. In DLS method, db determines the discrimination
level; accordingly, spectral lines are recognized as (formal)
outliers. |
In the next example we compare two methods of data fitting: our
DLS method and the multi-component fit (MCF). Here we estimate
only the parameters of the He II 468.6 nm Pashen alpha line (
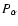 ), recorded in a high-voltage pulsed discharge (Djenize et al. 2004) - see Fig. 5. In the captured
spectrum, the central broad line is the
), recorded in a high-voltage pulsed discharge (Djenize et al. 2004) - see Fig. 5. In the captured
spectrum, the central broad line is the
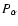 line, while
the two unambiguous peaks, left and right of the central line,
correspond to the O II 467.66 nm and the O II 469.93 nm lines,
respectively. Several low-magnitude peak-like crests visible on
both wings are treated as stochastic fluctuations. Note also the
presence of two typical outlying points, encircled in the lower
panel, probably caused by occasional misfire of the high-voltage
trigger. In this particular experiment, the high electron density
of the discharge, induces a notable Stark effect. Therefore, the
adequate model function for the spectral line is considered to be
of the Lorentz profile type
line, while
the two unambiguous peaks, left and right of the central line,
correspond to the O II 467.66 nm and the O II 469.93 nm lines,
respectively. Several low-magnitude peak-like crests visible on
both wings are treated as stochastic fluctuations. Note also the
presence of two typical outlying points, encircled in the lower
panel, probably caused by occasional misfire of the high-voltage
trigger. In this particular experiment, the high electron density
of the discharge, induces a notable Stark effect. Therefore, the
adequate model function for the spectral line is considered to be
of the Lorentz profile type
![$L(\lambda)=h/[1+(\frac{\lambda-c}{w})^2]$](/articles/aa/full/2008/03/aa5969-06/img129.gif) ,
depending on
wavelength
,
depending on
wavelength 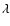 ,
and on the line parameters: height h,
center c, and half-width w. Since the wavelength interval of
the spectrum is rather narrow, it is enough to take the base line
in the form of a straight line:
,
and on the line parameters: height h,
center c, and half-width w. Since the wavelength interval of
the spectrum is rather narrow, it is enough to take the base line
in the form of a straight line:
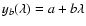 .
.
![\begin{figure}
\par\includegraphics[height=7.85cm,width=7.45cm,clip]{5969f5.eps}\end{figure}](/articles/aa/full/2008/03/aa5969-06/Timg132.gif) |
Figure 5:
Comparison of DLS and multi-component fit (MCF) of a
spectrum from a high-voltage pulsed discharge. The central line is
He II 468.6 nm Pashen alpha line (
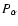 ). The two lateral
peaks are the O II 467.66 nm and O II 469.93 nm lines. In DLS fit,
the model function has the form ). The two lateral
peaks are the O II 467.66 nm and O II 469.93 nm lines. In DLS fit,
the model function has the form
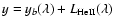 ,
with a straight base line ,
with a straight base line
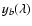 of slope b and y-intercept a and a
superimposed Lorentzian profile
of slope b and y-intercept a and a
superimposed Lorentzian profile
![$L(\lambda)=h/[1+(\frac{\lambda-c}{w})^2]$](/articles/aa/full/2008/03/aa5969-06/img129.gif) of height h, center c, and half-width w, describing the He II
of height h, center c, and half-width w, describing the He II
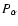 line. In MCF, we have also superimposed two Lorentzians, corresponding
to the O II lines. The obtained DLS and MCF best-fit parameters
coincide within the limits of their errors.
line. In MCF, we have also superimposed two Lorentzians, corresponding
to the O II lines. The obtained DLS and MCF best-fit parameters
coincide within the limits of their errors. |
In this problem, the proper DLS model function only consists of
the base line and the superimposed He II
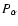 Lorentzian,
i.e.
Lorentzian,
i.e.
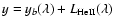 .
In contrast, if we apply
the multi-component fit, two additional Lorentzians, corresponding
to the lateral O II lines, have to be included as well; hence, the
proper MCF model function is:
.
In contrast, if we apply
the multi-component fit, two additional Lorentzians, corresponding
to the lateral O II lines, have to be included as well; hence, the
proper MCF model function is:
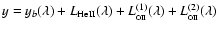 .
One can notice that sets of
.
One can notice that sets of
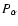 -line parameters, provided
by the DLS fit and by MCF, coincide within the limits of their
uncertainties. Note also that, though the base line was an
auxiliary feature (not shown in Fig. 5), both methods
give a fair agreement between the baseline parameters: the
y-intercept a and slope b.
-line parameters, provided
by the DLS fit and by MCF, coincide within the limits of their
uncertainties. Note also that, though the base line was an
auxiliary feature (not shown in Fig. 5), both methods
give a fair agreement between the baseline parameters: the
y-intercept a and slope b.
The specifics of both methods are clearly outlined by the
performed parallel fittings. The multi-component fit necessitates
a comprehensive form of model function with all (known) features
taken into account. In contrast, only the features of interest are
incorporated into the DLS model function, as the DLS merit
function enables removal of distant points. Some of these points
belong to the spectral lines, some are typical outliers, while the
rest of them cannot be easy classified. However, when a large
number of undocumented features and true outliers are expected,
instead of the foregoing straightforward MCF, the use of a
multi-component model function within the DLS approach is
recommended to reduce the risk of inaccurate parameter estimation.
In Fig. 6 we present an astrophysical spectrum - Far
Ultraviolet Spectroscopic Explorer (FUSE) composite spectrum,
originally reported in (Scott et al. 2004). The spectrum continuum is
supposed to be of a power-law type
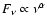 .
The best-fit power-law exponent quoted in (Scott et al. 2004) is
.
The best-fit power-law exponent quoted in (Scott et al. 2004) is
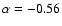 with standard deviation 0.11. We emphasize that the
reported estimate is obtained in a fit performed on selected
wavelength regions, free of emission lines: 630-750, 800-820,
850-900, 1095-1100, and 1135-1150 Å. The solid black line in
Fig. 6 shows this fit in wavelength scale, with the
power law
with standard deviation 0.11. We emphasize that the
reported estimate is obtained in a fit performed on selected
wavelength regions, free of emission lines: 630-750, 800-820,
850-900, 1095-1100, and 1135-1150 Å. The solid black line in
Fig. 6 shows this fit in wavelength scale, with the
power law
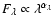 and
exponent
and
exponent
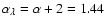 .
.
Contrary to the procedure adopted in Scott et al. (2004), the DLS fit
is performed on the whole spectrum range (630-1155 Å) of
the rest-frame wavelengths; the resulting best-fit curve is
represented by the solid gray line in Fig. 6. The DLS
best-fit exponent is
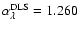 ,
while the
standard deviation, relying on the inherent noise, is estimated
to 0.034. Without any prior knowledge taken into account, the DLS
best-fit value
,
while the
standard deviation, relying on the inherent noise, is estimated
to 0.034. Without any prior knowledge taken into account, the DLS
best-fit value
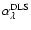 is slightly less than the
one quoted originally. It is indicative that the two tiny
wavelength intervals 1095 Å-1100 Å and 1135 Å-1150 Å,
(data in black line on the very right of Fig. 6),
recognized in (Scott et al. 2004) as regions of spectrum free of
emissions lines, have a significant impact on the best-fit value
of the power-law exponent. Inclusion of these intervals into the
continuum can be justified only if data pertaining to those
intervals are reliable and based on a priori knowledge, which
obviously has priority over any general procedure.
is slightly less than the
one quoted originally. It is indicative that the two tiny
wavelength intervals 1095 Å-1100 Å and 1135 Å-1150 Å,
(data in black line on the very right of Fig. 6),
recognized in (Scott et al. 2004) as regions of spectrum free of
emissions lines, have a significant impact on the best-fit value
of the power-law exponent. Inclusion of these intervals into the
continuum can be justified only if data pertaining to those
intervals are reliable and based on a priori knowledge, which
obviously has priority over any general procedure.
However, if we run DLS fit exactly on the same intervals as Scott
et al., the trough at about 720 Å is attributed again to
distant points signaling that this feature should be considered as
a candidate for rejection, even if the corresponding wavelength
interval is free of contamination. As mentioned in the preceding
example, by applying the DLS method independently, an unbiased
review and further insight into the considered problem could be
gained.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{5969f6.eps}\end{figure}](/articles/aa/full/2008/03/aa5969-06/Timg138.gif) |
Figure 6:
FUSE composite spectrum originally reported in
(Scott et al. 2004). Smooth solid lines represent best-fits of the
spectrum continuum to the power-law form
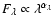 .
Scott et al. have
applied the fit only to selected wavelength intervals
(marked in black) that are free of spectral lines. Their best fit
(black line) corresponds to .
Scott et al. have
applied the fit only to selected wavelength intervals
(marked in black) that are free of spectral lines. Their best fit
(black line) corresponds to
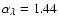 .
The best
power law according to DLS (gray line) is obtained on the
whole interval of wavelengths, and it corresponds to .
The best
power law according to DLS (gray line) is obtained on the
whole interval of wavelengths, and it corresponds to
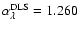 .
Data for DLS fit are recovered
from the original graph with limited accuracy, allowing only a
rough comparison of the two approaches. .
Data for DLS fit are recovered
from the original graph with limited accuracy, allowing only a
rough comparison of the two approaches. |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{5969f7.eps}\end{figure}](/articles/aa/full/2008/03/aa5969-06/Timg139.gif) |
Figure 7:
Time-integrated spectrum of an argon high-voltage pulsed
discharge recorded by a pocket-sized Ocean Optics spectrograph in
our plasma spectroscopy laboratory. The most intensive spectral
lines are clipped, in order to provide a noticeable continuum. By
DLS fitting of the spectrum continuum with Planck functions (15), we determined the time-averaged thermodynamic
temperature
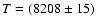 K. Its small uncertainty reflects a
low scattering of close points. K. Its small uncertainty reflects a
low scattering of close points. |
In Fig. 7 we present a time-averaged spectrum recorded
by a miniature Ocean Optics spectrograph during a single pulse of
an argon high-voltage pulsed discharge, operating in the Plasma
Spectroscopy Laboratory of the Faculty of Physics, University of
Belgrade. The spectrum covers the wavelength range from 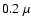 m
(near UV) to
m
(near UV) to 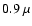 m (near IR). The created argon plasma is in
a state close to thermodynamic equilibrium (Djenize et al. 2006),
generating a spectrum with a large number of spectral lines and a
sizeable continuum. Consequently, the continuum profile defines
the base line of the spectrum. The simplest model function follows
from the Planck law of black body radiation, which relates the
intensity of radiation I at wavelength
m (near IR). The created argon plasma is in
a state close to thermodynamic equilibrium (Djenize et al. 2006),
generating a spectrum with a large number of spectral lines and a
sizeable continuum. Consequently, the continuum profile defines
the base line of the spectrum. The simplest model function follows
from the Planck law of black body radiation, which relates the
intensity of radiation I at wavelength 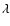 with the
thermodynamic temperature T. Within this example, we employ
Planck formula in the form
with the
thermodynamic temperature T. Within this example, we employ
Planck formula in the form
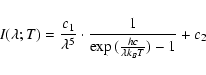 |
(15) |
where c1 comprises all requisite multiplicative factors
(including black-body corrections and spectrograph sensitivity),
while c2 takes the instrumental offset into account. In the
present approach, c1 and c2 are taken as fitting parameters
along with T. The DLS best-fit Planck function (15)
is presented in Fig. 7 by the solid line. The best-fit
value of time-averaged thermodynamic temperature is
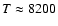 K. An independent temperature estimate based on the
Boltzmann-plot technique
K. An independent temperature estimate based on the
Boltzmann-plot technique![[*]](/icons/foot_motif.gif) gives
gives
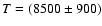 K.
This method requires a large number of pulsed discharge shots and
subsequent time averaging, thus adding a significant error to the
final result.
K.
This method requires a large number of pulsed discharge shots and
subsequent time averaging, thus adding a significant error to the
final result.
6 Discussion
In Sect. 2 we defined the merit function (2) on subsets s of a given data set s0 as arguments. Since the number of such subsets is typically huge
(2n0, n0 is the number of points in s0), it is evident
that the search for the merit function minimum by direct
inspection would be extremely inefficient. Therefore, some
substitute for the standard gradient methods, used in minimization
of ordinary functions (e.g. the steepest descent method), has to
be proposed.
Suppose that a data set s0, comprised of n0 points, is
given. In order to mimic a single step of a gradient method, we
remove point p from s0 so that the subset
s0(p),
obtained by its removal, has the minimum value of merit function
among all n0 subsets of s0 containing n0-1 points. Next,
we repeat the foregoing procedure on the subset
s0(p)instead of on s0, and so on. Though it is the closest
equivalent to the standard gradient minimization method, this
simple iterative procedure is still inefficient because, without
some additional criteria, the total number of subsets to be
scanned ( n02/2) is still large.
n02/2) is still large.
However, the structure of merit function (2) implies
that the outer points are the best candidates for removal. Indeed,
the greater the distance
|yp-f(xp,a(s))| of a
discarded point 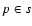 from the OLS best-fit curve
y=f(x,a(s)), the greater the local chances of
proceeding to the merit function minimum. Accordingly, if we
continue to remove the outermost points, the overall
chances of achieving the minimum of merit function (2) are greatest. Any other choice would reduce the prospects of reaching the minimum. Therefore, the ordered
collection
from the OLS best-fit curve
y=f(x,a(s)), the greater the local chances of
proceeding to the merit function minimum. Accordingly, if we
continue to remove the outermost points, the overall
chances of achieving the minimum of merit function (2) are greatest. Any other choice would reduce the prospects of reaching the minimum. Therefore, the ordered
collection
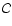 ,
introduced in Sect. 2, is an algorithmically optimal assortment of subsets, which provides an efficient way to find the minimum of
merit function (2). As in the case of standard
minimization, there is no full guarantee that a minimum found
within the ordered collection of subsets
,
introduced in Sect. 2, is an algorithmically optimal assortment of subsets, which provides an efficient way to find the minimum of
merit function (2). As in the case of standard
minimization, there is no full guarantee that a minimum found
within the ordered collection of subsets
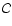 is the
absolute one.
is the
absolute one.
The rough estimate of errors in the best-fit parameters,
introduced in Sect. 4, is based on the
assumption that both - ordinary minimization algorithms employed
by DLS, as well the DLS itself - are exactly correct. The full
confidence limits on DLS best-fit parameters can be determined by
the Monte-Carlo method (Press et al. 2001) applied to the set of close
points, using 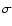 estimated according to Sect. 4.
estimated according to Sect. 4.
An important feature of the DLS method is its use of some OLS algorithm as a basic engine. Consequently, for a very broad class
of model functions depending linearly on their parameters (e.g.
polynomials), the solution is achieved without initial guess. This
is a serious advantage with respect to the original CPC method
(Bukvic & Spasojevic 2005), which requires the explicit use of a
minimization algorithm for all model functions, except for the
family of horizontal lines
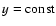 .
Nevertheless, if the model
function is a nonlinear function of its parameters, then the
explicit use of a minimization algorithm, like the
Levenberg-Marquardt algorithm (Press et al. 2001), is necessary.
.
Nevertheless, if the model
function is a nonlinear function of its parameters, then the
explicit use of a minimization algorithm, like the
Levenberg-Marquardt algorithm (Press et al. 2001), is necessary.
7 Conclusion
In this paper, we have proposed a new form of a merit function,
which measures the density of least squares (DLS) for subsets of a
given data set. The best-fit parameters are obtained by the
ordinary least-square method on a subset having a maximum density
of least squares. For a rapid approach to DLS maximum a simple
algorithm is put forward. Owing to its extreme robustness to the
presence of outlying points, DLS method enables flexible data
processing in which only features of interest are modeled. The
consequence is a notable reduction of fitting parameters and an
increased numerical stability, which are important in analyses of
complex real-world spectra.
The efficiency of DLS method has been illustrated by several
examples. Particularly persuasive is the low uncertainty
estimate of thermodynamic temperature from the continuum radiation
of a pulsed discharge.
The DLS method of data fitting allows plenty of extensions, which
we intend to study in the future.
Acknowledgements
This work was supported by the Serbian Ministry of Science
under projects 141010 and 141014 and by the Slovenian Research
Agency, under program P2-0056.
8 Appendix
8.1 Statistical underpinning of the DLS method
From the statistical point of view, many of the data-fitting
methods are local-M estimators![[*]](/icons/foot_motif.gif) . The basic assumption of the local-M approach is
that the probability density
P'(ym,x), of obtaining a
measured value ym at given x only depends on the relative
deviation
. The basic assumption of the local-M approach is
that the probability density
P'(ym,x), of obtaining a
measured value ym at given x only depends on the relative
deviation
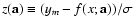 from the model function
f(x;a), so that
P'(ym,x)=P'(z(a)); here,
a stands for the
true model function parameters, whereas
from the model function
f(x;a), so that
P'(ym,x)=P'(z(a)); here,
a stands for the
true model function parameters, whereas 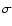 is the
uncertainty of ym.
is the
uncertainty of ym.
Assuming further that yi's are independent stochastic
variables, the overall probability density (of obtaining a data
set
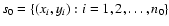 in a measurement) is
in a measurement) is
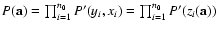 .
.
In practise, the true model function parameters are not known in
advance. In the maximum likelihood estimation, the
probability density
P(a) is taken as a
likelihood of parameters, so that the best-fit parameters
are those that maximize
P(a). Equivalently, one can
minimize the merit function
![$\mu(\mathbf{a})\equiv
-\ln[P(\mathbf{a})]$](/articles/aa/full/2008/03/aa5969-06/img150.gif) ,
commonly written as
,
commonly written as
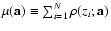 ,
where
,
where
![$\rho(z;\mathbf{a})\equiv -\ln[P'(z(\mathbf{a}))]$](/articles/aa/full/2008/03/aa5969-06/img152.gif) .
.
The best known local-M method is the OLS method. Here
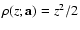 ,
so that the corresponding probability
distribution of relative deviations is the Gaussian distribution,
,
so that the corresponding probability
distribution of relative deviations is the Gaussian distribution,
![$P'\sim \exp[-z^2/2]$](/articles/aa/full/2008/03/aa5969-06/img154.gif) .
The consequence is that the OLS method
provides the best-fit parameters assuming a Gaussian noise. If,
however, the noise conforms to some other distribution, then the
OLS method will not be the most suitable; for example, in the
case of a double-exponential noise,
.
The consequence is that the OLS method
provides the best-fit parameters assuming a Gaussian noise. If,
however, the noise conforms to some other distribution, then the
OLS method will not be the most suitable; for example, in the
case of a double-exponential noise,
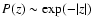 ,
it is
most appropriate to use a local-M estimator with
,
it is
most appropriate to use a local-M estimator with
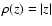 ,
i.e. to minimize the sum of absolute deviations. When applied to
data contaminated by outliers, this
least-absolute-deviation method is more robust than the OLS method because it gives less weight to large deviations.
,
i.e. to minimize the sum of absolute deviations. When applied to
data contaminated by outliers, this
least-absolute-deviation method is more robust than the OLS method because it gives less weight to large deviations.
By assigning less and less weight to suspiciously large
deviations, Lorentzian and Tukey's biweight methods
provide increasingly robust estimates. Eventually, one can decide
to discard suspicious points altogether, like in the
least-trimmed-square (LTS) method - see
(Rousseeuw 1984). The LTS method is based on the metric
trimming local-M estimator
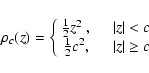 |
(16) |
where constant c>0 sets a boundary between c-distant
points (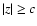 )
and c-close points
(|z|<c)
)
and c-close points
(|z|<c)![[*]](/icons/foot_motif.gif) . Furthermore,
with
. Furthermore,
with
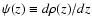 ,
one has
,
one has 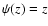 for
c-close points, and
for
c-close points, and 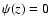 for c-distant
points
for c-distant
points![[*]](/icons/foot_motif.gif) . Hence, once recognized,
c-distant points do not enter the set of equations for the
best-fit parameters determined by
. Hence, once recognized,
c-distant points do not enter the set of equations for the
best-fit parameters determined by
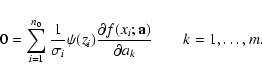 |
(17) |
The best-fit parameters, obtained from (17), are
actually the best-fit parameters from the OLS method
trimmed to the set of c-close points.
In what follows, we relate the proposed DLS to the LTS method. To
this end, we first demonstrate some of LTS basic features on a
pure Gaussian noise (4) with a
known standard deviation
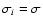 ,
and horizontal
lines y(x)=a taken as model functions. It follows that the
merit function is a sum of two terms,
,
and horizontal
lines y(x)=a taken as model functions. It follows that the
merit function is a sum of two terms,
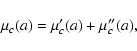 |
(18) |
the term comprising close-points contribution
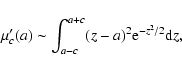 |
(19) |
and the term comprising distant-points contribution
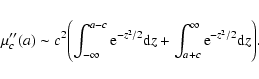 |
(20) |
All three quantities,
 ,
,
 ,
and
,
and
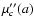 ,
are even functions of
a. Their respective derivatives are:
,
are even functions of
a. Their respective derivatives are:
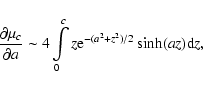 |
(21) |
![\begin{displaymath}%
\frac{\partial \mu'_c}{\partial a}\sim 2
\int\limits_{0}^cz^2{\rm e}^{-(a^2+z^2)/2}\cosh(az)[z\tanh(az)-a]{\rm d}z,
\end{displaymath}](/articles/aa/full/2008/03/aa5969-06/img176.gif) |
(22) |
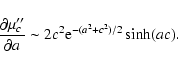 |
(23) |
From (21) and (23), it can be
shown that (for any c) both 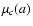 and
and
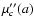 are
increasing (even) functions of a for a>0, so they both attain
their respective absolute minimum at a=0. In other words, y=0is the best horizontal line, as expected.
are
increasing (even) functions of a for a>0, so they both attain
their respective absolute minimum at a=0. In other words, y=0is the best horizontal line, as expected.
However, the close-points contribution 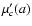 exhibits a less
simple behavior. Thus, for large c's,
exhibits a less
simple behavior. Thus, for large c's, 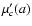 has two equal
and symmetrically positioned maxima. Between the maxima, there is
a single local minimum, located at a=0; cf.
Fig. 8. For decreasing c, i.e. for narrowing the
boundary, the minimum shallows and the adjacent maxima flatten
approaching each other, and eventually merge at a=0 as cattains its critical value cc. At the value cc, which
coincides with the solution of Eq. (6) for
k=2, the local minimum vanishes
has two equal
and symmetrically positioned maxima. Between the maxima, there is
a single local minimum, located at a=0; cf.
Fig. 8. For decreasing c, i.e. for narrowing the
boundary, the minimum shallows and the adjacent maxima flatten
approaching each other, and eventually merge at a=0 as cattains its critical value cc. At the value cc, which
coincides with the solution of Eq. (6) for
k=2, the local minimum vanishes![[*]](/icons/foot_motif.gif) .
.
In the region 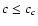 ,
the function
,
the function 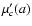 exhibits a
single absolute maximum at a=0; cf. Fig. 8. Hence,
one can find the best-fit parameters by maximizing the
close-points contribution
exhibits a
single absolute maximum at a=0; cf. Fig. 8. Hence,
one can find the best-fit parameters by maximizing the
close-points contribution 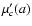 to the merit function,
instead of minimizing the merit function
to the merit function,
instead of minimizing the merit function 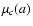 itself. We
will use this fact as a link between the LTS and DLS methods.
itself. We
will use this fact as a link between the LTS and DLS methods.
![\begin{figure}
\par\includegraphics[width=7.25cm,clip]{5969f8.eps}\end{figure}](/articles/aa/full/2008/03/aa5969-06/Timg184.gif) |
Figure 8:
LTS method: close-points contribution 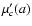 to
merit function, versus horizontal line level a for Gaussian
distribution of deviations. The five presented curves in
descending order correspond to the boundary c values 1.7, 1.5,
1.36876, 1.3, and 1.1, respectively. The critical value
cc=1.36876, separates the two modes of
to
merit function, versus horizontal line level a for Gaussian
distribution of deviations. The five presented curves in
descending order correspond to the boundary c values 1.7, 1.5,
1.36876, 1.3, and 1.1, respectively. The critical value
cc=1.36876, separates the two modes of 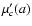 behavior.
For c>cc, the function
behavior.
For c>cc, the function 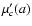 exhibits two maxima,
separated by a local minimum at a=0; when approaching the
critical value cc from above, the two maxima merge with the
local minimum. For
exhibits two maxima,
separated by a local minimum at a=0; when approaching the
critical value cc from above, the two maxima merge with the
local minimum. For 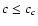 ,
the function ,
the function 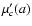 has an
absolute and single maximum at a=0.
has an
absolute and single maximum at a=0. |
Now, let us take
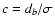 ,
where db is the width of the
best subset found by the DLS method for a given k - see Sect. 3.1. It can be recognized that the
best subset sb, having maximum density of least squares D(s),
is actually the set of c-close points
,
where db is the width of the
best subset found by the DLS method for a given k - see Sect. 3.1. It can be recognized that the
best subset sb, having maximum density of least squares D(s),
is actually the set of c-close points![[*]](/icons/foot_motif.gif) .
Furthermore, the LTS best-fit parameters are the OLS best-fit
parameters, obtained on the set of c-close points. They
coincide with DLS best-fit parameters, obtained by the same method
(OLS), and on the same subset (
.
Furthermore, the LTS best-fit parameters are the OLS best-fit
parameters, obtained on the set of c-close points. They
coincide with DLS best-fit parameters, obtained by the same method
(OLS), and on the same subset (
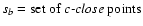 ). This indicates that DLS best-fit parameters are in fact
the maximum likelihood parameters for a suitably chosen
boundary value c separating close and distant points in the LTS method.
). This indicates that DLS best-fit parameters are in fact
the maximum likelihood parameters for a suitably chosen
boundary value c separating close and distant points in the LTS method.
At the end of this section, we would like to point out one major
difference between two methods, which is relevant, in particular,
when neither the width of noise nor the extent to which outliers
have contaminated the experimental data are known. In the LTS
method, the boundary c perfectly suits tuning the extent of
contamination, having the role of some kind of confidence level,
but requires the width of noise to be known in advance.
Though less obvious, the exponent k within the DLS method
serves the same purpose, with an essential advantage that
in the DLS method we do not need to know the width of noise
in advance. Instead, the width is estimated by the DLS method
itself, together with best-fit parameters.
8.2 Subroutine DLSFIT
In this section we present a subroutine DLSFIT that
implements the DLS method. The subroutine DLSFIT is not
self-contained, because it needs a linear and a nonlinear weighted
least-square (WLS) subroutine to be supplied as working engines.
For this purpose, we have chosen well-documented (Press et al. 2001)
subroutines: lfit (for general-linear WLS data fitting) and
mrqmin (for nonlinear WLS data fitting). These routines,
together with the subroutines: zbrent, gaussj,
covsrt, and mrqcof (called by DLSFIT,
lfit and mrqmin), are available on-line on the
official Numerical Recipes (NR) site http://www.nr.com, governed by Cambridge
University Press.
Here we present a FORTRAN code of DLSFIT subroutine. To
keep it as short as possible, we use concise FORTRAN90 syntax. For
the same reason we refer to the simply portable FORTRAN77 (version 2.10) code of subroutines zbrent, gaussj,
covsrt, and mrqcof - see, for instance,
http://www.nrbook.com/a/bookfpdf/f15-7.pdf.
The program which calls DLSFIT
should be compiled in FORTRAN90 compiler environment with
DOUBLE PRECISION as default real kind.
SUBROUTINE DLSFIT(x,y,sig,n0,a,m,rp,&
& chisq,dls,db,ns,spos,sbno,&
& covar,ia,funcs,&
& lf,k,res)
! Remove the next line if Compaq compiler is not used
!USE numerical_libraries !Compaq compiler directive
REAL,PARAMETER:: Pi=3.1415926535897932384626433832795D0, q=1./3.
INTEGER ia(m),spos(n0),sbno
REAL x(n0),y(n0),sig(n0),k
REAL a(m),covar(m,m),dyda(m),afunc(m),da(m)
EXTERNAL funcs
LOGICAL lf
IF(k>2.9.OR.k<2.)RETURN
dtiny=(MAXVAL(y)-MINVAL(y))/10.**PRECISION(db);nt=n0;ns=1;dls=0.
CALL fit(x,y,sig,nt,a,ia,m,covar,chisq,funcs,lf)
DO WHILE (nt>m+3)
CALL NewMeritVals;IF(dbt==0) EXIT
CALL ArrangeLayer
END DO
CALL fit(x,y,sig,spos(sbno),a,ia,m,covar,chisq,funcs,lf)
CONTAINS
SUBROUTINE ArrangeLayer
! Rearranges arrays x,y,sig so that their first spos(i)
! elements belong to the i-th subset in ordered collection
dr=rp*dbt;ns=ns+1
DO
i=1;nto=nt
DO WHILE (i<=nt) !Remove sublayer
yc=fun(x(i))
IF(ABS(y(i)-yc)/sig(i)>=dr)THEN
yc=fun(x(nt))
IF (ABS(y(nt)-yc)/sig(i)<dr)THEN
swap=x(i);x(i)=x(nt);x(nt)=swap
swap=y(i);y(i)=y(nt);y(nt)=swap
swap=sig(i);sig(i)=sig(nt);sig(nt)=swap
END IF
nt=nt-1
ELSE
i=i+1
END IF
END DO
IF((nt==nto).OR.(nt<=m+3))EXIT
CALL fit(x,y,sig,nt,a,ia,m,covar,chisq,funcs,lf)
END DO
END SUBROUTINE ArrangeLayer
SUBROUTINE NewMeritVals
! Calculates new DLS value
spos(ns)=nt;dbt=0
DO i=1,nt
d=ABS(y(i)-fun(x(i)))/sig(i); IF(dbt<d) dbt=d
END DO
IF(dbt>dtiny)THEN
dlst=chisq/(dbt**k)
ELSE
os2=SUM((/(1./(sig(i)*sig(i)),i=1,nt)/))/nt
dlst=os2*(1.+q*(nt-1))*res**(2-k);dbt=0
END IF
IF(dlst>dls)THEN
dls=dlst;sbno=ns;db=dbt
END IF
END SUBROUTINE NewMeritVals
FUNCTION fun(x) ! For given x, calculates value of model function
IF(lf)THEN
CALL funcs(x,afunc,m);fun=DOT_PRODUCT(a,afunc)
ELSE
CALL funcs(x,a,fun,dyda,m)
END IF
END FUNCTION fun
END SUBROUTINE DLSFIT
SUBROUTINE fit(x,y,sig,n0,a,ia,m,covar,chisq,funcs,lf)
! If lf=.TRUE. performs linear fit by calling lfit
! Otherwise, drives mrqmin which performs non-linear fit
DIMENSION x(n0),y(n0),sig(n0)
DIMENSION a(m),ia(m),covar(m,m),al(m,m)
REAL:: lamda,lamdaO
EXTERNAL funcs
LOGICAL lf
PARAMETER (MaxIt=100,RelErr=1.D-5)
IF(lf)THEN
CALL lfit(x,y,sig,n0,a,ia,m,covar,m,chisq,funcs);RETURN
END IF
lamda=-1;chisqO=0;lamdaO=0;it=0
DO WHILE (it.LE.MaxIt)
CALL mrqmin(x,y,sig,n0,a,ia,m,covar,al,m,chisq,funcs,lamda)
IF(chisq<=0)EXIT
IF((ABS(chisqO-chisq)/chisq<RelErr).AND.(lamda<lamdaO))EXIT
chisqO=chisq;lamdaO=lamda;it=it+1
END DO
lamda=0.
CALL mrqmin(x,y,sig,n0,a,ia,m,covar,al,m,chisq,funcs,lamda)
END SUBROUTINE fit
The user supplies to DLSFIT subroutine a set of n0
experimental data points x(1:n0), y(1:n0), with
individual standard deviations sig(1:n0) of their yi's;
if sig(1:n0) are not available, then set all
sig(i)=1 prior to DLSFIT call. The next argument in
the DLSFIT calling list is array a(1:m) of length
m. On input, the user supplies initial values of model
function parameters in a(1:m) in the case when the model
function is a nonlinear function of its parameters; otherwise, the
input values supplied in a(1:m) are irrelevant. On output,
the main result of DLS method - the best-fit parameters associated
with the best subset - are returned in a(1:m).
The input parameter rp is the removal parameter, introduced
in Sect. 2. In our experience, when
0.9 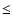 rp
rp 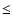 1 the best-fit parameters returned for
different values of rp coincide within the error
margins
1 the best-fit parameters returned for
different values of rp coincide within the error
margins![[*]](/icons/foot_motif.gif) .
.
Six parameters (chisq, dls, db, ns,
spos, sbno), which follow in DLSFIT calling
list, are output parameters. Thus, chisq is 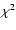 and
dls is the density of least squares obtained on the best subset in the ordered collection
and
dls is the density of least squares obtained on the best subset in the ordered collection
 (see Sect. 2), found by DLSFIT, while db
is the width of the best subset. Additionally, ns is the
total number of subsets in
(see Sect. 2), found by DLSFIT, while db
is the width of the best subset. Additionally, ns is the
total number of subsets in
 ,
spos(1:ns) is an
integer array that contains the number of data points in each
subset from
,
spos(1:ns) is an
integer array that contains the number of data points in each
subset from
 ,
and sbno is the ordinal number
of the best subset in
,
and sbno is the ordinal number
of the best subset in
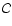 .
.
Note that the arrays x(1:n0), y(1:n0) and
sig(1:n0) are reordered on output so that the first
spos(i) data points belong to the subset
 .
In this way, the user can obtain relevant data for
each subset
.
In this way, the user can obtain relevant data for
each subset
 by applying the OLS method on the
first spos(i) elements of arrays x, y, and
sig.
by applying the OLS method on the
first spos(i) elements of arrays x, y, and
sig.
The next three parameters (covar, ia, funcs)
in the calling list of the DLSFIT subroutine are specific
to the applied lfit and mrqmin NR subroutines. Thus,
covar(1:m,1:m) is a two-dimensional array, which on output
contains the elements of covariance matrix. The integer array
ia(1:m) provides a convenient way to keep some of the
parameters frozen on their input values (ia(j)=0 for
frozen a(j), otherwise ia(j) is non-zero); the
values of all frozen parameters must be supplied on input in array
a. Finally, funcs is the name of a user-supplied
subroutine (fpoly from Press et al. 2001 in the case of
polynomial fit) proceeded to DLSFIT when DLSFIT is
called; when a general-linear fit is performed, then
funcs(x,afunc,m) should return the m basis functions
evaluated at x in the array afunc(1:m). In the
opposite case, funcs is a user supplied subroutine having
syntax funcs(x,a,y,dyda,m). For given x and model
function parameters
a, supplied in array a(1:m)
of length m, it returns the calculated value
f(x;a) of model function in variable y, together with values of all model function partial derivatives
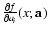 ,
returned in array
dyda(1:m).
,
returned in array
dyda(1:m).
The last three parameters in DLSFIT calling list are
lf, k, and res. The first of them, lf,
is a LOGICAL input parameter. When lf is set to
.TRUE., then DLSFIT performs general-linear WLS data
fitting by calling lfit subroutine; otherwise, nonlinear
fit is performed with an aid of mrqmin subroutine. The
value of DLS exponent k is supplied to DLSFIT subroutine
in the second parameter of the group, k. Finally, we must
also supply the value of
 (or
(or
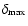 )
used in DLS calculations in the indefinite case - see Sect. 3.2. This is supplied through parameter
res - the original resolution of measurement.
)
used in DLS calculations in the indefinite case - see Sect. 3.2. This is supplied through parameter
res - the original resolution of measurement.
Note that the DLSFIT does not return errors in the best-fit
parameters. Estimation of errors, detailed in
4, is left to the user as it depends on
the specifics of actual data; nonetheless, a full-code example is
given in the online material only available in electronic form at
the CDS.
At the end, we explain the subroutine fit, called by
DLSFIT routine. The calling parameters have the same
meaning as for the DLSFIT routine. If model function
depends linearly on its parameters, then the subroutine fit
calls NR routine lfit, which performs the general linear
WLS data fitting. Otherwise, it serves as a simple driver for the
NR routine mrqmin, used for a nonlinear WLS data fitting.
The subroutine fit is singled out from DLSFIT in
order to provide a way for flexible estimation of the best-fit
parameters on any subset from the ordered collection of subsets
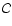 obtained by DLS method.
obtained by DLS method.
-
Barnett, V., & Lewis, T. 1994, Outliers in statistical data, 3rd edn. (New York: John Wiley and sons)
-
Bukvic, S., & Spasojevic, Dj. 2005, Spectrochim. Acta, Part B, 60, 1308
-
Contini, M., & Viegas, S. M. 2000, ApJ, 535, 721
-
Dietrich, M., Crenshaw, D. M., & Kraemer, S. B. 2005, ApJ, 623, 700
-
Dietrich, J. P., Clowe, D. I., & Soucail, G. 2002, A&A, 394, 395
-
Djenize, S., & Bukvic, S. 2001, A&A, 365, 252
-
Djenize, S., Bukvic, S., Sreckovic, A., & Platisa, M. 2004, A&A, 424, 561
-
Djenize, S., Sreckovic, A., Bukvic, S., & Vitas, N. 2006, Z. Naturforsch. A, submitted
-
Freudling, W., Corbin, M. R., & Korista, K. T. 2003, ApJ, 587, L67
-
Gabel, J. R., Arav, N., Kaastra, J. S., et al. 2005, ApJ, 623, 85G
-
Gilbert, K. M., & Peterson, B. M. 2003, ApJ, 587, 123
-
Hampel, F. R., Ronchetti, E. M., Rousseeuw, P. J., & Stahel, W. A. 1986, Robust
Statistics, The approach based on influence function (New York: John Wiley and
sons)
-
Hoaglin, D. C., Mosteller, F., & Tukey, J. W. 1983, Understanding robust and
exploratory data analysis (New York: John Wiley and sons)
-
Liu, Q. Z., & Yan, J. Z. 2005, New Astr., 11, 130
-
Liu, R. C., Markatou, M., & Tsai, C. L. 2005, Int. J. Pure Appl. Math., 21, 525
-
Marx, B. D. 1996, Technometrics, 38, 374
-
Meisel, L. V., & Cote, P. J. 1992, Phys. Rev. B, 46, 10822
-
Motulsky, H. J., & Brown, R. E. 2006, BMC Bioinformatics, 7, 123
-
Peterson, B. M., Berlind, P., Bertram, R., et al. 2002, ApJ, 581, 197
-
Popopovic, L. C. 2003, ApJ, 599, 140
-
Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2001, Numerical Recipes in
Fortran 77: The Art of Scientific Computing, Vol. 1 of Fortran Numerical Recipes, software version 2.10 (Cambridge: Cambridge University Press)
-
Rossa, J., Dietrich, M., & Wagner, S. J. 2000, A&A, 362, 501
-
Rousseeuw, P. J. 1984, J. Am. Stat. Assoc., 79, 871
-
Scott, J. E., Kriss, G. A., Brotherton, M., et al. 2004, ApJ, 615, 135
-
Spasojevic, Dj., Bukvic, S., Milosevic, S., & Stanley, E. 1996, Phys. Rev. E, 54, 2531
-
Wang, J., Wei, J. Y., & He, X. T. 2005, New Astron., 10, 353
Copyright ESO 2008
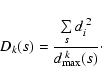
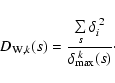
![\begin{figure}
\par\includegraphics[height=8.85cm,width=7.15cm,clip]{5969f1.eps}\end{figure}](/articles/aa/full/2008/03/aa5969-06/Timg45.gif)
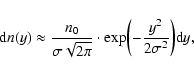
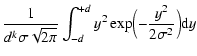
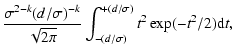
![\begin{figure}
\par\includegraphics[width=7.85cm,clip]{5969f2.eps}\end{figure}](/articles/aa/full/2008/03/aa5969-06/Timg73.gif)
![\begin{displaymath}%
\biggl(\frac{d_b}{\sigma}\biggr)^3\exp\biggl[-
\frac{d_b^{\...
...ma^2}\biggr]-k\int^{d_b/\sigma}_{0}
t^2\exp(-t^2/2){\rm d}t=0,
\end{displaymath}](/articles/aa/full/2008/03/aa5969-06/img75.gif)
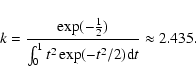
![\begin{displaymath}D_k(s)=\frac{\sum\limits_{i=1}^{n-1}d_i^2+d_{\rm max}^2}{d_{\...
..._{\rm max}\biggl[1+\sum_{i=1}^{n-1}d_i^2/d_{\rm max}^2\biggr],
\end{displaymath}](/articles/aa/full/2008/03/aa5969-06/img98.gif)
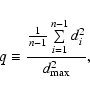
![\begin{displaymath}%
D_k(s)=d^{2-k}_{\rm max}\biggl[1+(n-1)q\biggr ].
\end{displaymath}](/articles/aa/full/2008/03/aa5969-06/img105.gif)
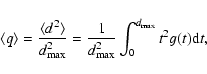
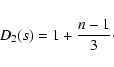
![\begin{displaymath}%
D_{w,k}(s)=\delta^{2-k}_{\rm max}\biggl [1+(n-1)q\biggr ],
\end{displaymath}](/articles/aa/full/2008/03/aa5969-06/img111.gif)
![\begin{figure}
\par\includegraphics[height=6.25cm,width=7.3cm,clip]{5969f3.eps}\end{figure}](/articles/aa/full/2008/03/aa5969-06/Timg127.gif)
![\begin{figure}
\par\includegraphics[height=6.25cm,width=7.3cm,clip]{5969f4.eps}\end{figure}](/articles/aa/full/2008/03/aa5969-06/Timg128.gif)
![\begin{figure}
\par\includegraphics[height=7.85cm,width=7.45cm,clip]{5969f5.eps}\end{figure}](/articles/aa/full/2008/03/aa5969-06/Timg132.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{5969f6.eps}\end{figure}](/articles/aa/full/2008/03/aa5969-06/Timg138.gif)
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{5969f7.eps}\end{figure}](/articles/aa/full/2008/03/aa5969-06/Timg139.gif)
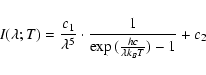
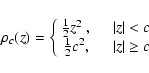
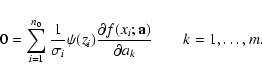
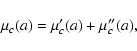
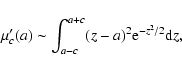
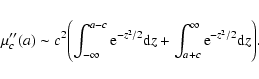
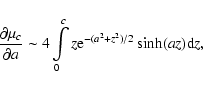
![\begin{displaymath}%
\frac{\partial \mu'_c}{\partial a}\sim 2
\int\limits_{0}^cz^2{\rm e}^{-(a^2+z^2)/2}\cosh(az)[z\tanh(az)-a]{\rm d}z,
\end{displaymath}](/articles/aa/full/2008/03/aa5969-06/img176.gif)
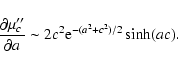
![\begin{figure}
\par\includegraphics[width=7.25cm,clip]{5969f8.eps}\end{figure}](/articles/aa/full/2008/03/aa5969-06/Timg184.gif)