- ... code
![[*]](/icons/foot_motif.gif)
- A full-code demo program is available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/477/967
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...layer
![[*]](/icons/foot_motif.gif)
- In applications the coarsened version of
this rule is of particular interest. The difference is only in the
first stage of this procedure: instead of removing a point with
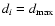 ,
we remove all points such that their distances
,
we remove all points such that their distances
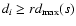 ,
where
,
where 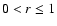 is a removal
parameter. For r=1 we are back at the original rule, while for
r< 1 we remove more points in a single step.
is a removal
parameter. For r=1 we are back at the original rule, while for
r< 1 we remove more points in a single step.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... holds
![[*]](/icons/foot_motif.gif)
- More precisely, for
subsets s such that
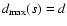 ,
the probability that the
opposite inequality
,
the probability that the
opposite inequality
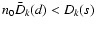 holds tends to zero
when n0 approaches infinity.
holds tends to zero
when n0 approaches infinity.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... DLS maximum
![[*]](/icons/foot_motif.gif)
- Let
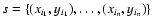 is a subset of s0 having
is a subset of s0 having
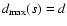 .
Its best horizontal line y(x)=a is
obtained for
.
Its best horizontal line y(x)=a is
obtained for
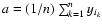 .
If s is not a subset
of sd, we translate it by amount a and obtain a set
.
If s is not a subset
of sd, we translate it by amount a and obtain a set
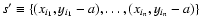 contained in
sd. Its best horizontal line is y(x)=0,
contained in
sd. Its best horizontal line is y(x)=0,
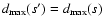 ,
so that
Dk(s)=Dk(s'), because the
least-square sums for subsets s and s' are equal as well. As
subset sd contains all points from s0 inside boundaries
,
so that
Dk(s)=Dk(s'), because the
least-square sums for subsets s and s' are equal as well. As
subset sd contains all points from s0 inside boundaries
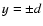 ,
and
,
and
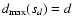 ,
it follows that
,
it follows that
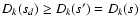 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sub-distribution
![[*]](/icons/foot_motif.gif)
- For simplicity, here we
take
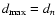 and
and
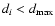 for all i<n.
for all i<n.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... technique
![[*]](/icons/foot_motif.gif)
- The Boltzmann-plot technique is
a common method for estimating electron temperatures in plasmas at
local thermodynamic equilibrium; for some typical applications in
astrophysics see (Popovic 2003).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... estimators
![[*]](/icons/foot_motif.gif)
- In this subsection we
closely follow the terminology and notations used in
Press et al. (2001)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)
![[*]](/icons/foot_motif.gif)
- The corresponding distribution is
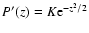 for |z|<c, and
for |z|<c, and
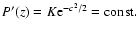 for
for
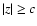 ,
where K is the normalization constant. Though the
particular value of K has no consequence for the analysis that
follows note, however, that K depends on c and on the
available interval of z, which is finite due to a finite
experimental range in which the data were collected.
,
where K is the normalization constant. Though the
particular value of K has no consequence for the analysis that
follows note, however, that K depends on c and on the
available interval of z, which is finite due to a finite
experimental range in which the data were collected.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
points
![[*]](/icons/foot_motif.gif)
- Note that the form of
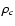 is unique,
if we want to relate it with the DLS method. Indeed, in the DLS method we treat close points like in the OLS method, whereas distant points are discarded. Therefore, in a related local-M
approach, one has
is unique,
if we want to relate it with the DLS method. Indeed, in the DLS method we treat close points like in the OLS method, whereas distant points are discarded. Therefore, in a related local-M
approach, one has
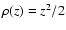 for close points and
for close points and 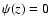 for distant points, implying that
for distant points, implying that
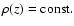 for distant
points. The only continuous
for distant
points. The only continuous 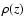 satisfying both conditions
is (16).
satisfying both conditions
is (16).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... vanishes
![[*]](/icons/foot_motif.gif)
- For a given c, let
a(c)>0 be the abscissa of the right-hand side maximum of
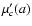 and let a=a(c) is the line of right-hand side
maxima. Along this line
and let a=a(c) is the line of right-hand side
maxima. Along this line
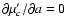 ,
hence the
first derivative of (22) satisfies
,
hence the
first derivative of (22) satisfies
![$0=c^2{\rm e}^{-c^2/2}[a\cosh(ac)-x\sinh(ac)]+\frac{{\rm d}a}{{\rm d}c}\int_0^cz^2
{\rm e}^{-z^2/2}[(1-x^2)\cosh(az)+a\sinh(az)]{\rm d}z$](/articles/aa/full/2008/03/aa5969-06/img179.gif) .
As
.
As 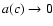 when
when
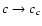 ,
the previous equation simplifies to
,
the previous equation simplifies to
![$0=\int_0^cz^2{\rm e}^{-z^2/2}[1-z^2]{\rm d}z$](/articles/aa/full/2008/03/aa5969-06/img182.gif) .
Finally, taking into account
.
Finally, taking into account
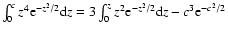 ,
we retrieve (6) for k=2.
,
we retrieve (6) for k=2.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... points
![[*]](/icons/foot_motif.gif)
- As in the
DLS method we adopt
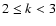 ,
and
,
and
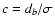 is obtained
from (6), it follows that
is obtained
from (6), it follows that 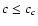 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
margins
![[*]](/icons/foot_motif.gif)
- Note that the bigger the value of the removal
parameter, the bigger the number of subsets found by DLSFIT, and
the longer the execution time, which is of particular importance
in the case of large data sets.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.