A&A 475, 109-114 (2007)
DOI: 10.1051/0004-6361:20077333
Cosmological hydrogen recombination: Lyn line feedback and continuum escape
J. Chluba1 - R. A. Sunyaev1,2
1 - Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1,
85741 Garching bei München, Germany
2 -
Space Research Institute, Russian Academy of Sciences, Profsoyuznaya 84/32,
117997 Moscow, Russia
Received 20 February 2007 / Accepted 16 September 2007
Abstract
We compute the corrections to the cosmological hydrogen
recombination history due to delayed feedback of Lyman-series photons
and the escape in the Lyman-continuum. The former
process is expected to slightly delay recombination, while the latter
should allow the medium to recombine a bit faster.
It is shown that the subsequent feedback of released Lyman-n photons on the lower lying Lyman-(n-1) transitions yields a maximal
correction of
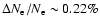 at
at
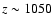 .
Including only Lyman-
.
Including only Lyman-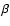 feedback onto the Lyman-
feedback onto the Lyman- transition, accounts for most of the effect.
We find corrections to the cosmic microwave background TT and EE power spectra with typical peak to peak amplitude
transition, accounts for most of the effect.
We find corrections to the cosmic microwave background TT and EE power spectra with typical peak to peak amplitude
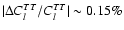 and
and
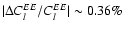 at
at
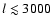 .
The escape in the Lyman-continuum and feedback of Lyman-
.
The escape in the Lyman-continuum and feedback of Lyman- photons on
the photoionization rate of the second shell lead to modifications of
the ionization history which are very small (less than
photons on
the photoionization rate of the second shell lead to modifications of
the ionization history which are very small (less than
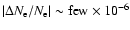 ).
).
Key words: cosmic microwave background - cosmology: miscellaneous
1 Introduction
The tremendous advances in observations of the cosmic microwave background
(CMB) temperature and polarization angular fluctuations
(e.g. Hinshaw et al. 2006; Page et al. 2006) and the prospects with the PLANCK
Surveyor![[*]](/icons/foot_motif.gif) have motivated several groups to
re-examine the problem of cosmological hydrogen recombination,
with the aim of identifying previously neglected physical processes
which could affect the ionization history of the Universe at the level of
have motivated several groups to
re-examine the problem of cosmological hydrogen recombination,
with the aim of identifying previously neglected physical processes
which could affect the ionization history of the Universe at the level of
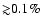 ,
and may lead to modifications of the cosmological hydrogen
recombination spectrum
(Chluba et al. 2007; Beigman & Sunyaev 1978; Burgin 2003; Kholupenko et al. 2005; Rybicki & dell'Antonio 1993; Dubrovich 1975; Rubiño-Martín et al. 2006; Wong et al. 2006; Chluba & Sunyaev 2006a; Dubrovich & Stolyarov 1995; Dubrovich & Shakhvorostova 2004), which could become observable in the future.
For example, effects connected with the two-photon transitions from
high s and d-states to the ground state (Dubrovich & Grachev 2005; Wong & Scott 2007; Chluba & Sunyaev 2007), the induced 2s-two-photon decay (Chluba & Sunyaev 2006b), the
increase in the 2s-two-photon absorption rate due to the large
Lyman-
,
and may lead to modifications of the cosmological hydrogen
recombination spectrum
(Chluba et al. 2007; Beigman & Sunyaev 1978; Burgin 2003; Kholupenko et al. 2005; Rybicki & dell'Antonio 1993; Dubrovich 1975; Rubiño-Martín et al. 2006; Wong et al. 2006; Chluba & Sunyaev 2006a; Dubrovich & Stolyarov 1995; Dubrovich & Shakhvorostova 2004), which could become observable in the future.
For example, effects connected with the two-photon transitions from
high s and d-states to the ground state (Dubrovich & Grachev 2005; Wong & Scott 2007; Chluba & Sunyaev 2007), the induced 2s-two-photon decay (Chluba & Sunyaev 2006b), the
increase in the 2s-two-photon absorption rate due to the large
Lyman- spectral distortion (Kholupenko & Ivanchik 2006), and details in the
evolution of the populations of the angular momentum sub-states
(Chluba et al. 2007; Rubiño-Martín et al. 2006) were discussed.
All these studies show that sub-percent-level corrections to the ionization
history do exist, which in principle could bias the values of the key
cosmological parameters (Lewis et al. 2006).
It is clear, that when reaching percent-level accuracy in the determination of
the key cosmological parameters or when considering signatures from inflation,
e.g. the possibility of a running spectral index, accurate theoretical
predictions of the ionization history are required.
Here we examine the effects due to feedback of hydrogen Lyman-series photons
and the escape of photons in the Lyman-continuum on the ionization history
during the epoch of hydrogen recombination, and the impact of this
process on the Lyman-
spectral distortion (Kholupenko & Ivanchik 2006), and details in the
evolution of the populations of the angular momentum sub-states
(Chluba et al. 2007; Rubiño-Martín et al. 2006) were discussed.
All these studies show that sub-percent-level corrections to the ionization
history do exist, which in principle could bias the values of the key
cosmological parameters (Lewis et al. 2006).
It is clear, that when reaching percent-level accuracy in the determination of
the key cosmological parameters or when considering signatures from inflation,
e.g. the possibility of a running spectral index, accurate theoretical
predictions of the ionization history are required.
Here we examine the effects due to feedback of hydrogen Lyman-series photons
and the escape of photons in the Lyman-continuum on the ionization history
during the epoch of hydrogen recombination, and the impact of this
process on the Lyman- distortion of the CMB blackbody spectrum.
distortion of the CMB blackbody spectrum.
The strongest distortions of the CMB spectrum arising during the epoch of
hydrogen recombination are due to the Lyman- transition and the 2s
two-photon decay (Peebles 1968; Zeldovich et al. 1968).
The feedback of these excess photons on the photoionization
rates of the second shell has been considered by Seager et al. (1999,2000),
with no significant changes for the number density of free electrons,
transition and the 2s
two-photon decay (Peebles 1968; Zeldovich et al. 1968).
The feedback of these excess photons on the photoionization
rates of the second shell has been considered by Seager et al. (1999,2000),
with no significant changes for the number density of free electrons, 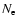 .
We confirm this statement for the feedback from Lyman-
.
We confirm this statement for the feedback from Lyman- photons and
find a maximal correction of
photons and
find a maximal correction of
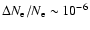 at
at
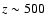 ,
the redshift which roughly corresponds to the time, when the
maximum of the CMB spectral distortion due to the Lyman-
,
the redshift which roughly corresponds to the time, when the
maximum of the CMB spectral distortion due to the Lyman- transition is
reaching the Balmer-continuum frequency.
transition is
reaching the Balmer-continuum frequency.
However, it has been shown by Kholupenko & Ivanchik (2006) that the huge excess of
photons in the Wien-tail of the CMB due to the Lyman- distortion leads
to an increase of the
distortion leads
to an increase of the
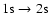 two-photon absorption
rate, which delays recombination and introduces corrections to the ionization
history at the percent-level.
Similarly, one expects some feedback of escaping Lyman-series photons on
lower lying Lyman-transitions and eventually the Lyman-
two-photon absorption
rate, which delays recombination and introduces corrections to the ionization
history at the percent-level.
Similarly, one expects some feedback of escaping Lyman-series photons on
lower lying Lyman-transitions and eventually the Lyman- transition.
Recently, this process was also considered by Switzer & Hirata (2007) for both
helium and hydrogen recombination, using an iterative approach.
Here we directly compute the escaping Lyman-n radiation within the Sobolev
approximation (e.g. see Chluba et al. 2007; Rubiño-Martín et al. 2006) and include the
feedback on the Lyman-(n-1) transition at all times by evaluating the
distorted spectrum at the corresponding frequency.
In addition, we assume that due to the huge optical depth in all the
Lyman-lines, at the end only the Lyman-
transition.
Recently, this process was also considered by Switzer & Hirata (2007) for both
helium and hydrogen recombination, using an iterative approach.
Here we directly compute the escaping Lyman-n radiation within the Sobolev
approximation (e.g. see Chluba et al. 2007; Rubiño-Martín et al. 2006) and include the
feedback on the Lyman-(n-1) transition at all times by evaluating the
distorted spectrum at the corresponding frequency.
In addition, we assume that due to the huge optical depth in all the
Lyman-lines, at the end only the Lyman- line remains and all the
Lyman-n lines will be completely re-processed by the closest lower lying
Lyman-(n-1) transition. Therefore, feedback always only works as
line remains and all the
Lyman-n lines will be completely re-processed by the closest lower lying
Lyman-(n-1) transition. Therefore, feedback always only works as
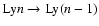 .
It is also important to ensure that the line is not producing any
feedback on itself.
.
It is also important to ensure that the line is not producing any
feedback on itself.
In addition, we estimate the escape probability for the
Lyman-continuum and include the approximate net rate for direct
recombinations into our multi-level code. As argued earlier
(Peebles 1968; Zeldovich et al. 1968), we find that the modification of the
ionization history due to this process is indeed completely negligible.
Table 1:
Appearance of the first few Lyman lines for the computations not including any
feedback. In particular we give the approximate redshift,
 ,
at
which
,
at
which
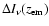 is maximal (see Fig. 1), and the
redshift at which the peak of the line reaches the next lower Lyman resonance,
is maximal (see Fig. 1), and the
redshift at which the peak of the line reaches the next lower Lyman resonance,
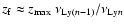 ,
where
,
where
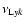 is the resonance frequency of the Lyman-k transition. Also
we give the approximate total number ofescaping photons per hydrogen nucleus for each transition.
is the resonance frequency of the Lyman-k transition. Also
we give the approximate total number ofescaping photons per hydrogen nucleus for each transition.
![\begin{figure}
\par\includegraphics[width=8.8cm]{eps/7333f001.eps}\\ [1mm]
\includegraphics[width=8.8cm]{eps/7333f002.eps}\end{figure}](/articles/aa/full/2007/43/aa7333-07/Timg44.gif) |
Figure 1:
Spectral distortions due to the first few Lyman-transitions at z = 0.
No feedback
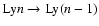 has been included.
Upper panel: as a function of the redshift of emission (see Eq. (1)
in Rubiño-Martín et al. 2006).
Lower panel: relative to the CMB blackbody as a function of observing
frequency
has been included.
Upper panel: as a function of the redshift of emission (see Eq. (1)
in Rubiño-Martín et al. 2006).
Lower panel: relative to the CMB blackbody as a function of observing
frequency  . .
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm]
{eps/7333f003.eps}\end{figure}](/articles/aa/full/2007/43/aa7333-07/Timg45.gif) |
Figure 2:
Changes in the free electron fraction due to inclusion of Lyman-series
feedback relative to the reference model without feedback.
The computations were performed for a 15-shell atom where for the Lyman-series
the escape of photons was modeled using the Sobolev approximation. The curves
are labeled according to the sequence of feedback that was included. For
example,
 indicates that Ly
indicates that Ly
 Ly Ly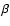 and Ly
and Ly
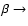 Ly
Ly feedback was taken into account.
Also the full result for the 30-shell hydrogen atom is shown, where feedback
up to n=30 was included.
feedback was taken into account.
Also the full result for the 30-shell hydrogen atom is shown, where feedback
up to n=30 was included. |
| Open with DEXTER |
2 Re-absorption of Lyman-series photons
Although in computations with no feedback, the contributions of the
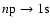 transitions from shells with n>2 to the total
Lyman-series are rather small (see Fig. 8 in Rubiño-Martín et al. 2006), in the
Wien-tail of the CMB the intensity of these lines is significantly larger than
the blackbody (see Fig. 1).
Therefore one expects that after redshifting each Lyman-transition from n>2will increase the absorption rate for the closest lower Lyman-series
transition (
transitions from shells with n>2 to the total
Lyman-series are rather small (see Fig. 8 in Rubiño-Martín et al. 2006), in the
Wien-tail of the CMB the intensity of these lines is significantly larger than
the blackbody (see Fig. 1).
Therefore one expects that after redshifting each Lyman-transition from n>2will increase the absorption rate for the closest lower Lyman-series
transition (
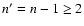 )
and thereby slightly delay hydrogen
recombination.
For example, the Lyman-
)
and thereby slightly delay hydrogen
recombination.
For example, the Lyman-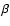 transition peaks at
transition peaks at
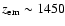 with
contribution
with
contribution
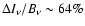 relative to the CMB blackbody
spectrum
relative to the CMB blackbody
spectrum 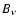 .
These excess photons reach the central frequency of the
Lyman-
.
These excess photons reach the central frequency of the
Lyman- transition at
transition at
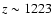 and increase the Lyman-
and increase the Lyman- absorption rate, thereby delaying recombination (see Table 1).
It is easy to estimate the total number of photons released in the
Lyman-
absorption rate, thereby delaying recombination (see Table 1).
It is easy to estimate the total number of photons released in the
Lyman-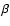 transition using Fig. 1. Its value is close
to
transition using Fig. 1. Its value is close
to
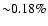 of the total number of hydrogen nuclei (see Table
1 for the other transitions).
At the time of maximal feedback (
of the total number of hydrogen nuclei (see Table
1 for the other transitions).
At the time of maximal feedback (
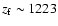 )
the number of free
electrons is roughly
)
the number of free
electrons is roughly 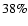 of the total number of hydrogen nuclei.
Therefore the maximal effect one can expect for the feedback-induced
corrections to the ionization history from the Lyman-
of the total number of hydrogen nuclei.
Therefore the maximal effect one can expect for the feedback-induced
corrections to the ionization history from the Lyman-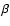 line is
line is
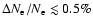 .
.
In Fig. 2 we present the results for detailed computations of
feedback-induced changes in the free electron fraction. Including
only Lyman-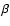 feedback on the Lyman-
feedback on the Lyman- transition accounts for most
of the effect, leading to a maximal difference of
transition accounts for most
of the effect, leading to a maximal difference of
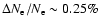 at
at
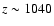 .
.
When including in addition the feedback of Lyman-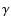 on Lyman-
on Lyman-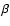 ,
the
maximal relative difference decreases to
,
the
maximal relative difference decreases to
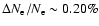 ,
now peaking at
,
now peaking at
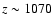 .
This behavior is expected, since the Lyman-
.
This behavior is expected, since the Lyman-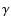 photon reduces the
transition rate in the Lyman-
photon reduces the
transition rate in the Lyman-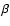 channel such that its feedback on the
Lyman-
channel such that its feedback on the
Lyman- line should become slightly smaller. In addition, the number of
electrons reaching the ground state via the Lyman-
line should become slightly smaller. In addition, the number of
electrons reaching the ground state via the Lyman-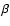 transition will be
reduced, which very likely leads to the small increase of the correction at
transition will be
reduced, which very likely leads to the small increase of the correction at
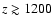 .
.
Subsequent inclusion of more feedback results in an alternating behavior of
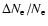 .
We found that for 30-shells, convergence is reached when including feedback
from np-levels with
.
We found that for 30-shells, convergence is reached when including feedback
from np-levels with
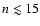 .
In Fig. 2 we also give the
full result including all feedback within a 30-shell hydrogen atom.
In addition we found that the correction barely depends on the total number of
included shells.
Therefore we expect that even for computations with up to 100-shells the total
feedback-induced relative difference will not change significantly.
.
In Fig. 2 we also give the
full result including all feedback within a 30-shell hydrogen atom.
In addition we found that the correction barely depends on the total number of
included shells.
Therefore we expect that even for computations with up to 100-shells the total
feedback-induced relative difference will not change significantly.
Examining the final differences in the Lyman- distortion and
the feedback-induced modifications of the Lyman-
distortion and
the feedback-induced modifications of the Lyman-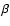 and
and 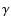 lines
before their absorption within the corresponding lower lying resonance
(see Fig. 3) shows that the situation is a bit more
complicated.
Including only Lyman-
lines
before their absorption within the corresponding lower lying resonance
(see Fig. 3) shows that the situation is a bit more
complicated.
Including only Lyman-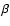 feedback the amount of emission in the
Lyman-
feedback the amount of emission in the
Lyman- line reduces by
line reduces by
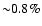 at
at
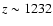 .
Note that this
redshift is very close to the expected value,
.
Note that this
redshift is very close to the expected value,
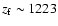 ,
for the
maximal feedback (see Table 1).
On the other hand, due to the feedback-induced small changes in the
populations of the levels, the net 2s-1s two-photon transition rate also
increases with a maximum of roughly
,
for the
maximal feedback (see Table 1).
On the other hand, due to the feedback-induced small changes in the
populations of the levels, the net 2s-1s two-photon transition rate also
increases with a maximum of roughly
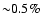 at
at
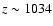 (see Fig. 4), which partially cancels the delaying feedback effect on the
Lyman-
(see Fig. 4), which partially cancels the delaying feedback effect on the
Lyman- transition.
transition.
When including Lyman-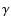 feedback, as expected, the emission in the
Lyman-
feedback, as expected, the emission in the
Lyman-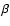 line reduces, with a maximal difference at the expected value
line reduces, with a maximal difference at the expected value
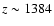 .
Adding Lyman-
.
Adding Lyman-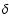 feedback reduces the strength of the
feedback of Lyman-
feedback reduces the strength of the
feedback of Lyman-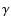 on the Lyman-
on the Lyman-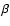 transition by a significant
fraction. Comparing the relative strength of the Lyman-
transition by a significant
fraction. Comparing the relative strength of the Lyman-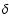 at its maximum
with the Lyman-
at its maximum
with the Lyman-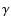 line at
line at 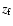 (Fig. 1) yields
(Fig. 1) yields
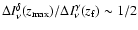 ,
which indicates that Lyman-
,
which indicates that Lyman-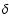 should be able to affect Lyman-
should be able to affect Lyman-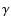 strongly.
Looking at the relative difference in the Lyman-
strongly.
Looking at the relative difference in the Lyman-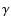 when including
Lyman-
when including
Lyman-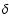 feedback shows that at
feedback shows that at
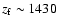 the line is
reduced by
the line is
reduced by
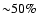 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm]
{eps/7333f004.eps}\\ [5.2mm]
\i...
...f005.eps}\\ [5.2mm]
\includegraphics[width=8.8cm]
{eps/7333f006.eps}\end{figure}](/articles/aa/full/2007/43/aa7333-07/Timg71.gif) |
Figure 3:
Feedback-induced changes of
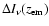 for the Lyman-
for the Lyman- and the modifications of the Lyman-
and the modifications of the Lyman-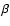 and
and 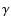 lines before
their absorption within the corresponding lower lying resonance.
The results are based on the computations for a 15-shell hydrogen atom.
lines before
their absorption within the corresponding lower lying resonance.
The results are based on the computations for a 15-shell hydrogen atom. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm]
{eps/7333f007.eps}\end{figure}](/articles/aa/full/2007/43/aa7333-07/Timg72.gif) |
Figure 4:
Changes in the net 2s-1s two-photon decay rate due to the inclusion of
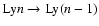 feedback, as labeled. The
results are based on the computation for a 15-shell hydrogen atom.
feedback, as labeled. The
results are based on the computation for a 15-shell hydrogen atom. |
| Open with DEXTER |
3 The Lyman-continuum escape
To estimate the maximal effect arising due to successful escape
of photons from the Lyman-continuum we shall neglect any re-absorption of
photons below the threshold frequency
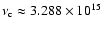 Hz. Although one can expect some modification due to the
forest of lines in the Lyman-series close to the
continuum
Hz. Although one can expect some modification due to the
forest of lines in the Lyman-series close to the
continuum![[*]](/icons/foot_motif.gif) , this approach will yield an upper limit on the effect,
which turns out to be very small in any case.
, this approach will yield an upper limit on the effect,
which turns out to be very small in any case.
With this in mind, in the vicinity of the Lyman-continuum the photon number
only changes by recombination and ionization to the ground state (we neglect
electron scattering):
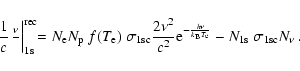 |
(1) |
Here 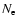 and
and 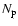 are the free electron and proton number densities,
are the free electron and proton number densities,
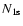 is the number density of hydrogen atoms in the ground state and
is the number density of hydrogen atoms in the ground state and
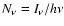 ,
where
,
where 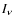 is the photon intensity. In addition,
is the photon intensity. In addition,
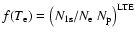 and
and
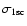 is the 1s-photoionization cross-section.
As can be seen from Eq. (1), photons are emitted with a
spectrum
is the 1s-photoionization cross-section.
As can be seen from Eq. (1), photons are emitted with a
spectrum![[*]](/icons/foot_motif.gif)
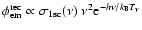 .
We now compute the probability that one single recombination will lead
to a successful escape of photons.
.
We now compute the probability that one single recombination will lead
to a successful escape of photons.
The optical depth for absorption of a photon, which has been emitted at
redshift
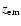 and is observed at frequency
and is observed at frequency
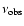 at redshift
at redshift
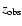 ,
within the Lyman-continuum is given by
,
within the Lyman-continuum is given by
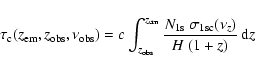 |
(2) |
where
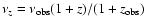 .
If we substitute
.
If we substitute
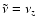 and use
and use
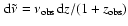 then we have
then we have
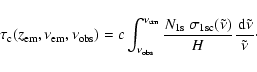 |
(3) |
Fixing the emission frequency and the emission redshift one can immediately
determine the current redshift as a function of
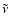 with
with
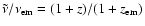 .
Now the escape probability in the Lyman-continuum can be directly given in
terms of the normalized emission profile
.
Now the escape probability in the Lyman-continuum can be directly given in
terms of the normalized emission profile
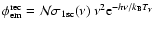 :
:
![\begin{displaymath}
P^{\rm Ly-c}_{\rm esc}(z_{\rm em})
=\int_{\nu_{\rm c}}^\inft...
...au_{\rm c}(z_{\rm em}, \nu', \nu_{\rm c})\right]{\,\rm d}\nu',
\end{displaymath}](/articles/aa/full/2007/43/aa7333-07/img95.gif) |
(4) |
where
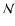 is determined from the condition
is determined from the condition
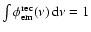 .
Because
.
Because
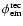 is sufficiently narrow (
is sufficiently narrow (
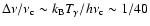 at
at
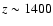 )
it only takes a very
short time to cross the emission profile via redshifting. Since the
characteristic time for changes of
)
it only takes a very
short time to cross the emission profile via redshifting. Since the
characteristic time for changes of
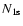 and H is much longer, one can
write
and H is much longer, one can
write
![\begin{displaymath}
P^{\rm Ly-c}_{\rm esc}(z_{\rm em})
\approx
\int_{\nu_{\rm c}...
...e{\nu})}{\tilde{\nu}}{\,\rm d}\tilde{\nu}
\right]{\,\rm d}\nu'
\end{displaymath}](/articles/aa/full/2007/43/aa7333-07/img101.gif) |
(5) |
where
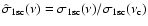 and the optical depth at the threshold frequency is
and the optical depth at the threshold frequency is
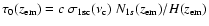 .
.
It is possible to simplify Eq. (5) even further. First,
since the emission profile is very narrow one may use
![$\phi^{\rm rec}_{\rm
em}\approx \tilde{\mathcal{N}} {\rm e}^{-h[\nu-\nu_{\rm c}]/k_{\rm B}T_{\gamma}}$](/articles/aa/full/2007/43/aa7333-07/img104.gif) ,
with the
corresponding normalization constant
,
with the
corresponding normalization constant
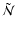 .
Assuming
.
Assuming
![$\hat{\sigma}_{\rm 1sc}\approx [\nu_{\rm c}/\nu]^3$](/articles/aa/full/2007/43/aa7333-07/img106.gif) one then obtains
one then obtains
![\begin{displaymath}
P^{\rm Ly-c}_{\rm esc}(z_{\rm em})\approx \int_0^\infty {\rm...
...sc}_{\rm c}]}
{\,\rm d}\xi=\frac{1}{1+\tau^{\rm esc}_{\rm c}},
\end{displaymath}](/articles/aa/full/2007/43/aa7333-07/img107.gif) |
(6) |
where
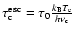 .
We see that interpreting the continuum profiles as a very narrow
line
.
We see that interpreting the continuum profiles as a very narrow
line![[*]](/icons/foot_motif.gif) ,
,
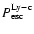 appears to be
similar to the Sobolev approximation for the escape of photons from resonance
lines.
In particular
appears to be
similar to the Sobolev approximation for the escape of photons from resonance
lines.
In particular
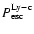 also scales as
also scales as
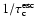 for large optical depth
for large optical depth
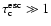 .
However,
unlike in the Sobolev approximation there is no symmetry between the
absorption and emission profile, which actually is one of the key requirements
that makes the Sobolev escape probability completely independent of the line
profile.
Comparing the results of Eqs. (5) and (6) shows that the latter equation provides a
sufficient approximation to
.
However,
unlike in the Sobolev approximation there is no symmetry between the
absorption and emission profile, which actually is one of the key requirements
that makes the Sobolev escape probability completely independent of the line
profile.
Comparing the results of Eqs. (5) and (6) shows that the latter equation provides a
sufficient approximation to
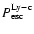 (see Fig. 5).
(see Fig. 5).
![\begin{figure}
\par\includegraphics[width=8.8cm]
{eps/7333f008.eps}\end{figure}](/articles/aa/full/2007/43/aa7333-07/Timg112.gif) |
Figure 5:
Escape probability for the Lyman-continuum as given by
Eq. (5) and Eq. (6). For
comparison we also show the Sobolev escape probability for the
Lyman- photons.
photons. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm]
{eps/7333f009.eps}\end{figure}](/articles/aa/full/2007/43/aa7333-07/Timg113.gif) |
Figure 6:
Changes in the free electron fraction due to inclusion of Lyman-continuum
escape relative to the reference model without any direct recombinations to
1s. The computations were performed for a 5-shell atom where for the
Lyman-series escape the Sobolev approximation was used. Note that the absolute
value of
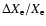 is
is
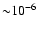 only.
only. |
| Open with DEXTER |
Using Eq. (6) it is easy to include the possibility of
direct recombinations to the ground state connected with the escape of
continuum photons. For this,one should add
![\begin{displaymath}
\Delta R_{\rm c1s}\approx P^{\rm Ly-c}_{\rm esc}(z_{\rm em})...
...rm 1s}~R_{{\rm 1sc}}-N_{\rm e}~N_{\rm p}~R_{{\rm c1s}}\right],
\end{displaymath}](/articles/aa/full/2007/43/aa7333-07/img114.gif) |
(7) |
to the rate equations of the electrons and subtract this term for the
1s-equation. Here
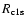 and
and
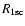 are the recombination
and photoionization rate of the ground state, respectively.
Note that we assume that on the blue side of the Lyman-continuum the
spectrum is Planckian. Therefore the photoionization rate
are the recombination
and photoionization rate of the ground state, respectively.
Note that we assume that on the blue side of the Lyman-continuum the
spectrum is Planckian. Therefore the photoionization rate
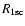 does
not include any spectral distortion. However, due to the release of photons
during
does
not include any spectral distortion. However, due to the release of photons
during
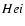 recombination some small distortions are created, which
lead to an increase of the photoionization rate.
recombination some small distortions are created, which
lead to an increase of the photoionization rate.
Comparing the escape probability for the Lyman-continuum with the Sobolev
escape probability for the Lyman- photons (see Fig. 5) one
can see that
photons (see Fig. 5) one
can see that
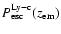 is roughly 10-100 times
larger at most times.
However, including the possibility of direct recombinations to the ground
state in our recombination code yields a tiny correction to
is roughly 10-100 times
larger at most times.
However, including the possibility of direct recombinations to the ground
state in our recombination code yields a tiny correction to 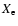 (see
Fig. 6), which shows that
(see
Fig. 6), which shows that
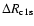 as given by
Eq. (7) is still many orders of magnitude smaller than the net
Lyman-
as given by
Eq. (7) is still many orders of magnitude smaller than the net
Lyman- transition rate. One can safely neglect direct recombinations
to the ground state of hydrogen for computations of the recombination history.
transition rate. One can safely neglect direct recombinations
to the ground state of hydrogen for computations of the recombination history.
![\begin{figure}
\par\includegraphics[width=8.8cm]
{eps/7333f010.eps}\end{figure}](/articles/aa/full/2007/43/aa7333-07/Timg121.gif) |
Figure 7:
Changes in the CMB temperature (TT) and polarization (EE) power spectra.
The differences were computed using our modified versions of
CMBEASY (Doran 2005), which allows loading of pre-calculated
recombination histories, and where the corresponding RECFAST-routine
was improved to achieve higher numerical accuracy with solvers from the
NAG-library. |
| Open with DEXTER |
4 Discussion
We have shown that
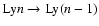 feedback leads to a
modification in the ionization history of
feedback leads to a
modification in the ionization history of
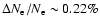 at
at
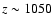 .
Since this is very close to the peak of the Thomson-visibility
function (Sunyaev & Zeldovich 1970), corrections to the CMB power spectra of similar
order are expected. Computing the CMB TT and EEpower spectra using the results for the ionization history with and without
the additional feedback we find changes with a typical peak to peak
amplitude
.
Since this is very close to the peak of the Thomson-visibility
function (Sunyaev & Zeldovich 1970), corrections to the CMB power spectra of similar
order are expected. Computing the CMB TT and EEpower spectra using the results for the ionization history with and without
the additional feedback we find changes with a typical peak to peak
amplitude
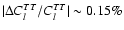 and
and
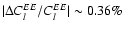 at
at
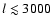 (see Fig. 7).
(see Fig. 7).
As shown by Chluba & Sunyaev (2007) due to two-photon processes
one can expect some asymmetries in the emission profiles of the higher
Lyman-series lines. This could modify the amount and time-dependence for the
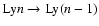 feedback process and may lead to
additional differences in the results presented above. However, because the
bulk of photons that escape in the red wing of a particular Lyman-transition
is expected to come from close to the line center, this may be of minor
importance. Here the most interesting aspect may be the changes in the
time-dependence of the feedback, but more detailed computations would be
necessary to understand this problem.
feedback process and may lead to
additional differences in the results presented above. However, because the
bulk of photons that escape in the red wing of a particular Lyman-transition
is expected to come from close to the line center, this may be of minor
importance. Here the most interesting aspect may be the changes in the
time-dependence of the feedback, but more detailed computations would be
necessary to understand this problem.
In addition one should look at the feedback-induced corrections in the
hydrogen recombination history due to the
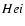 spectral
distortions, in particular due to the photons appearing in the
spectral
distortions, in particular due to the photons appearing in the
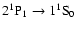 resonance transition, the
resonance transition, the
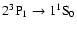 intercombination line and the
intercombination line and the
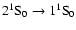 two-photon continuum.
It is clear that all high frequency
two-photon continuum.
It is clear that all high frequency
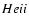 lines will be re-processed
during
lines will be re-processed
during
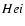 recombination, and correspondingly can only
affect the ionization history during that epoch.
However, for the feedback of the
recombination, and correspondingly can only
affect the ionization history during that epoch.
However, for the feedback of the
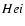 lines on hydrogen recombination
it will be important to compute the re-processing of photons in the
Lyman-continuum and all the subsequent Lyman-series transitions. Since all of these transitions are very optically thick a huge part of the
photons released during
lines on hydrogen recombination
it will be important to compute the re-processing of photons in the
Lyman-continuum and all the subsequent Lyman-series transitions. Since all of these transitions are very optically thick a huge part of the
photons released during
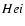 and
and
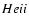 recombination will never reach the observer today, but due to
re-absorption by neutral hydrogen, they are fully converted to hydrogen
Lyman-
recombination will never reach the observer today, but due to
re-absorption by neutral hydrogen, they are fully converted to hydrogen
Lyman- and 2s-1s continuum photons (see
also Kholupenko et al. 2007; Rubiño-Martín et al. in preparation).
Since most of the helium
and 2s-1s continuum photons (see
also Kholupenko et al. 2007; Rubiño-Martín et al. in preparation).
Since most of the helium
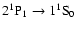 photons are
released at
photons are
released at
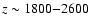 ,
they should be re-absorbed by neutral hydrogen
atoms at the early stages
,
they should be re-absorbed by neutral hydrogen
atoms at the early stages
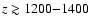 .
One can also conclude this from the paper of Kholupenko et al. (2007), where the
re-processed
.
One can also conclude this from the paper of Kholupenko et al. (2007), where the
re-processed
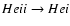 photons appear on the red
side of the hydrogen Lyman-
photons appear on the red
side of the hydrogen Lyman- distortion (most hydrogen Lyman-
distortion (most hydrogen Lyman- photons are released at
photons are released at
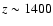 ). Therefore the helium photons affect the
hydrogen recombination history well before the maximum of the
Thomson-visibility function (
). Therefore the helium photons affect the
hydrogen recombination history well before the maximum of the
Thomson-visibility function (
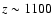 ), and hence should have a rather
small impact on the CMB power spectra. However, a more careful computation is
required and will be described in a forthcoming paper (Rubiño-Martín et al. in preparation).
), and hence should have a rather
small impact on the CMB power spectra. However, a more careful computation is
required and will be described in a forthcoming paper (Rubiño-Martín et al. in preparation).
Acknowledgements
The authors thank the anonymous referee for his useful
comments.
- Beigman,
I. L., & Sunyaev, R. A. 1978, preprint Leb. Phys.
Inst. N163
- Beigman,
I. L., Vainshtein, L. A., & Syunyaev, R. A.
1968, Soviet Phys. Uspekhi, 11, 411 [NASA ADS] [CrossRef]
- Burgin,
M. S. 2003, Astron. Rep., 47, 709 [NASA ADS] [CrossRef]
- Chluba, J.,
& Sunyaev, R. A. 2006a, A&A, 458, L29 [NASA ADS] [CrossRef] [EDP Sciences]
- Chluba, J.,
& Sunyaev, R. A. 2006b, A&A, 446, 39 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Chluba, J.,
& Sunyaev, R. A. 2007, ArXiv e-prints, 705
- Chluba, J.,
Rubiño-Martín, J. A., & Sunyaev, R. A.
2007, MNRAS, 374, 1310 [NASA ADS]
- Doran, M. 2005,
J. Cosmol. Astro-Part. Phys., 10, 11 [NASA ADS] (In the text)
-
Dubrovich, V. K. 1975, Sov. Astron. Lett., 1, 196 [NASA ADS]
- Dubrovich,
V. K., & Stolyarov, V. A. 1995, A&A, 302,
635 [NASA ADS]
-
Dubrovich, V. K., & Shakhvorostova, N. N. 2004,
Astron. Lett., 30, 509 [NASA ADS] [CrossRef]
-
Dubrovich, V. K., & Grachev, S. I. 2005, Astron.
Lett., 31, 359 [NASA ADS] [CrossRef]
- Hinshaw, G.,
Nolta, M. R., Bennett, C. L., et al. 2006, ArXiv
Astrophysics e-prints
- Kholupenko,
E. E., & Ivanchik, A. V. 2006, Astron. Lett., 32,
795 [NASA ADS] [CrossRef] (In the text)
- Kholupenko,
E. E., Ivanchik, A. V., & Varshalovich, D. A.
2005, Gravit. Cosmol., 11, 161
-
Kholupenko, E. E., Ivanchik, A. V., & Varshalovich,
D. A. 2007, MNRAS, L42
- Lewis, A.,
Weller, J., & Battye, R. 2006, MNRAS, 373, 561 [NASA ADS] (In the text)
- Page, L., Hinshaw,
G., Komatsu, E., et al. 2006, ArXiv Astrophysics e-prints
- Peebles,
P. J. E. 1968, ApJ, 153, 1 [NASA ADS] [CrossRef]
-
Rubiño-Martín, J. A., Chluba, J., & Sunyaev,
R. A. 2006, MNRAS, 371, 1939 [NASA ADS]
-
Rubiño-Martín, J. A., Chluba, J., & Sunyaev,
R. A. 2007, in preparation
- Rybicki,
G. B. & dell'Antonio, I. P. 1993, in Observational
Cosmology, ed. G. L. Chincarini, A. Iovino,
T. Maccacaro, & D. Maccagni, ASP Conf. Ser. 51,
548
-
Seager, S., Sasselov, D. D., & Scott, D. 1999, ApJ, 523,
L1 [NASA ADS] [CrossRef]
- Seager, S.,
Sasselov, D. D., & Scott, D. 2000, ApJS, 128, 407 [NASA ADS] [CrossRef]
- Sunyaev,
R. A. & Zeldovich, Y. B. 1970, Astrophysics and Space
Science, 7, 3 [NASA ADS] (In the text)
- Switzer,
E. R. & Hirata, C. M. 2007, ArXiv Astrophysics
e-prints
(In the text)
- Wong, W. Y.
& Scott, D. 2007, MNRAS, 375, 1441 [NASA ADS]
- Wong, W. Y.,
Seager, S., & Scott, D. 2006, MNRAS, 367, 1666 [NASA ADS]
- Zeldovich,
Y. B., Kurt, V. G., & Syunyaev, R. A. 1968,
Zhurnal Eksperimental noi i Teoreticheskoi Fiziki, 55, 278 [NASA ADS]
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=8.8cm]{eps/7333f001.eps}\\ [1mm]
\includegraphics[width=8.8cm]{eps/7333f002.eps}\end{figure}](/articles/aa/full/2007/43/aa7333-07/Timg44.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]
{eps/7333f003.eps}\end{figure}](/articles/aa/full/2007/43/aa7333-07/Timg45.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]
{eps/7333f004.eps}\\ [5.2mm]
\i...
...f005.eps}\\ [5.2mm]
\includegraphics[width=8.8cm]
{eps/7333f006.eps}\end{figure}](/articles/aa/full/2007/43/aa7333-07/Timg71.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]
{eps/7333f007.eps}\end{figure}](/articles/aa/full/2007/43/aa7333-07/Timg72.gif)
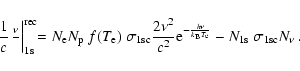
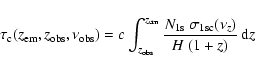
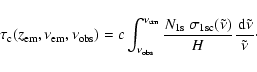
![\begin{displaymath}
P^{\rm Ly-c}_{\rm esc}(z_{\rm em})
=\int_{\nu_{\rm c}}^\inft...
...au_{\rm c}(z_{\rm em}, \nu', \nu_{\rm c})\right]{\,\rm d}\nu',
\end{displaymath}](/articles/aa/full/2007/43/aa7333-07/img95.gif)
![\begin{displaymath}
P^{\rm Ly-c}_{\rm esc}(z_{\rm em})
\approx
\int_{\nu_{\rm c}...
...e{\nu})}{\tilde{\nu}}{\,\rm d}\tilde{\nu}
\right]{\,\rm d}\nu'
\end{displaymath}](/articles/aa/full/2007/43/aa7333-07/img101.gif)
![\begin{displaymath}
P^{\rm Ly-c}_{\rm esc}(z_{\rm em})\approx \int_0^\infty {\rm...
...sc}_{\rm c}]}
{\,\rm d}\xi=\frac{1}{1+\tau^{\rm esc}_{\rm c}},
\end{displaymath}](/articles/aa/full/2007/43/aa7333-07/img107.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]
{eps/7333f008.eps}\end{figure}](/articles/aa/full/2007/43/aa7333-07/Timg112.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]
{eps/7333f009.eps}\end{figure}](/articles/aa/full/2007/43/aa7333-07/Timg113.gif)
![\begin{displaymath}
\Delta R_{\rm c1s}\approx P^{\rm Ly-c}_{\rm esc}(z_{\rm em})...
...rm 1s}~R_{{\rm 1sc}}-N_{\rm e}~N_{\rm p}~R_{{\rm c1s}}\right],
\end{displaymath}](/articles/aa/full/2007/43/aa7333-07/img114.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]
{eps/7333f010.eps}\end{figure}](/articles/aa/full/2007/43/aa7333-07/Timg121.gif)