A&A 474, 639-645 (2007)
DOI: 10.1051/0004-6361:20077396

Is a 2004 Leonid meteor spectrum captured in a 182 cm telescope?

T. Kasuga^1,3 - T. Iijima² - J. Watanabe³

1 - Institute for Astronomy (IfA), University of Hawaii, 2680 Woodlawn Drive, Honolulu, Hawaii 96822-1897, USA
2 - Obseservatorino Astrofisico, 36012 Asiago (Vi), Italy
3 - National Astronomical Observatory of the Japan (NAOJ), National Institute of Natural Science, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan

Received 2 March 2007 / Accepted 13 June 2007

Abstract
Context. It has been thought that fast-moving meteor spectra consist of only two excitation temperature regimes: the 5000 K main component and another hot component at 10 000 K. This belief does not always satisfy observed spectra due to the lack of sufficient physical correlation among derived excitation temperatures, observed fluxes, upper energy levels ($E_{\rm u}$), and Einstein A coefficients ( $A_{\rm ul}$) of each spectral emission line.
Aims. This work tries to correlate them and discovery new excitation temperature regimes in meteor spectra in the visual to near IR wavelength region.
Methods. We focus on the upper energy levels and Einstein A coefficients of observed spectral emission lines. A model fitting the first positive band of nitrogen (${\rm N_{2}}$) and total number of Si II under quasi-neutral conditions proved the key to identifying of new components.
Results. We have identified two new excitation temperature regions in meteor spectra. One is a Mid component at 8000 K for ${\rm N_{2}}$ and another a Jet component above 10 000 K for Si II. This breakthrough has allowed us to reproduce the meteor spectrum.
Conclusions. The spectra of high-speed meteors may consist of more than two excitation temperature regions including the main, Mid, hot, and Jet components.

Key words: meteors, meteoroids

1 Introduction

Many photographic and video-television techniques have been applied to meteor spectroscopy using slit less instruments. These studies have provided insight into the physical and chemical properties of meteoroids in meteor showers under a simple thermal equilibrium model (Ceplecha et al. 1998). Slit less and small instruments provide a wide field of view (FOV) and high statistics but a low-dispersion spectra data set. On the other hand, big telescopes can provide high-quality spectra with relatively high dispersion but with the problem of their smalls field of view (FOVs). The unpredictability of a meteor's appearance, position and their short duration rarely allow us to capture meteor spectra data on big telescopes. Therefore, it is most common to use small instruments and wait till bright meteors pass through the wide FOV - in other words, spectroscopic observations of meteors depend on "luck''.

	Figure 1: Spectra of V838 Mon and a meteor taken by the 182 cm telescope at ${\rm 2^{h}15^{m}24.3^{s}}$ UT 2004 Nov. 18. The telescope was pointing in a southerly direction at 1.56 airmass for V838 Mon, which is centered in the frame. The meteor spectrum was captured to the east (right) of V838 Mon, and a field star spectrum appears between them. The wavelength increases from bottom to top.
Open with DEXTER

Fortunately, 3 examples of sporadic meteor spectra in the wavelength range of 3500-10 500 $\AA$ have been reported. They appeared in high-dispersion slits on big telescopes by accident. On June 18, 1977, Stauffer & Spinrad (1978) first detected a sporadic meteor spectrum with the 3.05 m telescopes at Lick observatory (USA). Second, Borovicka & Zamorano (1995) obtained a spectrum of the scattered light of a bright and slow-moving fireball using the 2.2 m telescopes at the Calar Alto Observatory (Almeria, Spain) on Dec. 19, 1988. Last, on May 12, 2002, Jenniskens et al. (2004a) imaged a meteor spectrum that crossed the long slit of the European Southern Observatory (ESO) Very Large Telescope (VLT). These examples provide high-quality and high-resolution data (several $\AA$/pixel) to enable them to study metals, non-metallic emissions, and molecule bands. On the other hand, no spectra of meteoroids in the major meteor showers have been observed with big telescopes.

The Leonid meteor shower is one of the strongest activity showers in each year. Especially from 1998 to 2002, the Leonid meteor showers presented the increased activity associated with the passage of the parent comet 55P/Tempel-Tuttle in 1998. Understanding the physical and chemical properties of these meteors has benefit from the effort made during its recent active season using small instruments (Borovicka & Jenniskens 2000; Trigo-Rodrìguez et al. 2003; Borovicka et al. 1999; Kasuga et al. 2006). The high velocity of the Leonids (72 km  ${\rm s^{-1}}$) compared to other meteor showers results in their having the highest impact energy in Earth's atmosphere.

For very fast meteoroids, "the hot component condition'' is applied when attempting to unravel their spectra. This is the assumption of only two excitation temperature regions. One is a hot component at 10 000 K and the other the main component at around 5000 K. Emissions of neutral and ionized atoms and atmospheric molecular bands have been observed in the near-UV to near-IR wavelength region (Borovicka & Jenniskens 2000; Borovicka 1993; Ceplecha et al. 1998). The hot component theory has had success in deriving chemical compositions of meteoroids in the Leonid meteor showers so far, although little is known about the physical conditions of the theory.

In this paper we provide a meteor spectrum captured in a 182 cm telescope in the visual-near IR wavelength region. The 182 cm telescope of the Mount Ekar Station of the Astronomical Observatory of Padova was observing the spectrum of V838 Mon. During a 3600 s exposure in slit spectroscopic mode, a meteor crossed the slit. Thus, we obtained a meteor spectrum at the same time as that of V838 Mon. The possible Leonid meteor spectrum enabled us to study the excitation temperatures of spectral emission lines of non-metallic and metallic elements and molecular bands. First positive band of nitrogen (${\rm N_{2}}$) and ionized silicon emissions (Si II), which had been classified into typical components, may need to be grouped into new components. Our goal is to suggest new excitation temperature regions for satisfying the observed meteor spectrum. In this paper we describe the possibility that high-speed meteor plasma spectra consist of more than two excitation temperature regions.

2 Observation

The primary target was V838 MON (RA ${\rm07^h04^m05^s}$, Dec. ${\rm -03^{\circ}50'51''}$), using the 182 cm telescope of the Mount Ekar Station of the Astronomical Observatory of Padova. The observatory is located at latitude $+45^{\circ}50'36''$N, longitude $0^{\circ}46'17''$E, and altitude 1350 m. The exposure began at ${\rm 2^{h}15^{m}24.3^{s}}$ UT 2004 Nov. 18, and a meteor crossed the slit during a 3600 s exposure in slit spectroscopic mode. Therefore, spectra of both the meteor and V838 Mon were obtained at the same time (Fig. 1) .

A TK512CB1 charged-coupled device (CCD) was employed at the f/9 Cassegrain focus. The system is sensitive to the visible-near IR wavelength region (5800-7085 Å) using a Boller & Chivens spectrograph with a grating of 600 lines ${\rm mm^{-1}}$. A spectral resolution of $\lambda / \Delta \lambda \sim 800$ was achieved with a dispersion of 120 $\AA$ ${\rm mm^{-1}}$ (2.36 $\AA$ ${\rm pixel^{-1}}$), and the data were recorded as 16-bit images.

Reduction of the spectrum at the Asiago Observatory was carried out using standard tasks in the NOAO IRAF package. After subtraction of the CCD bias, the image was divided by a normalized flat-field to correct for pixel-to-pixel sensitivity variations. The wavelength calibration was made with the emission lines of a Fe-Ar lamp, and the spectral response of the instrument was calibrated with a spectrum of the standard star HD60778 taken on the same night.

3 Analysis and result

3.1 Line identification

Figure 2: 1D meteor spectrum extracted from the spectra shown in Fig. 1. Calibrated flux density is in units of ${\rm 10^{-14}~erg~s^{-1}~cm^{-2}~\AA^{-1}}$. The red curve shows the observed spectrum, while the blue curve is the best-fit model using atomic catalog lines and first positive band of ${\rm N_{2}}$. Residuals to the fit are shown with black fine dots below the spectrum. The green curve represents the model of the first positive band of ${\rm N_{2}}$ with a derived excitation temperature of ${\rm N_{2}}$ $8010\pm 260$ K. Excitation temperature of O I, N I, ${\rm H_\alpha }$ I, Si II, and Na I are set as 10 000 K and 5500 K, respectively.

Open with DEXTER

Figure 1 shows the raw CCD spectrum of the meteor while Fig. 2 provides line identification in the reduced 1D spectrum. Neutral metallic atom emission lines at 5891.42 $\AA$ (Na I-doublet) and ionized metallic lines at 6346.31 $\AA$ and 6370.47 $\AA$ (Si II) were clearly identified. Nonmetallic emission lines at 6157.35 $\AA$(O I), 6482.54 $\AA$ (N I), 6562.26 $\AA$ ( ${\rm H_\alpha }$ I) and molecular bands of the first positive band of ${\rm N_{2}}$ ( ${\rm B^{3}\Pi _g - A^{3}\Sigma ^{+}_{u}}$ 5880-7085 $\AA$) were also identified. These features are common to spectra obtained for other fast-moving meteors such as the Leonids, Perseids, and Coma Berenecids (e.g. Borovicka 1994; Harvey 1977). Most of the emission features at wavelengths longer than 6000 $\AA$ originate in the Earth's atmosphere. They were identified using a line catalog as shown in Table B.1. Emission lines of O I, N I, ${\rm H_\alpha }$ I, and Si II suggest the presence of the high-excitation temperature region that corresponds to the hot component condition (Borovicka 1993,1994).

A few emission lines of neutral non-metallic atoms and ionized metallic atoms also exist in the spectrum. These lines should be weak because of their high upper energy levels. In order to explain them, Borovi ${\rm \check{c}}$ka (1993) employed two types of spectra. One is the hot component with a high-excitation temperature of 10 000 K, which is composed of O I, N I, ${\rm H_{\alpha}~I}$, and Si II in the near-IR and Mg II (4481 $\AA$), Ca II (3933, 3968 $\AA$) in the near-UV to visual range (Borovicka & Jenniskens 2000; Borovicka 1993). The other is the main component with a low-excitation temperature of 5000 K mainly consisting of neutral metallic atoms. Borovicka (1994) suggests that the hotter component is produced by a meteor shock wave associated with fast-moving meteors. Indeed, our meteor exhibited strong atomic emission lines that belong to the hot component and imply that its entry velocity must be fast. Taking the observed emission lines and the image date and the direction into consideration, we believe that this object is probably a Leonid meteor. Hereafter, we assume that this is the case.

  
3.2 Model fitting

The Boltzmann distribution for the population of each energy level was assumed for the model fitting (Kasuga et al. 2005b). The total number of neutral atoms $N_{\rm u}$ in the upper energy level $E_{\rm u}$ is expressed as

$$N_{\rm u} = \frac{g_{\rm u}}{g_0} N_{0}\exp\left(-\frac{E_{\rm u}}{k_{\rm B} T_{\rm ex}}\right),$$ (1)

where N₀ is the total number of neutral atoms at the ground-state energy level, $g_{\rm u}$ and g₀ are the statistical weights of the upper and ground state energy levels respectively, $T_{\rm ex}$ is the electronic excitation temperature, and $k_{\rm B}$ the Boltzmann's constant. 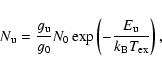The g-value of each energy level is taken from the Physical Reference Data of the National Institute of Standard and Technology (NIST) as listed in Table B.1.

Here the optically thin model was assumed for the observed spectrum. The self-absorption effect is suggested by estimating the emissions' curve of growth using only small numbers of Fe I-multiplets. However, this technique should not be applied for other elements and other emission lines (Ceplecha 1973; Borovicka 1993).

The flux $\widetilde{f}(\lambda)$ of a line emitted by atoms in a transition from a state u in the upper energy level $E_{\rm u}$ to a state l in the lower energy level $E_{\rm l}$ is expressed as

$$\widetilde{f}(\lambda) = \frac{N_0}{4\pi r^2} hc\nu_{\rm ul} ... ...(\frac{ - (\lambda - \lambda_{0})^{2}}{2 \sigma^{2}} \right) ,$$ (2)

where h is the Plank constant, c the velocity of light, $A_{\rm ul}$ is the Einstein transition probability of spontaneous emission, $\nu_{\rm ul} = (E_{\rm u} - E_{\rm l})/hc$ is the wavenumber of the line, r the distance from the meteor to the observer, and $N_0 / 4\pi r^2$ the column density. The spectral profile was assumed to be Gaussian with $\lambda_{0}$ the wavelength of the line center and $\sqrt{2} \sigma$the width of the instrumental profile. First, to determine $\sigma$, we fit the ionized atomic emission lines of Si II (6346.31 $\AA$ and 6370.47 $\AA$) because they were not convoluted with other features. We derived $\sigma = 2.40 \pm 0.31~\AA$ and hereafter apply it to all the spectral lines. These, N₀ for Si II was an arbitrary value and $T_{\rm e}$ was fixed at 10 000 K for the hot component condition (Borovicka 1993).

First positive band of ${\rm N_{2}}$ ( ${\rm B^{3}\Pi_g - A^{3}\Sigma^{+}_{\rm u}}$) was fit to the observed meteor wavelength range (5880-7085 $\AA$) as shown in Fig. 2. Second, we fit the three strong band sequences of the first positive band system as the baseline of the observed spectrum. The vibrational quantum numbers are v of $\Delta v=+2$, $\Delta v=+3$, and $\Delta v=+4$. Their band position, Einstein A coefficient, and the calculation procedure for the first positive band of ${\rm N_{2}}$ is given in Appendix A. We do not take the blackbody continuum into account because Harvey (1977) confirmed that most of the meteor spectrum in the near-IR wavelength region is caused by the first positive band.

Third, we fit the atomic emission lines of O I, N I, ${\rm H_\alpha }$ I, Si II, and Na I using Eq. (2). The number of O I, N I, ${\rm H_\alpha }$ I, Si II, Na I at the ground-state energy level and ${\rm N_{\rm 2}}$ at all energy levels were evaluated from the observed fluxes. The excitation temperature of ${\rm N_{\rm 2}}$ was derived to be $8010\pm 260$ K (see Appendix A). We found that $T_{\rm ex}$ of ${\rm N_{2}}$ was between the hot and the main components. We propose it as "the Mid component'', and this possibility is discussed in Sect. 4.1. Excitation temperatures of O I, N I, ${\rm H_\alpha }$ I, and Si II were assumed to be 10 000 K and 5500 K for Na I to follow the hot and main component conditions for the Leonids (Borovicka & Jenniskens 2000; Trigo-Rodrìguez et al. 2003; Kasuga et al. 2005a). The model fit result for the Leonid meteor spectrum is shown in Fig. 2, where we considered all the catalog lines listed in Table B.1 for the calculation.

Atoms in the ground state and all excited levels were summed to obtain the total number. This modification successfully resulted in the derivation of total neutral and/or ionized atomic abundance. To transform column density into number density, we assumed the typical thickness of meteor plasma volume to be about 10 m (Babadzhanov & Kokhirova 2004; Boyd 2000).

Since the telescope was pointed at an elevation of $39.9^{\circ}$ (at an airmass of 1.56) when the meteor spectrum was captured, we could estimate the distance from the meteor to observer to be about 171.59 km with the assumption that the altitude of Leonid meteor visibility is 110 km (Millman et al. 1971).

  
3.3 Electron density

Electron density is needed in the Saha equation to obtain the total number of each atomic species. It lets us derive the degree of the numbers of singly ionized and neutral atoms (Allen 1999). Hereafter, the ionization temperatures (= $T_{\rm ion}$) for the hot and main components are given the same value for the excitation temperatures (= $T_{\rm ex}$) for each component. To derive the electron density under the hot component condition, we defined the Saha's functions that satisfy the equals of total metal abundances and pressure of the radiant gas between the main and the hot components (Kasuga et al. 2005a). Unfortunately, the method requires two species of both neutral and ionized emission lines, such as Ca I, Mg I, Ca II, Mg II, for the main and hot components respectively, and none of these emission lines appear in the observed wavelength range. Then, to obtain electron density we applied the quasi-neutrality theory defined by Saha equation. We can consider a total number of the singly ionized one as the same value that of electron density if more highly ionized atoms had no need to be concerned (Borovicka 1993). Results are shown in Table 1.

Table 1: Results of the excitation temperatures of Si II, corresponding total number of Si II (=$n_{\rm e}$), and abundance ratios of N/O, H/O under the hot component condition.

Kasuga et al. (2006) found values for electron densities derived from 2002 Leonid meteor spectra of $10^{13} \sim 10^{15}~{\rm cm^{-3}}$. Those results agree with other studies obtained from the electron volume density ( ${\sim} 10^{12}~{\rm cm^{-3}}$); (Nagawasa 1978) and the condition of neutrality with the geometrical model of meteors ( $10^{12} \sim 10^{13}~{\rm cm^{-3}}$); (Borovicka 1993). Babadzhanov & Kokhirova (2004) carried out their both methods used the Ca II concentration and conclude that free electron densities are in the range of ${\sim}10^{13} \sim 10^{15}~{\rm cm^{-3}}$.

In this study the analysis process under the hot component condition was applied to the Leonid spectrum as stated above. Even though our application derived too high a value for the electron density ( $n_{\rm e} = 1.0 \pm0.3 \times 10^{18}~{\rm cm^{-3}}$); (see Table 1) the excitation temperature for the hot component was fit at 10 000 K. The derived value is not in the range of previous studies. The Si II (6347.10, 6371.36 Å) emissions can be much weaker due to the extremely small values of Einstein A coefficients ( ${\sim}10^{-1}~{\rm s^{-1}}$) and their high upper energy levels (${\sim}10$ eV) (see details in Sect. 4). However, we find strong Si II (6347.10, 6371.36 Å) emissions in the meteor, implying that these lines originate in the much higher-excitation temperature component.

For the purpose of deriving a realistic electron density from Si II emission lines, we assume that these lines belong to a "Jet component'' that has a much higher excitation temperature than the hot one. We try to raise the $T_{\rm ex}$ of Si II from 10 000 K to 20 000 K for every additional 1000 K and estimate the total number of Si II. As shown in Table 1 we can follow a value of electron density that gets close to a realistic value with the increase in the excitation temperature of the Jet component. We discovered that a realistic electron density is obtained at an excitation temperature for the Jet component of $T_{\rm e}^{\rm Jet} = 17~000$ K because its value is within the realistic range $10^{13} \sim 10^{15}~{\rm cm^{-3}}$ (see Sect. 4.2).

To derive total abundances, the electron density for the hot, mid, and main component are obtained from the Saha equation using the relationship for the pressure balances of continuous components, as expressed by

$$p = n_{\rm e}^{\rm Jet}k_{\rm B}T_{\rm ex}^{\rm Jet}=n_{\rm ... ...^{\rm Mid}= n_{\rm e}^{\rm Main}k_{\rm B}T_{\rm e}^{\rm Main}$$ (3)

where $n_{\rm e}^{\rm X} {\rm and} T_{\rm ex}^{\rm X}$ are electron density and excitation temperature for component X: the jet, hot, mid, and main components respectively. Then $n_{\rm e}^{X}$ can be rewritten as $n_{\rm e}^{\rm Jet} \cdot T_{\rm ex}^{\rm Jet} / T_{\rm ex}^{\rm X}$ and applied in the Saha equation to derive total abundances. The singly ionized nitrogen molecular band ( ${\rm N_{2}^{+}}$) is not considered because its dissociation energy $(9.76~{\rm eV})$ is clearly lower than the ionized energy $(15.58~{\rm eV})$ (Allen 1999). Derived results are included in Table 1.

  
4 Discussion

  
4.1 Upper energy levels and excitation temperature

A remarkable result is that our derived value of excitation temperature of the first positive band of ${\rm N_{2}}$ is $T_{\rm ex}=8,010\pm260$ K, which is much higher than the typical value of $\sim$4500 K (Jenniskens et al. 2004b,a,2000b). The difference may be caused by the source of meteor plasma, which may be either the body or the train (trail). However, we focus on the possibility that the difference is due to a dependence on upper energy levels ($E_{\rm u}$) of the first positive band of ${\rm N_{2}}$ as argued by other researchers.

Harvey (1977) and Ceplecha et al. (1998) have suggested that the ${\rm N_{2}}$ is due to a higher excitation temperature region in the meteor body plasma. The former determined effective vibrational temperatures (= $T_{\rm ex}$) of ${\rm N_{2}}$ for relatively high-speed meteors such as Leonids, Perseids, and Coma Berenecids. Their excitation temperatures of 15 000-20 000 K indicated that these values are consistent with the radiation from moderately high upper energy levels ( $E_{\rm u} \sim 8~{\rm eV}$). The latter also discuss the possibility that ${\rm N_{2}}$ is one of the sources of the hot component due to its high upper energy level. Derived values from Harvey (1977) are higher than our excitation temperatures. This is because the second positive band of ${\rm N_{2}}$ ( ${\rm C}^{3}\Pi_{\rm u} - {\rm B}^{3}\Pi_{\rm g}$), which has higher upper energy levels ($\sim$11 eV) in the near UV to visual wavelength region, is also taken into account in their model even though they are very faint. Contamination of the second positive band and absolute majority of metallic emission lines in the wavelength range (Kasuga et al. 2005b) might let Harvey (1977) derive relatively higher excitation temperature.

Table 2: Four type components and their excitation temperatures, with representative elements for each component, the catalog of wavelength; $\lambda$, Einstein A coefficients; $A_{\rm ul}$, and upper energy level; $E_{\rm u}$. Bold fonts are keys to find new components and its category.

Ceplecha (1973) found upper energy levels corresponding to reasonable excitation temperature by visualizing Boltzmann distribution of levels for Fe I-multiplets. The correlation for other emission lines are possible. In order to review the correlation about other emission lines we summarize the representative emission lines observed in Leonid meteor spectra for the main and the hot components in Table 2 (Kasuga et al. 2005a).

Lines with high excitation energies, such as Si II ($\sim$10.0 eV), Mg II ($\sim$11.6 eV), O I lines ($\sim$12.7 eV), ${\rm H_\alpha }$ I ($\sim$12.09 eV), and N I($\sim$13.6 eV ), have been included in the hot component. On the other hand, lower excitation energy lines, such as Mg I ($\sim$5.1 eV), Fe I($\sim$4.3 eV), Ca I($\sim$2.9 eV), and Na I ($\sim$2.1 eV), are emitted from the main component. Their upper energy levels are closely correlated with their excitation temperatures, except for the emission lines of Ca II($\sim$3.1 eV).

The components of Ca II have been discussed by several authors. Borovicka (1993) considers them under the hot component condition; however, Borovicka (1994) and Borovicka & Jenniskens (2000) show that Ca II were also included in the main component. Babadzhanov & Kokhirova (2004) suggest that the excitation temperature of Ca II is in the 1500-2000 K range in consideration of their realistic values of the electron density.

Kasuga et al. (2007,2005a) discuss the origin of the Ca II emissions (3933.66, 3968.47 $\AA$) from the view point of their low upper energy levels. To derive the electron density under the hot component condition, we applied the Saha functions as described in Sect. 3.3. Ca II (3933.66, 3968.47 $\AA$) was assumed to be in the hot component (Borovicka 1993), which resulted in two types of electron densities: one with a positive value and the other negative. The appropriate electron density is selected as the positive value following Borovicka (1993). However, we found an unrealistic situation in that both derived values of the electron density are negative in some meteor spectra. This means Ca II are not always under the hot component. The collapse of the hot component so far is recognized by the unbalanced pressure of radiant gas and metal abundances among just two types of components. In that situation, CaII was assumed to be in the main component instead of the hot one due to its low upper energy levels ($\sim$3.1 eV) and extracted electron density.

We point out that the excitation energy of the upper energy level correlates closely with its excitation temperature and suggest that the origin of Ca II is likely to be in the main and not the hot component. Babadzhanov & Kokhirova (2004) derived relatively low excitation temperatures, which may be another possibility because it seems to be related to Ca II's upper energy levels. This means that the hot condition with only two types of components is not always satisfied, suggesting that other components corresponding to their upper energy levels may exist. Thus, we support Harvey (1977) and conclude that our derived excitation temperature for the first positive band of ${\rm N_{2}}$ is consistent with their upper energy level. We refer to the new excitation temperature region as the Mid component, which consists of the first positive band radiation at $T_{\rm ex} \sim 8000$ K (Table 2).

  
4.2 Einstein A coefficients and excitation temperature

Higher upper energy levels require higher excitation temperature. The intensity of observed fluxes also depends on those physical values and the Einstein A coefficients: $A_{\rm ul}$ as expressed in Eq. (2). Clearly observed atomic emission lines in our meteor spectra yield values of $A_{\rm ul} = 10^{6} \sim 10^{8}~{\rm s^{-1}}$(Kasuga et al. 2005a). However, in this work, we found extremely small $A_{\rm ul}$-values for Si II ( $10^{-1}~{\rm s^{-1}}$) and expect that its excitation temperature might be higher than those of the hot component (see Sect. 3.3). Here we approach the reason for the high value of our derived excitation temperature, $T_{\rm ex} = 17~000~{\rm K}$, from the view point of the small value of  $A_{\rm ul}$.

The excitation temperature of Si II has been set to 10 000 K, and this value is assumed to be same as that of Mg II (Borovicka 1994). This is an unreasonable supposition if meteoroids are composed of solar abundance Mg/Si =  1.05^+0.27_-0.21 (Asplund et al. 2006). In Table 2, values of $A_{\rm ul}$ in Mg II (4481 Å) and other elements under the hot component show almost ${\rm 10^{6} \sim 10^{8}~s^{-1}}$, except for those of Si II $\sim$10^-1 s^-1. On the other hand, we can find that almost all elements in the hot component show similar values of upper energy levels. This fact enables us to expect that fluxes of Si II are much smaller than those of Mg II and that the ratio is about 10^-1:10⁸. However, both Fig. 2 in Borovicka (1994) and Fig. 19 in Borovicka (1993), which are relative intensities of spectra, show that Si II and Mg II do not reflect their values of $A_{\rm ul}$. The former derives a flux ratio of Si II:Mg II of about 1:2, while the latter finds a ratio of about 1:10. If Si II and Mg II are at the same excitation temperature of 10 000 K, their singly ionized numbers should almost have the same values. This is because, as Borovicka (1994) points out, ionization energies of Si and Mg are almost the same, 8.15 eV and 7.65 eV, respectively (Allen 1999). In this situation their relative fluxes can surely be attributed to their Einstein A coefficients, although it is not reflected in the observed spectra. Therefore, it is hard to argue that Si II and Mg II are at the same excitation temperature.

Our derived electron density at 10 000 K under the quasi-neutrality condition is also a questionable value ( $n_{\rm e} = 1.0 \pm0.3 \times 10^{18}~{\rm cm^{-3}}$) because it is out of the range of typical values derived by previous researchers (see Sect. 3.3). The abnormal value of our electron density may be caused by three factors: excitation temperature, geometrical thickness, or the altitude of the meteor illumination. To resolve the issue, we first tried to raise the excitation temperature of the Si II emissions to produce a more realistic electron density under the assumption that they belong to a "Jet component'' that has a higher excitation temperature than the hot component. As the excitation temperature of the Jet component increases to 17 000 K, the electron density gets close to a realistic value. Second, we assumed the geometrical thickness was extremely large, which might let us obtain unusual values for the electron density. If the geometrical thickness of the meteor plasma increases beyond the normal size (to 50 m), a realistic electron density can be obtained at 14 000 K ( $n_{\rm e} = 7.4 \pm 1.8 \times 10^{15}~{\rm cm^{-3}}$). The excitation temperature of Si II is predicted to be higher than that of the hot component even if the geometrical thickness is up to $\sim$100 m thick. Third, the high-altitude meteor illumination at 200 km is supposed to be shown by earlier Leonids observation (Spurný et al. 2000). This hypothesis also gives an unrealistic electron density ( $n_{\rm e} = 3.6 \pm 0.9 \times 10^{16}~{\rm cm^{3}}$), even at 20 000 K. Much higher excitation temperature is expected if the altitude of meteor illuminations is above 110 km. Thus, we conclude that an excitation temperature of Si II is higher than 10 000 K, providing evidence of a higher temperature region than the hot component. To confirm this prediction, it is important for future work to derive electron density from the total number of Mg II under the quasi-neutrality condition.

  
4.3 New excitation temperature regions

Borovicka (1994) has hypothesized that in fast-moving meteor spectra there are two excitation temperature regions. One is the main component of 5000 K and another the hot component of 10 000 K. Intermediate or other temperature regions have not been confirmed (Borovicka 1994).

In this work we have found two new components. One is "the Mid component'' composed of mainly neutral ${\rm N_{2}}$ ( ${\rm B^{3}\Pi_{\rm g} - A^{3}\Sigma^{+}_{\rm u}}$), and the other "the Jet component'' composed of Si II. The excitation temperature of the "the Mid component'' is about 8000 K, while that of "the Jet component'' is above 10 000 K. Their upper energy levels $E_{\rm u}$ and Einstein A coefficients $A_{\rm ul}$ proved to be the keys to identifying the new components.

This study suggests that meteor plasma spectra consist of several temperature regions, such as the main component, the Mid component, the hot component, and the Jet component. The temperature increases gradually from the main to the Jet components. To confirm its validity, we should consider a pressure balance and an equivalence of metal abundances among four types of continuous components. The former is considered (Eq. (3)) in this study, but the latter in each component is not estimated. It might be good to apply to the Saha function to metal elements, especially to Si I and Si II, under the old and new components conditions. To derive them, we need high-resolution meteor spectra from the near UV to near IR wavelength region, which includes neutral and ionized atomic emission lines and the nitrogen band for each component.

5 Summary

A meteor spectrum was captured in a 182 cm telescope in the visual-near IR wavelength region. We identified emission lines of O I, N I, ${\rm H_\alpha }$ I, Si II, Na I and molecular bands of ${\rm N_{2}}$ ( ${\rm B^{3}\Pi _g - A^{3}\Sigma ^{+}_{u}}$). Concluding remarks are as follows.

1.

Hot component features as identified earlier in Leonid meteoroids were confirmed.

2.

The excitation temperature of the first positive band of ${\rm N_{2}}$ ( ${\rm B^{3}\Pi _g - A^{3}\Sigma ^{+}_{u}}$) is $\sim$8000 K with an upper energy level of ($8 \sim9$ eV) suggesting that the excitation energy of the upper energy level correlates closely with its excitation temperature.

3.

Emission lines of Si II (6346.31 $\AA$ and 6370.47 $\AA$) originate in an even higher excitation temperature region: the Jet component.

4.

A high-velocity meteor spectrum consists of more than two excitation temperature regions: a main, Mid, hot, and Jet component in order of increasing temperature.

Acknowledgements

T.K. thanks Profs. Tetsuo Yamamoto, Yasuhiro Hirahara, Robert Jedicke, and the JSPS Research Fellowships for young scientists. We pray for the repose of Mr. Atsushi Mori's soul. He made a great contribution to meteor science.

References

• Allen, C. W. 1999, Astronomical Quantities, Fourth edn, University of London (The Althone Press) (In the text)
• Arnold, J. O., Whting, E. E., & Lye, G. C. 1969, J. Quant. Spectrosc. Radiant. Trans., 9, 775 [NASA ADS] (In the text)
• Asplund, M., Grevesse, N., & Jacques, S. A. 2006, Nucl. Phys. A, 777, 1 [NASA ADS] (In the text)
• Babadzhanov, P. B., & Kokhirova, G. I. 2004, A&A, 424, 317 [NASA ADS] [CrossRef] [EDP Sciences]
• Borovicka, J. 1993, A&A, 279, 627 [NASA ADS]
• Borovicka, J. 1995, Plan. Space. Sci., 42, 145 [NASA ADS] [CrossRef]
• Borovicka, J., & Zamorano, J. 1995, A&A, 68, 217 (In the text)
• Borovicka, J., Stork, R., & Bocek, J. 1999, Meteor. Planet. Sci., 34, 987 [NASA ADS]
• Borovicka, J., & Jenniskens, P. 2000, Earth, Moon Plan., 82/83, 399
• Boyd, I. D. 2000, Earth, Moon Plan., 82/83, 93
• Ceplecha, Z. 1973, Bull. Astr. Inst. Czech., 24, 4
• Ceplecha, Z., Borovicka, J., Graham, E. W., et al. 1998, Space Sci. Rev., 84, 327 [NASA ADS] [CrossRef] (In the text)
• Drellishak, K. S. 1964, ADEC-TDR-64-22
• Forrest, R. G., Russ, R. L., & Patrick, J. E. 1992, J. Phys. Chem. Ref. Data, 21, 1005 (In the text)
• Harvey, G. A. 1977, J. Geophys. Res., 82, 15 [NASA ADS] (In the text)
• Herzberg, F. 1950, Molecular Spectra and Molecular Structure I: Spectra of Diatomic Molecules, 2nd Edn., D. Van Nostrand, Princeton, New Jersey (In the text)
• Huber, K. P., & Herzberg, F. 1979, Molecular Spectra and Molecular Structure IV: Constants of Diatomic Molecules, Van Nostrand Reinhold, New York (In the text)
• Jenniskens, P., & Rairden, et al. 2000b, Earth, Moon Plan., 82/83, 457
• Jenniskens, P., Jehin, E., Cabanac, R. A., et al., 2004a, Meteor. Planet. Sci., 39, 609 [NASA ADS] (In the text)
• Jenniskens, P., Laux, C. O., Wilson, M., et al., 2004b, Astrobiology, 4, 67 [NASA ADS]
• Jenniskens, P., & Mandell, A. M., 2004c, Astrobiology, 4, 123 [NASA ADS]
• Lofthus, A., & Krupenie, P. H. 1977, J. Phys. Chem. Ref. Data, 6, 113 [NASA ADS] (In the text)
• Spurný, P., Betlem, H., Jobse, K., et al. 2000, Meteor. Planet. Sci., 35, 5, 1109 (In the text)
• Stauffer, J., & Spinrad, H. 1978, PASP, 90, 222 [NASA ADS] [CrossRef] (In the text)
• Stupochenko, E. V., Stakhanov, I. P., & Samuilov, et al. 1961, Physical gas dynamics, ed. A.S. Predvoditelev (Oxford: Pergamon Press)
• Kasuga, T., Yamamoto, T., Watanabe, J., et al. 2005a, A&A, 435, 341 [NASA ADS] [CrossRef] [EDP Sciences]
• Kasuga, T., Watanabe, J., & Ebizuka, E., et al. 2005b, A&A, 438, L17 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Kasuga, T., Watanabe, J., Kawakita, H., et al. 2007, Adv. Space. Res., 39, 513 [NASA ADS]
• Kasuga, T., Watanabe, J., Yamamoto, T., et al. 2006, ApJ, 638, 1176 [NASA ADS] [CrossRef]
• Nagasawa, K., 1978, Ann. Tokyo Astron. Obs. 2nd Ser., 16, 157 (In the text)
• Trigo-Rodrìguez, J. M., Llorca, J., Borovicka, J., et al. 2003, Meteor. Planet. Sci., 38, 1283 [NASA ADS]
• Zahn, U. V., Gerding, M., Höffner, J., et al. 1999, Meteor. Planet. Sci., 34, 1017 [NASA ADS]

 

  
Online Material

Appendix A

Here we describe the model of the first positive band of nitrogen: ${\rm N_{2}}$ ( ${\rm B^{3}\Pi _g - A^{3}\Sigma ^{+}_{u}}$). Molecular band emissions consist of many individual emission lines (Herzberg 1950). Wave numbers of those emission lines correspond to the transitions between two electronic states and are given by

$$\nu = (T_{\rm e}^{'}-T_{\rm e}^{''}) + (G'(v')- G''(v'')) + (F'(J') - F''(J''))$$ (A.1)

where $\nu$ depends on the electronic energy of the state $T_{\rm e}$, vibrational energy G, rotational energy F, vibrational quantum number v, and total rotational quantum number J. The single-primed letters refer to the upper state, and the double-primed letters refer to the lower state. The energies $T_{\rm e}$, G, and F are in units of wave numbers  ${\rm cm^{-1}}$. The vibrational energy G(v)is approximated as

$$G(v) = \omega_{\rm e} \left(v+\frac{1}{2}\right) - \omega_{\r... ...mega_{\rm e} y_{\rm e} \left(v+\frac{1}{2}\right)^{3} + \cdots$$ (A.2)

where $\omega_{\rm e}$, $\omega_{\rm e} x_{\rm e}$ and $\omega_{\rm e} y_{\rm e}$ are vibrational constants.

For triplet transitions where spin splitting is ignored, the central component of the triplet is used as an effective emission line (Arnold et al. 1969). Then, we applied it to the triplets for the model fitting. Hence, the rotational energy F(J) is expressed in Herzberg (1950) as

$$F(J)= F(K) = B_v[K(K+1)+ 4Z_2] - D_v \left(K + \frac{1}{2}\right)^{4},$$ (A.3)

where K, B_v and D_v are rotational quantum number and two rotational constants for the vibrational level of v, respectively. The factor Z₂ is given by

$$Z_2 = \frac{\Lambda Y (Y-1) - \frac{4}{9} -2K(K+1)}{3\left[\Lambda^{2} Y (Y-4) + \frac{4}{3} +4K(K+1) \right]},$$ (A.4)

and

$$Y = \frac{A}{B_v}$$ (A.5)

is a measure of the coupling strength of the spin to the internuclear axis. We obtained the spin - orbit interaction constant A for the upper and lower states from Huber & Herzberg (1979). The rotational constants B_v and D_v are given by

 

$$B_{\rm e} - \alpha_{\rm e} \left(v + \frac{1}{2}\right) + \gamma_{\rm e} \left(v + \frac{1}{2}\right)^{2}$$                          B_v = (A.6)

$$D_{\rm e} +\beta_{\rm e} \left(v + \frac{1}{2} \right)$$ D_v = (A.7)

where $B_{\rm e}$, $D_{\rm e}$, $\alpha_{\rm e}$, $\beta_{\rm e}$, and $\gamma_{\rm e}$ are rotational constants at the equilibrium position. The constants applied in Eqs. (A.1) through (A.7) are obtained from Huber & Herzberg (1979) and Lofthus & Krupenie (1977) and references therein.

These transitions are characterized by strong P and R branches, although other branches are negligibly small (Arnold et al. 1969). The selection rule of the first positive band [${\rm N_{2}}$ ( ${\rm B^{3}\Pi _g - A^{3}\Sigma ^{+}_{u}}$)] is $\Delta J=\pm 1$ and the P-branch is $\Delta J=-1(J'=J''-1)$, while the R-branch is $\Delta J=+1 (J'=J''+1)$. The symbol J is replaced by the symbol K, which denotes rotational quantum number without spin. It is assumed to be $K_{\rm max}=100$ in the least - square model.

Table A.1: Bands of ${\rm N_{2}}$ ( ${\rm B^{3}\Pi _g - A^{3}\Sigma ^{+}_{u}}$), with the wavelength $\lambda$, and Einstein coefficient A_v'v'' (Forrest et al. 1992).

The spectral flux $f(\lambda)$ of emission from the rotational lines is written as

$$f(\lambda) = \frac{N'}{4\pi r^2}~h~c~\nu~A_{v'v''}\cdot\left(\frac{ - (\lambda - \lambda_{0})^{2}}{2 \sigma^{2}} \right)\cdot$$ (A.8)

The number N' of particles in their upper energy level is given by a Boltzmann distribution

$$N' = \frac{N_0 d'(2K'+1)}{Q(T_{\rm ex})_{\rm total}}~ {\rm ex... ...frac{hc}{k_{\rm B}T_{\rm ex}}(T'_{\rm e}+G'(v')+F'(K'))\right]$$ (A.9)

for the total number N₀ of ${\rm N_{2}}$ molecules in all energy levels, electronic multiplicity d, partition function $Q(T_{\rm ex})$, Planck constant h, Boltzmann constant $k_{\rm B}$, the velocity of light c, the wavenumber $\nu$ in Eq. (A.1), and the electronic excitation temperature $T_{\rm ex}$ of ${\rm N_{2}}$ (Arnold et al. 1969). Here, we assume vibrational and rotational excitation temperatures at the same value for $T_{\rm ex}$. Our model employed the Einstein coefficients A_v'v'' listed in Table A.1, which were calculated by integrating $\int \psi_v'^* R_{\rm e}(r) \psi_v''^*{\rm d}r$ where $\psi_v'^* \psi_v''^*$ are weighting functions and $R_{\rm e}(r)$ is the transition moment function (Forrest et al. 1992).

The electronic multiplicity d is given by $d = \delta$ (2S+1) where $\delta$ and S are the lambda doubling factor and quantum number of the resultant spin of ${\rm N_{2}}$ molecules respectively. For the upper electronic state of the first positive band $\delta$ and S are 2 and 1 respectively (e.g. Herzberg 1950). The approximated partition function Q (Drellishak 1964; Stupochenko et al. 1961) of diatomic molecules in all electronic states is calculated with

$$Q(T_{\rm ex})_{\rm total} = \sum^{n}_{i=1} \left[d_i {\rm exp... ...rac{hcG(v_j)} {k_{\rm B}T{_{\rm ex}}}\right) \right) \right]_i$$ (A.10)

where i is the electronic state number and $v_{\rm jmax}$ the cut-off vibrational quantum number (Arnold et al. 1969). As a first step, we take the transition of ${\rm B^{3}\Pi _g - A^{3}\Sigma ^{+}_{u}}$ (= $Q(T_{\rm ex})_{\rm B-A}$) into our fitting model for the simplicity, not $Q(T_{\rm ex})_{\rm total}$ that includes the transition of all electronic states. It lets us have the total number of ${\rm N_{2}}$ in the electronic state B - A (n = 1 in Eq. (A.10)) and the excitation temperature $8010\pm 260$ K. With the excitation temperature, the ratio of over twenty - seven electronic states $Q(T_{\rm ex})_{\rm total}$ compiled by Lofthus & Krupenie (1977) relative to $Q(T_{\rm ex})_{\rm B-A}$ is roughly calculated to be $Q(T_{\rm ex})_{\rm total}$ / $Q(T_{\rm ex})_{\rm B-A}$ $\sim$20 by focusing on electronic energy states. Therefore, the total number of ${\rm N_{2}}$ in all electronic energy states is found to be $6.4 \pm 2.4\times 10^{11}$  ${\rm cm}^{-3}$.

Appendix B

Table B.1: Metallic and nonmetallic emission lines in the visual - near IR wavelength range. Observed elements and their line positions, catalogued line position, the Einstein A coefficient, energy $E_{\rm l}$ and $E_{\rm u}$ respectively of the lower and upper levels, configurations, and statistical weights $g_{\rm l}$ and $g_{\rm u}$ of the lower and upper levels respectively.