A&A 473, 357-368 (2007)
DOI: 10.1051/0004-6361:20077412
R. Ouyed - D. Leahy - B. Niebergal
Department of Physics and Astronomy, University of Calgary, 2500 University Drive NW, Calgary, Alberta, T2N 1N4, Canada
Received 5 March 2007 / Accepted 24 July 2007
Abstract
We explore the formation and evolution of debris ejected around quark stars in the Quark Nova scenario,
and the application to Soft Gamma-ray Repeaters (SGRs) and Anomolous X-ray Pulsars (AXPs).
If an isolated neutron star explodes as a Quark Nova, an iron-rich shell of degenerate matter
forms from its crust.
This model can account for many of the observed features of SGRs
and AXPs such as: (i) the two types of bursts (giant and regular);
(ii) the spin-up and spin-down episodes during and following the bursts
with associated increases in ![]() ;
(iii) the energetics of the boxing
day burst, SGR1806+20; (iv) the presence of an iron line as observed in SGR1900+14;
(v) the correlation between the far-infrared and the X-ray fluxes during the bursting episode
and the quiescent phase; (vi) the hard X-ray component observed in SGRs
during the giant bursts, and (vii) the discrepancy between the ages of SGRs/AXPs and
their supernova remnants.
We also find a natural evolutionary relationship between SGRs and AXPs in our model
which predicts that the youngest SGRs/AXPs are the most likely to exhibit strong bursting.
Many features of X-ray Dim Isolated Neutron stars (XDINs) are also accounted for in our model
such as, (i) the two-component blackbody spectra; (ii) the absorption lines around
300 eV; and (iii) the excess optical emission.
;
(iii) the energetics of the boxing
day burst, SGR1806+20; (iv) the presence of an iron line as observed in SGR1900+14;
(v) the correlation between the far-infrared and the X-ray fluxes during the bursting episode
and the quiescent phase; (vi) the hard X-ray component observed in SGRs
during the giant bursts, and (vii) the discrepancy between the ages of SGRs/AXPs and
their supernova remnants.
We also find a natural evolutionary relationship between SGRs and AXPs in our model
which predicts that the youngest SGRs/AXPs are the most likely to exhibit strong bursting.
Many features of X-ray Dim Isolated Neutron stars (XDINs) are also accounted for in our model
such as, (i) the two-component blackbody spectra; (ii) the absorption lines around
300 eV; and (iii) the excess optical emission.
Key words: dense matter - accretion, accretion disks - stars: pulsars: general - X-rays: bursts - elementary particles
Soft ![]() -ray Repeaters (SGRs) are sources of recurrent,
short (
-ray Repeaters (SGRs) are sources of recurrent,
short (
![]() ), intense (
), intense (
![]() )
bursts of
)
bursts of ![]() -ray emission with a soft energy spectrum.
The normal patterns of SGRs are intense activity periods
which can last weeks or months, separated by quiescent phases
lasting years or decades.
The three most intense SGR bursts ever recorded
were the 5 March 1979 giant flare of SGR 0526-66
(Mazets et al. 1979), the similar 28 August 1998 giant
flare of SGR 1900+14 and the 27 December 2004 burst (SGR 1806-20).
AXPs are similar in nature but with a somewhat weaker intensities and
no recurrent bursting.
Several SGRs/AXPs have been found to be X-ray pulsars with
unusually high spin-down rates of
-ray emission with a soft energy spectrum.
The normal patterns of SGRs are intense activity periods
which can last weeks or months, separated by quiescent phases
lasting years or decades.
The three most intense SGR bursts ever recorded
were the 5 March 1979 giant flare of SGR 0526-66
(Mazets et al. 1979), the similar 28 August 1998 giant
flare of SGR 1900+14 and the 27 December 2004 burst (SGR 1806-20).
AXPs are similar in nature but with a somewhat weaker intensities and
no recurrent bursting.
Several SGRs/AXPs have been found to be X-ray pulsars with
unusually high spin-down rates of
![]() s-1,
usually attributed to magnetic braking caused by a super-strong
magnetic field.
s-1,
usually attributed to magnetic braking caused by a super-strong
magnetic field.
Occasionally SGRs enter into active episodes producing many short X-ray bursts;
extremely rarely (about once per 50 years per source), SGRs emit giant flares,
events with total energies at least 1000 times higher than their typical bursts.
Current theory explains this energy release as the result of a catastrophic
reconfiguration of a magnetar's magnetic field.
Magnetars are neutron stars whose X-ray emission are powered by ultrastrong magnetic fields,
![]() G. Although the magnetar model has had successes, in this paper
we present an alternative model which addresses outstanding questions.
G. Although the magnetar model has had successes, in this paper
we present an alternative model which addresses outstanding questions.
We explore these issues within the quark-nova (QN) scenario (Ouyed et al. 2002; Ouyed et al. 2004; Keranen et al. 2005). In our previous studies we have suggested that CFL (color-flavor locked) quark stars could be responsible for the activity of SGRs and AXPs (Ouyed et al. 2005; Niebergal et al. 2006), and in this paper we extend the QN model by studying in more details the evolution of the QN ejecta (as first discussed in Keränen & Ouyed 2003).
Following the QN explosion we show
that a high metalicity shell can form from the neutron star crust![]() .
If this matter gains sufficient angular momentum from the central quark
star it can form a torus-like structure via the propeller mechanism, which is discussed
in the second paper in this series (Ouyed et al. 2006; hereafter refered to as Paper II).
However if it does not, as we discuss in this paper, there is instead a
thin corotating shell suspended by the quark star's magnetic field pressure.
Because the quark star is in a superconducting state it's magnetic field
decay is coupled to its period in a manner prescribed by Niebergal et al. (2006),
such that as the field decays the shell will drift closer to the star.
This movement will shift sections of the shell above the line of neutrality,
loosely defined as the polar angle (measured from the equator) above which
the magnetic field vector is sufficiently parallel to the gravity vector to allow
material to break off from the shell, and fall into the star. Upon collision with
the star the pieces of the shell are instantly converted to CFL quark matter
(described by Lugones & Horvath 2002),
where excess energy is released as high-energy radiation (Ouyed et al. 2004).
We propose this as the mechanism responsible for SGR and AXP bursting activity,
and also show that SGRs and AXPs differ primarily by age. Another
class of objects are also explored, namely X-ray Dim Isolated Neutron stars (XDINs; e.g. Haberl 2004),
and we find that these may have evolved from SGRs/AXPs.
.
If this matter gains sufficient angular momentum from the central quark
star it can form a torus-like structure via the propeller mechanism, which is discussed
in the second paper in this series (Ouyed et al. 2006; hereafter refered to as Paper II).
However if it does not, as we discuss in this paper, there is instead a
thin corotating shell suspended by the quark star's magnetic field pressure.
Because the quark star is in a superconducting state it's magnetic field
decay is coupled to its period in a manner prescribed by Niebergal et al. (2006),
such that as the field decays the shell will drift closer to the star.
This movement will shift sections of the shell above the line of neutrality,
loosely defined as the polar angle (measured from the equator) above which
the magnetic field vector is sufficiently parallel to the gravity vector to allow
material to break off from the shell, and fall into the star. Upon collision with
the star the pieces of the shell are instantly converted to CFL quark matter
(described by Lugones & Horvath 2002),
where excess energy is released as high-energy radiation (Ouyed et al. 2004).
We propose this as the mechanism responsible for SGR and AXP bursting activity,
and also show that SGRs and AXPs differ primarily by age. Another
class of objects are also explored, namely X-ray Dim Isolated Neutron stars (XDINs; e.g. Haberl 2004),
and we find that these may have evolved from SGRs/AXPs.
This paper is presented as follows. In Sect. 2 we review the concepts of a quark-nova and the expansion/evolution of the ejected material into a shell. Section 3 contains discussions on the geometry of the resulting shell and its self-similar behaviour in time, leading to pieces of the shell breaking off. The subsequent high-energy bursting from these pieces falling into the quark star is then described in Sect. 4, along with methods for estimating the age of SGRs/AXPs. In Sect. 5 the quiescent phase of SGRs/AXPs is discussed in the context of our model, where a simple relation between luminosity and spin-down rate is derived. The changes in period and period derivative observed during bursts are then discussed within the framework of our model in Sect. 6. Section 7 contains case studies for specific SGRs (1806-20 and 1900+14), along with explanations for the presence of an iron line during bursts, correlated X-ray to infrared flux ratio, and the hard spectrum seen in giant flares. We then summarize in Sect. 7.5 some outstanding issues in the current understanding of SGRs/AXPs, and show how our model can provide explanations. Finally in Sect. 8, we discuss XDINs and show how many features are readily explained using our model. We then conclude in Sect. 9.
In the quark-nova (QN) scenario, the core of a neutron star (NS) shrinks to a stable, compact, quark object before the conversion of the entire star to (u, d, s) matter. By contracting, and physically separating from the overlaying material (hadronic envelope which is mostly made of crust material), the core drives the collapse (free-fall) of the overlaying matter leading to both gravitational and phase transition energy release as high as 1053 ergs in the form of neutrinos. The result is a quark star in the Color-Flavor Locked (CFL) superconducting phase, surrounded by an ejected shell. Although it has been shown that pure CFL matter is rigorously electrically neutral (Rajagopal & Wilczek 2001), other work (Usov 2004, and references therein) indicates that a thin crust is allowed around a quark star due to surface depletion of strange quarks. In our model we have assumed no depletion of strange quarks, which implies a bare quark star.
In the CFL phase there are a total of nine combinations between the gluons and the photon with eight of these combinations subject to the Meissner effect. The only one that does not suffer the Meissner effect involves a combination of electromagnetism and a U(1) subgroup of the color interactions (e.g. Ferrer et al. 2005). In other words the magnetic field will penetrate some phases of the color field but not others. Unfortunately, the relevant calculations are done in effective models of QCD which cannot accurately handle the details of the mixing and the corresponding back reaction of the quarks. Assumptions had to be made (e.g. Meissner effect) in order to proceed with our astrophysical model which implies that we are ignoring the one component that penetrates the superconductor. In the CFL quark star, given our basic assumptions, the magnetic field is contained in the vortex array so the internal field is uniform and equal to the surface field.
The QN ejecta consists mainly of the neutron star's metal-rich
outer layers heated by neutrino bursts. It was shown that up to
![]() can
be released during the QN (Keränen et al. 2005).
Thus our model proposes a high density, metal-rich ejecta surrounding
a superconducting quark star.
can
be released during the QN (Keränen et al. 2005).
Thus our model proposes a high density, metal-rich ejecta surrounding
a superconducting quark star.
Within our model there are four possible scenarios as to the outcome of the ejecta. First, if the ejecta is very light then it will become gravitationally unbound from the quark star, where the r-process begins creating heavier elements (Jaikumar et al. 2006). Second, if the ejecta is too heavy it will fall back into the quark star releasing tremendous amounts of energy. This we propose could lead to explosive events reminiscent of short gamma-ray bursts, which we are currently exploring. Third, is the case where the ejecta mass is such that it can be suspended above the surface by the quark star's magnetic pressure. Fourth, the ejecta was formed with enough angular momentum to move into a Keplerian orbit. The third case is discussed in this paper, whereas the fourth is discussed in the second paper of this series.
We consider the dynamics of the shell (of mass
![]() )
ejected during the QN.
If the shell's outward momentum is not too large, the interplay
between gravity and the QS's magnetic field is dominant.
Thus, as the highly conducting shell expands spherically
outwards, an electromotive (
)
ejected during the QN.
If the shell's outward momentum is not too large, the interplay
between gravity and the QS's magnetic field is dominant.
Thus, as the highly conducting shell expands spherically
outwards, an electromotive (
![]() )
force is induced
to oppose its motion, causing it to continuously decelerate
)
force is induced
to oppose its motion, causing it to continuously decelerate![]() .
The natural oscillatory motion created by the magnetic
pressure gradient and gravity is resultingly damped out,
resulting in the ejecta finding an equilibrium radius
where the forces due to the magnetic pressure gradient and gravity
are in balance. This equilibrium radius is then given by,
.
The natural oscillatory motion created by the magnetic
pressure gradient and gravity is resultingly damped out,
resulting in the ejecta finding an equilibrium radius
where the forces due to the magnetic pressure gradient and gravity
are in balance. This equilibrium radius is then given by,
For this equilibrium situation to be achieved the mass and initial velocity of the shell are confined to a somewhat narrow range of values. Although the mass of the shell is self-consistent with previous studies of neutron star crust masses (discussed below), the initial velocity is not similarly constrained. As such, we assume it can take on a range of values, with the small initial velocity case corresponding to the work presented in this paper, and the high velocity case is left for the second paper in this series. We feel that this dichotomy is physical, and explains some observed AXP features well.
Recent work studying natural mechanism of magnetic field amplification in quark matter (just before or during the onset of superconductivity; Iwazaki 2005), shows that 1015 G magnetic fields are readily achievable. This amplification can occur in quark matter due to the response of quarks to the spontaneous magnetization of the gluons. In contrast, for the magnetar model, the sole proposed mechanism for generating 1015 G fields requires millisecond proto-neutron stars. This seems to be challenged by recent observations (Allen & Hovarth 2006).
Thus, Eq. (1) implies that for magnetic fields in the range of 1014-
![]() ,
the maximum mass of the shell cannot exceed 10-8-
,
the maximum mass of the shell cannot exceed 10-8-
![]() .
A higher shell mass translates into
.
A higher shell mass translates into
![]() ,
meaning that the magnetic field is
not sufficiently strong to stop the shell from promptly falling back onto the star.
This situation is very possible but not considered in this paper, as it is left for future work.
,
meaning that the magnetic field is
not sufficiently strong to stop the shell from promptly falling back onto the star.
This situation is very possible but not considered in this paper, as it is left for future work.
The shell's size is determined by the NS crust density profile (Datta et al. 1995),
and is of the order of (0.012-
![]() corresponding to shell masses
of the order of (10-8-
corresponding to shell masses
of the order of (10-8-
![]() for densities of
for densities of
![]() -
-
![]() g/cc. We note that if degenerate,
the shell will always be in relativistic degeneracy since
the densities are above
g/cc. We note that if degenerate,
the shell will always be in relativistic degeneracy since
the densities are above
![]() g/cc (Lang 1974). Here,
g/cc (Lang 1974). Here,
![]() is the
mean mass per electron and is taken to be
is the
mean mass per electron and is taken to be
![]() since the
shell's maximum density is below the neutron drip density,
since the
shell's maximum density is below the neutron drip density, ![]()
![]() g cm-3 .
g cm-3 .
The transition from Fermi-Dirac to Boltzmann statistics occurs at the degeneracy temperature
![]() for a non-relativistic gas and
for a non-relativistic gas and
![]() for a relativistic gas (e.g. Lang, p. 253).
So, for the shell to be born degenerate at 10 MeV, it implies a minimum density
of
for a relativistic gas (e.g. Lang, p. 253).
So, for the shell to be born degenerate at 10 MeV, it implies a minimum density
of ![]() 1010 g/cc which translates to an ejected mass of
1010 g/cc which translates to an ejected mass of ![]()
![]() .
We note that even if the shell density at birth is less than
.
We note that even if the shell density at birth is less than ![]() 1010 g/cc,
(blackbody) cooling during the expansion of the ejecta to
1010 g/cc,
(blackbody) cooling during the expansion of the ejecta to ![]() results in a shell
temperature of less than 1 MeV, thus, yielding a degenerate shell.
results in a shell
temperature of less than 1 MeV, thus, yielding a degenerate shell.
Once the shell reaches the magnetic radius ![]() ,
it will have expanded
to a thickness of,
,
it will have expanded
to a thickness of,
![]() ,
such that it satisfies hydrostatic equilibrium.
Using the relativistic degenerate equation-of-state (
,
such that it satisfies hydrostatic equilibrium.
Using the relativistic degenerate equation-of-state (
![]() where
where
![]() ),
the width of the shell, positioned at
),
the width of the shell, positioned at ![]() ,
can be calculated to be,
,
can be calculated to be,
The internal energy of the expanding ejecta is
![]() where
where
![]() ,
is the total number of electrons.
The Fermi energy in this case is
,
is the total number of electrons.
The Fermi energy in this case is
![]() (e.g. Pathria pg. 200).
As a result of the heating of the electrons, the optically thick shell will radiate
approximately as a blackbody,
(e.g. Pathria pg. 200).
As a result of the heating of the electrons, the optically thick shell will radiate
approximately as a blackbody,
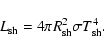 |
(4) |
We have not
investigated the fate of this energy release, whether it is absorbed by adiabatic
expansion losses or radiated.
What is crucial to our model is the fact that the shell remains
degenerate at ![]() which is guaranteed by hydrostatic equilibrium.
which is guaranteed by hydrostatic equilibrium.
For a magnetic radius, ![]() ,
larger than the corotation radius the propeller
will take effect (Schwartzman 1970; Illarionov & Sunyaev 1975),
deflecting the QN shell into a torus on the equatorial plane.
Using an angular momentum conservation argument, we can estimate the location
of such a torus by writing
,
larger than the corotation radius the propeller
will take effect (Schwartzman 1970; Illarionov & Sunyaev 1975),
deflecting the QN shell into a torus on the equatorial plane.
Using an angular momentum conservation argument, we can estimate the location
of such a torus by writing
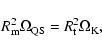 |
(6) |
However, in order to actually form a torus we require enough angular momentum
transfer to guarantee
![]() .
This translates into an upper limit
on the initial period of,
.
This translates into an upper limit
on the initial period of,
The area of a shell at the magnetic equilibrium radius, ![]() ,
is
,
is
![]() ,
where
,
where
![]() is the polar angle (measured from the equator) and defines the line of neutrality.
In other words, for
is the polar angle (measured from the equator) and defines the line of neutrality.
In other words, for
![]() the shell material is free to
"slip'' along the magnetic field lines onto the star, whereas for
the shell material is free to
"slip'' along the magnetic field lines onto the star, whereas for
![]() the
shell material is suspended by magnetic pressure.
Thus, the geometry is such that there is a thin shell at the equator subtending an angle of
the
shell material is suspended by magnetic pressure.
Thus, the geometry is such that there is a thin shell at the equator subtending an angle of
![]() ,
and empty regions at the poles. The shell is shaped in the star's distorted
magnetic dipole with an inward bulge at the equator, and the radius of the shell at the
equator, under hydrostatic balance, can be shown to be roughly half that at
,
and empty regions at the poles. The shell is shaped in the star's distorted
magnetic dipole with an inward bulge at the equator, and the radius of the shell at the
equator, under hydrostatic balance, can be shown to be roughly half that at
![]() .
.
The radius of the shell, ![]() ,
is proportional to the magnetic field strength
(i.e. Eq. (1)), so we use the magnetic field decay prescribed by
Niebergal et al. (2006) to calculate the radius in time. This is because the quark
star itself is in the superconducting phase, implying that vortex expulsion couples
field decay and period evolution.
,
is proportional to the magnetic field strength
(i.e. Eq. (1)), so we use the magnetic field decay prescribed by
Niebergal et al. (2006) to calculate the radius in time. This is because the quark
star itself is in the superconducting phase, implying that vortex expulsion couples
field decay and period evolution.
After a characteristic time, ![]() (as defined by Eq. (4) in Niebergal et al. 2006),
the shell will respond to the decaying field by moving towards the
star, resulting in a new equilibrium radius.
During this movement, sections of the shell will be shifted above the
line of neutrality,
(as defined by Eq. (4) in Niebergal et al. 2006),
the shell will respond to the decaying field by moving towards the
star, resulting in a new equilibrium radius.
During this movement, sections of the shell will be shifted above the
line of neutrality,
![]() ,
where they will be broken off
and fall into the star along the magnetic field lines. Upon colliding with
the quark star these shell pieces will be converted immediately to CFL quark matter,
releasing excess energy in the form of radiation, which in our model is an SGR/AXP burst.
We then have a new state, n+1, where the shell has moved towards the star, lost mass,
and is now sitting at radius
,
where they will be broken off
and fall into the star along the magnetic field lines. Upon colliding with
the quark star these shell pieces will be converted immediately to CFL quark matter,
releasing excess energy in the form of radiation, which in our model is an SGR/AXP burst.
We then have a new state, n+1, where the shell has moved towards the star, lost mass,
and is now sitting at radius
![]() with a mass
with a mass
![]() .
.
The new characteristic decay time, period of rotation, period derivative,
and magnetic field are respectively,
| (14) |
So after a time
![]() ,
the magnetic field decays and the shell
originally sitting at
,
the magnetic field decays and the shell
originally sitting at
![]() moves in closer to the star.
Now by keeping the mass of the shell constant as it slowly drifts in from
moves in closer to the star.
Now by keeping the mass of the shell constant as it slowly drifts in from ![]() to an inner
radius
to an inner
radius
![]() and applying Eq. (1) we can write,
and applying Eq. (1) we can write,
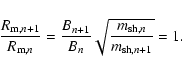 |
(17) |
In our model, AXPs are merely older versions of SGRs, thus one would expect SGR bursts to be more intense and frequent. As can be seen in Table 1 (where the objects are in order of decreasing estimated age), there is seemingly a decreasing trend in burst intensity and frequency as one moves from younger to older objects. It may be that both types of bursts have this trend, however, we do not feel there is enough events to draw any conclusions. This is a potential test for our model.
The magnetic energy due to field decay is released continuously over
a long timescale (thousands of years) and gives the steady x-ray luminosity
of SGRs and AXPs (see Sect. 5). What is
important and unique about the shell (i.e. the accretion energy) is that the energy is released
in bursts, and the shell sitting
at ![]() offers a natural mechanism/torque for sudden changes
in period derivative.
offers a natural mechanism/torque for sudden changes
in period derivative.
After time
![]() ,
the magnetic field decays substantially
and the entire shell moves in to
,
the magnetic field decays substantially
and the entire shell moves in to
![]() .
A larger
.
A larger ![]() means the shell moves closer to the star,
causing larger sections to be shifted above the line of neutrality,
implying larger bursts
means the shell moves closer to the star,
causing larger sections to be shifted above the line of neutrality,
implying larger bursts![]() .
.
Another possible scenario is that giant bursts are due to global instabilities like Rayleigh-Taylor while regular bursts are due to chunks breaking-off the edge of the shell. We assume that the Rayleigh-Taylor instability does not act due to the long timescale for magnetic penetration of the conducting shell (see Sect. 4.1 in Paper II). What is presented below is intended to present the overall scenario and follow-up work (i.e. numerical simulations) is necessary to investigate the effects global instabilities might have on this simplified picture.
If the time needed for the shell to move in sufficiently to have pieces broken off
is roughly equal to the characteristic field decay time, then ![]() ,
and
,
and ![]() 20%
of the shell's mass is lost during the burst.
According to Eq. (20), the corresponding energy release is,
20%
of the shell's mass is lost during the burst.
According to Eq. (20), the corresponding energy release is,
![\begin{figure}
\par\includegraphics[width=13cm,clip]{7412fig1.eps}
\end{figure}](/articles/aa/full/2007/38/aa7412-07/Timg116.gif) |
Figure 1:
The upper panel is a P- |
| Open with DEXTER | |
If pieces of the shell are able to break off as the shell
moves in by only a small amount, then
![]() .
This corresponds to small pieces of the shell falling into the star and,
in our model, leads to regular-sized bursts.
This process can be interpreted as small oscillations around
.
This corresponds to small pieces of the shell falling into the star and,
in our model, leads to regular-sized bursts.
This process can be interpreted as small oscillations around ![]() consistent with small fractional mass-loss episodes by the shell.
Observationaly, regular bursts are known to follow a power-law distribution in energies
which in our model would be due to a power-law distribution in
consistent with small fractional mass-loss episodes by the shell.
Observationaly, regular bursts are known to follow a power-law distribution in energies
which in our model would be due to a power-law distribution in ![]() .
Clearly, the detailed mechanism which determines
.
Clearly, the detailed mechanism which determines ![]() would be different
for giant bursts and regular bursts, and would require numerical simulations to understand.
would be different
for giant bursts and regular bursts, and would require numerical simulations to understand.
For
![]() ,
Eq. (18) approximates to
,
Eq. (18) approximates to
![]() which yields burst energies of,
which yields burst energies of,
Thus, in our model the difference between regular and giant bursts is due to the size of piece that breaks off the shell. Although the size is of a stochastic nature, we expect younger objects (i.e. the SGRs) to have a more unstable shell, resulting in more large pieces breaking off, causing more frequent and intense bursts. For older objects (i.e. the AXPs) the shell becomes more stable with age resulting in weaker, less frequent, bursts.
From Eqs. (10) and (12), the magnetic
field is related to the period and period derivative by,
To determine the exact age of AXPs/SGRs in our model, one would need to know the entire
bursting history of the object which is impossible.
For a real situation the burst sizes are variable implying a different ![]() for each burst. So to approximate the age in the simplest case
(when
for each burst. So to approximate the age in the simplest case
(when ![]() is constant over time on average), the age elapsed since the QN is,
is constant over time on average), the age elapsed since the QN is,
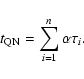 |
(27) |
One may be tempted to use the age of the associated parent supernova remnant to estime the age of the SGR/AXP, but in our model these ages are neccesarily different. This is due to the time required for a neutron star to reach quark deconfinement densities (Staff et al. 2006), as well as the time needed for strange quark nucleation (i.e. u,d to u,d,s) to occur (Bombaci et al. 2004). Together these delays can easily add up to the age difference between SGRs/AXPs and their supernova remnants.
The X-ray luminosity during the quiescent phase of SGRs/AXPs in our model
is due to vortex expulsion from spin-down. The magnetic field contained within
the vortices is also expelled, and the subsequent magnetic reconnection leads
to the production of X-rays. From Eq. (22) in Ouyed et al. (2004) and
Eqs. (10)-(12), the luminosty emitted from this process is,
The scatter in the AXPs/SGRs data can be explained within our model
by considerations of shell geometry and viewing angle.
More specifically, any X-rays being emitted from the star's surface towards the
solid angle filled by the shell (
![]() )
will be affected
due to absorption by the shell.
X-rays are then able to escape from an open area at the poles with a solid angle on the order of
)
will be affected
due to absorption by the shell.
X-rays are then able to escape from an open area at the poles with a solid angle on the order of
![]() .
Because we statistically observe viewing angles equally from all directions, this would imply
an average (geometrical mean) lumimosity of
.
Because we statistically observe viewing angles equally from all directions, this would imply
an average (geometrical mean) lumimosity of
![]() ,
assuming
,
assuming
![]() .
This is plotted by the dotted line
in the lower panel of Fig. 1. Thus, the scatter in data is a
combination of X-ray production efficiency and viewing angle effects.
The two "outliers'' namely, AXP 1E2259+586 and AXP 4U0142+615
can be explained as those AXPs/SGRs born in the
propeller regime so that they are surrounded by a degenerate torus instead
of a shell, and are discussed in more detail in Paper II.
.
This is plotted by the dotted line
in the lower panel of Fig. 1. Thus, the scatter in data is a
combination of X-ray production efficiency and viewing angle effects.
The two "outliers'' namely, AXP 1E2259+586 and AXP 4U0142+615
can be explained as those AXPs/SGRs born in the
propeller regime so that they are surrounded by a degenerate torus instead
of a shell, and are discussed in more detail in Paper II.
Our model provides an explanation to the two component blackbody spectrum
that may be seen in SGRs/AXPs (i.e. Israel 2002).
This is realized by considering the blackbody temperature as set by the X-ray continuum luminosity,
![]() ,
to be
,
to be![]()
The effective shell temperature in our model is also
set by the X-ray continuum luminosity,
![]() ,
and is
,
and is
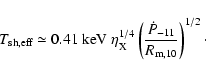 |
(32) |
Whether or not the blackbody component from the shell could actually be observed or not hasn't been considered. If it can not, then the magnetic field strengths around CFL quark stars is still at a magnitude that can produce the synchrotron break (i.e. blackbody plus power law) that is usually assumed for SGRs/AXPs. We only assert that if the blackbody emission from the shell could be observed, then its temperature is such that it correlates well with a two-component blackbody spectrum model.
Angular momentum exchange between the shell and the star occurs during the shell's inward and outward movements, and would manifest itself as changes in rotational period and period derivative during bursts. We start with the inward drift where the moment of inertia of the star decreases, causing it to spin-up.
In our model the inward shell drift occurs while the vortex (i.e. magnetic flux) expulsion
mechanism, as discussed in Niebergal et al. (2006), is coupling the spin period and
field decay as described in Eqs. (9)-(12).
The spin-up torque from a decreasing moment of inertia occurs slowly during
the magnetic field decay timescale over time
![]() ,
and is negligible compared to the spin-down due to vortex expulsion.
,
and is negligible compared to the spin-down due to vortex expulsion.
The shell eventually reaches an inner radius where it is unstable in the magnetic field
geometry, and pieces start to break off above
![]() .
As the pieces fall in along field lines to the polar regions and collide with the star,
angular momentum is transferred.
This transfer and the change in moment of inertia,
.
As the pieces fall in along field lines to the polar regions and collide with the star,
angular momentum is transferred.
This transfer and the change in moment of inertia, ![]() ,
as we show below would correspond to a star spinning-up during bursts (i.e. accretion
of chunks)
,
as we show below would correspond to a star spinning-up during bursts (i.e. accretion
of chunks)![]() .
The change in moment of inertia from the increase in mass and radius of the star is given by,
.
The change in moment of inertia from the increase in mass and radius of the star is given by,
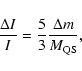 |
(33) |
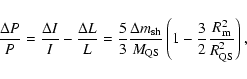 |
(34) |
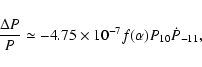 |
(36) |
If the accretion occurs during a time interval,
![]() ,
the spin-up rate,
,
the spin-up rate,
![]() ,
can be estimated by dividing both sides of Eq. (35) by
,
can be estimated by dividing both sides of Eq. (35) by
![]() .
By noting that
.
By noting that
![]() we arrive at
we arrive at
Following the accretion events, during the fast shell rebound,
angular momentum is transfered from the star to the shell to keep it
co-rotating, resulting in an increase in the spin-down rate of the star.
The magnetic coupling between the star and the shell implies that the
star will lose angular momentum and spin-down. As the star moves outward
from radius
![]() back to
back to ![]() ,
conservation of angular momentum of the star/shell system implies
,
conservation of angular momentum of the star/shell system implies
![]() .
That is
.
That is
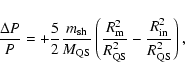 |
(38) |
Observationally, an increase in spin-down has been seen to last for ![]() 18 days,
as in the case of AXP1E2259, and
18 days,
as in the case of AXP1E2259, and ![]() 80 days for SGR1900+14.
In our model this is readily explained by the heating of the degenerate shell by the burst,
and the subsequent release of a portion of it's atmosphere.
Because a thin layer on the shell's surface is in the non-degenerate phase,
a fraction of it is blown away via the propeller mechanism,
removing angular momentum from the system over time.
80 days for SGR1900+14.
In our model this is readily explained by the heating of the degenerate shell by the burst,
and the subsequent release of a portion of it's atmosphere.
Because a thin layer on the shell's surface is in the non-degenerate phase,
a fraction of it is blown away via the propeller mechanism,
removing angular momentum from the system over time.
To determine the amount of atmosphere present on the shell during the quiescent phase,
we consider the critical density,
![]() ,
of the shell to ensure degeneracy which is found by setting
,
of the shell to ensure degeneracy which is found by setting
![]() ,
where the density is written in units of
,
where the density is written in units of
![]() .
So the gas will be non-degenerate below densities of,
.
So the gas will be non-degenerate below densities of,
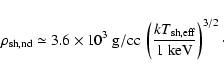 |
(40) |
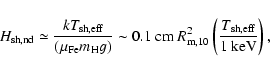 |
(41) |
Following a bright burst, with luminosity
![]() (in units of
(in units of
![]() ),
the shell gets reheated to temperatures of the order
),
the shell gets reheated to temperatures of the order
![]() .
The corresponding atmospheric (non-degenerate) mass in terms of the burst energy
(in units of
.
The corresponding atmospheric (non-degenerate) mass in terms of the burst energy
(in units of
![]() ), is then
), is then
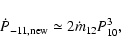 |
(44) |
The change in period due to mass lost at the light cylinder is also written as,
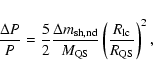 |
(45) |
Because the shell cools, there is decreasing amounts of matter available to drive the increased
spin-down rate. Thus this new rate is temporary and the timescale for it to decay back to the previous rate
can be estimated by,
![]() ,
or,
,
or,
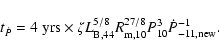 |
(47) |
The most recent and brightest giant flare came from SGR 1806-20 on Dec. 27, 2004.
This flare lasted about 5 min and had a peak luminosity of about
![]() .
For a distance to SGR 1806-20 of 15 kpc,
it is estimated that an (isotropic equivalent) energy release of
.
For a distance to SGR 1806-20 of 15 kpc,
it is estimated that an (isotropic equivalent) energy release of
![]() erg occured in the spike, and
erg occured in the spike, and
![]() erg in the tail.
erg in the tail.
In our model the energy is readily accounted for. The observed P and ![]() imply (from Eq. (25)) that
imply (from Eq. (25)) that
![]() G,
which translates to an energy of
G,
which translates to an energy of
![]() erg for
erg for ![]() and
and
![]() km (see Eq. (20)).
km (see Eq. (20)).
In the year leading up to the SGR 1806-20 giant flare,
well-sampled X-ray monitoring observations of the source with the Rossi X-ray Timing
Explorer (RXTE) indicated that it was also entering a very active phase, emitting more
frequent and intense bursts as well as showing enhanced persistent X-ray emission which was,
a prelude to the unprecedented giant flare.
In our model, this prelude would correspond to increasing amounts of shell
pieces breaking off above
![]() as the shell moves in rapidly
closer to the star. This situation is likely only when the quark star's magnetic field
is strong such that it is decaying quickly, implying the object is young,
which is the case with SGR 1806-20. Furthermore, because
as the shell moves in rapidly
closer to the star. This situation is likely only when the quark star's magnetic field
is strong such that it is decaying quickly, implying the object is young,
which is the case with SGR 1806-20. Furthermore, because ![]()
![]() of the shell's
mass was lost in this giant flare, the leftover smaller shell, once re-adjusted
to
of the shell's
mass was lost in this giant flare, the leftover smaller shell, once re-adjusted
to ![]() following the event, will have less capability to produce flares of the same magnitude
as the previous one (see Eq. (21)).
following the event, will have less capability to produce flares of the same magnitude
as the previous one (see Eq. (21)).
The sharp initial rise of the main spike
in the boxing day flare was of the order of 1 ms (Palmer et al. 2005).
In our model, a lower limit on the rise time,
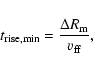 |
(48) |
For regular bursts (
![]() )
we find
)
we find
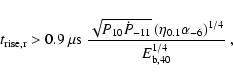 |
(50) |
The rotation period has been studied in detail for SGR 1900+14 during bursting
(i.e. Woods et al. 1999; and Palmer 2002), which allows us to test these features of our model.
The increase in period as given in our model (Eq. 46) following the burst is,
![]() using observed values for energy and period. Also, observed values for period and the new period derivative following the August 27th burst
give a mass loss rate of
using observed values for energy and period. Also, observed values for period and the new period derivative following the August 27th burst
give a mass loss rate of
![]() ,
and an upper limit for the
recovery time of
,
and an upper limit for the
recovery time of
![]() .
.
The magnetic equilibrium radius was estimated to be
![]() due to the presence
of iron line emission (Strohmayer & Imbrahim 2000) in which case for
due to the presence
of iron line emission (Strohmayer & Imbrahim 2000) in which case for
![]() we get
we get
![]() and
and
![]() days.
However as discussed in Sect. 7.2.1 for an ionized atmosphere, redshift
correction could move the radius to
days.
However as discussed in Sect. 7.2.1 for an ionized atmosphere, redshift
correction could move the radius to
![]() in which case a
in which case a
![]() gives
gives
![]() and
and
![]() days.
This is in good agreement with what can be inferred
from observations.
days.
This is in good agreement with what can be inferred
from observations.
Observations of Fe fluorescence lines in SGR 1900+14 (Strohmayer & Ibrahim 2000)
are a key feature in our quark star model. As discussed in Ouyed et al. (2002) and Keränen et al. (2005),
Fe and heavier metal production in the ejecta is significant during the formation of a quark star.
Strohmayer & Ibrahim state that the distance from the star's surface,
where the emission is created needs to be at least,
![]() ,
to account for the lack of redshift
,
to account for the lack of redshift![]() .
This distance gives an excellent confirmation to our model,
as it corresponds to the distance of the shell which possess an Fe-rich atmosphere.
.
This distance gives an excellent confirmation to our model,
as it corresponds to the distance of the shell which possess an Fe-rich atmosphere.
The atmosphere's column density can be calculated from Eq. (42) to be,
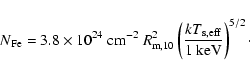 |
(51) |
Another observed feature in both SGRs and AXPs is the X-ray to infrared flux
ratio correlations.
The X-ray flux during the quiescent phase
(induced by the magnetic field decay) and/or during the
bursting phase (from accretion events) can be thermally reprocessed by the
shell into the far infrared. However, the efficiency is
too low due to the small shell size and cannot account for the observed
values of
![]() which are
which are ![]() 150 for
SGRs and
150 for
SGRs and ![]() 1500 for AXPs (e.g. Israel et al. 2003).
1500 for AXPs (e.g. Israel et al. 2003).
Alternatively one expects a much higher infrared flux related to vortex annihilation, which is always present in this model. The mechanism is synchrotron emission from mildly relativistic electrons accelerated by the magnetic reconnection events induced by vortex annihilation (see simulations in Ouyed et al. 2005). The X-rays are from the high energy electrons and the infrared from the low-energy electrons.
For a power-law electron energy distribution
![]() the optically thin synchrotron flux is given by
the optically thin synchrotron flux is given by
![]() (Longair 1992). This implies
(Longair 1992). This implies
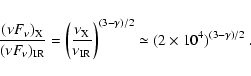 |
(52) |
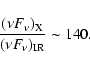 |
(53) |
Three of the four known SGRs have had hard spectrum (with photons
in the MeV energy) giant flares. Before showing how this can be accounted
for in our model, recall that in the case of quark
stars the surface emissivity of photons with energies below
![]()
![]() 23 MeV (
23 MeV (
![]() :
electromagnetic plasma frequency) is strongly suppressed
(Alcock et al. 1986; Chmaj et al. 1991;
Usov 1997). In Vogt et al. (2004) it was shown that
average photon energies in quark stars in the CFL phase
at temperatures T are
:
electromagnetic plasma frequency) is strongly suppressed
(Alcock et al. 1986; Chmaj et al. 1991;
Usov 1997). In Vogt et al. (2004) it was shown that
average photon energies in quark stars in the CFL phase
at temperatures T are ![]() 3T. Therefore, as soon
as the surface temperature of the star cools
below
3T. Therefore, as soon
as the surface temperature of the star cools
below
![]() MeV,
the photon emissivity is highly attenuated.
This is studied in more details in Ouyed et al. (2005)
where it was demonstrated that for temperatures above 7.7 MeV, neutrino cooling is dwarfed by the photons;
i.e., photon emission/cooling dominates as long as the star cools from
its initial temperature T0>7.7 MeV to
MeV,
the photon emissivity is highly attenuated.
This is studied in more details in Ouyed et al. (2005)
where it was demonstrated that for temperatures above 7.7 MeV, neutrino cooling is dwarfed by the photons;
i.e., photon emission/cooling dominates as long as the star cools from
its initial temperature T0>7.7 MeV to
![]() MeV. For temperatures
below 7.7 MeV, cooling is dictated by the slower neutrino processes.
MeV. For temperatures
below 7.7 MeV, cooling is dictated by the slower neutrino processes.
To a first approximation, the increase in the star's temperature,
![]() ,
following the accretion of shell pieces can be written as,
,
following the accretion of shell pieces can be written as,
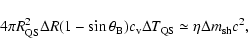 |
(54) |
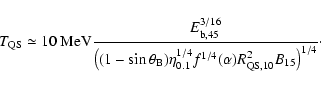 |
(55) |
The escaping photons are thermalized and cool the star at a rate
given by
![]() which leads to a cooling time of,
which leads to a cooling time of,
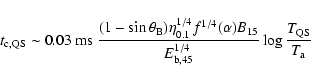 |
(56) |
We summarize this section by attempting to test our model against the open issues related to SGRs/AXPs as discussed in the literature (i.e. Israel 2006). These open issues are enumerated below.
Allen & Hovarth (2004) and Vink & Kuiper (2006) give good evidence in two cases for normal energy supernova shells around an AXP (1E1841-045) and an SGR (0526-66), which implies birth periods larger than tens of milliseconds. In our model there is no need for rapid rotation at birth.
A giant burst is due to the shell losing a larger
fraction of its mass as it moves towards the star, parameterized in our model by
![]() .
Regular bursts,
.
Regular bursts,
![]() ,
are due to smaller pieces breaking off the neutral line as the shell oscillates
around its equilibrium position. For SGR 1806-20 we argue the boxing
day event is one of the
first events experienced by this object following its birth.
Moreover, our model predicts (via Eq. (21)) that
we should continue to see a decreasing trend in both the burst intensity
and frequency going from younger to older objects.
,
are due to smaller pieces breaking off the neutral line as the shell oscillates
around its equilibrium position. For SGR 1806-20 we argue the boxing
day event is one of the
first events experienced by this object following its birth.
Moreover, our model predicts (via Eq. (21)) that
we should continue to see a decreasing trend in both the burst intensity
and frequency going from younger to older objects.
The far-IR emission and the correlation with the X-ray
emission can simply be explained as synchrotron emission
from the high-energy and low-energy electrons (see Sect. 7.3).
Our disk is in fact an iron-rich shell. It is passive because it is degenerate
and for most of its lifetime it remains in equilibrium at ![]() ,
co-rotating with the star.
,
co-rotating with the star.
AXPs/SGRs are quark stars and high-B radio pulsars are neutron stars that have not gone through a QN phase, probably because their core densities never reached deconfinement values (see Staff et al. 2006).
The hard X-ray spectrum in our model can be explained as MeV photons generated in the outer layers of the star. These photon bursts can only occur for accretion events capable of heating the star above 7.7 MeV. We find that only bursts with energies above 1043 erg can do so (see Sect. 7.4), thus explaining why only the giant SGR flares show a hard spectrum.
In our model the difference can be explained by the time
it takes the neutron star to reach deconfinement/nucleation densities as discussed in
Sect. 4.4. Simply put, the supernova age is the time for the neutron
star to reach quark deconfinment densities and experience a quark-nova, plus the time
needed for strange quark nucleation (
![]() ).
).
Massive stars (near the black hole line) exploding in high density ISM are most likely to lead to massive compact remnants. The high density ISM will confine the massive progenitor winds much closer to the star, causing the deceleration of the blast wave, and initiating the reverse shock inside the remnant (Truelove & McKee 1999). This would lead to more massive compact stars which are more likely to turn directly into quark stars.
In our model X-ray Dim Isolated Neutron Stars (XDINs) are old SGRs/AXPs
that have gone through their most active bursting
phase and are left with a thin shell in stable equilibrium
at ![]() .
We start by summarizing the
observed and measured features of XDINs before we apply our model
to these intriguing objects.
.
We start by summarizing the
observed and measured features of XDINs before we apply our model
to these intriguing objects.
These dim (
![]() )
isolated neutron stars are nearby at around 100-300 pc and show no SNR association. Three of them have known proper motions that are too fast to accrete. The main common properties of the "magnificent seven'' can be summarized as follows (see Haberl 2005 and references therein): (i) the blackbody: the X-ray spectra of XDINs obtained by the ROSAT PSPC are all
consistent with blackbody emission. The
soft X-ray spectra have a temperature in the range of 40-110 eV.
They show no non-thermal component; (ii) the Absorption lines:
the XMM-Newton spectra can be best modeled with a Planckian continuum including a broad, Gaussian shaped absorption line. The line centroid energies are in
the range 100-700 eV. The depth of the absorption line (or the equivalent width)
was found to vary with pulse phase. It has been suggested in the literature that these absorption
lines can be best explained as proton cyclotron resonance absorption features in
the 0.1-1 keV band with field strength in the range of
)
isolated neutron stars are nearby at around 100-300 pc and show no SNR association. Three of them have known proper motions that are too fast to accrete. The main common properties of the "magnificent seven'' can be summarized as follows (see Haberl 2005 and references therein): (i) the blackbody: the X-ray spectra of XDINs obtained by the ROSAT PSPC are all
consistent with blackbody emission. The
soft X-ray spectra have a temperature in the range of 40-110 eV.
They show no non-thermal component; (ii) the Absorption lines:
the XMM-Newton spectra can be best modeled with a Planckian continuum including a broad, Gaussian shaped absorption line. The line centroid energies are in
the range 100-700 eV. The depth of the absorption line (or the equivalent width)
was found to vary with pulse phase. It has been suggested in the literature that these absorption
lines can be best explained as proton cyclotron resonance absorption features in
the 0.1-1 keV band with field strength in the range of
![]() -
-
![]() G (Zane et al. 2001; Zavlin & Pavlov 2002) with the line broadening explained as
due to the variation of the magnetic field over the neutron star surface; (iii) the optical excess:
they show optical excess compared to the X-ray blackbody. In other words at optical
wavelengths they show a factor of about 3-14 excess when compared to the
extrapolation from X-rays (Pons et al. 2002; Motch & Haberl 1998;
Haberl et al. 2004; van Kerkwijk et al. 2004); (iv) the Lack of radio-emission:
it has been argued that the lack of pulsed radio-emission is because
their radio beam is very narrow due to the large light cylinder radius (i.e.,
large periods). However, there exist radio-pulsars with similar magnetic
field strengths and periods (e.g. Camilo et al. 2000) that are active in the radio.
In our model, the lack of radio pulsation is due to the fact that quark
stars in the CFL phase, unlike neutron stars, become aligned-rotators
following the QN (see Ouyed et al. 2005). We now go on to discuss the remaining properties.
G (Zane et al. 2001; Zavlin & Pavlov 2002) with the line broadening explained as
due to the variation of the magnetic field over the neutron star surface; (iii) the optical excess:
they show optical excess compared to the X-ray blackbody. In other words at optical
wavelengths they show a factor of about 3-14 excess when compared to the
extrapolation from X-rays (Pons et al. 2002; Motch & Haberl 1998;
Haberl et al. 2004; van Kerkwijk et al. 2004); (iv) the Lack of radio-emission:
it has been argued that the lack of pulsed radio-emission is because
their radio beam is very narrow due to the large light cylinder radius (i.e.,
large periods). However, there exist radio-pulsars with similar magnetic
field strengths and periods (e.g. Camilo et al. 2000) that are active in the radio.
In our model, the lack of radio pulsation is due to the fact that quark
stars in the CFL phase, unlike neutron stars, become aligned-rotators
following the QN (see Ouyed et al. 2005). We now go on to discuss the remaining properties.
Table 2:
Observed features of the X-ray dim radio-quiet isolated neutron stars
![]() .
.
As discussed in Sect. 5.1,
the first blackbody temperature is
set by the X-ray continuum luminosity from the surface of the quark star,
Similarly, the effective shell temperature (the second blackbody) is
Since
![]() in our model it implies
in our model it implies
![]() which means that the shell will act as an absorber of the hotter X-ray blackbody.
The maximum density,
which means that the shell will act as an absorber of the hotter X-ray blackbody.
The maximum density,
![]() ,
of the shell below
which the gas is non-degenerate is found by setting
,
of the shell below
which the gas is non-degenerate is found by setting
![]() ,
or,
,
or,
![]() .
The scale height of the non-degenerate, upper layers, of the shell can be estimated to be
.
The scale height of the non-degenerate, upper layers, of the shell can be estimated to be
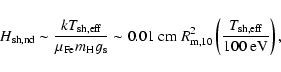 |
(59) |
| |
= | (60) | |
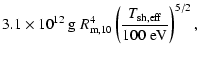 |
The shell's solid angle,
![]() ,
is
essentially providing the excess optical emission.
In the simplest case, one assumes a scattering atmosphere isotropizes
the optical emitted flux from the QS (i.e. blackbody tail) and the shell. Then
the ratio between the total optical flux and the optical contribution from the tail
of the blackbody can be expressed as
,
is
essentially providing the excess optical emission.
In the simplest case, one assumes a scattering atmosphere isotropizes
the optical emitted flux from the QS (i.e. blackbody tail) and the shell. Then
the ratio between the total optical flux and the optical contribution from the tail
of the blackbody can be expressed as
| |
= | 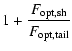 |
(62) |
| = |
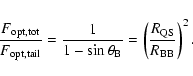 |
(63) |
In this paper we present a new model for SGRs and AXPs with possible applications to XDINs. This novel idea relies on the formation of bare CFL quark stars (within the quark-nova scenario) as the underlying engine, with the parent neutron star's crust material surrounding it. Despite the simplifications we have employed to study the dynamics of this ejected shell, specifically how it reaches the equilibrium radius and how it evolves once it is there, our model has a number of attractive features that can account for many observed SGR, AXP, and perhaps XDIN properties.
Missing from our study is the proper treatment of three-dimensional instabilities acting on the shell, such as Raleigh-Taylor or oscillations. Due to the high conductivity of the shell we expect the Raliegh-Taylor to not operate on very fast timescales, and any radial oscillations to be severly damped as the conducting shell will maintain the magnetic flux enclosed within. However, azimuthal oscillations may have a significant effect. For a more accuarate description, the dynamics of the shell will require numerical simulations, and is left as future work.
Acknowledgements
We thank K. Mori and P. Jaikumar for insightful discussions. This research is supported by grants from the Natural Science and Engineering Research Council of Canada (NSERC).
Table 1:
Observed features of SGRs and AXPs (Only AXPs and SGRs with measured P and ![]() are listed)+.
are listed)+.