- ... XDINs
![[*]](/icons/foot_motif.gif)
- Table 1 is only available in electronic form at http://www.aanda.org
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... crust
![[*]](/icons/foot_motif.gif)
- The
words "suspended crust'' has been used in a different context
already with respect to quark stars; i.e. the electro-magnetically suspended crust
at hundreds of Fermi's above the quark star surface (e.g. Alcock et al. 1986)
instead of a few quark star radii as in our case.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... decelerate
![[*]](/icons/foot_motif.gif)
- The damping term is by far the dominant term in the equations of motion
of the shell due to the high conductivity of the shell, estimated by
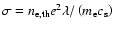 .
Here
.
Here
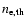 is the number density of thermal electrons,
is the number density of thermal electrons,
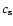 is the sound speed, the mean free path is given by
is the sound speed, the mean free path is given by
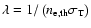 ,
and
,
and
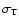 is the Thompson scattering cross section.
is the Thompson scattering cross section.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bursts
![[*]](/icons/foot_motif.gif)
- If
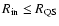 then
areas of the shell are in contact with the star.
In this case, it is easy to imagine that
the shell will experience a major disruption as inner sections are converted
to CFL matter during contact probably destroying the entire
shell; this could have applications to other explosive
phenomena and is beyond the self-similar picture presented here.
then
areas of the shell are in contact with the star.
In this case, it is easy to imagine that
the shell will experience a major disruption as inner sections are converted
to CFL matter during contact probably destroying the entire
shell; this could have applications to other explosive
phenomena and is beyond the self-similar picture presented here.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... be
![[*]](/icons/foot_motif.gif)
- Equation (31)
is a direct measure of the star's radius once
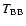 (or
(or 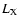 )
and
)
and 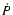 are measured.
This could become crucial for deriving the Mass-Radius relationship for these objects.
The mass (more precisely M/R) could be derived from photon redshifts.
are measured.
This could become crucial for deriving the Mass-Radius relationship for these objects.
The mass (more precisely M/R) could be derived from photon redshifts.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... chunks)
![[*]](/icons/foot_motif.gif)
- In the cases where the shell moves in and out without
pieces breaking off, there would be associated
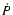 variations
without SGR bursts.
variations
without SGR bursts.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... redshift
![[*]](/icons/foot_motif.gif)
- If the line
is from ionized iron, the rest energy can increase up to
6.7 keV thus a redshift up to 5% is allowed, reducing the lower
limit on the distance of the iron emitting gas from the star to
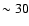 km.
km.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... thickness
![[*]](/icons/foot_motif.gif)
- The heat penetration depth is
given as
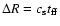 where
where
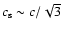 is the CFL sound speed and
is the CFL sound speed and
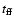 is the free fall timescale given by
Eq. (49). We get
is the free fall timescale given by
Eq. (49). We get
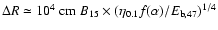 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... radius
![[*]](/icons/foot_motif.gif)
- It was suggested that the minimum radius of RXJ1856 might exceed 14 km thus favoring stiff equations of state (Trümper 2005). We argue that the inferred radius is in fact the location of the iron shell. Indeed, the temperature of the cool component was measured to be <33 eV at the
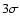 level (Burwitz et al. 2003). In our model, it implies
level (Burwitz et al. 2003). In our model, it implies
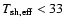 eV or
eV or
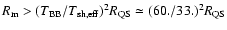 .
That is,
.
That is,
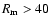 km assuming
km assuming
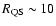 km.
km.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.