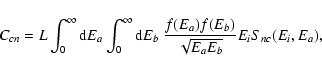A&A 472, L55-L58 (2007)
DOI: 10.1051/0004-6361:20078170
LETTER TO THE EDITOR
Hydrogen Balmer line formation in solar flares affected
by return currents
J. Stepán1,2 - J. Kasparová1 - M. Karlický1 - P. Heinzel1
1 - Astronomical Institute, Academy of Sciences of the Czech Republic, v.v.i.,
Fricova 298, 251 65 Ondrejov, Czech Republic
2 - LERMA, Observatoire de Paris-Meudon, CNRS UMR 8112, 5
place Jules Janssen, 92195 Meudon Cedex, France
Received 27 June 2007 / Accepted 30 July 2007
Abstract
Aims. We investigate the effect of the electric return currents in solar flares on the profiles of hydrogen Balmer lines. We consider the monoenergetic approximation for the primary beam and runaway model of the neutralizing return current.
Methods. Propagation of the 10 keV electron beam from a coronal reconnection site is considered for the semiempirical chromosphere model F1. We estimate the local number density of return current using two approximations for beam energy fluxes between 4 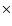 1011 and 1
1011 and 1 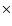
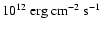 .
Inelastic collisions of beam and return-current electrons with hydrogen are included according to their energy distributions, and the hydrogen Balmer line intensities are computed using an NLTE radiative transfer approach.
.
Inelastic collisions of beam and return-current electrons with hydrogen are included according to their energy distributions, and the hydrogen Balmer line intensities are computed using an NLTE radiative transfer approach.
Results. In comparison to traditional NLTE models of solar flares that neglect the return-current effects, we found a significant increase emission in the Balmer line cores due to nonthermal excitation by return current. Contrary to the model without return current, the line shapes are sensitive to a beam flux. It is the result of variation in the return-current energy that is close to the hydrogen excitation thresholds and the density of return-current electrons.
Key words: Sun: flares - plasmas - line: formation - atomic processes
The ongoing study of nonthermal excitation of the flaring chromospheric plasmas
has been mainly concentrated on the effect of particle beams coming from
the coronal reconnection site
(Canfield et al. 1984; Fang et al. 1993; Kasparová & Heinzel 2002; Stepán et al. 2007; Hawley & Fisher 1994, and references therein).
However, Karlický & Hénoux (2002) and
Karlický et al. (2004) recently suggested that the role of neutralizing return currents can be
as important as the role of the primary beam itself, both for intensity and
linear polarization profiles.
Karlický et al. (2004) proposed a simple model of return current formed by the
runaway electrons and compared the rates of atomic transitions due to
collisions both with the thermal electrons and with the electrons of
the primary beam,
and due to collisions with the return current formed by the runaway electrons.
They showed that the rates due to the return current would dominate the
collisional processes in the atmospheric region of Balmer line formation.
However, no calculations of theoretical spectral line profiles were presented.
The aim of this paper is to take a first step towards
self-consistent modeling of the Balmer line formation
with return-current effects taken into account.
We use a semi-empirical model of
the flaring atmosphere as a basis for our NLTE radiative transfer model.
Then we use a standard model for electron-beam deceleration due to Coulomb
collisions with the ambient
atmosphere and combine it with the two different physical
models of the return-current generation. We incorporate the relevant processes
that enter the atomic statistical equilibrium equations and solve them
with the non-local equations of radiation transfer.
At the end, we discuss the results and validity of our models.
2 Electron beam and return-current propagation
We assume an electron beam that is accelerated in a coronal reconnection site
and injected into the cold chromosphere along the magnetic field lines. During
its propagation, the beam evolves under the influence of several processes
(Karlický 1997): (a) the beam generates the return current that decelerates
the beam in the return-current electric field, (b) the beam generates the
plasma waves causing the quasi-linear relaxation of the beam, and (c) the beam
electrons are decelerated and scattered due to collisions with the background
plasma particles. In the following model, we neglect the plasma wave processes
and the return current is taken in the form of runaway electrons
(Rowland & Vlahos 1985; van den Oord 1990; Norman & Smith 1978).
In this form, the
return-current losses are strongly reduced (Rowland & Vlahos 1985; Karlický et al. 2004).
Thus, only collisional losses, as described by Emslie (1978),
decelerate the electron beam in our case.
Let
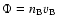 be the particle flux of the monoenergetic beam of the
energy
be the particle flux of the monoenergetic beam of the
energy
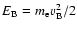 ,
where
,
where 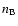 is the density of the beam
electrons,
is the density of the beam
electrons, 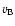 their velocity, and
their velocity, and 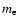 the mass of the electron. According
to Norman & Smith (1978) and Karlický et al. (2004), a fraction of background electrons
the mass of the electron. According
to Norman & Smith (1978) and Karlický et al. (2004), a fraction of background electrons
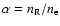 forms the current that moves in the opposite direction in
order to neutralize the electric current
forms the current that moves in the opposite direction in
order to neutralize the electric current 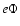 associated with the primary
beam. We use
associated with the primary
beam. We use 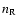 for the number density of the return-current electrons and
for the number density of the return-current electrons and
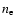 for the number density of the background electrons. The neutralization
condition can be expressed as
for the number density of the background electrons. The neutralization
condition can be expressed as
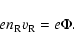 |
(1) |
We assume that all the return-current electrons move with
the same superthermal velocity 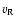 .
Note that the return-current flux only depends on the total flux of the
beam. For a realistic power-law distribution of the beam, the main part of the
beam flux is given by electrons with energy close to the low-energy cutoff of this
distribution. For these reasons and for simplicity, we consider
the monoenergetic beam in our model.
.
Note that the return-current flux only depends on the total flux of the
beam. For a realistic power-law distribution of the beam, the main part of the
beam flux is given by electrons with energy close to the low-energy cutoff of this
distribution. For these reasons and for simplicity, we consider
the monoenergetic beam in our model.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8170fig1}\end{figure}](/articles/aa/full/2007/36/aa8170-07/Timg25.gif) |
Figure 1:
From upper panel: H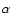 ,
H ,
H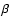 ,
and H ,
and H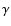 disk-center line profiles for disk-center line profiles for
 (dotted line, black),
(dotted line, black),
 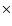 1011 (thick solid line, blue),
6
1011 (thick solid line, blue),
6 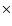 1011 (thick dash-dotted line, green),
8
1011 (thick dash-dotted line, green),
8 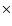 1011 (thin solid line, red), and
1.0
1011 (thin solid line, red), and
1.0 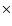 1012 (thin dash-dotted line, violet)
1012 (thin dash-dotted line, violet)
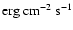 .
No return-current effects are taken into account. Note that nonthermal
profiles almost overlap in this range of beam fluxes. .
No return-current effects are taken into account. Note that nonthermal
profiles almost overlap in this range of beam fluxes. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8170fig2}\end{figure}](/articles/aa/full/2007/36/aa8170-07/Timg26.gif) |
Figure 2:
Same as Fig. 1 plus including collisions with return-current
electrons. The value of 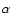 is given by Eq. (2).
is given by Eq. (2). |
| Open with DEXTER |
We used two models for estimating 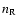 .
First, following
Norman & Smith (1978), the number of runaway electrons can be estimated as
.
First, following
Norman & Smith (1978), the number of runaway electrons can be estimated as
![\begin{displaymath}%
\alpha=\frac{n_{\rm R}}{n_{\rm e}}=\frac 12 \exp\left[ -\fr...
...}}-
\frac{\mathcal{E}}{\mathcal{E}_{\rm D}} \right)^2 \right],
\end{displaymath}](/articles/aa/full/2007/36/aa8170-07/img27.gif) |
(2) |
where
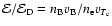 (see Xu et al. 2005; Karlický et al. 2004, for definition
of the electric field
(see Xu et al. 2005; Karlický et al. 2004, for definition
of the electric field
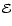 generated by the electron beam
and the Dreicer electric field
generated by the electron beam
and the Dreicer electric field
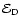 ),
and
),
and
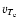 stands for the thermal velocity of the background electrons. In
the second model we assume that the return current is formed by a fixed
relative number of background electrons everywhere in the upper chromosphere:
stands for the thermal velocity of the background electrons. In
the second model we assume that the return current is formed by a fixed
relative number of background electrons everywhere in the upper chromosphere:
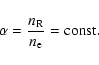 |
(3) |
In this model, 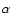 is obtained by averaging the values from the previous model over the Balmer line formation layers. The resulting value for each beam flux
can be found in Table 1.
is obtained by averaging the values from the previous model over the Balmer line formation layers. The resulting value for each beam flux
can be found in Table 1.
The normalized energy distribution of electrons can be locally expressed in
the form
![\begin{displaymath}%
f(E)~{\rm d}E=[c_{\rm M} f_{\rm M}(E)+c_{\rm B}\delta(E-E_{\rm B})+
c_{\rm R}\delta(E-E_{\rm R})]~{\rm d}E,
\end{displaymath}](/articles/aa/full/2007/36/aa8170-07/img33.gif) |
(4) |
where
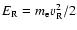 is the return-current energy and ci stands
for the normalization coefficients (i.e.,
is the return-current energy and ci stands
for the normalization coefficients (i.e.,
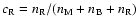 ,
etc.). The index M stands for the background electrons (without the runaway
ones), and they obey the Maxwell-Boltzmann energy distribution.
,
etc.). The index M stands for the background electrons (without the runaway
ones), and they obey the Maxwell-Boltzmann energy distribution.
To take the effect of the beam/return current into account, we have to
calculate all the electron-hydrogen excitation rates,
the rates of ionization by electron impacts, and the rates of the
inverse processes. We use the
data for total collisional cross-sections for the bound-bound and bound-free
transitions by Janev & Smith (1993), retrieved through the
GENIE database (http://www-amdis.iaea.org/GENIE/).
We do not consider any atomic polarization or angular dependence of the
collisional processes in this work.
The excitation or deexcitation rate of the 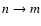 transition
between the two shells can be calculated using the common formula
transition
between the two shells can be calculated using the common formula
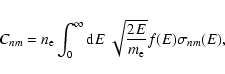 |
(5) |
where
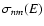 is the total cross-section of
is the total cross-section of 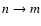 at impact energy E, and f(E) is electron energy distribution (4). The cross-sections for deexcitation
at impact energy E, and f(E) is electron energy distribution (4). The cross-sections for deexcitation 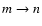 (m>n)
were calculated using the
(m>n)
were calculated using the 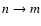 cross section and the
principle of detailed balance (e.g., Jefferies 1968),
cross section and the
principle of detailed balance (e.g., Jefferies 1968),
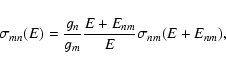 |
(6) |
where Enm is the excitation threshold of the transition and
gn/m the statistical weight of the given level.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8170fig3}\end{figure}](/articles/aa/full/2007/36/aa8170-07/Timg41.gif) |
Figure 3:
Same as Fig. 1 plus including collisions with return-current
electrons. The value of 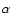 is constant along whole beam trajectory.
is constant along whole beam trajectory. |
| Open with DEXTER |
The rates of the inverse process of ionization by an electron impact,
the three-body recombination
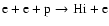 ,
must be treated separately
due to the nonthermal nature of the problem. Using the arguments of detailed
balance (Jefferies 1968; Fowler 1955) in the quasi-classical approximation of
the electron-hydrogen collisions, one can derive a formula for the recombination
rate. Let us consider the ionization of level n with the ionization energy En by an electron with energy Ei. Once cross-section
,
must be treated separately
due to the nonthermal nature of the problem. Using the arguments of detailed
balance (Jefferies 1968; Fowler 1955) in the quasi-classical approximation of
the electron-hydrogen collisions, one can derive a formula for the recombination
rate. Let us consider the ionization of level n with the ionization energy En by an electron with energy Ei. Once cross-section
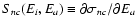 of
the encounter after which we find the two electrons with energies Ea and
Eb=Ei-En-Ea is known, one can write the total recombination rate as
of
the encounter after which we find the two electrons with energies Ea and
Eb=Ei-En-Ea is known, one can write the total recombination rate as
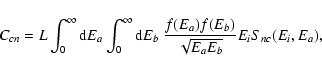 |
(7) |
where
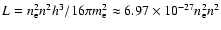 in
cgs units, and h stands for the Planck constant.
The expression (7) can be reduced to the well-known expression
in
cgs units, and h stands for the Planck constant.
The expression (7) can be reduced to the well-known expression
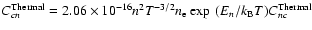 in the particular case of Maxwell-Boltzmann distribution, where
in the particular case of Maxwell-Boltzmann distribution, where
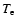 is the temperature of electrons and
is the temperature of electrons and 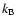 the Boltzmann constant.
For the cross section Snc we used the approximate
data of Omidvar (1965) at lower energies and the classical formula of
Thomson (1912) at high energies.
In our case, the electron energy distribution function given
by (4) leads to 9 terms
that contribute to the recombination rates.
We verified numerically that, in all our models,
the rates of three-body recombination involving the nonthermal electrons
of the return current are more than one order of magnitude below the rates
of the same processes involving the thermal electrons.
Our tests show that neglecting the nonthermal three-body recombination
affects the resulting profiles in a very negligible way.
The three-body recombinations involving the beam electrons are completely
negligible since their rates are several orders of magnitude below
the thermal ones. Thus, we took only
the thermal term containing
the Boltzmann constant.
For the cross section Snc we used the approximate
data of Omidvar (1965) at lower energies and the classical formula of
Thomson (1912) at high energies.
In our case, the electron energy distribution function given
by (4) leads to 9 terms
that contribute to the recombination rates.
We verified numerically that, in all our models,
the rates of three-body recombination involving the nonthermal electrons
of the return current are more than one order of magnitude below the rates
of the same processes involving the thermal electrons.
Our tests show that neglecting the nonthermal three-body recombination
affects the resulting profiles in a very negligible way.
The three-body recombinations involving the beam electrons are completely
negligible since their rates are several orders of magnitude below
the thermal ones. Thus, we took only
the thermal term containing
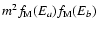 into account.
into account.
We calculated the NLTE radiative transfer for a 5-level plus continuum
hydrogen using the semiempirical 1D plane-parallel flare model F1 (Machado et al. 1980)
in which the temperature structure was kept fixed;
in this way, we found the differential effects on the
H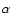 ,
H
,
H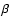 ,
and H
,
and H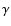 lines (cf. Kasparová & Heinzel 2002).
We used the preconditioned equations of statistical equilibrium (Rybicki & Hummer 1991)
and solved the coupled system
of NLTE equations by the accelerated lambda iteration (ALI) method.
For further details, see Heinzel (1995).
We found the equilibrium state
for several beam fluxes with or without the return current.
The initial beam fluxes chosen in our calculations were:
lines (cf. Kasparová & Heinzel 2002).
We used the preconditioned equations of statistical equilibrium (Rybicki & Hummer 1991)
and solved the coupled system
of NLTE equations by the accelerated lambda iteration (ALI) method.
For further details, see Heinzel (1995).
We found the equilibrium state
for several beam fluxes with or without the return current.
The initial beam fluxes chosen in our calculations were:
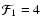
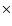 1011, 6
1011, 6  1011, 8
1011, 8  1011, and 1
1011, and 1 
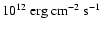 .
If the fluxes were lower, the number of runaway electrons would decrease fast
and their energy would exceed the beam energy in most depths.
This gives a limit for using of this simple model.
Higher fluxes, on the other hand, would be unrealistic.
The initial energy of beam electrons was set to E0=10 keV.
.
If the fluxes were lower, the number of runaway electrons would decrease fast
and their energy would exceed the beam energy in most depths.
This gives a limit for using of this simple model.
Higher fluxes, on the other hand, would be unrealistic.
The initial energy of beam electrons was set to E0=10 keV.
In Fig. 1, there are first three Balmer line profiles
that result from the nonthermal bombardment by the primary beam. The effects
of return current were completely ignored. In this sense, these calculations
are similar to the ones of Fang et al. (1993) and Kasparová & Heinzel (2002).
In spite of their probably limited physical relevance, these profiles
are useful for demonstrating the effects of return currents in the
more appropriate models that follow.
Figure 2 shows the situation where 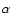 is calculated
using Eq. (2); i.e., the relative number of runaway
return-current electrons is calculated at each depth in the atmosphere.
Finally, in Fig. 3, there are profiles for
the model with
is calculated
using Eq. (2); i.e., the relative number of runaway
return-current electrons is calculated at each depth in the atmosphere.
Finally, in Fig. 3, there are profiles for
the model with 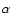 constant along the atmosphere.
In the layers of Balmer line formation,
constant along the atmosphere.
In the layers of Balmer line formation, 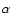 remains approximately
constant and its mean values are shown in Table 1.
Comparing Fig. 1 with Figs. 2 and 3, one can see that the effect of return current is very significant: All three lines show a prominent increase emission
in the line center.
remains approximately
constant and its mean values are shown in Table 1.
Comparing Fig. 1 with Figs. 2 and 3, one can see that the effect of return current is very significant: All three lines show a prominent increase emission
in the line center.
Table 1:
The properties of the return currents.
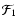 stands for
the initial flux of the 10 keV beam,
stands for
the initial flux of the 10 keV beam, 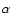 is the mean relative number
of runaway return-current electrons in the Balmer lines formation region,
and
is the mean relative number
of runaway return-current electrons in the Balmer lines formation region,
and 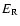 stands for the typical energy of the return-current electrons in
these layers. Both
stands for the typical energy of the return-current electrons in
these layers. Both 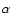 and
and 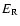 are average quantities which
can roughly characterize the return-current properties in the region
of interest.
are average quantities which
can roughly characterize the return-current properties in the region
of interest.
In the region of Balmer line formation, the energy of the return current can
be close to the excitation threshold of 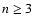 levels of hydrogen,
and it remains approximately constant along an extended trajectory.
The beam is finally
stopped on a very short path. The overall path of the beam is, however,
sensitive to the initial energy of the beam.
In order to model the beam propagation and line formation accurately,
one has to interpolate the original F1 model of Machado et al. (1980) by a number
of grid points in the layers of the Balmer line formation.
Since the return-current energy and density are sensitive to the beam flux
(see Table 1), the resulting variation of the nonthermal
collisional rates leads to a significant variation in line profiles.
For both models under consideration, a maximum emission is found for
the beam flux of 6
levels of hydrogen,
and it remains approximately constant along an extended trajectory.
The beam is finally
stopped on a very short path. The overall path of the beam is, however,
sensitive to the initial energy of the beam.
In order to model the beam propagation and line formation accurately,
one has to interpolate the original F1 model of Machado et al. (1980) by a number
of grid points in the layers of the Balmer line formation.
Since the return-current energy and density are sensitive to the beam flux
(see Table 1), the resulting variation of the nonthermal
collisional rates leads to a significant variation in line profiles.
For both models under consideration, a maximum emission is found for
the beam flux of 6 
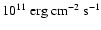 ,
although the
resulting profiles from these models differ slightly from each other.
In contrast to the case of 4
,
although the
resulting profiles from these models differ slightly from each other.
In contrast to the case of 4 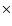
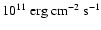 ,
for which
we found the least emission among the studied flux intervals,
the return-current density is higher by a factor of 5. It leads to
a significant increase in nonthermal excitation rates.
The disagreement of the profiles at fluxes below 6
,
for which
we found the least emission among the studied flux intervals,
the return-current density is higher by a factor of 5. It leads to
a significant increase in nonthermal excitation rates.
The disagreement of the profiles at fluxes below 6 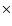
 is the result of the significant dependency of
is the result of the significant dependency of 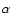 on the beam flux and
atmospheric depth.
The values of
on the beam flux and
atmospheric depth.
The values of 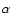 at low fluxes (shown in the Table 1)
are only a rough approximation for the Balmer line formation layers, and
the model with
at low fluxes (shown in the Table 1)
are only a rough approximation for the Balmer line formation layers, and
the model with
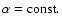 seems to be less accurate
than the one given by Eq. (2).
On the other hand, good correspondence between the models is found for high
fluxes. In this case, the variation in
seems to be less accurate
than the one given by Eq. (2).
On the other hand, good correspondence between the models is found for high
fluxes. In this case, the variation in 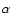 is less sensitive to the
beam flux and
does not strongly vary with atmospheric depth.
Then, the
is less sensitive to the
beam flux and
does not strongly vary with atmospheric depth.
Then, the
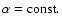 model seems to give the appropriate results.
The reason the higher beam fluxes lead to a lower emission in the
lines is that the energy of the return current is not sufficient to excite
hydrogen atoms as can be seen in Table 1.
model seems to give the appropriate results.
The reason the higher beam fluxes lead to a lower emission in the
lines is that the energy of the return current is not sufficient to excite
hydrogen atoms as can be seen in Table 1.
5 Conclusions and outlook
In this paper we used a simple model of the 10 keV electron beam
propagating in the chromosphere. We used two different models
of the return-current formation and calculated the differential effect
on the profiles of the hydrogen H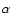 ,
H
,
H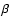 ,
and H
,
and H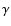 lines
of the semiempirical F1 model.
lines
of the semiempirical F1 model.
The return-current flux only depends on the total flux of the beam. For a
realistic power-law distribution of the beam, the main part of the beam
flux is given by electrons with energy close to the low-energy cutoff of
this distribution. Therefore, for simplicity we used the monoenergetic
beam in our model. Moreover, the excitation and ionization cross-sections
oflow-energy return-current electrons are larger than those for beam
electrons, which makes the return-current effects on line core formation
stronger. Taking high-energy beam electrons into account (i.e. using
power-law distribution) would lead to increased emission in the line
wings due to penetration of those electrons into the deeper atmospheric
layers. However, the total flux of the beam in these layers is significantly
lower than the initial beam flux, and the return current and
corresponding effects are also strongly reduced.
Even our simple model shows that the effect of return current is very
important for future study of the hydrogen lines formation
since the energy of the return current can be expected to be on the order of
the excitation threshold energies of upper hydrogen levels, for which
the excitation cross-sections are high. Moreover, the fluxes 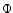 are high
enough to excite a sufficient number of atoms. As shown by Karlický et al. (2004),
the collisional rates from the nonthermal collisions can dominate
the collisional rates in the Balmer line formation regions.
The two models used in this
work lead to similar results for higher energy fluxes, but the result differs
for lower fluxes. The excitation threshold effects seem to play an
important role for higher fluxes, but they are very likely only a consequence of the
monoenergetic model we used.
The difference between the two models shows the used approximations to be
incompatible for lower fluxes, where the the approximation of constant
are high
enough to excite a sufficient number of atoms. As shown by Karlický et al. (2004),
the collisional rates from the nonthermal collisions can dominate
the collisional rates in the Balmer line formation regions.
The two models used in this
work lead to similar results for higher energy fluxes, but the result differs
for lower fluxes. The excitation threshold effects seem to play an
important role for higher fluxes, but they are very likely only a consequence of the
monoenergetic model we used.
The difference between the two models shows the used approximations to be
incompatible for lower fluxes, where the the approximation of constant 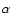 is not applicable.
A detailed description of the energy distribution of the
return-current electrons would lead to more realistic line intensities.
This complex issue will be subject of a forthcoming paper,
which will also study the impact polarization of the Balmer lines.
is not applicable.
A detailed description of the energy distribution of the
return-current electrons would lead to more realistic line intensities.
This complex issue will be subject of a forthcoming paper,
which will also study the impact polarization of the Balmer lines.
Acknowledgements
This work was partially supported by the grant 205/06/P135 of the Grant Agency of the Czech Republic, partially by the grant IAA300030701 of the Grant Agency of the Academy
of Sciences of the Czech Republic, and partially by the project LC06014
Center for Theoretical Astrophysics.
- Canfield,
R. C., Gunkler, T. A., & Ricchiazzi, P. J. 1984,
ApJ, 282, 296 [NASA ADS] [CrossRef]
- Emslie, A. G.
1978, ApJ, 224, 241 [NASA ADS] [CrossRef] (In the text)
- Fang, C., Henoux,
J. C., & Gan, W. Q. 1993, A&A, 274, 917 [NASA ADS]
- Fowler, R. H.
1955, Statistical mechanics (Cambridge University Press)
- Hawley, S. L.,
& Fisher, G. H. 1994, ApJ, 426, 387 [NASA ADS] [CrossRef]
- Heinzel, P. 1995,
A&A, 299, 563 [NASA ADS] (In the text)
- Janev, R. K.,
& Smith, J. J. 1993, in Atomic and plasma-material
interaction data for fusion, 4, 1
(In the text)
- Jefferies,
J. T. 1968, Spectral line formation (A Blaisdell Book in the
Pure and Applied Sciences, Waltham, Mass.: Blaisdell)
(In the text)
- Karlický,
M. 1997, Space Sci. Rev., 81, 143 [NASA ADS] [CrossRef] (In the text)
- Karlický,
M., & Hénoux, J.-C. 2002, A&A, 383, 713 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Karlický,
M., Kasparová, J., & Heinzel, P. 2004, A&A, 416,
L13 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
Kasparová, J., & Heinzel, P. 2002, A&A, 382, 688 [NASA ADS] [CrossRef] [EDP Sciences]
- Machado,
M. E., Avrett, E. H., Vernazza, J. E., & Noyes,
R. W. 1980, ApJ, 242, 336 [NASA ADS] [CrossRef] (In the text)
- Norman, C. A.,
& Smith, R. A. 1978, A&A, 68, 145 [NASA ADS]
- Omidvar, O. 1965,
Phys. Rev., 140, A26 [NASA ADS] [CrossRef] (In the text)
- Rowland,
H. L., & Vlahos, L. 1985, A&A, 142, 219 [NASA ADS]
- Rybicki,
G. B., & Hummer, D. G. 1991, A&A, 245, 171 [NASA ADS] (In the text)
-
Stepán, J., Heinzel, P., & Sahal-Bréchot, S. 2007,
A&A, 465, 621 [NASA ADS] [CrossRef] [EDP Sciences]
- Thomson,
J. J. 1912, Phil. Mag., 23, 449 (In the text)
- van den
Oord, G. H. J. 1990, A&A, 234, 496 [NASA ADS]
- Xu, Z., Hénoux,
J.-C., Chambe, G., Karlický, M., & Fang, C. 2005, ApJ,
631, 618 [NASA ADS] [CrossRef]
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8170fig1}\end{figure}](/articles/aa/full/2007/36/aa8170-07/Timg25.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8170fig2}\end{figure}](/articles/aa/full/2007/36/aa8170-07/Timg26.gif)
![\begin{displaymath}%
\alpha=\frac{n_{\rm R}}{n_{\rm e}}=\frac 12 \exp\left[ -\fr...
...}}-
\frac{\mathcal{E}}{\mathcal{E}_{\rm D}} \right)^2 \right],
\end{displaymath}](/articles/aa/full/2007/36/aa8170-07/img27.gif)
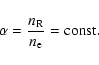
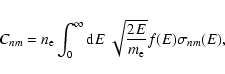
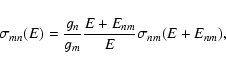
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8170fig3}\end{figure}](/articles/aa/full/2007/36/aa8170-07/Timg41.gif)