A&A 471, 717-730 (2007)
DOI: 10.1051/0004-6361:20067029

Thermal forces on planetary ring particles: application to the main system of Saturn^,

D. Vokrouhlický^1,2 - D. Nesvorný² - L. Dones² - W. F. Bottke²

1 - Institute of Astronomy, Charles University, V Holesovickách 2, 18000 Prague, Czech Republic
2 - Department of Space Studies, Southwest Research Institute, 1050 Walnut St., Boulder, CO 80302, USA

Received 26 December 2006 / Accepted 31 May 2007

Abstract
Context. The motion of small particles in planetary rings is affected in the long-term by radiation forces. While the Poynting-Robertson effect has been extensively discussed and applied to the dynamics of micron-sized ring particles, studies of thermal self-acceleration of particles are only in their infancy.
Aims. We extend the pioneering work of Rubincam (2006, Icarus 184, 532) by a more thorough analytical formulation of both planetary and solar thermal forces on ring particles.
Methods. Within a sparse disk model we analytically compute both seasonal and diurnal variants of the thermal forces and we demonstrate that the diurnal effect components vanish for a sample of rapidly rotating particles with randomly oriented spin axes. For sufficiently slowly rotating ring particles, though, these diurnal components might significantly modify the expected planetocentric secular drift rates of their orbits. We also take into account the orbital effects of Poynting-Robertson drag that begin to dominate the thermal forces for particles with sizes $\leq$5 mm. Our formulation of the Poynting-Robertson drag is the first to account properly for the influence of the planetary shadow.
Results. We critically review the previous suggestion that Saturn's A and B ring boundaries might correlate with radiative null-torque orbits of small particles. Using the best estimates of optical and thermal parameters of Saturn's ring particles, we show that the millimetre to several centimetre size particles mostly drift inward to the planet with a characteristic radial speed $\nu_{\rm r}\sim 3\times 10^{-6}$ cm/s, corresponding to drift across the whole main ring system in $\sim$ $(1{-}5)\times 10^8$ years if the effects of inter-particle collisions are neglected. The radial speed is comparable to, or even larger than, the effective radial drift rate of small particles due to redistribution of collisional ejecta from micrometeoroid impacts. Therefore, radiation forces may be important for estimating the evolution timescales of Saturn's rings as derived from the ballistic transport theory. We propose that, in addition to collisional coagulation, radiation forces may efficiently remove centimetre-sized particles and thus help explain the observed paucity of these particles in Saturn's rings. A population of particles with spin axes aligned with normal to the disk plane, if it exists, would experience a net outward drift provided their rotation rate is larger than their orbital frequency.

Key words: planets: rings - radiation mechanisms: non-thermal

1 Introduction

Analysis of dynamical consequences of thermal radiation, arising as a total recoil force and torque on translational and rotational motion, is currently attracting large interest in asteroidal science and meteoritics (for reviews see Bottke et al. 2002, 2006). For example, it helps to explain how meteorites and small asteroids are transported onto unstable orbits, asteroid families grow in time and/or orientation of asteroid spin axes are distributed in space and their rotation frequencies modified. Since ring particles in the main Saturnian system have sizes comparable (or slightly smaller) to meteorites (e.g., Cuzzi et al. 1984; Esposito et al. 1984), a question arises whether similar thermal effects could play some role in their dynamics. Despite the size correspondence, analysis of the dynamical consequences of thermal effects for planetary rings is vastly more complicated because ring particles are not isolated but live in dense populations. Effects of mutual light reflection and shadowing in optical wavelengths, and heating in thermal wavelengths, are considered important especially for the optically and thermally thick A and B rings. Moreover, solar incoming radiation is modulated by passages of ring particles through the planet's shadow, phenomenon without a counterpart in asteroidal applications. As far as this issue is concerned, though, lessons from space geodesy are in order, since artificial satellites (in spite of their vastly different composition) are susceptible to the same effects too (e.g., Rubincam 1987; Afonso et al. 1989).

A number of models for Saturn's rings radiation in mid-infrared has been developed, and compared to observations, since 1970s (e.g., Kawata & Irvine 1975; Froidevaux 1981; Kawata 1983). While taking into account inter-particle effects (shadowing and/or mutual irradiation in optical and thermal) at some approximation, many of these older models are based on the time-averaged energy balance only. Starting from the work of Aumann & Kieffer (1973), several more detailed models accounted also for the ring shadowing by Saturn and thus resolved time dependence of the particles' changing temperature as they revolve about the planet (especially when observations with the fine resolution became available in 1990s; e.g., Ferrari et al. 2005; Ferrari & Leyrat 2006). All these models, though, share the same approximation: they solve local-energy balance only without detailed analysis of temperature variation on the particles' surface (at best empirical factors are introduced to compare models of fast/slow rotating particles). In the notation and terminology used below this amounts to solving the monopole level of the particles' surface temperature distribution. However, the orbital thermal effects necessarily need to analyse the dipole level of particles' surface temperature distribution (e.g., Vokrouhlický 1998, 1999; Vokrouhlický & Farinella 1999). Thus the available thermal ring models do not provide enough information about the related orbital perturbations. Grasping the necessary more detailed information though brings difficulties and hence requires approximations, such that simpler models are analysed before resorting to more complex (and perhaps fully numerical) ones.

The first initiative toward application of the thermal effects for the ring particle dynamics has been taken by Rubincam (2004, 2006) who correctly identified the principal thermal effects at work. In particular, he showed that the different sources of the absorbed radiation by the ring particle - the planet and the Sun - produce two different versions of thermal drags when averaged over long periods of time. Interestingly, these two effects have opposite signs and their parametric-dependent composition could make ring particles migrate either inward or outward with respect to the planet. While developing similar approach the goal of our paper is twofold: (i) present somewhat more compact and general formulation of the thermal effects that allows us to proceed with analytical work beyond Rubincam's results, and (ii) discuss implications of the thermal forces for rings structure and their long term evolution. Our conclusions differ from that of Rubincam mainly because of different choice of parameters.

Ground based and Hubble space telescope observations, revisions of Voyager and new Cassini space-borne data are filling voids since 1990s, yet some uncertainties still persist. This is partially because the observations do not cover all necessary viewing geometries and do not span necessary spectral ranges (this is especially true in mid-infrared where we have much fewer observations available so far than in the optical band). Moreover, and possibly even more important, both optical and thermal data are difficult to interpret because an appropriately complete radiative transfer theory is not available. Different authors use different approximations and this may lead to comparable but not identical results. Inferences from our work (Sect. 6) are thus somewhat uncertain, and different from those in Rubincam (2004, 2006). However, we believe that the forthcoming data will hopefully constrain the prime parameters enough to make our work useful. In the same time, future work should make our model more complete, mainly as regards to inter-particle effects included and characterization of the ring particle rotation state.

In Sect. 2 we introduce our method for the approximate solution of the heat diffusion problem and determination of the thermal force on ring particles. In Sects. 3 and 4 two variants of thermal effects, relevant for a long-term orbital evolution of ring particles, namely the Yarkovsky effect and the Yarkovsky-Schach effect, are discussed. In both cases we analyse the orbital effects of the full thermal-force vector and we do not restrict to the spin-projected component only. We obtain analytic formulæ for the mean secular drift of the semimajor axis for circular orbits due to these thermal effects assuming a sample of particles with random orientation of spin axes. In Sect. 5 we estimate the typical drift rates of millimetre to decimetre ring particles and determine their dependence on principal unknown parameters. Importantly enough, we include in our analysis the effect of the Poynting-Robertson drag that is derived in Appendix B (note the Appendices are available in the on-line version of the paper). Probable implications from our work on long-term dynamics of rings are discussed in Sect. 6.

  
2 The heat diffusion problem for ring particles

Determination of a thermal force on particles orbiting a planet is a difficult enough problem to require a number of approximations if we want to deal with it analytically. The most important approximations are: (i) linearization of the boundary condition (Eq. (2)), (ii) constant thermal parameters, (iii) spherical shape of the particle, and (iv) circular orbit about the planet. In this paper we also adopt a model of a sparsely populated ring where different particles do not influence thermal state of each other, either by mutual eclipsing and/or mutual thermal radiation. This is an acceptable approximation when the ring thickness in optical or infrared bands is significantly less then unity. However, here we formally apply our results even to the Saturn's most optically thick ring, the B ring, relegating a much more complicated analysis of thermally interacting particles to a future work. We also assume that during one revolution about the planet the spin axis $\vec{s}$ of the ring particle is fixed in space. However, the final results are averaged over random orientations of $\vec{s}$, making our results representative for a sample of particles with randomly oriented axes. Here we adopt an assumption that mutual collisions of ring particles produce enough random re-orientations of their spin axis on a long-term, so that the sample-average of any quantity (such as the evolution of orbital elements) corresponds to a long-term time average for each of the particles. A simple model for a sample of particles with $\vec{s}$ aligned with normal to the disk-plane is discussed in Appendix D.

2.1 Heat diffusion equation and its scaling

Distribution of temperature T, determining thermal state of the ring particle, is obtained by solution of the heat diffusion equation (e.g., Landau & Lifshitz 1986)

$$\rho_{\rm b} C {\partial T\over \partial t} = K~\nabla^2 T ,$$ (1)

where $\rho_{\rm b}$ is the mean bulk density, C is the specific heat capacity and K is the thermal conductivity of the particle. The uniqueness of the solution stems from selecting appropriate boundary conditions. In the space domain this means regularity of T at the centre of the particle and energy conservation at the surface. The latter condition reads

$$\epsilon\sigma T^4 + K \left(\vec{n}\cdot{\partial T\over \partial \vec{r}}\right) = {\cal S}\;$$ (2)

for each of the infinitesimal surface elements with an outward directed unit vector $\vec{n}$. The first term here is the thermal energy radiated per unit of time by the particle to space and the second terms is the energy conducted per unit of time inside to the particle. Thermal emissivity $\epsilon$ is for simplicity taken unity throughout this paper (see also Spilker et al. 2003; Ferrari et al. 2005; Flasar et al. 2005). The effective boundary condition in the time domain is set by an assumption of periodicity of T in one revolution of the particle about the planet.

The source function ${\cal S}$ on the right hand side of Eq. (2) gives the amount of radiative energy impinging on a given surface element per unit of time. Since the local radiative field is principally compounded of the solar contribution at optical wavelengths, and the planet's contribution at thermal wavelengths, we write ${\cal S}=\alpha_{\rm V}~{\cal E}^{\rm V}+\alpha_{\rm I}~{\cal E}^{\rm I}$. Here $\alpha _{\rm V}$and $\alpha _{\rm I}$ are absorptivity coefficients of the particle in visible and infrared bands, while ${\cal E}^{\rm V}$ and ${\cal E}^{\rm I}$ are the respective optical and thermal radiative fluxes from the Sun and Saturn. We neglect in this work two other radiation sources: (i) solar radiation reflected by Saturn in optical, and (ii) the optical and infrared radiation of the neighboring particles in the ring. While conceptually simpler, the first effect presents difficulties for our analytic approach and that is the principal reason why we dropped its analysis. Rubincam (2006) showed that its contribution might be approximated as a few to about ten percent increase in strength of the seasonal Yarkovsky drag of the ring particles. The latter effect, radiation of other ring particles, is conceptually much more complicated. We, however, note that in the roughest approximation the irradiation might be seen as a time-variable but isotropic field when the particle is fully embedded in the ring. Then it only affects the effective temperature of the particles but does not have a long-term dynamical effect. The ring particles nevertheless would have a shielding effect that effectively diminishes the values of $\alpha _{\rm V}$ and $\alpha _{\rm I}$ to an extent that is also not modeled in this paper (this caveat mostly affects implications of our work for the A and B rings of Saturn). Similarly, dynamical models with particles of a spectrum of sizes predict smaller ones be dispersed over larger heights above the ring-plane, leaving large particles set in the mid-plane (e.g., Salo 1992; Salo & Karjalainen 2003). The small out-of-plane particles will thus experience an anisotropic local radiative field from other particles. We present another very rough model in Appendix C to show that the orbital effect would average out when isotropy of spin particles is assumed, but none of these effects is modeled in detail here.

Because we assume the ring particles are spherical it appears most natural to use spherical coordinates $(r,\theta,\phi)$, with the origin r=0 at the centre of the particle and colatitude $\theta$ measured from its spin axis $\vec{s}$. The origin of the longitude $\phi$ is not relevant for our work. To simplify the solution we chose the following set of the non-dimensional quantities (see also Vokrouhlický 1998, 1999):

• any quantity with spatial dimension will be scaled by the thermal length (the only exception is the planetocentric distance $\rho$ scaled by the planet's radius)
  

  $$\ell_{\rm s} = \sqrt{K\over \rho_{\rm b} C n} ,$$ (3)

  
  
  where n is the particle's mean motion about Saturn; in particular the radial coordinate r will have the scaled value $r' = r/\ell_{\rm s}$;
• the time t will be replaced by a complex variable $\zeta$ reading
  

  $$\zeta = \exp~({\rm i} n t)$$ (4)

  
  
  (here ${\rm i}=\sqrt{-1}$ is the imaginary unit; the time origin t=0 will be chosen below and may be different for each of the variants of the thermal effects discussed in Sects. 3 and 4);
• the temperature T will be scaled by an auxiliary value $T_\star$ defined by
  

  $$\epsilon \sigma T_\star^4 = {\cal S}_\star = \alpha_{\rm V} {\cal E}_\star^{\rm V}+ \alpha_{\rm I} {\cal E}_\star^{\rm I} ,$$ (5)

  
  
  where ${\cal E}_\star^{\rm V}\simeq 15.05$ W/m² is the mean solar radiation flux at Saturn, and ${\cal E}_{\star 0}^{\rm I}\simeq \alpha_{\rm VS}\xi~{\cal E}_\star^{\rm V}/4 \simeq 4.41$ W/m² is the mean infrared flux from the surface of the planet. Here $\alpha_{\rm VS}\simeq 0.658$ is the mean absorptivity of Saturn in the optical ( $\alpha_{\rm VS}=1-A_{\rm VS}$, where $A_{\rm VS}$ is the Bond albedo) and $\xi\simeq 1.78$ is the radiation excess of Saturn in the thermal (e.g., de Pater & Lissauer 2001). At the distance $\rho$ from the planet the mean energy flux ${\cal E}_{\star}^{\rm I}$ through a spherical particle is attenuated for simple geometric reasons. In Appendix A we find that ${\cal E}_{\star}^{\rm I} ={\cal E}_{\star 0}^{\rm I} ~\psi(\rho)$, where
  

  $$\psi(\rho)=2\left(1-\sqrt{1-\frac{1}{\rho^2}}\right)$$ (6)

  
  
  and $\rho$ is measured in Saturn's radii. The resulting non-dimensional variable will be denoted by $T' = T/T_\star$, and similarly we define $\Delta T' = \Delta T/T_\star$;
• the energy source term ${\cal S}$ in the right hand side of (2) will be scaled by ${\cal S}_\star$, thus we introduce ${\cal S}'={\cal S}/{\cal S}_\star$.

With the scaling introduced, the fundamental Eqs. (1) and (2) now take the following form:

$${\rm i} \zeta {\partial T'\over \partial \zeta} = \nabla'^2 T' ,$$ (7)

and

$$T'^4 + \Theta \left(\vec{n}\cdot{\partial T'\over \partial \vec{r}'}\right) = {\cal S}' .$$ (8)

$\nabla'^2$ is the usual Laplace operator where coordinates have been replaced with their scaled values. As a result of the scaling, the system (7) and (8) contains a single and fundamental non-dimensional parameter $\Theta = \sqrt{K\rho_{\rm b} C}\sqrt{n}/(\epsilon\sigma T_\star^3)$often called the "thermal parameter''; we also note that $\sqrt{K\rho_{\rm b} C}$ in its numerator is the thermal inertia of the particle.

  
2.2 Linearized approximation

A major obstacle of an analytic solution of the heat diffusion is the non-linear term ($\propto$T⁴ and $\propto$T'⁴) in the surface boundary conditions (2) or (8). A standard procedure to handle this problem is to split T into a suitably chosen mean value $T_{\rm av}$ and some small increment $\Delta T$: $T = T_{\rm av} + \Delta T$ with $\Delta T\ll T_{\rm av}$ becoming the solved-for function instead of T. The difficult quartic term in the boundary condition is then approximated using linearization $T^4 \approx T_{\rm av}^4 + 4T_{\rm av}^3 \Delta T + \ldots$ with higher order terms in $\Delta T$ being neglected. The most natural choice of $T_{\rm av}$ is from

$$\epsilon \sigma T_{\rm av}^4 = \overline{\cal S} = \alpha_{\r... ...cal E}^{\rm V}}+ \alpha_{\rm I} \overline{{\cal E}^{\rm I}} ,$$ (9)

where the over-bar means an average value of the corresponding quantity over (i) particle's revolution about Saturn, and (ii) all surface elements. As a result $T_{\rm av}\neq T_\star$.

Figure 1: Ring geometry, parameters of the particle orbit about Saturn and other quantities introduced in the text: $\vec{n}_0$ is the unitary vectortoward the Sun, tilt from the Saturn spin axis by $\theta _0$, $\vec{s}$ is the unitary spin axis of the particle and $\rho$ radius of its planetocentric orbit. The shaded zone on the ring plane indicates shadow cast by the planet. For given $\rho$ and $\theta _0$, the angular width $\Delta$ of the shadow along the orbit is given by Eq. (10).

Open with DEXTER

One easily shows that $\overline{{\cal E}^{\rm I}}={\cal E}_\star^{\rm I}/4$; this is because the spherical particle in equilibrium absorbs radiation through its cross-section, while it re-radiates it through the whole surface (see Appendix A). The determination of $\overline{{\cal E}^{\rm V}}$ is a little more complicated. Except the very outer part of the A ring and when the tilt of ring plane from the solar direction is maximum, the ring particles always enter the Saturn shadow during their revolution about the planet. The shadow is modeled here with a step function $\Gamma(\zeta)$ whose value is zero in the shadow and unity outside (we neglect the penumbra phase). Let us denote $\Delta$ the angular width of the shadow along the orbit at a planetocentric distance $\rho$ and we fix the arbitrary origin of time t to the middle point of the shadow. This is an appropriate choice in the case of the Yarkovsky-Schach effect, where Saturn's shadow plays essential role (Sect. 4). We also denote the angular tilt of solar direction from Saturn's spin axis by $\theta _0$, which spans an interval of values $\pi/2 \pm \varepsilon$, where $\varepsilon\simeq 26.73^\circ$ is Saturnian obliquity (see Fig. 1 for the planet-particle-Sun parameters introduced in the text). One easily shows that for $\rho\le\rho_\star=1/\cos\theta_0$we have $\Delta\ge 0$, namely

$$\tan\frac{\Delta}{2} = \sqrt{\frac{1-\rho^2\cos^2\theta_0}{\rho^2-1}}\cdot$$ (10)

The shadow function is expanded using

$$\Gamma(\zeta) = \sum c_k~ \zeta^k ,$$ (11)

with coefficients c_k given by

  

$$c_{0} = 1-\frac{\Delta}{2\pi} ,$$ (12)

$$c_{k} = -\frac{\sin~(k\Delta/2)}{k\pi} ,$$ (13)

where the second row applies when $k\neq 0$ (see, e.g., Ferraz-Mello 1972). Of particular interest is c₀ since it corresponds to the mean value of $\Gamma$ over one revolution of the particle about the planet. Obviously, for $\rho\ge\rho_\star$we have $\Delta=0$ and thus $\Gamma=1$ (c₀=1, c_k=0 for $k\neq 0$). It is interesting to note that the minimum value of $\rho_\star$ during Saturn's revolution about the Sun is $1/\sin\varepsilon\simeq 2.223$which nearly coincides with the outer radius of the A ring (at $\simeq$2.270). In other words, ring particles always enter the planetary shadow during their orbit about Saturn (an exception is the outer $\sim$19% strip of the A ring that, for a short period of time, resides fully outside Saturn's shadow). This fact, unrelated to any gravitational effects, attracted attention of Rubincam (2004, 2006) who considered it an important clue for a possible role of thermal forces on ring particles. Below, however, we challenge this conclusion suggesting it is a mere coincidence.

With the Fourier expansion (11) of the shadow function we can now write: $\overline{{\cal E}^{\rm V}}= c_0~{\cal E}_\star^{\rm V}/4$ (the factor 4 is here for the same reason as in the infrared flux). Combining Eqs. (5) and (9) we thus obtain

 

$$T_{\rm av}'^4\equiv \frac{\omega}{4} = \frac{1}{4}~\frac{\alpha_{... ...\psi(\rho)}{4~\alpha_{\rm V} + \alpha_{\rm I}\alpha_{\rm VS}\xi\psi(\rho)}\cdot$$ (14)

When the particle orbit does not intercept the planet's shadow, we have $\omega=1$; generally though $\omega<1$ as can be easily seen in Eq. (14). Moreover, since c₀ is a function of the time-dependent solar tilt angle $\theta _0$ from Saturn's spin axis, the mean temperature  $T_{\rm av}$ for the particle is constant during its revolution about the planet but variable as Saturn revolves about the Sun.

With the scaled variables introduced and with the mean temperature defined in Eq. (14), the heat diffusion problem (7) and (8) now becomes

 

$${\rm i} \zeta {\partial \over \partial \zeta}~ \Delta T'(r';\thet... ...) + \Lambda\left(\theta, \phi\right)\right\}~ \Delta T'(r';\theta,\phi;\zeta) ,$$ (15)

with the operator $\Lambda(\theta,\phi)$ given by

$$\Lambda\left(\theta,\phi\right) = {1\over \sin\theta}\left[{\... ...1\over \sin\theta}{\partial^2 \over \partial \phi^2}\right] ,$$ (16)

and the linearized boundary condition (2) reads

$$\sqrt{2}~\omega^{3/4} \Delta T'+ \Theta\left({\partial \Delta T'\over \partial r'}\right)_{R'} = \Delta {\cal S}' .$$ (17)

Here we denoted the particle radius with R and its scaled value $R'=R/\ell_{\rm s}$, and $\Delta {\cal S}' = {\cal S}'- \overline{{\cal S}'}$.

2.3 Solution of the linear heat diffusion problem

Given the assumed spherical geometry of the particle, it is natural to represent $\Delta T'$ in multipole series:

$$\Delta T'(r';\theta,\phi;\zeta) = \sum_{n\geq 1}~\sum_{k=-n}^n t'_{nk}(r';\zeta)~Y_{nk}(\theta,\phi) ,$$ (18)

with $Y_{nk}(\theta,\phi)$ denoting spherical functions. Inserting this expansion in Eq. (15) we find that the radial- and time-dependent amplitudes t'_nk fulfill a system of decoupled equations

$${\rm i} \zeta {\partial \over \partial \zeta}~ t'_{nk}(r';\... ... r'}\right) - n\left(n+1 \right)\right\}~ t'_{nk}(r';\zeta) ,$$ (19)

and at the surface r'=R' must satisfy

$$\sqrt{2}~\omega^{3/4} t'_{nk}(R';\zeta) + \Theta\left({\parti... ...'_{nk}\over \partial r'}\right)_{(R';\zeta)} = s_{nk}(\zeta) .$$ (20)

The time dependent right hand sides $s_{nk}(\zeta)$ of (20) are coefficients of the radiation source expansion $\Delta {\cal S}' (\zeta;\theta,\phi) =\sum_{n\geq 1}~\sum_{k=-n}^n s_{nk}(\zeta)~Y_{nk} (\theta,\phi)$. We summarize explicit expressions of $s_{nk}(\zeta)$necessary for our work in Appendix A.

Assuming now a particular Fourier mode in the time development of $s_{nk}(\zeta)$, namely $s_{nk}(\zeta) = s_{nk}^b~\zeta^b$ (with b integer and nonzero), Eqs. (19) and (20) admit solution $t'_{nk}(r';\zeta)= t^{\prime b}_{nk}(r')~\zeta^b$ with

$$t^{\prime b}_{nk}(r') = \frac{s_{nk}^b}{\sqrt{2}~ \omega^{3/... ...}{1+\chi~ \frac{Z}{j_n(Z)}~\frac{{\rm d} j_n(Z)}{{\rm d}Z}} ,$$ (21)

which is regular at r'=0. Here we denoted $z=\sqrt{-{\rm i} b}~r'$, $Z=\sqrt{-{\rm i} b}~R'$ and

$$\chi=\frac{\Theta}{\sqrt{2}~\omega^{3/4}~R'}\cdot$$ (22)

j_n(z) is a spherical Bessel function of the degree n of complex argument z (e.g., Abramowitz & Stegun 1970). Note while both $\Theta$ and R' depend on mean motion (or any other frequency they would be related to), $\chi$ becomes independent of it. A special attention is to be paid to the degree one coefficients with n=1. In this case, we have (recall $j_1(z)=(\sin z - z\cos z)/z^2$)

 

$$t^{\prime b}_{1k}(r') \frac{s_{1k}^b}{\sqrt{2}~ \omega^{3/4}}~\frac{j_1(z)}{j_1(Z)}~\frac{1}{1+\chi~ \frac{Z}{j_1(Z)}~\frac{{\rm d} j_1(Z)}{{\rm d}Z}}$$ =

$$\frac{s_{1k}^b}{\sqrt{2}~\omega^{3/4}~(1+\chi)}~\frac{j_1(z)} {j_1(Z)}~\frac{A(x_{\rm b})+{\rm i} B(x_{\rm b})}{C(x_{\rm b})+{\rm i} D(x_{\rm b})}$$ = (23)

$$\frac{s_{1k}^b}{\sqrt{2}~\omega^{3/4}~(1+\chi)}~ \frac{j_1(z)}{j_1(Z)}~E(x_{\rm b})\exp\left[{\rm i} \delta\left(x_{\rm b} \right)\right] ,$$ =

where $x_{\rm b}=\sqrt{2b}~R'$. The auxiliary functions A(x), B(x), C(x), D(x) are given, e.g., in Vokrouhlický (1998, 1999). It turns suitable to express the complex number $(A+{\rm i} B)/(C+{\rm i} D)$in amplitude-phase representation $E\exp({\rm i} \delta)$ as it has been used in the last row of (23). The angle $\delta<0$ plays the role of a thermal lag. For b<0 though, it is more convenient to write $x_{\rm b}=\sqrt{2\vert b\vert} ~R'$ and $E\exp({\rm i} \delta)$ becomes complex conjugate, namely $E\exp~(-{\rm i} \delta)$. These modes describe thermal advance rather than thermal lag. In Appendix D we note this case is appropriate for ring particles whose rotation rate is slower than their mean motion about the planet.

2.4 Thermal force computation

With the aim to compute the thermal recoil acceleration $\vec{f}$ on the particle we show now that only a very limited number of amplitude terms t'_nk is needed, a property which greatly simplifies analytical solution. In agreement with previous work we assume thermal radiation of the particle's surface isotropic (Lambert's law). Integrating over all contributions from infinitesimal oriented surface elements d $\vec{S}=R^2~{\rm d}\Omega~\vec{n}$, where ${\rm d}\Omega = \sin\theta~ {\rm d}\theta {\rm d}\phi$, we have (e.g., Milani et al. 1987; Bottke et al. 2002)

$$\vec{f}(\zeta) = -\int R^2{\rm d}\Omega~\frac{2}{3}\frac{\epsilon \sigma T^4}{mc}~\vec{n} .$$ (24)

Here we denoted particle's mass with m and the light velocity with c; the minus sign indicates thermal radiation recoils on the body. Using again linearization of the T⁴ term and introducing scaled quantities from our solution above, we obtain

$$\vec{f}(\zeta) = -{2\sqrt{2}\over 3\pi}~\omega^{3/4} \Phi \int {\rm d}\Omega~ \Delta T'(R';\theta,\phi;\zeta)~ \vec{n} ,$$ (25)

with $\Phi = ({\cal S}_\star \pi R^2/mc)$ the characteristic radiation force factor. It is now important to recall that components of the unitary vector $\vec{n}$ can be expressed using a linear combination of spherical function of degree 1, namely $n_X\pm{\rm i} ~n_Y = \mp~ 2\sqrt{\frac{2\pi}{3}}~Y_{1\pm 1}$ and  $n_Z=2\sqrt{\frac{\pi}{3}}~Y_{10}$. With these relations, and orthogonality property of spherical functions, we easily find that the thermal acceleration components (f_X,f_Y,f_Z) in an arbitrary frame whose axis Z is that of the particle's spin $\vec{s}$ read

  

$$f_X(\zeta) \pm {\rm i} f_Y(\zeta) \mp {8\over 3\sqrt{3\pi}}~ \omega^{3/4}\Phi~ t'_{1\mp 1}(R';\zeta) ,$$ = (26)

$$f_Z(\zeta) -{4\over 3}\sqrt{2\over 3\pi}~\omega^{3/4} \Phi~ t'_{10}(R';\zeta) .$$ = (27)

We conclude, that only dipole coefficients t'_1k are needed to compute thermal acceleration in the linearized theory (e.g., Rubincam 1998; Vokrouhlický 1998, 1999). For that reason, we omit computation of other coefficients below.

2.5 Orbital averaging of the thermal force

The second important simplification stems from our goal to determine the long-term effect of the thermal forces on the planetocentric orbital semimajor axis a. With zero eccentricity, we have

$$\frac{{\rm d}a}{{\rm d}t} = \frac{2}{n}~f_\tau ,$$ (28)

where $f_\tau = \vec{f}\cdot\vec{\tau}$ is a transverse component of the thermal acceleration. The unitary vector $\vec{\tau}$ transverse to the orbit, and expressed in the planetocentric orbital frame, reads: $\tau_x=\frac{{\rm i}}{2} (\zeta-\zeta^{-1})$, $\tau_y=\frac{1}{2}(\zeta+\zeta^{-1})$, $\tau_z=0$. Secular perturbations arose as orbit-averages of the right hand sides of Gauss perturbation equations such as (28) for semimajor axis. Since $\vec{\tau}$ depends on the first powers of $\zeta$ only, we need to identify the appropriate terms in the planetocentric frame development of $\vec{f}$. However, the solution of the heat diffusion problem becomes more natural in the ring-particle-fixed frame, so we undertake the other possible approach and transform $\vec{\tau}$ to this latter frame. Its algebraic form becomes different for the effects due to the Z-axis force component (often called the seasonal component) parallel to the particle spin axis direction $\vec{s}$ and the XY-plane force components (often called the diurnal components) in the particle's equatorial plane. We thus analyse the two cases separately in the following two sections.

  
2.5.1 Seasonal component

Assume $t'_{10}(R';\zeta)$ in the particle-fixed frame developed in Fourier series

$$t'_{10}(R';\zeta) = \varphi^+\zeta +\varphi^-\zeta^{-1}+ \ldots$$ (29)

Since the transformation of the orbit transverse vector $\vec{\tau}$ to the particle-fixed frame yields

$$f_\tau = \frac{{\rm i} f_Z}{2}\left(s_-\zeta-s_+\zeta^{-1}\right) ,$$ (30)

we note only the highlighted $\propto$ $\zeta^{\pm 1}$ terms in development of  $t'_{10}(R';\zeta)$ in (29) give nonzero long-term orbital effects (after averaging over $\zeta$). In Eq. (30) we also introduced a notation $s_\pm = s_1\pm {\rm i} s_2$, where s₁ and s₂ are projection of the particle's spin vector $\vec{s}$ onto x- and y-axes of a planetocentric reference frame whose xy-plane coincides with the ring plane, x-axis is the origin of time for the orbital motion (thus $\zeta=1$). The choice of x-direction in the ring-plane is arbitrary and should make the analytic computation easier. This is why this choice is different for the Yarkovsky and the Yarkovsky-Schach effects and will be introduced in Sects. 3 and 4. After averaging over particle's motion about the planet, that will be denoted with square brackets with index 1, we have the mean transverse acceleration

$$\left[f_\tau\right]_1 = -{4\over 3}\sqrt{2\over 3\pi}~ \omega^{3/4} \Phi~\Im\left(s_+\varphi^+\right) ,$$ (31)

where $\Im(z)$ denote the imaginary part of a complex number z.

  
2.5.2 Diurnal component

For the diurnal components computation we shall follow the general approach of Vokrouhlický (1999). To confine the problem periodic, we shall assume the ratio of rotation frequency $\Omega$to the planetocentric revolution frequency n is an integer parameter $m=\Omega/n$ (it is however easy to generalize the results for an arbitrary real value of m). In this case, we highlight the following Fourier components in the development of $t'_{11}(R';\zeta)$:

$$t'_{11}(R';\zeta) = \tau^+\zeta^{m+1} +\tau^-\zeta^{m-1}+ \ldots$$ (32)

After transforming $\vec{\tau}$ into the particle-fixed frame we obtain the orbit-averaged transverse thermal acceleration due to the diurnal force components

$$\left[f_\tau\right]_1 = -{8\over 3\sqrt{3\pi}}~ {\omega^{3/4... ...mma}{2}~\tau^-s_- +\sin^2\frac{\gamma}{2} ~\tau^+s_+\right) ,$$ (33)

where $\Re(z)$ denote the real part of a complex number z and $\gamma$ is the obliquity of $\vec{s}$ (i.e. the angle between $\vec{s}$ and the planet's spin axis direction perpendicular to the ring-plane).

  
3 Planetary Yarkovsky effect

Having outlined the general scheme, we shall now apply it to the two possible heating sources for the ring particles: (i) thermal radiation of the planet (this section), and (ii) the optical radiation of the Sun (Sect. 4). We always split the computation of the seasonal- and diurnal-force components into separate sections, starting with the seasonal part.

3.1 Seasonal component

The seasonal variant of the Yarkovsky effect has been introduced in orbital mechanics by Rubincam (1987) who studied the secular decrease of semimajor axis of the Earth-bound artificial satellite Lageos. The "cartoon-based'' illustration of the seasonal thermal effect has been repeated many times in the literature (e.g., Rubincam 1987, 1995, 1998; Bottke et al. 2002). It has to do with time lag in thermal radiation of northern and southern hemispheres of a body as it revolves about the radiating center (a star or a planet). For low-eccentricity orbits it always leads to orbital decay toward the centre.

The seasonal thermal force is produced, technically speaking, by choosing the planet's thermal radiation as a radiative source and the along-spin component f_Z of the thermal force (Sect. 2). The most suitable choice of time origin t=0 along the orbital motion of ring particle is when the spin axis is perpendicular to the planetocentric position vector. With $\gamma$being the particle's spin axis obliquity, this choice of the planetocentric reference frame implies s₁=0, $s_2=\sin\gamma$ and $s_3=\cos\gamma$, such that $s_+={\rm i}\sin\gamma$. One can show that the dipole source term reads

$$s_{10}(R';\zeta) = \frac{{\rm i}}{2}~\sqrt{\frac{\pi}{3}}~\fr... ...2~{\cal S}_\star}~\sin\gamma~ \left(\zeta-\zeta^{-1}\right) .$$ (34)

With the aid of Eq. (23) we obtain

$$\varphi^+ = \frac{{\rm i}}{2}~\sqrt{\frac{\pi}{6}}~\frac{\alp... ...1+\chi)}~E(x)\exp\left[{\rm i} \delta\left(x \right)\right] ,$$ (35)

with $x=\sqrt{2}~R'$; for simplicity we shorten $E(x)\exp\left[ {\rm i} \delta\left(x\right)\right] = E\exp({\rm i}\delta)$ in the following text. Combining the expression for s₊ with the source coefficient $\varphi^+$ from Eqs. (35) and (31) we finally obtain

 

$$\left[f_\tau\right]_1 \frac{2}{9}~\Phi~\frac{\alpha_{\rm I} {\cal E}^{\rm I}_{\star 0}}{\rho^2~{\cal S}_\star}~ \frac{E\sin\delta}{1+\chi}~\sin^2\gamma$$ = (36)

$$\frac{2}{9}~\Phi_1~\frac{E\sin\delta}{1+\chi}~\sin^2\gamma ,$$ =

for the orbit-averaged transverse component of the seasonal thermal acceleration. Here we introduced

$$\Phi_1 = \frac{\alpha_{\rm I}{\cal E}^{\rm I}_{\star 0}}{\rho^2}~ \frac{\pi R^2}{mc}\cdot$$ (37)

Equation (28) yields the secular change of the planetocentric semimajor axis (e.g., Vokrouhlický & Farinella 1999; Vokrouhlický 1999)

$$\left[\frac{{\rm d}a}{{\rm d}t}\right]_1 = \frac{4}{9n}~\Phi_1~\frac{E\sin\delta}{1 +\chi}~\sin^2\gamma .$$ (38)

Since $\delta<0$, both $\left[f_\tau\right]_1$ and $[{\rm d}a/{\rm d}t]_1$ are always negative. Put in other words, the seasonal Yarkovsky effect permanently drains angular momentum from the particle's orbital motion at a rate  $(ma~\left[f_\tau\right]_1)$.

A characteristic timescale of the ring particles' revolution about Saturn is of the order of a few hours. This is much shorter than any scale that might interest as far as the long-term ring fate is concerned. To bring our result closer to the relevant level we must now average previous results for the mean transverse force (36) or semimajor axis drift (38) over two longer timescales:

• Saturn's motion about the Sun ($\simeq$years), and
• a characteristic timescale over which the spin axis $\vec{s}$ orientation in space of the particles evolves.

To make our formalism clear, we shall denote the result of the second averaging (over Saturn's motion about the Sun) with  $[\ldots]_2$ and the result of the third averaging (over particle spin axis evolution) with $[\ldots]_3$. When the first (orbit revolution) and second averaging are done, the result will be denoted $[\ldots]_{12}$, etc.

The second averaging is conceptually simple and it only means that the geometry of the planet's shadow cast on the ring-plane changes over Saturn' revolution about the Sun (this is because of its significant obliquity). Neglecting the eccentricity of Saturn's orbit about the Sun and denoting its longitude in orbit with $\lambda$ we have

$$\cos\theta_0=\sin\varepsilon~\cos\lambda .$$ (39)

Recall $\theta _0$ is the angular tilt of direction toward the Sun from Saturn's spin axis whose obliquity is denoted $\varepsilon$. We arbitrarily chose $\lambda= 0^\circ$ when $\theta _0$ is minimum (i.e. maximum angular elevation of the Sun above the ring-plane). Recall the $\omega$ function in Eq. (14) depends on $\theta _0$ via the mean shadow function coefficient c₀. In the same time, the $\chi$ parameter in Eq. (22) depends on $\omega$ and thus also on Saturn's revolution phase about the Sun. We thus write

$$\left[f_\tau\right]_{12} = \frac{2}{9}~\Phi_1~\left[ \frac{E\sin\delta}{1+\chi}\right]_2~\sin^2\gamma ,$$ (40)

where

$$\left[\frac{E\sin\delta}{1+\chi}\right]_2 = \frac{1}{2\pi}\int_0^{2\pi} {\rm d}\lambda~\frac{E\sin\delta}{1+\chi}\cdot$$ (41)

This averaging can only be performed numerically. In the most rough approximation, we might neglect $\lambda$-dependence of $\omega$ adopting its value for $\lambda=90^\circ$ (thus $\theta_0=90^\circ$).

The third averaging, related to the ring particles' spin axis evolution, is much more complicated and the least certain issue in our solution. We adopt only a very crude approach in this paper, but most of the formalism and results in Sect. 2 are ready for adopting different schemes about ring particle rotation states. Here we assume that particle collisions eventually lead to randomization of $\vec{s}$ (see Appendix D for an alternative model of particles with $\vec{s}$ aligned with the disk-plane normal). The timescale on which this happens, if it does really happen, is not known exactly but we always assume the second and third averaging steps are decoupled. Assuming thus a sample of many particles with randomly oriented spin axis in space, we easily determine that $[\sin^2\gamma]_3=2/3$. As a result, the long-term mean seasonal thermal acceleration reads

$$\left[f_\tau\right]_{123}=\left[f_\tau\right]_{132} = \frac{4}{27}~\Phi_1 ~\left[\frac{E\sin\delta}{1+\chi}\right]_2\cdot$$ (42)

The same value is adopted for a long-term average of the transverse thermal acceleration for a single ring particle in orbit about Saturn whose spin axis undergoes collisions capable of random re-orientations of its spin axis.

3.2 Diurnal component

The diurnal component of the Yarkovsky effect is related to the equatorial force components f_X and f_Y given by Eq. (26). It represents the original version of the Yarkovsky effect analysed by Öpik (1951). For low-enough surface thermal conductivity, it typically dominates in strength the effects of the previously discussed seasonal variant, but for a sample of bodies with an isotropic distribution of spin axes it typically produces a null average orbital displacement. For that reason it has been thought to have a negligible long-term effect (see, e.g., discussion in Burns et al. 1979), and thus was dropped by Rubincam (2006) from his initial analysis of the thermal forces acting on ring particles.

Here, however, we decided to include the diurnal variants of both Yarkovsky and Yarkovsky-Schach effects in our analysis and comment on their potential importance for two reasons. First, while usually producing zero net orbital change for a sample of objects with an isotropic spin-axis distribution, the diurnal Yarkovsky effect can still produce a net semimajor axis dispersion growing with time (such as a random walk process). This may result in leaking the objects if the sample is bracketed by some boundary (e.g., the case of near-Earth asteroids leaking from the main belt reservoir through the adjacent resonances; e.g., Morbidelli & Vokrouhlický 2003). Second, the general result of a null mean orbital effect due to the diurnal Yarkovsky forces is only true for very fast spinning bodies (such as asteroids or meteoroids). As first studied by Vokrouhlický (1999), when the rotation period of the bodies becomes comparable to the revolution period, so that m is not much larger than unity in Sect. 2.5.2, the diurnal effect can result in a net secular change of orbits even for a sample of bodies with spin-axis isotropy. The works of Richardson (1994), and lately Salo & Karjalainen (2003), Ohtsuki & Toyama (2005), Morishima & Salo (2006) and Ohtsuki (2006), indicate that the small ring particles most appropriate for our work acquire collisional equilibrium with a mean rotation rate about one or two orders of magnitude higher than the orbital rate. The obliquity distribution is nearly isotropic, with only a small preference to retrograde spins. By itself, the $m\sim 10$ratio is small enough to motivate a check of the diurnal Yarkovsky effect's importance even for the ring particles (though we do not study here in detail the orbit-diffusion aspect of the diurnal Yarkovsky forces). Moreover, the largest particles in the rings rotate typically very slowly. Their appropriate m is even smaller than unity, with minimum values of $m\sim 0.3$. Their spin axis tends to be preferentially aligned with the normal of ring-plane. For this population of ring particles the diurnal components of the thermal effects are definitely important and we shall discuss this special case in Appendix D.

After transforming the source (planet) position into the particle-fixed frame we obtain

$$s_{11}(R';\zeta) = \sqrt{\frac{\pi}{6}}~\frac{\alpha_{\rm I} ... ...ma}{2}~\zeta^{m+1}+\cos^2\frac{\gamma}{2}~ \zeta^{m-1}\right)$$ (43)

for the appropriate term needed in the boundary condition (20). Using the general scheme for the linearized heat diffusion solution, Eqs. (23) and (32), we obtain

  

$$\tau^+ = \frac{1}{2}~\sqrt{\frac{\pi}{3}}~\frac{\alpha_{\rm I} {\... ...{\omega^{3/4}(1+\chi)}~E(x_+) \exp\left[{\rm i} \delta\left(x_+\right)\right] ,$$ (44)

$$\tau^- = \frac{1}{2}~\sqrt{\frac{\pi}{3}}~\frac{\alpha_{\rm I} {\... ...{\omega^{3/4}(1+\chi)}~E(x_-) \exp\left[{\rm i} \delta\left(x_-\right)\right] ,$$ (45)

with $x_\pm=\sqrt{2~(m\pm 1)}~R'$; to shorten notation we further use $E(x_\pm)\exp~[{\rm i}\delta(x_\pm)]=E_\pm\exp~[{\rm i}\delta_\pm]$. The general formula (33) then straightforwardly results in

$$\left[f_\tau\right]_1 = \frac{4}{9}~\Phi_1~\left(\sin^4 \fra... ...cos^4 \frac{\gamma}{2}\frac{E_-\sin\delta_-}{1+\chi}\right) ,$$ (46)

which gives the orbit-averaged Yarkovsky acceleration due to the diurnal effect on a body with an obliquity $\gamma$. The second-level time-averaging over the planet's motion about the Sun is straightforward as in the previous Section (and will again be denoted by a $[\ldots]_2$ symbol). Averaging over an isotropic distribution of spin axes then only requires $[\sin^4 \gamma/2]_3= [\cos^4 \gamma/2]_3=1/3$, giving thus our final form for the diurnal Yarkovsky acceleration:

$$\left[f_\tau\right]_{123} = \frac{4}{27}~\Phi_1~\left(\left[ ... ..._2-\left[\frac{E_-\sin \delta_-}{1+\chi}\right]_2\right)\cdot$$ (47)

As anticipated above, when $m\gg 1$, $x_+ \simeq x_-$ such that $E_+\sin\delta_+ \simeq E_-\sin\delta_-$ and the net diurnal effect vanishes. When m is not large, and surface conductivity low, the resulting effect is a slight net outward drift of the orbits. In the extreme case m<1 we have $x_-=\sqrt{2~(1-m)}~R'$ and the sign in $E_-\sin\delta_-$ should be changed.

  
4 Yarkovsky-Schach effect

Like the seasonal thermal drag, this variant of the thermal thrust has been discovered when analyzing tiny orbit decay of the Lageos satellite. Rubincam (1982) describes it as "tilted shadow effect'', while a more detailed quantitative analysis has been developed by Afonso et al. (1989) and others. Recently, Vokrouhlický et al. (2005) discuss how this variant of the thermal effects could affect the relative motion of binary asteroids, and Rubincam (2006) pointed out its possible importance for the ring particle motion.

Unlike in the case of the seasonal Yarkovsky effect in Sect. 3, the radiation source is now the Sun in the visible band. If there were no interruptions due to entries into the planet's shadow, the corresponding thermal force on the particle would be approximately constant in space (it would only slowly change as the planet revolves about the Sun). With that, the average semimajor axis change would be zero. However, when the planetocentric orbit of the particle is intercepted by shadow periods the particle cools in the shadow and heats in the sunlight. These two processes do not exactly compensate and a net transverse acceleration is produced. This is the essence of the Yarkovsky-Schach thermal thrust.

The Yarkovsky-Schach effect has been mostly studied in the limit of a fast particle rotation ($m\gg 1$), the case of an initial orbital-evolution phase of Lageos. Motivated by this spacecraft fast despinning, Farinella & Vokrouhlický (1996) attempted to develop a theory of the diurnal Yarkovsky-Schach effect, but their theory remained approximate. In Sect. 4.2 we give a first fully consistent approach to the diurnal Yarkovsky-Schach effect for a spherical body.

  
4.1 Seasonal component

The most suitable planetocentric reference frame to study the Yarkovsky-Schach effect derives from the symmetry of the planetary shadow. The ring-plane axis x coincides with the symmetry axis of the shadow. Time origin, t=0, thus $\zeta=1$, is when the ring particle crosses this axis. As always in our paper the z-axis is along Saturn's spin axis. In this frame the solar direction unitary vector has components $(-\sin\theta_0,0,\cos\theta_0)^T$ and the particle's spin axis is set at an arbitrary $\vec{s}= (s_1,s_2,s_3)^T$.

With that choice of reference frames, the transformation of the solar direction in the particle-fixed frame yields the zonal dipole source coefficient:

$$s_{10}(R';\zeta) = - \sqrt{\frac{\pi}{3}}~\frac{\alpha_{\rm V... ...\left(s_1\sin\theta_0-s_3 \cos\theta_0\right)~\Gamma(\zeta) .$$ (48)

Since the Sun is assumed fixed in space over the timescale of particle revolution about the planet, the time dependence of s₁₀ in (48) arises entirely from the shadow function $\Gamma(\zeta)=\sum c_k~\zeta^k$ (see Sect. 2.2). Sorting out the necessary Fourier terms from its development, we obtain

$$\varphi^+ = - \frac{\alpha_{\rm V}{\cal E}^{\rm V}_\star}{{\c... ... c_1~\frac{E\exp~({\rm i} \delta)}{\omega^{3/4}~(1+\chi)}\cdot$$ (49)

This is the amplitude of the Fourier term proportional to $\zeta$ in development of the temperature zonal dipole coefficient (Eq. (29)). The first degree coefficient of the shadow function $\Gamma(\zeta)$reads (Eqs. (10) and (13))

$$c_1 = -\frac{\sin~(\Delta/2)}{\pi} = -\frac{\sqrt{1-\rho^2\cos^2\theta_0}}{\pi\rho\sin\theta_0}\cdot$$ (50)

The orbit-averaged transverse acceleration is easily accomplished using Eq. (31) with the result

 

$$\left[f_\tau\right]_1 = \frac{4}{9}~\Phi_2~\frac{c_1 E}{1+\chi}~ ... ...\sin\theta_0-s_3\cos\theta_0\right) \left(s_1\sin\delta+s_2\cos \delta\right) ,$$ (51)

where

$$\Phi_2 = \alpha_{\rm V}{\cal E}^{\rm V}_\star~\frac{\pi R^2}{mc}\cdot$$ (52)

At the second step we aim to compute the average over a timescale of the planet's motion about the Sun. This is a sufficient interval for $\cos\theta_0$ to have a zero mean (Eq. (39)), such that we obtain

$$\left[f_\tau\right]_{12} = \frac{4}{9}~\Phi_2~\left[c_1\sin\t... ...ft(s_1\sin\delta+s_2\cos\delta\right)}{1+\chi} \right]_2\cdot$$ (53)

As above, thanks to enough-complicated functional form of the arguments the $[\ldots]_2$-averaging should be performed numerically. Interestingly, the s₃ projection of $\vec{s}$ entirely dropped from this expression.

Finally, adopting the model of random re-orientations of the spin axis for ring particles we note that [s₁²]₃ = 1/3 while [s₁ s₂]₃ = 0. Thus the overall mean of the thermal transverse component due to the seasonal component of the Yarkovsky-Schach effect reads

$$\left[f_\tau\right]_{123} = \left[f_\tau\right]_{132} =-\frac... ...{1+\chi}~\frac{\sqrt{1-\rho^2 \cos^2\theta_0}}{\rho}\right]_2$$ (54)

(here we inserted c₁ from Eq. (50)). It has been pointed out by Rubincam (2006) that $\left[f_\tau\right]_{123}$ in (54) is always positive because the thermal-lag angle $\delta$ is negative. Unlike the seasonal thermal drag, the Yarkovsky-Schach effect thus on average supplies angular momentum to the orbital motion of ring particles on a long term.

  
4.2 Diurnal component

With the same planetocentric reference system we now obtain the tesseral dipole coefficients of the particle insolation

$$s_{11}(R';\zeta) = \sqrt{\frac{\pi}{6}}~ \frac{\alpha_{\rm V... ...S}_\star}~\sigma_- \frac{\zeta^m~\Gamma(\zeta)}{\sin\gamma} ,$$ (55)

where we introduced

$$\sigma_\pm = s_2\sin\theta_0\pm {\rm i}~\left(s_1\cos\gamma \sin\theta_0+\sin^2\gamma\cos\theta_0\right) .$$ (56)

Equation (23) then provides the corresponding amplitude of the Fourier terms proportional to $\zeta^{m\pm 1}$ in tesseral dipole coefficient of the temperature development

  

$$\tau^+ = \frac{1}{2}~\sqrt{\frac{\pi}{3}}~\frac{\alpha_{\rm V} {\... ...-~c_1} {\sin\gamma}~\frac{E_+\exp~({\rm i} \delta_+)}{\omega^{3/4} ~(1+\chi)} ,$$ (57)

$$\tau^- = \frac{1}{2}~\sqrt{\frac{\pi}{3}}~\frac{\alpha_{\rm V} {\... ..._1} {\sin\gamma}~\frac{E_-\exp~({\rm i} \delta_-)}{\omega^{3/4} ~(1+\chi)}\cdot$$ (58)

We keep the same notation as in (44) and (45), namely $x_\pm=\sqrt{2~(m\pm 1)}~R'$. While straightforward, the averaging over different timescales and the isotropic distribution of spin axes gives a rather busy formula. We just give the final result after all algebra is completed

 

$$\left[f_\tau\right]_{123} = -\frac{4}{27\pi}~\Phi_2~\Biggl( \left... ...lta_-}{1+\chi}~\frac{\sqrt{1-\rho^2 \cos^2\theta_0}}{\rho}\right]_2\Biggr)\cdot$$ (59)

As in the case of diurnal planetary Yarkovsky effect (Eq. (47)), the net orbital effect of the diurnal force components of the Yarkovsky-Schach perturbation is zero for rapidly rotating particles ($m\gg 1$ and $x_+ \simeq x_-$). For a slowly-enough rotating sample of particles, the net diurnal effect (59) might again become non-zero and we shall test different assumptions below. In the extreme case m<1 we again have $x_-=\sqrt{2~(1-m)}~R'$ and the sign in $E_-\sin\delta_-$ should be changed.

  
5 Null-torque orbits and estimated drift rates of ring particles

For the sake of simplicity, we first consider the seasonal components of the thermal effects as in Rubincam (2004, 2006). The effects of the diurnal components are introduced in Sect. 5.3.

5.1 Low contrast in optical and infrared absorptivities

Rubincam (2004, 2006) proposed that boundaries of the two main Saturn's rings are related to thermal drifts of their constituents. Namely, he associated them with the null-torque orbits $[f_\tau ]_{123}=0$ (we analyze location of these orbits in Appendix E and show they can be reasonably determined using simple analytic formulae). Here, however, we bring several arguments to critically review this scenario.

First we point out a large sensitivity of the critical no-torque distance to the obliquity $\varepsilon$ of Saturn. Figure 2 shows the long-term average transverse acceleration due to the combined seasonal Yarkovsky and Yarkovsky-Schach effects. We assumed an icy particle with size D=1 cm, $\rho _{\rm b}=0.5$ g/cm³ and C=820 J/kg/K and the thermal conductivity K=10^-4 W/m/K. We also set $\alpha _{\rm V}= 0.5$ and $\alpha _{\rm I}=0.665$ in this particular case, such that all our parameters are identical to those in Rubincam (2006). The four curves correspond to obliquity values $24^\circ$, $25^\circ$, $26.73^\circ$ (the current value) and $28^\circ$. We note that small changes in Saturn's obliquity produce significant modifications of the results, especially (i) displacement of the outer critical orbit for smaller $\varepsilon$ values, and (ii) produces no solution for larger $\varepsilon$ values. Obviously, this is mainly because the Yarkovsky-Schach effect is strongly sensitive to the minimum extension of Saturn's shadow. The same behavior is observed in Fig. 3 where we plot the position of the no-torque orbits in the plane defined by the ratio of infrared and optical absorptivities $\alpha _{\rm I}/\alpha _{\rm V}$ and distance from Saturn $\rho$.

Figure 2: Long-term mean thermal transverse acceleration (in pm/s2) for D=1 cm ring particles as a function of the planetocentric distance $\rho$ (in planet's radii). We assume bulk density $\rho _{\rm b}=0.5$ g/cm3, specific thermal capacity C=820 J/kg/K and thermal conductivity K=10-4 W/m/K. Optical and thermal absorptivities are $\alpha _{\rm V}= 0.5$ and $\alpha _{\rm I}=0.665$. Four different curves are for different assumptions about Saturn's obliquity $\varepsilon$: (i) $24^\circ$ (label 1), (ii) $25^\circ$ (label 2), (iii) $26.73^\circ$ (the current value; thick line), and (iv) $28^\circ$ (label 3).

Open with DEXTER

Figure 3: Distance from Saturn where zero mean thermal torque $[f_\tau ]_{123}=0$ applies on the orbital motion of ring particles as a function of ratio between their absorptivity in thermal $\alpha _{\rm I}$ and optical $\alpha _{\rm V}$ bands. We assume particles of diameter D=1 cm, bulk density $\rho _{\rm b}=0.5$ g/cm3, specific thermal capacity C=820 J/kg/K and thermal conductivity K=10-4 W/m/K. Current position of the A and B rings is shown by the shaded zones. The three curves are for three possible values of Saturn's obliquity $\varepsilon$: (i) $24^\circ$ (label 1), (ii) $26^\circ$ (label 2), and (iii) $28^\circ$ (label 3).

Open with DEXTER

Figure 4: Isolines of positive (solid) and negative (dashed) values of the mean transverse acceleration $[f_\tau ]_{123}$ resulting from composition of thermal and P-R effects in the plane of distance from Saturn ($\rho$ in planetary radii) and size of the ring particle (D in cm). The four plots correspond to four possible values of Saturn's obliquity: (i) $\varepsilon =24^\circ$ ( left and top), (ii) $\varepsilon =26^\circ$ ( right and top), (iii) $\varepsilon =26.73^\circ$ ( left and bottom; current value), and (iii)  $\varepsilon =28^\circ$ ( right and bottom). The level curve distance is 0.25 pm/s2 for positive values, and -1 pm/s2 for negative values. In the two top figures the thick solid isoline is where $[f_\tau ]_{123}=0$ pm/s2, while in the bottom two figures (where no positive $[f_\tau ]_{123}$ occur) the thick dashed line is for $[f_\tau ]_{123}=-1$ pm/s2. The ring particles are assumed to have the following thermal parameters: bulk density $\rho _{\rm b}=0.5$ g/cm3, specific heat capacity C=820 J/kg/K, thermal conductivity K=10-4 W/m/K and ratio of thermal and optical absorptivity $\alpha _{\rm I}/\alpha _{\rm V}=1.33$ and $\alpha _{\rm V}= 0.5$. Shaded zones indicate position of the main B and A rings.

Open with DEXTER

It is interesting to note that a model by Ward & Hamilton (2004) and Hamilton & Ward (2004), provides a natural arena for such small but significant changes in Saturn's obliquity. In their view, Saturn's spin axis is presently trapped in a secular spin-orbit resonance s₈, librating with a large amplitude about Cassini state 2. If true, this resonance forces Saturn's obliquity to undergo variations that make it change in between maximum limits of $\simeq$$24^\circ$ to $\simeq$$30^\circ$(Hamilton & Ward 2004). The corresponding libration period is $\sim$100 My. The Cassini mission may provide more accurate data about Saturn's spin axis direction and precession rate (moments of inertia), which may modify the quantitative results in Hamilton & Ward (2004). In this situation we consider their model as a likely possibility and investigate its implications for the ring particle migration by the thermal effects. For instance, if the A and B ring boundaries were indeed strictly linked to the null-torque orbits, the rings would - for constant optical and thermal parameters - hardly survive one obliquity cycle since when the obliquity achieves its minimum value they disappear. Obviously, such considerations concern small-enough particles only.

More importantly, though, the previous results change significantly when Poynting-Robertson (P-R; see Appendix B) drag is added into our analysis. Figure 4 shows isolines of mean transverse acceleration $[f_\tau ]_{123}$ due to combined radiativeeffects (both the P-R and the seasonal thermal forces). We assumed the same thermal parameters as before: bulk density $\rho _{\rm b}=0.5$ g/cm³, specific thermal capacity C=820 J/kg/K, thermal conductivity K=10^-4 W/m/K and ratio of thermal and optical absorptivity  $\alpha _{\rm I}/\alpha _{\rm V}=1.33$ which holds for values $\alpha _{\rm V}= 0.5$ and $\alpha _{\rm I}=0.665$ suggested by Rubincam (2004, 2006). We again show results for different values of Saturn's obliquity $\varepsilon =24^\circ$, $26^\circ$, $\varepsilon =26.73^\circ$ (current value) and $28^\circ$.

We note that for particles smaller than $\simeq$3 mm in size, the P-R drag becomes dominant and makes all ring particle orbits decay toward the planet with an increasing rate for smaller sizes (approximately as $\propto$1/D). For low enough obliquities, $\varepsilon\leq 26^\circ$ in our examples, the Yarkovsky-Schach effect overcomes both inward drifts (seasonal Yarkovsky and P-R effects) in some distance range from the planet. This distance range is weakly dependent on the size of the particles, as expected from the discussion in Appendix E (obviously though, the outward drift values become very small for larger particles). For the present value of Saturn's obliquity, and larger values, no particles migrate outward from the planet and the thermal effects result only in an anomalous increase of the inward drag roughly in the A ring zone.

Figure 5: The same as in Fig. 4 but now for different ratios of the absorptivity coefficients in optical $\alpha _{\rm V}$ and infrared $\alpha _{\rm I}$: (i) left and top figure corresponds to $\alpha _{\rm V}=0.4$ and $\alpha _{\rm I}/\alpha _{\rm V}=2.25$ (a guess for the B ring particle values), (ii) right and top figure corresponds to $\alpha _{\rm V}= 0.5$ and $\alpha _{\rm I}/ \alpha _{\rm V}=1.8$ (a guess for the A ring particle values), (iii) left and bottom figure corresponds to $\alpha _{\rm V}= 0.75$ and $\alpha _{\rm I}/\alpha _{\rm V}=1.2$ (a guess for the C ring particle values), and (iv) right and bottom figure corresponds to $\alpha _{\rm V}=0.6$ and $\alpha _{\rm I}/\alpha _{\rm V}=1.5$ (a guess for the Cassini division particle values). Nominal value $\varepsilon =26.73^\circ$ of Saturn's obliquity and low conductivity K=10-4 W/m/K are assumed here. Dashed are isolines of negative $[f_\tau ]_{123}$ values with constant step -3 pm/s2 (the bold dashed curves correspond to $[f_\tau ]_{123}=-3$ pm/s2). Solid are isolines of positive $[f_\tau ]_{123}$ values with constant step +1 pm/s2 (the bold solid curve on the left and bottom panel is $[f_\tau ]_{123}=0$ pm/s2).

Open with DEXTER

5.2 High contrast in optical and infrared absorptivities

Perhaps the most serious caveat of the previous results is that the assumed mid-infrared albedo value $A_{\rm I}=0.335$ (giving thus $\alpha _{\rm I}=0.665$) is too high. In spite of a large uncertainty in its value, previous evidence points toward a much lower value $A_{\rm I}\sim 0.1$ (e.g., Irvine & Pollack 1968; Kawata & Irvine 1975; Hudgins et al. 1993). This means that relatively more Saturn's infrared radiation gets absorbed by the ring particles ( $\alpha_{\rm I}\sim 0.9$) and this increases the strength of the planetary Yarkovsky effect.

Bringing together our best estimates of Bond albedo in the optical for different ring-zones we shall re-derive our best estimates of radiative drift rates for particles with typical sizes of a few centimetres. Data from Porco et al. (2005) confirm, with much higher resolution then available before, the following values for the optical albedo: (i) $A_{\rm V}\simeq 0.25$ for the C ring, (ii)  $A_{\rm V}\simeq 0.6$ for the B ring (especially its outer part), (iii)  $A_{\rm V}\simeq 0.4$ for particles in the Cassini division, and (iv) $A_{\rm V}\simeq 0.5$ for the A ring (consistent values have been obtained in the previous literature, e.g., Dones et al. 1993, or Esposito et al. 1984, and references therein). There are certainly variations across the rings extension but in the first approximation we adopt these characteristic values. In all cases we consider our nominal value of the Bondalbedo in the mid-infrared $A_{\rm I}= 0.1$. Except for the C ring particle parameters, the ratio $\alpha _{\rm I}/\alpha _{\rm V}$ absorptivities in infrared and optical is larger than the critical value $\sim$1.37 (Fig. E.1) and the resulting thermal effects are expected to make the particles migrate inward. Saturn's obliquity is given its current value $\varepsilon =26.73^\circ$ and thermal parameters are as before. To proceed in clear conceptual steps, we keep the seasonal thermal forces in the analysis, postponing discussion of the possible role of the diurnal components to the next section.

Figure 5 shows the results. We note that in all cases the ring particles drift inward; this holds true also for the C ring zone. The thermal effects increase the migration rate of centimetre to decimetre size particles in the B and A rings by nearly two orders of magnitude as compared to their (small) drift rates by the P-R drag. This appears to be a significant modification. Neglecting other dynamical effects, such as viscosity and gravitational perturbations by satellites, we may estimate the timescale $\tau$ to migrate radial distance $\delta\rho$ at $\rho$ when the net transverse acceleration is $f_\tau$. Adopting planetary radii as units of $\delta\rho$ and $\rho$, and pm/s² for $f_\tau$ we obtain

$$\tau \simeq 400~\left[\frac{\delta\rho}{\rho^{3/2}~f_\tau}\right] \;\;\hbox{\rm [My]} .$$ (60)

Results in Fig. 5 show that $\simeq$(0.5-5) cm size ring particles have $\tau\simeq 30{-}50$ My to move a fair fraction $\delta \rho\sim 0.5$ of the whole main ring system. This $\tau$value is comparable or shorter than the expected obliquity cycle. Even if $\Psi\sim 0.01$ (see Appendix F) the timescale of sweeping small particles from the B and A ring zone would be smaller than the solar system age. The same size rocky pebbles, with higher thermal conductivity K and bulk density $\rho_{\rm b}$, are much less sensitive to the thermal effects and they would evolve on a timescale which is about an order of magnitude longer. The same applies to larger icy ring particles up to about 50 cm in size.

Of particular interest is to estimate the timescale of migration through the Cassini division from its outer to the inner edge. This is a region with optical depth ($\sim$0.075; e.g., Collins et al. 1984) such that the assumptions of our model meet reality more closely than, for instance, in the denser B ring. We also note that Porco et al. (2005) report, from analysis of the damping length of Atlas' 5:4 and Pan's 7:6 density waves, a characteristic particle size in the Cassini division to be $\simeq$0.4-0.6 m, an order of magnitude smaller than in the B and A rings (see also French & Nicholson 2000; and Tiscareno et al. 2007) and closer to the size range susceptible to radiative perturbations. A typical timescale of a centimetre to decimetre size particle to drift across the Cassini division is surprisingly short from our work $\simeq$3-10 My only. Either viscous effects make a strong obstacle to this drift, which seems unlikely (we would assume $\Psi$ close to unity in this case, see Appendix F), or small particles of the relevant composition are permanently leaking from the bottom ramp of the A ring toward the Cassini division. It has been previously determined that the ramp is built by the ballistic transport from the innermost part of the A ring (e.g., Durisen et al. 1989, 1992, 1996). The putative fast effacement of the particles from the Cassini division by the radiative drags would require the ballistic transport to be perhaps more efficient than expected so far or the rings to be younger. In any case, our findings put stronger constraints on sustaining the Cassini division population of particles on a long term.

Figure 6: The same as in Fig. 5 but now the results include effects of the diurnal variants of the thermal forces. All particles are assumed to have a rotation period five times shorter than the revolution period (i.e. m=5). The four panels are again appropriate for Saturn's B ring ( top left), A ring ( top right), C ring ( bottom left) and Cassini division ( bottom right). Nominal value $\varepsilon =26.73^\circ$ of Saturn's obliquity and low conductivity K=10-4 W/m/K are assumed here. Dashed are isolines of negative $[f_\tau ]_{123}$ values with constant step -3 pm/s2 (the bold dashed curves correspond to $[f_\tau ]_{123}=-3$ pm/s2). Solid are isolines of positive $[f_\tau ]_{123}$ values with constant step +10 pm/s2 (the bold solid curve on the left and bottom panel is $[f_\tau ]_{123}=0$ pm/s2) with the exception of the bottom left panel where the step is +1 pm/s2 only.

Open with DEXTER

  
5.3 Effect of the particle rotation rate

So far we have been analyzing effects of the seasonal variants of the Yarkovsky and Yarkovsky-Schach forces. As such the results were entirely independent from the rotation rate of the ring particles. Here we shall include the diurnal variants of the thermal forces and find this dependence on the particles rotation rate. Our theoretical analysis from Sects. 3.2 and 4.2 indicates that for rapidly rotating particles their role is negligible (we numerically verified this conclusion holds true for $m\ga 10$), but as the parameter $m=\Omega/n$ becomes smaller the diurnal components could modify previous results by an unknown extent. We shortly explore their potential role.

Keeping the same physical parameters for each of the ring sections we repeated our estimation of the long-term drifts of small particles now with the diurnal components of the thermal effects included. For definiteness we assigned m=5 for particles of each size. Figure 6 indicates that our results do not change for large particles ($D\ga 5$ mm, say) but get significantly modified for small ones ($D\la 5$ mm). For large enough $A_{\rm V}$ values, as in the case of the A and B rings and particles in the Cassini division, the diurnal component of the planetary Yarkovsky effect (46) becomes positive and dominates the seasonal component for a limited range of $m\leq 10$. We note a large gradient of the drift rates for $\sim$1 mm size particles across the B to A ring zones.

While theoretically interesting, we would like to draw a caution here. First, our thermal model assumes spherical and homogeneous particles. At millimetre and smaller sizes, though, the particles are likely to have an irregular shape with enough porosity to invalidate the assumptions of our solution. Moreover, collisional models (e.g., Richardson 1994; Salo & Karjalainen 2003; Ohtsuki & Toyama 2005; Morishima & Salo 2006; Ohtsuki 2006) predict that small ring particles will rotate fast ($m\ga 10$). These works indicate $m\propto 1/D$, with $m\sim 1$ or less for the largest particles in the population, as a rule of thumb. Nevertheless, our understanding of the small ring particle rotation state is still somewhat puzzling due to several contradictory hints (e.g., inaccurate constraints on the size distribution of the ring particles that prevent us from determining whether large or small particles dominate the cross-section, a population that might be rotating slowly; e.g., Ferrari et al. 2005; Flasar et al. 2005) and possibly missing physical effects in the theoretical models (such as radiation torques on the small particles; Rubincam 2000; Vokrouhlický & Capek 2002; Capek & Vokrouhlický 2004). Since the collisional evolution of the ring particles is coupled with their orbital and spin state, we cannot rule out peculiar rotation rates for small particles in the population yet.

5.4 Effect of the particle thermal conductivity

We note that previous results would significantly change if much higher thermal conductivity K was assumed. For instance with $K\sim 6$ W/m/K, appropriate for pure, non-porous crystalline ice (e.g., Ross et al. 1977), we find that semimajor axis drift rates due to thermal effects drop below the value of the P-R drag. This is because efficient thermal conduction across the particles make them basically isothermal and this will render the thermal effects much less important for the particle dynamics. Whether there exists a subpopulation of ring particles with these properties (e.g., compacted by micrometeoroid impacts) remains hypothetical, but observations of disk temperature profiles in the planetary shadow rather support the very low value of K used above (e.g., Spilker et al. 2003, 2006; Flasar et al. 2004; Ferrari et al. 2005).

  
6 Implications and conclusions

In spite of many approximations, and a need of further substantiation of our model, we believe our results might be pointing toward important implications.

First, all previous studies based on observations from optical to radar range suggest the rings are devoid of small particles. For instance French & Nicholson (2000) give a lower cut-off for a single power-law fit of the B ring and the inner A ring population size distribution at $\sim$30 cm, while about 0.1-1 cm for the C ring, Cassini division and the outer A ring. Recent Cassini radar observations (e.g., http://photojournal.jpl.nasa.gov/catalog/PIA07875 and Thomson et al. 2005) also suggest rings are depleted of small particles, placing the lower cut-off at centimetre to decimetre range. Moreover, they also confirm a gradient toward a larger value of the size-distribution lower cut-off at smaller distances from Saturn. A standard explanation is that particle agglomeration during soft-velocity collisions might drive small particles to build larger ones (Borderies et al. 1984; Longaretti 1992; Karjalainen & Salo 2004; Albers & Spahn 2006). Smaller sizes at the very outer part of the A ring was also suggested to be due to energetic collisions with small particles in the E ring (Dones et al. 1993, and references therein). But these models have uncertainties in physical parameters. Here we propose that small particles might be additionally swept from Saturn's rings by radiation forces both size- and saturnocentric-dependent (Fig. 5). By contrast with Rubincam (2006), we find that for plausible parameter values, particles drift inward at locations throughout the ring system.

It is also yet to be seen whether the thermal drifts computed above are important enough to modify the conclusions of the standard theory for the ballistic transport in the rings (e.g., Durisen et al. 1989, 1992, 1996; Cuzzi & Estrada 1998). Note, for instance, that centimetre to decimetre size particles in the Cassini division are expected to migrate inward due to radiative effects with a radial speed $v_{\rm r}\sim 3\times 10^{-6}$ cm/s. This may be larger than the estimated drift rates resulting from transport of angular momentum by the ballistic transport itself and viscosity (e.g., Durisen et al. 1989, 1996). However, numerical models of ring evolution are needed in order to determine the long-term effects on the structure of the ring system. We plan to construct such models in future work.

Acknowledgements

Part of this work was supported by the Czech Grant Agency through grant GACR 205/05/2737 and the Research Program MSM0021620860 of the Czech Ministry of Education. We also thank M. Broz for help in producing Fig. 1 and D. P. Rubincam who, as a referee, helped to improve the first version of this paper.

References

• Abramowitz, M., & Stegun, I. A. 1970, Handbook of Mathematical Functions (New York: Dover Publications) (In the text)
• Afonso, G., Barlier, F., Carpino, M., et al. 1989, Ann. Geophys., 7, 501 [NASA ADS] (In the text)
• Albers, N., & Spahn, F. 2006, Icarus, 181, 292 [NASA ADS] [CrossRef] (In the text)
• Aumann, H. H., & Kieffer, H. H. 1973, ApJ, 186, 305 [NASA ADS] [CrossRef] (In the text)
• Bertotti, B., Farinella, P., & Vokrouhlický, D. 2003, Physics of the Solar System (Dordrecht: Kluwer Academic Publishers) (In the text)
• Borderies, N., Goldreich, P., & Tremaine, S. 1984, in Planetary Rings, ed. R. Greenberg, & A. Brahic (Tucson: University of Arizona Press), 713 (In the text)
• Bottke, W. F., Vokrouhlický, D., Rubincam, D. P., & Broz, M. 2002, in Asteroids III, ed. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: University of Arizona Press), 395 (In the text)
• Bottke, W. F., Vokrouhlický, D., Rubincam, D. P., & Nesvorný, D. 2006, Annu. Rev. Earth Planet. Sci., 34, 157 [NASA ADS] (In the text)
• Burns, J. A., Lamy, P. L., & Soter, S. 1979, Icarus, 40, 1 [NASA ADS] [CrossRef] (In the text)
• Burns, J. A., Hamilton, D. P., & Showalter, M. R. 2001, in Interplanetary Dust, ed. E. Grün, B. A. S. Gustafson, S. F. Dermott, & H. Fechtig (Berlin: Springer-Verlag), 641 (In the text)
• Byrd, P. F., & Friedman, M. D. 1971, Handbook of Elliptic Integrals for Engineers and Scientists (Berlin: Springer-Verlag) (In the text)
• Capek, D., & Vokrouhlický, D. 2004, Icarus, 172, 526 [NASA ADS] [CrossRef] (In the text)
• Collins, F., Diner, J. A., Garneau, G. W., et al. 1984, in Planetary Rings, ed. R. Greenberg, & A. Brahic (Tucson: University of Arizona Press), 737 (In the text)
• Cuzzi, J. N., Lissauer, J. J., Esposito, L. W., et al. 1984, in Planetary Rings, ed. R. Greenberg, & A. Brahic (Tucson: University of Arizona Press), 73 (In the text)
• de Pater, I., & Lissauer, J. J. 2001, Planetary Sciences (Cambridge: Cambridge University Press) (In the text)
• Dones, L., Cuzzi, J. N., & Showalter, M. R. 1993, Icarus, 105, 184 [NASA ADS] [CrossRef] (In the text)
• Durisen, R. H., Cramer, N. L., Murphy, B. W., et al. 1989, Icarus, 80, 136 [NASA ADS] [CrossRef] (In the text)
• Durisen, R. H., Bode, P. W., Cuzzi, J. N., Cederbloom, S. E., & Murphy, B. W. 1992, Icarus, 100, 364 [NASA ADS] [CrossRef] (In the text)
• Durisen, R. H., Bode, P. W., Dyck, S. G., et al. 1996, Icarus, 124, 220 [NASA ADS] [CrossRef] (In the text)
• Esposito, L. W., Cuzzi, J. N., Holberg, J. B., et al. 1984, in Saturn, ed. T. Gehrels, & M. S. Matthews (Tucson: University of Arizona Press), 463 (In the text)
• Esposito, L. W., Colwell, J. E., Larsen, K., et al. 2005, Science, 307, 1251 [NASA ADS] [CrossRef]
• Farinella, P., & Vokrouhlický, D. 1996, Planet. Sp. Sci., 44, 1551 [NASA ADS] [CrossRef] (In the text)
• Ferrari, C., & Leyrat, C. 2006, A&A, 447, 745 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Ferrari, C., Galdemard, P., Lagage, P. O., Pantin, E., & Quoirin, C. 2005, A&A, 441, 379 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Ferraz-Mello, S. 1972, Cel. Mech., 5, 80 [NASA ADS] [CrossRef] (In the text)
• Flasar, F. M., Kunde, V. G., Abbas, M. M., et al. 2004, Space Sci. Rev., 115, 169 [NASA ADS] [CrossRef] (In the text)
• Flasar, F. M., Achterberg, R. K., Conrath, B. J., et al. 2005, Science, 307, 1247 [NASA ADS] [CrossRef] (In the text)
• French, R. G., & Nicholson, P. D. 2000, Icarus, 145, 502 [NASA ADS] [CrossRef] (In the text)
• Froidevaux, L., Matthews, K., & Neugebauer, G. 1981, Icarus, 46, 18 [NASA ADS] [CrossRef] (In the text)
• Goldreich, P., & Tremaine, S. 1978, Icarus, 34, 240 [NASA ADS] [CrossRef] (In the text)
• Goldreich, P., & Tremaine, S. 1982, ARA&A, 20, 249 [NASA ADS] (In the text)
• Guess, A. W. 1962, ApJ, 135, 855 [NASA ADS] [CrossRef] (In the text)
• Hamilton, D. P., & Ward, W. R. 2004, AJ, 128, 2510 [NASA ADS] [CrossRef] (In the text)
• Hudgins, D. M., Sandford, S. A., Allamandola, L. J., & Tielens, A. G. G. M. 1993, ApJ, 86, 713 [NASA ADS] [CrossRef] (In the text)
• Irvine, W. M., & Pollack, J. B. 1968, Icarus, 8, 324 [NASA ADS] [CrossRef] (In the text)
• Karjalainen, R., & Salo, H. 2004, Icarus, 172, 328 [NASA ADS] [CrossRef] (In the text)
• Kawata, Y., & Irvine, W. M. 1975, Icarus, 24, 472 [NASA ADS] [CrossRef] (In the text)
• Kawata, Y. 1983, Icarus, 56, 453 [NASA ADS] [CrossRef] (In the text)
• Kouchi, A., Greenberg, J. M., Yamamoto, T., & Mukai, T. 1992, ApJ, 388, L73 [NASA ADS] [CrossRef] (In the text)
• Landau, L. D., & Lifshitz, E. M. 1986, Hydrodynamics (Moscow: Nauka) (In the text)
• Longaretti, P. Y. 1992, in Interrelations Between Physics and Dynamics for Minor Bodies in the Solar System, ed. D. Benest, & C. Froeschlé (Paris: Societé Française des Spécialistes d'Astronomie), 453 (In the text)
• Mignard, F. 1984, in Planetary Rings, ed. R. Greenberg, & A. Brahic (Tucson: University of Arizona Press), 333 (In the text)
• Milani, A., Nobili, A. M., & Farinella, P. 1987, Non-gravitational Perturbations and Satellite Geodesy (Bristol: A. Hilger) (In the text)
• Morbidelli, A., & Vokrouhlický, D. 2003, Icarus, 163, 120 [NASA ADS] [CrossRef] (In the text)
• Morishima, R., & Salo, H. 2006, Icarus, 181, 272 [NASA ADS] [CrossRef] (In the text)
• Ohtsuki, K. 2006, Icarus 183, 384 (In the text)
• Ohtsuki, K., & Toyama, D. 2005, AJ, 130, 1302 [NASA ADS] [CrossRef] (In the text)
• Öpik, E. J. 1951, Proc. Roy. Irish Acad. 54, 165 (In the text)
• Poulet, F., & Cuzzi, J. N. 2002, Icarus, 160, 350 [NASA ADS] [CrossRef]
• Poulet, F., Cruikshank, D. P., Cuzzi, J. N., et al. 2003, A&A, 412, 305 [NASA ADS] [CrossRef] [EDP Sciences]
• Porco, C. C., Baker, E., Barbara, J., et al. 2005, Science, 307, 1226 [NASA ADS] [CrossRef] (In the text)
• Richardson, D. C. 1994, MNRAS, 269, 493 [NASA ADS] (In the text)
• Ross, R. G., Andersson, P., & Bæckstroem, G. 1977, High Temp. - High Press., 9, 87 (In the text)
• Rubincam, D. P. 1982, Celest. Mech., 26, 361 [NASA ADS] (In the text)
• Rubincam, D. P. 1987, J. Geophys. Res., 92, 1287 [NASA ADS] (In the text)
• Rubincam, D. P. 1995, J. Geophys. Res., 100, 1585 [NASA ADS] [CrossRef] (In the text)
• Rubincam, D. P. 1998, J. Geophys. Res., 103, 1725 [NASA ADS] [CrossRef] (In the text)
• Rubincam, D. P. 2000, Icarus, 148, 2 [NASA ADS] [CrossRef] (In the text)
• Rubincam, D. P. 2004, BAAS, 36, 710 (In the text)
• Rubincam, D. P. 2006, Icarus, 184, 532 [NASA ADS] [CrossRef] (In the text)
• Salo, H. 1992, Icarus, 96, 85 [NASA ADS] [CrossRef] (In the text)
• Salo, H., & Karjalainen, R. 2003, Icarus, 164, 428 [NASA ADS] [CrossRef] (In the text)
• Spilker, L. J., Ferrari, C., Cuzzi, J. N., et al. 2003, Planet. Space Sci., 51, 929 [NASA ADS] [CrossRef] (In the text)
• Spilker, L. J., Pilorz, S. H., Edgington, S. G., et al. 2005, Earth, Moon, and Planets, 96, 149
• Spilker, L. J., Pilorz, S. H., Wallis, B. D., et al. 2006, Planet. Space Sci., 54, 1167 [NASA ADS] [CrossRef] (In the text)
• Thomson, F., Wong, K., Marouf, E., et al. 2005, Scattered signal observations during Cassini radio occultations by Saturn's rings, AGU meeting abstract #P33B-0247 (In the text)
• Tiscareno, M. S., Burns, J. A., Nicholson, P. D., Hedman, M. M., & Porco, C. C. 2007, Icarus, in press (In the text)
• Vokrouhlický, D. 1998, A&A, 335, 1093 [NASA ADS] (In the text)
• Vokrouhlický, D. 1999, A&A, 344, 362 [NASA ADS] (In the text)
• Vokrouhlický, D., & Farinella, P. 1999, AJ, 118, 3049 [NASA ADS] [CrossRef] (In the text)
• Vokrouhlický, D., & Capek, D. 2002, Icarus, 159, 449 [NASA ADS] [CrossRef] (In the text)
• Vokrouhlický, D., Capek, D., Chesley, S. R., & Ostro, S. J. 2005, Icarus, 179, 128 [NASA ADS] [CrossRef] (In the text)
• Ward, W. R., & Hamilton, D. P. 2004, AJ, 128, 2501 [NASA ADS] [CrossRef] (In the text)
• Wyatt, S. P., & Whipple, F. L. 1950, ApJ, 111, 134 [NASA ADS] [CrossRef] (In the text)

 

  
Online Material

Appendix A: Radiation source term ${\cal S}$ for surface of a spherical body

In what follows we compute necessary coefficients of the multipole series

$${\cal S}' = \sum_{n\ge 0} \sum_{k=-n}^n s_{nk}~ Y_{nk}(\theta, \phi)$$ (A.1)

for radiation source terms ${\cal S}'$ that are relevant for our work. They are determined through

$$s_{nk} = \int {\rm d}\Omega~ {\cal S}' Y^*_{nk}(\theta,\phi) ,$$ (A.2)

where the star upper index means complex conjugation.

A.1 Impinging plane wave

The simplest source of radiation is a plane wave. We denote the associated radiation flux ${\cal E}^{\rm V}_\star$ and characterize direction of its propagation by $-\vec{n}_{\rm pw}$. Radiation flux through an infinitesimal surface element ${\rm d}\vec{S}=\vec{n}~{\rm d}S$ of a sphere is given by

  

$${\cal S}' {\cal E}^{\rm V}_\star~(\vec{n}\cdot\vec{n}_{\rm pw})\qquad \hbox{for}\quad(\vec{n}\cdot \vec{n}_{\rm pw})>0 ,$$ = (A.3)

$$0\qquad\qquad\qquad\; \hbox{for}\quad (\vec{n}\cdot \vec{n}_{\rm pw})\le 0 .$$ = (A.4)

Obviously, the scalar product $(\vec{n}\cdot\vec{n}_{\rm pw})$ determines whether ${\rm d}\vec{S}$ is illuminated from the $\vec{n}_{\rm pw}$ or not. In an arbitrary local reference system of the spherical body, such that the Z-axis is oriented along the spin vector as used in the main text, we can write

$$\vec{n}_{\rm pw} = \left[\begin{array}{c} \sin\theta_{\rm S} ... ...sin\phi_{\rm S} \\ \cos\theta_{\rm S} \end{array}\right] ,$$ (A.5)

so that $\theta_{\rm S}$ and $\phi_{\rm S}$ are the local colatitude and longitude of the radiation source.

Inserting (A.3) and (A.4) into Eq. (A.2) we readily obtain (recall scaling of the source term with ${\cal S}_\star$; Sect. 2)

$$s_{00} = \frac{\sqrt{\pi}}{2}~ \frac{\alpha_{\rm V} {\cal E}^{\rm V}_\star}{{\cal S}_\star}$$ (A.6)

for the monopole coefficient. With $Y_{00} = 1/(2\sqrt{\pi})$ we directly obtain $s_{00}Y_{00} = \alpha_{\rm V} {\cal E}^{\rm V}_\star/(4{\cal S}_\star)$. This is the factor 4 from the "cross-section vs surface'' argument in definition of the mean radiation terms $\overline{{\cal E}^{\rm V}}$ and $\overline{{\cal E}^{\rm I}}$ used in Sect. 1.

With the same algebra we obtain (also Vokrouhlický 1999)

  

$$s_{10} = \sqrt{\frac{\pi}{3}}\cos \theta_{\rm S}~ \frac{\alpha_{\rm V} {\cal E}^{\rm V}_\star}{{\cal S}_\star} ,$$ (A.7)

$$s_{1\pm 1} = \mp\sqrt{\frac{\pi}{6}}\sin\theta_{\rm S}~ \exp({\mp... ... i}\phi_{\rm S}})~ \frac{\alpha_{\rm V} {\cal E}^{\rm V}_\star}{{\cal S}_\star}$$ (A.8)

for the dipole coefficients. We could have continued to compute higher multipole coefficients, but the discussion in Sect. 2 indicates this is not needed for our work.

A.2 Spherical source

Next we examine a spherical source of radiation such as a planet. For simplicity, we assume each surface element of the planet emits thermal radiation isotropically and all surface elements are identical (no latitudinal thermal variations). Radiation intensity at the thermal wavelengths is denoted I, so that the radiation temperature $T_{\rm rad}$ of the planet reads ${\cal E}^{\rm I}_{\star 0}=\sigma T_{\rm rad}^4 = \pi I$ (for Saturn we have $T_{\rm rad}\simeq 95$ K; e.g., de Pater & Lissauer 2001; Bertotti et al. 2003). Since we are interested in ring particles of metre-size at maximum, we shall neglect their characteristic size with regards to the size of the planet and the particle planetocentric distance $\rho$. With that approximation, we may assume each of the planetary surface elements visible from the particle contributes to its illumination with a plane wave propagating along their mutual direction. The carried radiation intensity is still I, that of the source.

Since we model the radiation impinging on the ring particle with a composition of plane waves from different surface elements on the planet, the coefficients of the multipole expansion of ${\cal S}'$ are now obtained by integration of (A.6)-(A.8) over the source. In particular for the monopole term we obtain

$$s_{00} = \psi(\rho)~\frac{\sqrt{\pi}}{2}~\frac{\alpha_{\rm I} {\cal E}^{\rm I}_{\star 0}}{{\cal S}_\star} ,$$ (A.9)

where $\psi(\rho)$ is given by Eq. (6). Obviously at $\rho\rightarrow \infty$ we have the expected quadratic falloff $\psi(\rho)\propto 1/\rho^2$. On the other hand, for $\rho\rightarrow 1$ we obtain $\psi(1)=2$ where our approximation of plane wave illumination ceases to be valid. However, for any $\rho$ relevant in the Saturnian ring system our results apply (note the inner edge of the C ring is at $\rho\simeq 1.236$).

With the same approach we obtain in the case of dipole coefficients:

  

$$s_{10} = \frac{1}{\rho^2}~\sqrt{\frac{\pi}{3}}\cos \theta_{\rm S}~ \frac{\alpha_{\rm I} {\cal E}^{\rm I}_{\star 0}}{{\cal S}_\star} ,$$ (A.10)

$$s_{1\pm 1} = \mp \frac{1}{\rho^2}~\sqrt{\frac{\pi}{6}}\sin\theta_... ...\rm S}})~\frac{\alpha_{\rm I} {\cal E}^{\rm I}_{\star 0}}{{\cal S}_\star} \cdot$$ (A.11)

Interestingly, here the $1/\rho^2$ flux falloff is recovered exactly.

Appendix B: Poynting-Robertson drag on ring particles

Here we briefly review the Poynting-Robertson (P-R) drag, a velocity-dependent correction of the radiation pressure for particles moving with respect to the radiation source (e.g., Burns et al. 1979, 2001; Bertotti et al. 2003). As in the case of the thermal forces, we have two variants corresponding to the two possible radiation sources: the Sun and the Saturn.

The orbital decay due to a radiation source at the force center has been studied by Wyatt & Whipple (1950). We only adopt here a generalization to an extended spherical source of radiation developed by Guess (1962). The latter author showed that the transverse (P-R) force acting on a perfectly absorbing particle of radius R is given by

$$f_\tau = -\frac{1}{3}~\frac{\pi R^2 {\cal E}^{\rm I}_{\star 0... ...8+\frac{1}{\rho^2}\right) \sqrt{1-\frac{1}{\rho^2}} \right] ,$$ (B.1)

where the notation is similar to the main text and v is the planetocentric orbital velocity. Since v may be as large as $\simeq$20 km s^-1 at the inner edge of the B ring, we have $v/c\leq 10^{-4}$ or smaller in the A and B rings.

The solar radiation can be modeled at Saturn's distance with a plane wave approximation. Surprisingly, we have not found the general result for the P-R solar component in the literature and we believe it is given here for the first time. For that reason, we pay some attention to its derivation.

The general formula for the P-R acceleration is given by (e.g., Burns et al. 1979, 2001; Bertotti et al. 2003)

$$\vec{f} = -\frac{\pi R^2 {\cal E}^{\rm V}_{\star 0}}{mc^2}~\l... ...{V}_{\rm s}\cdot\vec{N}_{\rm s}\right)\vec{N}_{\rm s}\right] ,$$ (B.2)

where $\vec{N}_{\rm s}$ is the unit position vector of the ring particle with respect to the radiation source (Sun) and $\vec{V}_{\rm s}$ is their relative velocity. The latter decomposes into the planet's relative velocity $\vec{V}$ with respect to the Sun and the particle relative velocity $\vec{v}$ with respect to the planet: $\vec{V}_{\rm s}=\vec{V}+\vec{v}$ (see also Mignard 1984). We neglect the angular distance of the particle from the planet as seen from the Sun and set $\vec{N}_{\rm s}=\vec{N}$, where $\vec{N}$ is the planet's position vector with respect to the Sun. Assuming zero eccentricity of the planet's orbit about the Sun, and referring its longitude in orbit $\lambda$ to the instant when the Sun is at extreme latitude above the ring-plane, we have

$$\vec{N} = (N_x,N_y,N_z)^{\rm T} = \left[\begin{array}{c} -\... ... \phantom{-}\sin\varepsilon\cos\lambda \end{array}\right] ,$$ (B.3)

and

$$\vec{V} = (V_x,V_y,V_z)^{\rm T} = V~ \left[\begin{array}{c} ... ... \phantom{-}\sin\varepsilon\sin\lambda \end{array}\right] ,$$ (B.4)

with $\varepsilon$ the obliquity of the planet's rotation axis and $V\simeq 9.7$ km s^-1 is the mean orbital velocity of Saturn. The $\vec{N}$ and $\vec{V}$ components in Eqs. (B.3) and (B.4) are given in the planetary reference system with the z axis along the planet's rotation axis and the xy plane that of the ring-plane. The Sun at its maximum position above the ring-plane is located in the xz plane.

Assuming the shadow function $\Gamma(\zeta)$ is given in terms of Fourier series (11) we have altogether

$$\vec{f} = -\frac{\pi R^2 {\cal E}^{\rm V}_{\star 0}}{mc^2}~\l... ...left(\vec{v}\cdot\vec{N}\right)\vec{N}\right]~\Gamma(\zeta) .$$ (B.5)

Note the complex orbital parameter $\zeta$ from (4) is unity at the center of the planet's shadow, which constrains the shadow-function coefficients (12) and (13). Denoting the longitude of the shadow axis in the ring-plane by $\varphi_0$, we have

$$\exp(\pm {\rm i}\varphi_0) = -\frac{N_\pm}{\sin\theta_0} ,$$ (B.6)

where we introduced $N_\pm=N_x\pm {\rm i} N_y$ and the solar angular distance from the planet's rotation axis $\theta _0$ given by (39); for further use we also define $V_\pm=V_x\pm {\rm i} V_y$. The ring particle velocity $\vec{v}$, given in the (xyz) reference system, reads

$$\vec{v} = \frac{v}{2}~\left[\begin{array}{c} {\rm i}~\left(\... ...\rm i}\varphi_0\right)\phantom{]} \\ 0 \end{array}\right] .$$ (B.7)

The semimajor axis drift derives from the transverse component $f_\tau$ of the perturbing acceleration (e.g., Eq. (28))

$$f_\tau = -\frac{\pi R^2 {\cal E}^{\rm V}_{\star 0}}{mc}~\frac... ...ft(\vec{v}\cdot \vec{N}\right)^2}{v^2}\right]~\Gamma(\zeta) .$$ (8)

Averaging over a particle revolution about the planet, denoted by $[\ldots]_1$in the main text, is straightforward when using

  

$$\vec{v}\cdot\vec{V} = -\frac{{\rm i}~ v}{2\sin\theta_0}~\left(V_-N_+\zeta- V_+N_-\zeta^{-1}\right) ,$$ (B.9)

$$\vec{v}\cdot\vec{N} = -\frac{{\rm i}~ v}{2}~\sin\theta_0~\left(\zeta- \zeta^{-1}\right) .$$ (B.10)

Inserting these formulae in (B.8), and dropping all $\zeta$-dependent terms, we finally obtain

 

$$\left[f_\tau\right]_{1} = -\frac{\pi R^2 {\cal E}^{\rm V}_\star}{... ...n}{\sin\theta_0} ~c_1 + \frac{1}{2}~\sin^2\theta_0~\left(c_0-c_2\right)\Bigr] .$$ (B.11)

Recall (c₀,c₁,c₂) are the the first three coefficients of the shadow function $\Gamma(\zeta)$. It is not straightforward to average (B.11) over the planet's revolution cycle about the Sun analytically, but it is always possible to be done numerically. The only obvious exception is when the particles avoid visiting the planet shadow ( $\rho\ge\rho_\star=1/\cos\theta_0$) such that c₀=1, c₁=c₂=0. In this case we obtain (see, e.g., Goldreich & Tremaine 1982; Mignard 1984)

$$\left[f_\tau\right]_{12} = -\frac{1}{4}~\frac{\pi R^2 {\cal E... ...}_\star}{mc}~ \frac{v}{c}~ \left(5+\cos^2\varepsilon\right) .$$ (B.12)

The formulæ (B.1) through (B.12), which are both of the same order of magnitude, are used here mainly to find a parameter threshold for which the P-R drags would dominate the thermal effects (see Fig. 4).

Appendix C: A simplified model for the disk-radiation effects

Dropping the optical or thermal radiation of the neighboring particles in the ring was one of the major approximations in this paper. A full analysis of its role for altering the dipole anisotropy of the particle temperature, relevant for the orbital effects, lies beyond the scope of our work. Here we only argue that a very simple model can be developed using the results developed in Sects. 2 to 4.

Assume a small ring particle on a slightly inclined orbit toward a large, infinitesimally thin disk of radiating particles. During half of the revolution about the planet, namely along the arc extending from ascending to descending nodes, the particle is irradiated roughly along direction of the z-axis, while in the opposite direction along the complementary part of the orbit. We shall assume that the radiation flux is roughly constant, but the results hold true also when the flux is an arbitrary function of the vertical distance from the disk. These assumptions amount to the following formal parameters in the previous theory of the Yarkovsky-Schach effect: (i) fictitious "shadow function'' $\Gamma(\zeta)=\mp 1$ above/below the ring-plane, and (ii) radiation source along the z axis, thus $\theta_0=0^\circ$(the time origin t=0, and orientation of the x axis in the ring-plane is set equal to the ascending node of the particle orbit). With only these two simple modifications we can now use the previous theory to show that the corresponding dipole source coefficients of the seasonal/diurnal effects read:

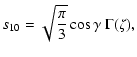$$s_{10} = \sqrt{\frac{\pi}{3}} \cos\gamma~\Gamma(\zeta) ,$$ (C.1)

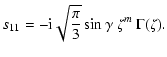$$s_{11} = -{\rm i} \sqrt{\frac{\pi}{3}} \sin\gamma~\zeta^m~ \Gamma(\zeta) .$$ (C.2)

The Fourier-series development of the shadow function now reads $\Gamma = \sum c_k \zeta^k$ with $c_k=\frac{2{\rm i}}{k\pi}~ \sin^2 (k\pi/2)$.

Without giving unnecessary details we note that the orbit-averaged thermal accelerations $[f_\tau]_1$ for both the seasonal and diurnal variants are linear functions of $s_\pm$. Since one easily shows that for an arbitrary function of obliquity $\Phi(\gamma)$ we have  $[\Phi(\gamma)~s_\pm]_3 = 0$, the mean transverse acceleration averaged over a sample of bodies with isotropically distributed spin axes vanishes. From this toy model we preliminarily conclude that the orbital effect of ring particle radiation is small compared to the effects discussed in the main text above.

Appendix D: The case of spin axes aligned with normal to the disk-plane

So far we have investigated the long-term averaged Yarkovsky drift for a sample of particles with an isotropic distribution of spin axes. This is likely justified for small particles, but observations tend to indicate that large particles might rotate slowly and their spin axis might be aligned with the direction of their orbital angular momentum. Here we briefly analyse this case.

Figure D.1: The same as in Fig. 6 but now the results assume a population of particles with zero obliquity (such that their spin axes are aligned with the normal to the disk plane). Two values of particle rotation rate are investigated: (i) m=2 ( left), and (ii) m=0.3 ( right). Thermal and optical parameters of icy particles of appropriate to the A ring assumed and the nominal value $\varepsilon =26.73^\circ$ of Saturn's obliquity. Particles with m>1 at any planetocentric distance migrate outward since the diurnal variant of the planetary Yarkovsky effect is stronger than the corresponding component of the Yarkovsky-Schach effect. However, the situation reverses for the extreme case m<1. We plot isolines of $[f_\tau ]_{12}$ with a constant step 1 pm/s2 (starting with the bold curve corresponding to $[f_\tau ]_{12}=1$ pm/s2 in the left panel and $[f_\tau ]_{12}=-1$ pm/s2 in the right panel). Solid/dashed curves apply to positive/negative $[f_\tau ]_{12}$ values.

As a toy model assume all particles have zero obliquity ( $\gamma=0^\circ$). With the analysis in Sects. 2 and 3 we than easily determine the mean orbital acceleration of these particles due to planetary Yarkovsky and the Yarkovsky-Schach effects (notation as above):

 

$$\left[f_\tau\right]_{12} = -\frac{4}{9}\;\;~\Phi_1 \left[\frac{E_... ...\sin\delta_-}{1+\chi} ~\frac{\sqrt{1-\rho^2\cos^2\theta_0}}{\rho}\right]_2\cdot$$ (D.1)

We note the seasonal components of the thermal effects have been dropped, while the only remaining contribution is due to the diurnal components. This is an important circumstance since with low surface conductivity the diurnal variant of the thermal effect typically provides faster orbital drifts (e.g., Bottke et al. 2002, 2006). For particles whose rotation rate equals that of the mean motion about the planet (m=1) the total effect would vanish because $E_-\sin\delta_-(m=1)=0$. When m<1, the sign in the right hand side of Eq. (D.1) should be changed as discussed in Sects. 2.3, 3.2 and 4.2.

Figure D.1 shows expected values of the mean transverse acceleration $\left[f_\tau\right]_{12}$ from (D.1) for a population of slowly rotating icy particles whose physical parameters are those of the A ring (in particular we have K=10^-4 W/m/K, $A_{\rm V}=0.5$, $A_{\rm I}= 0.1$, C=820 J/kg/K and $\rho _{\rm b}=0.5$ g/cm³). In the left panel we assumed m=2 and thus particles of all sizes and at any planetocentric distance migrate outward, since their high optical albedo makes the Yarkovsky-Schach effect be smaller than the planetary Yarkovsky effect. Because of the postulated zero obliquity, the latter now makes particles migrate from the planet. Particles up to a half metre size can have $\left[f_\tau\right]_{12} \sim 1$ pm/s². Using Eq. (60) we estimate they can drift across the whole width of the Cassini division in $\sim$50 My. As mentioned above, however, when $m\rightarrow 1$ (particles rotating synchronously with their revolution period around the planet) $\left[f_\tau\right]_{12}\rightarrow 0$ and this timescale would diverge. A population of particles rotating more slowly than revolving about the planet, e.g., m=0.3 in the right panel, would migrate toward the planet. This is because for them then hotter ("afternoon'') side leads rather than trails the trajectory as usual for fast rotating objects (we thank D.P. Rubincam for pointing this situation to us). The dominant diurnal variant of the planetary Yarkovsky force thus produces a net drag on the particle motion. The drift rates are comparable to the case of m=2 particles.

We speculate that inward/outward thermal drift of larger ring particles with spin axes normal to the disk-plane might have contributed to the formation of the Cassini division (see Goldreich & Tremaine 1978, for a standard theory). This is because outward migration of the icy particles with $m\sim (1{-}10)$ would be halted at the location of the 2/1 mean motion resonance with Mimas (inner edge of the Cassini division). In course of time a gap would be opened this way and the width of the Cassini division would be constrained by the age of the main A and B rings and the relevant thermal drift rate of the dominating population of ring particles. It is however yet to be understood by detailed modelling if this scenario is a viable possibility.

For the sake of completeness we note that for $\gamma=180^\circ$ obliquity we would have obtained

 

$$\left[f_\tau\right]_{12} = \phantom{-}\frac{4}{9}\;\;~\Phi_1 \lef... ...\sin\delta_+}{1+\chi} ~\frac{\sqrt{1-\rho^2\cos^2\theta_0}}{\rho}\right]_2\cdot$$ (D.2)

In this case all particles migrate toward the planet.

  
Appendix E: Null-torque orbits

Rubincam (2006) suggested that some of the ring boundaries, namely the outer edge of the A ring and the inner edge of the B ring, might correlate with the saturnocentric distance where the long-term mean thermal torques produced by the seasonal Yarkovsky and Yarkovsky-Schach effects vanish. Pursuing this idea we investigate where such zero-torque orbits are located in our model. For the sake of simplicity, though, we consider seasonal-effect torques in this section only.

Figure E.1: Distance from Saturn where the total thermal torque on the orbital motion of ring particles is zero as a function of ratio between its absorptivity in thermal $\alpha _{\rm I}$ and optical $\alpha _{\rm V}$ bands. Seasonal components of the Yarkovsky and Yarkovsky-Schach effects were taken into account. For sake of illustration we assume particle of diameter D=1 cm, bulk density $\rho _{\rm b}=0.5$ g/cm3 and specific thermal capacity C=820 J/kg/K. The light curves correspond to three values of thermal conductivity: (i) K=10-4 W/m/K (label 1), (ii) K=10-2 W/m/K (label 2), and (iii) K=1 W/m/K (label 3). The bold curve was calculated from approximate conditions (E.2) and (E.3). Position of the A and B rings is shown by the shaded zones. For large enough $\alpha _{\rm I}/\alpha _{\rm V}$ ratio the approximate method provides a very good means to compute the no-torque orbits independently on the ring particle thermal parameters and size. When $\alpha _{\rm I}/ \alpha _{\rm V}\leq 1$ (physically unlikely case) all ring orbits would gain orbital momentum.

No acceleration, thus null-torque, orbits $[f_\tau ]_{123}=0$ are determined by

$$\Phi_1~\left[\frac{E\sin\delta}{1+\chi}\right]_2 = \frac{1}{\... ...i}~\frac{\sqrt{1-\rho^2 \cos^2\theta_0}}{\rho}\right]_2 \cdot$$ (E.1)

In full accuracy, the square brackets $[\ldots]_2$ are to be determined numerically using integration over Saturn's longitude in orbit $\lambda$ from (39). We find interesting that the factor $E\sin\delta/(1+\chi)$changes little during Saturn's revolution about the Sun (except in the unlikely case $\alpha_{\rm I}\ll \alpha_{\rm V}$). Neglecting its variations we thus, in a rough but surprisingly satisfactory approximation, can drop this term from both sides in Eq. (E.1). In that case, the dependence of the condition (E.1) on thermal parameters and size of the ring particle entirely disappears. Moreover, the second averaging can be performed analytically and the condition Eq. (E.1) acquires a simplified form. We only need to distinguish two cases. First, when $\rho\sin\varepsilon\le 1$ the planetocentric orbit is always shadowed and we have

$$\frac{\alpha_{\rm I}}{\alpha_{\rm V}} = \frac{{\cal E}^{\rm V... ...} ~\frac{2\rho}{\pi^2}~ E\left(\rho \sin\varepsilon\right) ,$$ (E.2)

where E(x) is the complete elliptic integral of the second kind. When $\rho\sin\varepsilon > 1$, the orbit is entirely illuminated during part of the solar revolution cycle. In that case we obtain

 

$$\frac{\alpha_{\rm I}}{\alpha_{\rm V}} = \frac{{\cal E}^{\rm V}_\s... ...-1}{\rho \sin\varepsilon} K\left(\frac{1}{\rho \sin\varepsilon}\right)\right] ,$$ (E.3)

where K(x) is the complete elliptic integral of the first kind. In fact, Eq. (E.3) can be obtained from (E.2) by an appropriate Gauss transformation (e.g., Abramowitz & Stegun 1970; Byrd & Friedman 1971).

To check applicability of our simplified method we numerically determined roots in $\rho$ from Eqs. (E.1) for an icy particle with size D=1 cm, $\rho _{\rm b}=0.5$ g/cm³ and C=820 J/kg/K and three different values of the thermal conductivity K=10^-4, 10^-2 and 1 W/m/K (with the lowest value here appropriate for particles composed of or covered with fluffy amorphous aggregates of ice; e.g., Froidevaux et al. 1981; Kouchi et al. 1992; Spilker et al. 2003; Flasar et al. 2004; Ferrari et al. 2005). The roots were determined for different values of the ratio $\alpha _{\rm I}/\alpha _{\rm V}$ of the thermal and optical absorptivities of the particle. The result, shown in Fig. E.1, has been compared to the solution of Eqs. (E.2) and (E.3), in this case independent of the thermal parameters and the size of the particle. We note that in a fair range of the $\alpha _{\rm I}/\alpha _{\rm V}$ values the approximate method gives a very accurate position of the no-torque orbits. We find this result interesting because of the above mentioned independence on thermal parameters and size of the ring particle. Obviously, at very small (sub-mm) sizes the Poynting-Robertson drag modifies this result causing orbital decay to the planet (Figs. 4 and 5).

Appendix F: Collective motion of ring particles

The results given in this paper describe the motion of a single ring particle. The dense packing of particles in rings such as A and B around Saturn affects not only illumination by shadowing and mutual irradiation effects, but it also affects orbital motion by mutual collisions. While a complete solution of the problem is left for future numerical work, here we give an upper limit on modification of the single-particle thermal drift $[{\rm d}a/{\rm d}t]_{123}$ from Eq. (28) by collective effects. This method has been developed by Rubincam (2006). Here we slightly generalize it for any size distribution of the ring particles and, mainly, give heuristic result for a rarefied medium such as in the Cassini division (Sect. F.1).

Assume an infinitesimal ringlet of zero eccentricity particles with semimajor axis a. The particles have sizes D in the range $D_1\leq D\leq D_2$ and the population is described with a size distribution function $\Sigma(D)$: ${\rm d}N/{\rm d}D = \Sigma(D)$ such that there are dN particles in the size interval $(D,D+{\rm d}D)$. An extreme opposite assumption to free particle motion is a complete locking of the particle system as a unit via tight collisions. In this approximation, the ringlet would migrate as a whole, not letting the smallest particles escape first. The collective migration of the ringlet is obtained by relating the total (long-term) torque T produced by thermal forces

$$T = \frac{\pi}{6}~\rho a \int_{D_1}^{D_2} {\rm d}D~D^3~\Sigma(D) ~[f_\tau]_{123}(D)$$ (F.1)

to the change of the ringlet angular momentum L = M na² (here M is the mass of the ringlet):

$$\left[\frac{{\rm d}L}{{\rm d}t}\right]_{123} = \frac{M~na}{2}~ \left[\frac{{\rm d}a}{{\rm d}t}\right]_{123} = T .$$ (F.2)

As a result we obtain

$$\left[\frac{{\rm d}a}{{\rm d}t}\right]_{123} = \frac{2}{n}~ ... ...u]_{123}(D)} {\int_{D_1}^{D_2} {\rm d}D~D^3~\Sigma(D)} \cdot$$ (F.3)

Obviously, this equation could be also understood as a "mass-weighted'' form of Eq. (28).

Assume now that we are interested in migration of the smallest particles with size D₁ in the system. In the large-size regime, that applies for particles size $\geq$1 cm roughly, the long-term average thermal acceleration $[f_\tau ]_{123}$scales inversely proportionally with the size of the particle. In this limit, Eq. (F.3) takes the following form

$$\left[\frac{{\rm d}a}{{\rm d}t}\right]_{123} \simeq \frac{2}{n}~ [f_\tau]_{123}(D_1)~\Psi .$$ (F.4)

We intentionally pulled out the single-particle acceleration  $[f_\tau]_{123}(D_1)$ of the smallest members in the population on the right hand side of (F.4) so that the effective ringlet migration speed is compared to the migration speed of the smallest particles. This leaves us with the reduction factor $\Psi$ that reads

$$\Psi = \frac{D_1~\int_{D_1}^{D_2} {\rm d}D~D^2~\Sigma(D)} {\int_{D_1}^{D_2} {\rm d}D~D^3~\Sigma(D)}\cdot$$ (F.5)

The size distribution function $\Sigma(D)$ is not known exactly, but previous works set some limits. French & Nicholson (2000) fit a single-power law $\Sigma(D) = \Sigma_0~D^{-\gamma}$, and also derive D₁ and D₂ limits, in various parts of the Saturn's ring system using 1989 occultation data of 28 Sgr. Their value of $\gamma$ is close to 3, being slightly shallower $\sim$2.75 in the B ring, Cassini division and the inner part of the A ring while slightly steeper $\sim$3.1 in the C ring. We may consider the case $\gamma=3$, see also Rubincam's (2006) $\beta$-factor, and obtain $\Psi \simeq -\Lambda~{\rm ln}~\Lambda$ with $\Lambda = D_1/D_2$. With $D_1\simeq 30$ cm and $D_2\simeq 20$ m in the B ring, we have $\Psi\simeq 0.06$; with $D_1\simeq 1$ cm reported for the C ring and outer part of the A ring we would have $\Psi\simeq 0.007$. For a generic power-law distribution $\Sigma(D) = \Sigma_0~D^{-\gamma}$(with $\gamma\neq 3$) and sufficiently large $\Lambda$, we obtain: (i) $\Psi = [(4-\gamma)/(3-\gamma)]~\Lambda~(1-\Lambda^{3-\gamma})/ (1-\Lambda^{4-\gamma})\simeq [(4-\gamma)/(3-\gamma)]~\Lambda$ when $\gamma< 3$, and (ii) $\Psi =[(4-\gamma)/(\gamma-3)]~\Lambda^{4-\gamma} ~(1-\Lambda^{\gamma-3})/(1-\Lambda^{4-\gamma})\simeq [(4-\gamma)/ (\gamma-3)]~\Lambda^{4-\gamma}$ when $3<\gamma<4$.

As expected, the values of $\Psi$ range in between a few parts in 10^-3 to few parts in 10^-2, suggesting that the migration due to thermal torques becomes hindered in the approximation where all particles are tightly collisionally locked. This is because for shallow size distribution functions $\Sigma(D)$, such as appropriate for the ring system, the mass of the system is dominated by the largest particles. Since these have very small thermal migration rates, they effectively drag the motion of small particles too. The dependence becomes a little relaxed for $\gamma>3$, where at least small particles begin to dominate cross-section of the population and for that reason the $\Psi$ dependence on $\Lambda$becomes less. It disappears only for $\gamma\geq 4$ when the smallest particles in the system start dominating also the total mass of the ringlet. Such steep $\Sigma$-distributions are, however, inadequate for the ring systems, partly also because thermal effects might help deplete small particles (see below).

F.1 The role of collisions in a rarefied medium

The reality, that can be tested only through direct numerical modelling of the ring particle collisional system with thermal forces included, should perhaps reside somewhere in between the two simplified models: the single-particle and tight-locking systems. We may hypothesize, that Eq. (F.3) would still apply for migration of the smallest particles in the system, but now the $\Psi$-factor should get modified to account for the exact collisional coupling in between the particles. Since the latter is roughly characterized with the optical thickness $\tau$ of the ring, we may imagine a modification such as

$$\Psi(\Lambda) \rightarrow \frac{g(\tau)~\Psi(\Lambda)}{1+g(\tau)~ \Psi(\Lambda)} ,$$ (F.6)

where g is some function of the optical thickness and other parameters. We expect $g\rightarrow \infty$ for $\tau\rightarrow 0$and $g\rightarrow 1$ for $\tau\rightarrow \infty$. A proof, however, remains beyond the scope of this paper. We only give a hint of how important the collision effects might be in the limit of very small $\tau$. This is relevant for the rarefied C ring and Cassini division, where $\tau \sim 0.1$ except for narrow ringlets. In a numerical example we focus on the environment in the Cassini division.

Assume a rarefied portion of the ring with low $\tau$. Drift of the smallest particles with size D₁ in the population is a steady migration with the single-particle rate $[f_\tau]_{123}(D_1)$ from (28) over a collisional timescale $T_{\rm coll} \simeq \pi/(n\tau)$ (e.g., Goldreich & Tremaine 1982). After this characteristic timescale has elapsed, the particle typically undergoes a collision in which it obtains a velocity kick $\sim$n D₂ triggering a change in semimajor axis $\sim$2 D₂. The role of collisions after time T is seen by comparing the steady accumulated semimajor axis change $\simeq$ $[{\rm d}a/{\rm d}t]_{123}(D_1)~T$ and the characteristic diffusion length acquired by the collisions

$$\sigma_{\rm coll}^2\sim \frac{T}{T_{\rm coll}}~4D_2^2 .$$ (F.7)

For instance, considering typical conditions in the Cassini division, $\tau \sim 0.1$, $[f_\tau]_{123}(D_1)\sim 3\times 10^{-12}$ m/s² (see below), $D_2\sim 5$ m and $T\sim 5$ My, we obtain

$$\frac{\sigma_{\rm coll}}{\vert[{\rm d}a/{\rm d}t]_{123}(D_1)~T\vert} \sim 0.05 .$$ (F.8)

This choice of T corresponds to our estimated single-particle drift time of $D_1\sim 1$ cm size particles across the Cassini division (Sect. 5.2). The small value of the right hand side of Eq. (F.8) seemingly suggests that the role of mutual collisions in the Cassini division does not significantly hinder the drift of the smallest particles, thus making g in Eq. (F.6) effectively very large.

In the main text we shall use the single particle drift rates for the sake of discussion. Their attenuation by the $\Psi$ factor should be remembered when appropriate.