- ... Saturn
![[*]](/icons/foot_motif.gif)
- This work is dedicated to late Paolo
Farinella (1953-2000) who was prompting one of us (D.V.)
to analyse orbital effects of thermal forces on ring
particles back in 1998. Flooded with many other ideas,
Paolo never came to analyse this problem in detail.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](/icons/foot_motif.gif)
- Appendices are only available in electronic form at http://www.aanda.org
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Saturn
![[*]](/icons/foot_motif.gif)
- The absorptivities
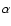 are assumed here to be the effective
values, spectrally integrated about the peak of the source emissivity.
In the optical, the ring particle albedo increases toward larger
wavelengths becoming then flat enough up to
are assumed here to be the effective
values, spectrally integrated about the peak of the source emissivity.
In the optical, the ring particle albedo increases toward larger
wavelengths becoming then flat enough up to
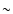
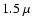 m (e.g., Poulet & Cuzzi 2002; Porco et al. 2005)
so that
m (e.g., Poulet & Cuzzi 2002; Porco et al. 2005)
so that
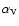 is about the value in the green filter.
The situation is much less known in the mid-infrared where Saturn's
emissivity is maximum. Measurements of optical parameters for polluted
ices by Hudgins et al. (1993) in the relevant temperature and spectral
range reveal several absorption features. Generally, though the
mid-infrared absorptivity
is about the value in the green filter.
The situation is much less known in the mid-infrared where Saturn's
emissivity is maximum. Measurements of optical parameters for polluted
ices by Hudgins et al. (1993) in the relevant temperature and spectral
range reveal several absorption features. Generally, though the
mid-infrared absorptivity
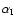 is assumed to be close to
unity for the inferred composition (e.g., Irvine & Pollack 1968;
Kawata & Irvine 1975; Hudgins et al. 1993; Poulet & Cuzzi 2002;
Poulet et al. 2003).
is assumed to be close to
unity for the inferred composition (e.g., Irvine & Pollack 1968;
Kawata & Irvine 1975; Hudgins et al. 1993; Poulet & Cuzzi 2002;
Poulet et al. 2003).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
acceleration
![[*]](/icons/foot_motif.gif)
- This is a part of a more general formula giving orbital
mean values of both the radial
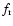 and transverse
and transverse 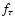 acceleration
components:
acceleration
components:
![$\left[f_{\rm r}+{\rm i} f_\tau\right]_1 = -{4\over 3}
\sqrt{2\over 3\pi}~\omega^{3/4}~ \Phi~s_+\varphi^+$](/articles/aa/full/2007/32/aa7029-06/img174.gif) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... mid-infrared
![[*]](/icons/foot_motif.gif)
- Cassini observations reported by Spilker et al. (2005)
provide empiric values of ring emissivities. While no detailed
attempt to translate these values into the Bond albedo of the individual
particles was done using a radiative transfer theory, we may
consider them to provide an upper bound on
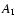 ,
namely: (i)
,
namely: (i)
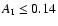 for the B ring, (ii)
for the B ring, (ii)
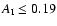 for the A ring, and
(iii)
for the A ring, and
(iii)
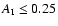 for the C ring. We re-ran simulations presented
in the main text with these upper bound values of
for the C ring. We re-ran simulations presented
in the main text with these upper bound values of 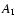 and found
no significant change in results.
and found
no significant change in results.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.