A&A 471, 301-309 (2007)
DOI: 10.1051/0004-6361:20077704
Grand minima and maxima of solar activity: new observational constraints
I. G. Usoskin1 - S. K. Solanki2 - G. A. Kovaltsov3
1 - Sodankylä Geophysical Observatory (Oulu unit), POB 3000, University of Oulu, Finland
2 - Max-Planck-Institut für Sonnensystemforschung, 37191
Katlenburg-Lindau, Germany
3 - Ioffe Physical-Technical Institute, Politekhnicheskaya 26, 194021 St. Petersburg, Russia
Received 24 April 2007 / Accepted 25 May 2007
Abstract
Aims. Using a reconstruction of sunspot numbers stretching over multiple millennia, we analyze the statistics of the occurrence of grand minima and maxima and set new observational constraints on long-term solar and stellar dynamo models.
Methods. We present an updated reconstruction of sunspot number over multiple millennia, from 14C data by means of a physics-based model, using an updated model of the evolution of the solar open magnetic flux. A list of grand minima and maxima of solar activity is presented for the Holocene (since 9500 BC) and the statistics of both the length of individual events as well as the waiting time between them are analyzed.
Results. The occurrence of grand minima/maxima is driven not by long-term cyclic variability, but by a stochastic/chaotic process. The waiting time distribution of the occurrence of grand minima/maxima deviates from an exponential distribution, implying that these events tend to cluster together with long event-free periods between the clusters. Two different types of grand minima are observed: short (30-90 years) minima of Maunder type and long (>110 years) minima of Spörer type, implying that a deterministic behaviour of the dynamo during a grand minimum defines its length. The duration of grand maxima follows an exponential distribution, suggesting that the duration of a grand maximum is determined by a random process.
Conclusions. These results set new observational constraints upon the long-term behaviour of the solar dynamo.
Key words: Sun: activity - solar-terrestrial relations - sunspots
The Sun is the only star whose magnetic activity can be studied on long time scales.
Direct solar observations since 1610 reveal great variability of the cycle averaged
magnetic activity level of the Sun - from the extremely quiet Maunder minimum (second half of 17th century) up to the modern episode of enhanced activity since the middle of the 20th century. The Maunder minimum is representative of grand minima of solar activity (e.g., Eddy 1977a), when sunspots almost completely vanished from the solar surface, while the solar wind appeared to continue blowing, although at a reduced pace (Cliver et al. 1998; Usoskin et al. 2001).
A grand minimum is believed to correspond to a special state of the dynamo
(Sokoloff 2004; Miyahara et al. 2006), and its very existence poses a challenge for solar dynamo theory. It is noteworthy that dynamo models do not agree how often such episodes occur in the Sun's history
and whether their appearance is regular or random.
For example, the commonly used mean-field dynamo yields a fairly regular 11-year cycle,
while there are also dynamo models, deterministic (e.g., Tobias 1996; Moss & Brooke 2000) or including a stochastic driver (e.g., Choudhuri 1992; Schmitt et al. 1996; Ossendrijver 2000; Weiss & Tobias 2000; Minini et al. 2001; Charbonneau 2001, 2004)
which predict intermittency of the solar magnetic activity. The presence of grand maxima of solar activity has been mentioned (Eddy 1977a; Usoskin et al. 2003; Solanki et al. 2004) but has not yet been studied in great detail.
Thanks to the recent development of precise technologies, including accelerator mass
spectrometry, solar activity can be reconstructed over multiple millenia
from concentrations of cosmogenic isotopes 14C and 10Be in terrestrial archives. This allows one to study the temporal evolution of solar magnetic activity,
and thus of the solar dynamo, on much longer time scales than available from
direct measurements. Consequently, a number of attempts to investigate the occurrence of grand minima in the past,
using radiocarbon 14C data in tree rings, have been undertaken.
E.g., Eddy (1977a) identified major excursions in the available 14C record as grand minima and maxima of solar activity and presented a list of 6 grand minima and 5 grand maxima for the last 5000 years.
Stuiver & Braziunas (1989) studied grand minima as systematic excesses of the high-pass filtered 14C record and suggested two distinct types of the grand minima: shorter Maunder-type and longer Spörer-like minima (cf. Stuiver et al. 1991).
Later Voss et al. (1996) defined grand minima in a similar manner
and provided a list of 29 such events for the last 8000 years.
A similar analysis of excursions of the 14C production rate has been
presented by Goslar (2003). However, because of the lack of adequate physical
models relating the radicarbon abundance to the solar activity level, such
studies retained a qualitative element.
The use of high-pass filtered 14C data is based on the assumption that
solar activity variations are important only on short times, while
all the long-term changes in radiocarbon production are attributed solely to
the slowly changing geomagnetic field.
This method ignores any possible long-term changes in the solar activity
(e.g., on time scales longer than 500 years for Voss et al. 1996).
There is, however, increasing evidence that solar activity varies on multi-centennial to multi-millennial time scales (McCracken et al. 2004; Usoskin et al. 2006a).
A recently developed approach, based on physics-based modelling of all
links relating the measured cosmogenic isotope abundance to the level of
solar activity, allows for quantitative reconstruction of the solar activity
level in the past, and thus, for a more realistic definition of
the periods of grand minima or maxima.
Here we study the statistics of occurrence of grand minima/maxima throughout the
Holocene and impose additional observational constraints on the dynamo models of the Sun and Sun-like stars.
Solar activity on multi-millenial time scales has been recently reconstructed
using a physics-based model from measurements of 14C in tree rings
(see full details in Solanki et al. 2004; Usoskin et al. 2006a).
The validity of the model results for the last centennia has been proven by
independent data on measurements of 44Ti in stony meteorites (Usoskin et al. 2006b).
The reconstruction depends on the knowledge of temporal changes of the
geomagnetic dipole field, which must be estimated independently by paleomagnetic
methods. Here we compare two solar activity reconstructions, which are based on alternative paleomagnetic models: one which yields an estimate of the virtual aligned dipole moment (VADM) since 9500 BC (Yang et al. 2000), and the other a recent paleomagnetic
reconstruction of the true dipole moment since 5000 BC (Korte & Constable 2005).
We note that the geomagnetic dipole moment obtained by Korte & Constable (2005) lies systematically lower than that of Yang et al. (2000), leading to a systematically higher solar activity reconstruction in the past (Usoskin et al. 2006a). While the geomagnetic reconstruction of the VADM by Yang et al. (2000) provides an upper bound for the true dipole moment, the more recent work of (Korte & Constable 2005) may underestimate it. Thus we consider both models as they bound a realistic case. We note that the Yang et al. (2000) data run more than 4000 years longer and give a more conservative estimate of the grand maxima.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7704fig1.eps}\end{figure}](/articles/aa/full/2007/31/aa7704-07/Timg5.gif) |
Figure 1:
Long-term solar activity reconstruction from 14C data. All data are decadal averages. Solid (denoted as "Y00'') and grey ("K05'') curves are based on the paleo-geomagnetic reconstructions of Yang et al. (2000) and Korte & Constable (2005), respectively. A) The modulation potential 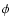 .
Big circles ("NM'') denote the .
Big circles ("NM'') denote the 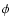 values obtained from direct cosmic ray measurements since 1951 (Usoskin et al. 2005). B) Open flux values obtained from direct cosmic ray measurements since 1951 (Usoskin et al. 2005). B) Open flux 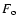 .
Reconstruction from sunspot numbers (Krivova et al. 2007) is used after 1610. C) Sunspot numbers reconstructed here. The Y00 and K05 curves are called SN-L and SN-S series, respectively throughout the paper. Observed group sunspot numbers (Hoyt & Schatten 1998) are shown after 1610. .
Reconstruction from sunspot numbers (Krivova et al. 2007) is used after 1610. C) Sunspot numbers reconstructed here. The Y00 and K05 curves are called SN-L and SN-S series, respectively throughout the paper. Observed group sunspot numbers (Hoyt & Schatten 1998) are shown after 1610. |
| Open with DEXTER |
Different indices of the reconstructed solar activity are shown in Fig. 1.
Most directly related to the 14C production in the atmosphere is the modulation
potential 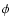 (e.g., Castagnoli & Lal 1980; Masarik & Beer 1999; Usoskin et al. 2002) whose variations are shown in panel A. The modulation potential
(e.g., Castagnoli & Lal 1980; Masarik & Beer 1999; Usoskin et al. 2002) whose variations are shown in panel A. The modulation potential 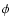 is a parameter describing the spectrum of galactic
cosmic rays (see definition and full description of this index in Usoskin et al. 2005).
Using a model of the heliospheric transport of cosmic rays, the modulation potential
can be nearly linearly related to the open solar magnetic flux
is a parameter describing the spectrum of galactic
cosmic rays (see definition and full description of this index in Usoskin et al. 2005).
Using a model of the heliospheric transport of cosmic rays, the modulation potential
can be nearly linearly related to the open solar magnetic flux 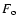 .
The reconstructed long-term variations of the open solar magnetic flux are shown
in panel B.
Next, using a model of the open magnetic flux formation, one can
estimate the sunspot numbers from the
.
The reconstructed long-term variations of the open solar magnetic flux are shown
in panel B.
Next, using a model of the open magnetic flux formation, one can
estimate the sunspot numbers from the 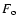 data.
This was done earlier using the open flux model by Solanki et al. (2000, 2002).
However, the model relating sunspots to the open magnetic flux, has been updated
recently by Krivova et al. (2007).
Starting from sunspot numbers (SN) they computed open and total magnetic flux as well as
the total solar irradiance (from SN and total magnetic flux).
Besides the active regions, the influence of ephemeral active regions is included.
They determined the free parameters of the models used by requiring the model output to
reproduce the best available data sets (of open and total fluxes as well as total solar irradiance)
with the help of a genetic algorithm. In particular, the improved total flux data set of Arge et al. (2002) and the total irradiance composite of Fröhlich (2006) set tight constraints, which could only be met by revising the relationship between SN and total emergent magnetic flux.
This revised relationship is employed here too. Accordingly, here we use this updated model to convert
data.
This was done earlier using the open flux model by Solanki et al. (2000, 2002).
However, the model relating sunspots to the open magnetic flux, has been updated
recently by Krivova et al. (2007).
Starting from sunspot numbers (SN) they computed open and total magnetic flux as well as
the total solar irradiance (from SN and total magnetic flux).
Besides the active regions, the influence of ephemeral active regions is included.
They determined the free parameters of the models used by requiring the model output to
reproduce the best available data sets (of open and total fluxes as well as total solar irradiance)
with the help of a genetic algorithm. In particular, the improved total flux data set of Arge et al. (2002) and the total irradiance composite of Fröhlich (2006) set tight constraints, which could only be met by revising the relationship between SN and total emergent magnetic flux.
This revised relationship is employed here too. Accordingly, here we use this updated model to convert 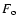 into the sunspot number (Eq. (A.17)), which is described in detail in Appendix A.
into the sunspot number (Eq. (A.17)), which is described in detail in Appendix A.
A comparison between the sunspot number series obtained using the new open flux
model with those published by Solanki et al. (2004) is shown in Fig. 2.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7704fig2.eps}\end{figure}](/articles/aa/full/2007/31/aa7704-07/Timg6.gif) |
Figure 2:
Scatter plot of decadal sunspot numbers for 9500 BC - 1900 AD published
by Solanki et al. (2004), 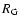 (S04), vs. sunspot numbers obtained in this work in a way identical to S04 but using the updated open solar flux model of Krivova et al. (2007). (S04), vs. sunspot numbers obtained in this work in a way identical to S04 but using the updated open solar flux model of Krivova et al. (2007). |
| Open with DEXTER |
The scatter in the relationship is very small (correlation coefficient 0.995),
but there is a small systematic difference between the two series.
The newly obtained sunspot numbers are slightly higher, with
the mean difference being about 1.6 and the standard deviation about 2.
At large SN values, however, the opposite is observed, with the new reconstructed SN
being smaller by values up to 14.
This reduces the largest peaks (grand maxima) somewhat.
This difference is a result of the different relationship between SN
and total emerging magnetic flux in active regions used by Krivova et al. (2007) than by Solanki et al. (2000, 2002).
We note that the difference is kept within the uncertainty of the
reconstruction, which is about 8 for the last millenia and up to 15-20 in the beginning of the Holocene (see Supplementary Material to Solanki et al. 2004).
The difference between the original sunspot numbers published in Usoskin et al. (2006a)
based on the paleomagnetic model by Korte & Constable (2005) and those obtained here using the updated open flux model has a mean of 1.0 and standard deviation about 2.4.
The 11 000-yr long data sets of the decadal sunspot number
similar to that by Solanki et al. (2004) but with the updated open flux model
is shown in Fig. 1C. It is called the SN-L series throughout the paper.
The shorter series (Fig. 1C), which is similar to that by Usoskin et al. (2006a), is called SN-S henceforth. After 1610 AD, the actually observed group sunspot numbers (Hoyt & Schatten 1998) has been used instead of the reconstructions.
Before identifying the grand minima and maxima, the decadal resolution data have been smoothed with the Gleissberg (1-2-2-2-1) filter, which is regularly applied when studying long-term variations of solar activity in order to suppress the noise (e.g., Gleissberg 1944; Soon et al. 1996; Mursula & Ulich 1998).
In order to check the effect of the filter we have studied a number of artificial SN series containing a total of 1000 grand
minima of 60-yr duration (at the level of
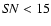 )
each.
A noise with
)
each.
A noise with 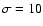 has been added to the series, and the grand minima have been identified
again as
has been added to the series, and the grand minima have been identified
again as
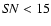 in both the raw and 1-2-2-2-1 smoothed noised series.
We found that 35% of grand minima are incorrectly identified (too short, too long or split in two short episodes, comparing to the "real'' signal) in the raw noisy series.
The filtering reduces the mis-identification to
in both the raw and 1-2-2-2-1 smoothed noised series.
We found that 35% of grand minima are incorrectly identified (too short, too long or split in two short episodes, comparing to the "real'' signal) in the raw noisy series.
The filtering reduces the mis-identification to 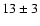 %, i.e. 3-fold.
Thus, the use of the 1-2-2-2-1 Gleissberg filter reduces the effect of noise on the
grand minima/maxima definition and makes the results more robust.
This smoothing, however, leads to a reduction in the amplitude and a slight underestimate (about 7% according to the above numerical experiment) of the number and duration of short, less than 30 years long minima and maxima.
%, i.e. 3-fold.
Thus, the use of the 1-2-2-2-1 Gleissberg filter reduces the effect of noise on the
grand minima/maxima definition and makes the results more robust.
This smoothing, however, leads to a reduction in the amplitude and a slight underestimate (about 7% according to the above numerical experiment) of the number and duration of short, less than 30 years long minima and maxima.
The filtered SN-L and SN-S series are shown in Figs. 3 and 4, respectively. We analyze both reconstructed SN data sets in equal details.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7704fig3.eps}\end{figure}](/articles/aa/full/2007/31/aa7704-07/Timg10.gif) |
Figure 3:
Sunspot activity SN-L throughout the Holocene (see text) smoothed with a 1-2-2-2-1 filter. Blue and red areas denote grand minima and maxima, respectively. The entire series is spread over two panels for better visibility. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7704fig4.eps}\end{figure}](/articles/aa/full/2007/31/aa7704-07/Timg11.gif) |
Figure 4:
Sunspot activity SN-S (see text) smoothed with a 1-2-2-2-1 filter. Blue and red areas denote grand minima and maxima, respectively. |
| Open with DEXTER |
3.1 Grand minima
We have defined a grand minimum as a period when the (smoothed) SN level
is less than 15 during at least two consecutive decades - this corresponds to
blue-filled (lower dark grey in b/w printing) areas in Figs. 3 and 4.
However, taking into account the uncertainty of the SN reconstruction and the influence
of the filtering, we have also considered as minima clear dips in the SN whose bottom is between 15 and 20 and the depth (with respect to surrounding plateaus/maxima) exceeds 20.
Therefore, such periods as, e.g., ca. 6400 BC are considered as
grand minima (see Fig. 3) even though their bottoms are above 15.
On the other hand, the period ca. 4450 BC is not counted as a grand minimum
because its minimum lies above 15 and its depth is less than 20.
All 27 grand minimum periods thus defined in the SN-L series are
listed in Table 1 together with their approximate duration,
defined as the period of time when SN was below 15 (20) as discussed above.
Among them there are two periods (ca 9200 BC and 7500 BC) when the dominant
grand minima are interrupted by a 1-2 decades long upward excursions.
We regard these period as continuous Spörer-like minima. Together these grand minima have a total duration of 1880 years, so that the Sun spends about 17% of the time in a grand minimum state.
We note that all the grand minima after 3000 BC discussed by Eddy (1977a, 1977b) are present in Table 1, which however contains also minima at ca. 1040 BC and
2860 BC not found by Eddy. On the other hand, all the grand minima listed in the table are mentioned by Voss et al. (1996), but the latter![[*]](/icons/foot_motif.gif) list more minima, e.g., three
minima between 200 BC and 200 AD which do not appear in our series.
Most of the minima listed here can also bee seen in Fig. 2 of Goslar (2003).
Therefore, we conclude that our definition of grand minima applied to the
present data set gives results generally in agreement
with earlier studies but not identical to them.
In particular, it gives more details than the study by Eddy (1977a)
but discards some small fluctuations mentioned by Voss et al. (1996).
list more minima, e.g., three
minima between 200 BC and 200 AD which do not appear in our series.
Most of the minima listed here can also bee seen in Fig. 2 of Goslar (2003).
Therefore, we conclude that our definition of grand minima applied to the
present data set gives results generally in agreement
with earlier studies but not identical to them.
In particular, it gives more details than the study by Eddy (1977a)
but discards some small fluctuations mentioned by Voss et al. (1996).
Table 1:
Approximate dates (in -BC/AD) of grand minima in the SN-L series (see text).
The grand minima listed in Table 1 dating after 5000 BC are identical for both SN-L and SN-S series (except for one minimum ca. 1385 BC in the SN-S series which does not match the formal definition). These grand minima will be used for the further analysis.
Similar to Solanki et al. (2004), we define as a grand maximum of solar activity a period when SN exceeds 50 during at least two consecutive decades (see red filled (upper dark grey in b/w printing) areas in Figs. 3 and 4). If two consecutive maxima are separated by less than 30 years they are considered as a single maximum (e.g., ca. 9000 BC in the SN-L series), i.e. they are treated in a way similar to grand minima. We have identified 19 grand maxima (of a total duration of 1030 years, corresponding to about 9% of the time)
in the SN-L series since 9500 BC, including also the modern maximum.
These are listed in Table 2.
Four out of six grand maxima found here after 3000 BC coincide with those pointed out
by Eddy (1977a,b). In the SN-S series, 23 grand maxima (of a total duration of 1560 years, corresponding to about 22% of the time) are identified since
5000 BC, as listed in Table 3. All maxima identified in the SN-L series are present also in the SN-S series, but
the latter yields more maxima satisfying the same definition before
1500 BC (after ca. 1500 BC the maxima are nearly identical). This indicates that the identification of maxima is less robust than for grand minima, and is more dependent on the definitions and model assumptions.
Table 2:
Approximate dates (in -BC/AD) of grand maxima in the SN-L series.
Table 3:
Approximate dates (in -BC/AD) of grand maxima in the SN-S series.
3.3 Waiting time distribution
The interval between two consequent events is called the waiting time.
The statistical distribution of waiting times (WTD - waiting time distribution)
reflects the nature of a process which produces the studied events.
For instance, an exponential WTD is a clear indicator of a purely random,
"memoryless'' process (e.g., Poisson process), when the behaviour of a system
does not depend on its preceding evolution on both short or long time-scales.
Any significant deviation of the WTD from an exponential law
implies that the probability of an event to occur is not time-independent but
is related to the previous history of the system.
We note that the occurrence of events generally is random also for a non-exponential
distribution, but the probability is not uniform in time.
This can be interpreted in different ways:
self-organized criticality (e.g., de Carvalho & Prado 2000; Freeman et al. 2000), time-dependent
Poisson process (e.g., Wheatland 2003), some memory in the driving process
(e.g., Lepreti et al. 2001; Mega et al. 2003).
The most typical non-exponential WTD is a power law which is, e.g., a necessary but not sufficient indication of self-organized criticality (de Carvalho & Prado 2000).
A power law implies higher tails of the distribution, i.e.
higher probability (relative to the exponential function) of occurrence of both long and
short intervals between the events. A power law distribution of the waiting time has been obtained for many solar and terrestrial indices on different time scales from minutes
to 105 years:
e.g., intervals between major earthquakes (Bak et al. 2002; Mega et al. 2003);
intervals between successive solar flares (Pearce et al. 1993; Boffetta et al. 1999; Moon et al. 2001);
waiting time between successive coronal mass ejections (Wheatland 2003; Berhondo et al. 2006);
intervals between bursts in the solar wind (Freeman et al. 2000); repetition time of geomagnetic disturbances (Papa et al. 2006); intervals between the geomagnetic field reversals (Ponte-Neto & Papa 2006), etc. Note that many of these processes, which depict different degrees of self-organization, are related to energy accumulation and release.
Here we study the WTD of the occurrence of grand minima and maxima of solar activity in order to understand the nature of its long-term evolution. The waiting time is defined as the length x of an interval between centers of consequent events.
First we studied the differential distribution which is defined as
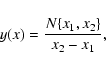 |
(1) |
where
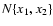 is the number of events with the waiting time
is the number of events with the waiting time
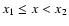 .
Statistical errors of the differential distribution are estimated from the Poisson statistics as
.
Statistical errors of the differential distribution are estimated from the Poisson statistics as
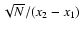 .
.
Since the statistics are poor (19-27 events) and differential WTD histograms are rough,
we have studied also the normalized cumulative distribution defined as
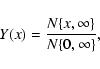 |
(2) |
which corresponds to the probability of finding a waiting time exceeding x. In this case the statistical errors cannot be determined since the points of the cumulative distribution are not independent.
The exponential WTD model is defined as
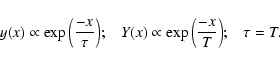 |
(3) |
The power law WTD model is defined as
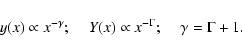 |
(4) |
The power law serves mainly to emphasize deviations from a purely exponential distribution, since the poor statistics hardly allow us to distinguish between a power law and other more-stretched-than-exponential distributions, e.g., log-Poisson.
We note that short intervals (shorter than a century) cannot be reliably defined because of noise and filtering. Statistics of very long intervals is not reliable either because of the limited length of the analyzed series. Therefore, when fitting the data we will ignore the shortest and longest intervals, i.e. first and last points of the cumulative distribution (the number of bins of the differential distribution is left unchanged).
First we have constructed histograms of the sunspot numbers.
The histogram for the SN-L series is shown in Fig. 5.
While being close to a normal distribution (
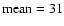 ,
,
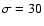 ), there is an apparent excess both at very low sunspot numbers, corresponding to the grand minima, and
at very high values, corresponding to grand maxima.
The overall distribution is consistent with the direct observational
record after 1610, suggesting that the latter is a representative
sample for the sunspot activity statistics, including grand minimum
and maximum
), there is an apparent excess both at very low sunspot numbers, corresponding to the grand minima, and
at very high values, corresponding to grand maxima.
The overall distribution is consistent with the direct observational
record after 1610, suggesting that the latter is a representative
sample for the sunspot activity statistics, including grand minimum
and maximum![[*]](/icons/foot_motif.gif) . This distribution with these excesses suggests that grand minima and maxima are special states of the solar dynamo that cannot be explained by random
fluctuations or noise in the data (see also forthcoming sections).
. This distribution with these excesses suggests that grand minima and maxima are special states of the solar dynamo that cannot be explained by random
fluctuations or noise in the data (see also forthcoming sections).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7704fig5.eps}\end{figure}](/articles/aa/full/2007/31/aa7704-07/Timg22.gif) |
Figure 5:
Histogram of the sunspot number SN series reconstructed here
for 9500 BC - 2000 AD. Hatched areas correspond to directly observed sunspots after 1610. The curve represents the best fit normal distribution. |
| Open with DEXTER |
Table 4:
Fitting of power law and exponential models to distributions of the grand minima and maxima occurrence: For the differential distribution the value of 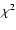 is shown together with the corresponding confidence level (in parentheses) for 4 degrees of freedom.
is shown together with the corresponding confidence level (in parentheses) for 4 degrees of freedom.
The distribution of the waiting time between grand minima is shown in the left-hand panel of Fig. 6 together
with the best fit approximations.
Parameters of the best-fit approximations are shown in Table 4 (row A).
The best fit exponential model (Eq. (3)) gives
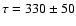 years, which roughly corresponds to the mean frequency of
grand minima occurrence. The exponential model agrees only relatively poorly with the observed WTD. The best fit power law model (Eq. (4)) agrees reasonably with the observed WTD.
years, which roughly corresponds to the mean frequency of
grand minima occurrence. The exponential model agrees only relatively poorly with the observed WTD. The best fit power law model (Eq. (4)) agrees reasonably with the observed WTD.
The cumulative WTD is shown in the right-hand panel of Fig. 6 together with the best fit approximations (Table 4, row A, Cols. 4 and 5).
The power law model agrees well with the bulk of the data
except for the very far tail (x>1000 years).
However, this tail contains only two events and is not representative.
(The 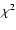 -test cannot be applied to the cumulative distribution since the points
are not independent.) The exponential model poorly reproduces the WTD.
As an additional test we compare the parameters of the models describing differential
and cumulative distributions, viz.
-test cannot be applied to the cumulative distribution since the points
are not independent.) The exponential model poorly reproduces the WTD.
As an additional test we compare the parameters of the models describing differential
and cumulative distributions, viz.
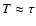 and
and
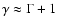 .
Both models pass this test.
.
Both models pass this test.
We conclude that a power law model better describes the observed WTD for
grand minima, although an exponential decay cannot be completely ruled out.
This is valid also for the SN-S series whose grand minima (except of one ca. 1385 BC) coincide with those in the SN-L series after 5000 BC.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7704fig6.eps}\end{figure}](/articles/aa/full/2007/31/aa7704-07/Timg55.gif) |
Figure 6:
Differential ( left panel) and cumulative ( right panel)
distribution of the waiting time between subsequent grand minima.
The histogram ( left) and circles ( right) represent the observed distribution, while solid and dotted lines depict best fit power law and exponential approximations, respectively. |
| Open with DEXTER |
A histogram of the duration of grand minima (Table 1) is shown in Fig. 7.
The mean duration is 70 year but the distribution is not uniform.
The minima tend to be either of a short duration, between 30 and 90 years
similar to the Maunder minimum, or rather long, longer than 110 years
similar to the Spörer minimum.
This agrees with the earlier conclusion on two different types of grand minima (Stuiver & Braziunas 1989; Goslar 2003).
This suggests that a grand minimum is a special state of the dynamo
whose duration is not random but is defined by some intrinsic process.
Note, however, that only 3 of the 5 Spörer-like minima are clear long grand minima while the other 2 are composed of multiple sub-minima (# 25 and 27 in Table 1 - see Sect. 3.1).
The distribution of the waiting time intervals between
subsequent maxima, listed in Table 2, is shown
in Fig. 8, with the parameters of best-fit approximations
shown in Table 4, row B. The differential distribution (left panel) can be well fitted by the power law model. An exponential model gives a formally insignificant
fit to the distribution.
The cumulative distribution is shown in the right panel and is
also close to a power law (see Table 4, rowB).
The exponential model fits
short-to-long intervals even better, but cannot reproduce the far tail,
with three intervals exceeding 1000 years.
Indices for the differential and cumulative models are
barely consistent with each other (
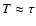 and
and
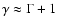 ).
Accordingly, for the SN-L series we cannot give a clear preference to either model.
).
Accordingly, for the SN-L series we cannot give a clear preference to either model.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7704fig8.eps}\end{figure}](/articles/aa/full/2007/31/aa7704-07/Timg57.gif) |
Figure 8:
Differential ( left panel) and cumulative ( right panel) distributions of the waiting time between grand maxima according to the SN-L series. |
| Open with DEXTER |
The statistics of WTD for the grand maxima using the SN-S series is shown in Fig. 9, with the best-fit parameters listed in Table 4, row C. The power law model satisfactory fits the differential WTD,
while the exponential law displays only a poor correspondence to it.
The cumulative WTD (right panel) is nicely fitted by a power law but poorly by an exponential. Both models pass the additional test (
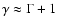 vs.
vs.
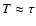 ).
).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7704fig9.eps}\end{figure}](/articles/aa/full/2007/31/aa7704-07/Timg58.gif) |
Figure 9:
Differential ( left panel) and cumulative ( right panel) distributions of the waiting time between grand maxima according to the SN-S series. |
| Open with DEXTER |
Therefore we conclude that, although the exponential model cannot be totally excluded, the power law model is more preferable in describing the WTD of grand maxima.
The distribution of the lengths of maxima in the SN-L series is shown in Fig. 10, with best-fit parameters listed in Table 4, row D.
The differential distribution (left panel) is reasonably fitted by an exponential law
but is poorly described by a power law. Although both models are seemingly good in fitting the observed cumulative WTD (right panel of Fig. 10), the additional test excludes the power law model, since
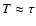 but
but
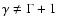 .
Therefore, we conclude that the distribution of the lengths of grand maximum
episodes is close to exponential, as noticed by Solanki et al. (2004).
.
Therefore, we conclude that the distribution of the lengths of grand maximum
episodes is close to exponential, as noticed by Solanki et al. (2004).
The differential distribution of the duration of maxima for the SN-S series is fitted
by none of the two models (see Table 4, row E). The best-fit parameters for the cumulative distribution also favor the exponential distribution (
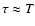 )
over the power law (
)
over the power law (
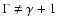 ).
).
We have also studied possible quasi-periodicities in the rate of grand minima/maxima
occurrence. We have found that the occurrence of grand minima depicts a weak (marginally
significant) quasi-periodicity of 2000-2400 years, which is a well-known period
in 14C data (e.g., Damon & Sonett 1991; Vasiliev & Dergachev 2002). No other periodicities are observed in the occurrence rate of grand minima. We have found no periodic feature in the occurrence of grand maxima in the
SN-L series, while a marginal hint for a periodicity of about 1200 years and its harmonics (about 600 and 400 years - cf. Usoskin et al. 2004) is found in SN-S data.
This indicates that the 2400-year periodicity is related likely to the clustering of
grand minima rather than to a long-term "modulation'' of solar activity.
Therefore, we conclude that the occurrence of grand minima and maxima is not
a result of long-term cyclic variability but is defined by stochastic/chaotic
processes as discussed in Sect. 6.
5 Summary of the results
We have studied the statistics of occurrence of grand minima and maxima
over the last 7-11 millennia. The main results can be summarized as follows.
- 1.
- We have presented lists of grand minima (Table 1) and maxima
(Tables 2 and 3), using updated physics-based reconstruction
of solar activity from 14C data measured by the INTCAL collaboration (Stuiver et al. 1998). The identification of grand minima is found to be more robust to the exact correction of the geomagnetic field than the grand maxima.
- 2.
- The occurrence of grand minima and maxima does not depict a dominant periodic behaviour.
Only a weak tendency exists for grand minima to cluster with a quasi-period
of about 2400 years, and no clear periodicities are observed in the occurrence of grand maxima.
- 3.
- The waiting time between grand minima depicts a distribution which deviates significantly from the exponential distribution
![[*]](/icons/foot_motif.gif) ,
although the latter cannot be completely ruled out because of poor statistics.
,
although the latter cannot be completely ruled out because of poor statistics.
- 4.
- The distribution of the duration of grand minima is bimodal, with a dominance of short
(30-90 yr) Maunder-like minima and a smaller number of long (longer than 110 yr)
Spörer-like minima.
- 5.
- The distribution of the waiting time between grand maxima also deviates from an exponential distribution (especially for the last 7000 years in the SN-S data series), but the latter cannot be completely ruled out.
- 6.
- Lengths of grand maxima correspond to an exponential distribution.
We have tested that the obtained results are robust with respect
to the uncertainties of the reconstruction.
The results remain qualitatively the same when varying the parameters
of Eq. (A.17) or when using the sunspot data obtained earlier (Solanki et al. 2004; Usoskin et al. 2006a) based on the old open flux model.
6 Discussion and conclusions
Using the above results we can formulate additional constraints on a dynamo model
aiming to describe the long-term evolution of solar magnetic activity.
- 1.
- The Sun spends around 3/4 of the time at moderate magnetic activity levels (averaged over 10 years). The remainder of the time is spent in the state of a grand minimum (about 17%) or a grand maximum (9% or 22% for the SN-L or SN-S series, respectively). The solar activity during modern times corresponds to the grand maximum state.
- 2.
- The occurrence of grand minima/maxima is not a result of long-term cyclic
variations but is defined by stochastic/chaotic processes.
This casts significant doubts on attempts of a long-term prediction of solar activity
using multi-periodic analyses.
- 3.
- The observed waiting time distribution of the occurrence of both grand minima and
grand maxima displays a deviation from an exponential distribution.
A relative excess of short and long waiting times indicates that the occurrence
of these events is not a time independent "memoryless'' Poisson-like process,
but tends to either cluster events together or produce long event-free periods.
Similar waiting time distributions are typical for many processes with, e.g.
self-organized criticality or processes related to accumulation and release of energy
(see Sect. 3.3).
- 4.
- We distinguish between grand minima of two different types: short minima of Maunder
type and long minima of Spörer type (cf., Stuiver & Braziunas 1989). This suggests that a grand minimum is a special state of the dynamo. Once falling into the grand minimum as a result of a stochastic/chaotic but non-Poisson process, the dynamo is "trapped'' in this state and its behaviour is driven by deterministic intrinsic features.
- 5.
- The duration of grand maxima follows an exponential distribution, in accord with
the earlier finding of Solanki et al. (2004).
This indicates that leaving a grand maximum is a random process, in contrast to the
grand minimum case.
In conclusion, we have presented an analysis of the occurrence of grand minima
and maxima of solar activity on time scales up to 11 000 years.
The results put important observational constraints upon the long-term behaviour of the solar dynamo. In view of the solar paradigm for the magnetic activity of cool stars, we expect these results to be applicable also to stellar dynamo models.
We note, however, that the current results depend on the reliability of the reconstruction of the sunspot numbers, which in turn depends on the reliability of the employed geomagnetic
field and other factors.
This mainly affects the definition of grand maxima, while the statistics of grand minima
occurrence remain fairly robust against these uncertainties.
Acknowledgements
Natalie Krivova and Laura Balmaceda are thanked for useful discussions and for
input that provided the basis for revising
the sunspot number reconstruction described in the appendix.
We are grateful to Monika Korte, Vincent Courtillot, Gauthier Hulot and Arnaud Chulliat for useful discussion on the paleomagnetic data. GAK gratefully acknowledges supports from the Academy of Finland and the Finnish Academy of Science and Letters Vilho, Yrjö and Kalle Väisälä Foundation as well as the Program of Presidium RAS N16-3-5.4.
Here we invert the updated model relating the sunspot number R to the open magnetic flux 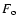 (Krivova et al. 2007 - referred henceforth as KBS07) to reconstruct
the decadal sunspot numbers from the open flux (cf. Usoskin et al. 2004) as follows.
From Eq. (3) of KBS07 one can obtain (henceforth
(Krivova et al. 2007 - referred henceforth as KBS07) to reconstruct
the decadal sunspot numbers from the open flux (cf. Usoskin et al. 2004) as follows.
From Eq. (3) of KBS07 one can obtain (henceforth
 denotes 10-year averaging):
denotes 10-year averaging):
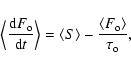 |
(A.1) |
where
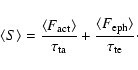 |
(A.2) |
From Eq. (1) of KBS07 it follows
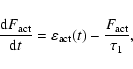 |
(A.3) |
where
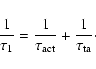 |
(A.4) |
Hereafter we adopt the parameter values from Table 1 (line 1) and Sect. 2.1 of KBS07
and express magnetic flux in units of 1014 Wb/month and time in months.
Equation (5) of KBS07 takes the form
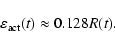 |
(A.5) |
Since
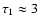 months is much shorter than the cycle length, one can assume that
months is much shorter than the cycle length, one can assume that
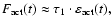 and after 10-year averaging we obtain:
and after 10-year averaging we obtain:
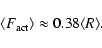 |
(A.6) |
Similarly, since
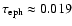 months is very small, one expects
months is very small, one expects
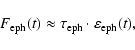 |
(A.7) |
where
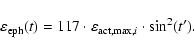 |
(A.8) |
Here t' runs over the length of ephemeral region cycle, which is longer than
a sunspot cycle. With the actual 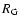 data since 1700 (Hoyt & Schatten 1998) we have tested that the amplitude of a solar cycle is related to the 10-yr averaged sunspot value as
data since 1700 (Hoyt & Schatten 1998) we have tested that the amplitude of a solar cycle is related to the 10-yr averaged sunspot value as
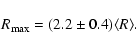 |
(A.9) |
Therefore, from (A.5)
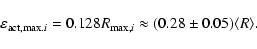 |
(A.10) |
Since
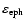 displays long cycles (of the mean duration of about 18 years) that partially overlap, the mean value of
displays long cycles (of the mean duration of about 18 years) that partially overlap, the mean value of
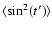 is
numerically found to be
is
numerically found to be
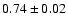 ,
and Eq. (A.7) becomes
,
and Eq. (A.7) becomes
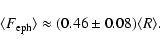 |
(A.11) |
From the above consideration one obtains that
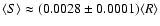 and
and
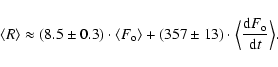 |
(A.12) |
In order to evaluate the decadal mean derivative we substitute the derivative by a slope.
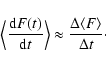 |
(A.13) |
However, from decadal data we cannot evaluate the value of
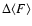 over a calendar decade:
over a calendar decade:
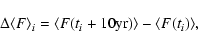 |
(A.14) |
where ti denotes the start year of a decade. Instead we have to use the value of
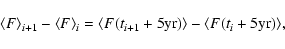 |
(A.15) |
which is displaced in time with respect to the exact definition of
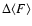 .
From the open flux computed by KBS07 we have evaluated that
.
From the open flux computed by KBS07 we have evaluated that
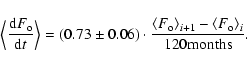 |
(A.16) |
Entering Eq. (A.16) into Eq. (A.12), one gets
 |
(A.17) |
We have tested the relation between actual 10-year averaged GSN and SN computed using Eq. (A.17) from the open flux (KBS07) for the period 1611-2000.
The scatter plot shown in Fig. A.1 displays a good correspondence between GSN and SN obtained from Eq. (A.17). The cross correlation is r=0.96, and the difference displays a nearly Gaussian distribution with an offset of -0.4 and
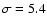 .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7704fi11.eps}\end{figure}](/articles/aa/full/2007/31/aa7704-07/Timg90.gif) |
Figure A.1:
Relation between the decadal group sunspot numbers (Hoyt & Schatten 1998)
and sunspot numbers computed using relation (A.17) from the open magnetic flux (KBS07) for 1610-2000. The diagonal, representing the expectation value, is shown by the solid line. |
Thus, we conclude that the conversion between 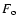 and SN decadal data can be done including the influence of ephemeral regions in a straightforward manner via Eq. (A.17) with an uncertainty of a few units in sunspot numbers.
and SN decadal data can be done including the influence of ephemeral regions in a straightforward manner via Eq. (A.17) with an uncertainty of a few units in sunspot numbers.
- Arge, C. N., Hildner,
E., Pizzo, V. J., & Harvey, J. W. 2002, J. Geophys. Res.,
107(A10), 1319
- Bak, P., Christensen, K.,
Danon, L., & Scanlon, T. 2002, Phys. Rev. Lett., 88,
178501 [NASA ADS] [CrossRef] (In the text)
- Damon, P. E., &
Sonett, C. P. 1991, in Sun in Time, ed. C. P. Sonett, M. S.
Giampapa, & M. S. Matthews (Tucson: Univ. Arizona Press),
360
(In the text)
- Berhondo, A. L. M.,
Taboada, R. E. R., & Larralde, L. A. 2006, Ap&SS, 302,
213 [NASA ADS] [CrossRef] (In the text)
- Boffetta, G., Carbone,
V., Giuliani, P., Vetri, P., & Vulpiani, A. 1999, Phys. Rev.
Lett., 83, 4662 [NASA ADS] [CrossRef] (In the text)
- Charbonneau, P. 2001,
Sol. Phys., 199, 385 [NASA ADS] [CrossRef] (In the text)
- Charbonneau, P.,
Blais-Laurier, G., & St-Jean, C. 2004, ApJ, 616, L183 [NASA ADS] [CrossRef]
- de Carvalho, J. X.,
& Prado, C. P. C. 2000, Phys. Rev. Lett., 84, 4006 [NASA ADS] [CrossRef] (In the text)
- Castagnoli, G., &
Lal, D. 1980, Radiocarbon, 22(2), 133
(In the text)
- Choudhuri, A. R. 1992,
A&A, 253, 277 [NASA ADS] (In the text)
- Cliver, E. W.,
Boriakoff, V., & Bounar, K. H. 1998, Geophys. Res. Lett., 25,
897 [NASA ADS] [CrossRef] (In the text)
- Eddy, J. A. 1977a, Sci.
Am., 236(5), 80
(In the text)
- Eddy, J. A. 1977b,
Clim. Change, 1, 173 [CrossRef]
- Freeman, M. P.,
Watkins, N. W., & Riley, D. J. 2006, Phys. Rev. E, 62,
8794 [NASA ADS] [CrossRef] (In the text)
- Fröhlich, C. 2006,
Space Sci. Rev., 125, 53 [NASA ADS] [CrossRef]
- Gleissberg, W. 1944,
Terr. Magnet. Atmosph. Electr., 49, 243 (In the text)
- Goslar, T. 2003, in:
PAGES News (Past Global Changes), 11(2-3), 12
(In the text)
- Hoyt, D. V., &
Schatten, K. 1998, Sol. Phys. 179, 189
(In the text)
- Korte, M., &
Constable, C. G. 2005, Earth Planet. Sci. Lett., 236, 348 [NASA ADS] [CrossRef] (In the text)
- Krivova, N. A.,
Balmaceda, L., & Solanki, S. K. 2007, A&A, 467, 335 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lepreti, F., Carbone,
V., & Veltri, P. 2001, Astrophys. J., 555, L133 [NASA ADS] [CrossRef] (In the text)
- Masarik, J., & J.
Beer 1999, J. Geophys. Res., 104(D10), 12099
(In the text)
- McCracken, K. G.,
McDonald, F. B., Beer, J. et al. 2004, J. Geophys. Res., 109,
A12103 [CrossRef] (In the text)
- Mega, M. S., Allegrini,
P., Grigolini, P. et al. 2003, Phys. Rev. Lett., 90, 188501 [NASA ADS] [CrossRef] (In the text)
- Mininni, P. D., Gomez,
D. O., & Mindlin, G. B. 2001, Sol. Phys., 201, 203 [NASA ADS] [CrossRef] (In the text)
- Miyahara, H., Sokoloff,
D., & Usoskin, I. G. 2006, The solar cycle at the Maunder
minimum epoch, in Advances in Geosciences, ed. W.-H. Ip, M. Duldig
(Singapore: World Scientific), 1
(In the text)
- Moon, Y.-J., Choe, G.
S., Yun, H. S., & Park, Y. D. 2001, J. Geophys. Res., 106,
29951 [NASA ADS] [CrossRef] (In the text)
- Moss, D., & Brooke,
J. 2000, MNRAS, 315, 521 [NASA ADS]
- Mursula, K., &
Ulich, Th. 1998, Geophys. Res. Lett., 25, 1837 [NASA ADS] [CrossRef] (In the text)
- Ossendrijver, M. A. J.
H. 2000, A&A, 359, 1205 [NASA ADS] (In the text)
- Papa, A. R. R.,
Barreto, L. M., & Seixas, N. A. B. 2006, J. Atmos. Solar-Terr.
Phys., 68, 930 [NASA ADS] (In the text)
- Pearce, G., Rowe, A.
K., & Yeung, J. 1993, Ap&SS, 208, 99 [NASA ADS] [CrossRef] (In the text)
- Ponte-Neto, C. F.,
& Papa, A. R. R. 2006, [arXiv:physics/0602122]
(In the text)
- Schmitt, D.,
Schüssler, M., & Ferriz-Mas, A. 1996, A&A, 311,
L1 [NASA ADS] (In the text)
- Sokoloff, D. D. 2004,
Sol. Phys., 224, 145 [NASA ADS] [CrossRef] (In the text)
- Solanki, S. K.,
Schüssler, M., & Fligge, M. 2000, Nature, 408, 445 [NASA ADS] [CrossRef]
- Solanki, S. K.,
Schüssler, M., & Fligge, M. 2002, A&A, 383, 706 [NASA ADS] [CrossRef] [EDP Sciences]
- Solanki, S. K.,
Usoskin, I. G., Kromer, B., Schüssler, M., & Beer, J.
2004, Nature, 431, 1084 [NASA ADS] [CrossRef] (In the text)
- Soon, W. H.,
Posmentier, E. S., & Baliunas, S. L. 1996, ApJ, 472, 891 [NASA ADS] [CrossRef] (In the text)
- Stuiver, M. 1980,
Nature, 286, 868 [NASA ADS] [CrossRef]
- Stuiver, M., &
Braziunas, T. F. 1989, Nature, 338, 405 [NASA ADS] [CrossRef] (In the text)
- Stuiver, M., Braziunas
T. F., Becker B., & Kromer, B. 1991, Quatern. Res., 35, 1 [CrossRef] (In the text)
- Stuiver, M., Reimer, P.
J., Bard, E. et al. 1998, Radiocarbon, 40, 1041 (In the text)
- Tobias, S. M. 1996,
A&A, 307, L 21
- Usoskin, I. G.,
Mursula, K., & Kovaltsov, G. A. 2001, J. Geophys. Res., 106,
16039 [NASA ADS] [CrossRef] (In the text)
- Usoskin, I. G., K.
Mursula, S. Solanki, Schüssler, M., & Kovaltsov, G. A.
2002, J. Geophys. Res., 107(A11), 1374
(In the text)
- Usoskin, I. G.,
Solanki, S. K., Schüssler, M., Mursula, K., & Alanko, K.
2003, Phys. Rev. Lett., 91, 211101 [NASA ADS] [CrossRef] (In the text)
- Usoskin, I. G., K.
Mursula, S. Solanki, Schüssler, M., & Alanko, K. 2004,
A&A, 413, 745 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Usoskin, I. G., K.
Alanko-Huotari, G. A. Kovaltsov, & K. Mursula 2005, J. Geophys.
Res., 110, A12108 [CrossRef] (In the text)
- Usoskin, I. G.,
Solanki, S. K., & Korte, M. 2006a, Geophys. Res. Lett., 33,
L08103 [CrossRef] (In the text)
- Usoskin, I. G., S. K.
Solanki, C. Taricco, N. Bhandari, & G. A. Kovaltsov 2006b,
A&A, 457, L25 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Vasiliev, S. S., &
V. A. Dergachev 2002, Ann. Geophys., 20, 115 [NASA ADS] (In the text)
- Voss, H., Kurths, J.,
& U. Schwarz 1996, J. Geophys. Res., 101, 15637 [NASA ADS] [CrossRef]
- Weiss, N. O., &
Tobias, S. M. 2000, Space Sci. Rev., 94, 99 [NASA ADS] [CrossRef] (In the text)
- Wheatland, M. S. 2003,
Sol. Phys., 214, 361 [NASA ADS] [CrossRef] (In the text)
- Yang, S., Odah, H.,
& Shaw, J. 2000, Geophys. J. Int., 140, 158 [NASA ADS] (In the text)
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7704fig1.eps}\end{figure}](/articles/aa/full/2007/31/aa7704-07/Timg5.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7704fig2.eps}\end{figure}](/articles/aa/full/2007/31/aa7704-07/Timg6.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{7704fig3.eps}\end{figure}](/articles/aa/full/2007/31/aa7704-07/Timg10.gif)
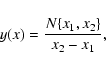
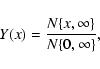
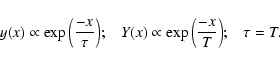
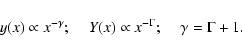
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7704fig5.eps}\end{figure}](/articles/aa/full/2007/31/aa7704-07/Timg22.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7704fig7.eps}\end{figure}](/articles/aa/full/2007/31/aa7704-07/Timg56.gif)
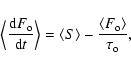
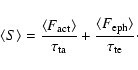
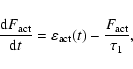
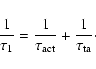
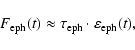
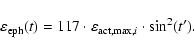
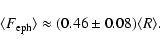
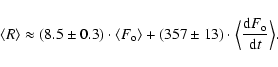
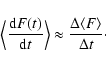
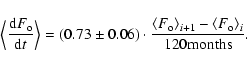
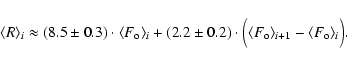
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7704fi11.eps}\end{figure}](/articles/aa/full/2007/31/aa7704-07/Timg90.gif)