A&A 471, 51-57 (2007)
DOI: 10.1051/0004-6361:20066774
Constraints on the parameters of radiatively decaying dark matter
from the dark matter halos of the Milky Way and Ursa Minor
A. Boyarsky1,2,3 -
J. Nevalainen4 -
O. Ruchayskiy5,2
1 - CERN, PH-TH, 1211 Geneve 23, Switzerland
2 -
École Polytechnique Fédérale de Lausanne, Institute of
Theoretical Physics, FSB/ITP/LPPC, BSP 720, 1015 Lausanne, Switzerland
3 -
On leave of absence from Bogolyubov Institute of Theoretical Physics, Kyiv, Ukraine
4 -
Helsinki University Observatory, Finland
5 -
Institut des Hautes Études Scientifiques, 91440 Bures-sur-Yvette, France
Received 20 November 2006 / Accepted 19 April 2007
Abstract
Aims. We improve the earlier restrictions on parameters of the warm dark matter (DM) in the form of a sterile neutrinos.
Methods. The results were obtained from not observing the DM decay line in the X-ray spectrum of the Milky Way (using the recent XMM-Newton PN blank sky data). We also present a similar constraint coming from the recent XMM-Newton observation of Ursa Minor - dark, X-ray quiet dwarf spheroidal galaxy.
Results. The new Milky way data improve on (by as much as the order of magnitude at masses 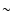 3.5 keV) existing constraints. Although the observation of Ursa Minor has relatively poor statistics, the constraints are comparable to those recently obtained using observations of the Large Magellanic Cloud or M 31. This confirms a recent proposal that dwarf satellites of the MW are very interesting candidates for the DM search and dedicated studies should be made to this purpose.
3.5 keV) existing constraints. Although the observation of Ursa Minor has relatively poor statistics, the constraints are comparable to those recently obtained using observations of the Large Magellanic Cloud or M 31. This confirms a recent proposal that dwarf satellites of the MW are very interesting candidates for the DM search and dedicated studies should be made to this purpose.
Key words: Galaxy: halo - galaxies: individual: Ursa Minor - cosmology: dark matter - X-rays: galaxies
This past year has seen a lot of activity, devoted to searching for the decay
signals of the DM particle in X-ray spectra of various astrophysical
objects (Boyarsky et al. 2006c; Riemer-Sørensen et al. 2006b; Boyarsky et al. 2006b; Riemer-Sørensen et al. 2006a; Boyarsky et al. 2006a; Watson et al. 2006, e.g). It was noticed long ago by Dodelson & Widrow (1994) that a right-handed neutrino with masses in the keV range presents a viable warm dark matter (WDM) candidate. Such a particle possesses a specific
radiative decay channel, so one can search for its decay line in the X-ray
spectra of astrophysical objects (Dolgov & Hansen 2002; Abazajian et al. 2001b).
Recently, the interest in the sterile neutrino as a DM candidate has been
greatly revitalized. First, the discovery of neutrino oscillations (see
e.g. Strumia & Vissani 2006, for a review) strongly suggest the existence of
right-handed neutrinos. Probably the easiest way to explain the data on
oscillations is by adding several right-handed, or sterile, neutrinos,
to the Standard Model. It has been demonstrated recently in Asaka et al. (2005)
and Asaka & Shaposhnikov (2005) that a simple extension of the Standard Model by three
singlet fermions with masses smaller than the electroweak scale (dubbed
the 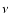 MSM in Asaka et al. 2005) allows accommodation of the data on neutrino
masses and mixings, allows baryon asymmetry of the Universe to be explained,
and provides a candidate for the dark matter particle in the form of the
lightest of the sterile neutrinos
MSM in Asaka et al. 2005) allows accommodation of the data on neutrino
masses and mixings, allows baryon asymmetry of the Universe to be explained,
and provides a candidate for the dark matter particle in the form of the
lightest of the sterile neutrinos![[*]](/icons/foot_motif.gif) .
.
Secondly, warm DM with the mass of particle in keV range can ease the
problem of the dark halo structures in comparison with the cold dark matter
scenario (Goerdt et al. 2006; Bode et al. 2001). By determining the matter power spectrum
from the Lyman-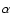 forest data from SDSS Seljak et al. (2006) and
Viel et al. (2006) argue that the mass of the DM particles should be in the range
forest data from SDSS Seljak et al. (2006) and
Viel et al. (2006) argue that the mass of the DM particles should be in the range
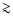
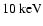 (
(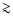
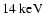 in the case of Seljak et al. 2006). As
this method gives direct bounds for the free-streaming length of the
neutrinos, the bounds on the mass of the DM particle depend on the momentum
distribution function of the sterile neutrinos and, therefore, on their
production mechanism. The results quoted above are claimed for the simplest
Dodelson-Widrow model (1994).
in the case of Seljak et al. 2006). As
this method gives direct bounds for the free-streaming length of the
neutrinos, the bounds on the mass of the DM particle depend on the momentum
distribution function of the sterile neutrinos and, therefore, on their
production mechanism. The results quoted above are claimed for the simplest
Dodelson-Widrow model (1994).
At the same time, studies of the Fornax dwarf spheroidal
galaxy (Strigari et al. 2006; Goerdt et al. 2006) disagree with the predictions of CDM models and suggest lower mass than in Seljak et al. (2006) and Viel et al. (2006) for
the DM particle
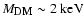 .
This result agrees with the earlier
studies of Hansen et al. (2002) and Viel et al. (2005), which used a different
dataset. For other interesting applications of the sterile neutrinos with the
mass
.
This result agrees with the earlier
studies of Hansen et al. (2002) and Viel et al. (2005), which used a different
dataset. For other interesting applications of the sterile neutrinos with the
mass 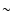 few keV see e.g. Kusenko (2006b), Biermann & Kusenko (2006),
Stasielak et al. (2006), Kusenko (2006a), and Hidaka & Fuller (2006).
few keV see e.g. Kusenko (2006b), Biermann & Kusenko (2006),
Stasielak et al. (2006), Kusenko (2006a), and Hidaka & Fuller (2006).
It has been argued in Boyarsky et al. (2006c) and Riemer-Sørensen et al. (2006a) that the
preferred targets for observations are objects from the local halo, including
our own Milky Way and its satellites. In particular, Boyarsky et al. (2006c)
showed that the best observational targets are the dwarf spheroidals (Ursa Minor, Draco, etc.). Indeed, these objects are X-ray quiet, while at the same
time one expects the DM decay signal from them, comparable to what comes from
galaxy clusters. Because at the time of writing of Boyarsky et al. (2006c) no
public data were available for these dwarf spheroidals, the observations of
the core of Large Magellanic Cloud (LMC) were used to produce the strongest
restrictions on parameters of the sterile neutrino. It was stressed
in Boyarsky et al. (2006c) that other dwarf satellite galaxies should be studied
as well, in order to minimize uncertainties related to the DM modeling in each
single object. In this paper we continue studies of the dwarf satellites of
the MW by analyzing the data from XMM-Newton observation of
Ursa Minor and confirm the restrictions of Boyarsky et al. (2006c).
It was also shown in Boyarsky et al. (2006c) that the improvement of the results
from MW DM halo can be achieved by using longer exposure data (notably, longer
exposure of the closed filter observations). In this paper, we improve our
restrictions, coming from the MW DM halo by using the blank sky dataset with
better statistics from Nevalainen et al. (2005).
2 DM with radiative decay channel
Although throughout this paper we are talking mostly about the sterile
neutrino DM, the results can be applied to any DM particle that
possesses the monoenergetic radiative decay channel, emits photon of energy 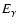 and has a decay width
and has a decay width 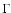 .
In the case of the sterile neutrino
(with mass below that of an electron), the radiative decay channel is into a photon and active neutrino Pal & Wolfenstein (1982). As the mass of an active neutrino is
much lower than keV,
.
In the case of the sterile neutrino
(with mass below that of an electron), the radiative decay channel is into a photon and active neutrino Pal & Wolfenstein (1982). As the mass of an active neutrino is
much lower than keV,
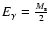 in this case. The width
in this case. The width 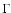 of radiative decay can be expressed (Pal & Wolfenstein 1982; Barger et al. 1995) in terms of mass
of radiative decay can be expressed (Pal & Wolfenstein 1982; Barger et al. 1995) in terms of mass 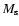 and mixing angle
and mixing angle 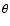 via
via
![\begin{displaymath}%
\Gamma = \frac{9~ \alpha~ G_F^2} {1024\pi^4}\sin^22\theta~ ...
...ta)
\left[\frac{M_{\rm s}}{{\rm keV}}\right]^5\;{\rm s}^{-1}.
\end{displaymath}](/articles/aa/full/2007/31/aa6774-06/img18.gif) |
(1) |
(The notation
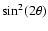 is used traditionally, although in all
realistic cases
is used traditionally, although in all
realistic cases
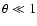 .) The flux of the DM decay from a given
direction is given by
.) The flux of the DM decay from a given
direction is given by
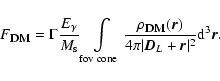 |
(2) |
Here 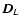 is the luminous distance between the observer and the
center of the observed object,
is the luminous distance between the observer and the
center of the observed object,
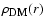 is the DM density, and the
integration is over the DM distribution inside the (truncated) cone - solid
angle, spanned by the field of view (FoV) of the X-ray satellite. If the
observed object is far
is the DM density, and the
integration is over the DM distribution inside the (truncated) cone - solid
angle, spanned by the field of view (FoV) of the X-ray satellite. If the
observed object is far![[*]](/icons/foot_motif.gif) ,
then Eq. (2) can be simplified:
,
then Eq. (2) can be simplified:
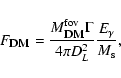 |
(3) |
where
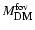 is the mass of DM within a telescope's field of view (FoV).
Equation (3) can be rewritten again as
is the mass of DM within a telescope's field of view (FoV).
Equation (3) can be rewritten again as
![\begin{displaymath}%
F_{{\textsc{dm}}}\! =\! 6.38 \!\times \!10^6\left(\frac{M_{...
...{\rm keV}}\right]^5\! \! \frac{{\rm keV}}{{\rm cm^2 \cdot s}}.
\end{displaymath}](/articles/aa/full/2007/31/aa6774-06/img26.gif) |
(4) |
In the absence of a clearly detectable line, one can put an upper limit on the
flux of DM from the astrophysical data, which will lead via Eq. (4)
to the restrictions of parameters of the sterile neutrino 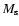 and
and 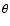 .
.
3 Restrictions from the blank sky observation
3.1 Modeling the DM halo of the MW
As shown in the previous section, one needs to know the distribution of the DM
to obtain the restrictions on parameters of the sterile neutrino. In the case
of nearby objects (including our own Galaxy and dwarf satellites from the
local halo), the DM distribution can be deduced e.g. by using the rotation
curves of the stars in the galaxy. Here we follow the analysis
of Boyarsky et al. (2006c). Various DM profiles, used to fit observed velocity
distributions, differ the most in the center of a distribution. In the case of
the MW we choose, as in Boyarsky et al. (2006c), to use the observations away from
the center, to minimize this uncertainty. In particular, in
references Klypin et al. (2002) and Battaglia et al. (2005) it was shown that the DM halo of the MW
can be described by the Navarro-Frenk-White (NFW) profile (Navarro et al. 1997)
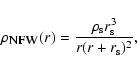 |
(5) |
with parameters, given in Table 1![[*]](/icons/foot_motif.gif) . The relation between virial parameters and
. The relation between virial parameters and
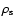 ,
,
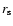 are given in the
Appendix A. Quoted halo parameters provide DM decay flux
(from the directions with
are given in the
Appendix A. Quoted halo parameters provide DM decay flux
(from the directions with
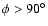 )
consistent within
)
consistent within 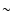
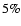 with
the one, given by Eqs. (6), (7). Only "maximal disk''
models in Klypin et al. (2002) would provide
with
the one, given by Eqs. (6), (7). Only "maximal disk''
models in Klypin et al. (2002) would provide 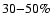 weaker restrictions;
however, these models are highly implausible, see Klypin et al. (2002). Similarly,
taking the lower limit for the virial mass of Battaglia et al. (2005), one would
obtain 25% weaker restrictions than the ones, presented in this
paper
weaker restrictions;
however, these models are highly implausible, see Klypin et al. (2002). Similarly,
taking the lower limit for the virial mass of Battaglia et al. (2005), one would
obtain 25% weaker restrictions than the ones, presented in this
paper![[*]](/icons/foot_motif.gif) .
.
Table 1:
Best-fit parameters of NFW model of the MW DM halo.
To compare the results from different (e.g. cuspy and cored) profiles, we can
also describe the DM distribution in the MW via an isothermal profile:
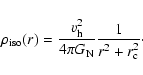 |
(6) |
The DM flux from a given direction 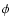 into the solid angle
into the solid angle
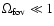 ,
measured by an observer on Earth (distance
,
measured by an observer on Earth (distance
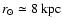 from
the galactic center), is given by
from
the galactic center), is given by
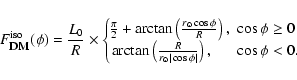 |
(7) |
Here
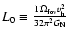 and
and
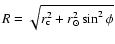 .
Angle
.
Angle 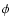 is related to the
galactic coordinates (b,l) via
is related to the
galactic coordinates (b,l) via
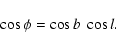 |
(8) |
Thus, the galactic center corresponds to
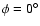 ,
and the anti-center
,
and the anti-center
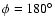 and the direction perpendicular to the galactic plane to
and the direction perpendicular to the galactic plane to
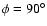 .
.
In Boyarsky et al. (2006c), the following parameters of isothermal profile were
chosen:
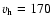 km s-1 and
km s-1 and
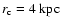 .
One can easily check (using
Table 1 and Eqs. (A.5), (A.6) in
Appendix A) that, in the directions
.
One can easily check (using
Table 1 and Eqs. (A.5), (A.6) in
Appendix A) that, in the directions
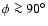 ,
the difference in predicted DM fluxes between the NFW model with parameters,
given in Table 1 and isothermal model with parameters just quoted
are completely negligible (less than 5%)
,
the difference in predicted DM fluxes between the NFW model with parameters,
given in Table 1 and isothermal model with parameters just quoted
are completely negligible (less than 5%)![[*]](/icons/foot_motif.gif) .
.
3.2 XMM-Newton PN blank sky data
To examine the Milky Way halo, we used the double-filtered, single+double
event XMM-Newton PN blank sky data from Nevalainen et al. (2005), which is a collection of 18 blank sky observations (see Table 2 in Nevalainen et al. 2005, for their observation IDs, positions, and exposures)![[*]](/icons/foot_motif.gif) . The exposure time of the co-added observations is 547 ks. We used a combination of closed-filter observations from Nevalainen et al. (2005) (total exposure time 145 ks) to model the
background of XMM-Newton PN instrument separately.
The data has been filtered using SAS expression "flag==0'', which rejects the data
from bad pixels and CCD gap regions. After removing the brightest point
sources, the total accumulation area is 603 arcmin2.
. The exposure time of the co-added observations is 547 ks. We used a combination of closed-filter observations from Nevalainen et al. (2005) (total exposure time 145 ks) to model the
background of XMM-Newton PN instrument separately.
The data has been filtered using SAS expression "flag==0'', which rejects the data
from bad pixels and CCD gap regions. After removing the brightest point
sources, the total accumulation area is 603 arcmin2.
Based on the >10 keV band count rates of the blank sky and the closed filter data,
we normalized the closed-filter spectrum by a factor of 1.07 before subtracting it from the
blank sky spectrum. The remaining sky-background spectrum consists mainly of the Galactic emission
and the cosmic X-ray background (CXB) due to unresolved extragalactic point sources.
We modeled the Galactic emission by a non-absorbed MEKAL model with Solar abundances.
For the CXB emission, we used a power-law model modified at the lowest energies by Galactic absorption with the value of 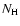 fixed to its exposure-weighted average over all blank sky observations
(
fixed to its exposure-weighted average over all blank sky observations
(
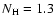
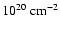 ).
).
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{6774fig1.ps} \end{figure}](/articles/aa/full/2007/31/aa6774-06/Timg65.gif) |
Figure 1:
Upper panel: the blank sky data of Nevalainen et al. (2005)
after subtraction of the closed filter data. The black crosses show the
data points, used for modeling the Galactic emission and CXB. The blue
crosses show the data points excluded from the fit. The best-fit model is
shown with the red line. The plotted spectrum is binned by a minimum of
20 000 counts per channel, different from that used in the actual fit (see
text). The error bars include the 5% systematic uncertainty used in the
analysis. Lower panel: the ratio of the data-to-model values in
each channel used in the fit. |
| Open with DEXTER |
The variable Galactic emission and geocoronal Solar wind-charge exchange
emission (see e.g. Wargelin et al. 2004) complicate the modeling at the
lowest energies. The remaining calibration uncertainties further complicate
the analysis in the lowest energies (see e.g. Nevalainen et al. 2006). Thus,
we omitted the channels below 0.8 keV. At energies above 7 keV, the particle
background dominates and the total flux is very sensitive to the background
normalization. We thus excluded channels above 7 keV.
The data are not well-described in the 1.45-1.55 and 5.8-6.3 keV bands with
the above model. These deviations probably originate from the variability of
the instrumental Al and Fe line emission. In order to minimize the effect of
the instrumental problems, we excluded these bands when finding the best-fit
sky background model (see below). Also, to account for possibly
remaining calibration inaccuracies, we added a systematic uncertainty of 5%
of the model value in each bin in quadrature to the statistical uncertainties.
We binned the spectrum using a bin size of 1/3 of the energy resolution and
fitted the data using models and channels as described above. The best-fit
(reduced 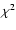 = 1.03 for 153 degrees of freedom) model agrees with the
data within the uncertainties (see Fig. 1), yielding a photon
index of 1.50
= 1.03 for 153 degrees of freedom) model agrees with the
data within the uncertainties (see Fig. 1), yielding a photon
index of 1.50 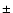 0.02 at 1
0.02 at 1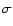 confidence level (see
Fig. 1), consistent with similar analyses
based on Chandra (Hickox & Markevitch 2006) and XMM-Newton MOS instrument
(De Luca & Molendi 2004). The best-fit temperature of the MEKAL component used to
model the Galactic emission is 0.19
confidence level (see
Fig. 1), consistent with similar analyses
based on Chandra (Hickox & Markevitch 2006) and XMM-Newton MOS instrument
(De Luca & Molendi 2004). The best-fit temperature of the MEKAL component used to
model the Galactic emission is 0.19 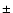 0.01 keV, consistent with
e.g. Hickox & Markevitch (2006).
0.01 keV, consistent with
e.g. Hickox & Markevitch (2006).
We then evaluated the level of possible DM flux above the background model
allowed by the statistical and systematic uncertainties in each channel. For
this, we modified the above best-fit model by adding a narrow (width = 1 eV)
Gaussian line to it. We then re-fitted the data, fixing the Gaussian centroid
for each fit to the central energy of a different channel. In these fits we
fixed the above continuum model parameters to the best-fit values and thus the
Gaussian normalization parameter is the only free parameter. We used the fits
to find the upper 3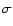 uncertainty of the Gaussian normalization, i.e.
the allowed DM flux. Note that here we included the channels 1.45-1.55 and
5.8-6.3 keV (excluded above when defining the sky background model). The
background is oversubtracted in the channels at 1.45-1.55 keV and
uncertainty of the Gaussian normalization, i.e.
the allowed DM flux. Note that here we included the channels 1.45-1.55 and
5.8-6.3 keV (excluded above when defining the sky background model). The
background is oversubtracted in the channels at 1.45-1.55 keV and 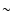 6.0 keV (see Fig. 1), which would formally require negative
normalization for the Gaussian. However, we forced the normalization to be
positive and thus obtained conservative upper limits in these energies.
6.0 keV (see Fig. 1), which would formally require negative
normalization for the Gaussian. However, we forced the normalization to be
positive and thus obtained conservative upper limits in these energies.
Finally, we converted the upper bound obtained for the flux per energy bin to the
restrictions on 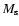 and
and
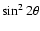 ,
using
Eqs. (1), (7) (we use exposure weighted average of DM fluxes (Eq. (7)) from all the observations, constituting the blank sky
dataset). This corresponds to the average "column density'' 1.22
,
using
Eqs. (1), (7) (we use exposure weighted average of DM fluxes (Eq. (7)) from all the observations, constituting the blank sky
dataset). This corresponds to the average "column density'' 1.22 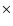 1028 keV/cm2. The results are shown in Fig. 2
1028 keV/cm2. The results are shown in Fig. 2
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{6774fig2.ps} \end{figure}](/articles/aa/full/2007/31/aa6774-06/Timg71.gif) |
Figure 2:
Exclusion plot based on the blank sky observations.
Bins
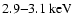 and
and
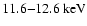 are excluded.
are excluded. |
| Open with DEXTER |
At energies above E=5 keV, the instrumental background of PN dominates over
the sky background (cf. Nevalainen et al. 2005). Therefore, the accuracy of
the co-added closed filter spectrum in predicting the particle background in
the blank sky observations becomes essential. We estimate this accuracy using
the variability of the individual closed-filter spectra in the 0.8-7.0 keV
band (Nevalainen et al. 2005) and propagate it by varying the normalization of
closed filter data by 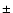
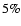 and repeating the above analysis. This leads
to a factor of 3 change in the results at
and repeating the above analysis. This leads
to a factor of 3 change in the results at
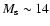 keV (see
Fig. 3). Therefore, for
keV (see
Fig. 3). Therefore, for 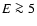 keV we choose the more
conservative normalization (see Fig. 7 below).
keV we choose the more
conservative normalization (see Fig. 7 below).
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{6774fig3.eps} \end{figure}](/articles/aa/full/2007/31/aa6774-06/Timg74.gif) |
Figure 3:
Dependence of the results on closed filter normalization. Red
(solid) and green (long-dashed) lines are the same as in
Fig. 2. |
| Open with DEXTER |
4 Restrictions from observations of Ursa Minor
It was argued in Boyarsky et al. (2006c) that dwarf satellite galaxies should
provide the best restrictions, based on their high concentration of DM and low
X-ray signal. At the moment of writing of Boyarsky et al. (2006c), no public data
on preferred dwarf satellites were available, therefore the observation of
core of LMC were used as a demonstration. Recently, the Ursa Minor dwarf (UMi)
was observed with XMM-Newton (obs IDs.: 0301690201, 0301690301,
0301690401, 0301690501, observed in August-September 2005)![[*]](/icons/foot_motif.gif) .
Unfortunately, most of these observations are strongly contaminated by
background flares and the observations have very small exposure times. Below we present the
analysis of only one observation (obsID: 0301690401), which "suffered'' the
least from background contamination.
.
Unfortunately, most of these observations are strongly contaminated by
background flares and the observations have very small exposure times. Below we present the
analysis of only one observation (obsID: 0301690401), which "suffered'' the
least from background contamination.
4.1 DM modeling for UMi
The DM distribution in UMi has a cored profile (see e.g. Gilmore et al. 2007; Kleyna et al. 2003; Wilkinson et al. 2006; Gilmore et al. 2006)![[*]](/icons/foot_motif.gif) .
We adopt the following parameters of isothermal profile (6) for UMi:
.
We adopt the following parameters of isothermal profile (6) for UMi:
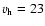 km s-1,
km s-1,
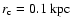 (see
e.g. Wilkinson et al. 2006)
(see
e.g. Wilkinson et al. 2006) ![[*]](/icons/foot_motif.gif) .
We adopt the distance to UMi
.
We adopt the distance to UMi
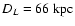 (Mateo 1998). The DM mass within the circular FoV with the radius
(Mateo 1998). The DM mass within the circular FoV with the radius
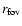 ,
centered at the center of the galaxy is given by
,
centered at the center of the galaxy is given by
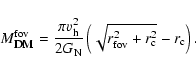 |
(9) |
In our case, the radius of FoV is 13.9', which corresponds to
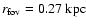 (i.e. about
(i.e. about
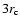 ). Therefore
). Therefore
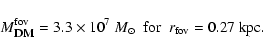 |
(10) |
Using Eqs. (10) and (3), one can compute the expected DM flux from UMi:
![\begin{displaymath}%
F_{{\textsc{dm}}} = 4.79 \ \frac{{\rm keV}}{{\rm cm^2\cdot s}} \left[\frac{M_{\rm s}}{{\rm keV}}\right]^5 \sin^2(2\theta).
\end{displaymath}](/articles/aa/full/2007/31/aa6774-06/img83.gif) |
(11) |
4.2 PN data analysis
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{6774fig4.ps} \end{figure}](/articles/aa/full/2007/31/aa6774-06/Timg84.gif) |
Figure 4:
Hard band light curve for the UMi observation 0301690401. The crosses show the PN > 10 keV band rate of the full FOV in 1 ks bins. The dashed line shows the average, when excluding first 2 time bins. The dotted line shows the corresponding quiescent value in the
co-added blank sky data (Nevalainen et al. 2005). |
| Open with DEXTER |
We processed the Ursa Minor observation 0301690401 using epchain
version 8.56 and filtered the event file with SAS expressions
"PATTERN<=4'' and "FLAG==0''. We applied the blank sky-based XMM-Newton background method of Nevalainen et al. (2005) for Ursa Minor.
The >10 keV band light curve from the full FOV (Fig. 4)
shows that the count rate in observation 0301690401 (excluding first 2 ks)
exceeds that of the blank sky quiescent average by 25%. This level is
higher, but close to what is used in the blank sky accumulation (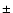 20%
filtering around the quiescent level). Thus we accepted the data from all
instants after the initial 2 ks, and we approximated the background
uncertainties with those in Nevalainen et al. (2005).
20%
filtering around the quiescent level). Thus we accepted the data from all
instants after the initial 2 ks, and we approximated the background
uncertainties with those in Nevalainen et al. (2005).
The hydrogen column density in the direction of Ursa Minor is small (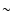
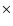
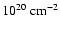 )
and consistent with the variation in the blank
sky sample. Thus we can also apply the blank sky background method to
channels below 2 keV.
)
and consistent with the variation in the blank
sky sample. Thus we can also apply the blank sky background method to
channels below 2 keV.
As noted in the above XMM-Newton blank sky study, the >10 keV band-based
scaling of the background only works up to a factor of 1.1, beyond which the
background prediction becomes worse. Furthermore, the correlation of
background rates in the >10 keV band is very poor with the rates below 2 keV band. Thus, in order to achieve the best possible background prediction
accuracy, we scaled the blank sky background spectrum by a factor of 1.1 at
channels above 2 keV, and we applied no background scalingat lower energies.
We removed this scaled background spectrum from the Ursa Minor spectrum (see
Fig. 5). As shown in Nevalainen et al. (2005), the background
accuracy is worse at lower energies. We used those estimates to propagate the
background uncertainties at 1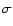 confidence level to our results by
examining how the results change when varying the 0.8-2.0 keV and 2.0-7.0 keV band background by 15% and 10%, respectively.
confidence level to our results by
examining how the results change when varying the 0.8-2.0 keV and 2.0-7.0 keV band background by 15% and 10%, respectively.
4.3 Ursa Minor data and restrictions on the sterile neutrino parameters
The X-ray spectrum of UMi is similar to that of LMC: above 2 keV the flux is
zero within statistical limits (see Fig. 5). (Of course, the
data set has rather low statistics: after the cleaning of flares the UMi
observation only contains 7 ks.) Therefore, for such data, we utilized the "total flux'' method. Namely, we restricted the DM flux in the given energy bin to be bounded from above by the
measured total flux in this energy bin plus its 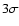 uncertainty
(Fig. 5). As each energy bin has a width of twice the FWHM at
a given energy, the flux from a DM line would not "spill'' into nearby bins.
Using Eq. (11), we find the restrictions on the sterile neutrino
parameters, represented in Fig. 6.
uncertainty
(Fig. 5). As each energy bin has a width of twice the FWHM at
a given energy, the flux from a DM line would not "spill'' into nearby bins.
Using Eq. (11), we find the restrictions on the sterile neutrino
parameters, represented in Fig. 6.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6774fig5.eps} \end{figure}](/articles/aa/full/2007/31/aa6774-06/Timg87.gif) |
Figure 5:
Flux from UMi (obs. ID 0301690401). Energy bins have the width of
twice the spectral resolution. Shown are the 1, 2, and 3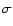 errors.
One can see that, above 2 keV, flux in most energy bins is zero within errors.
One can see that, above 2 keV, flux in most energy bins is zero within
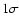 limits (blue crosses) and for the rest it is zero within limits (blue crosses) and for the rest it is zero within
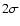 limits (green crosses). Similarly, below 2 keV black, cyan and
yellow crosses represent 1, 2, and 3 limits (green crosses). Similarly, below 2 keV black, cyan and
yellow crosses represent 1, 2, and 3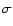 error correspondingly. The
solid black line represents the 3 error correspondingly. The
solid black line represents the 3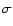 upper bound on total flux in a given energy bin, which we use to put the limit on DM parameters. upper bound on total flux in a given energy bin, which we use to put the limit on DM parameters. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.05cm,clip]{6774fig6.eps} \end{figure}](/articles/aa/full/2007/31/aa6774-06/Timg88.gif) |
Figure 6:
Exclusion from UMi (red solid line), as compared to LMC (green
long-dashed line). The blue short-dashed smooth curve shows hypothetical
restrictions from UMi observations with 100 ks exposure. |
| Open with DEXTER |
These restrictions should be compared with those, obtained from another
satellite galaxy - Large Magellanic Cloud (Boyarsky et al. 2006c). As one
clearly sees from Fig. 6, in spite of the low exposure time, it
is fully consistent with the earlier bounds from LMC, thus confirming the
results of Boyarsky et al. (2006c). Improvement of the exposure for UMi
observations should, presumably lead to the improvement of results (at least
for energies above 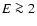 keV). For example, for a 100 ks observation,
we expect the results to improve by roughly a factor
keV). For example, for a 100 ks observation,
we expect the results to improve by roughly a factor
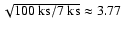 .
.
5 Results
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6774fig7.eps} \end{figure}](/articles/aa/full/2007/31/aa6774-06/Timg91.gif) |
Figure 7:
Results and comparison with previous bounds (a region ofparameter
space above a curve is excluded). |
| Open with DEXTER |
5.1 Restrictions from the blank sky data
By analyzing the blank sky data set with better statistics, we improved on the
previous results of Boyarsky et al. (2006c), Riemer-Sørensen et al. (2006a), Watson et al. (2006) (by as much as the factor of 10 for
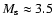 keV and by the
negligible amount for
keV and by the
negligible amount for
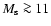 keV). The result is shown in
Fig. 7 in red solid line. The best previous bounds are also
shown: bound from LMC (Boyarsky et al. 2006c) with a blue short-dashed line and
bound from M 31 (Watson et al. 2006) with a dotted magenta line. We see that in the
region 3.5 keV
keV). The result is shown in
Fig. 7 in red solid line. The best previous bounds are also
shown: bound from LMC (Boyarsky et al. 2006c) with a blue short-dashed line and
bound from M 31 (Watson et al. 2006) with a dotted magenta line. We see that in the
region 3.5 keV 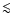
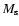
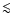 11 keV the new blank sky data improves
on previous results. These results can be converted (using
Eq. (1)) into restrictions on the decay rate
11 keV the new blank sky data improves
on previous results. These results can be converted (using
Eq. (1)) into restrictions on the decay rate 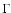 of any
DM particle, that possesses radiative decay channel and emits a photon
of any
DM particle, that possesses radiative decay channel and emits a photon 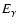 (see Fig. 8). Our results provide more than an order
of magnitude improvement over similar restrictions derived in Riemer-Sørensen et al. (2006a) (which used the Chandra blank sky background), as one can clearly see
by comparing Fig. 8 with Fig. 2 in Riemer-Sørensen et al. (2006a), where
the exclusion plot is above
(see Fig. 8). Our results provide more than an order
of magnitude improvement over similar restrictions derived in Riemer-Sørensen et al. (2006a) (which used the Chandra blank sky background), as one can clearly see
by comparing Fig. 8 with Fig. 2 in Riemer-Sørensen et al. (2006a), where
the exclusion plot is above
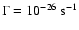 line for all
energies. (In Riemer-Sørensen et al. 2006a, the restriction were made, based on the total
flux of Chandra satellite, without subtraction of the instrumental
background, which explains a much weaker restrictions.)
line for all
energies. (In Riemer-Sørensen et al. 2006a, the restriction were made, based on the total
flux of Chandra satellite, without subtraction of the instrumental
background, which explains a much weaker restrictions.)
The empirical fit to the MW data is given by the following expression:
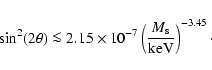 |
(12) |
5.2 Restrictions from Ursa Minor dwarf
Restrictions from XMM observation of UMi are shown in Fig. 7
by the green long-dashed line. These results are slightly weaker than LMC or
M 31 results, which is due to the very low statistics of the UMi observation.
Improvement of the statistics should lead to improvement of the current bound
(as shown in Fig. 6). These results confirm the recent claims
(Boyarsky et al. 2006c) that dwarfs of the local halo are promising
candidates for the DM-decay line search and, as such, should be studied
dedicatedly.
In searching for the DM signatures, it is important to understand that the
uncertainties of the DM modeling for any given object can be large, and
therefore it is important to study many objects of given type, as well as many
different types of objects (where DM distributions are deduced by independent
methods). To this end, although UMi data does not provide any improvement over
existing bounds, it makes those bounds more robust as the existence of DM in
UMi is deduced by independent observations, and the rotation curves of UMi are
measured quite well, since it has less perturbed dynamics, compared to e.g. LMC.
6 Discussion
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6774fig8.eps} \end{figure}](/articles/aa/full/2007/31/aa6774-06/Timg96.gif) |
Figure 8:
Restrictions on parameters of any DM particle with the radiative
decay width 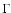 ,
emitting photon of energy ,
emitting photon of energy 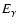 .
Shaded region
is excluded. .
Shaded region
is excluded. |
| Open with DEXTER |
In this paper we continued to search for the best astrophysical objects, from
the point of view of restricting parameters of DM particles with the radiative
decay channel. Several comments are in order here.
- (1)
- Although throughout this paper we have spoken about the sterile neutrinos and
restricted their parameters (namely, mass, and mixing angle), the constraints
can be readily converted into any other DM candidate that possesses a radiative decay channel
![[*]](/icons/foot_motif.gif) . Then the restrictions are formulated on the decay rate
. Then the restrictions are formulated on the decay rate 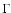 as a function of energy of the emitted photon
as a function of energy of the emitted photon 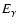 .
The results then can be presented in the form of an exclusion
plot, presented in Fig. 8.
.
The results then can be presented in the form of an exclusion
plot, presented in Fig. 8.
- (2)
- Clearly, if one could relate parameters of the sterile neutrino with
their relic abundance
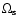 ,
this would allow one to put an upper limit
on the mass of the sterile neutrino. Unfortunately, such a computation is
strongly model-dependent. In Dodelson & Widrow (1994), Dolgov & Hansen (2002),
Abazajian et al. (2001a), Abazajian (2006), the relic abundance of the
sterile neutrinos was computed in a simple model with only one sterile
neutrino, assuming the absence of the sterile neutrinos above the
temperatures
,
this would allow one to put an upper limit
on the mass of the sterile neutrino. Unfortunately, such a computation is
strongly model-dependent. In Dodelson & Widrow (1994), Dolgov & Hansen (2002),
Abazajian et al. (2001a), Abazajian (2006), the relic abundance of the
sterile neutrinos was computed in a simple model with only one sterile
neutrino, assuming the absence of the sterile neutrinos above the
temperatures 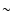 1 GeV. Yet, even the computation in this simplest model
is subject to a number of
uncertainties (Shaposhnikov & Tkachev 2006; Boyarsky et al. 2006c; Asaka et al. 2006a; Shi & Fuller 1999; Asaka et al. 2006b; Boyarsky et al. 2006a). In particular, in Dodelson & Widrow (1994), Dolgov & Hansen (2002), Abazajian et al. (2001a), Abazajian (2006), two assumptions were made:
(i) the absence of heavy particles, whose decay can dilute the relic
abundance,
(ii) the absence of lepton asymmetries.
In addition, simplifying assumptions about dynamics of hadrons at
temperatures
1 GeV. Yet, even the computation in this simplest model
is subject to a number of
uncertainties (Shaposhnikov & Tkachev 2006; Boyarsky et al. 2006c; Asaka et al. 2006a; Shi & Fuller 1999; Asaka et al. 2006b; Boyarsky et al. 2006a). In particular, in Dodelson & Widrow (1994), Dolgov & Hansen (2002), Abazajian et al. (2001a), Abazajian (2006), two assumptions were made:
(i) the absence of heavy particles, whose decay can dilute the relic
abundance,
(ii) the absence of lepton asymmetries.
In addition, simplifying assumptions about dynamics of hadrons at
temperatures
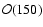 MeV were used. Recently, Asaka et al. (2007)
performed this computation from the first principles, showing that the
uncertainty due to QCD effects (between minimal and maximal values of
MeV were used. Recently, Asaka et al. (2007)
performed this computation from the first principles, showing that the
uncertainty due to QCD effects (between minimal and maximal values of
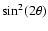 for given
for given 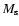 )
is about a factor of 8.
)
is about a factor of 8.
Taking away the assumptions about the absence of the sterile neutrinos
above the temperatures 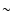 1 GeV makes any mixing angle possible. For
example, the DM neutrinos can be created due to the inflaton
decay Shaposhnikov & Tkachev (2006). Therefore, in this work we chose not to
derive an upper bound on the mass of the sterile neutrino.
1 GeV makes any mixing angle possible. For
example, the DM neutrinos can be created due to the inflaton
decay Shaposhnikov & Tkachev (2006). Therefore, in this work we chose not to
derive an upper bound on the mass of the sterile neutrino.
Acknowledgements
We would like to thank G. Gilmore, A. Neronov, M. Markevitch, I. Tkachev,
and M. Shaposhnikov for help during the various stages of this project. J.N.
acknowledges the support from the Academy of Finland. The work of A.B. was
(partially) supported by the EU 6th Framework Marie Curie Research and
Training network "UniverseNet'' (MRTN-CT-2006-035863). The work of O.R. was
supported in part by European Research Training Network contract 005104
"ForcesUniverse'' and by a Marie Curie International Fellowship
within the
 European Community Framework Programme.
European Community Framework Programme.
Appendix A: Determining parameters of NFW profile
Using the data on rotation curves, one usually obtains the following
parameters of DM distribution (see e.g. Klypin et al. 2002): virial mass
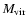 ,
virial radius
,
virial radius
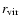 ,
and concentration parameter C. They have
the following relation with the parameters of NFW profile (5)
,
and concentration parameter C. They have
the following relation with the parameters of NFW profile (5) 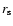 and
and
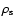 :
:
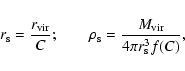 |
(A.1) |
where in terms of function f(x)
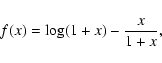 |
(A.2) |
one obtains the mass within the radius r:
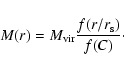 |
(A.3) |
If DM distribution in the Milky Way is described by the NFW model (as in
Klypin et al. 2002; Battaglia et al. 2005), the flux from a direction 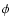 is
given by
is
given by
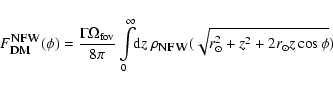 |
(A.4) |
(notations are the same as in Eqs. (7), (8)). Let us
consider two cases, when the integral in (A.4) can be easily computed.
Namely, we have for
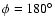
![\begin{displaymath}%
F_{\textsc{dm}}^{\textsc{nfw}}(180^\circ)=\frac{\Gamma\Omeg...
...}{r_\odot}\right) -\frac{r_{\rm s}}{r_{\rm s}+r_\odot}\right],
\end{displaymath}](/articles/aa/full/2007/31/aa6774-06/img104.gif) |
(A.5) |
and for
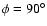
![$\displaystyle %
F_{\textsc{dm}}^{\textsc{nfw}}(90^\circ) =\frac{\Gamma\Omega_{{...
... -\frac54\right)\right] + \mathcal{O}\left(\frac{r_\odot^4}{r_{\rm s}^4}\right)$](/articles/aa/full/2007/31/aa6774-06/img105.gif) |
|
|
(A.6) |
(in the latter case the analytic expression is too complicated, so we present
Taylor expansion for the case 
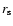 ).
).
-
Abazajian, K. 2006, Phys. Rev. D, 73, 063506 [NASA ADS] [CrossRef] (In the text)
- Abazajian,
K., & Koushiappas, S. M. 2006, Phys. Rev. D, 74,
023527 [NASA ADS] [CrossRef]
-
Abazajian, K., Fuller, G. M., & Patel, M. 2001a, Phys.
Rev. D, 64, 023501 [NASA ADS] [CrossRef] (In the text)
-
Abazajian, K., Fuller, G. M., & Tucker, W. H. 2001b,
ApJ, 562, 593 [NASA ADS] [CrossRef]
- Aguilar, A., et al.
2001, Phys. Rev. D, 64, 112007 [NASA ADS] [CrossRef]
- Asaka, T., &
Shaposhnikov, M. 2005, Phys. Lett. B, 620, 17 [NASA ADS] [CrossRef] (In the text)
- Asaka, T.,
Blanchet, S., & Shaposhnikov, M. 2005, Phys. Lett. B, 631,
151 [NASA ADS] [CrossRef] (In the text)
- Asaka, T., Kusenko,
A., & Shaposhnikov, M. 2006a, Phys. Lett. B, 638, 401 [NASA ADS] [CrossRef]
- Asaka, T., Laine,
M., & Shaposhnikov, M. 2006b, JHEP, 06, 053 [NASA ADS] [CrossRef]
- Asaka, T., Laine,
M., & Shaposhnikov, M. 2007, JHEP, 01, 091 [NASA ADS] [CrossRef] (In the text)
- Barger,
V. D., Phillips, R. J. N., & Sarkar, S. 1995, Phys.
Lett. B, 352, 365 [NASA ADS] [CrossRef]
- Battaglia,
G., et al. 2005, MNRAS, 364, 433 [NASA ADS] (In the text)
-
Berezhiani, Z. G., & Khlopov, M. Y. 1990, Sov. J.
Nucl. Phys., 52, 60
-
Berezhiani, Z. G., Vysotsky, M. I., & Khlopov,
M. Y. 1987, Sov. J. Nucl. Phys., 45, 1065
-
Berezhiani, Z. G., Vysotsky, M. I., Yurov, V. P.,
Doroshkevich, A. G., & Khlopov, M. Y. 1990, Sov. J.
Nucl. Phys., 51, 1020
- Biermann,
P. L., & Kusenko, A. 2006, Phys. Rev. Lett., 96,
091301 [NASA ADS] [CrossRef] (In the text)
- Bode, P., Ostriker,
J. P., & Turok, N. 2001, ApJ, 556, 93 [NASA ADS] [CrossRef]
- Boyarsky, A.,
Neronov, A., Ruchayskiy, O., & Shaposhnikov, M. 2006a, MNRAS,
370, 213 [NASA ADS]
- Boyarsky,
A., Neronov, A., Ruchayskiy, O., & Shaposhnikov, M. 2006b,
Phys. Rev. D, 74, 103506 [NASA ADS] [CrossRef]
- Boyarsky,
A., Neronov, A., Ruchayskiy, O., Shaposhnikov, M., & Tkachev,
I. 2006c, , 97, 261302
-
de Gouvea, A. 2005, Phys. Rev. D, 72, 033005 [NASA ADS] [CrossRef]
- De Luca, A.,
& Molendi, S. 2004, A&A, 419, 837 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- de Rujula,
A., & Glashow, S. L. 1980, , 45, 942
- Dodelson, S.,
& Widrow, L. M. 1994, Phys. Rev. Lett., 72, 17 [NASA ADS] [CrossRef] (In the text)
- Dolgov,
A. D., & Hansen, S. H. 2002, Astropart. Phys., 16,
339 [NASA ADS] [CrossRef]
-
Doroshkevich, A. G., Khlopov, M. I., & Klypin,
A. A. 1989, MNRAS, 239, 923 [NASA ADS]
- Ghigna, S.,
Moore, B., Governato, F., et al. 2000, ApJ, 544, 616 [NASA ADS] [CrossRef]
- Gilmore, G.,
Wilkinson, M., Kleyna, J., et al. 2006
[arXiv:astro-ph/0608528]
- Gilmore, G.,
et al. 2007 [arXiv:astro-ph/0703308]
- Goerdt, T.,
Moore, B., Read, J. I., Stadel, J., & Zemp, M. 2006,
MNRAS, 368, 1073 [NASA ADS]
- Hansen,
S. H., Lesgourgues, J., Pastor, S., & Silk, J. 2002,
MNRAS, 333, 544 [NASA ADS] (In the text)
- Hickox,
R. C., & Markevitch, M. 2006, ApJ, 645, 95 [NASA ADS] [CrossRef] (In the text)
- Hidaka, J., &
Fuller, G. M. 2006 [arXiv:astro-ph/0609425]
(In the text)
- Khlopov,
M. Y. 1997, Cosmoparticle Physics (World Scientific Pub Co
Inc)
- Kleyna,
J. T., Wilkinson, M. I., Gilmore, G., & Evans,
N. W. 2003, ApJ, 588, L21 [NASA ADS] [CrossRef]
- Klypin, A., Zhao,
H., & Somerville, R. S. 2002, ApJ, 573, 597 [NASA ADS] (In the text)
- Kusenko, A.
2006a [arXiv:astro-ph/0609375]
(In the text)
- Kusenko, A.
2006b, Phys. Rev. Lett., 97, 241301 [NASA ADS] [CrossRef] (In the text)
- Mateo, M. L.
1998, ARA&A, 36, 435 [NASA ADS] (In the text)
- Navarro,
J. F., Frenk, C. S., & White, S. D. M. 1997,
ApJ, 490, 493 [NASA ADS] [CrossRef] (In the text)
-
Nevalainen, J., Bonamente, M., & Kaastra, J. 2006
[arXiv:astro-ph/0610461]
(In the text)
-
Nevalainen, J., Markevitch, M., & Lumb, D. 2005, ApJ, 629,
172 [NASA ADS] [CrossRef] (In the text)
- Pal, P. B., &
Wolfenstein, L. 1982, Phys. Rev. D, 25, 766 [NASA ADS] [CrossRef] (In the text)
-
Riemer-Sørensen, S., Hansen, S. H., & Pedersen, K.
2006a, ApJ, 644, L33 [NASA ADS] [CrossRef]
-
Riemer-Sørensen, S., Pedersen, K., Hansen, S. H., &
Dahle, H. 2006b [arXiv:astro-ph/0610034]
- Seljak, U.,
Makarov, A., McDonald, P., & Trac, H. 2006, Phys. Rev. Lett.,
97, 191303 [NASA ADS] [CrossRef] (In the text)
-
Shaposhnikov, M., & Tkachev, I. 2006, Phys. Lett. B, 639,
414 [NASA ADS] [CrossRef]
- Shi, X.-d., &
Fuller, G. M. 1999, Phys. Rev. Lett., 82, 2832 [NASA ADS] [CrossRef]
- Stasielak,
J., Biermann, P. L., & Kusenko, A. 2006
[arXiv:astro-ph/0606435]
(In the text)
- Strigari,
L. E., et al. 2006 [arXiv:astro-ph/0603775]
- Strumia, A.,
& Vissani, F. 2006, hep-ph/0606054
(In the text)
- Viel, M.,
Lesgourgues, J., Haehnelt, M. G., Matarrese, S., & Riotto,
A. 2005, Phys. Rev. D, 71, 063534 [NASA ADS] [CrossRef] (In the text)
- Viel, M.,
Lesgourgues, J., Haehnelt, M. G., Matarrese, S., & Riotto,
A. 2006, Phys. Rev. Lett., 97, 071301 [NASA ADS] [CrossRef] (In the text)
- Wargelin,
B. J., Markevitch, M., Juda, M., et al. 2004, ApJ, 607,
596 [NASA ADS] [CrossRef] (In the text)
- Watson,
C. R., Beacom, J. F., Yuksel, H., & Walker,
T. P. 2006, Phys. Rev. D, 74, 033009 [NASA ADS] [CrossRef]
- Wilkinson,
M. I. et al. 2006 [arXiv:astro-ph/0602186]
- Wu, X. 2007
[arXiv:astro-ph/0702233]
Copyright ESO 2007
![\begin{displaymath}%
\Gamma = \frac{9~ \alpha~ G_F^2} {1024\pi^4}\sin^22\theta~ ...
...ta)
\left[\frac{M_{\rm s}}{{\rm keV}}\right]^5\;{\rm s}^{-1}.
\end{displaymath}](/articles/aa/full/2007/31/aa6774-06/img18.gif)
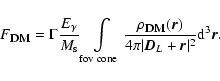
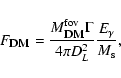
![\begin{displaymath}%
F_{{\textsc{dm}}}\! =\! 6.38 \!\times \!10^6\left(\frac{M_{...
...{\rm keV}}\right]^5\! \! \frac{{\rm keV}}{{\rm cm^2 \cdot s}}.
\end{displaymath}](/articles/aa/full/2007/31/aa6774-06/img26.gif)
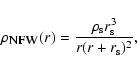
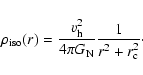
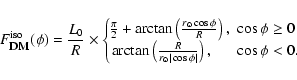
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{6774fig1.ps} \end{figure}](/articles/aa/full/2007/31/aa6774-06/Timg65.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{6774fig2.ps} \end{figure}](/articles/aa/full/2007/31/aa6774-06/Timg71.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{6774fig3.eps} \end{figure}](/articles/aa/full/2007/31/aa6774-06/Timg74.gif)
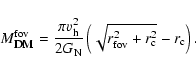
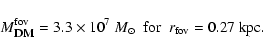
![\begin{displaymath}%
F_{{\textsc{dm}}} = 4.79 \ \frac{{\rm keV}}{{\rm cm^2\cdot s}} \left[\frac{M_{\rm s}}{{\rm keV}}\right]^5 \sin^2(2\theta).
\end{displaymath}](/articles/aa/full/2007/31/aa6774-06/img83.gif)
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{6774fig4.ps} \end{figure}](/articles/aa/full/2007/31/aa6774-06/Timg84.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6774fig5.eps} \end{figure}](/articles/aa/full/2007/31/aa6774-06/Timg87.gif)
![\begin{figure}
\par\includegraphics[width=8.05cm,clip]{6774fig6.eps} \end{figure}](/articles/aa/full/2007/31/aa6774-06/Timg88.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6774fig7.eps} \end{figure}](/articles/aa/full/2007/31/aa6774-06/Timg91.gif)
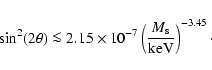
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6774fig8.eps} \end{figure}](/articles/aa/full/2007/31/aa6774-06/Timg96.gif)
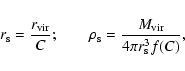
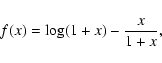
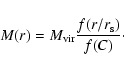
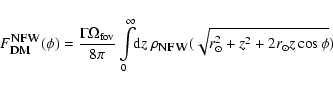
![\begin{displaymath}%
F_{\textsc{dm}}^{\textsc{nfw}}(180^\circ)=\frac{\Gamma\Omeg...
...}{r_\odot}\right) -\frac{r_{\rm s}}{r_{\rm s}+r_\odot}\right],
\end{displaymath}](/articles/aa/full/2007/31/aa6774-06/img104.gif)
![$\displaystyle %
F_{\textsc{dm}}^{\textsc{nfw}}(90^\circ) =\frac{\Gamma\Omega_{{...
... -\frac54\right)\right] + \mathcal{O}\left(\frac{r_\odot^4}{r_{\rm s}^4}\right)$](/articles/aa/full/2007/31/aa6774-06/img105.gif)