- ... neutrinos
![[*]](/icons/foot_motif.gif)
- The
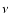 MSM does not explain the
unconfirmed results of the LSND experiment (Aguilar et al. 2001). There are other
models that try to account for it by introducing a sterile neutrino with the
mass around 1 eV. There are also models that explain not all, but only some
of these phenomena (e.g. LSND and DM, but not the baryon asymmetry as e.g.
in de Gouvea 2005) We do not give any review here. We would like to
stress that, although our work is motivated by the recent results on the
MSM does not explain the
unconfirmed results of the LSND experiment (Aguilar et al. 2001). There are other
models that try to account for it by introducing a sterile neutrino with the
mass around 1 eV. There are also models that explain not all, but only some
of these phenomena (e.g. LSND and DM, but not the baryon asymmetry as e.g.
in de Gouvea 2005) We do not give any review here. We would like to
stress that, although our work is motivated by the recent results on the
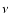 MSM, our method and results do not rely on any particular model.
MSM, our method and results do not rely on any particular model.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... far
![[*]](/icons/foot_motif.gif)
- Namely, if luminosity distance DL is much
greater than the characteristic scale of the DM distribution
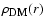 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](/icons/foot_motif.gif)
- According
to Klypin et al. (2002), the choice of e.g. the Moore profile Ghigna et al. (2000)
or a generalization thereof, as compared to the NFW profile, would change
the results by
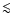
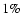 for
for
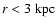 .
As we are using observations
away from the center, this difference is completely negligible, so we
choose to use the NFW profile.
.
As we are using observations
away from the center, this difference is completely negligible, so we
choose to use the NFW profile.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
paper
![[*]](/icons/foot_motif.gif)
- When quoting results of Klypin et al. (2002), we do not take the
effects of baryon compression on DM into account. While these effects make
DM distribution in the core of the MW denser, they are hard to compute
precisely. Thus the values we adopt give us a conservative lower bound on
the estimated DM signal.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...%)
![[*]](/icons/foot_motif.gif)
- Abazajian & Koushiappas (2006)
claim that the MW results of Boyarsky et al. (2006c); Riemer-Sørensen et al. (2006a) are
uncertain by about a factor of 3. This conclusion was based on the range of
virial masses of the MW DM halo
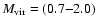
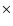
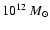 in Klypin et al. (2002). However, as just demonstrated, the authors
of Boyarsky et al. (2006c) have chosen parameters of DM halo conservatively. The
flux they used, corresponded to the favored models A1 or B1 in Klypin et al. (2002), with
in Klypin et al. (2002). However, as just demonstrated, the authors
of Boyarsky et al. (2006c) have chosen parameters of DM halo conservatively. The
flux they used, corresponded to the favored models A1 or B1 in Klypin et al. (2002), with
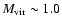
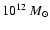 .
These
models provide the lowest bound on the derived flux of DM decay (if
one does not take into account the highly implausible "maximum disk''
(A2 or B2) models of Klypin et al. 2002). Even in the latter case, the
DM flux will be
.
These
models provide the lowest bound on the derived flux of DM decay (if
one does not take into account the highly implausible "maximum disk''
(A2 or B2) models of Klypin et al. 2002). Even in the latter case, the
DM flux will be 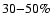 lower than the one used in
work Boyarsky et al. (2006c). Therefore, parameters of the MW DM halo
from Boyarsky et al. (2006c) provide the conservative estimate so we use them in
our work as well.
lower than the one used in
work Boyarsky et al. (2006c). Therefore, parameters of the MW DM halo
from Boyarsky et al. (2006c) provide the conservative estimate so we use them in
our work as well.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... exposures)
![[*]](/icons/foot_motif.gif)
- We processed the blank sky data with newer SAS distribution, xmmsas_20050815_1803-6.5.0, and obtained slightly different exposure times than those in the public data.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... August-September 2005)
![[*]](/icons/foot_motif.gif)
- We are
very grateful to Prof. T. Maccarone for sharing this data with us before it
became publicly available through the XMM data archive.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 2006)
![[*]](/icons/foot_motif.gif)
- As discussed
in Sect. 3.1, the estimates for DM flux do not vary significantly
if one uses NFW instead of the isothermal DM density profile. In the case of
UMi, the cored (isothermal) profile will clearly produce a more conservative
estimate than will the cuspy NFW profile. Indeed, taking NFW parameters for UMi from
the recent paper Wu (2007) gives a
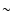 20% higher
estimate for the DM mass within the FoV.
20% higher
estimate for the DM mass within the FoV.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Wilkinson et al. 2006)
![[*]](/icons/foot_motif.gif)
- For the detailed studies of mass
distribution in dwarf spheroidals, see Gilmore et al. (2007). We are grateful to
Prof. G. Gilmore for sharing the numbers with us before their paper became
available. The statistical uncertainty in determining these numbers is
below 10%. The systematic uncertainties are much harder to estimate. One
of the major sources of the systematic errors comes from violation of the
main assumptions of the method: deviation from equilibrium and from the
spherical distribution of matter in a galaxy. In other known examples it
provides a factor of 2 uncertainty, which should be a conservative estimate
in the case of UMi, as it is rather spherical. Another typical uncertainty - determination of the mass of the stars - is not important for UMi, as it has a very high mass-to-light ratio.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... channel
![[*]](/icons/foot_motif.gif)
- For earlier works, discussing
cosmological and astrophysical effects of decaying DM,
see e.g. Berezhiani & Khlopov (1990); Doroshkevich et al. (1989); de Rujula & Glashow (1980); Berezhiani et al. (1987,1990). The extensive review of the results can also be found in the book Khlopov (1997).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.