A&A 469, 925-940 (2007)
DOI: 10.1051/0004-6361:20077511
R. A. Scheepmaker1 - M. R. Haas1 - M. Gieles1 - N. Bastian2 - S. S. Larsen1 - H. J. G. L. M. Lamers1
1 - Astronomical Institute, Utrecht University,
Princetonplein 5, 3584 CC Utrecht, The Netherlands
2 -
Department of Physics and Astronomy, University College London,
Gower Street, London, WC1E 6BT, UK
Received 20 March 2007 / Accepted 23 April 2007
Abstract
Context. Size measurements of young star clusters are valuable tools to put constraints on the formation and early dynamical evolution of star clusters.
Aims. We use HST/ACS observations of the spiral galaxy M 51 in F435W, F555W and F814W to select a large sample of star clusters with accurate effective radius measurements in an area covering the complete disc of M 51. We present the dataset and study the radius distribution and relations between radius, colour, arm/interarm region, galactocentric distance, mass and age.
Methods. We select a sample of 7698 (F435W), 6846 (F555W) and 5024 (F814W) slightly resolved clusters and derive their effective radii (
![]() )
by fitting the spatial profiles with analytical models convolved with the point spread function. The radii of 1284 clusters are studied in detail.
)
by fitting the spatial profiles with analytical models convolved with the point spread function. The radii of 1284 clusters are studied in detail.
Results. We find cluster radii between 0.5 and ![]() 10 pc, and one exceptionally large cluster candidate with
10 pc, and one exceptionally large cluster candidate with
![]() pc. The median
pc. The median
![]() is 2.1 pc. We find 70 clusters in our sample which have colours consistent with being old GC candidates and we find 6 new "faint fuzzy'' clusters in, or projected onto, the disc of M 51. The radius distribution can not be fitted with a power law similar to the one for star-forming clouds. We find an increase in
is 2.1 pc. We find 70 clusters in our sample which have colours consistent with being old GC candidates and we find 6 new "faint fuzzy'' clusters in, or projected onto, the disc of M 51. The radius distribution can not be fitted with a power law similar to the one for star-forming clouds. We find an increase in
![]() with colour as well as a higher fraction of clusters with
with colour as well as a higher fraction of clusters with
![]() in the interarm regions. We find a correlation between
in the interarm regions. We find a correlation between
![]() and galactocentric distance (
and galactocentric distance (
![]() )
of the form
)
of the form
![]() ,
which is considerably weaker than the observed correlation for old Milky Way GCs. We find weak relations between cluster luminosity and radius:
,
which is considerably weaker than the observed correlation for old Milky Way GCs. We find weak relations between cluster luminosity and radius:
![]() for the interarm regions and
for the interarm regions and
![]() for the spiral arm regions, but we do not observe a correlation between cluster mass and radius.
for the spiral arm regions, but we do not observe a correlation between cluster mass and radius.
Conclusions. The observed radius distribution indicates that shortly after the formation of the clusters from a fractal gas, the radii of the clusters have changed in a non-uniform way. We find tentative evidence suggesting that clusters in spiral arms are more compact.
Key words: galaxies: individual: M 51 - galaxies: star clusters
One of the most striking questions related to star cluster formation
concerns the transition from the densest parts of the star-forming
Giant Molecular Clouds (GMCs) to the clusters that emerge from them.
Observations show that the masses and radii of clouds follow a clear
relation of the form
![]() (e.g. Solomon et al. 1987; Larson 1981) down to the scale of the star
forming clumps (Williams et al. 1995). Such a relation is expected for
self-gravitating clouds, which are in virial equilibrium and pressure
bounded by their surroundings (e.g. Elmegreen 1989). The same
mass-radius relation is observed for complexes of multiple
clusters (Elmegreen & Salzer 1999; Elmegreen et al. 2001; Bastian et al. 2005a). Elliptical
galaxies and very massive (>
(e.g. Solomon et al. 1987; Larson 1981) down to the scale of the star
forming clumps (Williams et al. 1995). Such a relation is expected for
self-gravitating clouds, which are in virial equilibrium and pressure
bounded by their surroundings (e.g. Elmegreen 1989). The same
mass-radius relation is observed for complexes of multiple
clusters (Elmegreen & Salzer 1999; Elmegreen et al. 2001; Bastian et al. 2005a). Elliptical
galaxies and very massive (>
![]() )
stellar clusters follow
a similar relation (
)
stellar clusters follow
a similar relation (
![]() ,
Hasegan et al. 2005), which
advocates a possibility of forming very massive clusters by merging of
low mass clusters (Kissler-Patig et al. 2006; Fellhauer & Kroupa 2005).
,
Hasegan et al. 2005), which
advocates a possibility of forming very massive clusters by merging of
low mass clusters (Kissler-Patig et al. 2006; Fellhauer & Kroupa 2005).
However, for individual star clusters that emerge from the star forming clouds/clumps, a relation between mass and radius is not present (Jordán et al. 2005; Bastian et al. 2005b; Van den Bergh et al. 1991) or at least strongly weakened (Zepf et al. 1999; Lee et al. 2005; Hunter et al. 2003; Mackey & Gilmore 2003; Larsen 2004). Since this is already the case for very young clusters, it indicates that during, or shortly after (<10 Myr) the transition from clouds to clusters the mass and/or the radius of the objects change.
These changes in mass and/or radius are likely to be reflected in
changes in the mass and radius distributions (Ashman & Zepf 2001).
On the one hand, however, the mass distributions of both clouds and
clusters show great similarities. Both can be approximated by power
laws of the form
![]() ,
with the index
,
with the index ![]() in the range of 1.5-2.0 (see Fukui et al. 2001; Brand & Wouterloot 1995; Solomon et al. 1987; Harris & Pudritz 1994; Sanders et al. 1985; Elmegreen & Falgarone 1996 for clouds and see e.g. de Grijs et al. 2003; Zhang & Fall 1999; Ashman & Zepf 2001; Hunter et al. 2003; Bik et al. 2003 for
clusters). Recently, some studies have found evidence for an upper
mass truncation of the cluster mass distribution (Dowell et al. 2006; Gieles et al. 2006a), which is also found for the mass distributions of GMCs
(Rosolowsky 2005). On the other hand, the radius distributions are
less well constrained, especially for extra-galactic star clusters.
If we approximate the radius distributions by a power law of the form
in the range of 1.5-2.0 (see Fukui et al. 2001; Brand & Wouterloot 1995; Solomon et al. 1987; Harris & Pudritz 1994; Sanders et al. 1985; Elmegreen & Falgarone 1996 for clouds and see e.g. de Grijs et al. 2003; Zhang & Fall 1999; Ashman & Zepf 2001; Hunter et al. 2003; Bik et al. 2003 for
clusters). Recently, some studies have found evidence for an upper
mass truncation of the cluster mass distribution (Dowell et al. 2006; Gieles et al. 2006a), which is also found for the mass distributions of GMCs
(Rosolowsky 2005). On the other hand, the radius distributions are
less well constrained, especially for extra-galactic star clusters.
If we approximate the radius distributions by a power law of the form
![]() ,
the average value of the index for
GMCs is observed to be
,
the average value of the index for
GMCs is observed to be
![]() (Harris & Pudritz 1994; Elmegreen & Falgarone 1996), consistent with the gas having a fractal structure with
a fractal dimension
(Harris & Pudritz 1994; Elmegreen & Falgarone 1996), consistent with the gas having a fractal structure with
a fractal dimension
![]() (Mandelbrot 1983; Elmegreen & Elmegreen 2001). For young clusters in NGC 3256 Zepf et al. (1999) find
(Mandelbrot 1983; Elmegreen & Elmegreen 2001). For young clusters in NGC 3256 Zepf et al. (1999) find
![]() ,
while Bastian et al. (2005, from now on referred
to as "B05'') find
,
while Bastian et al. (2005, from now on referred
to as "B05'') find
![]() for star clusters in the disc
of M 51. This difference, however, seems to be caused by the erroneous
addition of +1 to the index in the result of
Ashman & Zepf (2001)
for star clusters in the disc
of M 51. This difference, however, seems to be caused by the erroneous
addition of +1 to the index in the result of
Ashman & Zepf (2001)![]() .
.
Our understanding of whether or not the mass and radius distribution of clouds and clusters are similar, and to which degree, is directly coupled to our understanding of star formation and the early evolution of star clusters. Besides that, possible explanations for the lack of a mass-radius relation for clusters which change the mass and/or the radius of the clusters in a non-uniform way, are likely to affect the mass and radius distributions (Ashman & Zepf 2001). It is therefore important to put better constraints on these distributions, and in this work we will focus on the radius distribution of young star clusters.
In the study presented here we exploit the superb resolution and large
field-of-view of the new HST Advanced Camera for Surveys
(ACS) observations of M 51, taken as part of the Hubble Heritage
Project. These observations allow us to measure the radii of a large
sample of clusters in an area covering, for the first time, the complete
disc of M 51 and its companion, NGC 5195 at a
![]() resolution.
In this work, which is the first in a series of papers, we
present the dataset and we study the radius distribution for the
complete cluster sample and for cluster samples with a different
background surface brightness ("background regions''). The
differences in background regions are likely to reflect differences in
environmental conditions, which could have an impact on the early
evolution of star clusters.
resolution.
In this work, which is the first in a series of papers, we
present the dataset and we study the radius distribution for the
complete cluster sample and for cluster samples with a different
background surface brightness ("background regions''). The
differences in background regions are likely to reflect differences in
environmental conditions, which could have an impact on the early
evolution of star clusters.
The radii of star clusters in M 51 have already been studied by B05 and Lee et al. (2005). However, these studies used lower resolution HST/WFPC2 data and were not covering the complete disc. Besides this, we use different selection criteria for the clusters than B05, based on the clusters actually being resolved and clearly separated from nearby contaminating sources. In combination with the larger field-of-view and the higher resolution of the ACS data, this leads to a larger sample of clusters, divided in different background regions.
The structure of this paper is as follows: in Sect. 2 we describe the dataset, the selection of sources and background regions and the photometry. The radius measurements are described in Sect. 3 and in Sect. 4 we describe experiments with artificial clusters to determine the accuracy and detection limits of our methods. Our selection criteria and a description of our cluster sample are presented in Sect. 5, followed by a comparison between ACS and WFPC2 data in Sect. 6. The radius distribution is presented in Sect. 7, and we search for correlations between mass, radius and galactocentric distance in Sect. 8. In Sect. 9 we finish with the summary and conclusions.
We make use of the HST/ACS dataset of M 51 (NGC 5194, a late type
Sbc galaxy), taken as part of the Hubble Heritage Project in January
2005 (proposal ID 10452, PI: S. V. W. Beckwith). The dataset consists
of 6 ACS pointings using the Wide Field Channel (WFC) in
F435W (![]() B), F555W (
B), F555W (![]() V), F814W (
V), F814W (![]() I) and F658N (
I) and F658N (![]()
![]() ), with 4 dithered exposures per filter, as is
summarized in Table 1. The observations
were reduced and drizzled into one mosaic image by Mutchler et al. (2005).
In summary, the standard ACS pipeline (CALACS) was used for bias,
dark and flat-field corrections of the individual dithered images.
The corrected images were then combined into one mosaic image using
the MultiDrizzle task (Koekemoer et al. 2002; Fruchter & Hook 2002), which
also corrects for filter-specific geometric distortion, cosmic rays
and bad pixels. For a complete description of the dataset we refer to
Mutchler et al. (2005) and the M 51 mosaic website
(http://archive.stsci.edu/prepds/m51/). For details on the
standard pipeline processing we refer to the ACS Data Handbook
(Pavlovsky et al. 2005).
), with 4 dithered exposures per filter, as is
summarized in Table 1. The observations
were reduced and drizzled into one mosaic image by Mutchler et al. (2005).
In summary, the standard ACS pipeline (CALACS) was used for bias,
dark and flat-field corrections of the individual dithered images.
The corrected images were then combined into one mosaic image using
the MultiDrizzle task (Koekemoer et al. 2002; Fruchter & Hook 2002), which
also corrects for filter-specific geometric distortion, cosmic rays
and bad pixels. For a complete description of the dataset we refer to
Mutchler et al. (2005) and the M 51 mosaic website
(http://archive.stsci.edu/prepds/m51/). For details on the
standard pipeline processing we refer to the ACS Data Handbook
(Pavlovsky et al. 2005).
The resulting mosaic image covers a region of
![]() (=
(=
![]() kpc) with a resolution of 2.0 pc per pixel, where
we assumed a distance modulus of
m-M = 29.62 from
Feldmeier et al. (1997), i.e. a distance of
kpc) with a resolution of 2.0 pc per pixel, where
we assumed a distance modulus of
m-M = 29.62 from
Feldmeier et al. (1997), i.e. a distance of
![]() Mpc. The
covered region is large enough to include the complete spiral disc of
M 51, as well as its companion NGC 5195 (a dwarf barred spiral of early
type SB0), while at the same time the resolution is good enough to
resolve stellar cluster candidates, i.e. to distinguish them
from stars by measuring their sizes and comparing these to the
Point Spread Function (PSF) of the HST/ACS camera.
Mpc. The
covered region is large enough to include the complete spiral disc of
M 51, as well as its companion NGC 5195 (a dwarf barred spiral of early
type SB0), while at the same time the resolution is good enough to
resolve stellar cluster candidates, i.e. to distinguish them
from stars by measuring their sizes and comparing these to the
Point Spread Function (PSF) of the HST/ACS camera.
Table 1: Overview of the filters and exposure times used. The limiting magnitude is for a point source with S/N = 5.
For source selection we used the SExtractor package (Bertin & Arnouts 1996, version
2.3.2). SExtractor first generates a background map by
computing the mean and standard deviation of every section of the
image with a user defined grid size for which we choose
![]() pixels. In every section the local background histogram is clipped
iteratively until every remaining pixel value is within
pixels. In every section the local background histogram is clipped
iteratively until every remaining pixel value is within ![]()
![]() of the median value. The mean of the clipped histogram is then taken
as the local background value. Every area of at least three adjacent
pixels that exceeded the background by at least
of the median value. The mean of the clipped histogram is then taken
as the local background value. Every area of at least three adjacent
pixels that exceeded the background by at least ![]() was called a
source. For details on the background estimation and the source
selection we refer to the SExtractor user manual (Bertin & Arnouts 1996) or
Holwerda (2005). The coordinates of the sources in F435W
F555W and F814W were matched and only sources that were detected
in all three filters within two pixel uncertainty were kept. This
resulted in a list of 75 436 sources, including cluster candidates
but also many stars and background galaxies. We did not apply any
selection criteria based on shape, sharpness or size during the
source selection with SExtractor. However, in Sect. 5 we use individual radii measurements to select a large
sample of cluster candidates from the source list.
was called a
source. For details on the background estimation and the source
selection we refer to the SExtractor user manual (Bertin & Arnouts 1996) or
Holwerda (2005). The coordinates of the sources in F435W
F555W and F814W were matched and only sources that were detected
in all three filters within two pixel uncertainty were kept. This
resulted in a list of 75 436 sources, including cluster candidates
but also many stars and background galaxies. We did not apply any
selection criteria based on shape, sharpness or size during the
source selection with SExtractor. However, in Sect. 5 we use individual radii measurements to select a large
sample of cluster candidates from the source list.
In order to study any possible relations between radius and
environment, and to perform completeness and accuracy tests for
different background levels, we divided the image in three regions
according to the background surface brightness. These background regions
were selected by smoothing the F555W image with a boxcar average of
200 pixels. Consequently, pixels with a value
<
![]() (corresponding to a surface
brightness
(corresponding to a surface
brightness
![]() mag arcsec-2) were flagged "low
background''. Pixel values
mag arcsec-2) were flagged "low
background''. Pixel values ![]()
![]() and
<
and
<
![]() (
(
![]() mag arcsec-2) were flagged "intermediate
background'' and pixels with a value
mag arcsec-2) were flagged "intermediate
background'' and pixels with a value
![]()
![]() (
(
![]() mag arcsec-2) were
flagged "high background''. These values were chosen because they
resulted in a contour map, shown in Fig. 1,
in which the high background region clearly follows most of the inner
spiral arms, covering most areas that would be marked "high
background'' if the selection would take place by eye. The
"intermediate'' region should be considered as a transition region to
clearly separate cluster samples within a low and high background
region.
mag arcsec-2) were
flagged "high background''. These values were chosen because they
resulted in a contour map, shown in Fig. 1,
in which the high background region clearly follows most of the inner
spiral arms, covering most areas that would be marked "high
background'' if the selection would take place by eye. The
"intermediate'' region should be considered as a transition region to
clearly separate cluster samples within a low and high background
region.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7511f01.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg54.gif) |
Figure 1: The contours outlining the three background regions, superimposed on the HST/ACS mosaic image in the F555W passband. The solid lines enclose "high background'' regions, and everything outside the dashed lines indicates the "low background'' regions. The regions in between solid and dashed lines are called "intermediate background''. |
| Open with DEXTER | |
For our photometry, radius measurements and artificial cluster experiments we need a filter dependent PSF. Since there are not enough bright, isolated point sources in the M 51 mosaic image to determine the PSF accurately, the PSF was observationally determined from a crowded star field on a drizzled image of the Galactic globular cluster 47 Tuc (NGC 104, HST proposal GO-9281, PI: J. E. Grindlay). For each filter a separate PSF was determined.
With drizzled data, the size of the PSF depends on the choice of the
drizzle kernel and the accuracy with which the flux from multiple
images is combined. We note that the image of 47 Tuc was drizzled in a
slightly different way than the M 51 image. The 47 Tuc images were
drizzled using a square kernel with a size of one pixel
(i.e.
![]() ,
Fruchter & Hook 2002), while a Gaussian
kernel with
,
Fruchter & Hook 2002), while a Gaussian
kernel with
![]() was used for M 51. Therefore, we
expect some differences between the PSFs, with the M 51 PSF possibly being
larger than the 47 Tuc PSF. This could lead to an overestimation of
the measured radii. However, tests by Larsen (2004) have shown
that the lower limit down to which Ishape can detect a source as
being resolved is
was used for M 51. Therefore, we
expect some differences between the PSFs, with the M 51 PSF possibly being
larger than the 47 Tuc PSF. This could lead to an overestimation of
the measured radii. However, tests by Larsen (2004) have shown
that the lower limit down to which Ishape can detect a source as
being resolved is ![]() 10% of the FWHM of the PSF. At the distance
of M 51 and with a FWHM of the ACS PSF of
10% of the FWHM of the PSF. At the distance
of M 51 and with a FWHM of the ACS PSF of ![]() 2.1 pixels, this
corresponds to an effective radius (
2.1 pixels, this
corresponds to an effective radius (
![]() )
of
)
of ![]() 0.5 pc. We indeed
find a very strong peak in the
0.5 pc. We indeed
find a very strong peak in the
![]() distribution of all the measured
sources below 0.5 pc, consistent with the majority of the sources
(faint stars) being fit as point sources.
distribution of all the measured
sources below 0.5 pc, consistent with the majority of the sources
(faint stars) being fit as point sources.
This peak of point sources implies that the measured radii are
not biased towards larger values. We therefore conclude that
the empirical PSF we use, although drizzled in a slightly different
way than the image of M 51, is not too small. It shows that
other effects on the PSF, like combining the flux of multiple separate
images, are more important than the differences in the drizzle
parameters. In Sect. 6 we
also show that there are no large systematic offsets between our
measured radii and the radii of some clusters that were independently
measured by B05 using WFPC2 data. We can therefore use the empirical
PSF from the image of 47 Tuc and we will use as a lower-limit for the
measured
![]() a value of 0.5 pc.
a value of 0.5 pc.
We performed aperture photometry on all the sources in the source list
using the IRAF![]() /DAOPHOT package. We used a 5 pixel aperture radius and a
background annulus with an inner radius of 10 pixels and a width of 3 pixels.
/DAOPHOT package. We used a 5 pixel aperture radius and a
background annulus with an inner radius of 10 pixels and a width of 3 pixels.
The aperture correction (
![]() )
for resolved
sources from the 5 pixel aperture to 10 pixels (=
)
for resolved
sources from the 5 pixel aperture to 10 pixels (=
![]() )
depends
on the size of the source. Larger sources will have more flux outside
the measuring aperture, and therefore need a larger (i.e. more
negative) aperture correction. We measured the aperture corrections
on artificial sources with different effective (i.e. projected
half-light) radii between
)
depends
on the size of the source. Larger sources will have more flux outside
the measuring aperture, and therefore need a larger (i.e. more
negative) aperture correction. We measured the aperture corrections
on artificial sources with different effective (i.e. projected
half-light) radii between ![]() 1 pc and
1 pc and ![]() 5 pc, generated by the
BAOlab package (Larsen 1999,2004). For these artificial
sources we used Moffat profiles (Moffat 1969) with a power-law
index of -1.5, which we convolved with the filter dependent PSF of
the HST/ACS. The aperture correction was then measured by comparing
the photometry between a 5 and 10 pixel aperture.
5 pc, generated by the
BAOlab package (Larsen 1999,2004). For these artificial
sources we used Moffat profiles (Moffat 1969) with a power-law
index of -1.5, which we convolved with the filter dependent PSF of
the HST/ACS. The aperture correction was then measured by comparing
the photometry between a 5 and 10 pixel aperture.
The measured aperture corrections in all the three filters (F435W,
F555W and F814W) show a clear linear relation with the measured
size of the analytical cluster. Figure 2 shows theresults
for F435W. The relations between
![]() and
measured effective radius (
and
measured effective radius (
![]() )
for the different filters can be
written as:
)
for the different filters can be
written as:
![\begin{figure}
\par\includegraphics[width=7cm,clip]{7511f02.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg63.gif) |
Figure 2:
The aperture correction (
|
| Open with DEXTER | |
We could use Eq. (1) to apply a size-dependent aperture
correction to every source based on their radius measurement.
However, this could introduce new and unknown systematic uncertainties
due to the limitations of the radius measurements. We therefore
decided to use a fixed aperture correction, determined for a 3 pc
source. We are aware that this introduces uncertainties in the flux
as a function of the sizes of the sources (Anders et al. 2006). We will
underestimate the flux with ![]() 0.3 mag for a 9 pc source and
overestimate the flux with
0.3 mag for a 9 pc source and
overestimate the flux with ![]() 0.1 mag for a 0.5 pc source (also see
Sect. 4). However, it is
preferred to deal with these systematic uncertainties of known origin
rather than introducing new uncertainties due to the less well
determined uncertainties of the sizes. Moreover, since the
coefficients in Eq. (1) are very similar for the different
filters, uncertainties in the aperture corrections practically cancel
out when we consider colours instead of fluxes. Nevertheless, when
necessary we will mention how our results change if we use the
size-dependent aperture corrections.
0.1 mag for a 0.5 pc source (also see
Sect. 4). However, it is
preferred to deal with these systematic uncertainties of known origin
rather than introducing new uncertainties due to the less well
determined uncertainties of the sizes. Moreover, since the
coefficients in Eq. (1) are very similar for the different
filters, uncertainties in the aperture corrections practically cancel
out when we consider colours instead of fluxes. Nevertheless, when
necessary we will mention how our results change if we use the
size-dependent aperture corrections.
The filter dependent aperture corrections from
![]() to
infinity (the "infinity corrections'') were taken from Table 5 of
Sirianni et al. (2005), which were determined for point sources. In
principle, with these infinity corrections for point sources we are
slightly underestimating the infinity corrections for resolved
sources. However, in Sect. 4 we
will show, using artificial cluster experiments, that with the
infinity corrections for point sources we are not introducing
systematic offsets in the photometry for 3 pc sources.
to
infinity (the "infinity corrections'') were taken from Table 5 of
Sirianni et al. (2005), which were determined for point sources. In
principle, with these infinity corrections for point sources we are
slightly underestimating the infinity corrections for resolved
sources. However, in Sect. 4 we
will show, using artificial cluster experiments, that with the
infinity corrections for point sources we are not introducing
systematic offsets in the photometry for 3 pc sources.
A final correction for Galactic foreground extinction of E(B-V) = 0.038 in the direction of M 51 was applied, according to Appendix B of Schlegel et al. (1998). This corresponds to an additional correction in F435W, F555W and F814W of -0.152, -0.117 and -0.068 mag, respectively.
We did not apply any CTE corrections, since on the drizzled mosaic
image the exact location of every source on the CCD is not easily
retrieved, nor did we do photometry on the single
(i.e. "un-stacked'') exposures, both of which are necessary to
calculate the CTE corrections. We have estimated the CTE corrections
to be of the order of -0.02 mag and therefore ignoring them does not
lead to large systematic effects. We also did not apply a correction
for the impact of the red halo (Sirianni et al. 2005) on our
F814W photometry, since clusters in the spiral disc of M 51 are
mainly blue objects and the red halo effect is most significant for
very red objects observed in the F850LP filter. Using Tables 6
and 8 from Sirianni et al. (2005) we estimate that the error in the
infinity correction for our F814W photometry would be of the order
of ![]() 0.01 mag, if the clusters would be red objects. This shows
that the red halo effect has no significant effect on our photometry.
0.01 mag, if the clusters would be red objects. This shows
that the red halo effect has no significant effect on our photometry.
We exploit the resolution of the ACS camera by measuring the effective radii of all the 75 436 detected sources in F435W, F555W and F814W. These radii can than be used to distinguish slightly resolved stellar cluster candidates from stars (Sect. 5) and to study the size distribution of a large sample of stellar cluster candidates (Sect. 7). With "slightly resolved'' we mean that the cluster candidates have an intrinsic size which is comparable to or smaller than the FWHM of the PSF.
For the radius measurements we used the Ishape routine, which is
part of the BAOlab package (Larsen 1999,2004). Ishape convolves analytic profiles for the surface brightness distribution of
a cluster with different effective radii with the PSF and then fits
these to each source in the data. The best fitting
![]() is then
determined by minimizing the
is then
determined by minimizing the ![]() in an iterative process. For
the analytic profiles we used the same ones as for the measured
aperture corrections described in Sect. 2.5, namely
Moffat profiles with a power-law index of -1.5 (i.e. a Moffat 15
profile). These profiles were found to be the best-fitting profiles
to young stellar clusters in the LMC (Elson et al. 1987).
in an iterative process. For
the analytic profiles we used the same ones as for the measured
aperture corrections described in Sect. 2.5, namely
Moffat profiles with a power-law index of -1.5 (i.e. a Moffat 15
profile). These profiles were found to be the best-fitting profiles
to young stellar clusters in the LMC (Elson et al. 1987).
Because the M 51 ACS data was drizzled, the cores of the surface brightness profiles of the young clusters in M 51 could have been slightly changed. We did not quantify this effect, but instead stick to the Moffat 15 profiles, since the outer regions of the profiles, which in the case of Moffat 15 profiles approximate power laws, are not expected to change.
The average surface brightness profile of Galactic globular clusters (GCs) is a King 30 profile (King 1962; Harris 1996). Tests by Larsen (1999) have shown that when clusters that follow a King profile are measured using a Moffat 15 profile, the effective radius is reproduced quite well. Therefore, even in the case where the true profiles of stellar clusters in M 51 are not perfect Moffat 15 profiles, the use of this profile will likely not lead to large systematic errors.
The radii of the sources were measured using the flux within a 5 pixel radius around the centre of the source (i.e. using an Ishape fitting radius of 5 pixels). To avoid neighbouring sources to affect the radius measurements, we rejected all sources which have a neighbour in the original source list within 5 pixels (see Sect. 5 for a full description of the applied selection criteria).
Since stellar cluster profiles are almost never perfectly spherically
symmetric, we fitted them with elliptical profiles. We transformed
the measured FWHM (in pixels) along the major axis into an effective
radius according to the formulae from the Ishape user's guide:
To test how our selection of stellar cluster candidates (Sect. 5) depends on the brightness and size of the cluster and the background region, and how accurate our radius measurements are, we performed tests with artificial clusters for all three filters, different background regions and different cluster sizes. The results of these tests will be used in Sect. 5 to select a sample of stellar cluster candidates with accurate radii.
First we created artificial clusters using the MKCMPPSF and MKSYNTH tasks, which are part of the BAOlab package (Larsen 1999). For every filter we convolved the PSF with a Moffat profile with a power-law index of -1.5 and effective radii between 1 and 9 pc, in steps of 2 pc. These artificial clusters were then scaled to a range of magnitudes between 18 and 26 mag with steps of 0.5 mag. For every magnitude 100 clusters were added at random locations to every background region on the mosaic image by combining MKSYNTH with the imarith task in IRAF. We made sure that the minimum distance between these random locations was at least 30 pixels, in order not to introduce artificial crowding effects.
We then performed the cluster selection on these sources in a similar
way as with the normal data. We performed these tests for every
filter individually, since taking into account the matching of every
source in three filters, as we did with the normal data, would imply
creating artificial clusters with a range of colours (i.e. ages) for
every magnitude, drastically increasing the computing time. However,
by comparing analytical spectral energy distributions (SEDs) from
GALEV simple stellar population (SSP) models (Schulz et al. 2002) to the
measured detection limits, we tested that for cluster ages up to
![]() 1 Gyr, the F814W filter is always the most limiting filter for
detecting clusters. We therefore do not expect that using the results
of these tests for individual filters is introducing large
age-dependent biases in the derived detection limits.
1 Gyr, the F814W filter is always the most limiting filter for
detecting clusters. We therefore do not expect that using the results
of these tests for individual filters is introducing large
age-dependent biases in the derived detection limits.
The artificial clusters were recovered by running SExtractor, followed
by photometry in all three filters and by performing size measurements
in F435W and F555W. For F435W and F555W, we considered a
cluster to be recovered when we found a resolved source (i.e. with a
![]() larger than our adopted lower limit of 0.5 pc (see
Sect. 5) and a
larger than our adopted lower limit of 0.5 pc (see
Sect. 5) and a ![]() which is lower
than the
which is lower
than the ![]() using only a PSF) within 1 pixel from the input
coordinate and with a distance to the nearest neighbouring source of
>5 pixels. For F814W we considered a cluster to be recovered when
we found a source within 1 pixel from the input coordinate and with a
distance to the nearest neighbouring source of >5 pixels.
The recovered fraction as a function of F435W magnitude for the
different background regions and input radii is plotted in
Fig. 3. For the F555W and F814W passbands the results are similar, except that the turn-off of the
completeness curves happens at brighter magnitudes due to a lower S/N
ratio of the F555W and F814W data (see below).
using only a PSF) within 1 pixel from the input
coordinate and with a distance to the nearest neighbouring source of
>5 pixels. For F814W we considered a cluster to be recovered when
we found a source within 1 pixel from the input coordinate and with a
distance to the nearest neighbouring source of >5 pixels.
The recovered fraction as a function of F435W magnitude for the
different background regions and input radii is plotted in
Fig. 3. For the F555W and F814W passbands the results are similar, except that the turn-off of the
completeness curves happens at brighter magnitudes due to a lower S/N
ratio of the F555W and F814W data (see below).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{7511f03.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg68.gif) |
Figure 3:
The recovered fraction of artificial clusters as a function
of magnitude and
|
| Open with DEXTER | |
The recovered fraction shown in Fig. 3 is
scaled to the number of clusters recovered at magnitude 18. We note,
however, that a certain fraction of even the brightest artificial
clusters is not recovered due to their vicinity within 5 pixels from a
neighbouring source. Our completeness tests show that these initial
losses will be ![]() 3,
3, ![]() 13 and
13 and ![]() 28% for the low,
intermediate and high background, respectively. This shows that due
to crowding effects one can never select a sample which is 100%
complete. Depending on the selection criteria and background region,
one will lose up to
28% for the low,
intermediate and high background, respectively. This shows that due
to crowding effects one can never select a sample which is 100%
complete. Depending on the selection criteria and background region,
one will lose up to ![]() 28% of the initial sample present in the
data. This number will be even higher when one considers that young
clusters are not randomly distributed across the spiral disc, but will
mostly be clustered themselves in high background regions.
28% of the initial sample present in the
data. This number will be even higher when one considers that young
clusters are not randomly distributed across the spiral disc, but will
mostly be clustered themselves in high background regions.
Figure 3 shows that larger clusters are harder to recover than smaller clusters with the same brightness. This is expected, since larger clusters have a lower surface brightness, which makes them easier to blend into the background. We define the magnitude at which 90% of the artificial cluster was recovered to be the 90% completeness limit. The values we found this way for the different filters, cluster sizes and background regions are plotted in Fig. 4.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{7511f04.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg69.gif) |
Figure 4:
The 90% completeness limits versus effective radius (
|
| Open with DEXTER | |
For our current study, where we look at the radius distribution of
stellar clusters, it is not only important to detect clusters by
measuring their radii, but the measured radii also have to be
accurate. To test the limitations of our radius measurements, we
looked at how the difference between input and measured radius of the
artificial clusters depends on magnitude, input size and background
region. In Fig. 5 we plot the 50th (i.e. the median), 68th and 90th percentile of ![]() versus
the magnitude in F435W, where we define
versus
the magnitude in F435W, where we define ![]() as the relative
difference between input and measured radius:
as the relative
difference between input and measured radius:
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{7511f05.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg73.gif) |
Figure 5:
The median ( top), 68th percentile ( middle) and 90th
percentile ( bottom) of |
| Open with DEXTER | |
We also used the results of our artificial cluster experiments to test
the robustness of our photometry and the accuracy of the applied
aperture corrections described in Sect. 2.5. In
Fig. 6 we show the mean difference between the
measured magnitude and the input magnitude (![]() mag) versus
F435W magnitude for different sizes in the high background region.
We applied the constant aperture correction for a 3 pc source
according to Eq. (1) and the infinity correction for point
sources from Sirianni et al. (2005) that we described in
Sect. 2.5. First of all, Fig. 6
shows that the applied aperture correction is very accurate, since the
photometry of 3 pc clusters is almost perfectly reproduced to
mag) versus
F435W magnitude for different sizes in the high background region.
We applied the constant aperture correction for a 3 pc source
according to Eq. (1) and the infinity correction for point
sources from Sirianni et al. (2005) that we described in
Sect. 2.5. First of all, Fig. 6
shows that the applied aperture correction is very accurate, since the
photometry of 3 pc clusters is almost perfectly reproduced to
![]() 22.5 mag. This shows that applying the point source infinity
correction to 3 pc sources does not introduce systematic offsets in
the photometry. Second, the range covered in
22.5 mag. This shows that applying the point source infinity
correction to 3 pc sources does not introduce systematic offsets in
the photometry. Second, the range covered in ![]() mag shows that
when there is no information about the radius of the cluster, the
uncertainty in the photometry can be as large as
mag shows that
when there is no information about the radius of the cluster, the
uncertainty in the photometry can be as large as ![]() 0.5 mag for
clusters with radii in the range 1-9 pc.
0.5 mag for
clusters with radii in the range 1-9 pc.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{7511f06.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg75.gif) |
Figure 6: The mean difference between the measured magnitude and the input magnitude of the recovered artificial clusters versus F435W magnitude for different sizes in the high background region. The truncated line for the largest and faintest clusters means none of these artificial clusters were recovered. |
| Open with DEXTER | |
We used the radius estimates to distinguish the resolved clusters from unresolved objects. In this section we select two different cluster samples: a "resolved sample'' with clearly resolved clusters, and a smaller subset from this sample, a "radius sample''. The radius sample satisfies extra criteria that make the radii more reliable, and will be used to study the radius distribution (Sect. 7) and the correlations between mass, radius and distance (Sect. 8). The resolved sample will be used in another study of the luminosity function of stellar clusters in M 51 (Gieles et al. 2006a; Haas et al. 2007, in prep.).
The cluster selection process is hampered by various factors like an irregular background (spiral arms, dust lanes), contaminating background galaxies and crowding effects which causes many sources to be (partially) blended with neighbouring sources, biasing the radius measurements. We tried to automate the selection of stellar cluster candidates as much as possible, taking into account all these factors. However, it was unavoidable to subject the automatically selected sample to visual inspection, to filter out any remaining contaminants or the stellar cluster candidates of which the radii measurements could not be trusted.
We created small images in all three filters for all the sources that fulfilled the above mentioned criteria, and by visual inspection we looked for:
To see if there are any possible old (![]() 10 Gyr) GC candidates
in our cluster sample, we applied the colour criteria
10 Gyr) GC candidates
in our cluster sample, we applied the colour criteria
![]() and
and
![]() to our cluster sample, typical for old MW GCs. There are
only 70 clusters satisfying these criteria, showing that the majority
of our cluster sample consists of young clusters, but a small fraction
of
to our cluster sample, typical for old MW GCs. There are
only 70 clusters satisfying these criteria, showing that the majority
of our cluster sample consists of young clusters, but a small fraction
of ![]() 5% is probably part of an old GC population or highly
reddened. A more detailed identification of GC candidates in M 51 will be carried out in future studies.
5% is probably part of an old GC population or highly
reddened. A more detailed identification of GC candidates in M 51 will be carried out in future studies.
We note that our dataset covers the same field used by Hwang & Lee (2006, from
here on referred to as "HL06''), who detect 49 "faint
fuzzy'' star clusters around the companion of M 51, NGC 5195. Faint
fuzzy clusters were introduced by Larsen & Brodie (2000), because they
formed a sub-group in a radius-colour diagram of star clusters in
NGC 1023. In Fig. 9 we show
![]() versus
versus ![]() for the
clusters in our sample. Six clusters in our sample satisfy
the criteria of a faint fuzzy, namely
for the
clusters in our sample. Six clusters in our sample satisfy
the criteria of a faint fuzzy, namely
![]() ,
,
![]() and
and
![]() pc. These faint fuzzy candidates are indicated in
Fig. 9. The figure shows that the faint fuzzy candidates
indeed form a separate group in a radius-colour diagram and are not
simply the largest clusters in the tail of a continuous radius
distribution.
pc. These faint fuzzy candidates are indicated in
Fig. 9. The figure shows that the faint fuzzy candidates
indeed form a separate group in a radius-colour diagram and are not
simply the largest clusters in the tail of a continuous radius
distribution.
![\begin{figure}
\par\includegraphics[width=27mm]{7511f07.ps}\includegraphics[widt...
...ics[width=27mm]{7511f14.ps}\includegraphics[width=27mm]{7511f15.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg91.gif) |
Figure 7:
A selection of F435W images centered on sources that were
rejected from the sample after visual inspection. The size of each
image is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=27mm]{7511f16.ps}\includegraphics[widt...
...ics[width=27mm]{7511f23.ps}\includegraphics[width=27mm]{7511f24.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg92.gif) |
Figure 8:
A selection of isolated stellar cluster candidates in F435W that passed the visual inspection. The size of each image is
60 |
| Open with DEXTER | |
Table 2: The selection of the sample of stellar cluster candidates with accurate radii. The numbers indicate the amount of sources that satisfy the mentioned criterion and all the criteria mentioned above it, split in the low, intermediate and high background region.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{7511f25.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg95.gif) |
Figure 9:
|
| Open with DEXTER | |
The six faint fuzzy candidates seem randomly located in (or projected
onto) the disc of M 51. None of the 49 faint fuzzy candidates of HL06
are therefore recovered in our cluster sample. This is because all
these 49 candidates are fainter than the magnitude limits we apply.
This is expected, since we apply rather conservative magnitude limits
in order to achieve accurate radius measurements, also for large
clusters in high background regions (Sect. 5.1). If we would drop our conservative magnitude limits from
the selection criteria, we would have 37 of the 49 faint fuzzy
candidates from HL06 in our sample. The 12 remaining candidates are
removed from our sample based on "inaccurate radii'' criteria (large
radius difference between F435W and F555W or a ![]() larger
than
larger
than
![]() ). The six faint fuzzy candidates in our
sample are not in the sample of HL06, because these authors focused
on the region around NGC 5195 and were therefore not covering the disc
of M 51.
). The six faint fuzzy candidates in our
sample are not in the sample of HL06, because these authors focused
on the region around NGC 5195 and were therefore not covering the disc
of M 51.
One cluster candidate in our radius sample, with our ID number
"212995'', clearly stands out from the other cluster candidates
in radius. The cluster candidate, positioned at
RA = 13
![]() 29
29
![]() 51
51
![]() 94,
Dec = +47
94,
Dec = +47![]() 11
11![]() 19
19
![]() 63 and shown in Fig. 10,
has an (ellipticity corrected)
63 and shown in Fig. 10,
has an (ellipticity corrected)
![]() pc in F435W. The
projected galactocentric distance of this cluster candidate is
1.02 kpc. Its brightness in F435W, F555W and F814W is 22.27,
21.52 and 20.48 mag, respectively, with corresponding
pc in F435W. The
projected galactocentric distance of this cluster candidate is
1.02 kpc. Its brightness in F435W, F555W and F814W is 22.27,
21.52 and 20.48 mag, respectively, with corresponding ![]() and
and ![]() of 0.75 and 1.05, respectively. These colours make this source both an
old GC and faint fuzzy candidate. Assuming the source is a cluster,
we can make an estimate of its age and mass by using GALEV SSP models.
However, since we only have photometry in three filters, this estimate
suffers from an age-extinction-metallicity degeneracy, introducing
rather large uncertainties. Assuming a low extinction (
E(B-V)< 0.1)
and a metallicity in the range of 0.2-1.0
of 0.75 and 1.05, respectively. These colours make this source both an
old GC and faint fuzzy candidate. Assuming the source is a cluster,
we can make an estimate of its age and mass by using GALEV SSP models.
However, since we only have photometry in three filters, this estimate
suffers from an age-extinction-metallicity degeneracy, introducing
rather large uncertainties. Assuming a low extinction (
E(B-V)< 0.1)
and a metallicity in the range of 0.2-1.0
![]() ,
the
best estimate for the age is
2.7+2.8-1.8 Gyr. The
corresponding best estimate for the mass is
,
the
best estimate for the age is
2.7+2.8-1.8 Gyr. The
corresponding best estimate for the mass is
![]() ,
which is a lower
limit due to the underestimation of the aperture correction for the
photometry for such a large source. Assuming the metallicity is
,
which is a lower
limit due to the underestimation of the aperture correction for the
photometry for such a large source. Assuming the metallicity is
![]() ,
the best estimates for the age and mass are
13.2+2.8-9.7 Gyr and
,
the best estimates for the age and mass are
13.2+2.8-9.7 Gyr and
![]() ,
respectively.
However, the possibility of the source being a highly reddened young
cluster is not fully excluded. There is also a possibility that this
cluster candidate is actually a background galaxy, but this
possibility is considered to be unlikely, since the
cluster is located (in projection) very close to the centre of M 51,
where the extinction of the background source and the surface brightness
of the foreground (M 51) is high.
,
respectively.
However, the possibility of the source being a highly reddened young
cluster is not fully excluded. There is also a possibility that this
cluster candidate is actually a background galaxy, but this
possibility is considered to be unlikely, since the
cluster is located (in projection) very close to the centre of M 51,
where the extinction of the background source and the surface brightness
of the foreground (M 51) is high.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7511f26.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg108.gif) |
Figure 10:
Cluster "212995'', the largest cluster in our sample with a
|
| Open with DEXTER | |
As a test of the robustness of our methods, we compared the photometry
and the radii of our clusters to the data of B05. B05 derived ages,
masses, extinctions and effective radius estimates of stellar clusters
covering the central ![]()
![]() kpc of M 51 using HST NICMOS and WFPC2 data. We calculated the transformation
between a mosaic of the F555W WFPC2 images and the ACS mosaic
image with the GEOMAP task in IRAF, by identifying 10 sources by eye
that were clearly visible in both data sets. We then transformed the
coordinates of all the clusters in their sample to our ACS mosaic frame using the GEOXYTRAN task in IRAF, and we matched sources
which were within 1 pixels from a cluster in our sample, which had
photometry in F435W (
kpc of M 51 using HST NICMOS and WFPC2 data. We calculated the transformation
between a mosaic of the F555W WFPC2 images and the ACS mosaic
image with the GEOMAP task in IRAF, by identifying 10 sources by eye
that were clearly visible in both data sets. We then transformed the
coordinates of all the clusters in their sample to our ACS mosaic frame using the GEOXYTRAN task in IRAF, and we matched sources
which were within 1 pixels from a cluster in our sample, which had
photometry in F435W (![]() B), F555W (
B), F555W (![]() V) and F814W (
V) and F814W (![]() I) in both data sets and which had a measured radius on the
WFPC2 data
I) in both data sets and which had a measured radius on the
WFPC2 data
![]() pc. This resulted in 271 matched
clusters, of which a few will be mismatched due to the uncertainties
in the transformation and most importantly, geometric distortion of
the WFPC2 images.
pc. This resulted in 271 matched
clusters, of which a few will be mismatched due to the uncertainties
in the transformation and most importantly, geometric distortion of
the WFPC2 images.
For these 271 clusters we compared the ![]() and
and ![]() colours of B05
with our results, after we removed our filter dependent infinity
corrections and Galactic foreground extinction corrections, since
these were constant for the photometry of B05. In
Fig. 11 we plot the difference between the
ACS and WFPC2 colours versus the ACS colour. For the mean
differences we find:
colours of B05
with our results, after we removed our filter dependent infinity
corrections and Galactic foreground extinction corrections, since
these were constant for the photometry of B05. In
Fig. 11 we plot the difference between the
ACS and WFPC2 colours versus the ACS colour. For the mean
differences we find:
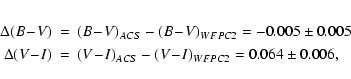
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{7511f27.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg113.gif) |
Figure 11: The differences between the colours of clusters matched between our ACS dataset and the WFPC2 dataset of Bastian et al. (2005), versus the colour in the ACS dataset.The dashed lines show a difference of 0 as a reference for the eye. |
| Open with DEXTER | |
We also compared the effective radii of the 271 matched clusters on
the F555W image. In Fig. 12 we show the
difference between the ACS and WFPC2 radius versus the ACS radius. No clear trend is visible, except that the average ACS radius of the clusters is slightly smaller than the WFPC2 radius.
The mean difference between the ACS and WFPC2 radius is
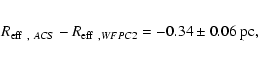
Now that we have selected a sample of clusters with accurate radii, we will study the distribution of their radii and possible dependencies between radius, background region and colour in this section. Possible correlations between radius and luminosity, mass and galactocentric distance will be the subject of the next section.
We show the effective radius distribution![]() of our sample
of 1284 clusters with linear bins in Fig. 13 and with logarithmic bins in Fig. 14. In both figures we plot the radius distributions for cluster
in the low and high background region separately. We see that the
radius distribution peaks around 1-2 pc and then drops to a maximum
radius of
of our sample
of 1284 clusters with linear bins in Fig. 13 and with logarithmic bins in Fig. 14. In both figures we plot the radius distributions for cluster
in the low and high background region separately. We see that the
radius distribution peaks around 1-2 pc and then drops to a maximum
radius of ![]() 10 pc. In the remainder of this section we will first
focus on the slope of the radius distribution at
10 pc. In the remainder of this section we will first
focus on the slope of the radius distribution at
![]() pc and then
focus on the location of the peak.
pc and then
focus on the location of the peak.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{7511f28.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg118.gif) |
Figure 12: The differences between the effective radii of the clusters matched between our ACS dataset and the WFPC2 dataset of Bastian et al. (2005), versus the effective radius in the ACS dataset. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{7511f29.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg119.gif) |
Figure 13: The effective radius distribution of the total sample of 1284 clusters, measured on the F435W image, using linear radius bins (solid line). Also shown are the radius distribution of only the sources in the low background region (dotted line) and the sources in the high background region (dashed line). For better readability, only the (Poissonian) error bars of the total sample are shown. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{7511f30.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg120.gif) |
Figure 14: The effective radius distribution of the total sample of 1284 clusters, measured on the F435W image, using logarithmic radius bins (solid line). Also shown are the radius distribution of only the sources in the low background region (dotted line) and the sources in the high background region (dashed line). For better readability, only the (Poissonian) error bars of the total sample are shown. For comparison we also show a power law with a slope of -2.3, typical for a fractal radius distribution of star-forming gas clouds, and a slope of -1.2 as determined by B05 for the radius distribution of 407 star clusters in M 51 with WFPC2 data. |
| Open with DEXTER | |
It has been observed that the mass distributions of both
star-forming clouds (Fukui et al. 2001; Brand & Wouterloot 1995; Solomon et al. 1987; Harris & Pudritz 1994; Sanders et al. 1985; Elmegreen & Falgarone 1996) and star clusters (de Grijs et al. 2003; Zhang & Fall 1999; Ashman & Zepf 2001; Hunter et al. 2003; Bik et al. 2003) can be approximated by power laws of the
form
![]() ,
with the index
,
with the index ![]() in
the range of 1.5-2.0. Star-forming clouds also show a power-law
radius distribution of the form
in
the range of 1.5-2.0. Star-forming clouds also show a power-law
radius distribution of the form
![]() (Harris & Pudritz 1994; Elmegreen & Falgarone 1996). For the clouds,
the power-law mass and radius distributions are consistent with the
clouds having a fractal structure with a fractal dimension of 2.3
(Mandelbrot 1983; Elmegreen & Elmegreen 2001). Since the mass distribution of
clusters is similar to the mass distribution of clouds, one might
naively expect the radius distributions also to be similar. We
plotted the radius distribution of star clusters in M 51 in
Fig. 14, using logarithmic bins. In
this figure a power law would be a straight line. We plotted two lines
with a slope of -2.3 and -1.2. The first slope is consistent with
the power-law distribution of the form
(Harris & Pudritz 1994; Elmegreen & Falgarone 1996). For the clouds,
the power-law mass and radius distributions are consistent with the
clouds having a fractal structure with a fractal dimension of 2.3
(Mandelbrot 1983; Elmegreen & Elmegreen 2001). Since the mass distribution of
clusters is similar to the mass distribution of clouds, one might
naively expect the radius distributions also to be similar. We
plotted the radius distribution of star clusters in M 51 in
Fig. 14, using logarithmic bins. In
this figure a power law would be a straight line. We plotted two lines
with a slope of -2.3 and -1.2. The first slope is consistent with
the power-law distribution of the form
![]() or
or
![]() ,
observed
for star-forming gas clouds on every length scale (down to the
smallest scales of
,
observed
for star-forming gas clouds on every length scale (down to the
smallest scales of ![]() 0.1 pc). We see in Fig. 14 that the radius distribution of the clusters in
M 51 between
0.1 pc). We see in Fig. 14 that the radius distribution of the clusters in
M 51 between ![]() 3 and
3 and ![]() 10 pc can not be approximated by
the same power law as the one for the star-forming gas
clouds
10 pc can not be approximated by
the same power law as the one for the star-forming gas
clouds![]() .
.
The slope of -1.2, indicated in Fig. 14, is consistent with the power-law distribution of
![]() ,
found by B05 for 407 clusters between 2-15 pc
in M 51 using WFPC2 data. Although the slope of our observed radius
distribution in the range
,
found by B05 for 407 clusters between 2-15 pc
in M 51 using WFPC2 data. Although the slope of our observed radius
distribution in the range ![]() 3-6 pc is similar to the slope
observed by B05, our observed radius distribution is considerably
steeper at larger radii. However, we note that we used a larger
sample of clusters, measured at twice the resolution and which was
checked by visual inspection for contaminants and blends. The cluster
sample of B05 is therefore expected to have a larger fraction of
contaminants and blends than the current sample. We note however,
that the current sample is still biased against clusters in crowded
regions, but for the remainder of this study we assume that the
current sample is representative of the entire star cluster
population of M 51.
3-6 pc is similar to the slope
observed by B05, our observed radius distribution is considerably
steeper at larger radii. However, we note that we used a larger
sample of clusters, measured at twice the resolution and which was
checked by visual inspection for contaminants and blends. The cluster
sample of B05 is therefore expected to have a larger fraction of
contaminants and blends than the current sample. We note however,
that the current sample is still biased against clusters in crowded
regions, but for the remainder of this study we assume that the
current sample is representative of the entire star cluster
population of M 51.
Figure 14 shows that the radius distribution of star clusters in M 51 is not consistent with a fractal structure. This suggests that after the formation of the clusters from a fractal gas, their radii have changed in a non-uniform way. Unfortunately, at the small radius end of the distribution a possible bias against small clusters can not be completely ruled out, since in a fractal gas the smallest clusters are expected to form in groups closest together. These small clusters could have been rejected from our sample by the close neighbour criterion (Sect. 5). Without this criterion, however, our sample would also be biased against small clusters due to blends. This bias is not expected at the large radius end of the distribution, where the radius distribution of star clusters in M 51 is clearly not consistent with a fractal distribution.
The picture in which the radii of the clusters change shortly after their formation is consistent with various suggested explanations for the lack of the mass-radius relation of clusters (see Sect. 8.2). One possible explanation is that interactions between young star clusters and gas clouds lead to dynamical heating and therefore expansion of the clusters (e.g. Gieles et al. 2006b). This expansion will be strongest for the largest and least concentrated clusters because of their lower density and it will therefore make an initial power-law distribution more shallow. Although cluster-cloud interactions are probably part of the explanation for the lacking mass-radius relation, on its own this scenario fails to explain the expansion of the smallest clusters, which is necessary to weaken the mass-radius relation.
Another suggested explanation for the weak or missing mass-radius relation of clusters is a star formation efficiency (SFE) which scales with the mass of the clouds (Ashman & Zepf 2001) combined with the early residual gas loss from clusters (Geyer & Burkert 2001; Hills 1980; Goodwin & Bastian 2006). In this scenario the forming clusters initially follow the same mass-radius relation as the clouds. However, the removal of binding energy will lead to the expansion of preferably small clusters, since they form from low-mass clouds which lose relatively more residual gas. On its own, however, this explanation will lead to a steeper radius distribution of clusters compared to clouds, i.e. with a slope <-2.3, contrary to what we observe (Fig. 14).
Although Fig. 14 suggests that the radii of the clusters have changed shortly after their formation, our radius distribution is consistent with neither scenario. Perhaps a scenario including a combination of stochastic cluster-cloud interactions, expansion due to residual gas expulsion and a mass-dependent SFE can change the radius distribution in a way that is more consistent with the observed radius distribution. However, a fundamental problem of the missing mass-radius relation of clusters is that there are also high-mass clusters with small radii. The existence of these clusters can not be explained by the scenarios mentioned so far, which all rely on the expansion of clusters. Therefore, we need better scenarios and more insight in cluster formation theory to account for the differences in the radius distributions between clouds and clusters.
In Fig. 13 we see that there is a peak
in the radius distribution around ![]() 1.5 pc. If we assume that
the star clusters in M 51 formed from a fractal gas, this is consistent
with the suggestion of the expansion of preferably the smallest
clusters, i.e. cluster with
1.5 pc. If we assume that
the star clusters in M 51 formed from a fractal gas, this is consistent
with the suggestion of the expansion of preferably the smallest
clusters, i.e. cluster with
![]() pc which expanded to radii >1.5 pc.
pc which expanded to radii >1.5 pc.
Figures 13 and 14 also show that the radius distribution of
clusters in the low background region (the dotted lines) shows a more
pronounced turnover, i.e. there are relatively fewer small clusters in
the low background region compared to the high background region.
This suggests that generally the smallest clusters are mainly found in
the high background regions (e.g. inside the spiral arms). The
medians also show this trend: while the median
![]() of our complete
cluster sample is 2.1 pc, it is 1.9 pc for the high background and
2.7 pc for the low background region.
of our complete
cluster sample is 2.1 pc, it is 1.9 pc for the high background and
2.7 pc for the low background region.
We stress that it is not very likely that this trend is biased due to selection effects, since we applied magnitude limits that are brighter than the 90% completeness limits in the high background region (Sect. 4), and visual inspection removed most background galaxies in the low background region and possible blends in the high background region. Also, the more compact clusters are easier to detect, so it is not likely that there is a selection effect against small clusters in the low background regions.
Figure 15 shows the ![]() colour distribution
of clusters in the low and high background region. The high
background region has a higher fraction of blue clusters (
colour distribution
of clusters in the low and high background region. The high
background region has a higher fraction of blue clusters (
![]() )
than the low background region. This fraction is expected to
be stronger when extinction is taken into account, since clusters in
the high background region are likely more strongly reddened than
clusters in the low background region.
)
than the low background region. This fraction is expected to
be stronger when extinction is taken into account, since clusters in
the high background region are likely more strongly reddened than
clusters in the low background region.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{7511f31.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg126.gif) |
Figure 15:
The normalized |
| Open with DEXTER | |
Figures 14 and 15
suggest that there is a relation between
![]() and colour. In
Fig. 16 we show the radius
distribution for 2 equal-sized samples with
and colour. In
Fig. 16 we show the radius
distribution for 2 equal-sized samples with
![]() ("blue'') and
("blue'') and
![]() ("red''). We indeed see a shift in the radius
distribution towards larger radii for our red subsample. The median
value follows this shift: for the blue sample the median
("red''). We indeed see a shift in the radius
distribution towards larger radii for our red subsample. The median
value follows this shift: for the blue sample the median
![]() is
1.8 pc, while for the red sample it is 2.5 pc. In
Fig. 17 we show the median
is
1.8 pc, while for the red sample it is 2.5 pc. In
Fig. 17 we show the median
![]() versus
versus ![]() and
and ![]() colour. Because all bins contain an equal number of
clusters, size-of-sample effects are excluded. Both for low and high
background regions and
colour. Because all bins contain an equal number of
clusters, size-of-sample effects are excluded. Both for low and high
background regions and ![]() and
and ![]() colours we see a similar trend of
a median
colours we see a similar trend of
a median
![]() increasing with colour, although the scatter is high
and the trend is strongest for
increasing with colour, although the scatter is high
and the trend is strongest for ![]() colours.
colours.
Therefore, the observed difference in the radius distribution between
low and high background regions can be explained by a higher fraction
of red clusters in low background regions, which are generally
slightly larger. For young clusters, colours become redder with age.
This is consistent with a larger fraction of blue clusters in high
background regions, since these regions follow the high density spiral
arms, where most clusters are expected to form. If the observed
spread in colour is also a spread in the age of the clusters, the
slight increase in median
![]() with colour in
Fig. 17 suggests a dynamical evolution of the
clusters with age. The fact that the increase in radius is
strongest for
with colour in
Fig. 17 suggests a dynamical evolution of the
clusters with age. The fact that the increase in radius is
strongest for ![]() colours supports this suggestion, because
colours supports this suggestion, because ![]() is
more sensitive to age than
is
more sensitive to age than ![]() .
.
In this hypothesis, newly formed clusters in spiral arms are generally
small, reflecting the high pressure and density of their parental gas
clouds. In the subsequent early evolution of the clusters an increase
in size is expected, likely due to dynamical heating from
cluster-cluster and cluster-cloud encounters and due to the removal of
binding energy when the clusters lose mass (Goodwin 1997; Boily & Kroupa 2003). Clusters also expand when moving out of the spiral arm, due
to tidal forces from the spiral density wave (Gieles et al. 2007). This
hypothesis is consistent with the low background regions containing a
relatively larger fraction of older, more evolved clusters with
therefore slightly larger radii![]() .
.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{7511f32.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg129.gif) |
Figure 16:
The effective radius distribution split in a sample with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{7511f33.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg130.gif) |
Figure 17:
The median
|
| Open with DEXTER | |
If clusters expand, they will do this on a dynamical (crossing)
timescale of a few Myr (Lada & Lada 2003). The typical timescale for a cluster
to move from the high to low background region will be about half the
time between 2 spiral arm passages, which for a 2-armed spiral galaxy
is
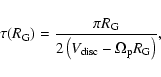 |
(4) |
We have used the 271 matched clusters with an age estimate from B05 to
search for a correlation between age and
![]() .
These clusters show a
weak relation between radius and age of the form
.
These clusters show a
weak relation between radius and age of the form
![]() ,
with a large scatter. This is consistent
with the relation Lee et al. (2005) observe for clusters in M 51 using
WFPC2 data (best fit slope of
,
with a large scatter. This is consistent
with the relation Lee et al. (2005) observe for clusters in M 51 using
WFPC2 data (best fit slope of
![]() ). Figure 18 shows the radius distribution for the matched
clusters, split in two equal-sized samples with log (age) < 7.5 and
log (age) > 7.5. The distributions are not very different, although a
weak trend is visible since the older sample has slightly more large
clusters than the younger sample. However, these differences are
within the statistical errors and also a K-S test did not give a
significant result (p = 0.126). The median
). Figure 18 shows the radius distribution for the matched
clusters, split in two equal-sized samples with log (age) < 7.5 and
log (age) > 7.5. The distributions are not very different, although a
weak trend is visible since the older sample has slightly more large
clusters than the younger sample. However, these differences are
within the statistical errors and also a K-S test did not give a
significant result (p = 0.126). The median
![]() follows a similar
trend: the median
follows a similar
trend: the median
![]() is 1.8 and 2.2 pc for the younger and older
population, respectively.
is 1.8 and 2.2 pc for the younger and older
population, respectively.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{7511f34.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg140.gif) |
Figure 18: The radius distribution of the 271 matched clusters for which we have age estimates from B05, split in a sample with log (age) > 7.5 and log (age) < 7.5. |
| Open with DEXTER | |
We compared the mean and median
![]() of our cluster sample to other
work, but we note that these comparisons can easily be biased by
differences in the lower limits of the radius and other selection
criteria. The mean and median
of our cluster sample to other
work, but we note that these comparisons can easily be biased by
differences in the lower limits of the radius and other selection
criteria. The mean and median
![]() of our total sample are 2.5 and
2.1 pc, respectively. The mean and median
of our total sample are 2.5 and
2.1 pc, respectively. The mean and median
![]() of the 70 GC
candidates in our sample are
of the 70 GC
candidates in our sample are ![]() and 2.4 pc, respectively,
where 0.4 is the standard error of the mean (the standard deviation
is 3.4 pc). If we restrict ourselves to clusters in the low
background regions, the mean and median
and 2.4 pc, respectively,
where 0.4 is the standard error of the mean (the standard deviation
is 3.4 pc). If we restrict ourselves to clusters in the low
background regions, the mean and median
![]() are 2.9 and
2.7 pc, respectively. This last value is the same as the mean
are 2.9 and
2.7 pc, respectively. This last value is the same as the mean
![]() Jordán et al. (2005) found for thousands of GCs observed in 100 early-type
galaxies of the ACS Virgo Cluster Survey.
Larsen (2004) studied the effective radii of stellar clusters in 18 nearby spiral galaxies using HST WFPC2 images, and he found a
mean
Jordán et al. (2005) found for thousands of GCs observed in 100 early-type
galaxies of the ACS Virgo Cluster Survey.
Larsen (2004) studied the effective radii of stellar clusters in 18 nearby spiral galaxies using HST WFPC2 images, and he found a
mean
![]() of
of
![]() pc. Lee et al. (2005) studied the radii of
clusters in M 51 using HST WFPC2 observations covering parts of the
mosaic image used in our study, and they found a mean and median
pc. Lee et al. (2005) studied the radii of
clusters in M 51 using HST WFPC2 observations covering parts of the
mosaic image used in our study, and they found a mean and median
![]() of 3.7 and 3.1 pc, respectively. The ACS camera has about
twice the resolution of the WFPC2 camera and can therefore detect
small clusters more efficiently. This could explain why our mean and
median
of 3.7 and 3.1 pc, respectively. The ACS camera has about
twice the resolution of the WFPC2 camera and can therefore detect
small clusters more efficiently. This could explain why our mean and
median
![]() are smaller than the values from Lee et al. (2005). The
median
are smaller than the values from Lee et al. (2005). The
median
![]() for Galactic GCs is
for Galactic GCs is ![]() 3.3 pc (Harris 1996), very
similar to the value Barmby et al. (2006) found for their sample of blue
clusters in M101, namely 3.2 pc. We see that the mean and median
values of
3.3 pc (Harris 1996), very
similar to the value Barmby et al. (2006) found for their sample of blue
clusters in M101, namely 3.2 pc. We see that the mean and median
values of
![]() of our cluster sample are somewhat smaller than what
is generally found, although the differences become smaller when we
restrict ourselves to the clusters in the low background regions or
the GC candidates.
of our cluster sample are somewhat smaller than what
is generally found, although the differences become smaller when we
restrict ourselves to the clusters in the low background regions or
the GC candidates.
In this section we will combine the effective radii of the clusters
with other parameters, such as their galactocentric distance,
luminosity and for some clusters their mass. Correlations between
these parameters for clusters in M 51 have already been studied by B05,
using WFPC2 data of the inner 5 kpc of the disc of M 51. We again
search for correlations, but now using the ACS data out to a
galactocentric distance of ![]() 10 kpc.
10 kpc.
For Galactic GCs there is a relation between the distance to the
Galactic centre,
![]() ,
and the half-light diameter D0.5, of the form
,
and the half-light diameter D0.5, of the form
![]() (Van den Bergh et al. 1991). This same trend is observed for the core radii
of old clusters in the LMC (Mateo 1987; Hodge 1962) and for the sizes
of old GCs in NGC 5128 (Hesser et al. 1984). However, these cluster
populations are all old and mainly residing in the outer regions or
halo of their host galaxies, while we are studying a population of
mostly young clusters in a disc.
(Van den Bergh et al. 1991). This same trend is observed for the core radii
of old clusters in the LMC (Mateo 1987; Hodge 1962) and for the sizes
of old GCs in NGC 5128 (Hesser et al. 1984). However, these cluster
populations are all old and mainly residing in the outer regions or
halo of their host galaxies, while we are studying a population of
mostly young clusters in a disc.
For the GCs, different explanations for the observed relation between
radius and galactocentric distance have been suggested. One
possibility could be that the sizes of GCs reflect the densities of
the gas clouds from which they formed, i.e. compact GCs
preferentially formed from dense gas clouds near the centres of
galaxies, while larger GCs preferentially formed in the less dense
halo regions (Van den Bergh et al. 1991).
Harris & Pudritz (1994) use the
Ebert-Bonnor relations (Ebert 1955; Bonnor 1956) to show that
Another possible explanation for the observed relation between radius
and galactocentric distance for GCs is more evolutionary in nature.
It assumes that the GCs have reached tidal equilibrium with their host
galaxy. The tidal radius of a cluster in an external logarithmic
potential field scales as:
In Fig. 19 we show the median
![]() versus
the galactocentric distance for the clusters in M 51. There seems to
be a slight increase in
versus
the galactocentric distance for the clusters in M 51. There seems to
be a slight increase in
![]() with distance, but the scatter is large
(reflected in the large error bars). We have tried to fit a function
of the form
with distance, but the scatter is large
(reflected in the large error bars). We have tried to fit a function
of the form
 |
(8) |
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{7511f35.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg158.gif) |
Figure 19:
The median
|
| Open with DEXTER | |
The radius distribution changes for different galactocentric distance bins, as shown in Fig. 20. The radius distribution close to the centre of M 51 (distance <3 kpc) is shifted towards smaller radii compared to the radius distributions at larger distances. A K-S test confirmed that it is unlikely (p < 0.001) that the radius distribution for distance <3 kpc and >5.5 kpc are drawn from the same parent distribution.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{7511f36.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg159.gif) |
Figure 20:
The effective radius distributions for three different
galactocentric distance regions in M 51. The solid line shows clusters
close to the centre of M 51 (distance < 3 kpc), the dotted line shows
clusters at intermediate distances (3 < distance < 5.5 kpc) and the
dashed line shows clusters at large galactocentric distances
(>5.5 kpc). The changes in the distributions are consistent with a
slight increase in
|
| Open with DEXTER | |
Since we observe a relation between
![]() and color
(Fig. 17), any increase in radius with
galactocentric distance could be the result of an increase in colour
with galactocentric distance. In Fig. 21 we
show
and color
(Fig. 17), any increase in radius with
galactocentric distance could be the result of an increase in colour
with galactocentric distance. In Fig. 21 we
show ![]() versus galactocentric distance for the 1284 clusters that
were also shown in Fig. 19. No obvious
trend is visible, which is expected since at all galactocentric radii
we encounter clusters in both arm and interarm regions. The arm
regions are mostly high background regions and will therefore contain
mostly blue clusters, while the interarm regions are mostly low
background regions and will therefore contain mostly red clusters
(Fig. 15). The observed
versus galactocentric distance for the 1284 clusters that
were also shown in Fig. 19. No obvious
trend is visible, which is expected since at all galactocentric radii
we encounter clusters in both arm and interarm regions. The arm
regions are mostly high background regions and will therefore contain
mostly blue clusters, while the interarm regions are mostly low
background regions and will therefore contain mostly red clusters
(Fig. 15). The observed
![]() is therefore not likely a result of the
relation between radius and colour.
is therefore not likely a result of the
relation between radius and colour.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{7511f37.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg160.gif) |
Figure 21:
The median |
| Open with DEXTER | |
B05 did not find a relation between
![]() and
and
![]() for
for
![]() kpc. For
kpc. For
![]() kpc we
find a weak relation, but this relation is considerably weaker than
the observed relations for old GCs. Therefore, the clusters we
observe in the disc of M 51 are either forming under different
conditions than the GCs, or the observed relation for GCs emerged
during their longer dynamical evolution. We consider the first
explanation to be the most likely one, since GCs probably formed
outside a spiral disc, in regions where the surface pressure of their
parental clouds decreased with distance (Eq. (6)). For
clusters in spiral arms it is not expected that the surface pressure
scales in a similar way with distance. Likely, the higher pressure
inside spiral arms decreases less strongly with galactocentric
distance. Rix & Rieke (1993) find that the arm/interarm density
contrast for M 51 increases with galactocentric distance, consistent
with this picture. In this case
a strong radius-distance correlation for the clusters is not expected.
kpc we
find a weak relation, but this relation is considerably weaker than
the observed relations for old GCs. Therefore, the clusters we
observe in the disc of M 51 are either forming under different
conditions than the GCs, or the observed relation for GCs emerged
during their longer dynamical evolution. We consider the first
explanation to be the most likely one, since GCs probably formed
outside a spiral disc, in regions where the surface pressure of their
parental clouds decreased with distance (Eq. (6)). For
clusters in spiral arms it is not expected that the surface pressure
scales in a similar way with distance. Likely, the higher pressure
inside spiral arms decreases less strongly with galactocentric
distance. Rix & Rieke (1993) find that the arm/interarm density
contrast for M 51 increases with galactocentric distance, consistent
with this picture. In this case
a strong radius-distance correlation for the clusters is not expected.
One of the most peculiar properties of star clusters is the lack of a
clear relation between their mass and radius. Star clusters are
believed to form from Giant Molecular Clouds (GMCs), for which a clear
relation between mass and radius is observed. Larson (1981) finds
that the internal velocity dispersion of GMCs, ![]() ,
scales with
their size,
,
scales with
their size,
![]() ,
as
,
as
![]() .
Assuming the GMCs are in virial
equilibrium, this leads to a mass-radius relation of the form
.
Assuming the GMCs are in virial
equilibrium, this leads to a mass-radius relation of the form
![]() .
Also assuming
virial equilibrium, Solomon et al. (1987) find
.
Also assuming
virial equilibrium, Solomon et al. (1987) find
![]() .
These observations are consistent with GMCs having a constant surface
density (
.
These observations are consistent with GMCs having a constant surface
density (
![]() ).
).
From the Ebert-Bonnor relations for pressure bounded,
self-gravitating, isothermal spheres (Ebert 1955; Bonnor 1956), both
Eq. (5) as well as:
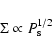 |
(9) |
When clusters emerge from GMCs, the mass-radius relation appears to be
erased, indicating that high-mass clusters have higher stellar
densities than low-mass clusters. A constant stellar density
would predict
![]() ,
which is not
observed. Zepf et al. (1999) find
,
which is not
observed. Zepf et al. (1999) find
![]() for young
clusters in NGC 3256, where L is the luminosity of the cluster which
scales directly with the mass (since their cluster sample suggests
that colour is independent of luminosity and therefore they assume
that the mass-to-light ratio is mostly independent on luminosity).
For clusters in a sample of (non-interacting) spiral galaxies,
Larsen (2004) finds
for young
clusters in NGC 3256, where L is the luminosity of the cluster which
scales directly with the mass (since their cluster sample suggests
that colour is independent of luminosity and therefore they assume
that the mass-to-light ratio is mostly independent on luminosity).
For clusters in a sample of (non-interacting) spiral galaxies,
Larsen (2004) finds
![]() .
The effective radius of the old Galactic GCs also does not
seem to correlate with their luminosity and thus their mass
(Van den Bergh et al. 1991). Mackey & Gilmore (2003) report that for a sample of 53 rich LMC clusters, there seems to be no strong correlation between
their mass and core radius, either.
.
The effective radius of the old Galactic GCs also does not
seem to correlate with their luminosity and thus their mass
(Van den Bergh et al. 1991). Mackey & Gilmore (2003) report that for a sample of 53 rich LMC clusters, there seems to be no strong correlation between
their mass and core radius, either.
In Fig. 22 we show
![]() versus
magnitude in F435W for the M 51 clusters, split in the low and
high background region. For these clusters we do not have mass
estimates. However, it is expected that the age range for the largest
fraction of this cluster sample is not very large, because most
clusters are blue and located in the spiral arms. Many clusters are
therefore expected to have similar mass-to-light ratios and therefore
any mass-radius relation should also be visible as a relation between
magnitude and radius. Figure 22 shows
that clusters in the high background regions show a slight trend of
radius decreasing with luminosity. Clusters in the low background
regions show a less obvious trend, although the median
versus
magnitude in F435W for the M 51 clusters, split in the low and
high background region. For these clusters we do not have mass
estimates. However, it is expected that the age range for the largest
fraction of this cluster sample is not very large, because most
clusters are blue and located in the spiral arms. Many clusters are
therefore expected to have similar mass-to-light ratios and therefore
any mass-radius relation should also be visible as a relation between
magnitude and radius. Figure 22 shows
that clusters in the high background regions show a slight trend of
radius decreasing with luminosity. Clusters in the low background
regions show a less obvious trend, although the median
![]() of the
brightest bin is considerably larger, especially compared to the
brightest bin in the high background region. A fit on the unbinned
data points of the form
of the
brightest bin is considerably larger, especially compared to the
brightest bin in the high background region. A fit on the unbinned
data points of the form
![]() ,
with L the luminosity
in the F435W passband, resulted in
,
with L the luminosity
in the F435W passband, resulted in
![]() and
and
![]() for the low and high background region, respectively.
We verified that applying the size-dependent aperture correction of
Eq. (1), instead of the constant aperture correction for a
3 pc source (Sect. 2.5), would not change this result
considerably (
for the low and high background region, respectively.
We verified that applying the size-dependent aperture correction of
Eq. (1), instead of the constant aperture correction for a
3 pc source (Sect. 2.5), would not change this result
considerably (
![]() and
and
![]() for the low and
high background, respectively).
for the low and
high background, respectively).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{7511f38.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg177.gif) |
Figure 22:
The median
|
| Open with DEXTER | |
It is not likely that this observed differences in power-law
indices is a bias due to our detection limits, since we use magnitude
limits (Sect. 5.1) brighter than the 90%
completeness limits for ![]() 8 pc sources in the high background
regions. Due to the lack of age estimates of these clusters, there is
a degeneracy between age and mass. Therefore it is not certain if any
evolution in
8 pc sources in the high background
regions. Due to the lack of age estimates of these clusters, there is
a degeneracy between age and mass. Therefore it is not certain if any
evolution in
![]() with luminosity is mainly caused by age effects,
mass effects, or a combination of both. More measurements of the ages and masses of
clusters which also have accurate radii estimates are necessary to
break this age/mass degeneracy (e.g. through additional U-band
imaging).
with luminosity is mainly caused by age effects,
mass effects, or a combination of both. More measurements of the ages and masses of
clusters which also have accurate radii estimates are necessary to
break this age/mass degeneracy (e.g. through additional U-band
imaging).
Using the 271 clusters that were matched with the cluster sample of
B05 and for which we therefore have mass estimates, we show
![]() versus mass in Fig. 23. No apparent
relation is visible. This sample is too small to make a distinction
between clusters in low and high background regions, since it mostly
covers the inner high background regions of M 51.
versus mass in Fig. 23. No apparent
relation is visible. This sample is too small to make a distinction
between clusters in low and high background regions, since it mostly
covers the inner high background regions of M 51.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{7511f39.ps}
\end{figure}](/articles/aa/full/2007/27/aa7511-07/Timg178.gif) |
Figure 23:
|
| Open with DEXTER | |
We conclude that we do not find evidence for any direct relation between mass and radius of the clusters, although we find weak relations between luminosity and radius, changing with background region. The suggested explanations for a lacking mass-radius relation were already mentioned in Sect. 7.1, but we stress again that none of these scenarios are currently capable of explaining the observed differences in the radius distributions between clouds and clusters.
We have used the HST ACS mosaic image of M 51 to detect 7698, 6846
and 5024 stellar clusters across the spiral disc in F435W, F555W and F814W respectively, based on effective radius (
![]() )
measurements. We presented the dataset and described the methods used
to select our cluster sample, including tests with artificial clusters
to show the accuracy, limits and robustness of our methods. We
divided the data in 3 regions with respectively a low, intermediate
and high background, where the high background traces the spiral arms.
We selected a sample of 1284 clusters with the most accurate radius
estimates to study the radius distribution and relations between
radius, mass, luminosity, galactocentric distance and background
region. From these studies we conclude the following:
)
measurements. We presented the dataset and described the methods used
to select our cluster sample, including tests with artificial clusters
to show the accuracy, limits and robustness of our methods. We
divided the data in 3 regions with respectively a low, intermediate
and high background, where the high background traces the spiral arms.
We selected a sample of 1284 clusters with the most accurate radius
estimates to study the radius distribution and relations between
radius, mass, luminosity, galactocentric distance and background
region. From these studies we conclude the following:
Acknowledgements
We thank Peter Anders for useful discussions, tips and comments. We also thank Marcelo Mora at ESO/Garching for discussions and for kindly providing us with the empirical PSFs. We would like to thank Max Mutchler, Richard Hook and Andrew Fruchter for discussions regarding the effects of the drizzle routine on the PSF. We thank Narae Hwang for kindly providing us the list of faint fuzzies around NGC 5195.