- ... M 51
![[*]](/icons/foot_motif.gif)
- Based
on observations made with the NASA/ESA Hubble Space Telescope,
obtained from the data archive at the Space Telescope Institute. STScI
is operated by the association of Universities for Research in
Astronomy, Inc., under the NASA contract NAS 5-26555.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Ashman & Zepf (2001)
![[*]](/icons/foot_motif.gif)
- Fitting a function of the form
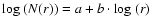 results in
results in
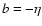 .
However, using logarithmic binning, one fits
.
However, using logarithmic binning, one fits
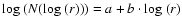 ,
in which
,
in which
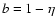 .
This extra term +1 can easily cause confusion when
comparing different distributions. Also see B05 and
Elmegreen & Falgarone (1996).
.
This extra term +1 can easily cause confusion when
comparing different distributions. Also see B05 and
Elmegreen & Falgarone (1996).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... IRAF
![[*]](/icons/foot_motif.gif)
- The Image Reduction and Analysis Facility
(IRAF) is distributed by the National Optical Astronomy Observatories,
which are operated by the Association of Universities for Research in
Astronomy, Inc., under cooperative agreement with the National Science
Foundation.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... distribution
![[*]](/icons/foot_motif.gif)
- Strictly speaking,
the term distribution refers to linear intervals, i.e.
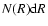 ,
and the term function refers to logarithmic intervals,
i.e.
,
and the term function refers to logarithmic intervals,
i.e.
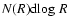 .
In this work, however, we will not make
this distinction. We will only use the term distribution and we
will specify the type of interval used when necessary.
.
In this work, however, we will not make
this distinction. We will only use the term distribution and we
will specify the type of interval used when necessary.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
clouds
![[*]](/icons/foot_motif.gif)
- Between 0.5 and
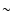 10 pc a log-normal
distribution provides a reasonable fit to the data (not shown here).
10 pc a log-normal
distribution provides a reasonable fit to the data (not shown here).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... radii
![[*]](/icons/foot_motif.gif)
- If one would actually quantify any
age-radius relation one needs to be aware of possible biases, due to a
slight mass-radius relation or size-of-sample effects. E.g. at older
ages, the low-mass clusters will first fade below the detection limit,
so any observed age-radius relation could then result from a possible
mass-radius relation. Also, if one would let the absolute age
intervals increase with age (i.e. logarithmic binning), one would
sample the radius distribution up to larger radii for older ages and
the average radius would seem to increase with age.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.