A&A 469, 387-404 (2007)
DOI: 10.1051/0004-6361:20066017
P. Tisserand1,![]() -
L. Le Guillou1,
-
L. Le Guillou1,![]() -
C. Afonso1,
-
C. Afonso1,![]() -
J. N. Albert2 -
J. Andersen5 -
R. Ansari2 -
É. Aubourg1,
-
J. N. Albert2 -
J. Andersen5 -
R. Ansari2 -
É. Aubourg1,![]() -
P. Bareyre1 -
J. P. Beaulieu3 -
X. Charlot1 -
C. Coutures1,3 -
R. Ferlet3 -
P. Fouqué7,8 -
J. F. Glicenstein1 -
B. Goldman1,
-
P. Bareyre1 -
J. P. Beaulieu3 -
X. Charlot1 -
C. Coutures1,3 -
R. Ferlet3 -
P. Fouqué7,8 -
J. F. Glicenstein1 -
B. Goldman1,![]() -
A. Gould6 -
D. Graff6,
-
A. Gould6 -
D. Graff6,![]() -
M. Gros1 -
J. Haissinski2 -
C. Hamadache1 -
J. de Kat1 -
T. Lasserre1 -
É. Lesquoy1,3 - C. Loup3 -
C. Magneville1 -
J. B. Marquette3 -
É. Maurice4 -
A. Maury8,
-
M. Gros1 -
J. Haissinski2 -
C. Hamadache1 -
J. de Kat1 -
T. Lasserre1 -
É. Lesquoy1,3 - C. Loup3 -
C. Magneville1 -
J. B. Marquette3 -
É. Maurice4 -
A. Maury8,![]() -
A. Milsztajn1 -
M. Moniez2 -
N. Palanque-Delabrouille1 -
O. Perdereau2 -
Y. R. Rahal2 -
J. Rich1 -
M. Spiro1 -
A. Vidal-Madjar3 -
L. Vigroux1,3 -
S. Zylberajch1
-
A. Milsztajn1 -
M. Moniez2 -
N. Palanque-Delabrouille1 -
O. Perdereau2 -
Y. R. Rahal2 -
J. Rich1 -
M. Spiro1 -
A. Vidal-Madjar3 -
L. Vigroux1,3 -
S. Zylberajch1
(The EROS-2 collaboration)
1 -
CEA, DSM, DAPNIA,
Centre d'Études de Saclay, 91191 Gif-sur-Yvette Cedex, France
2 -
Laboratoire de l'Accélérateur Linéaire,
IN2P3 CNRS, Université de Paris-Sud, 91405 Orsay Cedex, France
3 -
Institut d'Astrophysique de Paris,
UMR 7095 CNRS, Université Pierre & Marie Curie,
98 bis boulevard Arago, 75014 Paris, France
4 -
Observatoire de Marseille,
2 place Le Verrier, 13248 Marseille Cedex 04, France
5 -
The Niels Bohr Institute, Copenhagen University, Juliane Maries Vej 30,
2100 Copenhagen, Denmark
6 -
Department of Astronomy, Ohio State University, Columbus,
OH 43210, USA
7 -
Observatoire Midi-Pyrénées, Laboratoire d'Astrophysique (UMR 5572),
14 av. E. Belin, 31400 Toulouse, France
8 -
European Southern Observatory (ESO), Casilla 19001, Santiago 19, Chile
Received 11 July 2006 / Accepted 10 April 2007
Abstract
Aims. The EROS-2 project was designed to test the hypothesis that massive compact halo objects (the so-called "machos'') could be a major component of the dark matter halo of the Milky Way galaxy. To this end, EROS-2 monitored over 6.7 years
![]() stars in the Magellanic clouds for microlensing events caused by such objects.
stars in the Magellanic clouds for microlensing events caused by such objects.
Methods. In this work, we use only a subsample of
![]() bright stars spread over
bright stars spread over
![]() of the LMC and
of the LMC and
![]() of the SMC. The strategy of using only bright stars helps to discriminate against background events due to variable stars and allows a simple determination of the effects of source confusion (blending). The use of a large solid angle makes the survey relatively insensitive to effects that could make the optical depth strongly direction dependent.
of the SMC. The strategy of using only bright stars helps to discriminate against background events due to variable stars and allows a simple determination of the effects of source confusion (blending). The use of a large solid angle makes the survey relatively insensitive to effects that could make the optical depth strongly direction dependent.
Results. Using this sample of bright stars, only one candidate event was found, whereas ![]() 39 events would have been expected if the Halo were entirely populated by objects of mass
39 events would have been expected if the Halo were entirely populated by objects of mass
![]() .
Combined with the results of EROS-1, this implies that the optical depth toward the Large Magellanic Cloud (LMC) due to such lenses is
.
Combined with the results of EROS-1, this implies that the optical depth toward the Large Magellanic Cloud (LMC) due to such lenses is
![]() (95% CL), corresponding to a fraction of the halo mass of less than 8%. This optical depth is considerably less than that measured by the MACHO collaboration in the central region of the LMC. More generally, machos in the mass range
(95% CL), corresponding to a fraction of the halo mass of less than 8%. This optical depth is considerably less than that measured by the MACHO collaboration in the central region of the LMC. More generally, machos in the mass range
![]() are ruled out as the primary occupants of the Milky Way Halo.
are ruled out as the primary occupants of the Milky Way Halo.
Key words: Galaxy: halo - cosmology: dark matter - gravitational lensing
Since the proposal (Petrou 1981; Paczynski 1986) that dark matter in
the form of faint compact objects
(machos![]() )
could be found through
gravitational microlensing,
the EROS, MACHO, OGLE, MOA and SuperMACHO collaborations have
monitored millions of stars in the
Magellanic Clouds to search for microlensing events.
Such events would be due to
a lensing object passing near the line of sight
toward a background Magellanic star, causing a
transient magnification of the star's primary image
as well as creating a secondary image.
Neither the image separation nor the
image size are normally resolvable, so the only easily observable
effect during an event
is an apparent transient amplification of the star's flux.
The amplification is greater than a factor 1.34 if the
line of sight to the star passes within the lens's Einstein ring of
squared radius
)
could be found through
gravitational microlensing,
the EROS, MACHO, OGLE, MOA and SuperMACHO collaborations have
monitored millions of stars in the
Magellanic Clouds to search for microlensing events.
Such events would be due to
a lensing object passing near the line of sight
toward a background Magellanic star, causing a
transient magnification of the star's primary image
as well as creating a secondary image.
Neither the image separation nor the
image size are normally resolvable, so the only easily observable
effect during an event
is an apparent transient amplification of the star's flux.
The amplification is greater than a factor 1.34 if the
line of sight to the star passes within the lens's Einstein ring of
squared radius
![]() where
where ![]() is the distance
to the star and
is the distance
to the star and
![]() is the distance to the lens of mass M.
The optical depth for microlensing,
i.e. the probability that
at a given time a given star
is amplified by more than a factor 1.34, is
is the distance to the lens of mass M.
The optical depth for microlensing,
i.e. the probability that
at a given time a given star
is amplified by more than a factor 1.34, is
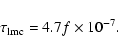 |
(2) |
Magellanic stars can also be lensed by non-halo
stars, either in the Magellanic Clouds or in the Milky Way
disk. Lensing by disk stars is expected to have
an optical depth of order 10-8 (Alcock et al. 2000b).
The optical depth for lensing by "self-lensing'', i.e. lensing
by stars in the Clouds,
is expected to range from ![]()
![]() in the
center of the LMC bar to
in the
center of the LMC bar to ![]()
![]() at
at ![]() from the bar (Mancini et al. 2004).
For the SMC, the self-lensing optical depth
is expected to be somewhat larger,
from the bar (Mancini et al. 2004).
For the SMC, the self-lensing optical depth
is expected to be somewhat larger, ![]()
![]() averaged over the central
averaged over the central
![]() (Graff & Gardiner 1999).
(Graff & Gardiner 1999).
Microlensing events are characterized by a timescale ![]() giving the time for the lens to travel a distance corresponding
to its Einstein radius,
giving the time for the lens to travel a distance corresponding
to its Einstein radius,
![]() where vt is the
lens's transverse velocity relative to the line of sight.
For high amplification events,
where vt is the
lens's transverse velocity relative to the line of sight.
For high amplification events,
![]() is the time over which the amplification is A>1.34.
Since
is the time over which the amplification is A>1.34.
Since ![]() is proportional to the square root of the
lens mass M, the mean
is proportional to the square root of the
lens mass M, the mean ![]() will scale like M1/2.
The S model has a 3-dimensional macho velocity dispersion
of
will scale like M1/2.
The S model has a 3-dimensional macho velocity dispersion
of
![]() and gives
and gives
Bennett (2005) argued that the MACHO optical depth should be reduced
to
![]() in order to take into account
contamination by variable stars. This paper made use of
the observation by the EROS collaboration (Tisserand 2004) of further
variability of one of the MACHO A candidates, indicating intrinsic stellar
variability.
The paper also noted that the spectrum of the MACHO B candidate MACHO-LMC-22 indicated that the source is
an active background galaxy,
as reported in Alcock et al. (2001b) where the event was eliminated
from the sample for studying high-mass lenses.
Using four MACHO A candidates whose microlensing nature was
confirmed by precision photometry and the one A candidate rejected
as a variable star,
Bennett (2005) performed a likelihood analysis to argue that
in order to take into account
contamination by variable stars. This paper made use of
the observation by the EROS collaboration (Tisserand 2004) of further
variability of one of the MACHO A candidates, indicating intrinsic stellar
variability.
The paper also noted that the spectrum of the MACHO B candidate MACHO-LMC-22 indicated that the source is
an active background galaxy,
as reported in Alcock et al. (2001b) where the event was eliminated
from the sample for studying high-mass lenses.
Using four MACHO A candidates whose microlensing nature was
confirmed by precision photometry and the one A candidate rejected
as a variable star,
Bennett (2005) performed a likelihood analysis to argue that ![]() of the 13 A candidates are likely to be microlensing events, yielding
the revised optical depth.
of the 13 A candidates are likely to be microlensing events, yielding
the revised optical depth.
Machos can also be searched for by monitoring M31 and looking for temporal variations of surface brightness consistent with a star in M31 being microlensed. Candidate events have been reported by the VATT (Uglesich et al. 2004), WeCAPP (Riffeser et al. 2003), POINT-AGAPE (Calchi Novati et al. 2005), MEGA (de Jong et al. 2006) and Nainital (Joshi et al. 2005) collaborations. The POINT-AGAPE and MEGA collaborations presented efficiency calculations allowing them to constrain the content of the M31 and Milky Way halos. The disagreement between these two collaborations parallels that between the MACHO and EROS collaborations with the AGAPE collaboration finding a halo fraction in the range 0.2<f<0.9, while the MEGA collaboration finds a halo fraction f<0.3.
In this paper, we extend our previous analysis to find
![]() (95% CL) for
(95% CL) for
![]() ,
corresponding to f<0.08.
Unlike the previous EROS limit, this is significantly
lower than the optical depth measured by the MACHO collaboration.
Unlike all previous analyses,
we use only
a bright, well-measured subsample of the Magellanic stars,
about 20% of the total. We believe that the use of this
bright subsample gives more reliable limits on the
optical depth than measurements using faint stars.
There are two reasons for this.
First, bright stars have well reconstructed
light curves that permit discrimination of intrinsically variable
stars.
Second, the use of bright stars makes it relatively simple to estimate
so-called blending effects
where reconstructed fluxes can receive contributions from more
than one star, complicating the interpretation of events.
,
corresponding to f<0.08.
Unlike the previous EROS limit, this is significantly
lower than the optical depth measured by the MACHO collaboration.
Unlike all previous analyses,
we use only
a bright, well-measured subsample of the Magellanic stars,
about 20% of the total. We believe that the use of this
bright subsample gives more reliable limits on the
optical depth than measurements using faint stars.
There are two reasons for this.
First, bright stars have well reconstructed
light curves that permit discrimination of intrinsically variable
stars.
Second, the use of bright stars makes it relatively simple to estimate
so-called blending effects
where reconstructed fluxes can receive contributions from more
than one star, complicating the interpretation of events.
EROS-2 is a second generation microlensing experiment. The
first generation, EROS-1, consisted of two programs, both
at the European Southern Observatory (ESO) at La Silla, Chile.
The first program (Ansari et al. 1996a) used Schmidt photographic plates
to monitor a
![]() region containing the LMC bar
during the southern summer from October, 1990 through April, 1993.
With a sampling frequency of up to one image per night, it was sensitive
mostly to machos in the range
region containing the LMC bar
during the southern summer from October, 1990 through April, 1993.
With a sampling frequency of up to one image per night, it was sensitive
mostly to machos in the range
![]() .
The second program (Renault et al. 1998) used
a
.
The second program (Renault et al. 1998) used
a
![]() CCD mosaic from December 1991 through March, 1995
to monitor one field in the LMC bar
and another in the SMC. With up to 40 images taken per night,
this program was sensitive
mostly to machos in the range
CCD mosaic from December 1991 through March, 1995
to monitor one field in the LMC bar
and another in the SMC. With up to 40 images taken per night,
this program was sensitive
mostly to machos in the range
![]() .
The results of these two EROS-1 programs are summarized in Renault et al. (1997).
.
The results of these two EROS-1 programs are summarized in Renault et al. (1997).
The second generation program described here, EROS-2,
used the Marly 1 meter telescope
at ESO, La Silla.
The telescope was equipped with two
![]() CCD mosaics to monitor
CCD mosaics to monitor
![]() in the Magellanic Clouds,
in the Magellanic Clouds,
![]() in the Galactic Bulge, and
in the Galactic Bulge, and
![]() in the spiral arms
of the Milky Way.
The observations were performed between
July 1996 and February 2003 (JD between 2 450 300 and 2 452 700).
in the spiral arms
of the Milky Way.
The observations were performed between
July 1996 and February 2003 (JD between 2 450 300 and 2 452 700).
Besides the Magellanic results presented here, EROS-2 has also published measurements of the optical depth toward the Galactic Bulge (Hamadache et al. 2006; Afonso et al. 2003b). The measured optical depth is in agreement with that measured by MACHO (Popowski et al. 2005), and OGLE-2 (Sumi et al. 2006) and with the predictions of Galactic models (Bissantz & Gerhard 2002; Han & Gould 2003; Evans & Belokurov 2002; Wood & Mao 2005).
EROS-1 and EROS-2 overlapped with the MACHO program that
monitored ![]()
![]() of the LMC from July, 1992
through January, 2000. Three other wide-angle microlensing
searches are now in operation:
MOA
of the LMC from July, 1992
through January, 2000. Three other wide-angle microlensing
searches are now in operation:
MOA![]() (since August, 1998),
OGLE-3
(since August, 1998),
OGLE-3![]() (since June, 2001)
and SuperMACHO
(since June, 2001)
and SuperMACHO![]() (since October, 2001).
(since October, 2001).
In this article, we report on the analysis of the full EROS-2 data set (July 1996 till February 2003) toward the Magellanic Clouds. Our previous analyses reported on 5 years of data and 5 million stars toward the SMC (Afonso et al. 2003a), and 2 years of data and 17 million stars toward the LMC (Lasserre et al. 2000). An update of the LMC analysis was reported in Milsztajn et al. (2001) and Lasserre (2000), which dealt with 25 million stars and 3 years. The limits determined in the previous analyses are refined in the analysis presented here. More details about the present analysis can be found in Tisserand (2004).
The plan of the article is as follows. In Sect. 2, we recall the basics of the EROS-2 setup, give the general characteristics of the data sample and describe the data reduction steps used to produce the light curves. Section 3 presents the Bright-Star Sample of stars to be used in the measurement of the optical depth. In Sect. 4, we describe the selection criteria used to choose the microlensing candidates in the Bright-Star Sample. (Selection of events in the full sample is described in Appendix A.) Section 5 presents the final sample of selected events from the Bright-Star Sample as well as events found by relaxing the selection criteria. In Sect. 6 we discuss the status of former EROS-1 and EROS-2 microlensing candidates as well as those of the MACHO collaboration. In Sect. 7, we describe the computation of the EROS-2 detection efficiency. Section 8 presents the limit on the optical depth and on the abundance of machos in the Galactic halo by combining all EROS-1 and EROS-2 data. We conclude in Sect. 9 with a discussion of the significance of the limit, and a comparison with the results of Alcock et al. (2000b).
The EROS-2 Marly telescope, camera, telescope operations and data reduction are described in Bauer et al. (1997), Palanque-Delabrouille et al. (1998), and references therein. Here we give only general information, and details or modifications that are specific to the present analysis.
The Marly telescope is a one meter diameter Ritchey-Chrétien
(f=5.14 m), equipped with two wide angle CCD cameras.
Each camera is a mosaic of 8 CCDs, 2 along right ascension and 4 along declination. Each CCD has
![]() pixels of
pixels of
![]() m2 size, corresponding to
m2 size, corresponding to
![]() arcsec2.
Images were taken simultaneously in two wide passbands,
so-called
arcsec2.
Images were taken simultaneously in two wide passbands,
so-called
![]() centered
close to the
centered
close to the ![]() standard band, and
standard band, and
![]() intermediate between the standard V and R bands.
While no results presented here depend on the photometric
calibration, almost all of our fields could be calibrated using
stars from the catalogs of the
Magellanic Clouds Photometric Survey (Zaritsky et al. 2004). For
intermediate between the standard V and R bands.
While no results presented here depend on the photometric
calibration, almost all of our fields could be calibrated using
stars from the catalogs of the
Magellanic Clouds Photometric Survey (Zaritsky et al. 2004). For
![]() ,
the calibration was checked with the
OGLE-II catalog (Udalski et al. 2000b).
To a precision of
,
the calibration was checked with the
OGLE-II catalog (Udalski et al. 2000b).
To a precision of ![]()
![]() ,
the EROS magnitudes satisfy
,
the EROS magnitudes satisfy
| (4) |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{6017fg01.eps} \end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg89.gif) |
Figure 1:
Map of the EROS-2 LMC and SMC fields in equatorial coordinates.
A total of 88 LMC and 10 SMC
fields were monitored. The first number in each field is the field
number and the second is the number of bright stars
(as defined in Sect. 3)
in the field
in units of 104.
The two shaded regions (the larger one centered on the LMC bar)
are the
|
| Open with DEXTER | |
The ten SMC fields were imaged with a similar sampling, except in 2001 and 2002 when the inner six fields were imaged twice as often as the four outer ones. The number of photometric measurements, per star and per band, ranges from 600 to 900 in these SMC fields.
After rejection of bad images (11%) due to bad seeing, high sky background or instrumental problems, the average numbers of measurements used in the analysis, per star and per band, are about 430 and 780 in the LMC and SMC fields respectively.
The production of light curves proceeded in three steps: template image construction, star catalog production from the templates, and photometry of individual images to obtain the light curves.
The template images were obtained by co-adding 15 images of each field; they were resampled so that the templates have twice as many pixels as the original images. The 15 images were chosen among the best ones available, i.e. with low sky background, good seeing, and with a large number of stars (as estimated from a quick first look algorithm). All images susceptible to enter the template construction were checked for the absence of long tracks, caused by satellites, planes or meteors. For technical reasons linked to computing and to PSF variation within one CCD, the CCD images were divided in four quadrants, such that there were in total 6272 template images (98 fields, 8 CCDs, 4 quadrants, 2 passbands). In order to ensure relatively uniform zeropoints of the 6272 templates, we required that the first image used in template construction (to which the other 14 images were photometrically aligned) be registered within a short time interval with good and uniform sky conditions (23rd to 26th, November 2000). For each field, the same epochs were used in the construction of the templates in the two passbands.
The stars were identified on the template images using a pseudo-image that we call a correlation image. Each pixel of this image contains the correlation coefficient of neighboring pixels of the template itself with a two-dimensional Gaussian PSF. Each group of pixels satisfying some threshold value on the pseudo-image was retained as a star in the catalog. In previous EROS-2 analyses, the thresholds were identical for all templates; this had led to over 20% failures in this cataloging step. The present analysis has chosen to progressively relax the thresholds when such failures occur; in this way, the cataloging step failures were drastically reduced. (The number of identified stars on fields using relaxed thresholds was lower on average.) The star catalogs obtained from the template images in the two passbands were then merged. A star was retained only if it was detected in both. The overall efficiency of the template plus star catalog construction was excellent; only 24 CCD quadrants could not be processed out of a total of 3136.
Examples of color-magnitude diagrams can be found in Figs. 7 to 10 and A.1 to A.5. They are all characterized by a prominent group of clump giants and a main sequence whose relative strength varies from field to field. There are also stars that are redder than Magellanic red giants. Most of them are likely to be foreground stars in the disk of the Milky Way and their number is consistent with the predictions of Galactic models (Robin et al. 2003).
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{6017fg02.eps} \end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg90.gif) |
Figure 2:
The photometric precision as a function of
|
| Open with DEXTER | |
Photometry was then performed on each image of a given quadrant in turn with software specifically designed for crowded fields, PEIDA (Photométrie et Étude d'Images Destinées à l'Astrophysique) (Ansari et al. 1996b). First, the image was geometrically aligned with the template. Then, imposing the star position determined from the template image, PSF-fitting photometry was performed for all stars by a linear least-squares method involving the star and all neighbors closer than 11 pixels, plus a sky background. An estimate of the error on this flux measurement was computed that depends on the photon statistics and on the overall quality of the photometered image. Typical photometric precisions are shown in Fig. 2.
Before the analysis was started, we removed from the light curves measurements
taken under far from normal conditions. This happened not infrequently, as the
data taking policy was to work whenever possible, leaving to the analysis
the task of rejecting these abnormal measurements. These were identified by
extreme values of the sky background, seeing or absorption. In addition,
images where the photometry failed for over 40% of cataloged stars were
eliminated, as well as images for which more than 12% of the stars showed an
excursion from their average flux larger than three standard deviations.
Depending on the CCD, the number of rejected images varied between 7 and 18%, with an average of 11%![]() .
.
To reduce systematic errors in the photometry, each light curve was searched for significant linear correlations between the measured flux and three observational variables, the seeing, the hour angle and the airmass. This was done independently in the two passbands. The measured fluxes were corrected linearly by requiring a vanishing correlation coefficient between the corrected fluxes and the given variable. The largest correlation was found with the seeing, in both passbands. For the bright stars considered in this work, the correction has only a small influence on the point-to-point dispersion of the lightcurves, reducing it on average by 6%.
A potential problem with this correction is that an artificial correlation can be induced if a real flux variation happens to occur during a period of poor seeing (for example). In this case, application of the correction would reduce the amplitude of the real flux variation but increase the point-to-point dispersion of the curve by making an incorrect flux correction. To guard against this possibility, we did not apply the correction if it increases the point-to-point dispersion of the light curves.
A total of 58.4 million objects
were found on the template images of both passbands
- 51.8 million in the LMC and 6.6 million in
the SMC.
We chose to ignore
those stars for which the association between the objects
detected separately in the two passbands was doubtful or ambiguous
(8.4 million) and objects that are dimmer than about twice the typical
size of sky background fluctuations (14.9 million). We rejected light curves
for which more than half of the photometry points are absent (1.0 million).
Finally, we did not consider stars whose photometry is unstable due to
its environment. This includes stars close to a very bright field star
(
![]() ,
probably in the Galactic disk) and stars close to a visible
diffraction feature in the PSF of bright stars; these two categories
contain respectively 1.1% and 0.8% of the remaining stars.
,
probably in the Galactic disk) and stars close to a visible
diffraction feature in the PSF of bright stars; these two categories
contain respectively 1.1% and 0.8% of the remaining stars.
We removed from consideration stars in field lm003, CCD0 which
has numerous events caused by light echos from SN1987a. The
echos generate arc-like images
that appear to move a few arcsec per year![]() ,
causing false variations of a star's flux as the arc passes
through the star's position.
,
causing false variations of a star's flux as the arc passes
through the star's position.
After these cuts, 33.4 million objects remained, 29.2 million in the LMC and 4.2 million in the SMC. This constitutes the Full Sample of EROS-2 stars. In the next section we describe the selection of the Bright-Star Sample used for the measurement of optical depths.
We have chosen to restrict our analysis to the Bright Sample of stars defined below. Besides the obvious advantage of ensuring a good photometric resolution, we do this to simplify the evaluation of the number of expected events predicted by a model. In crowded fields, this evaluation is complicated by "blending'', i.e. the fact that photometry of a given object can be influenced by more than one star. We shall see that these effects are rather small and simple to evaluate for the Bright-Star Sample (which should, strictly speaking, be called the Bright-Object Sample).
Limiting the number of studied objects limits the sensitivity
of the experiment so the magnitude cut must be a compromise
between quantity and quality of objects.
The efficiency calculations of Sect. 7 for unblended sources
indicated that keeping only the ![]()
![]() brightest
stars reduces by only
brightest
stars reduces by only ![]()
![]() the number of simulated microlensing events
that pass our selection criteria.
We therefore initially
decided to accept a nominal
the number of simulated microlensing events
that pass our selection criteria.
We therefore initially
decided to accept a nominal ![]()
![]() loss of events
by requiring
loss of events
by requiring
![]() ,
where
,
where
![]() is
the median
is
the median
![]() for simulated unblended microlensing events passing
our event selection criteria.
for simulated unblended microlensing events passing
our event selection criteria.
![]() ranges from
ranges from ![]() 18.2 in the densest fields to
18.2 in the densest fields to ![]() 20.5 in the sparsest.
However,
for sparse fields far from the LMC bar,
in order to have a reasonable object reconstruction efficiency,
a stricter cut was found to be necessary,
20.5 in the sparsest.
However,
for sparse fields far from the LMC bar,
in order to have a reasonable object reconstruction efficiency,
a stricter cut was found to be necessary,
![]() .
.
The final sample of bright stars is therefore defined by
The position of the magnitudes cut are shown in the color-magnitude diagrams of Figs. 7 to 10 and A.1 to A.5. Generally speaking, the cut includes clump giants but not the numerous main sequence stars seen far below the clump. Other than the small number of bright main sequence stars, we therefore employ stars of colors and magnitudes similar to those used in Galactic Bulge measurements that use clump giants (Hamadache et al. 2006).
It turns out that the cut (5) gives a rather uniform
photometric precision for the Bright-Star Sample. Figure 3
shows the distribution of precision with a mean in both bands
of ![]()
![]() .
The precision in dense fields hardly differs from
that in sparse fields and the precision in the LMC hardly differs
from that in the SMC.
.
The precision in dense fields hardly differs from
that in sparse fields and the precision in the LMC hardly differs
from that in the SMC.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{6017fg03.eps} \end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg100.gif) |
Figure 3:
The flux precision,
|
| Open with DEXTER | |
The number of EROS-2 objects in the Bright-Star Sample
defined by (5) is
6.05 million in the
LMC and 0.90 million in the SMC.
We must subtract from these numbers the expected
number of foreground stars in the Milky Way disk.
The Besançon model of the Milky Way (Robin et al. 2003)
predicts that 0.56 million (LMC) and 0.04 million (SMC) are foreground Milky Way stars,
consistent with the number of stars
we observe that are redder than Magellanic red giants.
The number of Bright-Sample stars to be used for optical
depth measurements must therefore be reduced by 9% (4%) for the LMC (SMC),
giving
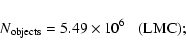 |
(6) |
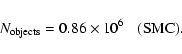 |
(7) |
EROS photometry is performed on
a set of "objects'' found on a reference image. In crowded
fields, the correspondence between objects and stars is not
straightforward. Generally speaking, most objects are dominated
by one star, i.e. by the brightest star in the object's
seeing disk. However, if a fainter star in the seeing disk is
microlensed, EROS photometry will assign some of the extra flux to
the object with the remainder assigned to sky background.
It is thus convenient to rewrite (8) as
If there were no blending, the
efficiency could be estimated by modifying a sample of light
curves with measured fluxes F0(t) by
For blended events only a fraction ![]() of an object's
flux is amplified. If the fraction is independent of amplification,
the resulting light curve is
of an object's
flux is amplified. If the fraction is independent of amplification,
the resulting light curve is
![\begin{figure}
\par\includegraphics[width=15.8cm,clip]{6017fg04.eps}\end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg115.gif) |
Figure 4:
The effects of blending on artificial stars added to
the dense field lm009 ( left) and the sparse field lm048 ( right).
The top two panels show the distribution of |
| Open with DEXTER | |
A simple example is two superimposed stars of the
same magnitude and color. In this case
![]() and
and
![]() .
Before efficiency corrections, the
event rate would be
0.7+0.7=1.4 times the rate calculated ignoring blending.
If the two stars
have colors differing by
.
Before efficiency corrections, the
event rate would be
0.7+0.7=1.4 times the rate calculated ignoring blending.
If the two stars
have colors differing by
![]() ,
the requirement that
,
the requirement that
![]() in both
colors yields a rate that is increased by
a factor 1.3 over the rate for
in both
colors yields a rate that is increased by
a factor 1.3 over the rate for ![]() .
.
To statistically evaluate the distribution of the ![]() for Bright-Sample
objects,
a spectrum of 8000 artificial stars was placed at
random positions on real EROS images
(lm009, lm019, lm034, lm048)
to give artificial images (xm009, xm019, xm034, xm048).
These fields were chosen as representative of the crowding
variations over the LMC fields.
The stars were given fluxes according to randomly
chosen microlensing events (one per artificial star).
Reference xm images were created using these images and photometry
performed in the same manner as for the normal (lm)
images.
for Bright-Sample
objects,
a spectrum of 8000 artificial stars was placed at
random positions on real EROS images
(lm009, lm019, lm034, lm048)
to give artificial images (xm009, xm019, xm034, xm048).
These fields were chosen as representative of the crowding
variations over the LMC fields.
The stars were given fluxes according to randomly
chosen microlensing events (one per artificial star).
Reference xm images were created using these images and photometry
performed in the same manner as for the normal (lm)
images.
After photometry, the light curves of xm objects falling near
artificial stars were studied to
find values of the ![]() .
In practice, one median value of
.
In practice, one median value of ![]() was calculated for each lightcurve
using points for which
was calculated for each lightcurve
using points for which
![]() ,
though no nonlinearity was
observed that made this a crucial point.
Of the
8000 artificial stars that
were added to each of the four fields, most are
not usable for various (understandable) reasons: star in a
masked region of the CCD, event during a period with no observations,
or the reconstructed magnitude
not satisfying the Bright Sample cuts.
For the field xm009, a total of 1123 lightcurves were usable for determining
,
though no nonlinearity was
observed that made this a crucial point.
Of the
8000 artificial stars that
were added to each of the four fields, most are
not usable for various (understandable) reasons: star in a
masked region of the CCD, event during a period with no observations,
or the reconstructed magnitude
not satisfying the Bright Sample cuts.
For the field xm009, a total of 1123 lightcurves were usable for determining ![]() .
Of these lightcurves, 982 concerned objects
for which the artificial star
is the primary component, while in the remaining 141 objects the
artificial star falls
underneath a preexisting bright object on the original image.
We use the
first type of object to determine the distribution of
.
Of these lightcurves, 982 concerned objects
for which the artificial star
is the primary component, while in the remaining 141 objects the
artificial star falls
underneath a preexisting bright object on the original image.
We use the
first type of object to determine the distribution of ![]() ,
the value of
,
the value of ![]() for the primary star associated
with each object.
for the primary star associated
with each object.
Figure 4 (top) shows the distribution of ![]() for
the dense field lm009 and the sparse field lm048.
The other two fields give similar distributions.
The distributions of
for
the dense field lm009 and the sparse field lm048.
The other two fields give similar distributions.
The distributions of ![]() are characterized by
peaks at
are characterized by
peaks at
![]() due
to artificial stars falling more than
due
to artificial stars falling more than ![]()
![]() from any
pre-existing lm object. This happens for about half the artificial
stars in the densest field (lm009) so blending has little
effect on about half the bright stars in dense fields.
Stars falling on pre-existing stars
yield the tail at
from any
pre-existing lm object. This happens for about half the artificial
stars in the densest field (lm009) so blending has little
effect on about half the bright stars in dense fields.
Stars falling on pre-existing stars
yield the tail at
![]() .
This can be seen in the middle plots that show, for artificial
stars within
.
This can be seen in the middle plots that show, for artificial
stars within
![]() of pre-existing stars, the correlation
between
of pre-existing stars, the correlation
between ![]() and the magnitude difference between artificial
and pre-existing stars. The distribution follows closely the
expected form
and the magnitude difference between artificial
and pre-existing stars. The distribution follows closely the
expected form
![]() where f1 is the flux of
the artificial star and f2 is the flux of the preexisting star.
For example, when
where f1 is the flux of
the artificial star and f2 is the flux of the preexisting star.
For example, when
![]() the cloud of points passes
near
the cloud of points passes
near
![]() .
.
The mean value of
![]() is
is ![]() 0.86 equivalent to a mean value of u1 of 0.92. This means
that the (efficiency uncorrected)
rate of events with amplifications of the primary
component greater than 1.34 is
reduced by a factor 0.92 from the rate calculated assuming no
blending.
0.86 equivalent to a mean value of u1 of 0.92. This means
that the (efficiency uncorrected)
rate of events with amplifications of the primary
component greater than 1.34 is
reduced by a factor 0.92 from the rate calculated assuming no
blending.
The loss of 8% of the events is compensated by extra events due to stars
under the primary component.
Since
![]() ,
we can expect
that
,
we can expect
that
![]() for superimposed objects.
However, the superposition is not perfect so
for superimposed objects.
However, the superposition is not perfect so ![]() must
be a decreasing function of the separation between the
object and star 2.
The artificial
events due to artificial stars falling under brighter pre-existing objects
are well described by
must
be a decreasing function of the separation between the
object and star 2.
The artificial
events due to artificial stars falling under brighter pre-existing objects
are well described by
![\begin{figure}
\par\includegraphics[width=7cm,clip]{6017fg05.eps}\end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg130.gif) |
Figure 5:
The distribution of u1 (solid line) and
(u1+u2) dashed line for the sparse EROS field lm048 ( top panel)
the dense EROS field lm009 ( middle panel) and the very dense HST field in lm009, ccd3 ( bottom panel) as described in the text.
The distributions of u1 are all characterized by a peak
near |
| Open with DEXTER | |
The compensation is seen in Fig. 5 histogramming u1 and u1+u2. The sum u1+u2 gives the rate for event with amplifications >1.34 compared to that calculated assuming ![]() .
In lm048, events due to the second star compensate
for the loss of events on the first star
while in the dense field lm009 there is a 10% overcompensation.
As we will see in Sect. 7, the efficiency to observe
the blended events is degraded compared to unblended events,
so the overall number of expected events is about 10% less than
what one would calculate ignoring blending.
.
In lm048, events due to the second star compensate
for the loss of events on the first star
while in the dense field lm009 there is a 10% overcompensation.
As we will see in Sect. 7, the efficiency to observe
the blended events is degraded compared to unblended events,
so the overall number of expected events is about 10% less than
what one would calculate ignoring blending.
We have checked our calculations by studying public HST images of
a small part of the densest EROS region, that of lm009 ccd 3.
A catalog of stars for this region was produced and images with
EROS seeing were fabricated. As in the previous
analysis, images with some amplifications were compared with
reference images. Figure 5 shows the distribution of u1for bright objects on the convoluted images.
Because of the very high density of stars, u1 is somewhat
smaller than that calculated with the artificial
images:
![]() as opposed to
as opposed to
![]() .
This lower value of
u1 is, as expected, compensated by higher values of u2.
Figure 5 shows the
histogram of u1+u2 indicating that the
event rate is raised by 15% over the unblended rate. Including
the loss of efficiency modifies this so that the event rate is
only 5% higher than the unblended rate.
.
This lower value of
u1 is, as expected, compensated by higher values of u2.
Figure 5 shows the
histogram of u1+u2 indicating that the
event rate is raised by 15% over the unblended rate. Including
the loss of efficiency modifies this so that the event rate is
only 5% higher than the unblended rate.
The present analysis aims at detecting luminosity excursions, due to
microlensing, on otherwise constant light curves. The smallest reachable
microlensing timescale, ![]() ,
is determined by the sampling of the fields;
in practice, except for a few fields,
the detection efficiency is very low below 2-3 days.
The largest detectable timescale, about 800 days, is determined by the
reduction in the detection efficiency when the timescale becomes so
large that the baseline flux is not seen during the observing period.
,
is determined by the sampling of the fields;
in practice, except for a few fields,
the detection efficiency is very low below 2-3 days.
The largest detectable timescale, about 800 days, is determined by the
reduction in the detection efficiency when the timescale becomes so
large that the baseline flux is not seen during the observing period.
The analysis is guided using the simulation of microlensing described in Sect. 7, which also serves to determine the efficiency of the selection procedure.
In the present analysis, luminosity excursions are defined with respect to
the baseline stellar flux; the first
task is thus to determine this baseline. To that end, we order the N
measured fluxes ![]() of the light curve by increasing values of
of the light curve by increasing values of ![]() .
For each of the N-1 middle values of the flux intervals
.
For each of the N-1 middle values of the flux intervals
![]() ,
we count the number
,
we count the number
![]() of runs,
i.e. groups of consecutive points on the light curve that are on the same
side of
of runs,
i.e. groups of consecutive points on the light curve that are on the same
side of
![]()
![]() .
The baseline flux is defined as that value of
.
The baseline flux is defined as that value of
![]() which maximizes
which maximizes
![]() .
This way of defining
the baseline has a precision similar to that of a simple average of the
fluxes, but it proves much more robust to aberrant measurements, and
less biased for most variable stars. We have checked on the simulated
microlensing
light curves that there is no visible bias for timescales
.
This way of defining
the baseline has a precision similar to that of a simple average of the
fluxes, but it proves much more robust to aberrant measurements, and
less biased for most variable stars. We have checked on the simulated
microlensing
light curves that there is no visible bias for timescales ![]() shorter
than
shorter
than ![]()
![]() .
The bias is non-negligible above
.
The bias is non-negligible above ![]() ,
but this is taken into account in the efficiency calculation.
,
but this is taken into account in the efficiency calculation.
Next, we determine the point-to-point dispersion in the light curve
![]() ,
from the comparison of each measured flux with the linear
interpolation of its two neighboring (in time)
fluxes. This is done separately for
the 7 seasons of data taking, as we have observed a progressive degradation
of the photometric scatter in the last 3 seasons.
,
from the comparison of each measured flux with the linear
interpolation of its two neighboring (in time)
fluxes. This is done separately for
the 7 seasons of data taking, as we have observed a progressive degradation
of the photometric scatter in the last 3 seasons.
Using the baseline flux and the photometric scatter, we then search for
luminosity excursions defined as
a group of consecutive points with fluxes
sufficiently far from
the baseline flux.
These should have at least 5 consecutive measurements
more than
![]() from the baseline.
In practice, to increase
the detection efficiency for short duration phenomena, we allow small
"holes'' within the excursion
(series of points less than
from the baseline.
In practice, to increase
the detection efficiency for short duration phenomena, we allow small
"holes'' within the excursion
(series of points less than
![]() from the baseline)
provided that each hole contains
exactly one measurement.
We call positive (negative) excursions those
comprised of fluxes higher (lower) than the baseline.
from the baseline)
provided that each hole contains
exactly one measurement.
We call positive (negative) excursions those
comprised of fluxes higher (lower) than the baseline.
The relative significance of each excursion is then estimated using the
probability that it corresponds to a statistical fluctuation of a normal
law. We use the variable LPN, the co-logarithm of this probability
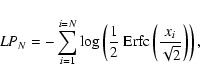
Table 1: The number of light curves surviving the cuts C1 to C12 as described in the text.
We now describe the 12 selection criteria, C1-C12, used to
select microlensing candidates.
C1 requires at least one significant positive excursion:
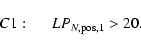
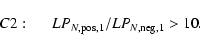
All light curves passing C1-3 are fitted with a simple microlensing
curve (10),
independently in the two passbands. The results of the fits, i.e. the fitted
parameters t0, u0 and ![]() and the values of
and the values of ![]() ,
are used in
cuts C5-C10.
,
are used in
cuts C5-C10.
Cuts C4 and C5 eliminate light curves with significant variability
outside the main positive excursion.
We first require that the second positive excursion be much less significant
than the first one:
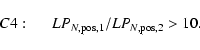
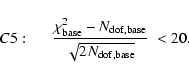
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{6017fg06.eps} \end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg156.gif) |
Figure 6:
The u0 (mean of those for
|
| Open with DEXTER | |
Cuts C6 and C7 require that the main fluctuation occur at a time when
the light curve is sufficiently well sampled.
In order to discriminate against stellar variations with very asymmetric peaks
we thus require that the time t0 be
within the observing
interval:
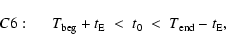
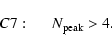
![\begin{figure}
\par\includegraphics[width=15cm,clip]{6017fg07.eps} \end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg161.gif) |
Figure 7: The light curves of EROS-2 microlensing candidate EROS2-SMC-1 (star sm005-4m-5761). Also shown is the color-magnitude diagram of the star's CCD-quadrant and the excursion of the event. |
| Open with DEXTER | |
We next require that the
microlensing fit to the light curves in both passbands be significantly
better than the fit of a constant flux:
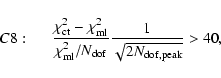
We then require a reasonably good fit to the microlensing curve
within the peak:
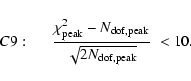
We identify blue bumpers first from their position in the color-magnitude
diagram and their low, chromatic amplification.
For stars with
![]() and
and
![]() (LMC) or
(LMC) or
![]() (SMC), we require
(SMC), we require

There are 10 LMC light curves and 4 SMC light curves that
pass cuts C1-C10. Four of these light curves are most likely
supernovæ (SN) exploding in
galaxies far behind the Magellanic Clouds.
In the analysis of the Full Sample of EROS-2
Magellanic light curves (Tisserand 2004), 31
such supernovae were found.
All SN in our sample have fitted timescales in the range 25-50 days,
asymmetric light curves with a faster rise time, and larger variations in
the bluer passband. For a fraction of them, about 20%, the host galaxy is visible,
which makes them indisputable SN. In order to identify the remaining SN,
we have devised a fitting function with a time asymmetry parameter S;
the function reduces to simple microlensing for S = 0. The fitting
function is obtained from simple microlensing (10)
by replacing the Einstein timescale ![]() by the "supernova''
varying timescale
by the "supernova''
varying timescale
![\begin{displaymath}t_{\rm S} = t_{\rm E} \: \left[ 1 + S \: \arctan
\left( \frac{t - t_0}{t_{\rm E}}\right) \right] \cdot
\end{displaymath}](/articles/aa/full/2007/26/aa6017-06/img172.gif) |
(13) |
Table 2:
Events found in the analysis of the full sample of
EROS-2 stars (Tisserand 2004).
Only event EROS2-SMC-1
is in the Bright-Star Sample and passes the cuts C1-C12 and therefore
is used for limits on the optical depth.
All fits assume zero blending and no intrinsic variability.
The two values of the fitted parameters t0, ![]() and u0 are
for
and u0 are
for
![]() (first line) and
(first line) and
![]() (second line). (There are no
(second line). (There are no
![]() points during the event for EROS2-LMC-12.)
The time of maximum, t0 is given as JD-2450000.
points during the event for EROS2-LMC-12.)
The time of maximum, t0 is given as JD-2450000.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{6017fg08.eps} \end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg178.gif) |
Figure 8:
The light curves of EROS-2 star lm057-0n-29305 (
|
| Open with DEXTER | |
After the cuts described in the previous two sections have been applied,
only one candidate microlensing event remains in the Bright-Star Sample,
EROS2-SMC-1.
Its light curve is
shown in Fig. 7 and its characteristics are
given on the first entry in Table 2.
It has been known since 1997 (Alcock et al. 1997b; Palanque-Delabrouille et al. 1998) and is
identical to candidate MACHO-97-SMC-1. It has one of the two
longest timescales (![]() )
and the highest luminosity of all
published microlensing
candidates reported toward the Magellanic Clouds.
The star is separated by
)
and the highest luminosity of all
published microlensing
candidates reported toward the Magellanic Clouds.
The star is separated by
![]() from another star that
is
from another star that
is
![]() fainter
(Udalski et al. 1997) causing
fainter
(Udalski et al. 1997) causing ![]()
![]() blending in EROS-2 images.
Including the blend in the light curve fit increases
blending in EROS-2 images.
Including the blend in the light curve fit increases
![]() to
to ![]()
![]() .
The star displays a 4-5% variability with a period
P = 5.12 d (Palanque-Delabrouille et al. 1998). For further details on this event, see
Palanque-Delabrouille et al. (1998), Afonso et al. (1999,2003a) and Assef et al. (2006).
.
The star displays a 4-5% variability with a period
P = 5.12 d (Palanque-Delabrouille et al. 1998). For further details on this event, see
Palanque-Delabrouille et al. (1998), Afonso et al. (1999,2003a) and Assef et al. (2006).
Table 3:
The 17 microlensing candidates of the MACHO collaboration (Alcock et al. 2000b).
Candidates 20, 22 and 27 (marked B)
are low signal-to-noise candidates not satisfying the
MACHO "A'' requirements.
Candidate 9 is due to a binary lens and does not satisfy their A requirements.
The values of ![]() and maximum amplification
and maximum amplification
![]() are from the MACHO fit assuming no blending, and t0 is given
as JD-2 450 000.
Candidates 18 and 25 are each within
are from the MACHO fit assuming no blending, and t0 is given
as JD-2 450 000.
Candidates 18 and 25 are each within
![]() of an object of similar
magnitude that is resolved by the MACHO analysis but blended in the EROS
analysis.
Candidates 14 and 20 occurred during EROS-2 observations, and the
EROS-2 values of
of an object of similar
magnitude that is resolved by the MACHO analysis but blended in the EROS
analysis.
Candidates 14 and 20 occurred during EROS-2 observations, and the
EROS-2 values of ![]() and
and
![]() are shown in parentheses
(averages of
are shown in parentheses
(averages of
![]() and
and
![]() measurements).
measurements).
As a check on the cuts C1-12 leading to EROS2-SMC-1 and to
search for nonstandard microlensing events
(e.g. those due to binary lenses),
a large number of light curves were visually scanned.
Among them were
all events satisfying C1-C8 and u0<1,
all events satisfying C1-C7 and u0<0.5,
all events satisfying C1-C10,
and all events satisfying C1-C12 but with
![]() increased by
increased by
![]() .
Only one interesting event was found, EROS2-LMC-15
shown in Fig. 8.
The beginning of the event is very similar to a standard microlensing
event but subsequent points are too high
.
Only one interesting event was found, EROS2-LMC-15
shown in Fig. 8.
The beginning of the event is very similar to a standard microlensing
event but subsequent points are too high![]() .
It was rejected by the
.
It was rejected by the
![]() cut (C9) but it may, in fact, be a lensing
event due to a binary lens.
Note that its position in the color-magnitude
diagram suggests that the star is either
not in the LMC or behind a foreground Milky Way star.
cut (C9) but it may, in fact, be a lensing
event due to a binary lens.
Note that its position in the color-magnitude
diagram suggests that the star is either
not in the LMC or behind a foreground Milky Way star.
An important verification of the analysis of the Bright-Star Sample
presented here
comes from an analysis of the
Full Sample of
Magellanic light curves described in Tisserand (2004).
Because faint stars were analyzed, the cuts,
given in Appendix A, were generally slightly
stricter than those described in Sect. 4.
However, the analysis did not require observation of the
event in both colors. It therefore provides an important
check on our analysis. The candidates found in this
analysis are listed in Table 2 and their
light curves shown in Appendix A.
Two candidates EROS2-SMC-1 and 5 are in the Bright-Star Sample.
Candidate 5 does not pass the cuts presented here because
it fails C12. We also note that it shows non-microlensing-like
variations in the light curve of the MACHO
collaboration![]() .
.
Two other independent analyses were performed on the SMC data, restricted to the first five years of data. In both cases, the only event found in the Bright-Star Sample was EROS2-SMC-1. The first analysis, reported in Afonso et al. (2003a), was based on a larger set of stars (5.2 million); the number of analysis cuts common to it and the present analysis is small; the computer programs were written independently. The second analysis followed a complete reprocessing using a new implementation of differential photometry developed by Le Guillou (2003). The technique would allow us to find events not on cataloged stars.
We attempted to check our efficiency for finding
microlensing events by considering the events published
by the MACHO collaboration.
The 13-17 events (Alcock et al. 2000b) used by them to measure
the optical depth toward the LMC are listed in
Table 3.
Only 2 of the 17 stars (MACHO-LMC-18 and 25)
are bright enough to be in our Bright-Star Sample.
Three of the 17 events occurred after the beginning of EROS-2
operations but none of these three events occurred on stars
in our Bright-Star Sample.
One of the three (MACHO-LMC-15) was on a star too dim
to be seen by EROS-2![]() .
The two other events
(MACHO-LMC-14 and 20) are seen in the
EROS-2 images and give microlensing parameters compatible with
those measured by MACHO (see Table 3).
.
The two other events
(MACHO-LMC-14 and 20) are seen in the
EROS-2 images and give microlensing parameters compatible with
those measured by MACHO (see Table 3).
MACHO-LMC-14 was selected in the MACHO A analysis.
In EROS-2, it was located in a defective zone of
![]() pixels on
CCD 7 of our blue camera, near the edge of the mosaic.
The corresponding star was not cataloged in this band, and the star
failed the requirement to be observed in both passbands.
Consequently, it does not appear in Table 2.
pixels on
CCD 7 of our blue camera, near the edge of the mosaic.
The corresponding star was not cataloged in this band, and the star
failed the requirement to be observed in both passbands.
Consequently, it does not appear in Table 2.
MACHO-LMC-20 was selected in the MACHO B analysis. In EROS-2, it is located 35 arcsec from a very bright Galactic star (about V = 10 vs. 21 for the candidate). In this analysis, stars too near bright stars were eliminated so this candidate does not appear in Table 2.
In this section, we review and update the status of the published Magellanic microlensing candidates of the EROS and MACHO collaborations.
EROS has, in the past, used 11 candidates to place upper limits on the optical depth toward the LMC and to measure the depth toward the SMC. Six of the candidates are in the Bright-Star Sample considered here. The candidates and their present status are given in Table 4.
Table 4: The 11 events of the EROS collaboration used in the past to set upper limits on the microlensing optical depth toward the LMC and to measure the depth toward the SMC. Candidates marked "B-S'' in Col. 2 occur on stars in the EROS-2 Bright-Star Sample. All candidates except EROS2-SMC-1 have been eliminated as variable stars or as supernovae.
Of the candidates in Table 4 only EROS2-SMC-1 remains as a candidate microlensing event. The others have been eliminated either because continued observations of the same stars show further variability on the light curves, or because improved photometry, in some cases complemented by spectroscopy, lead to re-interpreting the candidates as variable stars. Before the analysis presented here, the following EROS candidates were eliminated: EROS1-LMC-2, presented in Aubourg et al. (1993) and which displayed a new variation 8 years later (Lasserre et al. 2000); and candidate EROS2-LMC-4, presented in Lasserre et al. (2000) and eliminated in Milsztajn et al. (2001).
Before this analysis started, there were 5 surviving LMC microlensing candidates from EROS, one from EROS-1 (number EROS1-LMC-1) and four from EROS-2 (numbered EROS2-LMC-3, 5, 6 and 7).
The EROS-1 candidate EROS1-LMC-1 displayed a new variation in the EROS-2 data (Fig. 9) in 1998, 6.3 years after the first one, of similar amplitude (a factor two) and timescale (27 days). This second variation is well fitted by a microlensing light curve. Because they are separated in time by more than 80 Einstein timescales, the probability that these two bumps correspond to the microlensing of a double source star is lower than half a percent, even in the favorable case of the two stars being of equal luminosity. This candidate was thus rejected. Let us recall that it was already known to be a Be star (Beaulieu et al. 1995) and was thus already suspected of being variable (Paczynski 1996). Candidate EROS2-LMC-3 also displayed new variations between 1999 and 2002, of a more irregular nature, and was thus rejected.
The light curves of candidates EROS2-LMC-5, 6 and 7 have been improved, due to the better template images in the present analysis. The reduced photometric scatter, compared to Milsztajn et al. (2001), made apparent an asymmetry in rise and fall times; the asymmetry test (C11) allowed us to identify and reject them as supernovæ. EROS2-LMC-5 is identical to MACHO-LMC-26, which had been rejected by Alcock et al. (2000b) for the same reason.
The conclusion is that none of the former EROS LMC microlensing candidates are still considered valid. Four displayed further variability, and three were identified as SN thanks to improved photometry.
There have been four EROS-2 SMC candidates, EROS2-SMC-1 discussed in Sect. 5, and EROS2-SMC-2, 3 and 4 presented in Afonso et al. (2003a). Candidates 2, 3 and 4 were described as doubtful candidates, as all three display very long timescale variations, and look more like irregular variable stars. Another analysis of the same SMC data using differential photometry (Le Guillou 2003) allowed us to reduce the photometric errors and substantiate this interpretation. The additional two years of data since Afonso et al. (2003a) have confirmed this, as further irregular variations have been observed. They are not selected in the present analysis, and are now considered as definitively rejected.
We have also searched for further variations in the 17 stars used by the MACHO collaboration to measure the optical depth toward the LMC (Table 3). One of the candidates, MACHO-LMC-23, showed a further variation in the EROS-2 data (Tisserand 2004), 6.8 years after its first variation in the MACHO data. Its EROS-2 lightcurve is shown in Fig. 10. As such, we can eliminate it as a microlensing candidate. In spite of this, both the variation shown in Fig. 10 and the original variation in the MACHO data are quite achromatic, indicating that achromaticity is not a fool-proof criterion for selecting microlensing events. We note however that Bennett et al. (2005) argued that, even without considering its further variation seen in the EROS-2 data, the form of its light curve made MACHO-LMC-23 a weak microlensing candidate.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{6017fg09.eps} \end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg190.gif) |
Figure 9: The EROS-2 light curve of EROS-1 microlensing candidate EROS1-LMC-1. The curve shows a second variation, 6.3 years after the variation observed in EROS-1. Also shown is the color-magnitude diagram of the star's CCD-quadrant and the excursion of the event. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{6017fg10.eps} \end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg191.gif) |
Figure 10: The EROS-2 light curve of MACHO microlensing candidate MACHO-LMC-23. The curve shows a second variation, 6.8 years after the variation seen by MACHO. Also shown is the color-magnitude diagram of the star's CCD-quadrant and the excursion of the event. |
| Open with DEXTER | |
The MACHO collaboration has also reported candidate events found by their alert system. The most notable is MACHO99-LMC-2 that was studied by Bond et al. (2002). This impressive microlensing candidate was on a star too faint to be in the EROS Full Sample.
Besides the 17 LMC events of the MACHO collaboration, they have
reported two candidates in the SMC, though they have reported no
systematic search for SMC events.
The first MACHO SMC candidate (Alcock et al. 1997b)
is identical to EROS2-SMC-1 (Sect. 5). The second
candidate, MACHO-98-SMC-1, concerned a star too faint
to be included in our Full Sample of SMC stars.
The event
was detected by the alert
system of the MACHO group in May 1998 and a probable caustic
crossing due to a double lens was announced soon after.
The source star was monitored by most microlensing groups,
including EROS-2. The second caustic crossing was fully measured,
which allowed the determination of the relative proper motion between
the lens and source, allowing
one to conclude that the event was due
to a lens in the SMC (Afonso et al. 1998,2000)![]() .
.
To measure the optical depth from the detected events, or limits
on this quantity, we first need to evaluate the detection efficiency
as a function of the time scale ![]() .
This was determined by using
Monte Carlo simulated light curves: we superimpose artificial
microlensing events on a representative sample of light curves,
corresponding to 2% of the Bright-Star Sample from each of the 98 monitored fields. The light curve for a simple microlensing event
(i.e. point-source point-lens zero-blending) is described by
three parameters of (10):
date of maximum amplification t0, impact parameter u0 and time scale
.
This was determined by using
Monte Carlo simulated light curves: we superimpose artificial
microlensing events on a representative sample of light curves,
corresponding to 2% of the Bright-Star Sample from each of the 98 monitored fields. The light curve for a simple microlensing event
(i.e. point-source point-lens zero-blending) is described by
three parameters of (10):
date of maximum amplification t0, impact parameter u0 and time scale ![]() .
Blended events have the additional parameter
.
Blended events have the additional parameter ![]() in (11).
The microlensing
parameters are chosen at random: t0 follows a flat distribution over
our 2500 days observing period, JD 2 450 242 till 2 452 742; u0 is
picked randomly between 0 and 1.2; and
in (11).
The microlensing
parameters are chosen at random: t0 follows a flat distribution over
our 2500 days observing period, JD 2 450 242 till 2 452 742; u0 is
picked randomly between 0 and 1.2; and ![]() is chosen at random from a
distribution flat in
is chosen at random from a
distribution flat in
![]() ,
between 1 and 1000 days. Each star in
the 2% sample is actually used thrice in the simulation, once per decade
in
,
between 1 and 1000 days. Each star in
the 2% sample is actually used thrice in the simulation, once per decade
in ![]() .
The simulation takes into account the relative variation of
photometric errors.
.
The simulation takes into account the relative variation of
photometric errors.
Simulated light curves were then fed into the analysis chain to find
the fraction that are recovered by our detection algorithm. The detection
efficiency in a given ![]() bin,
bin,
![]() ,
is then given by the ratio between the
number of events passing all selection criteria in this bin and the
number of microlensing events generated in the same bin with u0<1.
,
is then given by the ratio between the
number of events passing all selection criteria in this bin and the
number of microlensing events generated in the same bin with u0<1.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{6017fg11.eps} \end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg196.gif) |
Figure 11:
The detection efficiency for unblended ( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{6017fg12.eps} \end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg197.gif) |
Figure 12:
The ratio between the summed efficiency,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{6017fg13.eps}\end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg199.gif) |
Figure 13:
The detection efficiency for simple microlensing
light curves (10) as a function of u0 ( top)
and of
|
| Open with DEXTER | |
Figure 11 shows the LMC and SMC efficiencies for
unblended events (![]() )
as a
function of
)
as a
function of ![]() .
For the range of
.
For the range of ![]() of interest for this work, the efficiency
varies from
of interest for this work, the efficiency
varies from ![]() 0.25 at
0.25 at
![]() to
to ![]() 0.45 at
0.45 at
![]() .
.
Blended events have an efficiency that is reduced because an impact
parameter smaller than unity is necessary to produce an amplification
of 1.34.
The efficiency is also modified because the time scale is reduced.
To sufficiently good approximation we find
 |
(14) |
To evaluate the summed detection efficiency for a realistic distribution
of ![]() and
and ![]() we used the pairs from the artificial
images of Sect. 3, Fig. 4.
Figure 12 shows the ratio between the calculated
sum (for the four studied fields) and the unblended efficiency.
For
we used the pairs from the artificial
images of Sect. 3, Fig. 4.
Figure 12 shows the ratio between the calculated
sum (for the four studied fields) and the unblended efficiency.
For
![]() the efficiency is reduced by a factor ranging
from 0.90 in the sparse fields lm048 and lm034 to 0.92 and 0.97
in the denser fields lm019 and lm009.
The brightest star, i=1 accounts for 95% of the rate in the sparse
fields and 88% in the dense fields.
the efficiency is reduced by a factor ranging
from 0.90 in the sparse fields lm048 and lm034 to 0.92 and 0.97
in the denser fields lm019 and lm009.
The brightest star, i=1 accounts for 95% of the rate in the sparse
fields and 88% in the dense fields.
Figure 13 shows the efficiency for unblended events
as a function of u0 and of
![]() for events with
for events with
![]() .
The efficiency for the Bright-Star Sample
has a much weaker dependence on u0 and
.
The efficiency for the Bright-Star Sample
has a much weaker dependence on u0 and
![]() than that for the Full Sample. For the Full Sample
the efficiency falls rapidly with increasing u0and
than that for the Full Sample. For the Full Sample
the efficiency falls rapidly with increasing u0and
![]() (Tisserand 2004).
(Tisserand 2004).
The efficiencies in Figs. 11 and 13 are for
the detection of microlensing events due to simple lenses.
Events due to binary lenses
with caustic crossings are discriminated
against, mostly by C9.
Of the 17 LMC events of the MACHO collaboration (Alcock et al. 2000b)
only 1 event, MACHO-LMC-9,
is of this type and would not pass our selection criteria.
This event corresponds to ![]()
![]() of their optical depth.
We note also that toward the Galactic Bulge
of their optical depth.
We note also that toward the Galactic Bulge ![]()
![]() of the
observed microlensing events are
due to binary lenses (Udalski et al. 2000a).
To compensate for
this loss of efficiency, we conservatively reduce the efficiency
of Fig. 11 by a factor 0.9when calculating limits on the optical depth.
of the
observed microlensing events are
due to binary lenses (Udalski et al. 2000a).
To compensate for
this loss of efficiency, we conservatively reduce the efficiency
of Fig. 11 by a factor 0.9when calculating limits on the optical depth.
The microlensing optical depth, ![]() ,
is defined as the probability that
any given star, at a given time, is amplified by at least 1.34,
i.e. with an impact parameter u < 1.
From a set of
,
is defined as the probability that
any given star, at a given time, is amplified by at least 1.34,
i.e. with an impact parameter u < 1.
From a set of
![]() events,
events, ![]() can be
estimated from
can be
estimated from
In the LMC we have found no events so we can only
give an upper limit on ![]() by calculating
the expected number of events as a function of
by calculating
the expected number of events as a function of ![]() as given by (9).
For this analysis we use the
as given by (9).
For this analysis we use the ![]() distribution of the S model
(Alcock et al. 2000b)
shown in Fig. 14. It relates
distribution of the S model
(Alcock et al. 2000b)
shown in Fig. 14. It relates
![]() to the macho mass (assumed unique):
to the macho mass (assumed unique):
![]() .
Limits using other halo models or macho mass distributions
can be found to often good approximation
by simply scaling (9)
with
.
Limits using other halo models or macho mass distributions
can be found to often good approximation
by simply scaling (9)
with
![]() .
.
The expected number of LMC events for
![]() as a function of
lens mass, M, is shown in Fig. 15a.
For
as a function of
lens mass, M, is shown in Fig. 15a.
For
![]() ,
we have
,
we have
![]() ,
,
![]() ,
,
![]() and
and
![]() ,
giving 32 LMC events for EROS-2. We add 7 LMC events for EROS-1 to give
a total of 39 expected events for
,
giving 32 LMC events for EROS-2. We add 7 LMC events for EROS-1 to give
a total of 39 expected events for
![]() .
.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{6017fg14.eps}\end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg217.gif) |
Figure 14:
The |
| Open with DEXTER | |
For no observed events (N<3.0, 95% CL),
the 95% CL upper limit on the optical depth
is
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{6017fg15.eps} \end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg223.gif) |
Figure 15:
The top panel shows the numbers of expected events as a function of
macho mass M for the S model of Alcock et al. (2000b).
The expectations for EROS-2-LMC, SMC (this work) are shown along with
those of EROS-1 (Renault et al. 1997) with contributions
from the photographic plate program (Ansari et al. 1996a) and
CCD program (Renault et al. 1998).
The number of events for EROS-2-SMC supposes
|
| Open with DEXTER | |
For the SMC, the one observed event corresponds to an optical depth of
![]() (
(
![]() ).
Taking into account
only Poisson statistics on one event,
).
Taking into account
only Poisson statistics on one event,
![]() (90% CL) this gives
(90% CL) this gives
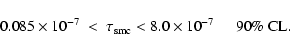 |
(19) |
We also note that the self-lensing interpretation is favored from the absence of an indication of parallax in the light curve (Assef et al. 2006).
We can combine the LMC data and the SMC data to give
a limit on the
halo contribution to the optical depth by supposing that the SMC optical
depth is the sum of a halo contribution,
![]() (
(
![]() )
and a self-lensing contribution
)
and a self-lensing contribution
![]() .
(We conservatively ignore contributions from LMC self-lensing
and from lensing by stars in the disk of the Milky Way.)
For one observed SMC event with
.
(We conservatively ignore contributions from LMC self-lensing
and from lensing by stars in the disk of the Milky Way.)
For one observed SMC event with
![]() and zero
observed LMC events, the likelihood function
is
and zero
observed LMC events, the likelihood function
is
![\begin{displaymath}L(\tau_{\rm lmc},\tau_{\rm sl}) ~\propto~
\left[
\alpha\tau_...
...E})
\right]
\exp\left[-~N(\tau_{\rm lmc},\tau_{\rm sl})\right]
\end{displaymath}](/articles/aa/full/2007/26/aa6017-06/img235.gif)
A possible systematic error in our result could come from our assumption
that the optical depth due to binary lenses is small, 10% of the total.
An alternative strategy would have been to relax the cuts so as to include
the event shown in Fig. 8.
We have chosen not to do this because the light curve itself
is not sufficiently
well sampled to establish the nature of the event (other than that it is not
a simple microlensing event) and also because of its anomalous position in the
color-magnitude diagram. We note also that the optical depth
associated with the event,
![]() ,
is
a factor
,
is
a factor ![]() 4 below the
upper limit (17).
4 below the
upper limit (17).
Another important question concerns the influence on our results
of the Bright-Sample magnitude cut. Since the cut was not established
before the event search, it is natural to ask if the position of the
cut was chosen to give a strong limit. In fact, elimination of the
cut would not change significantly the conclusions of this paper.
Four additional events
(EROS2-LMC-8, 9, 10 and 11 from Table 2)
were found with the analysis described in Appendix A.
The baselines of the source stars of these events are
on average 0.9 mag below the Bright Sample cut. An additional
event (EROS2-LMC-12) with no
![]() data during the variation was found.
The values of
data during the variation was found.
The values of ![]() for these events are in the range 10-60 days, similar
to those in the MACHO sample.
The optical depth associated with the four events seen in two colors
is
for these events are in the range 10-60 days, similar
to those in the MACHO sample.
The optical depth associated with the four events seen in two colors
is
![]() (Tisserand 2004),
not in contradiction with the limit from
the Bright-Sample analysis.
The 95% CL limit on the halo fraction is 12% at
(Tisserand 2004),
not in contradiction with the limit from
the Bright-Sample analysis.
The 95% CL limit on the halo fraction is 12% at
![]() .
We prefer to use the limit from the Bright Sample
for the reasons already mentioned: better understanding of blending and
a superior photometry allowing better rejection of variable stars.
Indeed, inspection of the light curves of EROS2-LMC-8-12 in
Figs. A.1-A.5 indicates that most are not
especially convincing candidates. An exception is
EROS2-LMC-8 but its position in the color-magnitude diagram
and strongly chromatic magnification indicate that
the event is most likely due to a lens in the Milky Way disk.
.
We prefer to use the limit from the Bright Sample
for the reasons already mentioned: better understanding of blending and
a superior photometry allowing better rejection of variable stars.
Indeed, inspection of the light curves of EROS2-LMC-8-12 in
Figs. A.1-A.5 indicates that most are not
especially convincing candidates. An exception is
EROS2-LMC-8 but its position in the color-magnitude diagram
and strongly chromatic magnification indicate that
the event is most likely due to a lens in the Milky Way disk.
The limits shown in Fig. 15 rule out machos as the
majority of Galactic dark matter over the range
![]() .
The limits are f<0.04 for
.
The limits are f<0.04 for
![]() and f<0.1 for
and f<0.1 for
![]() .
We note that even stronger limits in the range
.
We note that even stronger limits in the range
![]() were found (Alcock et al. 1998) by
combining the data from the EROS-1 CCD program with
those of the MACHO program.
These data gave f<0.07 for
were found (Alcock et al. 1998) by
combining the data from the EROS-1 CCD program with
those of the MACHO program.
These data gave f<0.07 for
![]() .
It should also be possible to improve limits in the range
.
It should also be possible to improve limits in the range
![]() by combining the results presented here with the MACHO high mass results
(Alcock et al. 2001b).
This may narrow the small remaining allowed macho mass range
between the range excluded by microlensing and that excluded
by the abundance of halo wide binary stars (Yoo et al. 2004).
by combining the results presented here with the MACHO high mass results
(Alcock et al. 2001b).
This may narrow the small remaining allowed macho mass range
between the range excluded by microlensing and that excluded
by the abundance of halo wide binary stars (Yoo et al. 2004).
Initially,
the EROS and MACHO programs were primarily motivated by the
search for halo brown dwarfs of mass
![]() .
Such objects
are clearly ruled out as primary components of the Milky Way halo
by Fig. 15 (implying f<0.04) and
the data of the MACHO collaboration (Alcock et al. 2000b).
.
Such objects
are clearly ruled out as primary components of the Milky Way halo
by Fig. 15 (implying f<0.04) and
the data of the MACHO collaboration (Alcock et al. 2000b).
The observation of 17 events by MACHO with
![]() suggested the existence of machos of
suggested the existence of machos of
![]() .
Such objects could be invisible (e.g. primordial black holes) or
faint (e.g. cool white dwarfs). However, the latter
are not seen at the corresponding level
in multi-color surveys (Gates et al. 2004)
and high
proper-motion surveys (Reid 2005; Goldman et al. 2002, and references therein).
.
Such objects could be invisible (e.g. primordial black holes) or
faint (e.g. cool white dwarfs). However, the latter
are not seen at the corresponding level
in multi-color surveys (Gates et al. 2004)
and high
proper-motion surveys (Reid 2005; Goldman et al. 2002, and references therein).
At any rate,
the EROS limit (17) is significantly less than the MACHO result
![]() .
However,
there are considerable differences between the EROS and MACHO
data sets that may
help to resolve
the conflict. Generally speaking, MACHO uses faint stars in dense fields
(
.
However,
there are considerable differences between the EROS and MACHO
data sets that may
help to resolve
the conflict. Generally speaking, MACHO uses faint stars in dense fields
(
![]() stars over
stars over
![]() )
while EROS-2 uses bright stars in
sparse fields (
)
while EROS-2 uses bright stars in
sparse fields (
![]() stars over
stars over
![]() ).
Of these bright EROS-2 stars,
).
Of these bright EROS-2 stars,
![]() are in MACHO fields.
are in MACHO fields.
The use of dense fields by the MACHO group suggests that the higher MACHO optical depth may be due, in part, to self-lensing in the inner parts of the LMC. This would contradict LMC models (Mancini et al. 2004) which suggest that only 1-3 MACHO events should be expected to be due to self-lensing. In fact, MACHO-LMC-14 is known to be due to self-lensing (Alcock et al. 2001c) because it has a binary source and the form of the accompanying deformation of the lightcurve with respect to the simple microlensing lightcurve requires that the lens be in the LMC. A second event, MACHO-LMC-9, is due to a binary lens and the self-lensing interpretation can be avoided only by assuming that the source is also a binary system and that each of the two widely separated components happened to land on the caustic on the two successive observations made of the caustic entrance (Alcock et al. 2000a).
If it turns out that the self-lensing rate is higher than
the model estimates
in the MACHO fields but still negligible in the outer fields of
the LMC, the disagreement between MACHO and this work is considerably
reduced. Since only 1/3 of our Bright Sample stars are in MACHO fields,
the EROS-2 95% CL upper limit on ![]() for the MACHO fields is the limit (17)
multiplied by a factor 3,
consistent with the Alcock et al. (2000b)
result as modified by Bennett (2005).
for the MACHO fields is the limit (17)
multiplied by a factor 3,
consistent with the Alcock et al. (2000b)
result as modified by Bennett (2005).
A possible explanation for the discrepancy that is similar to self-lensing is the possibility that the events are due to halo lenses but the Halo is clumpy and that the MACHO-fields lie behind a clump of size less than that of the EROS-2 fields. The effect of a clumpy halo on the optical depth was discussed by Holopainen et al. (2006) though they did not discuss directly the possibility that it could resolve the EROS-MACHO controversy. At any rate, if this is the cause of the discrepancy, the EROS-2 result gives the more representative optical depth because it is based on a larger solid angle.
The use of faint stars by MACHO may also give an explanation of the disagreement. Only two of the 17 MACHO candidates (MACHO-LMC-18 and 25) are sufficiently bright to be in our Bright-Star Sample. Of these two, MACHO-LMC-18 is in the EROS Bright-Sample only because the EROS starfinder mixed two similar objects that are resolved by the MACHO starfinder.
The use of faint stars by MACHO suggests two possible explanations for the disagreement. The first would be contamination by variable stars that, in our Bright-Star Sample, are either not present or identified as such because of superior photometric precision. The low photometric precision for the faint LMC stars makes most of the events less convincing than the events on bright stars in the Galactic Bulge or the one EROS event in the SMC. Indeed, one of the MACHO A events, MACHO-LMC-23, has been identified as a variable star by a second variation in the EROS-2 data shown in Fig. 10 (Tisserand 2004). As already noted, Bennett et al. (2005) argued that MACHO-LMC-23 was, in any case, a weak candidate and that its variability doesn't call into question the nature of the other MACHO candidates. Indeed, some of the MACHO candidates are very convincing microlensing candidates. In particular, MACHO-LMC 1, 5, 9, 14 and 21 are strong candidates based only on MACHO photometry while Bennett et al. (2005) argued that MACHO-LMC-4, 13 and 15 are strong candidates because of high precision followup photometry. We might note, however, that of these candidates, MACHO-LMC-14 is most likely due to LMC self-lensing and MACHO-LMC-5 is due to lensing by a normal red-dwarf star in the disk of the Milky Way (Alcock et al. 2001d; Gould 2004).
The second possible explanation related to the use of faint source stars is the large blending effects that must be understood. Alcock et al. (2001a,2000b) suggest a 30% systematic error to reflect this uncertainty. The experience with the use of faint stars in the Galactic Bulge suggests that this uncertainty may be underestimated, though in principle the star distribution is better understood in the LMC than in the Bulge. At any rate, the extension of the limits presented here, either by EROS or by OGLE-3 or SuperMACHO, will require the use of faint stars and a good understanding of blending.
Acknowledgements
Over the last 17 years, the EROS collaboration has profited from discussions with members of the MACHO collaboration, especially Charles Alcock (who introduced us to machos and microlensing), Dave Bennett, Kim Griest and Chris Stubbs. We thank Annie Robin for help with the Galactic model calculations. We are grateful to the technical staff of ESO, La Silla for the support given to the EROS-2 project. We thank J.-F. Lecointe and A. Gomes for the assistance with the online computing and the staff of the CC-IN2P3, especially the team in charge of the HPSS storage system, for their help with the data management. A.G. was supported by grant AST-0452758 from the NSF and J.A. by the Danish Natural Science Research Council. Finally, we thank the referee for questions and comments that led to significant improvements in this paper.
In this paper we have concentrated on the analysis of the Bright-Star Sample of stars because this leads to the most reliable limits of the optical depth. A search for microlensing events on the full sample of stars was also performed (Tisserand 2004). The candidates found in this search are listed in Table 2 and displayed in Figs. A.1-A.5. In this section we list the selection criteria leading to this set of candidates.
The criteria are very similar to those described in Sect. 4 for the Bright-Star Sample. However, the problems encountered with analyzing low precision light curves necessarily led to more complicated criteria to avoid the many spurious events caused by photometric problems. In all, 17 criteria, c1-c17, were applied compared to the 12 criteria, C1-C12, applied to the Bright-Star Sample.
The first four criteria are identical to those applied to
the Bright-Star Sample:
For excursions with a regular variation, the point-to-point dispersion
of the measured fluxes within the excursion,
![]() ,
obtained from the comparison of each measured flux with the linear
interpolation of its two neighbors (in time), is normally smaller than the
global dispersion,
,
obtained from the comparison of each measured flux with the linear
interpolation of its two neighbors (in time), is normally smaller than the
global dispersion,
![]() ,
i.e. the width of the distribution of all fluxes within the excursion.
To exclude irregular variations, we require that their ratio be sufficiently
small;
,
i.e. the width of the distribution of all fluxes within the excursion.
To exclude irregular variations, we require that their ratio be sufficiently
small;
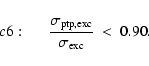
The next two criteria are similar to C5 and C9 applied to the
Bright-Star Sample
![\begin{displaymath}c7:\hspace*{5mm} \left[\frac{ \chi^2 - N_{\rm dof} }
{ \sqrt{2 N_{\rm dof} }}\right]_{\rm base}\;
<\; 15 ,
\end{displaymath}](/articles/aa/full/2007/26/aa6017-06/img265.gif)
![\begin{displaymath}c8:\hspace*{5mm}
\left[\frac{ \chi^2 - N_{\rm dof} }{ \sqrt{2 N_{\rm dof} }}\right]_{\rm peak}\;
<\; 10 .
\end{displaymath}](/articles/aa/full/2007/26/aa6017-06/img266.gif)
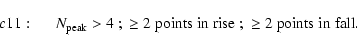
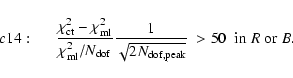
The first six events in Table 2 passed the cuts c1-c17. A monochromatic analysis was performed where c10 was removed and candidates were only required to pass the other criteria in either of the two colors. About 500 events were scanned by eye. Only one event, EROS2-LMC-12, was found, the others being due to photometric problems or long period variable stars.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{6017ap01.eps} \end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg275.gif) |
Figure A.1: The light curves of EROS-2 star lm055-7m-23303. Also shown is the color-magnitude diagram of the star's CCD-quadrant and the excursion of the event. |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{6017ap02.eps} \end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg276.gif) |
Figure A.2: The light curves of EROS-2 star lm042-1l-2622. Also shown is the color-magnitude diagram of the star's CCD-quadrant and the excursion of the event. |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{6017ap04.eps} \end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg278.gif) |
Figure A.4: The light curves of EROS-2 star lm061-4m-15782. Also shown is the color-magnitude diagram of the star's CCD-quadrant and the excursion of the event. |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{6017ap05.eps} \end{figure}](/articles/aa/full/2007/26/aa6017-06/Timg279.gif) |
Figure A.5: The light curves of EROS-2 star lm085-6l-14234. Also shown is the color-magnitude diagram of the star's CCD-quadrant and the position of the source's baseline. |