A&A 467, 359-369 (2007)
DOI: 10.1051/0004-6361:20065091
National Astronomical Observatory of Japan, Mizusawa, 2-12, Hoshigaoka-cho, Mizusawa-ku, Oshu-shi, Iwate-ken, 023-0861, Japan
Received 25 February 2006 / Accepted 13 December 2006
Abstract
Aims. An alternative to the traditional method for modeling the kinematics of the Earth's rotation is proposed. The purpose of developing the new approach is to provide a self-consistent and simple description of the Earth's rotation in a way that can be estimated directly from observations without using intermediate quantities.
Methods. Instead of estimating the time series of pole coordinates, the UT1-TAI angles, their rates, and the daily offsets of nutation, the method for estimating coefficients of the expansion of a small perturbational rotation vector into basis functions is proposed. The resulting transformation from the terrestrial coordinate system to the celestial coordinate system is formulated as the product of the a priori matrix of a finite rotation and an empirical vector of a residual perturbational rotation. In the framework of this approach, the specific choice of the a priori matrix is irrelevant, provided the angles of the residual rotation are small enough to neglect their squares. The coefficients of the expansion into the B-spline and Fourier bases, together with estimates of other nuisance parameters, are evaluated directly from observations of time delay or time range in a single least square solution.
Results. This approach was successfully implemented in a computer program for processing VLBI observations. The dataset from 1984 through 2006 was analyzed. The new procedure adequately represents the Earth's rotation, including slowly varying changes in UT1-TAI and polar motion, the forced nutations, the free core nutation, and the high frequency variations of polar motion and UT1.
Key words: reference systems - Earth - techniques: interferometric
As we learn from an elementary physics course in high school, the rotation of a rigid body can be represented by three angles. Euler angles are usually selected as parameters, although it is not the only choice. We can say that rotation of an arbitrary body is defined if a functional dependence of Euler angles on time is known.
However, when we are dealing with the Earth, the traditional way of representing the kinematics of the Earth's rotation is not as simple. In modern textbooks that follow the formalism of Newcomb-Andoyer, for instance Seidelmann (1992), the Earth's rotation is represented as the product of 9 matrices that depend on many parameters. Analytical expressions are provided for some of them, but other parameters are supposed to be determined from observations. These parameters are defined though intermediate quantities. These intermediate quantities, like the Earth's rotation axis, the celestial ephemeris pole, the true equinox of date, the non-rotating origin, and others, are not objects that can be observed, but idealistic concepts that do not have a clear, intuitive interpretation.
According to the traditional approach (e.g. McCarthy & Petit 2004), in order to get the Earth's orientation at any given moment, one should first compute the values of intermediate parameters that have more than a thousand terms, then interpolate tables of corrections produced by smoothing results of analysis of observations, and finally compute the product of rotational matrices that depend on these intermediate quantities.
At first glance it seems that the complexity of representing the Earth's
rotation is unavoidable, since it should reflect the complexity of a theory
for modeling the Earth's rotation at the level of the accuracy of observations,
i.e. on the order of 10-10 rad![]() . This would be
true if theoretical models were precise to that level. Roughly speaking,
the Earth's rotation can be considered as consisting of two components, the tidally driven component with precisely known frequencies
and the component driven by an exchange of the angular momentum between
the solid Earth and geophysical fluids. The latter component is not
predictable in principle. The atmosphere contributes to the UT1 at a level
of 10-6 rad, more than three orders of magnitude higher than the
accuracy of observations. For a long period of time, it was considered that
the quasi-diurnal motion of the pole, namely the precession and nutation,
can be modeled with a precision comparable to the accuracy of observations.
First results of VLBI analysis presented by Herring et al. (1986) shattered this
belief. It was discovered that even the most advanced nutation theory
of Wahr (1980) was not accurate enough. Numerous attempts to build
a theory of tidally driven quasi-diurnal motion were made, but they were
not completely successful. In order to reduce the disagreement between
theories and observations, the authors had to resort to adjusting some
parameters of their theories to quantities derived from the same
observations of the quasi-diurnal motion
(Mathews et al. 1991; Getino & Ferrandiz 2001; Mathews et al. 2002). It was also soon realized that
there are two other constituents of the quasi-diurnal polar motion at the
level of 1 nanoradian: the free core nutation (Moritz 1987) and the nutation
excited by the atmosphere (Bizouard et al. 1998). These constituents currently
cannot be predicted and, presumably, they cannot be predicted in principle.
Therefore, even if a precise theory of forced nutation is developed in
the future, one should apply parameters determined from observations in
order to represent the quasi-diurnal motion.
. This would be
true if theoretical models were precise to that level. Roughly speaking,
the Earth's rotation can be considered as consisting of two components, the tidally driven component with precisely known frequencies
and the component driven by an exchange of the angular momentum between
the solid Earth and geophysical fluids. The latter component is not
predictable in principle. The atmosphere contributes to the UT1 at a level
of 10-6 rad, more than three orders of magnitude higher than the
accuracy of observations. For a long period of time, it was considered that
the quasi-diurnal motion of the pole, namely the precession and nutation,
can be modeled with a precision comparable to the accuracy of observations.
First results of VLBI analysis presented by Herring et al. (1986) shattered this
belief. It was discovered that even the most advanced nutation theory
of Wahr (1980) was not accurate enough. Numerous attempts to build
a theory of tidally driven quasi-diurnal motion were made, but they were
not completely successful. In order to reduce the disagreement between
theories and observations, the authors had to resort to adjusting some
parameters of their theories to quantities derived from the same
observations of the quasi-diurnal motion
(Mathews et al. 1991; Getino & Ferrandiz 2001; Mathews et al. 2002). It was also soon realized that
there are two other constituents of the quasi-diurnal polar motion at the
level of 1 nanoradian: the free core nutation (Moritz 1987) and the nutation
excited by the atmosphere (Bizouard et al. 1998). These constituents currently
cannot be predicted and, presumably, they cannot be predicted in principle.
Therefore, even if a precise theory of forced nutation is developed in
the future, one should apply parameters determined from observations in
order to represent the quasi-diurnal motion.
Recognizing that both components in the Earth rotation cannot be predicted with accuracy comparable to the precision of observations, prompts us to reconsider approaches to representing the Earth's rotation and the role of the theory. The quasi-diurnal motion should be described with the use of parameters determined by continuous observations in a similar way as the UT1 and Chandler polar motion. The theory of nutation should be considered not as a tool for data reduction or for predicting the Earth's orientation, but as a means for validating geophysical models. At the same time, a theory of the Earth's rotation can provide valuable guidance for building empirical mathematical models.
The goals of this paper are to build such an empirical mathematical model, to demonstrate using a long dataset of observations that it is feasible, and to show that this approach describes the Earth rotation at least as well as the traditional way. It should be noted that an empirical mathematical model has a different meaning than a theoretical model. The theoretical model relates a function of time that describes the Earth rotation with specific properties of the Earth's body in the form of a solution of the equation of dynamics. The empirical mathematical model relates this function of time to observations using a parameter estimation technique. A minimal requirement for an empirical model is to represent the phenomena with the least possible errors for the entire interval of observations and to provide estimates of uncertainties. We will also try to satisfy two additional requirements: the model should be simple and the parameters of the model should not be strongly correlated. If parameter estimates are strongly correlated, their comparison with theoretical predictions becomes problematic. We will represent the Earth orientation parameters (EOP) in the form of an expansion over a family of basis functions.
The procedure for developing an empirical model of the Earth's rotation is presented in the rest of the paper. The choice of the a priori model and basis functions is described in Sect. 2, the proposed mathematical models is described in Sect. 3, the strategy of analysis of the 22 year long dataset of VLBI observations is presented in Sect. 4, and the results of solutions are discussed in Sect. 5. Concluding remarks are given in Sect. 6.
We consider here that N stations observe K celestial physical bodies.
It is assumed that each station is associated with a reference point.
In the case of VLBI antennas with intersecting axes, this is the intersection
point of the axes. Observing stations receive electromagnetic radiation
emitted by celestial bodies, and each sample of the received signal
is associated with a time stamp from a local frequency standard synchronized
with the GPS time. Analysis of voltage and time stamps of received radiation
eventually allows us to derive photon propagation time from reference
points of observed bodies to reference points of observing stations.
These distances depend on the relative positions of stations with respect
to the observed bodies. The instantaneous coordinate vector of station i,
![]() ,
at a given moment of time is represented as the
sum of a rotation and translation applied to a vector
,
at a given moment of time is represented as the
sum of a rotation and translation applied to a vector
![]() at initial epoch t0 as
at initial epoch t0 as
The displacement vector
![]() characterizes the motion of an individual station, while matrix
characterizes the motion of an individual station, while matrix
![]() and
vector
and
vector ![]() describe the motion of the entire network. Assuming the
stations are solidly connected to the Earth's crust, we consider that this
part of motion represents the motion of the entire Earth. In particular,
matrix
describe the motion of the entire network. Assuming the
stations are solidly connected to the Earth's crust, we consider that this
part of motion represents the motion of the entire Earth. In particular,
matrix
![]() describes the Earth's rotation.
Schematically, the mechanical model of observations can be viewed as the
motion of the polyhedron of observing stations with respect to the polyhedron
of observed bodies (Fig. 1). It should be noted that the
EOP are defined here as the parameters of an estimation model, while in the
framework of the traditional approach, they are defined as angles between
big circles on a sphere.
describes the Earth's rotation.
Schematically, the mechanical model of observations can be viewed as the
motion of the polyhedron of observing stations with respect to the polyhedron
of observed bodies (Fig. 1). It should be noted that the
EOP are defined here as the parameters of an estimation model, while in the
framework of the traditional approach, they are defined as angles between
big circles on a sphere.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.1cm,clip]{5091fig1.eps}\end{figure}](/articles/aa/full/2007/19/aa5091-06/Timg18.gif) |
Figure 1: The polyhedron of observing stations (black) and the polyhedron of observed bodies (grey). The relative orientation of two polyhedrons is estimated from observations of projections of vectors between observing stations and observed bodies and interpreted as the Earth's rotation. |
| Open with DEXTER | |
Since both
![]() and vector
and vector
![]() are
functions of time, i.e. infinite sets of points, they can be evaluated from
a finite set of observations only in the form of an expansion in some functions.
When we say that the matrix
are
functions of time, i.e. infinite sets of points, they can be evaluated from
a finite set of observations only in the form of an expansion in some functions.
When we say that the matrix
![]() is determined
from observations, this should not be understood literally, but instead it
should be construed that a mathematical model for the dependence of
is determined
from observations, this should not be understood literally, but instead it
should be construed that a mathematical model for the dependence of
![]() on time is assumed, either explicitly or
implicitly. The model depends on a finite set of unknown parameters that
are determined from observations.
on time is assumed, either explicitly or
implicitly. The model depends on a finite set of unknown parameters that
are determined from observations.
The choice of the mathematical model is not unique. On one hand, the mathematical model should approximate the rotation with errors comparable to uncertainties of observations during the full interval of observations. On the other hand, we should be able to estimate robustly all the parameters of the model. Let us consider several approaches.
The easiest way to represent a rotation is to estimate the matrix
![]() at certains moment of time and, thus, generate the time series. The 3
at certains moment of time and, thus, generate the time series. The 3 ![]() 3 matrix
3 matrix
![]() has 9 elements, but only three of them are
linearly independent. An arbitrary rotation matrix can be decomposed in
a product of several elementary rotation matrices with respect to coordinate
axes at certain angles. Therefore, it is sufficient to determine these rotation
angles in order to determine the matrix
has 9 elements, but only three of them are
linearly independent. An arbitrary rotation matrix can be decomposed in
a product of several elementary rotation matrices with respect to coordinate
axes at certain angles. Therefore, it is sufficient to determine these rotation
angles in order to determine the matrix
![]() from observations.
from observations.
The fundamental problem is that no observation technique, except the laser gyroscope, is sensitive to the instantaneous Earth's rotation vector or to its time derivatives directly. The rotation angles can be derived using the least square estimation procedure, together with evaluating other parameters. It requires accumulating sufficient amount of data in order to separate variables. The estimates of the Earth's rotation angles cannot be sampled too fast. A typical sampling rate of estimates is one day, since this allows compensation for a certain type of systematic error. In some cases the sampling rate can be reduced to several hours.
Unfortunately, one cannot neglect changes in the Earth's rotation angles
during the sampling interval. The accuracy in determining rotation angles
for the 24-h period is nowadays at the level of 2-5 ![]() 10-10 rad. The amplitude of the quasi-diurnal motion around axes 1 and 2
is growing with a rate that is an order of magnitude of
7
10-10 rad. The amplitude of the quasi-diurnal motion around axes 1 and 2
is growing with a rate that is an order of magnitude of
7 ![]() 10-12 rad s-1. Therefore, this motion should first be
separated from the slowly varying components. In the era of optical
astrometry, some components of this motion, namely precession and nutation,
were determined separately from observations of slowly varying components
using a different technique and even different instruments. The observations
of slowly varying constituents in the Earth's rotation angles were corrected
with a model of the quasi-diurnal motion. Herring et al. (1986) have demonstrated
that corrections to the model of the quasi-diurnal motion around axes 1 and 2
can be estimated together with slowly varying components of the Earth rotation,
if the rotation angles around coordinate axes Ai(t) are parameterized
in the form
10-12 rad s-1. Therefore, this motion should first be
separated from the slowly varying components. In the era of optical
astrometry, some components of this motion, namely precession and nutation,
were determined separately from observations of slowly varying components
using a different technique and even different instruments. The observations
of slowly varying constituents in the Earth's rotation angles were corrected
with a model of the quasi-diurnal motion. Herring et al. (1986) have demonstrated
that corrections to the model of the quasi-diurnal motion around axes 1 and 2
can be estimated together with slowly varying components of the Earth rotation,
if the rotation angles around coordinate axes Ai(t) are parameterized
in the form
However, it is important to realize the limitations of the time series approach. First, the raw time series of estimates provides the values of rotation angles only at specific discrete moments. They do not determine a functional dependence of rotation angles on time. An end user needs to have a tool for computing Earth's orientation at any moment of time within the interval of observations. Thus, the raw time series are the basis for the second step of processing that involves smoothing and interpolation. Smoothing and interpolation of the time series ck, sk, b1k, b2k, b3k implicitly assumes that Ai(t) satisfies some mathematical model that appears to be different from the model in expression (2) used in the estimation process. The resulting smooth function of rotation angles does not provide the best fit to observations; if it did, no smoothing would have been needed.
Second, at the present level for accuracy of observations, the estimation
model corresponding to Eqs. (2) is not adequate: one cannot neglect
changes in
c(t), s(t) and
![]() over the interval
of estimation, typically 24 hours. Adjusting time derivatives
over the interval
of estimation, typically 24 hours. Adjusting time derivatives
![]() makes estimates of these parameters so strongly
correlated that they do not have a practical value.
makes estimates of these parameters so strongly
correlated that they do not have a practical value.
Changes in the a priori model for slowly varying components of rotation
angles affect all estimated parameters, including c(t) and s(t). In order
to demonstrate this, two VLBI solutions using 3563 twenty four hour observing
sessions from 1984 through 2006 were computed. The USNO Finals EOP time series
of pole coordinates and UT1-TAI with a time span of
1 day (Dick & Richter 2004)![]() were used as the a priori model
in the reference solution. The Gaussian noise with standard deviation
1 nrad was added to all components of the USNO Finals EOP series, and these
modified time series were used in the trial solution. The rms of differences
in the total values of
b(t), c(t), s(t), i.e., the sum of a priori
values and adjustments over the 24 h time intervals, was
0.14 nrad for b(t) and 0.16 nrad for c(t) and s(t). Since the accuracy
of estimates of
b(t), c(t), s(t) from 24 h VLBI experiments is currently
at a 0.3 nrad level, the accuracy of the a priori EOP series should be better
than 1 nrad in order to reduce the contribution its errors to a negligible
level: 1/2 of the random error in estimates. In a similar way, the change
in the a priori model for the quasi-diurnal motion also affects estimates of
c(t), s(t) and bi(t). Although one can expect that
a continuous process or refining the a priori model and subsequent least
square estimation should converge, this does not happen in practice. It is
known among analysts who process raw data that, if the initial a priori values
are changed, the total angles, i.e. the sum of the a priori and the
adjustments, come out different. Researchers who process time series are not
always aware of these complications and tend to consider the results
of processing the same observations by different analysts as independent
"data'', so they attribute the differences between them to so-called
"analyst noise''. These discrepancies occur due to an internal inconsistency
between the estimation model, the a priori model, and the post-processing
procedure.
were used as the a priori model
in the reference solution. The Gaussian noise with standard deviation
1 nrad was added to all components of the USNO Finals EOP series, and these
modified time series were used in the trial solution. The rms of differences
in the total values of
b(t), c(t), s(t), i.e., the sum of a priori
values and adjustments over the 24 h time intervals, was
0.14 nrad for b(t) and 0.16 nrad for c(t) and s(t). Since the accuracy
of estimates of
b(t), c(t), s(t) from 24 h VLBI experiments is currently
at a 0.3 nrad level, the accuracy of the a priori EOP series should be better
than 1 nrad in order to reduce the contribution its errors to a negligible
level: 1/2 of the random error in estimates. In a similar way, the change
in the a priori model for the quasi-diurnal motion also affects estimates of
c(t), s(t) and bi(t). Although one can expect that
a continuous process or refining the a priori model and subsequent least
square estimation should converge, this does not happen in practice. It is
known among analysts who process raw data that, if the initial a priori values
are changed, the total angles, i.e. the sum of the a priori and the
adjustments, come out different. Researchers who process time series are not
always aware of these complications and tend to consider the results
of processing the same observations by different analysts as independent
"data'', so they attribute the differences between them to so-called
"analyst noise''. These discrepancies occur due to an internal inconsistency
between the estimation model, the a priori model, and the post-processing
procedure.
Third, the second step in the analysis, smoothing and interpolation, is rather subjective. A different degree of smoothing produces a different series.
Finally, the time series cannot be used directly for making an inference about the physical processes that affect the Earth's rotation. The time series are transformed by various analysis procedures. The dependence of the series on the a priori model and the correlations between the elements of time series are usually ignored. The correlations between the elements are not zero, because the elements themselves were estimated together with other parameters like global site velocity or source positions that are considered common for the entire interval of observations. Although these correlations are not strong, typically at a level of 0.1, their contribution is significant when long time series are processed.
Due to the complexity of the a priori model, analysts who process the time series of estimates usually do not handle the total angles of the Earth's rotation, but rather adjustments to the a priori values, tacitly assuming that analysts who processed the raw data strictly followed a standardized procedure for data reduction. In reality this is often not the case. This creates an additional source of confusion and errors.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{5091fig2.eps} \end{figure}](/articles/aa/full/2007/19/aa5091-06/Timg28.gif) |
Figure 2:
The logarithm of the power spectrum of the tide generating
potential in
|
| Open with DEXTER | |
These complications prompt us to look for a one-step procedure of estimation of the Earth's orientation parameters.
While Eqs. (2) represent rotation angles within a short period
of time, 24 h, they are not adequate for a longer period of time. We need
to find a mathematical model which would be valid for the entire period
of observations, i.e. several decades. The matrix
![]() has a non-linear dependence on its
arguments. A linear estimator, the least square method, allows us to evaluate
not the matrix itself, but its small perturbation. The coordinate
transformation of a vector
has a non-linear dependence on its
arguments. A linear estimator, the least square method, allows us to evaluate
not the matrix itself, but its small perturbation. The coordinate
transformation of a vector ![]() from the terrestrial coordinate system
to the celestial coordinate system is then written as
from the terrestrial coordinate system
to the celestial coordinate system is then written as
In order to find an appropriate basis for expanding of
![]() ,
we
need to use an a priori knowledge of the process under consideration.
The Earth's rotation can be considered in terms of a response to external
forces. The external forces that affect rotation of the solid Earth are
caused 1) by redistribution of geophysical fluids and 2) by tidal attraction
of external bodies. The first process is not predictable and
is dominating at frequencies by modulo much less than the diurnal frequency
,
we
need to use an a priori knowledge of the process under consideration.
The Earth's rotation can be considered in terms of a response to external
forces. The external forces that affect rotation of the solid Earth are
caused 1) by redistribution of geophysical fluids and 2) by tidal attraction
of external bodies. The first process is not predictable and
is dominating at frequencies by modulo much less than the diurnal frequency
![]() .
The tide-generating potential exerted by external bodies can
be considered to be known precisely. Its spectrum has a comb of very sharp
lines as shown in Fig. 2.
.
The tide-generating potential exerted by external bodies can
be considered to be known precisely. Its spectrum has a comb of very sharp
lines as shown in Fig. 2.
To characterize the Earth's response, we should take into account
that the triaxiality of the Earth's inertia tensor (B-A)/C is small,
about 2 ![]() 10-5. Therefore, the differential equations of the Earth's
rotation are linear. First, this leads to decoupling rotation around the axes 1 and 2, i.e. the polar motion, and rotation around the axis 3, the diurnal
motion. Second, the response to harmonic external forces will result
in harmonic variations of the component 2 of
10-5. Therefore, the differential equations of the Earth's
rotation are linear. First, this leads to decoupling rotation around the axes 1 and 2, i.e. the polar motion, and rotation around the axis 3, the diurnal
motion. Second, the response to harmonic external forces will result
in harmonic variations of the component 2 of ![]() with the same
amplitude as component 1 with the phase shifted by
with the same
amplitude as component 1 with the phase shifted by ![]() .
Third,
the excitation at the diurnal frequency will result in the appearance of
cross-terms
.
Third,
the excitation at the diurnal frequency will result in the appearance of
cross-terms
![]() and
and
![]() (Moritz 1987).
(Moritz 1987).
Considering these factors, the following mathematical model for the
the vector of a small perturbational rotation is proposed:
The B-spline basis functions were first introduced by Schönberg (1946). The
B-spline function of degree m depends on time and on a monotonically
nondecreasing sequence of n knots at the interval
[t1, tn]. In order
to introduce splines, let us extend this sequence by adding m elements at
the beginning of the sequence and m-1 elements at the end of the sequence
such that
![]() and
and
![]() .
At a given extended sequence of n+2m-1 knots, n+m-1 B-spline functions with
the pivot element
.
At a given extended sequence of n+2m-1 knots, n+m-1 B-spline functions with
the pivot element
![]() are defined through
a recursive relationship.
are defined through
a recursive relationship.
The B-spline of the 0th degree with the pivot knot ![]()
![]() on the knots sequence
on the knots sequence
![]() ,
such that
,
such that
![]() ,
is determined by
,
is determined by
In general, knots can be selected arbitrarily. Test runs have shown that a set
of B-spline functions of the 3rd degree with equidistant knots with a time
span of 3 days for components 1, 2, and 1 day for component 3 of the vector
![]() adequately represents the slowly varying component of
the Earth's rotation. Weak constraints on values of B-splines, its first
and second derivatives can be imposed to ensure the stability of the solution
at intervals with considerable gaps in observations and at the beginning
and the end of the data set.
adequately represents the slowly varying component of
the Earth's rotation. Weak constraints on values of B-splines, its first
and second derivatives can be imposed to ensure the stability of the solution
at intervals with considerable gaps in observations and at the beginning
and the end of the data set.
Modeling the quasi-diurnal components is more challenging. The tides exerted
by the Moon and the Sun cause variations in sea currents and the sea
surface at tidal frequencies. These variations excite changes in all
components of the Earth's rotation. The resonance near the retrograde diurnal
frequency causes a significant amplification at that frequency band for
components 1 and 2 of the vector
![]() .
The theoretical spectrum
of this motion referred to as nutation computed by
Souchay & Kinoshita (1996,1997) and Souchay et al. (1999) for the model of the
rigid Earth, the REN-2000 expansion, is presented in Fig. 3.
.
The theoretical spectrum
of this motion referred to as nutation computed by
Souchay & Kinoshita (1996,1997) and Souchay et al. (1999) for the model of the
rigid Earth, the REN-2000 expansion, is presented in Fig. 3.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5091fig3.eps}\end{figure}](/articles/aa/full/2007/19/aa5091-06/Timg61.gif) |
Figure 3:
The logarithm of the power spectrum of quasi-diurnal variations
in q1, q2 components of the rotation vector according to
the REN-2000 expansion in
|
| Open with DEXTER | |
The problem is that the spectrum is very dense, and observations during a finite period of time cannot resolve all the constituents. The REN-2000 spectrum has 560 constituents with amplitudes greater than 10-11 rad and 1551 constituents with amplitudes greater than 10-12 rad with the frequency difference between some of them as low as 10-15 rad s-1.
Several strategies can be used for overcoming this problem. First,
we can select frequencies with maximal amplitudes from the theoretical
spectrum and ignore constituents with an angular frequency separation
less than
![]() ,
where
,
where ![]() is the interval
of observations. No signal will be mismodeled if the frequency separation
between the constituents
is the interval
of observations. No signal will be mismodeled if the frequency separation
between the constituents
![]() ,
since in this
case the two constituents will be indistinguishable.
,
since in this
case the two constituents will be indistinguishable.
However, if the constituents are not very close, the mismodeled signal will
leak into adjustments at other frequencies. The sidelobe with the amplitude A2 and frequency ![]() of the main constituent with the
frequency
of the main constituent with the
frequency ![]() can be omitted if the quantity
can be omitted if the quantity
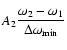 is less than a certain
threshold. Depending on the threshold level, there are several hundred constituents in the tidal spectrum for which this condition is not valid.
is less than a certain
threshold. Depending on the threshold level, there are several hundred constituents in the tidal spectrum for which this condition is not valid.
One way to mitigate this problem is to estimate the amplitude of close
sidelobes, together with the amplitude of main constituents, and to impose
strong constraints on the amplitude of sidelobes by using some a priori
information. It is plausible to assume that the a posteriori amplitudes
of constituents of the quasi-diurnal motion for the real Earth differ from
the theoretical amplitudes computed for the rigid Earth by multiplicative
factors called transfer function, which is a smooth function of frequency
according to theory. Then we can assume that the transfer function for two close constituents with theoretical amplitudes P be the same, i.e.
the ratio of complex amplitudes A of two close constituents
is the same as for the a priori rigid Earth amplitudes, and, therefore,
should satisfy this equation:
An alternative to constraining sidelobes is the strategy of estimating
a wide range of constituents that are multiples of
![]() or, in
other words, indirectly performing the discrete Fourier transform of
the perturbational rotation. With this approach, in general we are
in a position to discard our a priori knowledge about the frequency structure
of the signal. Estimating the signal at discrete frequencies that are
multiples of
or, in
other words, indirectly performing the discrete Fourier transform of
the perturbational rotation. With this approach, in general we are
in a position to discard our a priori knowledge about the frequency structure
of the signal. Estimating the signal at discrete frequencies that are
multiples of
![]() ,
from the zero frequency through the Nyquist frequency, recovers any signal according to the sampling theorem. However,
this kind of approach applied to estimating the vector
,
from the zero frequency through the Nyquist frequency, recovers any signal according to the sampling theorem. However,
this kind of approach applied to estimating the vector
![]() has a practical value only if the number of non-negligible constituents in
the discrete spectrum is significantly less than the total number of samples.
Since the spectrum of the tide-generating potential consists of a set of
discrete frequencies that are not commensurate to each other, the frequencies
that are multiples of
has a practical value only if the number of non-negligible constituents in
the discrete spectrum is significantly less than the total number of samples.
Since the spectrum of the tide-generating potential consists of a set of
discrete frequencies that are not commensurate to each other, the frequencies
that are multiples of
![]() cannot coincide with all tidal
frequencies. If the amplitude of a narrow-band harmonic signal is not
estimated at its frequency, but estimated at a set of nearby frequencies
that are multiples of
cannot coincide with all tidal
frequencies. If the amplitude of a narrow-band harmonic signal is not
estimated at its frequency, but estimated at a set of nearby frequencies
that are multiples of
![]() ,
the signal will be recovered only
partially. The wider the range of frequencies, the better the approximation.
The rate of convergence depends on the amplitude of the signal and the
difference between its frequency and the closest frequency used for estimation.
Selection of reasonably good a priori
,
the signal will be recovered only
partially. The wider the range of frequencies, the better the approximation.
The rate of convergence depends on the amplitude of the signal and the
difference between its frequency and the closest frequency used for estimation.
Selection of reasonably good a priori
![]() values may significantly
reduce the number of frequencies needed for estimation to reach a given
level of accuracy of approximation.
values may significantly
reduce the number of frequencies needed for estimation to reach a given
level of accuracy of approximation.
Other important constituents of the signal at the retrograde diurnal
band are the free near-diurnal wobble (Moritz 1987) and the atmospheric
nutations (Yseboodt et al. 2002; Bizouard et al. 1998). Since this signal is excited by
a broad-band stochastic process, it is expected that these constituents in the
Earth's rotation are also relatively broad-band. To model this
signal, the constituents at frequencies within the range of that band need
to be added to the list of constituents at tidal frequencies. It follows
from the sampling theorem of Kotelnikov (1933) that a band limited signal with
frequencies in the range of
![]() is completely recovered
when the estimates of the sine and cosine amplitudes of the spectrum are
made at discrete frequencies
is completely recovered
when the estimates of the sine and cosine amplitudes of the spectrum are
made at discrete frequencies
![]() .
.
The tidal spectrum also has constituents with low frequencies, so-called
zonal tides. They affect component 3 in the vector of the perturbational
rotation. Their contribution dominates the rate of change for this component.
It would be desirable to estimate the complex amplitude of this variations.
Since the residual rate of change of ![]() is a factor of 3-10 less,
constraints on a rate of change for the residual component of
is a factor of 3-10 less,
constraints on a rate of change for the residual component of ![]() ,
modeled with an expansion over the B-spline basis can be set stronger without
introducing a bias in the estimates. This improves the solution stability during
intervals of time with gaps in observations. For the same reason, it would
be desirable to estimate variations in components 1 and 2 of the Earth's
rotation vector at the annual and Chandler frequencies:
1.990968
,
modeled with an expansion over the B-spline basis can be set stronger without
introducing a bias in the estimates. This improves the solution stability during
intervals of time with gaps in observations. For the same reason, it would
be desirable to estimate variations in components 1 and 2 of the Earth's
rotation vector at the annual and Chandler frequencies:
1.990968 ![]() 10-7 and 1.678
10-7 and 1.678 ![]() 10-7 rad s-1,
respectively.
10-7 rad s-1,
respectively.
It should be noted that the estimates of harmonic constituents with lower
periods than the time span between nodes of B-spline will so highly correlate
with B-spline coefficients that the system of equations will be very close
to singular. Decorrelation constraints on coefficients of the B-spline should
be imposed in order to overcome this problem. We require that the product
of expansion over basic B-spline and Fourier functions for the jth frequency be zero over the interval of observations:
A set of estimates of group delays at frequency bands centered around 2.2 and 8.6 GHz from January 1984 through January 2006 was used to validate the proposed approaches. The International VLBI Service for Geodesy and Astrometry (IVS) (Vandenberg 1999) provides online access to the collection of all observations made in the geodetic mode under various astrometric and geodynamics programs from 1979 through now at http://ivscc.gsfc.nasa.gov. The VLBI data set shows a substantial spatial and time inhomogeneity. Typically, observations are made in sessions with a duration of about 24 h. Observations were sporadic in the early 80s, but in January 1984 a regular VLBI campaign for the determination of the Earth orientation parameters started first with 5-day intervals, from May 1993 with weekly intervals, and from 1997 twice a week. In addition to these observations, various other observing campaigns were running. On average, 150 sessions per year have been observed since 1984.
During that period 153 stations participated in observations, although
a majority of them observed only during short campaigns. The observations
at stations that participated in less than 20 000 observations, and the
stations that only participated in at regional networks with sizes of 2000 km
and less were discarded. Forty four stations remained. Observations of
sources that were observed in less than 4 sessions and gave less than
64 usable pairs of dual-band group delays were excluded. The data before
January 1984 were also discarded. In total, ![]() 5% of the observations
were excluded, and the remaining data from 3563 sessions between January 1984 to August 2006, more than 4.6 million of dual-band pairs of group
delays, were used in the analysis.
5% of the observations
were excluded, and the remaining data from 3563 sessions between January 1984 to August 2006, more than 4.6 million of dual-band pairs of group
delays, were used in the analysis.
The number of participating stations in each individual session varies from 2 to 20, although 4-7 is a typical number. No station participated in all sessions, but every station participated in sessions with many different networks. All networks have common nodes and, are therefore, tied together. Networks vary significantly, but more than 70% of them have a size exceeding the Earth's radius.
The state of the art theoretical models were used for computing the theoretical time delay and its partial derivatives. The procedure in general follows the approach presented by Sovers et al. (1998) with some minor refinements. The expression for time delay derived by Kopeikin & Schäfer (1999) in the framework of general relativity was used. The displacement caused by the Earth's tides were computed using a rigorous algorithm Petrov & Ma (2003) with a truncation at a level of 0.05 mm using the numerical values of the generalized Love numbers presented by Mathews (2001). The displacements caused by ocean loading were computed by convolving the Greens' functions with ocean tide models using the NLOADF algorithm of Agnew (1997). The GOT00 model (Ray 1999) of diurnal and semi-diurnal ocean tides, the NAO99 model (Matsumoto et al. 2000) of ocean zonal tides, the equilibrium model of the pole tide and the tide with period of 18.6 years were used. The atmospheric pressure loading was computed by convolving the Greens' functions with the numerical model of the atmosphere NCEP Reanalysis (Kalnay et al. 1996). The algorithm of computations is described in full details in Petrov & Boy (2004).
The a priori path delay in the atmosphere caused by the hydrostatic component was calculated as a product of the zenith path delay computed on the basis of surface pressure using the Saastamoinen (1972) expression and the isobaric mapping function (Niell & Petrov 2004) computed using the geopotential height of the 20 kPa pressure layer provided by the numerical weather model NCEP Reanalysis. The isobaric mapping function describes the dependence of path delay on the angle between the local axis of symmetry of the atmosphere and the direction to the observed sources. The direction of this axis from the zenith was considered to coincide with the normal to the surface of the geopotential height at the 20 kPa pressure level. This normal was computed using the NCEP Reanalysis dataset.
Since the accuracy requirements to the of the a priori Earth rotation model
are very low in the framework of the present approach, we can exploit
this to use the simplest possible model. The following expression for
the a priori matrix of the Earth's rotation
![]() according to the Newcomb-Andoyer formalism was used:
according to the Newcomb-Andoyer formalism was used:
Several solutions were produced. Each solution used the basic parameterization which was common for all runs, and a specific parameterization for an individual solution. Basic parameters belong to one of the three groups:
Several solutions have been computed with different a priori vectors of
the perturbational rotation
![]() and with a different set of
harmonic constituents of the vector
and with a different set of
harmonic constituents of the vector
![]() .
.
In solution A, the a priori vector
![]() was set to zero.
A set of sine and cosine amplitudes of the perturbational rotation vector was
estimated as global parameters. The frequencies of these estimates were
selected according to the following process. First, the frequencies for
components 1 and 2 of this vector in the range of the near-diurnal
retrograde wobble
[-7.310955
was set to zero.
A set of sine and cosine amplitudes of the perturbational rotation vector was
estimated as global parameters. The frequencies of these estimates were
selected according to the following process. First, the frequencies for
components 1 and 2 of this vector in the range of the near-diurnal
retrograde wobble
[-7.310955 ![]()
![]()
![]()
![]() and hypothetical near-diurnal prograde wobble (see, for
instance, Dehant 1993) [-7.284405
and hypothetical near-diurnal prograde wobble (see, for
instance, Dehant 1993) [-7.284405 ![]()
![]()
![]()
![]() ]
were sampled with step 9.0
]
were sampled with step 9.0 ![]()
![]() .
This step of frequency sequences corresponds to
.
This step of frequency sequences corresponds to
![]() where
where ![]() is the interval of observations, 22.6 years. Then the frequencies
of constituents with the amplitudes exceeding 1
is the interval of observations, 22.6 years. Then the frequencies
of constituents with the amplitudes exceeding 1 ![]()
![]() in the REN-2000 expansion were added to the list of constituents in order
of decreasing their amplitudes, provided the minimal difference in the
frequencies of the constituents was less than
9.0
in the REN-2000 expansion were added to the list of constituents in order
of decreasing their amplitudes, provided the minimal difference in the
frequencies of the constituents was less than
9.0 ![]()
![]() .
If two constituents have
difference in frequencies less than that, the constituent with smaller
amplitude was discarded.
.
If two constituents have
difference in frequencies less than that, the constituent with smaller
amplitude was discarded.
Second, all constituents at positive and negative diurnal, semi-diurnal,
and ter-diurnal bands of the tide-generating potential with amplitudes greater
than 0.003 of the amplitude of the M2 tide were selected. At negative
frequencies, all three components of the vector
![]() were estimated,
while only the components 1 and 2 were estimated at positive frequencies.
The same rejection criteria for the constituents with close frequencies
was enforced.
were estimated,
while only the components 1 and 2 were estimated at positive frequencies.
The same rejection criteria for the constituents with close frequencies
was enforced.
Third, the harmonic signal in components 1 and 2 of ![]() at
the Chandler and annual frequencies, and the harmonic signal in the
component 3 at 14 frequencies of zonal tides with amplitudes greater
than 3% of the amplitude of the tide generating potential at the
Mf frequency 5.323414
at
the Chandler and annual frequencies, and the harmonic signal in the
component 3 at 14 frequencies of zonal tides with amplitudes greater
than 3% of the amplitude of the tide generating potential at the
Mf frequency 5.323414 ![]() 10-6 rad s-1 were estimated.
Decorrelation constraints were imposed on estimates of B-spline coefficients.
10-6 rad s-1 were estimated.
Decorrelation constraints were imposed on estimates of B-spline coefficients.
Solution B is similar to solution A, but constituents at the 76 frequencies
that have a close companion, a sidelobe, and that satisfy the criteria in
Sect. 3,
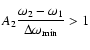
![]()
![]() ,
were not rejected as in solution A, but remained on the list. Strong
constraints with reciprocal weight
,
were not rejected as in solution A, but remained on the list. Strong
constraints with reciprocal weight
![]() in the form
of Eq. (7) were imposed. The purpose of this solution was
to investigate the effects of omitted sidelobes.
in the form
of Eq. (7) were imposed. The purpose of this solution was
to investigate the effects of omitted sidelobes.
A family of solutions C was computed. The purpose of this solution
was to evaluate a harmonic signal at non-tidal frequencies.
In addition to the frequencies used in the solution A, a possible non-tidal
signal was sought in eight frequency bands at the frequencies equally
sampled with the step 9.0 ![]()
![]() .
The low and high edges of each frequency band are shown in Table 1.
The total number of constituents of the perturbational rotation vector
estimated for components 1 and 2 was 20 093 and and for component 3 was 9885.
Since the total number of global parameters was at a level of 70 000,
well beyond the capabilities of a personal computer, 20 individual solutions
were performed. In each individual solution of family C, the sine and cosine
amplitudes of constituents at
.
The low and high edges of each frequency band are shown in Table 1.
The total number of constituents of the perturbational rotation vector
estimated for components 1 and 2 was 20 093 and and for component 3 was 9885.
Since the total number of global parameters was at a level of 70 000,
well beyond the capabilities of a personal computer, 20 individual solutions
were performed. In each individual solution of family C, the sine and cosine
amplitudes of constituents at ![]() 2000 frequencies were estimated.
The estimates of constituents are correlated at a level of 0.02-0.20,
since other common parameters were estimated, such as source coordinates and
station positions. Strictly speaking, the procedure of estimating
the spectrum by parts is not perfectly correct. But it was assumed that
such a procedure may result in a false detection, but not miss the
signal present in the data. In the final run of a solution of family C,
680 non-tidal frequencies were selected. The signal was detected at
a 95% confidence level at these frequencies in the previous runs.
2000 frequencies were estimated.
The estimates of constituents are correlated at a level of 0.02-0.20,
since other common parameters were estimated, such as source coordinates and
station positions. Strictly speaking, the procedure of estimating
the spectrum by parts is not perfectly correct. But it was assumed that
such a procedure may result in a false detection, but not miss the
signal present in the data. In the final run of a solution of family C,
680 non-tidal frequencies were selected. The signal was detected at
a 95% confidence level at these frequencies in the previous runs.
Table 1:
The range of frequency bands for estimation of a non-tidal
signal. The last column refers to components of
![]() vector of perturbational rotation that were estimated.
vector of perturbational rotation that were estimated.
The purpose of solution D was to investigate whether the process of
frequency selection for solution A picked up all the signals in the diurnal
band. In this solution the a priori vector
![]() was generated from
the REN-2000 nutation expansion. It had all the constituents with
amplitudes greater than 1
was generated from
the REN-2000 nutation expansion. It had all the constituents with
amplitudes greater than 1 ![]() 10-9 rad, except the constituents with
frequencies -7.331937
10-9 rad, except the constituents with
frequencies -7.331937 ![]() 10-5 -7.293186
10-5 -7.293186 ![]() 10-5,
-7.291047
10-5,
-7.291047 ![]() 10-5, and -7.252295
10-5, and -7.252295 ![]() 10-5 rad s-1, because they
had already been included in the matrix
10-5 rad s-1, because they
had already been included in the matrix
![]() .
For selection of the frequencies, at which the harmonics of the
perturbational rotation vector was to be estimated, the time series
of
.
For selection of the frequencies, at which the harmonics of the
perturbational rotation vector was to be estimated, the time series
of
![]() on the interval [1984.0, 2006.6] with a step of 0.125 days were produced, and its power
spectrum was computed. Here
on the interval [1984.0, 2006.6] with a step of 0.125 days were produced, and its power
spectrum was computed. Here
![]() is the vector of the adjustments
of perturbational rotation in solution B and vectors
is the vector of the adjustments
of perturbational rotation in solution B and vectors
![]() ,
where
,
where
![]() are the a priori perturbational vectors used.
The frequencies of constituents run from 0 through 2.9
are the a priori perturbational vectors used.
The frequencies of constituents run from 0 through 2.9 ![]()
![]() with step 9.0
with step 9.0 ![]()
![]() .
Not all of them were estimated, but only those
that had the frequency by module less than 9.3
.
Not all of them were estimated, but only those
that had the frequency by module less than 9.3 ![]()
![]() and that satisfied one of the three conditions:
a) to be in the range [7.20
and that satisfied one of the three conditions:
a) to be in the range [7.20 ![]() 10-5, 7.38
10-5, 7.38 ![]() 10-5] rad s-1 for taking the near-diurnal wobble
and the signal excited by the atmosphere into account, or
b) to have the square root of the power greater than 1
10-5] rad s-1 for taking the near-diurnal wobble
and the signal excited by the atmosphere into account, or
b) to have the square root of the power greater than 1 ![]() 10-11 rad
for taking the signal at tidal frequencies into account, or
or c) to be in the range of non-tidal frequencies identified in solutions C.
In total, 3676 parameters at 1706 frequencies, which are a multiple of the
frequency 9.0
10-11 rad
for taking the signal at tidal frequencies into account, or
or c) to be in the range of non-tidal frequencies identified in solutions C.
In total, 3676 parameters at 1706 frequencies, which are a multiple of the
frequency 9.0 ![]()
![]() ,
were selected.
,
were selected.
Table 2: The weighted root mean squares of the differences between estimates of the Earth rotation model from analysis of VLBI observations and the USNO Finals EOP model for the period of [1996.0, 2006.0]. The statistics in rows 1 and 2 correspond to solution B, which follows the proposed approach. The statistics in row 3 correspond to solution gsf2006c, which follows the traditional approach.
The software Calc/Solve was used for these solutions. Results of analysis are available on the Web at http://vlbi.gsfc.nasa.gov/erm.
Analysis of the results showed that the approach for the direct estimation
of the perturbational rotation vector in the form of expansion into basic
functions from VLBI observations allows us to represent the Earth's rotation
adequately. The fit of the least square solutions, 21.9 ps, was
the same as the fit in solutions that followed the traditional time series
approach. The slowly varying component was compared with the USNO EOP model.
The USNO Finals EOP time series with 1 day steps was derived by averaging
results of analysis of GPS and VLBI observations and smoothing. To compare
results, the USNO series of polar motion,
![]() ,
and UT1-TAI with
respect to the a priori Earth rotation model in expressions (13):
,
and UT1-TAI with
respect to the a priori Earth rotation model in expressions (13):
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{5091fig4.eps} \end{figure}](/articles/aa/full/2007/19/aa5091-06/Timg122.gif) |
Figure 4: The component 1 of the residual perturbational vector with respect to the Earth rotation USNO Finals EOP model. |
| Open with DEXTER | |
The differences for component 1 between the USNO model and our results from solution B after removal the contribution of harmonic variations with periods less than 2 days are shown in Fig. 4. No pattern of systematic differences is revealed. The statistics of these differences for all three components of the small vector of the Earth rotation and their time derivatives computed at the equidistant grid with time interval 2.5 h are presented in the 1st row of Table 2.
Since the VLBI observations are not carried out continuously due to budget
limitations, the accuracy of the Earth orientation model is the highest within
an interval of observations and the lowest at moments of time when there were
no observations. In the framework of the traditional approach, the EOP are
estimated on moments of time in the middle of a 24 h observing
session. The statistics of the differences of the EOP series from analysis
of VLBI observations gsf2006c![]() for moments in the middle of
1426 observing sessions are shown in the 3rd row of Table 2.
For comparison, the EOP were computed from results of solution B at exactly
the same epochs, and these statistics of the differences with respect to the
USNO model are presented in the 2nd row of this table.
for moments in the middle of
1426 observing sessions are shown in the 3rd row of Table 2.
For comparison, the EOP were computed from results of solution B at exactly
the same epochs, and these statistics of the differences with respect to the
USNO model are presented in the 2nd row of this table.
Analysis of statistics shows that the differences in components 1 and 2 of the Earth's orientation according to the proposed and traditional approaches do not exceed 20%. At the same time the proposed approach gives the estimates of all the components of the Earth's angular velocity vector by a factor of 1.5-2.0 closer to the GPS results than the estimates produced in the framework of the traditional approach. According to the traditional approach, the EOP rates and nutation daily offsets are computed for each session independently, which makes them less stable. With the proposed approach, at a given epoch several experiments contribute to estimates of EOP rate, which makes them more robust.
Analysis of the differences in amplitudes of the harmonic terms of
components 1 and 2 of the vector of perturbational rotation at the retrograde
diurnal band with respect to the semi-empirical MHB2000 expansion
(Mathews et al. 2002), showed they can reach 0.2 nrad for some terms. Detailed
analysis of these differences is beyond the scope of the present paper.
In order to test results, the empirical Earth rotation model from
solution B was used as the a priori for the solution that estimated the
time series of daily offset to nutations. The weighted root mean square of
the differences for the period of [1996.0, 2006.0] is 0.39 nrad when results
of solution B were used as the a priori, and 0.98 nrad when the MHB2000 was
used. The daily offsets to nutation in obliquity
![]() with
respect to both models are shown in Figs. 5-6.
with
respect to both models are shown in Figs. 5-6.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{5091fig5.eps} \end{figure}](/articles/aa/full/2007/19/aa5091-06/Timg124.gif) |
Figure 5:
The time series of the estimates of the daily offsets of nutation
in obliquity when the empirical Earth rotation model from
solution B was used as the a priori. The wrms is
3.9 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{5091fig6.eps} \end{figure}](/articles/aa/full/2007/19/aa5091-06/Timg125.gif) |
Figure 6:
The time series of the estimates of the daily offsets of nutation
in obliquity when the MHB2000 nutation expansion
was used as the a priori. The wrms is
9.8 |
| Open with DEXTER | |
Analysis of estimates of the harmonic components showed excessive power
near the frequency of the near-diurnal retrograde wobble, as was expected.
The spectrum turned out rather broad, spanning a rather wide band, and it
partly overlaps with the tidal frequency -7.312026 ![]()
![]() that corresponds to the annual retrograde
nutation as shown in Fig. 7. It was found by Herring et al. (1986)
that the near-diurnal wobble cannot be represented by a purely harmonic model
with a constant amplitude. This means that when this component of the Earth's
rotation is represented in the frequency domain, several constituents in the
spectrum will correspond to it.
that corresponds to the annual retrograde
nutation as shown in Fig. 7. It was found by Herring et al. (1986)
that the near-diurnal wobble cannot be represented by a purely harmonic model
with a constant amplitude. This means that when this component of the Earth's
rotation is represented in the frequency domain, several constituents in the
spectrum will correspond to it.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{5091fig7.eps} \end{figure}](/articles/aa/full/2007/19/aa5091-06/Timg126.gif) |
Figure 7:
The power spectrum of the estimates of the quasi-diurnal variations
of components 1 and 2 of the perturbational vector of the Earth's
rotation from solution A in the vicinity of the frequency of the
near-diurnal free wobble. The estimate for the frequency
-7.312026 |
| Open with DEXTER | |
Analysis of the results of the C family solutions revealed several
constituents with the non-tidal signal. The spectrum of components 1 and 2
in the vicinity of the frequency
![]() ,
i.e. the K2 tide, turned out
rather broad. The excerpt of the power spectrum produced from estimates of
sine and cosine amplitudes of the components 1 and 2 is shown in
Fig. 8. This signal cannot be attributed to the spectral leakage,
since no excessive power was found in the vicinity of even a stronger tide
at the M2 frequency. A relatively broad-band signal in the vicinity of
the
,
i.e. the K2 tide, turned out
rather broad. The excerpt of the power spectrum produced from estimates of
sine and cosine amplitudes of the components 1 and 2 is shown in
Fig. 8. This signal cannot be attributed to the spectral leakage,
since no excessive power was found in the vicinity of even a stronger tide
at the M2 frequency. A relatively broad-band signal in the vicinity of
the
![]() frequency, i.e. K3, was found at the 3rd component
of the rotation vector. The excerpt of the power spectrum produced from
estimates of sine and cosine amplitudes of the component 3 is shown in
Fig. 9. A weaker signal in the estimates can also be revealed in the
vicinity of the
frequency, i.e. K3, was found at the 3rd component
of the rotation vector. The excerpt of the power spectrum produced from
estimates of sine and cosine amplitudes of the component 3 is shown in
Fig. 9. A weaker signal in the estimates can also be revealed in the
vicinity of the
![]() frequency. A similar signal can
be seen at prograde frequencies in the vicinity
K2, K3, K4 at
components 1 and 2
frequency. A similar signal can
be seen at prograde frequencies in the vicinity
K2, K3, K4 at
components 1 and 2![]() .
.
Another peculiarity of the spectrum are sharp peaks at frequencies
![]()
![]() ,
,
![]()
![]() at a level of 2-7
at a level of 2-7![]() above the
noise level. No convincing explanation was found, but it is suspected
that this signal in the estimates may be an artifact caused by errors in
modeling by analogy with a detection of a very strong signal in estimates
of the harmonic constituents of the perturbational Earth's rotation from
GPS time series at frequencies that are multiple to the diurnal frequency:
S1, S2, S3, S4, etc., reported by Rothacher et al. (2001). It should be noted
that no non-tidal signal at S3, S4 frequencies is seen from analysis
of VLBI group delays.
above the
noise level. No convincing explanation was found, but it is suspected
that this signal in the estimates may be an artifact caused by errors in
modeling by analogy with a detection of a very strong signal in estimates
of the harmonic constituents of the perturbational Earth's rotation from
GPS time series at frequencies that are multiple to the diurnal frequency:
S1, S2, S3, S4, etc., reported by Rothacher et al. (2001). It should be noted
that no non-tidal signal at S3, S4 frequencies is seen from analysis
of VLBI group delays.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{5091fig8.eps} \end{figure}](/articles/aa/full/2007/19/aa5091-06/Timg134.gif) |
Figure 8:
The power spectrum of the estimates of the quasi-diurnal variations
of components 1 and 2 of the perturbational vector of the Earth's
rotation from solution C in the vicinity of the -K2 frequency.
The estimate for the frequency
-1.458423 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{5091fig9.eps} \end{figure}](/articles/aa/full/2007/19/aa5091-06/Timg135.gif) |
Figure 9: The portion of the power spectrum of estimates of the ter-diurnal variations of components 1 and 2 of the perturbational vector of the Earth's rotation vector in the ter-diurnal band. The broad peak is seen near the -K3 frequency. |
| Open with DEXTER | |
Solution D did not reveal other missed harmonic signals in the diurnal band.
The formal uncertainties of the amplitudes on harmonics constituents can be
evaluated on the basis of the signal-to-noise ratio of fringe phases
used for computing group delay by invoking the law of error propagation.
These uncertainties are in a range of 5-12 prad. Analysis of the estimates
of the constituents at the frequency bands where no tidal or no-tidal
signal was detected provides a more reliable measure of noise in adjustments.
It is 16 prad for components 1, 2 and 13 prad for component 3 for the
diurnal band; 13 prad and 10 prad for these components at other frequency
bands. This corresponds to displacements of 0.06-0.12 mm at the Earth's
surface. Evaluation of the level of systematic errors is more problematic.
The major possible source of systematic errors is considered to be a residual
motion of the individual stations. In fact, the rotation of the station
polyhedron was evaluated, and it was assumed that the motion of this
polyhedron is a representative measure of the Earth's rotation. This assumption
is valid to the extent that residual horizontal motion of individual
observing stations is negligible. Petrov & Ma (2003) estimated harmonic
site position variations and found that the accuracy of modeling the horizontal
motion of individual stations is at the level of 0.4 mm. In the case of the
errors of modeling being completely uncorrelated, this error will be diluted as
![]() ,
where
,
where
![]() is the effective number of
observing stations, 10-44, depending on how to define the effective number
of stations. Unfortunately, the distribution of residual motions of stations
at tidal frequencies shows a pattern of a systematic behavior, which does
not support the hypothesis of uncorrelated errors. A conservative estimate
of the possible contribution of the unmodeled residual motion of the network
of stations to the estimates of harmonic constituents of the perturbational
rotation suggests a dilution factor of 2, i.e. the surface displacements
is the effective number of
observing stations, 10-44, depending on how to define the effective number
of stations. Unfortunately, the distribution of residual motions of stations
at tidal frequencies shows a pattern of a systematic behavior, which does
not support the hypothesis of uncorrelated errors. A conservative estimate
of the possible contribution of the unmodeled residual motion of the network
of stations to the estimates of harmonic constituents of the perturbational
rotation suggests a dilution factor of 2, i.e. the surface displacements
![]() 0.2 mm. That means systematic errors may be two times greater
than random errors.
0.2 mm. That means systematic errors may be two times greater
than random errors.
Dehant et al. (2003) investigated the influence of systematic errors due to the neglect of the modeling source structure. It was suggested to split the observed radio sources into two classes, "stable'' and "unstable'', and either to remove unstable sources from analysis or to estimate the time series of their positions. In this paper a different approach was used: proper motion of those sources that had a long enough history of observations was estimated. This method is supposed to reduce systemic errors in the estimates of the harmonic constituents in the perturbational rotation vector.
It was demonstrated that the empirical Earth rotation model can be determined directly from observations over a period of 22 years using the least square estimation technique. The advantage of the proposed approach is that a continuous function describing the Earth's orientation is determined in one step without producing intermediate time series. The consistency between station positions, source coordinates, and the empirical Earth rotation model is automatically achieved. Another advantage of the proposed approach is that a simplified a priori model with only 31 numerical parameters is sufficient, while the traditional approach needs a complicated a priori model of precession, nutation, high frequency harmonic variations of the Earth's rotation, and a filtered and smoothed time series of the Earth orientation parameters produced in the previous analysis, in total 46 000 numerical parameters (McCarthy & Petit 2004).
The traditional approach to describing the Earth's rotation follows the formalism of either Newcomb and Andoyer or Guinot (1979) and Capitaine et al. (1986), and involves such notions as the celestial intermediate pole, the point of the vernal equinox, the non-rotating origin, the ecliptic, and other axes, points, planes, and circles on the celestial sphere. The advantage of the empirical Earth rotation model is that it is conceptually simpler, since it is built entirely kinematically and does not require introduction of intermediate points, axes, planes that are not observable.
It was demonstrated that the empirical Earth rotation model derived from analysis of VLBI observations gives the differences with respect to the EOP derived from analysis of independent GPS observations at moments of observation at the same level, within 20%, as the differences of the VLBI EOP series produced with the traditional approach. The advantage of the proposed approach is that the estimates of the EOP rates are a factor of 1.5-2.0 closer to the GPS time series than the VLBI EOP rates estimated following the traditional approach.
When results of analysis of observations are compared with theoretical predictions, two approaches can be taken: a) the parameters that describe empirical data are formulated through parameters of the theoretical models; b) theoretical predictions are transformed to a form that can be unambiguously determinedfrom the observations. Representation of the Earth's rotation in the form of the expansion into basis functions establishes a foundation for the second approach.
Scientific interpretation of the results of estimation of the empirical Earth rotation model will be given in the next paper.
Acknowledgements
This work was done while the author worked at the National Observatory of Japan, Mizusawa, as a visiting scientist. The author would like to thank S. Manabe, T. Sato, Y. Tamura, D. Rowlands, Ch. Bizouard and an anonymous referee for useful discussion that helped to improve the manuscript.
Table 3: Numerical values of the a priori Earth rotation model parameters used in data reduction.