A&A 466, 1131-1144 (2007)
DOI: 10.1051/0004-6361:20067017
Relation between photospheric magnetic field and chromospheric emission
R. Rezaei1 - R. Schlichenmaier1 - C. A. R. Beck1,2 - J. H. M. J. Bruls1 -
W. Schmidt1
1 - Kiepenheuer-Institut für Sonnenphysik, Schöneckstr. 6, 79 104 Freiburg, Germany
2 -
Instituto de Astrofísica de Canarias (IAC), 38 205 La Laguna, Espain
Received 22 December 2006 / Accepted 25 January 2007
Abstract
Aims. We investigate the relationship between the photospheric magnetic field and the emission of the mid chromosphere of the Sun.
Methods. We simultaneously observed the Stokes parameters of the photospheric iron line pair at 630.2 nm and the intensity profile of the chromospheric Ca II H line at 396.8 nm in a quiet Sun region at a heliocentric angle of 53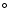 .
Various line parameters have been deduced from the Ca II H line profile. The photospheric magnetic field vector has been reconstructed from an inversion of the measured Stokes profiles. After alignment of the Ca and Fe maps, a common mask has been created to define network and inter-network regions. We perform a statistical analysis of network and inter-network properties. The H-index is the integrated emission in a 0.1 nm band around the Ca core. We separate a non-magnetically,
.
Various line parameters have been deduced from the Ca II H line profile. The photospheric magnetic field vector has been reconstructed from an inversion of the measured Stokes profiles. After alignment of the Ca and Fe maps, a common mask has been created to define network and inter-network regions. We perform a statistical analysis of network and inter-network properties. The H-index is the integrated emission in a 0.1 nm band around the Ca core. We separate a non-magnetically,
 ,
and a magnetically,
,
and a magnetically,
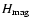 ,
heated component from a non-heated component,
,
heated component from a non-heated component,
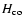 in the H-index.
in the H-index.
Results. The average network and inter-network H-indices are equal to 12 and 10 pm, respectively. The emission in the network is correlated with the magnetic flux density, approaching a value of
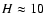 pm for vanishing flux. The inter-network magnetic field is dominated by weak field strengths with values down to 200 G and has a mean absolute flux density of about 11 Mx cm-2.
pm for vanishing flux. The inter-network magnetic field is dominated by weak field strengths with values down to 200 G and has a mean absolute flux density of about 11 Mx cm-2.
Conclusions. We find that a dominant fraction of the calcium emission caused by the heated atmosphere in the magnetic network has non-magnetic origin (
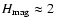 pm,
pm,
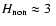 pm). Considering the effect of straylight, the contribution from an atmosphere with no temperature rise to the H-index (
pm). Considering the effect of straylight, the contribution from an atmosphere with no temperature rise to the H-index (
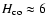 pm) is about half of the observed H-index in the inter-network. The H-index in the inter-network is not correlated to any property of the photospheric magnetic field, suggesting that magnetic flux concentrations have a negligible role in the chromospheric heating in this region. The height range of the thermal coupling between the photosphere and low/mid chromosphere increases in presence of magnetic field. In addition, we demonstrate that a poor signal-to-noise level in the Stokes profiles leads to a significant over-estimation of the magnetic field strength.
pm) is about half of the observed H-index in the inter-network. The H-index in the inter-network is not correlated to any property of the photospheric magnetic field, suggesting that magnetic flux concentrations have a negligible role in the chromospheric heating in this region. The height range of the thermal coupling between the photosphere and low/mid chromosphere increases in presence of magnetic field. In addition, we demonstrate that a poor signal-to-noise level in the Stokes profiles leads to a significant over-estimation of the magnetic field strength.
Key words: Sun: photosphere - Sun: chromosphere - Sun: magnetic fields
The dominant pattern covering the entire solar surface, except sunspots, is granulation,
the top of small-scale convection cells with diameters of 1-2 Mm.
On a larger scale of 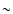 20 Mm supergranules are observed
which show the same pattern as granulation: a horizontal flow from the center towards the boundary of the cell.
These large scale convection cells have a
mean lifetime of 20 h, much longer than the granular time-scale (some 10 min).
The chromospheric network forms at the boundary of the supergranular cells.
The network is presumably formed by the long-time advection of magnetic flux to the
boundaries of the supergranules (Priest et al. 2002; Cattaneo et al. 2003). The interior of the network cells,
the inter-network, has much less magnetic field than the network (e.g., Keller et al. 1994).
The magnetic and thermodynamic properties of the network and inter-network are different (e.g., Lites 2002).
20 Mm supergranules are observed
which show the same pattern as granulation: a horizontal flow from the center towards the boundary of the cell.
These large scale convection cells have a
mean lifetime of 20 h, much longer than the granular time-scale (some 10 min).
The chromospheric network forms at the boundary of the supergranular cells.
The network is presumably formed by the long-time advection of magnetic flux to the
boundaries of the supergranules (Priest et al. 2002; Cattaneo et al. 2003). The interior of the network cells,
the inter-network, has much less magnetic field than the network (e.g., Keller et al. 1994).
The magnetic and thermodynamic properties of the network and inter-network are different (e.g., Lites 2002).
The chromospheric heating mechanism is one of the main challenges of solar
physics (Narain & Ulmschneider 1996, and references therein).
The core emission of the Ca II H and K lines is an important source of radiative losses
in the chromosphere.
Moreover, this emission is an important tool to study the temperature stratification
and the magnetic activity of the outer atmosphere of the Sun and other stars (e.g., Schrijver & Zwaan 2000).
Most of the observational studies based on these lines
use either the calcium intensity
profile (e.g., Cram & Damé 1983; Lites et al. 1993) or combinations of
calcium filtergrams and magnetograms (e.g., Berger & Title 2001).
From the observation of the calcium spectrum alone,
it is not possible to distinguish between the magnetic and non-magnetic heating components.
Combining calcium filtergrams with magnetograms allows to separate those components,
but the spectral information is lost.
Simultaneous observations that allow to reconstruct the magnetic field and record the spectrum for the Ca II H line are
rare (e.g., Lites et al. 1999) and only available at lower spatial resolution.
Therefore, it is not surprising that none of the present theories,
mechanical and Joule heating, was confirmed or rejected observationally (Socas-Navarro 2005; Fossum & Carlsson 2005).
![\begin{figure}
\par {\includegraphics[width=16.8cm,clip]{7017fig1.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg16.gif) |
Figure 1:
From left to right: a) the Fe I 630 nm continuum intensity,
b) the calcium wing intensity at 396.490 nm which was calibrated to FTS
data (Stenflo et al. 1984), c) the outer calcium wing intensity (W1),
d) the inner calcium wing intensity (W3), e) the H-index,
f) the masks which separate network (white) from the inter-network (gray),
and g) the magnetic flux density obtained from the inversion.
We did not use the black region between the network and inter-network.
Each small tickmark is 1 arcsec. Note that sampling in x and y directions are different. |
| Open with DEXTER |
Schrijver (1987) studied a sample of late-type stars and
introduced the concept of the basal flux to separate the
non-magnetic heating from the magnetic one.
The Sun is not a very active star, with a chromospheric radiative loss on the order of the
basal flux for Sun-like stars (Fawzy et al. 2002b).
Carlsson & Stein (1997) presented a semi-empirical
hydrodynamic model where enhanced chromospheric emission
is due to outward propagating acoustic waves.
This model was criticized in subsequent investigations (e.g., Kalkofen et al. 1999; Fossum & Carlsson 2005),
which was partly due to disagreements on the temperature stratification in
higher layers (e.g., Wedemeyer-Böhm et al. 2005; Ayres 2002).
In addition, it is not clear whether high- or low-frequency acoustic waves play the dominant
role in the energy transport to higher layers (Fawzy et al. 2002a; Jefferies et al. 2006).
While there are theoretical indications that the magnetic filling factor
discriminates between different regimes of heating (Solanki & Steiner 1990), there
is no canonic model reproducing thermal, dynamical and
magnetic properties of the solar chromosphere (Judge & Peter 1998; Rutten 1999).
The POlarimetric LIttrow Spectrograph (POLIS, Schmidt et al. 2003; Beck et al. 2005a) was designed to
provide co-temporal and co-spatial measurements of the magnetic field in the photosphere
and the Ca II H intensity profile.
We use POLIS to address the question of the chromospheric heating mechanism,
by comparing properties of network and inter-network in photosphere and chromosphere
by a statistical analysis.
With the information on the photospheric fields,
we separate the contributions of the magnetically and non-magnetically heated component.
For the first time we study the
correlation of the chromospheric emission with the corresponding
amplitude/area asymmetry and Stokes-V zero-crossing velocity at the corresponding photospheric position.
We also investigate the magnetic field strength distribution of the inter-network to check whether
it consists of weak fields (e.g., Faurobert et al. 2001; Collados 2001) or
kilo-Gauss fields (e.g., Sánchez Almeida et al. 2003a,b).
Observations and data reduction are
explained in Sects. 2 and 3. Histograms of the obtained parameters are presented in Sect. 4.
Correlations between the chromospheric and photospheric parameters are addressed in Sect. 5.
The heating contributions are elaborated in Sect. 6.
Discussion and conclusions are presented in Sects. 7 and 8, respectively. Details of the
magnetic field parameters in the inter-network are discussed in Appendix A.
The straylight contamination and calibration uncertainties for the POLIS Ca channel
are estimated in Appendix B. An overview of some of our results also appears in Rezaei et al. (2007).
We observed a network area close to the active region NOAA 10675 on September 27, 2004,
with the POLIS instrument at the German Vacuum Tower Telescope (VTT) in Tenerife.
The observations were part of a coordinated observation campaign in the International
Time Program, where also the Swedish Solar Telescope (SST), Dutch Open Telescope (DOT)
and the Télescope Héliographique pour
l'Étude du Magnétisme et des Instabilités Solaires (THÉMIS) participated.
Here we analyze a series of thirteen maps of the same network
region at a heliocentric angle of 53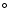 ,
taken during several hours.
We achieved a spatial resolution of around 1.0 arcsec, estimated from the
spatial power spectrum of the intensity maps.
,
taken during several hours.
We achieved a spatial resolution of around 1.0 arcsec, estimated from the
spatial power spectrum of the intensity maps.
All maps were recorded with a slit width of 0.5 arcsec,
a slit height of 47.5 arcsec, and an exposure time per slit position of 4.92 s.
The scan extension for the first three maps was 40.5, 55.5, and 20.5 arcsec,
while it was 25.5 arcsec for the remaining ten maps.
The Ca II H line and the visible neutral iron lines at 630.15 nm, 630.25 nm, and
Ti I 630.38 nm were observed with the blue (396.8 nm) and red (630 nm) channels of POLIS.
The spatial sampling along the slit (y-axis in Fig. 1) was 0.29 arcsec. The scanning step was 0.5 arcsec for all maps.
The spectral sampling of 1.92 pm for the blue channel
and 1.49 pm for the red channel leads to a velocity dispersion of
1.45 and 0.7 km s-1 per pixel, respectively.
The spectropolarimetric data of the red channel
were corrected for instrumental effects and telescope
polarization with the procedures described by Beck et al. (2005b,a).
![\begin{figure}
\par {\includegraphics[width=8cm,clip]{7017fig2.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg17.gif) |
Figure 2:
Sample averaged calcium profile of one of the maps
(the average profile is similar for all other maps).
The bands are explained in Table 1. |
| Open with DEXTER |
Table 1:
The definition of the characteristic parameters of the Ca II H profile
for the peak sample (upper part) and the band sample (lower part) (see also Fig. 2).
Wavelengths are in nm.
Figure 1 displays an overview of one of the thirteen maps after spatial alignment.
The map (a) shows the Fe I 630 nm continuum intensity normalized to
the average quiet Sun intensity.
The map (b) shows the Ca II H wing intensity, taken close
to 396.490 nm (for a definition of line parameters see Fig. 2 and Table 1).
These two maps were used for the spatial alignment of the red and blue channels.
The next two maps (c and d) show the intensities in the outer and inner
wings (W1, respectively, W3).
The inner wing samples a wavelength band close to the core; hence, it is more influenced
by the line-core emission and shows higher contrast of the network than the outer wing.
The next map (e) is the H-index, i.e., the intensity of the calcium core integrated over
0.1 nm (cf. Table 1).
The network features appear broadest and show the highest contrast in this map.
The map (f) demonstrates network and inter-network masks (Sect. 3.1).
The map (g) shows the magnetic flux density obtained from
the spectro-polarimetric data (Sect. 3.2).
In this section we discuss characteristic parameters of the calcium profile and the Fe I 630 nm line pair.
We briefly explain the inversion method that was used to infer the vector magnetic field.
For each map, we created a mask to distinguish between the network and inter-network regions (Fig. 1f).
This was done manually on the basis of the magnetic flux and the H-index.
We did not use the black region in Fig. 1f which separates network from inter-network.
To study structures in these two regions, we define two statistical samples:
Each member of this sample has a regular V profile and a double reversal in the calcium core.
For this sample, we study quantities related to
the Ca II H emission peaks (Table 1, upper part).
The number of data points in the network and inter-network
are 19 509 and 1712, respectively.
We emphasize that the few inter-network points in this sample are not distributed uniformly.
They usually belong to small-scale magnetic elements surrounded by large areas without
magnetic signal above the noise level.
All network and inter-network points, marked in the masks, are present in this sample.
Since some of these profiles do not have two emission peaks in the calcium core,
we use integrated intensities in a fixed spectral range (Cram & Damé 1983) at the
core and wing of the calcium profile (Table 1, lower part).
This definition retrieves reasonable chromospheric parameters.
In total from all the maps, 24 225 points were selected as network (white in Fig. 1f)
and 20 855 as inter-network positions (gray in Fig. 1f).
We averaged profiles over a large area (including network) to obtain an average
profile for each map. These average profiles are the mean of more than three thousand profiles each time;
an example is shown in Fig. 2.
We then normalized the intensity at the line wing at 396.490 nm to the FTS profile (Stenflo et al. 1984).
The same normalization coefficient was applied to all profiles of the map.
Hence, all profiles are normalized to the average continuum intensity.
Table 1 lists the characteristic parameters we define for each calcium profile:
- a)
- The intensity of the Ca II H core, H3, and the amplitudes of the emission
peaks,
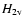 and
and
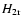 ,
and their respective
positions,
,
and their respective
positions,
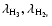 ,
and
,
and
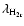 (peak sample).
(peak sample).
- b)
- Intensities in the outer (W1), middle (W2), and inner line wings (W3),
which are integrated over spectral bands with a fixed spectral range (band sample).
From these quantities we derive:
- 1.
- the ratio of the emission peaks,
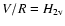 /
/
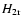 ,
and
,
and
- 2.
- the emission strength which is the intensity of the violet emission peak
divided by the core,
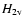 /H3.
/H3.
The band intensities are defined such that the wavelength intervals are fixed for all the
profiles and do not depend on the peak/core positions (Table 1, lower part).
Figure 3 shows a comparison between the
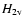 parameters derived from
the band and peak definitions.
The correlation is very strong (also for other peak parameters).
Thus, it is justified to use the values from the band sample to improve the statistics for the inter-network.
parameters derived from
the band and peak definitions.
The correlation is very strong (also for other peak parameters).
Thus, it is justified to use the values from the band sample to improve the statistics for the inter-network.
![\begin{figure}
\par {\includegraphics[width=8cm,clip]{7017fig3.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg23.gif) |
Figure 3:
Scatter plot of the
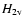 band vs. peak definition.
In the band definition, a fixed spectral range was used.
Gray and black show the network and inter-network, respectively.
band vs. peak definition.
In the band definition, a fixed spectral range was used.
Gray and black show the network and inter-network, respectively. |
| Open with DEXTER |
![\begin{figure}
\par {\includegraphics[width=16.5cm,clip]{7017fig4.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg24.gif) |
Figure 4:
Histograms of the intensity parameters for the network (thick) and
inter-network (thin), using the band sample: a) the H-index, b)
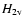 ,
c) ,
c)
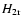 ,
d) W3 (the inner wing intensity), e) W2 (the middle wing intensity),
f) W1 (the outer wing intensity), g) the calcium wing intensity at 396.490 nm which
was used for normalization (see Fig. 2),
and h) Fe I 630.2 nm normalized continuum intensity (see Table 1 for definitions). ,
d) W3 (the inner wing intensity), e) W2 (the middle wing intensity),
f) W1 (the outer wing intensity), g) the calcium wing intensity at 396.490 nm which
was used for normalization (see Fig. 2),
and h) Fe I 630.2 nm normalized continuum intensity (see Table 1 for definitions). |
| Open with DEXTER |
The data of the red channel of POLIS were treated with the standard polarimetric calibration
procedures described in Beck et al. (2005b,a).
The spectral line curvature was removed using the telluric O2 line at 630.20 nm with a routine
described in Rezaei et al. (2006).
The polarization signal in
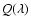 ,
,
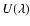 ,
and
,
and
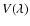 is
normalized to the local continuum intensity,
is
normalized to the local continuum intensity, 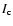 ,
for each pixel.
The rms noise level of the Stokes parameters in the continuum
was
,
for each pixel.
The rms noise level of the Stokes parameters in the continuum
was
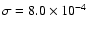
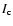 .
Only pixels with V signals greater than 3
.
Only pixels with V signals greater than 3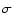 were
included in the profile analysis.
For regular Stokes-V signals above the threshold,
we derived positions and amplitudes of the profile extrema
in all Stokes parameters by fitting a parabola to each lobe.
were
included in the profile analysis.
For regular Stokes-V signals above the threshold,
we derived positions and amplitudes of the profile extrema
in all Stokes parameters by fitting a parabola to each lobe.
An inversion was performed using the SIR code (Ruiz Cobo & del Toro Iniesta 1992).
We used the same setup as in Bellot Rubio & Beck (2005) and Beck et al. (2006):
a two-component solar atmosphere model with one magnetic and one field-free component.
Additionally, a variable amount of straylight was allowed for.
This accounts for unresolved magnetic fields inside each pixel.
We did not consider any gradient for the atmospheric parameters except for the temperature.
The inversion yields the magnetic field vector and an estimate for the magnetic filling fraction.
The flux density map (magnetic flux per pixel, Fig. 1g) is
based on the inversion results.
The network patches are brighter than the inter-network at all wavelengths:
in the core and wing of the Ca II H line and in Fe I 630 nm continuum.
The distributions of the intensity parameters at different wavelengths are shown in Fig. 4.
Thick and thin curves show network and inter-network, respectively.
A comparison between the network and inter-network histograms indicates that
the calcium core parameters (H-index,
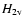 ,
,
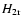 )
are more shifted than the wing/continuum intensities (Figs. 4a-c).
In other words, the intensity contrast increases from the continuum toward
the wing and peaks at the core.
Moreover, the wing intensities show different behaviors
due to their respective distances to the core:
the closer the selected wavelength band to the core, the larger the shift between
network and inter-network distributions.
Hence, the histogram of
the inner wing intensity (Fig. 4d) has a larger shift than the middle and outer wings (Figs. 4e and f).
The distribution of the Ca II H wing
)
are more shifted than the wing/continuum intensities (Figs. 4a-c).
In other words, the intensity contrast increases from the continuum toward
the wing and peaks at the core.
Moreover, the wing intensities show different behaviors
due to their respective distances to the core:
the closer the selected wavelength band to the core, the larger the shift between
network and inter-network distributions.
Hence, the histogram of
the inner wing intensity (Fig. 4d) has a larger shift than the middle and outer wings (Figs. 4e and f).
The distribution of the Ca II H wing![[*]](/icons/foot_motif.gif) and Fe I 630 nm continuum
intensities also show a shift between the network and
inter-network: the peak of the distribution in the network is slightly brighter than in the
inter-network in 396.490 nm and also in the 630 nm continuum (Figs. 4g and h).
and Fe I 630 nm continuum
intensities also show a shift between the network and
inter-network: the peak of the distribution in the network is slightly brighter than in the
inter-network in 396.490 nm and also in the 630 nm continuum (Figs. 4g and h).
![\begin{figure}
\par {\includegraphics[width=15cm,clip]{7017fig5.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg30.gif) |
Figure 5:
Histograms of the magnetic field parameters for the network (thick) and
inter-network (thin), using the peak sample: a) the absolute magnetic flux density,
b) the field strength, c) Stokes-V amplitude, d) Fe I 630.25 nm V velocity,
e) the amplitude asymmetry, and f) the area asymmetry. |
| Open with DEXTER |
From the inversion, we obtain the magnetic field and the magnetic flux
in the photosphere. The statistics of these quantities in the network and inter-network are
discussed here; the relation with the chromospheric parameters is discussed
in the next section. We restrict the analysis
to those profiles with a regular Stokes-V and a double emission calcium profile,
although there are only 1712 profiles in the inter-network.
The histogram of the absolute magnetic flux density,
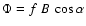 ,
is shown in Fig. 5a,
where f is the magnetic filling factor, B is the field strength, and
,
is shown in Fig. 5a,
where f is the magnetic filling factor, B is the field strength, and 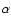 is the angle
between the magnetic field orientation and the line-of-sight.
The histogram for the inter-network has a narrow distribution, which peaks at some
is the angle
between the magnetic field orientation and the line-of-sight.
The histogram for the inter-network has a narrow distribution, which peaks at some
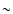 4 Mx cm-2 whereas there is a long tail
up to
4 Mx cm-2 whereas there is a long tail
up to 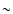 250 Mx cm-2 for the network.
The distribution function of the magnetic field strength (Fig. 5b) has a peak around
250 Mx cm-2 for the network.
The distribution function of the magnetic field strength (Fig. 5b) has a peak around 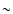 1.3 kG for the
network elements and increases with decreasing field strength for the inter-network.
The peak at 200 G is due to the detection limit of the polarization signal.
The histogram of the V amplitude (Fig. 5c) shows weak inter-network signals with a
V amplitude far less than 1%.
The distribution of the inter-network V amplitude
1.3 kG for the
network elements and increases with decreasing field strength for the inter-network.
The peak at 200 G is due to the detection limit of the polarization signal.
The histogram of the V amplitude (Fig. 5c) shows weak inter-network signals with a
V amplitude far less than 1%.
The distribution of the inter-network V amplitude![[*]](/icons/foot_motif.gif) peaks at
peaks at
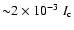 whereas the network shows a broad distribution up to
whereas the network shows a broad distribution up to
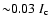 .
.
![\begin{figure}
\par {\includegraphics[width=8.1cm,clip]{7017fig6.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg35.gif) |
Figure 6:
Upper panels: correlation between the
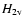 and
and
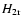 based on the
peak sample and the H-index.
Lower left: correlation between W1 and the H-index.
Lower right: correlation of the ( V/R) ratio with the calcium core position.
Gray and black show the network and inter-network, respectively (for abbreviations, see Table 1).
based on the
peak sample and the H-index.
Lower left: correlation between W1 and the H-index.
Lower right: correlation of the ( V/R) ratio with the calcium core position.
Gray and black show the network and inter-network, respectively (for abbreviations, see Table 1). |
| Open with DEXTER |
The V velocity distribution is shown in Fig. 5d. Although it has a peak around zero both for the
network and inter-network, the inter-network shows a larger fraction of high-velocity V profiles.
The amplitude and area asymmetries in the network peak at small positive values of 10% and
3%, respectively (Figs. 5e and f).
In contrast, there is no tendency to positive or negative values for the inter-network asymmetries.
This is in agreement with other studies of quiet Sun magnetic fields (Sigwarth et al. 1999; Khomenko et al. 2003; Sigwarth 2001).
There is a strong correlation between the H-index, H3,
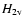 ,
,
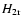 ,
and the inner wing intensity (with a correlation coefficient
,
and the inner wing intensity (with a correlation coefficient 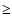 0.8, see Fig. 6).
Therefore, we adopt the H-index as a proxy for the calcium core emission.
It also has the advantage to be the calcium intensity parameter closest to the widely used
filtergrams
0.8, see Fig. 6).
Therefore, we adopt the H-index as a proxy for the calcium core emission.
It also has the advantage to be the calcium intensity parameter closest to the widely used
filtergrams![[*]](/icons/foot_motif.gif) .
.
The (V/R) ratio is an indicator for the H3 line-core position (Rutten & Uitenbroek 1991; Cram & Damé 1983).
There is a strong correlation between the (V/R) ratio
and 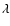 (H3): the redshifted
and blueshifted calcium profiles correspond to (V/R) ratios
smaller and larger than one, respectively (Fig. 6, lower right panel)
(H3): the redshifted
and blueshifted calcium profiles correspond to (V/R) ratios
smaller and larger than one, respectively (Fig. 6, lower right panel)![[*]](/icons/foot_motif.gif) .
We find a similar correlation between the emission strength and the (V/R) ratio:
the larger the (V/R) ratio, the larger the emission strength.
The lower left panel of Fig. 6 shows the correlation between the outer wing intensity and the H-index.
While there is a correlation in the network (gray), there is no significant correlation in the inter-network (Table 2).
We calculated the correlation coefficient between the H-index and all
intensities in the line wing to investigate this difference in more
detail (Table 2). In the network, there is a stronger correlation than
in the inter-network for all the wing bands considered.
We return to this point in Sect. 7.
.
We find a similar correlation between the emission strength and the (V/R) ratio:
the larger the (V/R) ratio, the larger the emission strength.
The lower left panel of Fig. 6 shows the correlation between the outer wing intensity and the H-index.
While there is a correlation in the network (gray), there is no significant correlation in the inter-network (Table 2).
We calculated the correlation coefficient between the H-index and all
intensities in the line wing to investigate this difference in more
detail (Table 2). In the network, there is a stronger correlation than
in the inter-network for all the wing bands considered.
We return to this point in Sect. 7.
There is a strong correlation between the
amplitude and area asymmetries, both in the network and inter-network (Fig. 7, top left panel).
In contrast, there is no correlation between either amplitude or area asymmetries and
the V velocity (bottom left panel, Fig. 7).
These are typical properties of the quiet Sun magnetic field (e.g., Sigwarth et al. 1999).
The right panels of Fig. 7 show scatter plots of the V asymmetries versus V amplitude.
There is a tendency for high amplitude V signals to have small asymmetries.
On the other hand,
histograms of the asymmetries peak at a positive value.
Implications of these two findings will be discussed in Sect. 5.3.2.
Table 2:
Correlation coefficients between the band intensities and the H-index in
the network and inter-network using the band sample.
![\begin{figure}
\par {\includegraphics[width=8.3cm,clip]{7017fig7.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg37.gif) |
Figure 7:
Top left: scatter plot of the amplitude vs. area asymmetries.
Bottom left: scatter plot of the area asymmetry vs. the V velocity.
Right panels: scatter plots of the amplitude and area asymmetries vs. the Fe I 630.25 nm V amplitude.
Gray and black show the network and inter-network, respectively. |
| Open with DEXTER |
The upper panel of Fig. 8 shows the relation between the photospheric magnetic flux and the
chromospheric emission for the network.
For lower flux values (<100 Mx cm-2), there is a clear increase of emission with flux.
However, for higher
magnetic flux densities, the H-index increases slowly.
To reproduce the observed relation, we utilize a power law fit to the data,
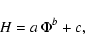 |
(1) |
where 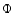 is the absolute magnetic flux density, H is the H-index,
a is a constant coefficient,
b is the power index, and c is the non-magnetic contribution (see Sect. 5.3.2).
We use a variable lower threshold of 0, 3, .., 20 Mx cm-2 (cf. Table 3)
for the fit and neglect all
data points with fluxes below this level.
We find that the power exponent, b, depends strongly on the threshold.
The higher the threshold, the better the fit curve resembles a straight line, as first reported
by Skumanich et al. (1975).
If we keep all the points, including inter-network, we obtain a value for the power exponent b of
is the absolute magnetic flux density, H is the H-index,
a is a constant coefficient,
b is the power index, and c is the non-magnetic contribution (see Sect. 5.3.2).
We use a variable lower threshold of 0, 3, .., 20 Mx cm-2 (cf. Table 3)
for the fit and neglect all
data points with fluxes below this level.
We find that the power exponent, b, depends strongly on the threshold.
The higher the threshold, the better the fit curve resembles a straight line, as first reported
by Skumanich et al. (1975).
If we keep all the points, including inter-network, we obtain a value for the power exponent b of 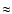 0.2.
0.2.
![\begin{figure}
\par {\includegraphics[width=7.2cm,clip]{7017fig8.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg41.gif) |
Figure 8:
Upper panel: correlation between the H-index and the absolute
magnetic flux density. Gray is the original data and black is the binned data: each point is average of 25 points.
The middle curve shows a fit of a power law to the original data (Eq. (1)), the other two curves give the
1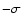 error range of the fit. Lower panel: there is no correlation between the H-index and the
magnetic flux density in inter-network.
error range of the fit. Lower panel: there is no correlation between the H-index and the
magnetic flux density in inter-network. |
| Open with DEXTER |
![\begin{figure}
\par {\includegraphics[width=16.9cm,clip]{7017fig9.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg42.gif) |
Figure 9:
Correlation between the H-index and amplitude/area asymmetry and V velocity.
Plusses and squares show network and inter-network, respectively. The binning method is similar to Fig. 8. |
| Open with DEXTER |
The calcium core emission in the inter-network does not correlate with the magnetic flux,
at least with the concentrated magnetic field within the Zeeman sensitivity (Fig. 8, lower panel).
The value of the offset, c, of the fit to the network (Table 3) for low magnetic flux densities
is around 10 pm, which is consistent with the average H-index value of all the inter-network profiles
(10 pm for the peak sample). The value of the c parameter changes for different thresholds
of the flux density (Table 3). Implications of this finding
for the basal flux are discussed in Sect. 7.
Table 3:
The parameters of the fit to Eq. (1) to the network data.
The first column is the threshold for the magnetic flux density (Mx cm-2).
By increasing the threshold, we avoid the inter-network intrusions.
For a comparison to the peak inter-network flux density, see Appendix A.
There are different behaviors for the network and inter-network calcium core emission
with respect to V velocity and asymmetries (Fig. 9).
The core emission peaks at small positive amplitude/area symmetry in the network.
This is caused by strong V profiles that show small asymmetries (Fig. 7, right panels).
The highest H-index in the network corresponds to almost zero V velocity.
In its diagram (Fig. 9), the slope of the left branch (blueshift) is smaller than the right one.
Moreover for the strong upflow
or downflow in the magnetic atmosphere in the network, the H-index decreases
significantly. The H-index in the inter-network does not
depend on any parameter of the Stokes-V profile (Fig. 9).
Considering the fact that the amplitude and area asymmetries strongly
correlate with each other (top left panel, Fig. 7),
a natural consequence is that the left (right) branch of the scatter plot of the
H-index vs. amplitude asymmetry corresponds to the left (right) branch of the scatter plot
of the H-index vs. area asymmetry (Fig. 9).
However, if we compare only negative or positive branches of the scatter plots of the H-index vs. V
velocity and asymmetries in the network,
we realize that the left branch in the V velocity does not correspond to the
similar branch in the asymmetry plots.
The left diagrams in Fig. 10 consider only the profiles with a
negative V velocity, while in the right panels profiles with a negative area asymmetry are shown.
A positive V velocity may thus correspond to a positive or negative area asymmetry.
There is no relation between the amplitude/area
asymmetries and the V signal in the inter-network (right panels, Fig. 7).
The H-index includes the H1 (the minima outside the emission peaks), H2, and H3 spectral regions.
So its formation height extends from the higher photosphere to the middle chromosphere.
The Ca II H & K lines are one of the main sources of the chromospheric radiative loss.
We use the H-index as a proxy for the emission in the low/mid chromosphere, and
assume a linear relation between the H-index and the chromospheric radiative loss.
To derive the contribution of magnetic fields to the chromospheric emission, we
added the H-index of all points with magnetic flux above a given flux threshold.
The fractional H-index, 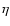 ,
is then defined by normalizing this quantity to the total
H-index of all points in the field of view
,
is then defined by normalizing this quantity to the total
H-index of all points in the field of view![[*]](/icons/foot_motif.gif) :
:
Table 4 lists the fractional H-index in different magnetic flux thresholds.
Some 20% of the total H-index is provided by strong flux
concentrations (
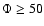 . Mx cm-2) while
the remaining 80% of that is produced by the weak magnetic field and/or field free regions.
. Mx cm-2) while
the remaining 80% of that is produced by the weak magnetic field and/or field free regions.
![\begin{figure}
\par {\includegraphics[width=7.2cm,clip]{7017fig10.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg45.gif) |
Figure 10:
In the left column diagrams,
only the points with a negative V velocity are plotted.
In the right panels, only points with a negative area asymmetry are plotted.
Pluses and squares show network and inter-network, respectively. |
| Open with DEXTER |
Table 4:
Fractional distribution of the total H-index, 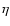 ,
for different magnetic flux thresholds.
,
for different magnetic flux thresholds.
The average H-index is 12.0 and 9.8 pm in the network and inter-network, respectively.
However, it contains some contributions from the photosphere (outside emission peaks) and a cool
chromosphere (without temperature rise).
Therefore, we decompose the observed calcium profiles in a
heated and a non-heated component,
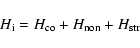 |
(2) |
where
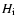 is the average H-index of the inter-network,
is the average H-index of the inter-network,
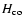 is the non-heated component,
is the non-heated component,
 is the
non-magnetically heated component, and
is the
non-magnetically heated component, and
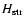 is the straylight contribution.
The non-heated component of the profile originates from the line-wing emission (photosphere)
and a cool chromosphere,
is the straylight contribution.
The non-heated component of the profile originates from the line-wing emission (photosphere)
and a cool chromosphere,
 .
.
We use the Holweger & Müller (1974) model atmosphere as a proxy
for those parts of the solar atmosphere that are not affected by
any heating process.
This model is very similar to a theoretical radiative equilibrium
model, but it was not constructed to strictly satisfy this condition.
We prefer this semi-empirical model over a theoretical
radiative equilibrium model because it results in slightly better
reproduction of the Ca II H line wings in a standard disk-center
atlas.
We note, however, that 3D (M)HD simulations of the solar atmosphere
commonly produce regions in the upper photosphere and chromosphere
with temperatures significantly lower than in the Holweger-Müller model.
These structures, however, are generally so small that their evolution
is strongly influenced by their surroundings, so that they cannot serve
as a model for those parts of the solar atmosphere that are not influenced
by any heating processes. That means that they are not suitable for determining
the absolute minimum value of the H-index.
We perform a consistent NLTE radiative transfer computation in plane-parallel
geometry, including effects of partial frequency redistribution, in order to
estimate the non-heated component of the H-index.
We added an isothermal hydrostatic extension up to a height of 2000 km
to the model in order to be able to compute the core parts of the Ca II H & K lines.
This may seem an arbitrary choice, but considering that the computed
intensity is essentially zero at the line core for models with such low
temperatures in the upper atmosphere, its influence on the H-index
is very small. This model atmosphere and the obtained profile are
similar to the COOLC model of Ayres et al. (1986) and the corresponding profile.
We find a value of
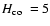 pm at disk center.
At a heliocentric angle of 53
pm at disk center.
At a heliocentric angle of 53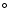 ,
the appropriate value is
,
the appropriate value is
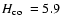 pm.
pm.
We find an upper limit of  12% for the straylight contamination of the
observed profiles (cf. Appendix B).
Therefore, we decompose the average H-index in the inter-network (
12% for the straylight contamination of the
observed profiles (cf. Appendix B).
Therefore, we decompose the average H-index in the inter-network (
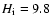 pm) to obtain
the non-magnetically heated component,
pm) to obtain
the non-magnetically heated component,
 :
:
We find an average non-magnetic heating of
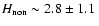 pm.
To decompose the average H-index of the network, we also consider the magnetically heated component,
pm.
To decompose the average H-index of the network, we also consider the magnetically heated component,
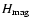 ,
and use the same method:
,
and use the same method:
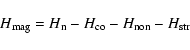 |
(4) |
where the magnetically heated contribution is the first term in Eq. (1).
Assuming a similar non-magnetically heated contribution,
 ,
for the network as in the
inter-network (which is supported by observations, e.g., Schrijver 1987,1995),
we find an average magnetically heated component of about
,
for the network as in the
inter-network (which is supported by observations, e.g., Schrijver 1987,1995),
we find an average magnetically heated component of about
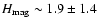 pm,
which is consistent with the difference between
the mean H-index in the network and inter-network.
Thus, the non-magnetically heated component has a larger contribution in the observed H-index
than magnetically heated one, both in the network and inter-network.
Our error estimates in Appendix B show that the uncertainties of the measurements do not
affect this result.
pm,
which is consistent with the difference between
the mean H-index in the network and inter-network.
Thus, the non-magnetically heated component has a larger contribution in the observed H-index
than magnetically heated one, both in the network and inter-network.
Our error estimates in Appendix B show that the uncertainties of the measurements do not
affect this result.
All intensity parameters, from the calcium core to the Fe I 630 nm continuum,
show different distributions in the network and inter-network: the network patches are
brighter not only at all observed wavelengths of the calcium profile, but also in the 630 nm
continuum (Figs. 7 and 4).
As noted by Cram & Damé (1983), this implies that the temperature fluctuations are spatially
coherent between the photosphere and the lower chromosphere.
This coherent intensity increase is presumably due to the fact that
the optical depth scale is shifted downwards in the evacuated magnetic part of the atmosphere.
The correlation between the inner wing intensity and H-index is strong,
both in the network and inter-network (Table 2). However, the correlation between
the outer wing intensity and the H-index is significant only in the network (Fig. 6, lower left panel).
This indicates that the height range of the thermal coupling between the photosphere
and low/mid chromosphere increases in presence of a magnetic field.
There are also suggestions that this coupling extends to the upper chromosphere (Rauscher & Marcy 2006).
The amount of energy deposited in the network depends on the
magnetic flux density. To reproduce the dependence of calcium
core emission on the magnetic flux with a power law, we find that
the exponent derived strongly depends on the inclusion (or exclusion)
of the weakest fluxes. We obtain a power
exponent, b, of about 0.3, which is smaller than the value given
by Schrijver et al. (1989) and Harvey & White (1999). We ascribe the
difference to the higher quality of our data set: better spatial
resolution, a lower detection limit for magnetic signals, an accurate
estimate of the magnetic flux due to the inversion of vector polarimetric
data instead of a magnetogram, and unlike these authors, we do not
consider an assumption for the background component prior to the fit.
Instead, we keep it as a free
parameter. In this way, we find a background component close to the mean H-index of the inter-network for
the weakest flux concentrations.
The rate of increase of the chromospheric emission vs. magnetic flux
reduces for strong magnetic flux densities. This implies that for large
flux concentrations, either the filling factor or the magnetic field strength saturates.
There are indications that it is the filling factor:
the available space is completely filled by expanding flux tubes (Hammer 1987; Schrijver et al. 1996; Saar 1996).
In contrast, a lower limit of chromospheric emission also exists.
In the inter-network, no relation between emission and the photospheric fields is found (Figs. 8 and 9).
The average value of the H-index in the inter-network of around 10 pm corresponds to the offset, c, Eq. (1).
This reflects a constant contribution to the H-index which is present even
without photospheric magnetic flux, in agreement with
Schrijver (1987,1995) who argued that
the basal flux does not depend on the magnetic activity.
The basal flux contains two components: the non-heated (cf. Sect. 6) and the non-magnetically heated contributions.
The non-heated contribution depends on the temperature stratification,
so that we speculate that the non-magnetically heated component
has an inverse dependence on the temperature stratification.
Figure 8 (upper panel) shows that there is a variable lower limit for the H-index versus the
magnetic flux density.
In contrast, the upper limit is less clearly defined, and would be in
agreement with a constant maximum value independent of the amount of magnetic flux.
There are also similar behaviors for the upper and lower limits in the scatter plots of
the H3,
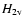 ,
and
,
and
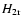 versus the magnetic flux density.
This is similar to upper and lower limits of the basal flux of stars vs. the color (B-V) where
the lower boundary changes but the upper one is almost constant (Fawzy et al. 2002b, their Fig. 2).
The situation for the inter-network is different: both the upper and lower limits are
independent of the magnetic flux density.
versus the magnetic flux density.
This is similar to upper and lower limits of the basal flux of stars vs. the color (B-V) where
the lower boundary changes but the upper one is almost constant (Fawzy et al. 2002b, their Fig. 2).
The situation for the inter-network is different: both the upper and lower limits are
independent of the magnetic flux density.
We interpret the solar Ca II H line profile as the superposition of a cool chromospheric profile,
the heated component and straylight components.
Oranje (1983) first applied this method to reproduce different observed Ca II K profiles from two
"basic'' profiles.
Later, Solanki et al. (1991) used the same idea to decompose the observed profiles by a
combination of two theoretically calculated profiles.
Our one-dimensional NLTE radiative transfer calculations reveal that
the H-index of a cool chromosphere is about 5.9 pm.
Since the chromospheric emission of the Sun as a star is slightly above the minimum among the
Sun-like stars (Schrijver & Zwaan 2000),
the average quiet Sun profile contains a heated component.
Subtraction of the cool chromospheric component from the measured H-index
(along with straylight considerations) leads to an estimation of
the pure non-magnetically and magnetically heated components in the measured H-index.
The non-magnetically heated component is almost 50% larger than the magnetically heated component.
The presence of a significant non-heated contribution in the H-index indicates
that not all of the chromospheric emission emerges from a hot chromosphere,
in contrast to findings from, e.g., Kalkofen et al. (1999).
The minimum heated component in a Ca profile provides evidence how cool the chromosphere may
be (e.g., Wedemeyer-Böhm et al. 2005).
Moreover, it favors theories in which the non-magnetic heating plays
the dominant role in the chromospheric heating (Fawzy et al. 2002a).
The fact that the non-magnetic chromospheric heating contributes significantly to
the chromospheric energy balance is also found in the relative contributions of mainly
field-free inter-network and network areas to the total emission in the field of view.
Magnetic flux densities above 50 Mx cm-2 add
only 20% to the total emission, which is also seen in the ratio of the mean H-index
in the network and inter-network, 12.0 /
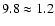 (Table 4).
(Table 4).
The main uncertainty in the non-magnetically and magnetically heated components is the presence
of some heating in our cool chromosphere profile.
The Holweger & Müller (1974) model atmosphere is close to an atmosphere in radiative equilibrium without
non-magnetic or magnetic heating, so no heated component (cf. Sect. 6) is expected
to be found on its Ca profile.
Since there is no general agreement how cool the chromosphere may
be (e.g., Ayres 2002; Kalkofen et al. 1999),
the best answer would be to use the observed calcium profile with the lowest H-index.
However, Solanki et al. (1991) concluded that it is not possible to observe a low activity
profile as presented by the COOLC model of Ayres et al. (1986), which is similar to the one employed by
us on base of the Holweger & Müller (1974) model atmosphere. Thus, our cool profile can
well serve as lower limit of the non-heated contribution to the H-index.
Note that a larger value for
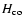 would increase
the contribution of the magnetically heated component, leading to a larger fractional contribution
for the magnetically heated to the total heated component.
would increase
the contribution of the magnetically heated component, leading to a larger fractional contribution
for the magnetically heated to the total heated component.
There may be some mixed polarity fields below our polarimetric detection limit which may
influence the ratio of the magnetically heated to the non-magnetically heated component.
From the relations of the chromospheric emission to quantities of the photospheric
magnetic field in the network, we find that the chromospheric emission peaks at
small positive values of the Stokes-V asymmetries and at zero Stokes-V velocity
(Fig. 5). It reflects the histograms of the respective photospheric field quantities
which show similar distributions even at disk center (e.g., Sigwarth et al. 1999).
However, in combination with the dependence of the emission on the flux density it is
inferred that the stronger flux concentrations mainly show small material flows
along with non-zero asymmetries.
The magnetically heated component is related to Stokes-V profiles with non-zero area and
amplitude asymmetries (Figs. 5 and 9).
A possible explanation for this finding would be the absorption of upward propagating
acoustic waves, generated by the turbulent convection, by the inclined fields of expanding
flux tubes. This would imply that the energy is deposited at the outer boundary
or in the canopy of flux concentrations rather than in the central, more vertical, part.
It is mainly because the non-magnetic cutoff frequency is lowered at the boundary of the flux tubes,
where the field lines are inclined.
This was first predicted by Suematsu (1990) and recently achieved some observational
support (Jefferies et al. 2006; Hansteen et al. 2006).
Figure 9 indicates that the maximum observed H-index has non-zero V asymmetry.
These asymmetric V profiles are consistent with the case when the line of sight passes through the canopy of
a magnetic element or through a flux tube axis (positive and negative asymmetries respectively, Steiner 1999).
Therefore our finding supports Suematsu (1990).
As a byproduct of our study on the relation between photospheric fields and chromospheric emission,
we obtained distributions of field strength for network and inter-network regions. For the inter-network fields,
for the first time an inversion of visible spectral lines in the weak field limit led to the
same distribution as results from the more sensitive infrared lines (Collados 2001).
This is discussed in Appendix A. Thus, we find that the inter-network magnetic field is dominated by
field strengths of the weak field regime which ranges up to some 600 G.
This rules out the argument that the inter-network is dominated by a
magnetic field with a strength of more than a kilo-Gauss (e.g., Sánchez Almeida et al. 2003a).
There is no correlation between the H-index and magnetic field parameters in the inter-network.
Therefore, we conclude that the magnetic field has a negligible role in
the chromospheric heating in the inter-network.
On the other hand, the H-index is a power law function of the magnetic flux density
in the network with a power index of 0.3.
The average H-index observed in the network and inter-network are 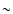 10 and 12 pm, respectively.
We find a non-magnetic component in the network (based on Eq. (1)) of about 10 pm which
shows the consistency of our analysis: the non-magnetic part of the
network H-index is equal to the H-index of the inter-network.
10 and 12 pm, respectively.
We find a non-magnetic component in the network (based on Eq. (1)) of about 10 pm which
shows the consistency of our analysis: the non-magnetic part of the
network H-index is equal to the H-index of the inter-network.
A NLTE radiative transfer calculation, using the Holweger-Müller model atmosphere,
indicates that the non-heated component of the H-index, emerging from a cool
chromosphere, is about 5.9 pm.
Comparison of this non-heated component and the average H-index in the inter-network
has two implications: a) some of the observed chromospheric emission does not originate from a hot chromosphere,
and b) the non-magnetically heated component is about 50% larger than the magnetically heated component.
From this, we conclude that the non-magnetically heated component has a larger contribution
in the chromospheric radiative loss than the
magnetically heated component, both in the network and inter-network.
In our statistical ensemble,
spatial positions with strong magnetic field (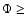 50 Mx cm-2) contribute about 20%
of the total H-index. Correlations and histograms of the different intensity bands in the Ca II H spectrum
indicate that above a magnetic threshold, photosphere and low/mid chromosphere are thermally
coupled. Moreover, our findings are consistent with the idea that the energy transfer in a flux tube
has a skin effect: the energy transfer is more efficient in the flux tube boundary (canopy)
than at its center (axis).
50 Mx cm-2) contribute about 20%
of the total H-index. Correlations and histograms of the different intensity bands in the Ca II H spectrum
indicate that above a magnetic threshold, photosphere and low/mid chromosphere are thermally
coupled. Moreover, our findings are consistent with the idea that the energy transfer in a flux tube
has a skin effect: the energy transfer is more efficient in the flux tube boundary (canopy)
than at its center (axis).
For the first time, we find a magnetic field distribution in the inter-network using visible lines
which is similar to results inferred from infrared lines with larger Zeeman splitting.
The distribution function increases with decreasing field strength. The peak at 200 G is due to the detection
limit of the polarization signal. The average
and distribution peak of the absolute flux density (of magnetic profiles)
in the inter-network are 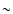 11 and 4 Mx cm-2, respectively.
We conclude that the combination of high spatial resolution and polarimetric accuracy is sufficient
to reconcile the different results on field strength found from infrared and visible lines.
11 and 4 Mx cm-2, respectively.
We conclude that the combination of high spatial resolution and polarimetric accuracy is sufficient
to reconcile the different results on field strength found from infrared and visible lines.
Acknowledgements
The principal investigator (PI) of the ITP observing campaign was P. Sütterlin, Utrecht, The Netherlands.
We wish to thank Reiner Hammer, Oskar Steiner, Thomas Kentischer, Wolfgang Rammacher, and Hector Socas-Navarro
for useful discussions.The POLIS instrument has been a joint development of the High
Altitude Observatory (Boulder, USA) and the Kiepenheuer-Institut.
Part of this work was supported by the Deutsche Forschungsgemeinschaft (SCHM 1168/8-1).
Traditional magnetic field strength distributions for the quiet Sun (inter-network) based on visible lines
have a broad peak centered around 1 kG (Sánchez Almeida et al. 2003a; Domínguez Cerdeña et al. 2006).
On the other hand, observations in the infrared lines show a clear peak at
lower field strengths and an almost exponentially
decreasing probability for higher fields strengths (Khomenko et al. 2003; Bellot Rubio & Collados 2003; Collados 2001).
This discrepancy between the retrieved parameters from the visible and infrared lines
has not been solved so far (Steiner 2003; Martínez González et al. 2006).
We achieved a magnetic field distribution for the inter-network
using the Fe I 630 nm pair that is similar to the infrared studies (Fig. 5b).
We elaborate on the effects of spatial resolution and signal-to-noise ratio on this finding.
We used the Kiepenheuer Adaptive Optics System (KAOS) to improve spatial
resolution and image stability (von der Lühe et al. 2003).
It provides stable sharp images in a certain field of view, and therefore
allows us to increase the exposure time to have better signal-to-noise ratio.
Figure A.1 is a close-up view of the inter-network magnetic flux distribution.
The lowest flux detected is 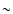 0.05 Mx cm-2. The distribution of the
flux decreases sharply for fluxes below
0.05 Mx cm-2. The distribution of the
flux decreases sharply for fluxes below
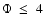 Mx cm-2, which is due
to the detection limit of the polarization signal. The small fluxes still detected
give us, however, confidence that the magnetic field strength distribution of Fig. 5b
is reliable as a consequence of the combination of high spatial resolution and good signal-to-noise ratio.
Mx cm-2, which is due
to the detection limit of the polarization signal. The small fluxes still detected
give us, however, confidence that the magnetic field strength distribution of Fig. 5b
is reliable as a consequence of the combination of high spatial resolution and good signal-to-noise ratio.
![\begin{figure}
\par {\includegraphics[width=8.3cm,clip]{7017fgA1.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg62.gif) |
Figure A.1:
Close up view of the flux density distribution for the inter-network.
At a value of  4.0 Mx cm-2, the histogram shows a peak. 4.0 Mx cm-2, the histogram shows a peak. |
To investigate the influence of noise on the inversion results,
we compare inversion results of the original datasets with and without adding noise.
In order to create "noisy'' data sets, the rms value of the noise in the original data
was increased to
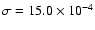
 ,
two times larger than the original value.
The spatial sampling was identical to the original data.
We emphasize that inversion was done using the same assumptions and initial model atmosphere.
Figure A.2 compares two sets of full Stokes profiles (black)
and the inversion fit (red). The upper four panels are the original profiles and the lower four
panels are the same profiles with noise. The fits and retrieved model atmospheres differ significantly.
Especially important is the fact that the noisy inversion leads to a magnetic field of 1.5 kG.
,
two times larger than the original value.
The spatial sampling was identical to the original data.
We emphasize that inversion was done using the same assumptions and initial model atmosphere.
Figure A.2 compares two sets of full Stokes profiles (black)
and the inversion fit (red). The upper four panels are the original profiles and the lower four
panels are the same profiles with noise. The fits and retrieved model atmospheres differ significantly.
Especially important is the fact that the noisy inversion leads to a magnetic field of 1.5 kG.
![\begin{figure}
\par {\includegraphics[width=8cm,clip]{7017fgA2.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg64.gif) |
Figure A.2:
The upper four plots show an example of the original Stokes profiles and the inversion fits.
The lower four figures show the same profile with a rms noise value two times larger and corresponding fits.
The magnetic field strength, magnetic filling factor, and macro turbulence velocity for the
original and noisy profiles are (842, 1543) G, (7.6, 5.3)%, and (2.95, 2.77) km s-1 respectively.
The x-axis shows the spectral coordinate in mÅ.
|
To compare the field strength obtained from the original and noisy datasets, their
histograms are shown in Fig. A.3. The distribution of the original field strength
peaks around  200 G (black histogram), while for the noisy data, it has a clear shift
toward higher values with a peak at 0.8 kG (red histogram).
This emphasizes the role of the noise in the existing discrepancy between visible and
infrared measurements (Bellot Rubio & Collados 2003).
200 G (black histogram), while for the noisy data, it has a clear shift
toward higher values with a peak at 0.8 kG (red histogram).
This emphasizes the role of the noise in the existing discrepancy between visible and
infrared measurements (Bellot Rubio & Collados 2003).
In brief, we find that higher spatial resolution of these observations along with low noise data
is an important step toward resolving disagreements between the visible and infrared polarimetric measurements.
The visible Fe I 630 nm pair shows higher Stokes amplitudes for small magnetic fields than the
infrared lines of Fe I 1.56 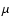 m. Hence, with an equal amount of noise in observational data,
the visible lines provide a higher signal-to-noise ratio than infrared lines.
Therefore, in contrast to Martínez González et al. (2006), we find the visible Fe I 630 nm pair to be a proper
tool to investigate the inter-network magnetic field. We ascribe the present disagreements
to the low spatial resolution of previous observations and different signal-to-noise ratios.
m. Hence, with an equal amount of noise in observational data,
the visible lines provide a higher signal-to-noise ratio than infrared lines.
Therefore, in contrast to Martínez González et al. (2006), we find the visible Fe I 630 nm pair to be a proper
tool to investigate the inter-network magnetic field. We ascribe the present disagreements
to the low spatial resolution of previous observations and different signal-to-noise ratios.
![\begin{figure}
\par {\includegraphics[width=7.6cm,clip]{7017fgA3.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg66.gif) |
Figure A.3:
Histograms of the inter-network field strengths of one of the maps
based on the inversion of original data (black) and noisy data (red). |
The POlarimetric LIttrow Spectrograph (POLIS) was designed to
facilitate co-temporal and co-spatial measurements of the vector magnetic field in the photosphere
and the Ca II H intensity profile (Schmidt et al. 2003; Beck et al. 2005a).
We try to elaborate on the uncertainties in
the intensity calibration, because it is critical for the estimates of
the various contributions (straylight, non-magnetic heating, etc.) to the observed calcium profiles.
Observations are discussed in Sect. B.1.
We study the linearity of the CCD camera for different light levels in Sect. B.2.
Then, we investigate instrumental and solar straylight contributions in Sect. B.3.
In Sect. B.4, we perform standard error propagation to quantify uncertainties
in our final calibrated spectra.
In order to study linearity of the POLIS CCD camera of the calcium channel
at different light levels, we observed a set of calcium spectra and flat field
data with different accumulations and slit widths at disk center.
A sunspot was also observed with a similar setup and an exposure time of 0.82 s and six accumulations.
Besides this,
we recorded dark current data using either the AO or POLIS field stop. We use these two data sets to
estimate the solar and instrumental straylight, respectively.
All spectra and profiles in this Appendix are dark subtracted raw data.
No other calibration process like flat fielding was applied.
In order to show intrinsic noise in the data, we did not spatially average darks or spectra.
In order to check the linearity of the calcium camera from profiles
by, e.g., comparing the ratio of the core to wing for different exposures,
we recorded spectra with different slit widths and identical modulation
speed (Mullikin et al. 1994).
Figure B.1 shows a comparison between the two flat field profiles taken on disk center
with identical illumination, but different slit widths.
The black and blue profiles correspond to a
slit width of 0.48 and 0.18 arcsec, respectively.
If one multiplies the blue curve with the ratio of the slit widths of 2.67,
the resulting curve agrees well with the profile of the broad slit for all wavelengths
including the line core.
We calculated the ratio of the two profiles with different slit widths as function of wavelength.
The rms variation of the ratio was 1%.
This can be used as an upper limit for non-linearity effects of the CCD camera.
![\begin{figure}
\par {\includegraphics[width=8.1cm,clip]{7017fgB1.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg67.gif) |
Figure B.1:
Comparison between two different slit widths and the same modulation speed.
The black and blue profiles
correspond to slit widths of 0.48 and 0.18 arcsec, respectively. The red profile is
the blue profile multiplied by a constant factor of 2.6 for all pixels.
The green profiles show the 1-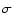 rms value (
rms value (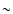 1%) from the mean curve (red). 1%) from the mean curve (red). |
![\begin{figure}
\par {\includegraphics[width=7.6cm,clip]{7017fgB2.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg68.gif) |
Figure B.2:
Dark subtracted spectrum of the umbra in a sunspot. |
We compare two sets of dark current images of the POLIS Fe channel:
one with a field stop right after the focal plane,
and another one with the field stop in front of the camera. In the second case,
all light sources inside the observing room are fully blocked. The difference
between the two measurements is about 0.9 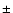 0.5%. This gives an upper
limit for the instrumental straylight in the POLIS Ca channel as well,
since most of the sources in the observing room will not emit in blue as efficient as red.
0.5%. This gives an upper
limit for the instrumental straylight in the POLIS Ca channel as well,
since most of the sources in the observing room will not emit in blue as efficient as red.
![\begin{figure}
\par {\includegraphics[width=16.9cm,clip]{7017fgB3.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg69.gif) |
Figure B.3:
Left: a single Ca II H spectrum of the umbra and quiet sun profiles in a sunspot.
Asterisks show spectral bands that were used to estimate the true signal (see Sect. B.3.2).
Right: close up view of the quiet sun and umbral profiles near the calcium line core.
The true signal (about 5% in the wing close to the Ca core according
to Wallace et al. (2000) was subtracted from the umbral profile.
The red curve shows 12% of the quiet sun profile.
The two cyan curves show an uncertainty interval of one sigma (1%). |
The calcium profile in the sunspot umbra is significantly weaker than a quiet sun profile.
However, there is a well known single emission peak in the calcium core (Linsky & Avrett 1970).
We thus compare an inner wing band close to the calcium core, but excluding the
core itself (asterisks in the left panel of Fig. B.3),
in an umbral profile and a normal profile from outside the spot to derive an
upper limit for the solar straylight contribution to observed profiles.
Figure B.2 shows a slit spectrum of the umbra.
To keep the sample profiles as uniform as possible, we chose two identical positions
along the slit (at about 30 arcsec, Fig. B.2).
The spectrum of the quiet sun and the
minimum spectrum of the umbra are shown in Fig. B.3 (left panel).
Wallace et al. (2000) presented a Fourier transform spectral atlas of the umbra.
In this atlas, the wing close to the umbral core
has an intensity of 5% in units of the umbral continuum,
while the wing close to the Fe I, Ti I, and Ni I lines at about
396.5 nm has an intensity of 38%. In our umbral profile,
this continuum has an intensity of about 80 counts (asterisks, Fig. B.3, left panel),
whereas close to the core the profile has about 45 counts.
Assuming no straylight in the atlas profile, only 11 counts (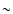 22% of the observed valued)
should be measured in the core. Thus, 78% of the observed signal have to be due
to straylight.
To reproduce 78% of the umbral profile, a straylight contribution of around 12% is needed.
If we assume that there is no real calcium signal in the umbra (which is wrong) and
take the observed calcium profile of the umbra as pure scattered light,
the ratio changes from 12% to 15%.
Therefore, uncertainties about the scattered light in the atlas profile have minor importance.
22% of the observed valued)
should be measured in the core. Thus, 78% of the observed signal have to be due
to straylight.
To reproduce 78% of the umbral profile, a straylight contribution of around 12% is needed.
If we assume that there is no real calcium signal in the umbra (which is wrong) and
take the observed calcium profile of the umbra as pure scattered light,
the ratio changes from 12% to 15%.
Therefore, uncertainties about the scattered light in the atlas profile have minor importance.
A close-up view of the spectral region close to the calcium core is shown in Fig. B.3 (right panel).
For the reason mentioned above,
in the right panel of Fig. B.3, the umbral profile was labeled umbra (78%).
The red curve shows 12% of the quiet sun profile. The two cyan curves also show
an uncertainty interval of one sigma (1%). Figure B.4 shows the
ratio of the umbra to the quiet sun profile. If we calculate mean and rms of the whole
spectrum, it gives a value of 10 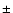 3% while considering only on the wing band
close to the calcium core, we obtain 12
3% while considering only on the wing band
close to the calcium core, we obtain 12 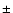 1%. We take this value as an upper limit
for the total straylight in the POLIS calcium channel.
In Sect. B.3.1, we concluded that the instrumental straylight is about 1%.
Hence, most of the obtained straylight originates from
the scattered solar light in the telescope and the earth atmosphere.
1%. We take this value as an upper limit
for the total straylight in the POLIS calcium channel.
In Sect. B.3.1, we concluded that the instrumental straylight is about 1%.
Hence, most of the obtained straylight originates from
the scattered solar light in the telescope and the earth atmosphere.
![\begin{figure}
\par {\includegraphics[width=8.2cm,clip]{7017fgB4.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg70.gif) |
Figure B.4:
Ratio of the umbral profile to a quiet sun profile.
If one considers all the spectrum, the ratio will be 10 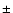 3% while considering only parts
of the wing close to the Ca II H core, the ratio will be 12 3% while considering only parts
of the wing close to the Ca II H core, the ratio will be 12 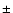 1%. Note to the
mismatch between the quiet sun and umbral profiles at spectral line positions due to different broadenings. 1%. Note to the
mismatch between the quiet sun and umbral profiles at spectral line positions due to different broadenings. |
![\begin{figure}
\par {\includegraphics[width=8.2cm,clip]{7017fgB5.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg71.gif) |
Figure B.5:
Distribution of the readout error in a set of 50 dark currents with 8 accumulations. |
There are three noise sources in a CCD camera (Mullikin et al. 1994):
- 1.
- readout noise because of the pre-amplifier;
- 2.
- dark current noise which is influenced by the chip temperature;
- 3.
- photon noise due to the quantum nature of light which obeys Poisson statistics.
The readout error of the camera was estimated by a set of 50 consecutive dark frames
with similar exposure and accumulations.
Here, we compare the number of counts on each pixel in different images.
We attribute the standard deviation of the count value mainly to the readout
error, and hence, obtain a readout error for each pixel separately.
The distribution of the readout errors is shown in Fig. B.5.
The readout noise is about
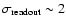 counts.
counts.
![\begin{figure}
\par {\includegraphics[width=8.3cm,clip]{7017fgB6.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg73.gif) |
Figure B.6:
Upper panel: a row in a dark frame with 6 accumulation. The red curve is a polynomial fit
to subtract systematic shift from the random noise.
Lower panel: the residual signal after subtraction of the polynomial, which is the real noise.
Note to the large difference between the rms of the map (excluding its borders) and the rms of the residuals. |
![\begin{figure}
\par {\includegraphics[width=8.2cm,clip]{7017fgB7.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg74.gif) |
Figure B.7:
A sample calcium profile. We use the calcium core minimum counts to estimate the photon noise.
In this case, the signal-to-noise ratio at the calcium core is more than 10. |
To investigate the thermal noise in the dark current, one has to
remove small systematic offsets between CCD columns
(probably due to thermal fluctuations of the AD system) before
considering statistical measures, e.g., rms, of a dark profile (a CCD row).
As it is shown in Fig. B.6, for a dark frame with 6 accumulations,
the resulting rms (after removing systematics)
is far less than the standard deviation of the whole map including a large-scale variation.
It provides an estimate for the thermal noise in the camera.
So the rms of the dark frame is about
 counts.
counts.
The total noise in the recorded data,
 ,
consists of three components:
,
consists of three components:
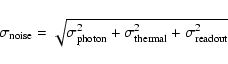 |
(A.1) |
where the photon noise originates from the Poisson fluctuations of the number of photons counted.
Assuming that
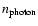 is the number of detected photons,
the corresponding rms,
is the number of detected photons,
the corresponding rms,
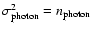 .
The calcium core is more influenced by the noise than the other points in the spectrum.
Figure B.7 shows a dark subtracted calcium spectrum with 6 accumulations and a narrow slit (0.18 arcsec).
The minimum number of counts in the core is 117, so
.
The calcium core is more influenced by the noise than the other points in the spectrum.
Figure B.7 shows a dark subtracted calcium spectrum with 6 accumulations and a narrow slit (0.18 arcsec).
The minimum number of counts in the core is 117, so
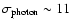 .
Therefore, the total noise in the core (Eq. (B.1)) will be
.
Therefore, the total noise in the core (Eq. (B.1)) will be
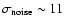 .
So the worst signal-to-noise ratio at the calcium core position will be better than 10.
Note that the data described in the paper were obtained with a wide slit (0.48 arcsec)
while the spectrum shown in Fig. B.7 was recorded with a narrow slit (0.18 arcsec),
so we have better signal-to-noise ratio in the data.
.
So the worst signal-to-noise ratio at the calcium core position will be better than 10.
Note that the data described in the paper were obtained with a wide slit (0.48 arcsec)
while the spectrum shown in Fig. B.7 was recorded with a narrow slit (0.18 arcsec),
so we have better signal-to-noise ratio in the data.
The relative intensity of the core to wing is defined as:
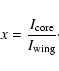 |
(A.2) |
To estimate their rms errors, we find the signal-to-noise ratio for the core and wing
intensities in some wing bands.
Since it is not possible to use the core intensity to obtain the noise due to intrinsic changes,
we use the average signal-to-noise of the left and right wings close to the calcium core
as the signal-to-noise of the core. So the real signal-to-noise of the core is probably worse than that.
The S/N ratio of the core and wing vary from 35 and 112 for two accumulations to
174 and 216 for twenty accumulations.
We use the worse S/N ratio corresponding to anexposure time of 1.64 s and
obtain the following values for the rms errors of the core and wing intensities:
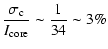 |
|
|
(A.3) |
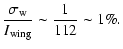 |
|
|
(A.4) |
So, we can obtain the
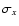 as follows:
as follows:
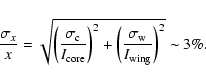 |
(A.5) |
Error sources of the final calibrated data include uncertainties from
the flat-field parameter, the straylight and the linearity of the detector.
The straylight uncertainty was obtained about 1% in Sect. B.3.
Assuming an upper limit for the uncertainty in the flat-field to be 5%
and some 1% uncertainty in linearity of the core to wing ratio,
an upper limit for the uncertainty in the calibrated spectrum will be:
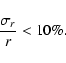
- Ayres, T. R.
2002, ApJ, 575, 1104 [NASA ADS] [CrossRef]
- Ayres,
T. R., Testerman, L., & Brault, J. W. 1986, ApJ, 304,
542 [NASA ADS] [CrossRef] (In the text)
- Beck, C.,
Schlichenmaier, R., Collados, M., Bellot Rubio, L., &
Kentischer, T. 2005a, A&A, 443, 1047 [NASA ADS] [CrossRef] [EDP Sciences]
- Beck, C., Schmidt,
W., Kentischer, T., & Elmore, D. 2005b, A&A, 437, 1159 [NASA ADS] [CrossRef] [EDP Sciences]
- Beck, C.,
Bellot Rubio, L., Schlichenmaier, R., & Sütterlin, P.
2006, A&A, submitted
(In the text)
-
Bellot Rubio, L. R., & Collados, M. 2003, A&A, 406,
357 [NASA ADS] [CrossRef] [EDP Sciences]
- Bellot Rubio,
L. R., & Beck, C. 2005, ApJ, 626, L125 [NASA ADS] [CrossRef] (In the text)
-
Berger, T. E., & Title, A. M. 2001, ApJ, 553,
449 [NASA ADS] [CrossRef] (In the text)
- Carlsson,
M., & Stein, R. F. 1997, ApJ, 481, 500 [NASA ADS] [CrossRef] (In the text)
-
Cattaneo, F., Emonet, T., & Weiss, N. 2003, ApJ, 588, 1183 [NASA ADS] [CrossRef]
- Collados, M.
2001, in Advanced Solar Polarimetry - Theory, Observation, and
Instrumentation, ed. M. Sigwarth, ASP Conf. Ser., 236,
255
- Cram,
L. E., & Damé, L. 1983, ApJ, 272, 355 [NASA ADS] [CrossRef]
- de Wijn,
A. G., Rutten, R. J., Haverkamp,
E. M. W. P., & Sütterlin, P. 2005, A&A,
441, 1183 [NASA ADS] [CrossRef] [EDP Sciences]
- Domínguez Cerdeña,
I., Almeida, J. S., & Kneer, F. 2006, ApJ, 646, 1421 [NASA ADS] [CrossRef]
-
Faurobert, M., Arnaud, J., Vigneau, J., & Frisch, H. 2001,
A&A, 378, 627 [NASA ADS] [CrossRef] [EDP Sciences]
- Fawzy,
D., Rammacher, W., Ulmschneider, P., Musielak, Z. E., &
Stepien, K. 2002a, A&A, 386, 971 [NASA ADS] [CrossRef] [EDP Sciences]
- Fawzy,
D., Ulmschneider, P., Stepien, K., Musielak, Z. E., &
Rammacher, W. 2002b, A&A, 386, 983 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Fossum, A.,
& Carlsson, M. 2005, Nature, 435, 919 [NASA ADS] [CrossRef]
- Hammer, R. 1987,
Solar and Stellar Physics, LNP, 292, 77
-
Hansteen, V. H., De Pontieu, B., Rouppe van der Voort, L., van
Noort, M., & Carlsson, M. 2006, ApJ, 647, L73 [NASA ADS] [CrossRef]
-
Harvey, K. L., & White, O. R. 1999, ApJ, 515,
812 [NASA ADS] [CrossRef] (In the text)
- Holweger, H.,
& Müller, E. A. 1974, Sol. Phys., 39, 19 [NASA ADS] [CrossRef] (In the text)
-
Jefferies, S. M., McIntosh, S. W., Armstrong, J. D.,
et al. 2006, ApJ, 648, L151 [NASA ADS] [CrossRef]
- Judge,
P. G., & Peter, H. 1998, Space Sci. Rev., 85,
187 [NASA ADS] [CrossRef]
-
Kalkofen, W., Ulmschneider, P., & Avrett, E. H. 1999, ApJ,
521, L141 [NASA ADS] [CrossRef]
- Keller,
C. U., Deubner, F.-L., Egger, U., Fleck, B., & Povel,
H. P. 1994, A&A, 286, 626 [NASA ADS] (In the text)
-
Khomenko, E. V., Collados, M., Solanki, S. K., Lagg, A.,
& Trujillo Bueno, J. 2003, A&A, 408, 1115 [NASA ADS] [CrossRef] [EDP Sciences]
- Linsky,
J. L., & Avrett, E. H. 1970, PASP, 82, 169 [NASA ADS] [CrossRef] (In the text)
- Lites, B. W.
2002, ApJ, 573, 431 [NASA ADS] [CrossRef] (In the text)
- Lites,
B. W., Rutten, R. J., & Kalkofen, W. 1993, ApJ, 414,
345 [NASA ADS] [CrossRef]
- Lites,
B. W., Rutten, R. J., & Berger, T. E. 1999, ApJ,
517, 1013 [NASA ADS] [CrossRef] (In the text)
-
Martínez González, M. J., Collados, M., & Ruiz
Cobo, B. 2006, A&A, 456, 1159 [NASA ADS] [CrossRef] [EDP Sciences]
- Mullikin,
J. C., van Vliet, L. J., Netten, H., et al. 1994, in
Image Acquisition and Scientific Imaging Systems, ed. H. C.
Titus, & A. Waks, Proc. SPIE, 2173, 73
(In the text)
- Narain, U.,
& Ulmschneider, P. 1996, Space Sci. Rev., 75,
453 [NASA ADS] [CrossRef] (In the text)
- Oranje,
B. J. 1983, A&A, 124, 43 [NASA ADS] (In the text)
- Priest,
E. R., Heyvaerts, J. F., & Title, A. M. 2002,
ApJ, 576, 533 [NASA ADS] [CrossRef]
-
Rauscher, E., & Marcy, G. W. 2006, PASP, 118, 617 [NASA ADS] [CrossRef] (In the text)
- Rezaei, R.,
Schlichenmaier, R., Beck, C. A. R., & Bellot Rubio,
L. R. 2006, A&A, 454, 975 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Rezaei, R.,
Schlichenmaier, R., Beck, C. A. R., & Schmidt, W.
2007, in Modern Solar Facilities-Advanced Solar Science, ed.
F. Kneer, K. G. Puschmann, & A. D. Wittmann, in
press
(In the text)
- Ruiz Cobo, B., & del
Toro Iniesta, J. C. 1992, ApJ, 398, 375 [NASA ADS] [CrossRef] (In the text)
- Rutten,
R. J. 1999, in Third Advances in Solar Physics Euroconference:
Magnetic Fields and Oscillations, ed. B. Schmieder,
A. Hofmann, & J. Staude, ASP Conf. Ser., 184,
181
- Rutten,
R. J., & Uitenbroek, H. 1991, Sol. Phys., 134,
15 [NASA ADS] [CrossRef]
- Saar, S. H.
1996, in Stellar Surface Structure, ed. K. G. Strassmeier,
& J. L. Linsky, IAU Symp., 176, 237
- Sánchez Almeida, J.,
Domínguez Cerdeña, I., & Kneer, F. 2003a, ApJ, 597,
L177 [NASA ADS] [CrossRef]
-
Sánchez Almeida, J., Emonet, T., & Cattaneo, F. 2003b,
ApJ, 585, 536 [NASA ADS] [CrossRef]
- Schmidt, W.,
Beck, C., Kentischer, T., Elmore, D., & Lites, B. 2003, Astron.
Nachr., 324, 300 [NASA ADS]
-
Schrijver, C. J. 1987, A&A, 172, 111 [NASA ADS] (In the text)
- Schrijver,
C. 1995, A&A Rev., 6, 181 [NASA ADS]
- Schrijver,
C. J., & Zwaan, C. 2000, Solar and Stellar Magnetic
Activity (Cambridge University Press)
(In the text)
- Schrijver,
C. J., Cote, J., Zwaan, C., & Saar, S. H. 1989, ApJ,
337, 964 [NASA ADS] [CrossRef] (In the text)
- Schrijver,
C. J., Shine, R. A., Hagenaar, H. J., et al.
1996, ApJ, 468, 921 [NASA ADS] [CrossRef]
- Sigwarth, M.
2001, ApJ, 563, 1031 [NASA ADS] [CrossRef]
- Sigwarth, M.,
Balasubramaniam, K. S., Knölker, M., & Schmidt, W.
1999, A&A, 349, 941 [NASA ADS]
-
Skumanich, A., Smythe, C., & Frazier, E. N. 1975, ApJ,
200, 747 [NASA ADS] [CrossRef] (In the text)
- Socas-Navarro,
H. 2005, ApJ, 633, L57 [NASA ADS] [CrossRef]
- Solanki,
S. K., & Steiner, O. 1990, A&A, 234, 519 [NASA ADS] (In the text)
- Solanki,
S. K., Steiner, O., & Uitenbroeck, H. 1991, A&A, 250,
220 [NASA ADS] (In the text)
- Steiner, O. 1999,
in Third Advances in Solar Physics Euroconference: Magnetic Fields
and Oscillations, ed. B. Schmieder, A. Hofmann, &
J. Staude, ASP Conf. Ser., 184, 38
(In the text)
- Steiner, O.
2003, in NATO Advanced Research Workshop: Turbulence, waves, and
instabilities in the solar plasma, ed. R. Erdelyi, &
K. Petrovay, 181
- Stenflo,
J. O., Solanki, S., Harvey, J. W., & Brault,
J. W. 1984, A&A, 131, 333 [NASA ADS] (In the text)
- Suematsu, Y.
1990, in Progress of Seismology of the Sun and Stars, ed.
Y. Osaki, & H. Shibahashi, LNP, 367, 211
(In the text)
- von der
Lühe, O., Soltau, D., Berkefeld, T., & Schelenz, T. 2003,
in Innovative Telescopes and Instrumentation for Solar
Astrophysics, ed. S. L. Keil, & S. V. Avakyan, Proc.
SPIE, 4853, 187
(In the text)
-
Wallace, L., Hinkle, K., & Livingston, W. 2000, An atlas of
sunspot umbral spectra in the visible, from 15 000 to
25 500 cm(-1) (3920 to 6664 [Å]) (NOAO)
(In the text)
-
Wedemeyer-Böhm, S., Kamp, I., Bruls, J., & Freytag, B.
2005, A&A, 438, 1043 [NASA ADS] [CrossRef] [EDP Sciences]
Copyright ESO 2007
![\begin{figure}
\par {\includegraphics[width=16.8cm,clip]{7017fig1.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg16.gif)
![\begin{figure}
\par {\includegraphics[width=8cm,clip]{7017fig2.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg17.gif)
![\begin{figure}
\par {\includegraphics[width=8cm,clip]{7017fig3.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg23.gif)
![\begin{figure}
\par {\includegraphics[width=16.5cm,clip]{7017fig4.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg24.gif)
![\begin{figure}
\par {\includegraphics[width=15cm,clip]{7017fig5.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg30.gif)
![\begin{figure}
\par {\includegraphics[width=8.1cm,clip]{7017fig6.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg35.gif)
![\begin{figure}
\par {\includegraphics[width=8.3cm,clip]{7017fig7.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg37.gif)
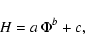
![\begin{figure}
\par {\includegraphics[width=7.2cm,clip]{7017fig8.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg41.gif)
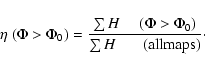
![\begin{figure}
\par {\includegraphics[width=7.2cm,clip]{7017fig10.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg45.gif)
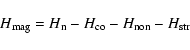
![\begin{figure}
\par {\includegraphics[width=8.3cm,clip]{7017fgA1.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg62.gif)
![\begin{figure}
\par {\includegraphics[width=8cm,clip]{7017fgA2.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg64.gif)
![\begin{figure}
\par {\includegraphics[width=7.6cm,clip]{7017fgA3.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg66.gif)
![\begin{figure}
\par {\includegraphics[width=8.1cm,clip]{7017fgB1.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg67.gif)
![\begin{figure}
\par {\includegraphics[width=7.6cm,clip]{7017fgB2.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg68.gif)
![\begin{figure}
\par {\includegraphics[width=16.9cm,clip]{7017fgB3.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg69.gif)
![\begin{figure}
\par {\includegraphics[width=8.2cm,clip]{7017fgB4.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg70.gif)
![\begin{figure}
\par {\includegraphics[width=8.2cm,clip]{7017fgB5.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg71.gif)
![\begin{figure}
\par {\includegraphics[width=8.3cm,clip]{7017fgB6.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg73.gif)
![\begin{figure}
\par {\includegraphics[width=8.2cm,clip]{7017fgB7.ps} }
\end{figure}](/articles/aa/full/2007/18/aa7017-06/Timg74.gif)