A&A 466, 627-639 (2007)
DOI: 10.1051/0004-6361:20066301
Q. Hu1, 2 - C. Wu2 - X.-B. Wu3
1 - Yuanpei Program, Peking University, Beijing, 100871,
PR China
2 - School of Physics, Peking
University, Beijing, 100871, PR China
3 - Department of Astronomy, Peking University, Beijing, 100871,
PR China
Received 26 August 2006 / Accepted 5 January 2007
Abstract
Aims. The SDSS Data Release 1 includes 1833 DA white dwarfs (WDs) and forms the largest homogeneous sample of WDs. This sample provides the best opportunity to study the statistical properties of WDs.
Methods. We adopt a recently established theoretical model to calculate the mass and distance of each WD using the observational data. Then we adopt a bin-correction method to correct for selection effects and use the 1/V weight-factor method to calculate the luminosity function, the continuous mass function and the formation rate of these WDs.
Results. The SDSS DA WD sample is incomplete and suffers seriously from selection effects. After corrections for the selection effects, only 531 WDs remain. From this final sample we derive the most up-to-date luminosity function and mass function, in which we find a broad peak of WD masses centered around 0.58 ![]() .
The DA WD space density is calculated as
.
The DA WD space density is calculated as
![]() pc-3 and the formation rate is
pc-3 and the formation rate is
![]() pc-3 yr-1.
pc-3 yr-1.
Conclusions. The statistical properties of the SDSS DA WD sample are generally in good agreement with previous observational and theoretical studies, and provide us information on the formation and evolution of WDs. However, a larger and more complete all-sky WD sample is still needed to explain some subtle disagreements and unresolved issues.
Key words: stars: fundamental parameters - stars: luminosity function, mass function - stars: statistics - white dwarfs
Studies of white dwarfs (WDs) have developed substantially in the last century. Chandrasekhar (1933, 1939) first developed a theoretical WD model by applying Fermi-Dirac statistics of electron and predicted a relationship between the mass and radius (M-R relation) of the WD. Hamada & Salpeter (1961) improved the model for the zero-temperature degenerate configuration by incorporating the assumption of various cores (H, He, C, O, Si, Mg, Fe) for different WDs. Wood (1990, 1995) considered more details such as the finite-temperature effect on the radius and the envelope of WDs, and derived theoretical models by calculating the stellar evolution. These models were widely employed in the following decade. Two of the latest model calculations are those of Panei et al. (2000) and Fontaine et al. (2001). On the observational side, thousands of WDs have been detected in large sky surveys, such as those of the Extreme Ultraviolet Explorer (EUVE), the Palomar-Green Surveys (PG), ROSAT All-sky Survey, 2DF QSO Survey and the Sloan Digital Sky Survey (SDSS). Various spectral and photometric parameters of these WDs have been obtained. McCook & Sion (1999) published a catalog including 2245 spectroscopically identified WDs. The SDSS Data Release 1 (DR1) included 2551 identified WDs (Kleinman et al. 2004), of which only a few WDs were already in the catalog of McCook & Sion (1999). The Hipparcos data (Schmidt 1996; Provencal et al. 1998) provided a reliable source of the proper motions and parallaxes of a few WDs. The orbital parameters of WDs in visual binaries (e.g. radial velocities of WDs in common proper motion (CPM) systems) can also be obtained from observations (see e.g. Thorstensen et al. 1978; Vennes et al. 1999; Wegner & Reid 1987; Wegner et al. 1989).
The
effective temperature
![]() and surface gravity
and surface gravity ![]() can
be derived from fitting the Balmer line profiles of WDs.
Detailed discussions about the fitting techniques can be
found in Bergeron et al. (1992, hereafter BSL) and
references therein.
can
be derived from fitting the Balmer line profiles of WDs.
Detailed discussions about the fitting techniques can be
found in Bergeron et al. (1992, hereafter BSL) and
references therein.
![]() can also be derived from the
photometric colors by using an atmosphere model. To test
the theoretical M-R relation, we need to estimate the mass and
radius of WDs by directly measuring the flux,
distance and the gravitational redshift of them. The distance of
a nearby WD can be obtained directly from the measured parallax.
The gravitational redshifts of some WDs in the CPM systems have
been measured (see Wegner & Reid 1987; Wegner et al. 1989).
However, these direct measurements can be done only for a few WDs.
can also be derived from the
photometric colors by using an atmosphere model. To test
the theoretical M-R relation, we need to estimate the mass and
radius of WDs by directly measuring the flux,
distance and the gravitational redshift of them. The distance of
a nearby WD can be obtained directly from the measured parallax.
The gravitational redshifts of some WDs in the CPM systems have
been measured (see Wegner & Reid 1987; Wegner et al. 1989).
However, these direct measurements can be done only for a few WDs.
Calculating the mass of WDs from the fundamental parameters
mentioned above (such as
![]() and
and ![]() )
is the key to obtain
the mass distribution of a large WD
sample. Currently there are four kinds of methods to
determinate the WD mass (see Sect. 3 for details). There are a number of
previous determination of WD masses (Koester et al. 1979; Weidemann & Koester 1984; McMahan 1989; Weidemann
1990; BSL; Finley et al. 1997; Marsh et al. 1997a,b;
Vennes et al. 1997; Vennes 1999; Napiwotzki et al. 1999;
Madej et al. 2004; Liebert et al. 2005). All of these obtained the
mass distribution based on the spectroscopic WD masses, while BSL,
Bergeron et al. (1995) and Reid (1996) obtained the
mass distribution based on the gravitational redshifts.
Although the gravitational redshift measurements are certainly
important, these can be obtained only for a few WDs.
For a large sample of WDs, estimating their masses from
the spectroscopic data is probably the only possible way.
)
is the key to obtain
the mass distribution of a large WD
sample. Currently there are four kinds of methods to
determinate the WD mass (see Sect. 3 for details). There are a number of
previous determination of WD masses (Koester et al. 1979; Weidemann & Koester 1984; McMahan 1989; Weidemann
1990; BSL; Finley et al. 1997; Marsh et al. 1997a,b;
Vennes et al. 1997; Vennes 1999; Napiwotzki et al. 1999;
Madej et al. 2004; Liebert et al. 2005). All of these obtained the
mass distribution based on the spectroscopic WD masses, while BSL,
Bergeron et al. (1995) and Reid (1996) obtained the
mass distribution based on the gravitational redshifts.
Although the gravitational redshift measurements are certainly
important, these can be obtained only for a few WDs.
For a large sample of WDs, estimating their masses from
the spectroscopic data is probably the only possible way.
Generally, the mass distribution, the luminosity and mass functions (LF and MF) of the WDs can be constructed when the sample of WDs is large and complete enough. The luminosity function (LF) and the mass function (MF) derived from a sufficiently large sample of WDs in the solar neighborhood are very helpful for the study of the WD formation history. The LF reveals the current formation rate or death rate of stars in the local Galactic disk, and the MF can display the roles of close binary evolution in the WD formation process (Schmidt 1959, 1963, 1968, 1975; Green 1980; Fleming et al. 1986; Liebert et al. 2005). In particular, Liebert et al. (2005) studied the mass distribution of a volume-limited sample, and obtained the luminosity and mass functions and the recent formation rate of DA WDs based on the 348 hot WDs from the PG survey.
The aim of the present paper is to derive the mass distribution and luminosity and mass functions of the large sample of DA WDs in the SDSS DR1, taking advantage of the larger volume of SDSS DR1 to obtain more reliable results. We have investigated the whole 1833 DA white dwarfs in the SDSS DR1, and calculated the mass, radius, bolometric magnitude, cooling age, and distance of these WDs using the recently published theoretical evolutionary models of Panei et al. (2000) (see also Althaus & Benvenuto 1998 and Benvenuto & Althaus 1998). These models cover a broader and denser parameter space than the models of Wood (1990, 1995), and are more able to be applied to obtain the spectroscopic masses for a large sample of WDs. Based on the derived parameters, we constructed the luminosity function, mass function and determined the formation rate of DA WDs. Due to the magnitude-limited selection effect of SDSS, the sample is far from the completeness needed to obtain statistically reliable results. Therefore, after introducing the sample and mass estimation method in Sect. 2, we investigate the sample completeness and correct the selection effects in Sect. 3. Then we study the luminosity function, mass function, formation rate and 3-dimensional distribution properties of DA WDs in Sects. 4 to 7. We briefly summarize and discuss our results in Sect. 8.
The SDSS is an ongoing imaging and spectroscopic survey of about
ten thousand square degrees in the north Galactic cap
to determine the brightness, positions, and obtain
optical spectra of various objects (York et al.
2000). Although it mainly focuses on the extragalactic objects,
there are many Galactic spin-off projects of which one is to
acquire high-quality stellar spectra from stars of different
spectral types. The spectroscopic survey in the SDSS DR1 covers an
area of 1360 deg2. Kleinman et al. (2004) published catalogs of
the spectroscopic WD and hot subdwarf sample from the
SDSS DR1 (Abazajian et al. 2003). They presented the spectral
fitting results of 2551 certain WDs, 240 hot subdwarf
stars and another 144 possible, but uncertain WDs and hot
subdwarf stars. In this paper, we
use the spectral data of 1833 DA WDs. Kleinman
et al. (2004) derived the effective temperatures ranging from 7220 K to 93 855 K, and the surface gravities ![]() from 6.25 to 9.00 (in cgs units), using the pure hydrogen
atmosphere model of Koester et al. (2001). The photometric
parameters include the five magnitudes in ugriz system (the
magnitudes at g band being from 15.20 to 20.55), the proper
motion velocity, the extinction index of g band and the value of
signal to noise. The WD data of the SDSS DR1 are available
at the SDSS website
from 6.25 to 9.00 (in cgs units), using the pure hydrogen
atmosphere model of Koester et al. (2001). The photometric
parameters include the five magnitudes in ugriz system (the
magnitudes at g band being from 15.20 to 20.55), the proper
motion velocity, the extinction index of g band and the value of
signal to noise. The WD data of the SDSS DR1 are available
at the SDSS website![]() .
.
Previous studies (e.g. Clemens 1993; Barstow et al. 1993) provided
evidence that a DA white dwarf most likely has a thick
hydrogen layer of about
![]() .
In addition, the suggestion that
most of high mass DA WDs have a C/O core
and the low-mass DA WDs have a helium core has been widely
accepted in former studies (e.g. Napiwotzki et al. 1999; Madej et al. 2004; Liebert et al. 2005).
Theoretical studies also show that when the mass of a WD is less than 0.45
.
In addition, the suggestion that
most of high mass DA WDs have a C/O core
and the low-mass DA WDs have a helium core has been widely
accepted in former studies (e.g. Napiwotzki et al. 1999; Madej et al. 2004; Liebert et al. 2005).
Theoretical studies also show that when the mass of a WD is less than 0.45 ![]() ,
the progenitors of these WDs could not reach high
enough central temperatures for helium to be ignited at the
center (Panei et al. 2000), providing further evidence for a helium core
of low-mass DA WDs.
BSL, Finley et al. (1997), Marsh et al. (1997a,b),
Vennes et al. (1997), Vennes (1999) and Liebert et al. (2005) all
adopted Wood's evolutionary model (Wood 1990, 1995) of a C/O-core
with a thick hydrogen envelope in their studies.
Madej et al. (2004) brought in the evolutionary
models of Panei et al. (2000) assuming a C/O core with
,
the progenitors of these WDs could not reach high
enough central temperatures for helium to be ignited at the
center (Panei et al. 2000), providing further evidence for a helium core
of low-mass DA WDs.
BSL, Finley et al. (1997), Marsh et al. (1997a,b),
Vennes et al. (1997), Vennes (1999) and Liebert et al. (2005) all
adopted Wood's evolutionary model (Wood 1990, 1995) of a C/O-core
with a thick hydrogen envelope in their studies.
Madej et al. (2004) brought in the evolutionary
models of Panei et al. (2000) assuming a C/O core with
![]() in the atmosphere of massive WDs and a helium
core with
in the atmosphere of massive WDs and a helium
core with
![]() for WDs with a mass less than 0.45
for WDs with a mass less than 0.45 ![]() .
In this paper, we use the evolutionary helium-core
model for WDs with mass less than 0.45
.
In this paper, we use the evolutionary helium-core
model for WDs with mass less than 0.45 ![]() and bring in the C/O-core model for those with mass
larger than 0.45
and bring in the C/O-core model for those with mass
larger than 0.45 ![]() .
Both models are from Panei et al. (2000).
In this
paper we
assume that all DA WDs (with either a C/O or helium core) have a thick
hydrogen layer (
.
Both models are from Panei et al. (2000).
In this
paper we
assume that all DA WDs (with either a C/O or helium core) have a thick
hydrogen layer (
![]() ,
z=0.001) for simplicity.
,
z=0.001) for simplicity.
![\begin{figure}
\par\includegraphics[width=7.2cm,height=6.5cm,clip]{6301f1CMJN.eps} \end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg28.gif) |
Figure 1:
The
|
| Open with DEXTER | |
The predictions of the models of Panei et al. (2000)
and the data (![]() ,
,
![]() )
of all DA non-magnetic WDs
in the SDSS DR1 are
plotted in Fig. 1. From it we can see that the models we chose
are appropriate for our study. The predicted parameters of two models
(He-core and C/O-core) cover a
lager parameter range in the figure. The C/O models cover
)
of all DA non-magnetic WDs
in the SDSS DR1 are
plotted in Fig. 1. From it we can see that the models we chose
are appropriate for our study. The predicted parameters of two models
(He-core and C/O-core) cover a
lager parameter range in the figure. The C/O models cover
![]() from about 4000 K to 100 000 K, and
from about 4000 K to 100 000 K, and ![]() from 7.43
to 9.03, while the He-core models cover
from 7.43
to 9.03, while the He-core models cover
![]() from 2500 K to 27 000 K and
from 2500 K to 27 000 K and ![]() from 6.2 to 7.7. Most observed data
of the DA WDs in the SDSS DR1 are within the range of these models.
Some high temperature WDs at the right part of Fig. 1
are not covered by any models. The parameters of
these extremely high-temperature WDs were discussed in BSL (they limited the
from 6.2 to 7.7. Most observed data
of the DA WDs in the SDSS DR1 are within the range of these models.
Some high temperature WDs at the right part of Fig. 1
are not covered by any models. The parameters of
these extremely high-temperature WDs were discussed in BSL (they limited the
![]() of their WD sample to less than 40 000 K).
There is a large discrepancy between the
effective temperatures obtained from two different methods of
fitting the Balmer lines when the
of their WD sample to less than 40 000 K).
There is a large discrepancy between the
effective temperatures obtained from two different methods of
fitting the Balmer lines when the
![]() of a WD is above
50 000 K. We eliminate the WDs with extremely high
of a WD is above
50 000 K. We eliminate the WDs with extremely high
![]() (
(
![]() K) from our samples. Because these WDs
(39 objects) are only a very small fraction (about 2%) of the
whole sample, their influence on the
completeness of the sample is small.
K) from our samples. Because these WDs
(39 objects) are only a very small fraction (about 2%) of the
whole sample, their influence on the
completeness of the sample is small.
To ensure that our calculation of WD parameters through the evolutionary
model is
reliable, we tested the model by comparing the WD masses derived
from the evolutionary model and spectroscopic parameters
(
![]() and
and ![]() )
with the masses obtained from other independent
methods. Currently there are three methods to
determine the masses of WDs without involving the evolutionary
models, namely:
)
with the masses obtained from other independent
methods. Currently there are three methods to
determine the masses of WDs without involving the evolutionary
models, namely:
Table 1: Comparison of white dwarf mass determinations from different methods.
Figure 2 shows the comparisons of the WD masses obtained from different methods.
WDs were divided into two groups, one with
![]() less than 12 000 K
(represented by crosses) and the other with
less than 12 000 K
(represented by crosses) and the other with
![]() higher than 12 000 K. We can see that except for several
WDs with
higher than 12 000 K. We can see that except for several
WDs with
![]() less than 12 000 K the masses estimated with different methods
are in good agreement.
For WDs with
less than 12 000 K the masses estimated with different methods
are in good agreement.
For WDs with
![]() less than 12 000 K, the differences in masses estimated by different methods
are obviously larger. This is because these cooler WDs
are likely to be convective. BSL have convincingly proved that
the convection effect leads to significant amounts of helium (which is
invisible in the spectra) entering the atmosphere,
producing higher pressure which would substantially affect the spectral
line profiles. The total effect on the spectral line is
indistinguishable from the increased surface gravity. In other
words, a low-temperature DA WD with large surface gravity might
actually be a helium-rich star with lower surface gravity (and correspondingly
with lower mass). So the scatter in the masses
estimated with different methods for cooler WDs possibly has less
to do with the evolutionary model that we adopted but is mainly due to
the techniques of analyzing the spectral lines. For this reason, we
remove these WDs from our statistical analyses.
less than 12 000 K, the differences in masses estimated by different methods
are obviously larger. This is because these cooler WDs
are likely to be convective. BSL have convincingly proved that
the convection effect leads to significant amounts of helium (which is
invisible in the spectra) entering the atmosphere,
producing higher pressure which would substantially affect the spectral
line profiles. The total effect on the spectral line is
indistinguishable from the increased surface gravity. In other
words, a low-temperature DA WD with large surface gravity might
actually be a helium-rich star with lower surface gravity (and correspondingly
with lower mass). So the scatter in the masses
estimated with different methods for cooler WDs possibly has less
to do with the evolutionary model that we adopted but is mainly due to
the techniques of analyzing the spectral lines. For this reason, we
remove these WDs from our statistical analyses.
There are still some high-temperature
WDs for which the different mass estimates do not match very well. A
few factors can contribute to this discrepancy, such as the
techniques of fitting the spectral lines, the uncertainties of the
observational parameters. etc. One of the most important
factors is that there seems to be no appropriate evolutionary model for
these high-temperature WDs. For example, G238-44, GD140, EG50, and
EG21 have relatively higher spectroscopic mass compared with the
mass derived from other methods. If we apply a thin hydrogen layer
model (
![]() ,
,
![]() )
or a metal core (like Fe core) for these
four WDs, their spectroscopic mass will be lower by
)
or a metal core (like Fe core) for these
four WDs, their spectroscopic mass will be lower by
![]() ,
and thus the mass comparison of these four WDs would
be better. Moreover, the presence of helium in the atmosphere
would also significantly influence the mass estimate. Boudreault &
Bergeron (2005) gave a detailed discussion of this effect. They
calculated the masses by using the models of Fontaine et al.
(2001) and assuming a mixed composition in the atmosphere with
,
and thus the mass comparison of these four WDs would
be better. Moreover, the presence of helium in the atmosphere
would also significantly influence the mass estimate. Boudreault &
Bergeron (2005) gave a detailed discussion of this effect. They
calculated the masses by using the models of Fontaine et al.
(2001) and assuming a mixed composition in the atmosphere with
![]() rather than a pure hydrogen atmosphere, and
obtained similar results that the mean
rather than a pure hydrogen atmosphere, and
obtained similar results that the mean
![]() of WDs in their
sample will be lower by 0.2
of WDs in their
sample will be lower by 0.2 ![]() .
Thus, if we adjust
the thickness of the envelope, the composition of the atmosphere
and the atom in the core, more than half of the WDs in Fig. 2 will
have their
.
Thus, if we adjust
the thickness of the envelope, the composition of the atmosphere
and the atom in the core, more than half of the WDs in Fig. 2 will
have their
![]() equal to the mass derived by the
other method. Therefore, we may find the most appropriate
evolutionary model for each WD by matching two kinds of mass
estimates, and then the discrepancy in Fig. 2 would be alleviated.
equal to the mass derived by the
other method. Therefore, we may find the most appropriate
evolutionary model for each WD by matching two kinds of mass
estimates, and then the discrepancy in Fig. 2 would be alleviated.
However, for most DA WDs from SDSS DR1 in our sample, we do not have parallax or gravitational redshift data to derive a second mass estimate and do not have further information about their internal structure and atmospheric composition. So we will just assume a theoretically appropriate model for our samples. From Fig. 2, we find that the comparison results are satisfactory in general, ignoring the low-temperature WDs. We then conclude that the assumptions of evolutionary models we adopted are generally reliable.
![\begin{figure}
\par\includegraphics[width=7.5cm,height=6.4cm,clip]{6301f2CMJN.eps} \end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg47.gif) |
Figure 2:
A comparison between the WD mass derived from the evolutionary
model and those determined by other methods without using a theoretical
M-R relation. Both axes are in unit of |
| Open with DEXTER | |
Table 2: Fundamental parameters of the DA white dwarfs from the Sloan Digital Sky Survey.
Using the methods described above, we can calculate
the radius R, luminosity L and bolometric magnitude
![]() for WDs.
Similar to the determination of mass, the cooling age of a WD
can be derived by interpolating the grids of the evolutionary
models, thus
for WDs.
Similar to the determination of mass, the cooling age of a WD
can be derived by interpolating the grids of the evolutionary
models, thus
![]() .
The bolometric
correction (BC) in the g band can be obtained by using the model
atmospheres of Bergeron et al. (1995b). BC is derived through
interpolating the
.
The bolometric
correction (BC) in the g band can be obtained by using the model
atmospheres of Bergeron et al. (1995b). BC is derived through
interpolating the
![]() and
and ![]() into the grid
of the model atmosphere in Bergeron et al. (1995b)
for the ugriz system,
into the grid
of the model atmosphere in Bergeron et al. (1995b)
for the ugriz system,
![]() .
The distance r (in pc) of the
star can be derived from the BC and the relationship between the
absolute magnitude and visual magnitude in the g band:
.
The distance r (in pc) of the
star can be derived from the BC and the relationship between the
absolute magnitude and visual magnitude in the g band:
![]() ,
,
![]() ,
where Ag is the extinction in the g band which is provided by the SDSS.
,
where Ag is the extinction in the g band which is provided by the SDSS.
To compare our results with other previous work, we also derived
the absolute magnitude of WDs in the V band which were commonly used in
previous studies. Using the results of Bergeron et al.
(1995b), we can easily convert the Mg of the ugriz system to the
MV of the UBV system. Bergeron et al. (1995b) provide the grids
in both ugriz and UBV systems and the relationship between them,
so we can obtain the bolometric correction in the V band and MV of
the UBV system by interpolating the
![]() and
and ![]() in the
grid. Both MV and BCV (bolometric correction at V band)
are a function of
in the
grid. Both MV and BCV (bolometric correction at V band)
are a function of
![]() and
and ![]() ,
namely,
,
namely,
![]() ,
and
,
and
![]() .
We also calculate the galactic coordinates (l, b)of WDs through the equatorial coordinates (
.
We also calculate the galactic coordinates (l, b)of WDs through the equatorial coordinates (![]() ,
,
![]() )
provided
by the SDSS.
)
provided
by the SDSS.
The uncertainties in the values of parameters can be estimated in the
following way. Assuming that a function is determined by several input
parameters,
![]() ,
the error in this
function f can be expressed as:
,
the error in this
function f can be expressed as:
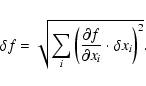 |
(1) |
In Table 2 we list our main results. As there are many WDs in the sample and every WD has many parameters, a subset of Table 2 only is shown here. A full table is available in electronic form at the CDS.
Madej et al. (2004) derived the SDSS WD mass distribution by counting the number of WDs in the sample. However, the SDSS detects WDs in the g magnitude range from about 16 to 20 mag, much fainter than the previous Palomar-Green Survey (Fleming et al. 1986; Liebert et al. 2005) and EUVE Survey (e.g., Vennes et al. 1997; Finley et al. 1997; Napiwotzki et al. 1999). Many WDs are several hundreds or even thousands of pc away from the Earth, thus the magnitude-limiting selection effect plays an essential role and the sample is often far from complete. One should first test the completeness of the sample and make necessary corrections to remove the selection effect; otherwise, the result will be seriously biased.
![\begin{figure}
\par\includegraphics[width=7.8cm,height=6.5cm,clip]{6301f3CMJN.eps} \end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg61.gif) |
Figure 3:
The value of
|
| Open with DEXTER | |
We use the method of Schmidt (1968), Green (1980) and Fleming et al. (1986) to calculate the corrections and derive the WD Luminosity Function (LF). Generally, for an all-sky WD
sample with upper visual magnitude limit
![]() ,
e.g. for Vband, given a specific WD with its absolute V magnitude MV and
distance r, the r defines a volume V, and and the
,
e.g. for Vband, given a specific WD with its absolute V magnitude MV and
distance r, the r defines a volume V, and and the
![]() define
a maximum distance
define
a maximum distance
![]() and consequently the maximum volume
and consequently the maximum volume
![]() with the following equation:
with the following equation:
![]() (we assume an average extinction which has been included in
(we assume an average extinction which has been included in
![]() ). The SDSS WD space distribution scale is about 1 kpc,
whereas the galaxy disk radius is about 10 kpc, so it is natural
to assume that the WD space radial distribution around the sun
is uniform. To correct the non-uniform height distribution, we
define d
). The SDSS WD space distribution scale is about 1 kpc,
whereas the galaxy disk radius is about 10 kpc, so it is natural
to assume that the WD space radial distribution around the sun
is uniform. To correct the non-uniform height distribution, we
define d
![]() and adopt z0=250 pc as the scale
height, as done by Fleming et al. (1986) and Liebert et al.
(2005). Thus, if the sample is complete, the average value
of
and adopt z0=250 pc as the scale
height, as done by Fleming et al. (1986) and Liebert et al.
(2005). Thus, if the sample is complete, the average value
of
![]() will be equal to 0.5 (Green 1980). Otherwise, to make
the sample uniform, one should lower the
will be equal to 0.5 (Green 1980). Otherwise, to make
the sample uniform, one should lower the
![]() and eliminate
the WDs with
and eliminate
the WDs with
![]() until
until
![]() .
.
Moreover, we make two small changes to the method:
(1) In addition to the upper magnitude limit
![]() ,
the SDSS
also has a lower magnitude limit
,
the SDSS
also has a lower magnitude limit
![]() ,
which defines a
minimum distance
,
which defines a
minimum distance
![]() and a volume
and a volume
![]() .
The reason is
that the SDSS's main focus is extragalactic objects whose
magnitudes are usually faint and the WDs are just its spin-off
projects (Kleinman et al. 2004). Thus the actual space where WDs
were detected is between
.
The reason is
that the SDSS's main focus is extragalactic objects whose
magnitudes are usually faint and the WDs are just its spin-off
projects (Kleinman et al. 2004). Thus the actual space where WDs
were detected is between
![]() and
and
![]() ,
and its volume
is
,
and its volume
is
![]() .
So we should use
.
So we should use
![]() instead of
instead of
![]() to test the sample's completeness.
to test the sample's completeness.
(2) The SDSS DR1 spectroscopic data cover only 1360 deg2 of the
whole sky (Abazajian et al. 2003), so the
volume is not a spherical or elliptical shape but a cone shape. We
also assume that the d![]() of the volume dV is apart from
its galactic latitude b. So the cubic angle
of the volume dV is apart from
its galactic latitude b. So the cubic angle ![]() is simply 1360 deg2. Then we derive the expression of volume V as a
function of r and b.
is simply 1360 deg2. Then we derive the expression of volume V as a
function of r and b.
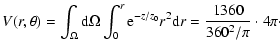 |
|||
![$\displaystyle \hspace*{2mm}\left(\frac{{z_0 }}{{\cos \theta }}\right)^3\left\{ ...
...os \theta }}{{z_0 }} + 2\right] \cdot {\rm e}^{ - r\cos \theta /z_0 } \right\},$](/articles/aa/full/2007/17/aa6301-06/img76.gif) |
(2) |
![\begin{figure}
\par\includegraphics[width=7.5cm,height=6.5cm,clip]{6301f4.eps}
\end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg79.gif) |
Figure 4:
Selection effect correction according to g band and the
comparison of the two correction methods. The crosses denote the
1794 SDSS DA WDs with
|
| Open with DEXTER | |
For g band magnitude, the
![]() value
of the 1794 non-magnetic SDSS DA WDs with
value
of the 1794 non-magnetic SDSS DA WDs with
![]() K is around 0.3, which suggests that the sample is far
from complete. If we lower the the upper magnitude limit
K is around 0.3, which suggests that the sample is far
from complete. If we lower the the upper magnitude limit
![]() (see Fig. 3) to about 18.2 mag,
the
(see Fig. 3) to about 18.2 mag,
the
![]() approaches 0.5
and the remaining sample is more complete. However, too many WDs
will be eliminated. We made a compromise: if
approaches 0.5
and the remaining sample is more complete. However, too many WDs
will be eliminated. We made a compromise: if
![]() ,
the
sample will be regarded as complete. This means that we eliminate the
most selection effect contaminated part of the sample. Setting the
upper limit
,
the
sample will be regarded as complete. This means that we eliminate the
most selection effect contaminated part of the sample. Setting the
upper limit
![]() for g band, the number of WDs in
the remaining sample is 864 out of 1794, almost half (see Fig. 4, we also required Mg<14.3, for the fainter WDs are difficult
to detect). Similarly, Green (1980) also set
for g band, the number of WDs in
the remaining sample is 864 out of 1794, almost half (see Fig. 4, we also required Mg<14.3, for the fainter WDs are difficult
to detect). Similarly, Green (1980) also set
![]() in his study.
in his study.
An improved method (hereafter named bin-correction, while the
above method is named uniform-correction or
ordinary-correction) is to consider the different magnitude upper limit
for different absolute magnitudes of a specific WD. We
divide the whole sample into 0.5-mag-width bins according to Mg(or 1-mag-width bins according to
![]() ), assuming that the
WDs within the same bins have the same upper magnitude limit and
the whole sample shares a lower magnitude limit. In each bin,
), assuming that the
WDs within the same bins have the same upper magnitude limit and
the whole sample shares a lower magnitude limit. In each bin,
![]() .
Figure 4
shows this bin-correction for g band. The number of WDs in the
remaining sample is 860. Although the number is more or less the
same as the 864 of the uniform-correction, the difference is obvious:
the upper magnitude limit at the brighter end is usually smaller than
the 18.984 mag of the uniform-correction. Such WDs observed
are relatively distant, whereas the fainter end's upper magnitude
limit is usually larger than the 18.984 mag, because only the
faint WDs that are near us can be observed and the magnitude-limiting
selection effect is relatively small for the nearby star sample.
Thus we prefer to use the improved bin-correction method.
.
Figure 4
shows this bin-correction for g band. The number of WDs in the
remaining sample is 860. Although the number is more or less the
same as the 864 of the uniform-correction, the difference is obvious:
the upper magnitude limit at the brighter end is usually smaller than
the 18.984 mag of the uniform-correction. Such WDs observed
are relatively distant, whereas the fainter end's upper magnitude
limit is usually larger than the 18.984 mag, because only the
faint WDs that are near us can be observed and the magnitude-limiting
selection effect is relatively small for the nearby star sample.
Thus we prefer to use the improved bin-correction method.
![\begin{figure}
\par\includegraphics[width=7.5cm,height=6.5cm,clip]{6301f5CMJN.eps} \end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg84.gif) |
Figure 5:
Selection effect bin-correction according to
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.3cm,height=6.5cm,clip]{6301f6.eps} \end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg85.gif) |
Figure 6: SDSS WD LF as a function of MV, compared with previous LFs: dashed, dot-dashed and dotted lines denotes the PG LF of Liebert et al. (2005), LF of Fleming et al. (1986) and LF of Green (1980), respectively. Solid lines denote the SDSS DA WD LF. |
| Open with DEXTER | |
We also made a 1-mag-width bin-correction
according to
![]() for the whole 1794 non-magnetic SDSS DA WD
sample with
for the whole 1794 non-magnetic SDSS DA WD
sample with
![]() K. The number of WDs in the remaining
sample is 893, as shown in Fig. 5. The reason why we choose
K. The number of WDs in the remaining
sample is 893, as shown in Fig. 5. The reason why we choose
![]() as a criterion is that the u, g, r, i, z or V bands have their own
magnitude limits and selection effects. The
extinction is also different from short wavelengths to long
wavelengths. But above all, the
as a criterion is that the u, g, r, i, z or V bands have their own
magnitude limits and selection effects. The
extinction is also different from short wavelengths to long
wavelengths. But above all, the
![]() can represent all these
factors. After
this selection effect correction, our analysis of SDSS WD samples
will be much less biased and more reliable.
can represent all these
factors. After
this selection effect correction, our analysis of SDSS WD samples
will be much less biased and more reliable.
The SDSS WD LF is calculated using the method of Green (1980) and
Fleming et al. (1986). Its distribution volume is
![]() ,
and the weight factor is
,
and the weight factor is
![]() which is similar to the 1/V'm used in some previous studies.
which is similar to the 1/V'm used in some previous studies.
![\begin{figure}
\par\includegraphics[width=7.2cm,height=6.5cm,clip]{6301f7.eps} \end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg89.gif) |
Figure 7:
The LF of SDSS WDs as a function of
|
| Open with DEXTER | |
Figure 6 shows the LF of SDSS non-magnetic DA WDs (solid line)
with
![]() K and MV<15.25. We also show other LFs
obtained previously: Liebert et al. (2005, dashed line, called the
PG sample and we select WDs with
K and MV<15.25. We also show other LFs
obtained previously: Liebert et al. (2005, dashed line, called the
PG sample and we select WDs with
![]() K in their
sample for comparison); Green (1980, dotted line); Fleming et al.
(1986, dot-dashed line). Briefly, the SDSS LF is in general
agreement with Liebert et al. (2005) and Fleming et al. (1986),
especially at the fainter end (MV>12). An obvious advantage of the
SDSS LF is that it extrapolates the fainter end of WD LF from 13.25 to 15.25 mag. Because the SDSS has a lower magnitude
limit, WDs with larger MV are usually nearer to
us. Their selection effects may
not be very strong and the result should be less biased. At the
brighter end, however, the SDSS LF is lower by about half an order
of magnitude than the PG LF. Some possible reasons that account for
such a difference:
(1) The PG Survey is an all-sky survey, whereas the SDSS DR1 just
covers 1360 deg2 of the whole sky.
(2) The SDSS sample may contain fewer WDs at the brighter end
where
K in their
sample for comparison); Green (1980, dotted line); Fleming et al.
(1986, dot-dashed line). Briefly, the SDSS LF is in general
agreement with Liebert et al. (2005) and Fleming et al. (1986),
especially at the fainter end (MV>12). An obvious advantage of the
SDSS LF is that it extrapolates the fainter end of WD LF from 13.25 to 15.25 mag. Because the SDSS has a lower magnitude
limit, WDs with larger MV are usually nearer to
us. Their selection effects may
not be very strong and the result should be less biased. At the
brighter end, however, the SDSS LF is lower by about half an order
of magnitude than the PG LF. Some possible reasons that account for
such a difference:
(1) The PG Survey is an all-sky survey, whereas the SDSS DR1 just
covers 1360 deg2 of the whole sky.
(2) The SDSS sample may contain fewer WDs at the brighter end
where
![]() .
Because SDSS has a low magnitude limit,
very bright WDs (with smaller MV) must be
very distant from us, as
shown in Fig. 8. These stars are extremely contaminated by the
selection effects and even after the bin-correction the result still may
be inaccurate. (3) Fleming et al. (1986) and Liebert et al. (2005) both pointed out that there may be problems of missing
binaries or double degenerates in the PG WD sample. Zuckerman &
Becklin (1992) and Marsh et al. (1995) have shown that
many low mass DA candidates (usually hot and with low absolute
magnitudes) are binaries, with the companion being either a low
mass main sequence star or another WD. Kleinman et al. (2004) also
mentioned this problem. Bergeron et al. (2001) made a
detailed analysis of this unresolved problem. Liebert et al.
(2005) even pointed out that double degenerates are likely in
the majority of cases. So we expect that the missing binaries in
the SDSS sample may account for a considerable number of missing stars.
.
Because SDSS has a low magnitude limit,
very bright WDs (with smaller MV) must be
very distant from us, as
shown in Fig. 8. These stars are extremely contaminated by the
selection effects and even after the bin-correction the result still may
be inaccurate. (3) Fleming et al. (1986) and Liebert et al. (2005) both pointed out that there may be problems of missing
binaries or double degenerates in the PG WD sample. Zuckerman &
Becklin (1992) and Marsh et al. (1995) have shown that
many low mass DA candidates (usually hot and with low absolute
magnitudes) are binaries, with the companion being either a low
mass main sequence star or another WD. Kleinman et al. (2004) also
mentioned this problem. Bergeron et al. (2001) made a
detailed analysis of this unresolved problem. Liebert et al.
(2005) even pointed out that double degenerates are likely in
the majority of cases. So we expect that the missing binaries in
the SDSS sample may account for a considerable number of missing stars.
![\begin{figure}
\par\includegraphics[width=7.5cm,height=6.5cm,clip]{6301f8CMJN.eps} \end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg91.gif) |
Figure 8:
Selection effect comparison. Dots denote PG DA WDs from Liebert
et al. (2005) and crosses the SDSS DA WDs after bin-correction. It is clear
that in the case of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,height=6.5cm,clip]{6301f9CMJN.eps} \end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg94.gif) |
Figure 9:
Mass function of SDSS DA WDs in different
|
| Open with DEXTER | |
The SDSS DA WD LF is consistent with the theoretical predictions of
Mestel (1952) and Lamb & van Horn (1975). The
Mestel law is:
![]() The evolutionary tracks obtained by Lamb & van Horn (1975) also agree
with the Mestel law in the
The evolutionary tracks obtained by Lamb & van Horn (1975) also agree
with the Mestel law in the
![]() range between 6.0 and 13.5. They explained that the
deviation below this range is due to the neutrino energy losses and
above this range due to the Debye cooling. Compared with
these, the SDSS DA WD LF is approximately a
straight line in the range of
range between 6.0 and 13.5. They explained that the
deviation below this range is due to the neutrino energy losses and
above this range due to the Debye cooling. Compared with
these, the SDSS DA WD LF is approximately a
straight line in the range of
![]() between 6.0 and 13.5, with
a linear fitting slope of 0.32, which is almost identical to the
slope 2/7 of the Mestel law (Fig. 7). The SDSS DA WD LF also shows a
trend of deviation when
between 6.0 and 13.5, with
a linear fitting slope of 0.32, which is almost identical to the
slope 2/7 of the Mestel law (Fig. 7). The SDSS DA WD LF also shows a
trend of deviation when
![]() is smaller than 6.0, which is
identical with the model of Lamb & van Horn (1975). For the fainter end where
is smaller than 6.0, which is
identical with the model of Lamb & van Horn (1975). For the fainter end where
![]() ,
the LF data does not cover a sufficiently broad
,
the LF data does not cover a sufficiently broad
![]() range to test the model of Lamb & van Horn (1975).
range to test the model of Lamb & van Horn (1975).
![\begin{figure}
\par\includegraphics[width=7.3cm,height=6.5cm,clip]{6301f10.eps} \end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg98.gif) |
Figure 10:
Mass function of SDSS DA WDs (solid line) with
|
| Open with DEXTER | |
Figure 9 shows the mass function (MF), i.e. the
![]() weighted mass distribution of the SDSS DA
WDs. Kleinman et al. (2004) pointed out that the
weighted mass distribution of the SDSS DA
WDs. Kleinman et al. (2004) pointed out that the ![]() value
determination of cooler WDs with
value
determination of cooler WDs with
![]() K has a systematic
offset to higher
K has a systematic
offset to higher ![]() and a possible interpretation is that a
moderate amount of helium has been convectively mixed into the
atmosphere (see Sect. 6 of Kleinman et al. 2004; also Bergeron et al. 1990; BSL; Liebert et al. 2005). Thus, the parameters and
mass functions of WDs with
and a possible interpretation is that a
moderate amount of helium has been convectively mixed into the
atmosphere (see Sect. 6 of Kleinman et al. 2004; also Bergeron et al. 1990; BSL; Liebert et al. 2005). Thus, the parameters and
mass functions of WDs with
![]() K may be inaccurate.
However we include these cool WDs in our MF in Fig. 9 for
reference. From both the PG and SDSS MFs in Fig. 9 we can see a
qualitative property of MF that in the massive part, the cool WDs'
space density is much larger than that of the hotter WDs. A
possible explanation is that the hot massive WDs usually evolve much
faster than cool WDs, which leads to its faintness (larger
K may be inaccurate.
However we include these cool WDs in our MF in Fig. 9 for
reference. From both the PG and SDSS MFs in Fig. 9 we can see a
qualitative property of MF that in the massive part, the cool WDs'
space density is much larger than that of the hotter WDs. A
possible explanation is that the hot massive WDs usually evolve much
faster than cool WDs, which leads to its faintness (larger
![]() )
and thus difficulty for observations. So the WDs we
observe are usually quite near to us, and consequently have a
small
)
and thus difficulty for observations. So the WDs we
observe are usually quite near to us, and consequently have a
small
![]() and larger
and larger
![]() (see Figs. 5 and 8), which will result in a higher space density. A
rough estimate leads to an important implication that cool
massive WDs may contribute a larger part to the galactic matter
than previous estimates. However, the confirmation of this
requires further investigation with more accurate
(see Figs. 5 and 8), which will result in a higher space density. A
rough estimate leads to an important implication that cool
massive WDs may contribute a larger part to the galactic matter
than previous estimates. However, the confirmation of this
requires further investigation with more accurate ![]() measurements.
measurements.
Figure 10 shows the usually discussed mass function (MF) of WDs with
![]() between 12 000 K and 48 000 K. It is more accurate because
we have more reliable estimates of the masses of these WDs
(see discussions in Sect. 2). In
many bins, the SDSS DA density is lower than the PG DA density,
and the reason is similar to those explained in Sect. 4.1. However, their relative distributions are similar. The SDSS MF is also
similar to other previous studies, e.g. Wiedemann & Koester
(1984), McMahan (1989), BSL, Marsh et al. (1997a), Vennes et al. (1997), Finley et al. (1997) and Napiwotzki et al. (1999),
etc. The majority of WDs clump between 0.5 and 0.7
between 12 000 K and 48 000 K. It is more accurate because
we have more reliable estimates of the masses of these WDs
(see discussions in Sect. 2). In
many bins, the SDSS DA density is lower than the PG DA density,
and the reason is similar to those explained in Sect. 4.1. However, their relative distributions are similar. The SDSS MF is also
similar to other previous studies, e.g. Wiedemann & Koester
(1984), McMahan (1989), BSL, Marsh et al. (1997a), Vennes et al. (1997), Finley et al. (1997) and Napiwotzki et al. (1999),
etc. The majority of WDs clump between 0.5 and 0.7 ![]() .
with some small clusters from 0.7 to 1.0
.
with some small clusters from 0.7 to 1.0 ![]() .
Another
peak is perhaps seen at 1.2
.
Another
peak is perhaps seen at 1.2 ![]() .
Nevertheless, since Kleinman et al. (2004) have artificially assigned an upper
.
Nevertheless, since Kleinman et al. (2004) have artificially assigned an upper ![]() limit of 9.0, we obtain no WDs with mass higher than about 1.2
limit of 9.0, we obtain no WDs with mass higher than about 1.2 ![]() .
In other words, the 1.2
.
In other words, the 1.2 ![]() cluster probably includes some WDs more
massive than 1.2
cluster probably includes some WDs more
massive than 1.2 ![]() .
For this reason, Madej et al. (2004)
concluded that this peak is not a real feature. Since our sample
has been corrected for selection effects and is more complete, we
conclude that there really is a cluster and a peak around 1.2
.
For this reason, Madej et al. (2004)
concluded that this peak is not a real feature. Since our sample
has been corrected for selection effects and is more complete, we
conclude that there really is a cluster and a peak around 1.2 ![]() ,
while the peak may be slightly larger than 1.2
,
while the peak may be slightly larger than 1.2 ![]() .
.
![\begin{figure}
\par\includegraphics[width=7cm,height=6.8cm,clip]{6301f11.eps} \end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg99.gif) |
Figure 11:
Comparison of the traditional discrete MF and our improved
continuous MF of 531 SDSS DA WDs with
|
| Open with DEXTER | |
Vennes et al. (1997) described a method to derive a continuous MF by
calculating
![]() ,
where N<M denotes the number of WDs with
mass less than a value M. At each mass point of a WD in the
sample, this
,
where N<M denotes the number of WDs with
mass less than a value M. At each mass point of a WD in the
sample, this
![]() will result in a Dirac
will result in a Dirac ![]() function. For this reason, they smoothed the function by
assuming a Gaussian distribution with a uniform FWHM of 0.1
function. For this reason, they smoothed the function by
assuming a Gaussian distribution with a uniform FWHM of 0.1 ![]() .
Here we try to improve their method. For a specific WD with
its observation-derived mass Mi and error
.
Here we try to improve their method. For a specific WD with
its observation-derived mass Mi and error
![]() ,
the
probability density function of this WD is a Gaussian distribution
function. The probability that this WD's mass equals M is equal
to
,
the
probability density function of this WD is a Gaussian distribution
function. The probability that this WD's mass equals M is equal
to
![]() and
and
![]() .
So the mass function here can be defined as:
.
So the mass function here can be defined as:
| |
= | ||
| = | 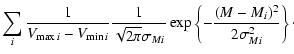 |
(3) |
Usually, the error of a SDSS WD mass is small enough to retain its
distribution properties and also large enough not to produce a
Dirac ![]() function. Figure 11 compares the traditional discrete
MF and our continuous MF of SDSS DA WDs with
function. Figure 11 compares the traditional discrete
MF and our continuous MF of SDSS DA WDs with
![]() between 12 000 K and 48 000 K. They are in good agreement and thus demonstrate
the reliability of our method. The continuous MF has many
advantages over the discrete one. From it, we determine that the
main peak of the SDSS DA mass distribution is at
between 12 000 K and 48 000 K. They are in good agreement and thus demonstrate
the reliability of our method. The continuous MF has many
advantages over the discrete one. From it, we determine that the
main peak of the SDSS DA mass distribution is at
![]() and two other obvious peaks at
and two other obvious peaks at
![]() and
and
![]() .
The
.
The
![]() peak is in perfect
agreement with previous studies (see Table 1 of Madej et al.
2004). The 0.58
peak is in perfect
agreement with previous studies (see Table 1 of Madej et al.
2004). The 0.58 ![]() peak, which is derived from
peak, which is derived from
![]() weighted MF of a complete sample after selection effect
corrections, is close to the 0.562
weighted MF of a complete sample after selection effect
corrections, is close to the 0.562 ![]() peak derived by
Madej et al. (2004), found by simply counting the number of
WDs in an incomplete sample. This implies that the main peak
of the WD mass distribution around 0.57
peak derived by
Madej et al. (2004), found by simply counting the number of
WDs in an incomplete sample. This implies that the main peak
of the WD mass distribution around 0.57 ![]() is very
insensitive to sample completeness, which puts in context the
agreement of our results with previous studies.
is very
insensitive to sample completeness, which puts in context the
agreement of our results with previous studies.
![\begin{figure}
\par\includegraphics[width=7.2cm,height=6.5cm,clip]{6301f12.eps} \end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg113.gif) |
Figure 12:
Normalized MF of 531 SDSS DA WDs (solid line) compared to 270 PG
DA WDs (Liebert et al. 2005, dashed line), both with
|
| Open with DEXTER | |
The total space density of SDSS DA WDs is
![]() pc-3 for WDs with
pc-3 for WDs with
![]() between 12 000 K and 48 000 K and
between 12 000 K and 48 000 K and
![]() pc-3 for WDs with
pc-3 for WDs with
![]() K. If we
include DB/DO WDs, the result will be
K. If we
include DB/DO WDs, the result will be
![]() pc-3and
pc-3and
![]() pc-3, respectively. The normalized MF is
shown in Fig. 12, assuming that the average error for the PG DA WD masses is 0.025
pc-3, respectively. The normalized MF is
shown in Fig. 12, assuming that the average error for the PG DA WD masses is 0.025 ![]() ,
equal to the bin-width of the discrete MF
to retain the distribution information. The two normalized MFs
agree well and show similar properties of distribution when
,
equal to the bin-width of the discrete MF
to retain the distribution information. The two normalized MFs
agree well and show similar properties of distribution when
![]() ,
e.g. the main peak around 0.57
,
e.g. the main peak around 0.57 ![]() and its width
(FWHM), despite the SDSS DR1 just covering a small area of the
whole sky. As we discussed in Sect. 6.2, if the artificial
and its width
(FWHM), despite the SDSS DR1 just covering a small area of the
whole sky. As we discussed in Sect. 6.2, if the artificial
![]() limit is relaxed, the SDSS 1.2
limit is relaxed, the SDSS 1.2 ![]() high
and thin peak would be lower and wider and move right-ward,
more like the PG 1.3
high
and thin peak would be lower and wider and move right-ward,
more like the PG 1.3 ![]() peak.
Our conclusion is that there is a small peak around or
above 1.2
peak.
Our conclusion is that there is a small peak around or
above 1.2 ![]() .
.
![\begin{figure}
\par\includegraphics[width=7.2cm,height=6.8cm,clip]{6301f13.eps} \end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg119.gif) |
Figure 13:
Detailed formation rates of SDSS WDs in linear and log Age scale.
The dashed lines denote SDSS DA samples with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.4cm,height=6.8cm,clip]{6301f14.eps} \end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg120.gif) |
Figure 14:
Detailed formation rates of SDSS WDs with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.3cm,height=6cm,clip]{6301f15a.eps}\p...
...*{2mm}
\includegraphics[width=7.3cm,height=6cm,clip]{6301f15b.eps} \end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg121.gif) |
Figure 15:
Cumulative age functions of SDSS WDs with
|
| Open with DEXTER | |
When we substitute WD age for the mass M in the continuous MF,
we will obtain the age Function, as shown in Fig. 13.
In fact, this age function is just the WD
formation rate as a function of Age (see Fig. 14). Although the
subtle details will be contaminated by fluctuation, the general
trend is much more reliable. Considering the complete sample
with
![]() K, including 893 WDs, we find a relatively
constant formation rate of about
K, including 893 WDs, we find a relatively
constant formation rate of about
![]() pc-3 yr-1 during the last 2 Gyr. There is a very high formation
rate peak around 3-3.5 Gyr (see dashed line in Fig. 13). The
real peak may not be as high as is
shown because of the artificial upper limit of
pc-3 yr-1 during the last 2 Gyr. There is a very high formation
rate peak around 3-3.5 Gyr (see dashed line in Fig. 13). The
real peak may not be as high as is
shown because of the artificial upper limit of
![]() by Kleinman et al. (2004). The massive WDs,
according to current SDSS data and models, are usually very old.
If we consider only the 531 WDs with
by Kleinman et al. (2004). The massive WDs,
according to current SDSS data and models, are usually very old.
If we consider only the 531 WDs with
![]() ,
another problem is seen: the formation rate declines rapidly
when the WD's age exceeds 0.1 Gyr (see Fig. 14). Liebert et al. (2005) noticed
this fact as well (see Sect. 5.1 and Fig. 16 of their paper).
An interpretation can be found: when we just consider the
hotter WDs, the sample will be incomplete due to the elimination of the
cooler ones which were much hotter many years ago when they were
born. So the formation rate of the hotter sample will decline
rapidly accompanying the WDs' cooling along time. The same thing
happens in the EUVE Survey sample (see Fig. 9 in Vennes et al.
1997). In their sample the formation rate declines even faster
(at 10 Myr) than in our work and Liebert et al. (2005)
because their sample is hotter than 20 000 K. The hotter the sample
is, the more incomplete it is and the more rapidly the formation
rate declines.
We integrate the Age (birth rate) Function to get the Cumulative Age
Function as shown in Figs. 15 and 16, which are similar to Fig. 9
in Vennes et al. (1997). In Fig. 15, the hotter sample shows a nearly
excellent straight line below 0.1 Gyr. By assuming a constant formation
rate in the last 2 Gyr to eliminate the influence of the fluctuation in
the continuous function, we can make a linear fit to obtain an
average formation rate equal to the fitting line's slope. The
complete sample also exhibits a
straight line below 2 Gyr, as is shown in Fig. 16. The result is
,
another problem is seen: the formation rate declines rapidly
when the WD's age exceeds 0.1 Gyr (see Fig. 14). Liebert et al. (2005) noticed
this fact as well (see Sect. 5.1 and Fig. 16 of their paper).
An interpretation can be found: when we just consider the
hotter WDs, the sample will be incomplete due to the elimination of the
cooler ones which were much hotter many years ago when they were
born. So the formation rate of the hotter sample will decline
rapidly accompanying the WDs' cooling along time. The same thing
happens in the EUVE Survey sample (see Fig. 9 in Vennes et al.
1997). In their sample the formation rate declines even faster
(at 10 Myr) than in our work and Liebert et al. (2005)
because their sample is hotter than 20 000 K. The hotter the sample
is, the more incomplete it is and the more rapidly the formation
rate declines.
We integrate the Age (birth rate) Function to get the Cumulative Age
Function as shown in Figs. 15 and 16, which are similar to Fig. 9
in Vennes et al. (1997). In Fig. 15, the hotter sample shows a nearly
excellent straight line below 0.1 Gyr. By assuming a constant formation
rate in the last 2 Gyr to eliminate the influence of the fluctuation in
the continuous function, we can make a linear fit to obtain an
average formation rate equal to the fitting line's slope. The
complete sample also exhibits a
straight line below 2 Gyr, as is shown in Fig. 16. The result is
![]() pc-3 yr-1 and
pc-3 yr-1 and
![]() pc-3 yr-1, for WDs with
pc-3 yr-1, for WDs with
![]() and
and
![]() K, respectively. If the formation rate is corrected
for nondegenerate companions and for those WDs that are likely to
be in binaries, it will be increased by a significant factor.
Compared with the recent calculated PNe formation rate of about
K, respectively. If the formation rate is corrected
for nondegenerate companions and for those WDs that are likely to
be in binaries, it will be increased by a significant factor.
Compared with the recent calculated PNe formation rate of about
![]() pc-3 yr-1 (Pottasch 1996;
Phillips 2002), there is a significant disagreement (see the detailed
discussion in Sect. 5.7 of Liebert et al. 2005). Previous
calculated WD formation rates have also been listed in Table 3 for
comparison with our result.
pc-3 yr-1 (Pottasch 1996;
Phillips 2002), there is a significant disagreement (see the detailed
discussion in Sect. 5.7 of Liebert et al. 2005). Previous
calculated WD formation rates have also been listed in Table 3 for
comparison with our result.
![\begin{figure}
\par\includegraphics[width=7cm,height=6.8cm,clip]{6301f16.eps} \end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg125.gif) |
Figure 16:
Cumulative age functions of SDSS WDs with
|
| Open with DEXTER | |
Table 3: Comparisons of our calculated WD formation rate with previous results.
Bergeron et al. (2001) have emphasized the importance of combining
the MF and LS into one distribution function for the comparison of
cooling time. The LF and other parameters of a sample of WDs
vary in different mass groups. For this reason, Liebert et al.
(2005) divided the whole PG sample into 3 groups with mass around
0.6 ![]() ,
,
![]() and
and
![]() ,
respectively. Their discussions of the other parameters such as
the formation rate are all based on this 3-group division.
However, this method also has some problems. (1) Even within each
group, the distribution and parameters are not uniform. (2) This 3-group division method is not universal, e.g. in the SDSS sample, as is shown in Figs. 10 and 12, this division is not
appropriate because the 0.578
,
respectively. Their discussions of the other parameters such as
the formation rate are all based on this 3-group division.
However, this method also has some problems. (1) Even within each
group, the distribution and parameters are not uniform. (2) This 3-group division method is not universal, e.g. in the SDSS sample, as is shown in Figs. 10 and 12, this division is not
appropriate because the 0.578 ![]() peak is too strong,
overwhelming the other groups and the 1.19
peak is too strong,
overwhelming the other groups and the 1.19 ![]() peak is
unreliable. Using the continuous distribution function we proposed
above, a more universal solution can be found by assuming that
every WD's contribution to the space density can be described as
a 2-dimensional Gaussian distribution weighted by
peak is
unreliable. Using the continuous distribution function we proposed
above, a more universal solution can be found by assuming that
every WD's contribution to the space density can be described as
a 2-dimensional Gaussian distribution weighted by
![]() .
We define the Mass-Luminosity Function
(MLF) as:
.
We define the Mass-Luminosity Function
(MLF) as:
| |
= | 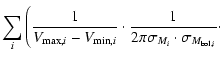 |
|
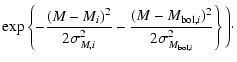 |
(4) |
![\begin{figure}
\par\includegraphics[width=7.8cm,height=6.2cm,clip]{6301f17CMJN.eps}
\end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg137.gif) |
Figure 17:
3-dimension mass-luminosity function for SDSS DA WDs with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,height=6.2cm,clip]{6301f18.eps}
\end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg138.gif) |
Figure 18:
3-dimension mass-luminosity function for SDSS DA WDs with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,height=6.8cm,clip]{6301f19.eps}
\end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg139.gif) |
Figure 19:
Mass-age distribution function for SDSS DA WDs with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,height=6.2cm,clip]{6301f20.eps} \end{figure}](/articles/aa/full/2007/17/aa6301-06/Timg141.gif) |
Figure 20:
H-R diagram for SDSS DA WDs with
|
| Open with DEXTER | |
Figure 17 shows the mass-luminosity function for SDSS DA WDs with
![]() .
The main cluster in Fig. 12 with many
subtle peaks is now decomposed into a "mountain'' along
.
The main cluster in Fig. 12 with many
subtle peaks is now decomposed into a "mountain'' along
![]() with several independent peaks. In this figure, the
maximum mass distribution peak is at about 0.65
with several independent peaks. In this figure, the
maximum mass distribution peak is at about 0.65 ![]() ,
which
is just a quasi-peak in Fig. 12, and the overwhelming peak at 0.58
,
which
is just a quasi-peak in Fig. 12, and the overwhelming peak at 0.58 ![]() is the integration along
is the integration along
![]() of the
"mountain ridge'' at about 0.55
of the
"mountain ridge'' at about 0.55 ![]() .
We can also see a
trend that the mass cluster moves to the massive end as the
.
We can also see a
trend that the mass cluster moves to the massive end as the
![]() goes to the fainter end. Thus, we can infer that if the
goes to the fainter end. Thus, we can infer that if the
![]() becomes fainter than 12 mag, the mass cluster will continue
to move to the massive end, and in Fig. 18 we confirm this inference.
This trend is partly interpreted by Fig. 19. If we assume that most
of the progenitors of these WDs formed almost simultaneously at
early stage of our galaxy, as massive stars usually evolve
faster than lighter ones, they will soon die out to produce
massive WDs and have a long cooling time to reach a present high
becomes fainter than 12 mag, the mass cluster will continue
to move to the massive end, and in Fig. 18 we confirm this inference.
This trend is partly interpreted by Fig. 19. If we assume that most
of the progenitors of these WDs formed almost simultaneously at
early stage of our galaxy, as massive stars usually evolve
faster than lighter ones, they will soon die out to produce
massive WDs and have a long cooling time to reach a present high
![]() .
Meanwhile the less massive stars have much longer lives and
die slowly and much later to give birth to recently born WDs,
which have had little time to cool and only retain a low
.
Meanwhile the less massive stars have much longer lives and
die slowly and much later to give birth to recently born WDs,
which have had little time to cool and only retain a low
![]() .
This
implies that the mass - age distribution of a complete WD sample
contains important information on the early main sequence stars and
our galaxy. Figure 20 gives the 3D H-R diagram which shows an
obvious evolutionary track of WDs.
.
This
implies that the mass - age distribution of a complete WD sample
contains important information on the early main sequence stars and
our galaxy. Figure 20 gives the 3D H-R diagram which shows an
obvious evolutionary track of WDs.
We have performed a study of a DA WD sample from SDSS DR1. To ensure that our adopted sample is accurate and complete, we have carried out many tests. We performed a mass determination comparison to test the accuracy of the model of Panei et al. (2000). By comparing the model-derived mass with that obtained from other methods, independent of the theoretical M-R relation, we find that the model of Panei et al. (2000) is reliable enough to be applied to the mass estimation of SDSS WDs, especially for the hotter WDs.
We tested the completeness of the SDSS WD sample
and corrected for selection effects. We found
that this sample is far from complete, mainly due to
the magnitude-limiting selection effect. Thus we lower the upper
magnitude limit by at least 1.5 mag to make the sample almost
complete. We also proposed a more detailed bin-correction method
to improve the accuracy. The remaining 531 DA WDs with
![]() still form the largest homogeneous
and complete DA WD sample to date.
still form the largest homogeneous
and complete DA WD sample to date.
We calculated the SDSS WD luminosity function based on the
methods of Green (1980) and Fleming et al. (1986), except for some
minor differences. The SDSS LF is generally in agreement with most
previous studies. In addition, the SDSS LF itself shows excellent
agreement with theoretical work, e.g.
the Mestel law. We also proposed some possible interpretations to
account for the disagreements between the SDSS and PG WD samples. We then introduced an improved continuous mass function
and a method to obtain the 3-dimensional distribution functions. We
derived a SDSS MF whose relative distribution and properties are
in good agreement with that of the PG sample, although the
absolute value is different. We thus obtained a 0.58 ![]() mass peak and found that in the 3D mass-luminosity function it is decomposed
into a "mountain ridge'' along
mass peak and found that in the 3D mass-luminosity function it is decomposed
into a "mountain ridge'' along
![]() at about 0.55
at about 0.55 ![]() and an actual peak at about 0.65
and an actual peak at about 0.65 ![]() for fainter WDs.
Evidence implies that there is a massive
WD peak or cluster above 1.2
for fainter WDs.
Evidence implies that there is a massive
WD peak or cluster above 1.2 ![]() ,
which mainly consists of
cool and faint WDs. The derived space
density is
,
which mainly consists of
cool and faint WDs. The derived space
density is
![]() and the formation rate is
about
and the formation rate is
about
![]() and
and
![]() ,
for SDSS DA WDs with
,
for SDSS DA WDs with
![]() and
and
![]() ,
respectively.
,
respectively.
As predicted by Kleinman et al. (2004), we can expect an additional 10 000 WDs or so by the time the SDSS is finished; a much larger and more complete sample of WDs will be available. Eisentein et al. (2006) published a catalog of 9316 spectroscopically confirmed WDs from the SDSS DR4, which includes 8000 DA WDs. A further study of the statistical properties of WDs with this enlarged sample is under way and will be reported in a future work. The theortical model of WDs adopted in our study is still quite simple. Any future progress in the theoretical models of WDs would be very helpful for a more accurate understanding of the statistical properties of WDs.
Acknowledgements
We are greatly indebted to Professor P. Bergeron for kindly providing us with the newly calculated WD bolometric correction data. We thank the referee, Professor Martin A. Barstow, for his careful annotations on the manuscript, which greatly improve our presentation. This research is supported by the President Fund of Peking University, the NFSC grants (No. 10473001 and No. 10525313), the RFDP grant (No. 20050001026) and the Key Grant Project of Chinese Ministry of Education (No. 305001).