A&A 464, 429-435 (2007)
DOI: 10.1051/0004-6361:20065486
M. González1,2 - E. Audit1,2 - P. Huynh3
1 - CEA-Saclay, DSM/DAPNIA/Service d'Astrophysique,
91191 Gif-sur-Yvette Cedex, France
2 -
AIM - Unité Mixte de Recherche CEA, CNRS, Université Paris VII,
UMR No. 7158, France
3 -
CEA-Saclay, DSI/DIR,
91191 Gif-sur-Yvette Cedex, France
Received 24 April 2006 / Accepted 8 November 2006
Abstract
Aims. We present a new three-dimensional radiation hydrodynamics code called HERACLES that uses an original moment method to solve the radiative transfer.
Methods. The radiation transfer is modelled using a two-moment model and a closure relation that allows large angular anisotropies in the radiation field to be preserved and reproduced. The radiative equations thus obtained are solved by a second-order Godunov-type method and integrated implicitly by using iterative solvers. HERACLES has been parallelized with the MPI library and implemented in Cartesian, cylindrical, and spherical coordinates. To characterize the accuracy of HERACLES and to compare it with other codes, we performed a series of tests including purely radiative tests and radiation-hydrodynamics ones.
Results. The results show that the physical model used in HERACLES for the transfer is fairly accurate in both the diffusion and transport limit, but also for semi-transparent regions.
Conclusions. This makes HERACLES very well-suited to studying many astrophysical problems such as radiative shocks, molecular jets of young stars, fragmentation and formation of dense cores in the interstellar medium, and protoplanetary discs.
Key words: radiative transfer - scattering - hydrodynamics - methods: numerical
Since we receive almost all the information from astrophysical objects in the form of photons, there has been a long tradition of radiative transfer in the astrophysical community. However, most of the time, radiation is used as a probe of the physical system under study. For that purpose radiative transfer is treated in great detail, using complex spectral opacities and without assuming local thermodynamical equilibrium (Kurucz 1996; Hauschildt et al. 1997). However, in many cases, radiation cannot be considered as a passive probe of the physical system, but it has to be considered as an important dynamical constituent.
For this reason, and thanks to the ever-increasing computing power available, there has been a rise in the interest in radiation-hydrodynamics, that is, in the dynamical coupling of gas and radiation. However, using the radiative transfer models developed in the context of spectral analysis for radiation-hydrodynamics is far out of the reach of present computers. Therefore, in order to study the dynamics of multi-dimensional systems including radiative transfer, one has to greatly simplify the full transfer equation, which depends upon six variables in a three-dimensional problem.
Our objective is to propose a radiative transfer model that can preserve and reproduce large angular anisotropies in the radiation field, which properly treats the time dependence of the radiation field and which couples naturally to the modern high-resolution numerical schemes used for hydrodynamics. All this, of course, has to be obtained at a reasonable numerical cost.
Different physical approximations have been developed to model radiative transfer in particular cases. Within the limit of large optical thickness, the diffusion approximation can be used (Turner & Stone 2001; Mihalas & Mihalas 1984; Dai & Woodward 1998). On the other hand, the transport limit is reached for transparent media. Particular methods have been implemented to describe this regime (Dai & Woodward 2000).
In many problems of physical interest, regions of large opacities are found next to transparent regions. One possibility for treating these problems is to couple two approximate models, i.e. one for each region. However, this introduces large drawbacks due to the domain partition, some loss in accuracy in the transition zone; and most of the time the semi-transparent regions would not be described correctly. Monte-Carlo codes that directly solve the transfer equation (Mihalas & Mihalas 1984; Pascucci et al. 2004, and references therein) can describe both regimes; however, they are difficult to couple to hydrodynamical codes and are very costly, especially in the diffusion regime.
Other techniques have therefore been developed based on discretization both in angles and space. One of them consists in choosing a set of discrete directions and in computing the integral over solid angle by a weighted sum over these directions. This technique, called the discrete ordinates method, can solve radiative transfer problems with relatively good accuracy and moderate computing cost. Although it has been greatly extended since Chandrasekhar first introduction, it still has two major drawbacks: ray effects and false scattering (Coelho 2002). False scattering (equivalent to the false diffusion in hydrodynamics) is due to the spatial discretization and may be reduced by refining the grid. The ray effect appears in free-streaming regions and consists in anomalous distortions of radiation intensity. Moreover, this method cannot properly treat the specularly reflected beams because of the choice of discrete directions.
To overcome this problem, both the short or the long characteristic methods choose the photons trajectories as privileged directions (Rukolaine et al. 2002). In these methods, the radiative transfer equation is integrated over ray propagation. In the long characteristic algorithm, the ray is projected from each grid point to the domain boundaries where specific intensity is known via boundary conditions. This method is unfortunately very time-consuming and not well-suited to three-dimensional problems. That is why, in the short characteristic method, the rays are projected only to the neighboring cells (van Noort et al. 2002). This is much less time-consuming, but the interpolations needed along grid lines make it more diffusive than the long characteristic one.
Instead of trying to solve the full transfer equation as in the Monte-Carlo, the discrete ordinates, or the characteristic methods, it is also possible to use another class of methods that consists in solving an approximate simplified model. This class is dedicated to model situations where radiative transfer is strongly coupled with other phenomena (fluid motion, chemical reactions, etc.) as is the case in our domain of interest. These methods consider the moments of the radiative transfer equation and consist in choosing a closure relation to solve them. The most common of these methods is the flux-limited diffusion, which solves the evolution of the first moment (radiative energy) and uses a closure relation valid in the diffusion limit, which is an isotropic radiative pressure tensor. In this scheme, the flux is always colinear and proportional to the gradient of radiative energy. In addition, the equation is modified with an ad-hoc function (the flux limiter) in order to ensure that the radiative flux remains in physically acceptable limits. This method is very useful in diffusive regions because it gives good results at a reasonable computational cost. Nevertheless, it should be used with care when dealing with free-streaming regions. Another method of closing the system is the variable tensor Eddington formalism (VTEF). It solves, in a first step, the moment equations with a fixed Eddington tensor and then computes the new tensor by solving the transfer equation locally with a fixed source function (Stone et al. 1992; Gehmeyr & Mihalas 1993) or with an approximate time dependence (Hayes & Norman 2003). If this procedure is iterated until the value of the source converges, one has a means of solving the transfer equation exactly. The VTEF methods give better results than the flux-limited diffusion but are much more complex because they require the local resolution of the transfer equation at each time step.
We have chosen in this work to use a moment model to describe radiative transfer but with a more general closure relation than the flux-limited diffusion, but one that is nevertheless analytical. This model allows treatment of radiative transfer from the diffusion to the free-streaming regime at, as we will show, a relatively low cost and with good accuracy. Furthermore, since we use a moment model, elastic scattering can be taken into account at almost no extra cost and with a reasonable accuracy, which is not the case for the other methods described before. In the next section, we present the moment model and our chosen closure. Section 3 describe the numerical scheme and its actual parallel implementation. The next section presents some multi-dimensional tests to verify our code both on purely radiative problems and on radiation hydrodynamics, as well as some performance analysis. Finally, the last section presents a summary and concluding remarks.
For most problems and for the foreseeable future, solving the full transfer equation in three dimensions is much too costly both in time and memory. This problem is even greater if one wants to couple the radiative transfer with hydrodynamics to study multi-dimensional time-dependent problems. For this reason, we decided to use a moment model that is much less expensive than the full transfer equation and couples naturally to hydrodynamics.
The radiative transfer equation for the specific intensity is
Integrating Eq. (1) and Eq. (1)
![]() over solid angle yields
over solid angle yields
Unfortunately, the previous system is not closed since the radiative
pressure is not known. The pressure is then often expressed as
![]() where
where
![]() is the Eddington
tensor. There are many physical approximations that can be used to
determine the Eddington tensor. The simplest one is to use the
Eddington tensor given by the diffusion limit:
is the Eddington
tensor. There are many physical approximations that can be used to
determine the Eddington tensor. The simplest one is to use the
Eddington tensor given by the diffusion limit:
![]() ,
where
,
where
![]() is the identity matrix. This corresponds
to an isotropic radiation field. We also chose an analytical
Eddington tensor in order to keep the method simple and cost
competitive. But, as we will see, the underlying photon distribution
function (or equivalently the specific intensity) is not isotropic,
which makes the method applicable to a wide range of conditions.
is the identity matrix. This corresponds
to an isotropic radiation field. We also chose an analytical
Eddington tensor in order to keep the method simple and cost
competitive. But, as we will see, the underlying photon distribution
function (or equivalently the specific intensity) is not isotropic,
which makes the method applicable to a wide range of conditions.
In order to close system (4), we want to express the
Eddington tensor, and therefore the underlying specific intensity,
only in terms of ![]() and
and
![]() .
It is then natural to suppose
that the direction of the radiative flux is an axis of symmetry of the
local specific intensity. With this assumption, the Eddington tensor
is given by (Levermore 1984)
.
It is then natural to suppose
that the direction of the radiative flux is an axis of symmetry of the
local specific intensity. With this assumption, the Eddington tensor
is given by (Levermore 1984)
We now need to specify the Eddington factor in order to close the
system. For that purpose we assume that the specific intensity of our
radiative transfer model is given by
![$\displaystyle B (\nu,f,T^*) =
\frac{2 h \nu^3}{c^2} \left[\exp \left(\frac{h \n...
...\Vert^2}}{\Vert\vec{ f}\Vert^2}\vec{f}.\vec{\Omega}\right)\right)-1\right]^{-1}$](/articles/aa/full/2007/11/aa5486-06/img32.gif) |
(6) |
![]() and
and
![]() is the reduced flux. Note that by
definition of
is the reduced flux. Note that by
definition of ![]() and
and
![]() ,
we have
,
we have
![]() ,
which means that radiative energy is transported at most at the speed
of light. This distribution can either be obtained by applying a
Lorentz transform to an isotropic one (Levermore 1984) or by
minimizing the radiative entropy (Dubroca & Feugeas 1999). As we shall see,
this simple assumption for the specific intensity allows us to compute
the Eddington factor easily and analytically, but one has to keep in
mind that there might be some cases where assuming such a simplified
geometry may be a very poor approximation.
,
which means that radiative energy is transported at most at the speed
of light. This distribution can either be obtained by applying a
Lorentz transform to an isotropic one (Levermore 1984) or by
minimizing the radiative entropy (Dubroca & Feugeas 1999). As we shall see,
this simple assumption for the specific intensity allows us to compute
the Eddington factor easily and analytically, but one has to keep in
mind that there might be some cases where assuming such a simplified
geometry may be a very poor approximation.
In the M1 model (Ripoll et al. 2001; Dubroca & Feugeas 1999), the previous form of the
specific intensity is used to compute the Eddington factor, therefore
closing system (4):
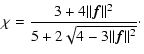 |
(7) |
We first start by describing the interaction between a static fluid and radiation. The fluid can only be heated or cooled and its evolution is determined by the classical energy conservation equation with a source term characterizing the energy exchanges between the fluid and the radiation.
To ensure a good conservation of energy, we consider the equation for
the total energy (radiation plus matter) instead of only matter
energy. The system to be solved is:
To numerically solve the system above, we use a second-order Godunov type algorithm for the hyperbolic subsystem formed by the last two equations. The first equation is then integrated using the flux obtained by the hyperbolic solver.
It is worth noticing that the wave speeds of this subsystem, which
mathematically correspond to the eigenvalues of its Jacobian matrix,
depend only on the norm of the reduced flux ![]() and on the angle
and on the angle ![]() of this flux with the considered interface. These wave
speeds describe the speed at which the information is transported in
the system, in the same way as the sound speeds in a fluid at rest.
Figure 1 illustrates the behavior of the eigenvalues
normalized by c for some characteristic values of
of this flux with the considered interface. These wave
speeds describe the speed at which the information is transported in
the system, in the same way as the sound speeds in a fluid at rest.
Figure 1 illustrates the behavior of the eigenvalues
normalized by c for some characteristic values of ![]() and
and ![]() .
.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{5486f1.eps}\end{figure}](/articles/aa/full/2007/11/aa5486-06/Timg47.gif) |
Figure 1: Eigenvalues of the Jacobian matrix normalized by c. |
| Open with DEXTER | |
The left plot corresponds to a flux perpendicular to the interface
(
![]() ), which is similar to the mono-dimensional problem (cf.
Fig. 1 of Audit et al. 2002). In particular, for a unit reduced flux
(points A), the four eigenvalues are equal to c so the transport limit
is correctly described.
The middle plot represents the case where the flux is parallel to the
interface. In that particular case, two eigenvalues are always equal
to zero and the two others are equal in norms but of opposite sign.
We can also notice that, when the reduced flux is unity (points C),
the four eigenvalues are null. This is particularly interesting
because it corresponds to the physical characteristic speeds of a
transverse flux and because it means that there is no transport
perpendicular to the radiative flux (cf. shadow test below).
In all cases, we find that for
), which is similar to the mono-dimensional problem (cf.
Fig. 1 of Audit et al. 2002). In particular, for a unit reduced flux
(points A), the four eigenvalues are equal to c so the transport limit
is correctly described.
The middle plot represents the case where the flux is parallel to the
interface. In that particular case, two eigenvalues are always equal
to zero and the two others are equal in norms but of opposite sign.
We can also notice that, when the reduced flux is unity (points C),
the four eigenvalues are null. This is particularly interesting
because it corresponds to the physical characteristic speeds of a
transverse flux and because it means that there is no transport
perpendicular to the radiative flux (cf. shadow test below).
In all cases, we find that for
![]() (points B), the
eigenvalues are {
(points B), the
eigenvalues are {
![]() }, which are the proper
propagation speeds in the diffusion limit.
These eigenvalues are then used in our Riemann solver, which is an
HLLE (Harten-Lax-van Leer-Einfeldt) scheme (Einfeldt et al. 1991), see
Appendix A for details.
}, which are the proper
propagation speeds in the diffusion limit.
These eigenvalues are then used in our Riemann solver, which is an
HLLE (Harten-Lax-van Leer-Einfeldt) scheme (Einfeldt et al. 1991), see
Appendix A for details.
Our scheme is of order two in space. It means that all quantities evaluated at the interfaces are reconstructed by using a linear reconstruction in each cell. To insure numerical stability, the results presented in this paper used a minmod limiter, but another limiter could easily be used instead. HERACLES has been implemented in order to work in either Cartesian, cylindrical, or spherical geometry (cf. Appendix B for the specific divergence discretization in these geometries).
Noticing that the time step given by the Courant condition is much smaller for radiation than for hydrodynamics, and since we are most often interested in studying system over hydrodynamical time scales, we need to develop an implicit algorithm for the radiation. The time step is then given by the explicit Courant condition for hydrodynamics and by controlling the variation of the variables for the implicit radiative solver. When doing radiation-hydrodynamics, the smallest of these two time steps is taken (see Appendix C for details).
We now have to solve a non-linear set of equations (the
non-linearities come from the Eddington factor and the T4 terms).
This is done using a Raphson-Newton method, which can eventually be
restricted to a single iteration if solving the linearized system is
enough. Either way, we have to invert a
![]() matrix, where d is the dimensionality of the problem and N the
number of cells along a direction. The typical scale of a simulation
makes a direct inversion out of reach, so we need to resort to an
iterative inversion method. We have implemented and tested two
different methods that are relevant in different physical situations,
each one efficient in one of the two limits of the transfer equation.
matrix, where d is the dimensionality of the problem and N the
number of cells along a direction. The typical scale of a simulation
makes a direct inversion out of reach, so we need to resort to an
iterative inversion method. We have implemented and tested two
different methods that are relevant in different physical situations,
each one efficient in one of the two limits of the transfer equation.
The Gauss-Seidel method (see Press et al. 1986, for further details) is
very efficient in the transport limit. For example, in one dimension
if we know a priori the direction in which the information
propagates, the algorithm converges theoretically in only one
iteration. To take advantage of this feature, we can also use a sweep
method that inverts the cells ordering at each iteration. All the
tests performed show that this method is very efficient both in time
and in memory requirements. One could be tempted to use the improved
method called successive overrelaxation (SOR), but it should be taken
with care. Indeed, in some cases, too large extrapolation could lead
to a non physical iterate that does not respect the condition
![]() and that breaks down the iterations because of the M1closure.
and that breaks down the iterations because of the M1closure.
On the other hand, the generalized minimal residual (GMRES) method (Saad & Schultz 1986), although more constraining in terms of memory requirement, is well-suited to the diffusion limit in which case the matrix is diagonally dominant. As each method dumps the residual in a different way, we also implemented a coupled version for which we switch between both methods. This version seems to have the best convergence rate (cf. Fig. D.2 and Appendix D for further details).
For both inversion methods, we need a convergence criterion. After trying various possibilities, we found that using the residual of the adimensioned equations gave the best results. In order to adimensionate the equation on the radiative flux, we divide it by the radiative energy times the speed of light and not by the radiative flux, which can be vanishing. In all the tests presented in this paper, the convergence is assumed to be achieved when this residual is less than 10-5.
As our code is parallelized with the MPI library, we also quantified the scaling of these two methods as the number of processors increased. We found that both of them show good scaling; however, the Gauss-Seidel algorithm is nearly perfect, whereas GMRES could have a loss in performance reaching 20% (cf. Appendix D).
We now generalize the previous analysis to a moving fluid. The fluid evolution is determined by the classical conservation equations (mass, momentum, and energy) with source terms characterizing the momentum and energy exchanges between the fluid and the radiation.
In order to write the radiation hydrodynamics equations, one has to choose the frame in which to evaluate the radiative quantities: laboratory frame or comoving frame (i.e. the frame moving with the fluid). The laboratory frame is convenient because the system remains globally conservative, which keeps the hyperbolic part (i.e. the left-hand side) of the system simple (Mihalas & Auer 2001). But in this frame, interactions with matter become complex because of Doppler and aberration effects that have to be incorporated in the source terms. On the other hand, using the radiative quantities expressed in the comoving frame (Lowrie et al. 2001) adds non-conservative terms to the equations. But the source terms remain unaffected by the fluid motions.
In HERACLES, we have chosen to express radiative quantities in the
comoving frame. The equations of radiation hydrodynamics can then be
written (Mihalas & Mihalas 1984) as
The resolution of the previous system is split into three steps. The
first one updates the hydrodynamical quantities using a classical
second-order Godunov type method. In the next step, the radiative
quantities are updated implicitly, as described in the previous
section. During this step, we use the velocity given by the hydro
solver. In the third and final step, the
![]() source term is added to the gas momentum and total energy. Since in
most cases this term is rather small, it is not necessary to treat it
in the implicit system. This allows the reduction of the number of
equations to be solved implicitly and makes the method more efficient:
source term is added to the gas momentum and total energy. Since in
most cases this term is rather small, it is not necessary to treat it
in the implicit system. This allows the reduction of the number of
equations to be solved implicitly and makes the method more efficient:
We performed a series of verification tests in order to better characterize the accuracy of HERACLES and to compare it with other codes. We reproduce here just the three that are particularly relevant to astrophysical conditions. Appendix E compiles others tests: beam test, pipe flow test, diffusion in a moving fluid, and a comparison with simple analytical models of matter-radiation coupling and Marshak wave.
We performed a 2D shadow test similar to the one presented in
Hayes & Norman (2003). This test consists in lighting an oblate spheroid clump
in a cylinder L=1 cm, R=0.12 cm. This spheroid is located on the
symmetric axis and at the centre of the box width:
![]() .
Its extension is
(z0,r0)=(0.1,0.06).
.
Its extension is
(z0,r0)=(0.1,0.06).
Initially, the medium is at equilibrium with radiation i.e.
![]() ,
and the density is homogeneous (
,
and the density is homogeneous (
![]() )
except for the clump with density
)
except for the clump with density ![]() one thousand times greater. The boundary of this region is smoothed,
such as
one thousand times greater. The boundary of this region is smoothed,
such as
![]() with
with
![]() .
The opacity of the medium is a function of density and
temperature
.
The opacity of the medium is a function of density and
temperature
![]() with
with
![]() .
Initially, the mean free path is then 10 cm in the
cylinder and 10-5 cm in the clump. At time t=0, a uniform
source is lighted at the left boundary with
.
Initially, the mean free path is then 10 cm in the
cylinder and 10-5 cm in the clump. At time t=0, a uniform
source is lighted at the left boundary with
![]() .
The mean free path of a photon being much smaller in the clump (by six
orders of magnitude), a shadow develops behind it. Until the light
has crossed the clump, the shadow should remain stable.
.
The mean free path of a photon being much smaller in the clump (by six
orders of magnitude), a shadow develops behind it. Until the light
has crossed the clump, the shadow should remain stable.
Figure 2 shows the radiative temperature for three runs
performed on a
![]() grid. The first run (upper panel) was performed
solving the diffusion equation. It corresponds to the time t=0.1 s,
which means
grid. The first run (upper panel) was performed
solving the diffusion equation. It corresponds to the time t=0.1 s,
which means
![]() light crossing times. The other two runs used
the M1 model and differs by the method of computing the
eigenvalues. In the first case (middle panel), we chose not to
compute these eigenvalues and to set them arbitrarily equal to
light crossing times. The other two runs used
the M1 model and differs by the method of computing the
eigenvalues. In the first case (middle panel), we chose not to
compute these eigenvalues and to set them arbitrarily equal to ![]() ,
whereas in the second run (lower panel), the eigenvalues were
computed. To compare with the results obtained in Hayes & Norman (2003), we
also plotted a radial profile of the radiative temperature at the
outer boundary (cf. Fig. 3).
,
whereas in the second run (lower panel), the eigenvalues were
computed. To compare with the results obtained in Hayes & Norman (2003), we
also plotted a radial profile of the radiative temperature at the
outer boundary (cf. Fig. 3).
One can see that there is no longer a shadow in the first case. This
is due to the fact that the diffusion equation is intrinsically
isotropic (
![]() ). Therefore, the photons can
go around the obstacle immediately. In the two other cases, the
shadow is better preserved even in the simple case without computing
eigenvalues. As could be expected, the first method is more diffusive
than the second one. The improvement obtained with the second method
is easy to understand when looking at the real eigenvalues (cf.
Sect. 3.1). The proper treatment of the propagation
speed in the HLLE scheme is effective enough to inhibit large
numerical diffusion between the shadowed and enlightened regions.
). Therefore, the photons can
go around the obstacle immediately. In the two other cases, the
shadow is better preserved even in the simple case without computing
eigenvalues. As could be expected, the first method is more diffusive
than the second one. The improvement obtained with the second method
is easy to understand when looking at the real eigenvalues (cf.
Sect. 3.1). The proper treatment of the propagation
speed in the HLLE scheme is effective enough to inhibit large
numerical diffusion between the shadowed and enlightened regions.
It is also interesting to compare the propagation speed of the
radiation between the diffusion approximation and the M1 model. For
the diffusion, the characteristic length scales as the square root of
time:
![]() where
where ![]() is the diffusion
coefficient. In our example, it means that radiation will cross the
box in a few 10-9 s, whereas in reality as radiation propagates
in a transparent medium, it goes at light speed and the crossing time
is
is the diffusion
coefficient. In our example, it means that radiation will cross the
box in a few 10-9 s, whereas in reality as radiation propagates
in a transparent medium, it goes at light speed and the crossing time
is
![]() s. In the two M1 model simulations, we recover
this value.
s. In the two M1 model simulations, we recover
this value.
| |
Figure 2: Radiative temperature in the shadow test using the diffusion equation ( upper panel), M1 closure with fixed eigenvalues ( middle panel), and M1 closure with calculated eigenvalues ( lower panel). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{5486f3.eps}\end{figure}](/articles/aa/full/2007/11/aa5486-06/Timg77.gif) |
Figure 3: Radial profiles of the radiative temperature in the shadow test using the diffusion equation (dotted line), M1 closure with fixed eigenvalues (dashed line), and M1 closure with calculated eigenvalues (solid line). |
| Open with DEXTER | |
We now present a test of HERACLES in a semi-transparent regime where the validity of the physical model used to treat the transfer has to be assessed. The following test can be seen as a star with solar luminosity illuminating its surrounding disc of gas at a distance approximately equal to 5 AU (which corresponds to the Sun-Jupiter distance).
The simulation box, whose dimensions are
![]() and
and
![]() ,
is at equilibrium, and at
t=0 an incoming horizontal radiative flux equal to
,
is at equilibrium, and at
t=0 an incoming horizontal radiative flux equal to
![]() is set. The box is filled
with matter at density
is set. The box is filled
with matter at density
![]() ,
while
there is a vacuum on the outside. The width of the box corresponds to
seven mean free paths (the absorption coefficient is
,
while
there is a vacuum on the outside. The width of the box corresponds to
seven mean free paths (the absorption coefficient is
![]() )
and is sampled over 50 cells. This box is therefore
a semi-transparent region, and this run will test the accuracy of the
M1 closure in this particular transient regime.
Figure 4 shows the isotherms obtained at equilibrium by
HERACLES and by a Monte-Carlo code (Dullemond & Natta 2003).
)
and is sampled over 50 cells. This box is therefore
a semi-transparent region, and this run will test the accuracy of the
M1 closure in this particular transient regime.
Figure 4 shows the isotherms obtained at equilibrium by
HERACLES and by a Monte-Carlo code (Dullemond & Natta 2003).
The two results agree with good precision. The differences could be due to the M1 model itself or to the slightly different treatment of the boundary conditions. It is important to note that the Monte-Carlo code solves the transfer equation exactly and, therefore, the agreement between these two approaches is a very good test to verify our model, both physically and numerically, in this semi-transparent regime.
| |
Figure 4: Left panel: HERACLES temperature map. Right panel: isotherms for HERACLES (solid lines) and a Monte-Carlo code (dashed lines). |
| Open with DEXTER | |
Scattering is a phenomenon that plays an important role in many astrophysical problems, such as in the interstellar medium where light is scattered by dust grains. The radiative model used in HERACLES allows us to treat scattering at no additional cost and with reasonable accuracy.
By definition, the importance of scattering compared to absorption is
quantified by the albedo:
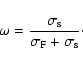
We wanted to perform the same test as above but with scattering; but
to have results to compare with, we changed the scale of the problem
and borrowed initial conditions from the engineering literature
(Crosbie & Schrenker 1984). We consider a two-dimensional box whose dimensions
are
![]() and
and
![]() where
where
![]() and
and
![]() are the optical
coordinates. This box is lit from left by a source at
are the optical
coordinates. This box is lit from left by a source at ![]() and the
steady state is achieved.
and the
steady state is achieved.
We reproduce the results of only one test here, but several others
were performed and show good agreement, too. We took
![]() ,
,
![]() ,
and each direction is sampled over 100 cells. We
chose this particular test because it reproduces a rectangular medium
for which the influence of albedo is very important.
Figure 5 shows the normalized radiative energy
,
and each direction is sampled over 100 cells. We
chose this particular test because it reproduces a rectangular medium
for which the influence of albedo is very important.
Figure 5 shows the normalized radiative energy
![]() isocontours at five values 0.3, 0.4, 0.5, 0.6, and 0.7,
for
isocontours at five values 0.3, 0.4, 0.5, 0.6, and 0.7,
for ![]() and
and
![]() .
This figure is very similar to
Fig. 12c of Crosbie & Schrenker (1984). As expected, the isocontours penetrate
deeper in the domain when there is no absorption. Radiative energy is
greater when absorption exists.
.
This figure is very similar to
Fig. 12c of Crosbie & Schrenker (1984). As expected, the isocontours penetrate
deeper in the domain when there is no absorption. Radiative energy is
greater when absorption exists.
The differences in terms of distance covered between our results and those of Crosbie & Schrenker (1984) remain lower than 5%. But for HERACLES, contrary to other methods, the treatment of scattering is nearly free in terms of computational cost. Indeed, in our case, taking scattering into account implies slightly modifying the source term in the radiative flux equation, but it does not change the number of operations needed at each iteration of the implicit solver. On the other hand, when solving the transfer equation, treating scattering implies computing an integral over solid angles of the specific intensity, which is very costly.
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{5486f5.eps}
\end{figure}](/articles/aa/full/2007/11/aa5486-06/Timg94.gif) |
Figure 5:
Normalized radiative energy isocontours for |
| Open with DEXTER | |
Radiative shocks might be encountered in various astrophysical systems: stellar accretion shocks, pulsating stars, interaction of either jets or supernovæ with the interstellar medium, etc. They are also reproduced in laboratory experiments, in a scaled manner, in order to better understand their underlying physics (González et al. 2006; Bozier et al. 1986).
There are two kinds of shocks depending on the initial fluid speed: subcritical and supercritical (Mihalas & Mihalas 1984). When the initial fluid speed is low, the matter temperature before the shock is much lower than the matter temperature behind it and the transition is sharp. The radiative temperature never overshoots the temperature behind the shock. Such shocks are called subcritical. On the other hand, when the initial fluid speed is high enough, the temperature on each side of the shock are equal. The transition is smoother, the radiative precursor is larger, and a matter temperature peak, which extends over roughly one mean free path, appears just behind the shock. This is a supercritical shock. The specific profiles and characteristics of these shocks are the result of the strong coupling between matter and radiation.
We consider a 1D homogeneous medium where the fluid moves uniformly
from right to left and the left boundary is a wall. A shock is
therefore generated at this boundary and travels the box from left to
right. The initial conditions are such that
![]() (divided in 300 cells) and
(divided in 300 cells) and
![]() .
The gas is perfect with an adiabatic coefficient of 7/5
and temperature at 10 K in equilibrium with radiation. The medium is
supposed to have a constant extinction coefficient:
.
The gas is perfect with an adiabatic coefficient of 7/5
and temperature at 10 K in equilibrium with radiation. The medium is
supposed to have a constant extinction coefficient:
![]() .
.
In all the above figures, we plot the temperatures as function of xi=x-u t to be able to compare our results with those obtained in Ensman (1994) and in Hayes & Norman (2003).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{5486f6.eps}
\end{figure}](/articles/aa/full/2007/11/aa5486-06/Timg100.gif) |
Figure 6: Subcritical shock: gas (solid line) and radiative (dashed line) temperatures at 1.7e4, 2.8e4, and 3.8e4 s obtained with the M1 model (thick lines) compared to a constant and isotropic Eddington tensor model (thin lines). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{5486f7.eps}\end{figure}](/articles/aa/full/2007/11/aa5486-06/Timg102.gif) |
Figure 7: Supercritical shock: temperatures (thick lines) of gas (solid line) and radiation (dashed line) at 4.0e3, 7.5e3, and 1.3e4 s and the corresponding reduced fluxes (thin lines). |
| Open with DEXTER | |
The ability of HERACLES to treat these radiative shocks properly shows that our resolution method divided in three steps (Eqs. (11)-(13)) does not alter the coupling between matter and radiation.
We have presented a new, parallelized, three-dimensional radiation hydrodynamics code called HERACLES. The radiative transfer is solved using a moment method and the M1 closure relation. We have shown that, even though approximate, this model gives an accurate solution even when the radiation field presents large angular anisotropies. The numerical scheme proposed for integrating the M1 model is implicit and allows us to numerically keep the correct physical properties of M1.
The tests performed and presented in this paper reveal the accuracy of HERACLES both in the diffusion and transport limit, and despite all the approximations, it compares well to codes that solve the exact transfer equation. In particular, and in opposition to flux limited diffusion, HERACLES can deal with semi-transparent and free-streaming regions. The possibility of easily treating scattering with reasonable accuracy is also an advantage to our method. Finally, it naturally couples to the modern high-resolution numerical schemes used for hydrodynamics, and its reasonable numerical cost allows the treatment of three-dimensional radiation hydrodynamics problems.
The tests presented in this paper show that HERACLES will be very well-suited to studying various astrophysical problems from the study of protoplanetary discs to the formation and fragmentation of dense cores in the interstellar medium. It has already been used to study and interpret multidimensional effects in laboratory astrophysics radiative shocks experiments carried out at the PALS laser (González et al. 2006). And a study of the interaction of molecular jets with the interstellar medium is in preparation (González et al. 2007).
Some further developments of the code are also envisaged. The most useful for astrophysical applications are implementation of a multigroup M1 model and coupling to an AMR grid to obtain a very high resolution while remaining cost competitive.
Acknowledgements
HERACLES is available at http://www-dapnia.cea.fr/Projets/COAST/heracles.htm or by sending an e-mail to edouard.audit@cea.fr
We would like to thank the CEA computing center, CCRT, where all the computations presented in this paper were done.
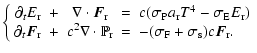 |
(A.1) |
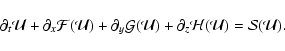
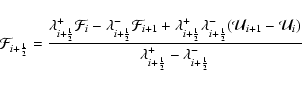 |
(A.2) |
The computation of these eigenvalues is rather time-consuming because
we need them at each iteration in a time step and at each interface of
the mesh. However, since they only depend on two parameters (i.e.
![]() and
and ![]() ), they can be tabulated easily. We
therefore decided to compute them once for a set of
), they can be tabulated easily. We
therefore decided to compute them once for a set of ![]() and fand to interpolate the value needed. This method performs well
because the eigenvalues have a smooth behavior. The maximum
difference obtained between the exact eigenvalues and the interpolated
ones never exceeds one percent using a
and fand to interpolate the value needed. This method performs well
because the eigenvalues have a smooth behavior. The maximum
difference obtained between the exact eigenvalues and the interpolated
ones never exceeds one percent using a
![]() interpolation grid.
interpolation grid.
Table B.1: Divergence in the three different geometries handled by HERACLES.
In one Cartesian dimension, noting down the time index n and n+1, the cell index i, and the interfaces indexes
One should take particular care in the discretization of these terms
in order to check three conditions. First, the discrete divergence of
a constant must be null. Second, when r tends to infinity, the
geometry effects vanish and one should recover the Cartesian
divergence. Finally, when the resolution increases (i.e. dr tends
to zero), the discrete scheme should not diverge. In order to verify
these three conditions in HERACLES, we then discretize the "nabla''
terms with the classical formula
![]() .
For the derivative terms, we use a discretization over
the direction considered involving interface values:
.
For the derivative terms, we use a discretization over
the direction considered involving interface values:
![]() and
and
![]() .
As
for the additional terms, they are cell-centered.
.
As
for the additional terms, they are cell-centered.
This discretization ensures us that the momentum in the hydrodynamics
equations is conserved. One can notice that the additive centered
terms drop naturally when the diffusion limit is reached, because in
such case the tensor of radiative pressure is isotropic:
![]() .
.
The time step in HERACLES is the smallest of the hydrodynamical and the radiative time steps. The hydrodynamical time step is simply given by a Courant condition using a Courant factor of 0.8. For the radiation, we compute two time steps. An explicit one, also given by a Courant condition, and an implicit one controlled by the variation in the variables involved in the implicit step (gas energy, radiative energy, and radiative flux). We set a limit on the allowed variation for these variables during a time step, and the implicit time step is increased (resp. lowered) if the actual variations are lower (resp. higher) than this limit. The final radiative time step is the implicit one if it is at least 10 times greater than the explicit one. This last condition ensures that implicit integration is done only when it is profitable.
We present here the performances obtained with HERACLES. The code is parallelized with the MPI library in order to run on a large parallel supercomputer. The parallelization scheme used is a classical domain decomposition. This splitting ensures a good equilibrium of charge between all the processors. The communications at the boundary between each domain always take a negligible time in all the tests we have done.
To test the performances, we ran different simulations over 1, 16, 36,
64, and 121 processors such that each processor worked on
![]() cells. In Fig. D.1, we plot the CPU time per
processor and per cell normalized by the Gauss-Seidel CPU time with
one processor. We can clearly see that the Gauss-Seidel method has a
nearly perfect scaling, whereas the GMRES method has a more complex
behavior with a loss of performance that can reach 20%. This is due
to the fact that the GMRES algorithm has a more complex communication
scheme and is therefore more sensitive to small load unbalances. We
can also see that one GMRES iteration nearly corresponds to three
Gauss-Seidel iterations in terms of CPU time. Another drawback of the
GMRES method is that it is very demanding in terms of memory space.
In conclusion, the GMRES method is appropriate if it significantly
accelerates the convergence (at least by a factor of 3) and if memory
is not a crucial issue.
cells. In Fig. D.1, we plot the CPU time per
processor and per cell normalized by the Gauss-Seidel CPU time with
one processor. We can clearly see that the Gauss-Seidel method has a
nearly perfect scaling, whereas the GMRES method has a more complex
behavior with a loss of performance that can reach 20%. This is due
to the fact that the GMRES algorithm has a more complex communication
scheme and is therefore more sensitive to small load unbalances. We
can also see that one GMRES iteration nearly corresponds to three
Gauss-Seidel iterations in terms of CPU time. Another drawback of the
GMRES method is that it is very demanding in terms of memory space.
In conclusion, the GMRES method is appropriate if it significantly
accelerates the convergence (at least by a factor of 3) and if memory
is not a crucial issue.
The convergence rate of the above algorithms can vary significantly from one test to the next. Figure D.2 shows the residual during one time step of a Marshak wave test. We can see that the Gauss-Seidel method in this particular test is far much efficient than the GMRES method. We have performed another Marshak wave test with higher opacities in order to be in a more diffusive regime. In that case, the results are inverted, with the GMRES method better than Gauss-Seidel. We recover the characteristics discussed in Sect. 3.2: Gauss-Seidel is more efficient in the transport limit and GMRES in the diffusion limit. However, we empirically discovered that coupling the two methods gives the best results. We first performed a few iterations with one method and then gave this result as initial guess to the other one. At the switch the residual drops by about one order of magnitude, due to the fact that for each method the first iterations are more efficient than what follows. Pushing this idea further, we tried the "yoyo'' method, which consists in switching back and forth between the two methods every 10 iterations. In all the tests we have done, this method was the most efficient (if the memory needed by GMRES can be afforded), even though the optimal number of iterations between each switch can vary somewhat.
In all our simulations, the CPU time needed for the radiative transfer was between 3 and 10 times the time taken by the hydrodynamics depending on the variation in the radiative quantities during one hydrodynamical time step and on the convergence criteria used. The memory needed by the radiative transfer is equal to the memory needed by the hydrodynamics if one uses the GS solver but it is higher when using the GMRES algorithm (depending on the size of the Krylov space used to find the solution).
![\begin{figure}
\par\includegraphics[width=6cm,clip]{5486fD1.ps}\end{figure}](/articles/aa/full/2007/11/aa5486-06/Timg138.gif) |
Figure D.1: Normalized CPU time as a function of the number of processors for simulations with a constant cell number per processor. |
In the shadow test, the numerical diffusion is limited because radiation propagates along mesh axis. In order to quantify this efect, we performed a test where a narrow beam of radiation propagates with a certain angle (cf. Richling et al. 2001).
For this test, we computed a
![]() mesh that covers the domain
x=[-1,1] and y=[-1,1]. The beam is introduced at x=-1 between
y=[-0.875, -0.750] with an angle of
mesh that covers the domain
x=[-1,1] and y=[-1,1]. The beam is introduced at x=-1 between
y=[-0.875, -0.750] with an angle of ![]() and with a unit
reduced flux. Initially, the temperature is at
and with a unit
reduced flux. Initially, the temperature is at
![]() and the beam is at
and the beam is at
![]() .
There is no scattering,
absorption, or emission:
.
There is no scattering,
absorption, or emission: ![]() .
The beam should therefore cross
the medium without dispersion.
.
The beam should therefore cross
the medium without dispersion.
If we plot a profile of the radiative energy, the beam is initially a step sampled over 8 cells. In the stationary state, we can see (cf. Fig. E.2) that, for fixed eigenvalues, the FWHM approximately corresponds to 30 cells. When the eigenvalues are computed, this FWHM falls to only 24 cells. The numerical diffusion has been therefore reduced by 20%. This test shows that the eigenvalue computation keeps the numerical diffusion under control even in a direction not along mesh axis.
| |
Figure E.1:
Radiative energy for the beam test: eigenvalues set to |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{5486fE2.ps}\end{figure}](/articles/aa/full/2007/11/aa5486-06/Timg146.gif) |
Figure E.2: Horizontal cut in Fig. E.1 at the middle height. Solid line corresponds to calculated eigenvalues and dashed line to fixed ones. |
This test, known as the pipe flow test (Gentile 2001), is not an astrophysical one, but it treats all the physics underlying the radiative transfer. It is very demanding because it involves at the same time regions of free-streaming, of diffusion, shadows, and the results depend strongly on the description of the heating and reemission of the walls.
In this problem, a cylindrical section of dense and opaque material is embedded in less dense and less opaque material (the pipe), which is itself embedded in a cylinder of the dense and opaque material. The geometry is sketched in Fig. E.3.
Both materials have a heat capacity
![]() ,
but the densities and opacities differ:
,
but the densities and opacities differ:
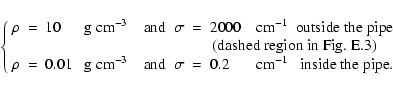
Initially, the medium is at equilibrium
![]() everywhere. At time t=0, a uniform source with
everywhere. At time t=0, a uniform source with
![]() is lighted on at the left side of the pipe.
is lighted on at the left side of the pipe.
In Fig. E.4, the problem is analyzed with the matter temperature at the five characteristic points A, B, C, D, and E. Points A and B are located in the pipe before the obstacle. Their temperature therefore depends on the code's ability to recover the free-streaming limit. These two plots show good agreement with the results published in Gentile (2001). The next three points depend closely on the physical equations solved. Indeed, in a diffusion model, photons would go round the obstacle very easily since the photon distribution function is isotropic, whereas in fact the photons have to be absorbed by the obstacle, which is heated, and then reemitted from the heated walls. This allows photons initially moving horizontally to go upward and then to go round the obstacle. For these three last points, our results are qualitatively good, although quantitatively some discrepancies exist: point E is heated faster, point C is heated a little bit later, etc. Only few people perform this test, so there are not many results to compare with. Nevertheless, we see that our model, although simple, compares well to exact codes with Monte-Carlo techniques.
This simple radiation hydrodynamics test compares diffusion in a
moving fluid and in a fluid at rest. We use a Cartesian grid of
![]() cells. At t=0, we initialize a Gaussian pulse of energy at
the center of the simulation box. First, we perform a test without
radiation. The energy radiation is advected as a passive scalar in the
fluid moving along the diagonal. Secondly, we look at a static
diffusion: we turn on both hydrodynamics and radiation, but the fluid
is at rest
cells. At t=0, we initialize a Gaussian pulse of energy at
the center of the simulation box. First, we perform a test without
radiation. The energy radiation is advected as a passive scalar in the
fluid moving along the diagonal. Secondly, we look at a static
diffusion: we turn on both hydrodynamics and radiation, but the fluid
is at rest
![]() .
Finally, we conjugate the two precedent tests
to look at dynamical diffusion: a Gaussian pulse is initialized in a
moving fluid. This test will characterize the relative importance of
advection and diffusion terms and will verify their coupling.
.
Finally, we conjugate the two precedent tests
to look at dynamical diffusion: a Gaussian pulse is initialized in a
moving fluid. This test will characterize the relative importance of
advection and diffusion terms and will verify their coupling.
| |
Figure E.5: Radiative energy for diffusion test: pure advection, static diffusion, diffusion in a moving fluid. |
Figure E.5 shows the radiative energy in these three cases
whereas Figs. E.6 and E.7 show slices
with the pulse always recentered by a factor
![]() .
In the first case, the Gaussian pulse should be advected without being
affected at all. We first verify that the advection speed is correct
because the two peaks are centered at the same position. Then we can
see that the pulse is slightly diffused (the maximum has decreased by 8% after crossing over 12 cells). This diffusion could easily be
lowered by using a more aggressive slope limiter. When we turn on
hydrodynamics, all the pulses are again properly centered, which means
that advection is still done at the right speed. Moreover, the
diffusion of the radiative pulse in the moving and in the static
fluids is very similar (the maximum discrepancy is less than 2%).
Therefore, our treatment of the comoving terms preserves the good
accuracy of the advection scheme and there is no problem in coupling
advection with diffusion terms.
.
In the first case, the Gaussian pulse should be advected without being
affected at all. We first verify that the advection speed is correct
because the two peaks are centered at the same position. Then we can
see that the pulse is slightly diffused (the maximum has decreased by 8% after crossing over 12 cells). This diffusion could easily be
lowered by using a more aggressive slope limiter. When we turn on
hydrodynamics, all the pulses are again properly centered, which means
that advection is still done at the right speed. Moreover, the
diffusion of the radiative pulse in the moving and in the static
fluids is very similar (the maximum discrepancy is less than 2%).
Therefore, our treatment of the comoving terms preserves the good
accuracy of the advection scheme and there is no problem in coupling
advection with diffusion terms.
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{5486fE6.eps}\end{figure}](/articles/aa/full/2007/11/aa5486-06/Timg158.gif) |
Figure E.6:
Radiative energy for pure advection: initial pulse (dashed line)
and pulse after crossing one eighth of the box (solid line). The pulse
is recentered by a factor
|
We now present a test of the matter-radiation coupling. If the
radiation energy density is much higher than the gas one, the
matter-radiation coupling can be solved analytically by assuming a
constant radiative energy (Turner & Stone 2001). The matter energy
then obeys the following equation where ![]() is constant:
is constant:
| (E.1) |
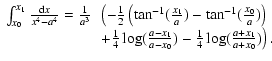 |
(E.2) |
We did two tests with a radiative energy
![]() erg cm-3(i.e.
erg cm-3(i.e.
![]() ), an opacity
), an opacity
![]() cm-1, and a heat capacity
cm-1, and a heat capacity
![]() .
In the first one, the initial gas energy was 102 erg cm-3 (i.e.
.
In the first one, the initial gas energy was 102 erg cm-3 (i.e.
![]() ), and in the
second one 1010 erg cm-3 (i.e.
), and in the
second one 1010 erg cm-3 (i.e.
![]() ). The corresponding results are plotted in
Fig. E.8. We can see that if the variation of the energy is
well-sampled (i.e. the time step is less than
). The corresponding results are plotted in
Fig. E.8. We can see that if the variation of the energy is
well-sampled (i.e. the time step is less than ![]() ), then the
analytical solution is properly reproduced. If the time step is large
compared to the coupling time, the shape of the energy variation moves
away from the analytical solution (as could be expected) but the
proper value for the equilibrium is nevertheless found.
), then the
analytical solution is properly reproduced. If the time step is large
compared to the coupling time, the shape of the energy variation moves
away from the analytical solution (as could be expected) but the
proper value for the equilibrium is nevertheless found.
A Marshak wave is the propagation of a radiation heating front in a
cold slab (Marshak 1958). An analytical solution of the Marshak wave
problem was proposed by Su & Olson (1996) in the context of the diffusion
equation and assuming that the gas heat capacity is proportional to T3 (i.e.
![]() ). We compared the solution obtained
by HERACLES to their solution for the case
). We compared the solution obtained
by HERACLES to their solution for the case
![]() .
.
Figure E.9 represents the radiative and gas energies
(normalized by their boundary values) obtained by HERACLES and by
Su & Olson (1996) at times given by
![]() (cf. their Fig. 3). At early times and at the foot of the
Marshak wave, we can see large differences between the two methods.
This was to be expected since in this region the radiation is instead
in the transport regime and the diffusion approximation is then
different from our M1 model. At later times and inside the wave,
the reduce flux is much smaller (i.e. the radiation is almost in the
diffusion regime) and, accordingly, the results given by M1 are in
good agreement with the analytical solution.
(cf. their Fig. 3). At early times and at the foot of the
Marshak wave, we can see large differences between the two methods.
This was to be expected since in this region the radiation is instead
in the transport regime and the diffusion approximation is then
different from our M1 model. At later times and inside the wave,
the reduce flux is much smaller (i.e. the radiation is almost in the
diffusion regime) and, accordingly, the results given by M1 are in
good agreement with the analytical solution.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{5486fE9.ps}\end{figure}](/articles/aa/full/2007/11/aa5486-06/Timg174.gif) |
Figure E.9: Marshak wave test: comparison of Heracles results (radiative energy with a solid line and gas energy with a dashed line) with the Su & Olson (1996) solution (radiative energy with stars and gas energy with crosses) at three different times. |