A&A 462, 43-55 (2007)
DOI: 10.1051/0004-6361:20066121
J. Machalski1 - K. T. Chyzy1 - ![]() .
Stawarz1,2 - D. Kozie
.
Stawarz1,2 - D. Kozie![]() 1
1
1 - Astronomical Observatory, Jagellonian University, ul. Orla 171, 30244 Cracow, Poland
2 - Landessternwarte Heidelberg, Königstuhl, and MPI für Kernphysik, Saupfercheckweg 1, 69117 Heidelberg, Germany
Received 27 July 2006 / Accepted 21 September 2006
Abstract
Context. Determining the ages of powerful radio sources is crucial for understanding galaxy evolution, the activity cycle of galactic nuclei, and their influence on the surrounding intergalactic medium. So far, several different methods for estimating the age of classical double radio galaxies have been proposed and widely used in the literature, although each of them faces difficulty due to observational limitations and/or freedom in choosing the underlying model assumptions.
Aims. We propose a new approach to determining the ages of FR II type radio sources that, on one hand exploits a dynamical model developed for these objects by Kaiser et al. (1997, MNRAS, 292, 723) and, on the other hand, uses multifrequency radio observations not necessarily restricted to the high-resolution ones.
Methods. In particular, we applied the assumed dynamical model to a number of FR II type radio galaxies observed at different radio frequencies and fit - for each frequency separately - the model's free parameters to the quantities of the observed sources. Such a procedure, which in fact enlarged a number of observables, enabled us to determine relatively precise ages and other crucial characteristics (like the jets' kinetic power) for the analyzed sources.
Results. The resulting age estimates agree very well with those obtained with the "classical'' spectral aging method for objects not older than 10 Myr, for which good-quality spectral data are available. However, this method is also applicable in the case of older sources than this and/or those for which the only available low-resolution radio data do not allow for detailed spectral aging studies. Interestingly, the estimated ages always correspond to the realistic values of the jets' advance velocity of ![]() 0.01-0.1 c.
0.01-0.1 c.
Conclusions. Our analysis indicates that the main factor precluding precise age determination for FR II type radio galaxies is related to the poorly known shape of the initial electron energy distribution injected by the jet's terminal shocks to the expanding lobes/cocoons. We briefly considered this issue and conclude that the broad-band single power-law form assumed here may be accurate enough for the age estimates, although most likely it does not strictly correspond to some well-defined realistic particle acceleration process. Instead, it should be considered as the simplest model approximation of the initial electron continuum, averaged over a very broad energy range and over the age of the source, with the effective spectral index that may be different for different sources, but within the relatively narrow range of p = 2.0-2.4 suggested by our modeling.
Key words: galaxies: active - galaxies: evolution - radio continuum: galaxies
The dynamical age of extragalactic radio sources is very important for first studying and then understanding details of the physical processes taking place in both active galactic nuclei (AGNs) which emit energy in the form of jets boring through the ambient intergalactic medium (IGM) and lobes or a cocoon consisting of shocked (backflowing) jet material and shocked IGM. The "standard model'' for classical double radio sources (Blandford & Rees 1974; Scheuer 1974) implies that the axial lengthening of the cocoon is governed by the balance between the jet's thrust and the ram pressure of the IGM, while the width of the cocoon is determined by its internal pressure. This scenario has formed the basis for all the later analytical models of the dynamics and radio-emission properties of powerful double radio sources (e.g., Begelman & Cioffi 1989; Falle 1991; Nath 1995; Kaiser et al. 1997; Chyzy 1997; Blundell et al. 1999; Manolakou & Kirk 2002; Kino & Kawakatu 2005).
All these dynamical models allow one to predict a number of observational parameters of the sources (e.g., linear size, width of the cocoon, radio power at different wavelengths) for their given ages and redshifts by assuming values of the models' basic free parameters (e.g., jet power, the external medium density and its gradient, etc.). A comparison of the predictions of the three main scenarios, i.e. those by Kaiser et al. (1997), Blundell et al. (1999), and Manolakou & Kirk (2002), was recently undertaken by Barai & Wiita (2006). They argued that no existing model could acceptably fit to the common properties of radio sources from the survey under consideration (3 CRR, 6CE, 7CRS), although the Manolakou & Kirk model gave "better overall results than do either of the other two''.
The age of a classical double radio source can be determined, in principle, from its apparent radio spectrum. There is no doubt that a radio continuum spectrum in different parts of a radio source should contain crucial information about its history, depending on the various energy losses (and gains) of the radiating particles. This simple idea, which relies on the determination of a single characteristic break frequency in the radio spectrum (at a given part of the source) caused by the above time-dependent losses, was used to estimate the radiative ages and expansion speeds in large samples of powerful 3CR sources (Myers & Spangler 1985; Alexander & Leahy 1987; Leahy et al. 1989; Carilli et al. 1991; Liu et al. 1992), as well as in samples of low-luminosity and intermediate-luminosity radio galaxies (Klein et al. 1995; Parma et al. 1999). However, the spectral break and steepening of the spectrum beyond this break need not be entirely due to radiative aging. A possible role of the local magnetic field structure and evolution, details of the backflow process of the cocoon material, or the difficulties in disentangling various energy losses of the radiating particles have been raised in a number of papers (e.g. Rudnick et al. 1994; Eilek & Arendt 1996; Jones et al. 1999).
The task of resolving some of the above difficulties was undertaken by Kaiser (2000, hereafter referred to as K2000), who constructed a 3-dimensional model of the synchrotron emissivity for a cocoon of an FR II-type radio source and applied it to the self-similar model of the cocoon's dynamics developed by Kaiser & Alexander (1997, hereafter referred to as KA) and its extension by Kaiser et al. (1997, hereafter KDA). In the K2000 model, the cocoon is split into small-volume elements whose surface-brightness evolution is traced individually. The author argues that the proposed careful analysis of the bulk backflow process and of the electron energy losses (both radiative and adiabatic) can accurately estimate the sources' spectral ages, in addition to agreement with the estimates of their dynamical ages. Blundell & Rawlings (2000) contend however, that this could only be the case if they were much younger than 10 Myr.
Analyzing the K2000 model, we realized that in the majority of the extended FR II-type radio sources - even those without distorted lobe structures - the surface-brightness profiles are far from the expected smooth shapes, making the fitted free parameters highly uncertain. In addition, the K2000 method requires rather high-resolution observations of the radio lobes. But usually high-resolution observations of low-brightness sources cause a serious loss of the flux density, so that the K2000 method can in fact only be applied to a few of the strongest sources such as Cyg A.
The KDA model has been successively used by Machalski et al. (2004a,b) to derive the basic physical parameters of the FR II-type radio sources with known ages, namely the jet power, the central density of the ambient medium, the cocoon's energy density and pressure, and the total energy deposited in the radio source. All of these values were derived by means of fitting the model free parameters to the observed parameters of the source: its redshift, monochromatic radio luminosity at 1.4 GHz, projected linear size, and the cocoon's axial ratio. In this paper we propose a simplified method of determining the age of powerful radio sources that is based on a further exploitation of the KDA model, which avoids the limitations present in the K2000 method. In particular, we show that performing this fitting procedure for a few observing frequencies, i.e. enlarging the number of the observables used by adding the radio spectrum data of the entire cocoon, a unique set of the age and values for the two fundamental model parameters - the jet power and the central density of the ambient medium - can be found. This, in turn, enables us to determine the age of the analyzed source relatively precisely, even if the available (low-resolution) radio data do not allow for detailed spectral aging studies.
The paper is organized as follows. First, a brief presentation of the analytical KDA model, together with its application to the dynamical aging studies, are given in Sect. 2. In Sect. 3 we present the dataset used in the subsequent analysis. Examples of the dynamical age determination for the radio galaxy Cygnus A and its dependence on the assumed model parameters are given in Sect. 4. A summary of how the method is applied to a variety of other FR II type radio sources is presented in Sect. 5. Remarks on the implications of the results for modeling the electron injection-spectrum in lobes of powerful radio sources are given in Sect. 6. Final conclusions are presented in Sect. 7.
In this section the model application is described more in details.
The dynamical expansion of an FR II-type radio source built in the KDA model comes
from the dynamics described in the self-similar KA model. Based on the original idea
of Blandford & Rees (1974) and Scheuer (1974), it assumes that the classical double
radio structure is formed by twin jets emerging from the AGN in opposite directions
into a surrounding tenuous environment. The jets terminate in strong shocks
where the jet particles are shocked, accelerated, and finally inflate the cocoon.
A density distribution of the unperturbed external gas is approximated by a power-law
radial distribution scaling with distance r>a0 from the center of the host galaxy as
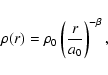
Half of the cocoon (from the core to the hotspot) is approximated by a cylinder of
length
![]() and base diameter b. Here
and base diameter b. Here ![]() is the
total deprojected length (linear size) of the source. The ratio of the source's length
to the base diameter is called the "axial ratio'' (AR); in the original KDA paper, half of the
cocoon has an axial ratio of
is the
total deprojected length (linear size) of the source. The ratio of the source's length
to the base diameter is called the "axial ratio'' (AR); in the original KDA paper, half of the
cocoon has an axial ratio of
![]() .
The cocoon expands along the jet axis driven
by the hotspot plasma pressure
.
The cocoon expands along the jet axis driven
by the hotspot plasma pressure ![]() and in the perpendicular direction by the cocoon
pressure
and in the perpendicular direction by the cocoon
pressure ![]() .
The rate at which energy is transported from the AGN along each jet,
i.e. the jet power
.
The rate at which energy is transported from the AGN along each jet,
i.e. the jet power
![]() ,
is assumed to be constant during the source's lifetime.
The model predicts self-similar expansion of the cocoon and gives analytical formula for
the time evolution of various geometrical and physical parameters, e.g. the length of the
jet (Eqs. (4) and (5) in KA)
,
is assumed to be constant during the source's lifetime.
The model predicts self-similar expansion of the cocoon and gives analytical formula for
the time evolution of various geometrical and physical parameters, e.g. the length of the
jet (Eqs. (4) and (5) in KA)
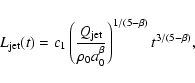 |
(1) |
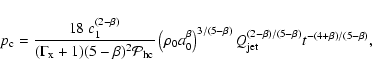 |
(2) |
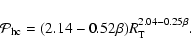
The energy delivered by the twin jets during the source lifetime is equal simply to
![]() .
Accounting for the energy losses of relativistic particles due to
adiabatic expansion within the time-dependent volume of the cocoon
.
Accounting for the energy losses of relativistic particles due to
adiabatic expansion within the time-dependent volume of the cocoon
![]() ,
the ratio of the jets' energy and the energy stored in the cocoon
,
the ratio of the jets' energy and the energy stored in the cocoon
![]() is
is
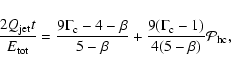
Following KDA, we assume that the cocoon is composed of many small-volume elements
filled with magnetized plasma and cosmic rays that are injected into the cocoon
at the jet head - the jet terminal shock. The initial energy distribution
![]() of injected particles with the Lorentz factor
of injected particles with the Lorentz factor
![]() is assumed to have a single
power-law form with the spectral index p:
is assumed to have a single
power-law form with the spectral index p:
![]() .
The unknown
normalization parameter n0 is given by integrating the initial power-law distribution
over the entire (assumed) energy range [
.
The unknown
normalization parameter n0 is given by integrating the initial power-law distribution
over the entire (assumed) energy range [
![]() ].
].
The relativistic particles injected into the cocoon lose their energies in a magnetic
field of energy density ![]() ,
and thus the cocoon's radio spectrum evolves with
time. Tracing the effects of adiabatic expansion, synchrotron losses (with the assumed
effective isotropization of the particles' pitch angle distribution), and inverse Compton
scattering on the cosmic background radiation in the volume
elements independently, the radio power of the cocoon
,
and thus the cocoon's radio spectrum evolves with
time. Tracing the effects of adiabatic expansion, synchrotron losses (with the assumed
effective isotropization of the particles' pitch angle distribution), and inverse Compton
scattering on the cosmic background radiation in the volume
elements independently, the radio power of the cocoon ![]() at a fixed observing
frequency
at a fixed observing
frequency ![]() is obtained by summing up the contributions from all volume elements,
resulting in an integral over time (see Eq. (16) in KDA). It depends on the source's age t,
redshift z, the jet power
is obtained by summing up the contributions from all volume elements,
resulting in an integral over time (see Eq. (16) in KDA). It depends on the source's age t,
redshift z, the jet power
![]() ,
the half-cocoon axial ratio
,
the half-cocoon axial ratio ![]() ,
the exponent in the initial power-law distribution of relativistic particles p, the
values of the low-energy and high-energy cut-offs
,
the exponent in the initial power-law distribution of relativistic particles p, the
values of the low-energy and high-energy cut-offs
![]() and
and
![]() ,
and on the ratio
,
and on the ratio ![]() of the magnetic field energy
of the magnetic field energy ![]() to the energy of relativistic
electrons
to the energy of relativistic
electrons ![]() .
The integral is not analytically solvable and has to be calculated
numerically.
.
The integral is not analytically solvable and has to be calculated
numerically.
On the basis of the above analytical model, we aim to predict the dynamical age and
the two physical parameters of the analyzed FR II-type radio sources:
![]() and
and ![]() .
In order to derive these parameters, all the other free parameters
of the model (
.
In order to derive these parameters, all the other free parameters
of the model (
![]() ,
,
![]() ,
a0,
,
a0,
![]() ,
,
![]() ,
p,
,
p,
![]() ,
,
![]() )
have to be fixed
(see Table 1).
)
have to be fixed
(see Table 1).
Table 1: Observational and model parameters (see Sects. 2.1-2.3 for detailed descriptions).
Following the KDA analysis, we adopt their Case 3 where both the cocoon and the ambient medium are
assumed to be described best by the "cold'' equation of state (
![]() ).
For the initial ratio of the energy densities of the cocoon's magnetic field and particles, we use
the equipartition condition
).
For the initial ratio of the energy densities of the cocoon's magnetic field and particles, we use
the equipartition condition
![]() ,
which is well supported by the
X-ray observations of the lobes in powerful radio sources (see Kataoka & Stawarz
2005; Croston et al. 2005, and references therein).
,
which is well supported by the
X-ray observations of the lobes in powerful radio sources (see Kataoka & Stawarz
2005; Croston et al. 2005, and references therein).
Selection of the particular (universal) values regarding external medium parameters a0
and ![]() requires some justification. We note that even careful 2-D modeling of a
distribution of radio emission for powerful sources with quite regular structure can lead
to values of a0 that are discrepant with those implied by the X-ray observations of the
intergalactic thermal environment. In our simplified approach, we assume a0=10 kpc for all the
analyzed sources, a conservative value between 2 kpc used by KDA, and the 50 kpc found by Wellman et al.
(1997). We also use a constant value of
requires some justification. We note that even careful 2-D modeling of a
distribution of radio emission for powerful sources with quite regular structure can lead
to values of a0 that are discrepant with those implied by the X-ray observations of the
intergalactic thermal environment. In our simplified approach, we assume a0=10 kpc for all the
analyzed sources, a conservative value between 2 kpc used by KDA, and the 50 kpc found by Wellman et al.
(1997). We also use a constant value of
![]() ,
in agreement with Daly
(1995), Blundell et al. (1999),
Willott et al. (1999), and K2000. Note that the assumed ambient medium profile is then slightly
flatter than the one adopted in the original KDA paper on the basis of the Canizares et al.
(1987) analysis, which found
,
in agreement with Daly
(1995), Blundell et al. (1999),
Willott et al. (1999), and K2000. Note that the assumed ambient medium profile is then slightly
flatter than the one adopted in the original KDA paper on the basis of the Canizares et al.
(1987) analysis, which found ![]() to be typical at about 100 kpc from the galactic nucleus (but see
Gopal-Krishna & Wiita 1987).
to be typical at about 100 kpc from the galactic nucleus (but see
Gopal-Krishna & Wiita 1987).
Another free parameter of the model is the orientation of the jet axis to the observer's
line of sight ![]() .
We assume
.
We assume
![]() for the giant-size radio galaxies
and
for the giant-size radio galaxies
and
![]() for `normal'-size radio galaxies. This latter value is justified
on the basis of the unified scheme for extragalactic radio sources. In this scheme,
the average orientation angle for radio galaxies is
for `normal'-size radio galaxies. This latter value is justified
on the basis of the unified scheme for extragalactic radio sources. In this scheme,
the average orientation angle for radio galaxies is
![]() (Barthel 1989). The apparent size D of a radio source then yields the
model cocoon length
(Barthel 1989). The apparent size D of a radio source then yields the
model cocoon length
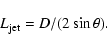 |
(3) |
The cut-off energies in the electron energy distribution injected by the jet terminal
shock to the expanding cocoon are poorly constrained by both observations and theory.
The values considered in the literature for
![]() vary from 104 up to
vary from 104 up to
![]()
![]() (see Barai & Wiita 2006). Here we initially studied a very broad
range
(see Barai & Wiita 2006). Here we initially studied a very broad
range
![]() -1010 (Sect. 4), in order to check how the results of
the proposed method depend on the choice of this particular model parameter. We found
that the effect is minor and note in this context that the high values of the
maximum Lorentz factors for electrons accelerated at the jet terminal shocks are more
likely, since a number of hotspots in powerful radio sources are established sources
of synchrotron X-ray emission, meaning that production of high-energy
(
-1010 (Sect. 4), in order to check how the results of
the proposed method depend on the choice of this particular model parameter. We found
that the effect is minor and note in this context that the high values of the
maximum Lorentz factors for electrons accelerated at the jet terminal shocks are more
likely, since a number of hotspots in powerful radio sources are established sources
of synchrotron X-ray emission, meaning that production of high-energy
(
![]() )
electrons thus seems to be a general property of radio
galaxies and quasars (see discussion in Hardcastle et al. 2004; Kataoka & Stawarz
2005, and references therein). For these reasons, later on in the analysis (Sect. 5) we
consider a slightly narrower range of
)
electrons thus seems to be a general property of radio
galaxies and quasars (see discussion in Hardcastle et al. 2004; Kataoka & Stawarz
2005, and references therein). For these reasons, later on in the analysis (Sect. 5) we
consider a slightly narrower range of
![]() -108.5.
-108.5.
As for the minimum electron energy, we note that most authors assume
![]() ,
although such a choice is made largely for the sake of simplicity.
Interestingly, Blundell et al. (2006) recently argued that the X-ray observations
of giant radio galaxy 4C 39.24 indicate an initial electron low-energy cut-off as
high as
,
although such a choice is made largely for the sake of simplicity.
Interestingly, Blundell et al. (2006) recently argued that the X-ray observations
of giant radio galaxy 4C 39.24 indicate an initial electron low-energy cut-off as
high as
![]() ;
see also in this context Carilli et al.
(1991) for the low-frequency radio observations of Cyg A hotspots.
We believe, however, that these data do not unambiguously show any sharp low-energy
cut-off of the electron energy distribution at some particular (ultrarelativistic) energy,
but instead indicate only spectral flattening at low (
;
see also in this context Carilli et al.
(1991) for the low-frequency radio observations of Cyg A hotspots.
We believe, however, that these data do not unambiguously show any sharp low-energy
cut-off of the electron energy distribution at some particular (ultrarelativistic) energy,
but instead indicate only spectral flattening at low (
![]() )
electron energies. Thus, hereafter we take
)
electron energies. Thus, hereafter we take
![]() ,
assuming that the particles
at the jet terminal shock are picked up by the acceleration process(es) directly from the
"thermal pool'' of the cold plasma carrying the bulk of the jet kinetic energy to form the
non-thermal electron energy distribution injected further into the expanding cocoon.
We checked, however, that taking
,
assuming that the particles
at the jet terminal shock are picked up by the acceleration process(es) directly from the
"thermal pool'' of the cold plasma carrying the bulk of the jet kinetic energy to form the
non-thermal electron energy distribution injected further into the expanding cocoon.
We checked, however, that taking
![]() (as favored by the analysis of
Barai & Wiita 2006) does not change our results obtained with
(as favored by the analysis of
Barai & Wiita 2006) does not change our results obtained with
![]() as presented in the next sections.
as presented in the next sections.
These choices regarding low- and high-energy electron cut-offs seem to be justified,
although they may lead to inconsistency with the main assumption of the model, namely
with the assumed single power-law form of the initial electron energy distribution.
If the low-energy spectral flattening of the electron spectrum is the case (as has to be
accepted if indeed
![]() ), it suggests that the particle distribution
injected by the jet terminal shocks to the lobes/cocoons is characterized by some more
complex spectral shape, for which a broken power-law could be for example a simple
approximation. Meanwhile, in the original KDA model, universal single power-law initial
energy distribution of the relativistic particles with the energy index p=2.14 was assumed,
corresponding to the radio spectral index
), it suggests that the particle distribution
injected by the jet terminal shocks to the lobes/cocoons is characterized by some more
complex spectral shape, for which a broken power-law could be for example a simple
approximation. Meanwhile, in the original KDA model, universal single power-law initial
energy distribution of the relativistic particles with the energy index p=2.14 was assumed,
corresponding to the radio spectral index
![]() .
This value agrees
perfectly with the one obtained for the classical FR II-type radio source Cyg A by means
of fitting its radio spectrum by the "continuum injection'' (C.I.) model (for the spectral
aging theory review see Myers & Spangler 1985; Carilli et al. 1991). It should be
noticed that p=2.14 is close to, although not exactly equal to, the model spectral
index of relativistic particles accelerated at non-relativistic shocks by the 1st-order
Fermi (diffusive) acceleration process.
.
This value agrees
perfectly with the one obtained for the classical FR II-type radio source Cyg A by means
of fitting its radio spectrum by the "continuum injection'' (C.I.) model (for the spectral
aging theory review see Myers & Spangler 1985; Carilli et al. 1991). It should be
noticed that p=2.14 is close to, although not exactly equal to, the model spectral
index of relativistic particles accelerated at non-relativistic shocks by the 1st-order
Fermi (diffusive) acceleration process.
Most importantly, the low-frequency radio observations of a number of powerful radio
sources imply a wide spread of the injection spectral index,
![]() .
This indicates that there may be no universal value to this parameter
for all cocoons. Moreover, we note that the low-frequency radio spectra usually
steepen with redshift (see Laing & Peacock 1980; Macklin
1982; Gopal-Krishna 1988;
van Breugel & McCarthy 1990). The physical reason for such a dependence is unclear,
although the effect seems to be real. Therefore, keeping in mind all the uncertainties
regarding
.
This indicates that there may be no universal value to this parameter
for all cocoons. Moreover, we note that the low-frequency radio spectra usually
steepen with redshift (see Laing & Peacock 1980; Macklin
1982; Gopal-Krishna 1988;
van Breugel & McCarthy 1990). The physical reason for such a dependence is unclear,
although the effect seems to be real. Therefore, keeping in mind all the uncertainties
regarding
![]() (or equivalently p), which reflect our poor understanding
of the particle acceleration processes taking place at mildly relativistic collisionless
astrophysical shocks, and also the observational limitations, we decided to treat the injection
spectral index as a free parameter, which may be different for different sources.
(or equivalently p), which reflect our poor understanding
of the particle acceleration processes taking place at mildly relativistic collisionless
astrophysical shocks, and also the observational limitations, we decided to treat the injection
spectral index as a free parameter, which may be different for different sources.
We also emphasize that the particular value of power-law index pobtained for a given source with the fitting procedure does not necessarily correspond to some well-defined acceleration process taking place at the jet terminal shock. Instead, it should be considered as an effective spectral index of the injected electron continuum (characterized most likely by more complex spectral shape), averaged over a very broad energy range and over the lifetime of the source. This issue will be discussed further in Sect. 6.
In Table 1 we summarize all the observational and model parameters characterizing the source's cocoon that are used in the present calculations.
Assuming a value for the source age t and having fixed all the free parameters of the model
as discussed in Sect. 2.3, we find the jet power
![]() and the central density of
the external medium
and the central density of
the external medium ![]() for an investigated source by an iterative solution of the
system of two equations: (i) Eq. (1) equated to Eq. (3) for the jet length
for an investigated source by an iterative solution of the
system of two equations: (i) Eq. (1) equated to Eq. (3) for the jet length
![]() and
(ii) the integral for the luminosity of the cocoon
and
(ii) the integral for the luminosity of the cocoon ![]() (Eq. (16) in KDA, see Sect. 2.2).
These equations require matches of the solution to the observed values of D to (i) and
(Eq. (16) in KDA, see Sect. 2.2).
These equations require matches of the solution to the observed values of D to (i) and ![]() to (ii) at a number of different frequencies, respectively. This fitting procedure proved to be
stable and always provides a unique solution.
to (ii) at a number of different frequencies, respectively. This fitting procedure proved to be
stable and always provides a unique solution.
Performing the above calculations![]() for a number of age values t assumed for a
given source, we obtain a set of solutions for
for a number of age values t assumed for a
given source, we obtain a set of solutions for
![]() and
and
![]() ,
which show a correlation of
,
which show a correlation of
![]() and anticorrelation of
and anticorrelation of ![]() ,
as expected,
with the source age t for a given apparent size D and total cocoon
luminosity
,
as expected,
with the source age t for a given apparent size D and total cocoon
luminosity ![]() .
An example of this effect for the four observing frequencies
is shown in Fig. 1. A perfect
intersection of all the
.
An example of this effect for the four observing frequencies
is shown in Fig. 1. A perfect
intersection of all the
![]() curves corresponding to different
observing frequencies at some particular "true'' age of a source is expected if
the observed shape of its total radio spectrum (used here to determine the radio
power at different frequencies) agrees with the theoretically predicted
one in the framework of the C.I. model and if the dynamical (KDA) model
applied here is indeed correct. However, the observed spectrum of a number of the
analyzed sources evidently departs from the predicted behavior. In such cases, the
sources' high-frequency spectra are steeper than expected, so that
the resultant
curves corresponding to different
observing frequencies at some particular "true'' age of a source is expected if
the observed shape of its total radio spectrum (used here to determine the radio
power at different frequencies) agrees with the theoretically predicted
one in the framework of the C.I. model and if the dynamical (KDA) model
applied here is indeed correct. However, the observed spectrum of a number of the
analyzed sources evidently departs from the predicted behavior. In such cases, the
sources' high-frequency spectra are steeper than expected, so that
the resultant
![]() curve corresponding to the highest observing
frequency bisects other curves at the age inconsistent with what is implied by the
remaining ones.
curve corresponding to the highest observing
frequency bisects other curves at the age inconsistent with what is implied by the
remaining ones.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{6121fig1.ps}\end{figure}](/articles/aa/full/2007/04/aa6121-06/Timg71.gif) |
Figure 1:
A set of
|
| Open with DEXTER | |
A "goodness'' of the intersection is quantified by the ![]() measure, which is
defined as follows:
indicating
measure, which is
defined as follows:
indicating
![]() and
and
![]() ,
we calculate
the mean separation between the points determined by the values of [
x(t), y(t)] in the
,
we calculate
the mean separation between the points determined by the values of [
x(t), y(t)] in the
![]() -
-
![]() plane as
plane as
![\begin{displaymath}\Delta(t)=\frac{2}{n(n-1)} \sum_{i=1}^{n-1}\left(\sum_{j=i}^{...
...{j+1}(t)]^{2}+
[y_{i}(t)-y_{j+1}(t)]^{2}\right\}^{1/2}\right),
\end{displaymath}](/articles/aa/full/2007/04/aa6121-06/img76.gif) |
(4) |
Table 2: List of sources and their observational parameters derived from radio maps and spectra with the radio power in units of W Hz-1 sr-1.
However, the calculations indicate that the "age solution'' depends significantly on
the exponent in the initial power-law energy distribution, p. In addition, they suggest
that there is no canonical value of this injection spectral index that would be good for
each and every source. (This in fact agrees with the preliminary notes given at the end of
the previous section; this issue will be discussed further in Sect. 6.)
For this reason, the best value of p (or equivalently
![]() ), needed for a
precise estimate of the dynamical age of a particular FR II-type radio source, is determined
below by finding the minimum of the jet kinetic energy delivered to the cocoon (see Sect. 4.3).
The age solution corresponding to the minimum jet energy is hereafter called the best
solution.
), needed for a
precise estimate of the dynamical age of a particular FR II-type radio source, is determined
below by finding the minimum of the jet kinetic energy delivered to the cocoon (see Sect. 4.3).
The age solution corresponding to the minimum jet energy is hereafter called the best
solution.
The data necessary for determining the age of a given radio source with the method
presented above are: its projected linear length D, its axial ratio AR, its total
radio power ![]() at a number of observing frequencies, and the source's redshift z.
at a number of observing frequencies, and the source's redshift z.
As we limit our method to FR II-type sources, D is invariant of frequency and can be precisely determined from the radio maps. The lateral size (base diameter b of the cocoon) is taken as the average of the widths of the two lobes. They are determined on the maps with the highest sensitivity to surface brightness as the deconvolved width of a transversal cross-section through the lobes measured halfway between the core and the outer edge of the source. Thus, AR=D/b.
The source power ![]() is determined at four frequencies:
is determined at four frequencies: ![]() ,
408, 1400, and
4800 MHz. Because not all the sources were observed at these particular frequencies,
the cocoon's spectrum was derived from the available flux densities with the
contributions from the radio core and the hotspots subtracted whenever possible. Next,
the simple analytical functions
,
408, 1400, and
4800 MHz. Because not all the sources were observed at these particular frequencies,
the cocoon's spectrum was derived from the available flux densities with the
contributions from the radio core and the hotspots subtracted whenever possible. Next,
the simple analytical functions
![]() ,
where
,
where ![]() [GHz] and
[GHz] and
![]() [mJy], were fitted to these flux densities weighted by their given
error. These two functions were found to provide the best fit (the least
[mJy], were fitted to these flux densities weighted by their given
error. These two functions were found to provide the best fit (the least ![]() )
to
the data. Then, the values of P151, P408, P1400, and P4800 were
calculated using flux densities found with the above functions and the appropriate radio
K-corrections
)
to
the data. Then, the values of P151, P408, P1400, and P4800 were
calculated using flux densities found with the above functions and the appropriate radio
K-corrections![]() .
.
The FR II-type radio sources analyzed in this paper and their observational parameters as used in the fitting procedure are given in Table 2. These sources, subjectively selected from the sample of Machalski et al. (2004a), include high-redshift and low-redshift, high-luminosity and low-luminosity, giant-sized and normal-sized radio galaxies. The sources in Table 2 do not include quasars whose jets' axes (and hence radio structures) may be strongly projected onto the sky.
In this section the dynamical age estimate and its dependence on the values of the model free parameters are presented for Cyg A.
Assuming
![]() and adopting (after K2000) parameters p=2.14 and
and adopting (after K2000) parameters p=2.14 and
![]() ,
the fitted values of
,
the fitted values of
![]() and
and ![]() for different hypothetical ages of
this source are shown as the
for different hypothetical ages of
this source are shown as the
![]() -
-
![]() diagram in Fig. 2. This figure shows that the four curves corresponding to the four observing frequencies intersect
at the age of about 10 Myr. The age solution giving a minimum of the
diagram in Fig. 2. This figure shows that the four curves corresponding to the four observing frequencies intersect
at the age of about 10 Myr. The age solution giving a minimum of the ![]() measure for the
set of the model free parameters (recalled in the caption of Fig. 2) is
measure for the
set of the model free parameters (recalled in the caption of Fig. 2) is
![]() Myr.
Myr.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6121fig2.ps}\end{figure}](/articles/aa/full/2007/04/aa6121-06/Timg86.gif) |
Figure 2:
|
| Open with DEXTER | |
As mentioned previously, a minimum of ![]() appears to be dependent on the assumed
parameters of the initial energy distribution of relativistic particles. The dependence
of
appears to be dependent on the assumed
parameters of the initial energy distribution of relativistic particles. The dependence
of ![]() on t for two different (rather extreme) values of
on t for two different (rather extreme) values of
![]() and =1010 is plotted in Fig. 3 for different values of
and =1010 is plotted in Fig. 3 for different values of
![]() .
As shown,
the age solution is not very sensitive to the particular choice of
.
As shown,
the age solution is not very sensitive to the particular choice of
![]() ,
especially if
,
especially if
![]() .
.
The dependence of the resulting age solution on
![]() for the same
two extreme values of
for the same
two extreme values of
![]() is shown in Fig. 4. It is
clear that the age solution increases strongly with the decreasing
is shown in Fig. 4. It is
clear that the age solution increases strongly with the decreasing
![]() ,
and hence that the minimum
,
and hence that the minimum ![]() measure is smaller for
higher assumed values of
measure is smaller for
higher assumed values of
![]() .
This is due to the fact that, in the
case of flatter and flatter initial electron energy distributions, more and more
time has to elapse for the radio continuum to steepen up to some given (observed)
level. As a result, the obtained age solution anticorrelates with the injection
spectral index, meaning that the minimum of
.
This is due to the fact that, in the
case of flatter and flatter initial electron energy distributions, more and more
time has to elapse for the radio continuum to steepen up to some given (observed)
level. As a result, the obtained age solution anticorrelates with the injection
spectral index, meaning that the minimum of ![]() also decreases with decreasing t.
Such a decrease continues until reaching the point where the radio continuum does not
have time to steepen at all, corresponding to the situation where all the curves
on the
also decreases with decreasing t.
Such a decrease continues until reaching the point where the radio continuum does not
have time to steepen at all, corresponding to the situation where all the curves
on the
![]() overlap each other. Such an ambiguous situation leads
to the question of which value of
overlap each other. Such an ambiguous situation leads
to the question of which value of
![]() one should really assume for a
given source to apply our method of the dynamical age estimate. This issue
will be addressed further in Sect. 4.3 below.
one should really assume for a
given source to apply our method of the dynamical age estimate. This issue
will be addressed further in Sect. 4.3 below.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{6121fig3.ps}\end{figure}](/articles/aa/full/2007/04/aa6121-06/Timg88.gif) |
Figure 3:
The influence of the initial energy distribution parameters on the "goodness''
of fit quantified by the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{6121fig4.ps}\end{figure}](/articles/aa/full/2007/04/aa6121-06/Timg89.gif) |
Figure 4:
The influence of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6121fig5.ps}\end{figure}](/articles/aa/full/2007/04/aa6121-06/Timg90.gif) |
Figure 5:
The influence of |
| Open with DEXTER | |
The fitting results indicate that the effect due to changing particular values of the
![]() ,
AR, and
,
AR, and ![]() parameters is of minor importance for the resulting age solution.
Figure 5 shows the influence of the exponent
parameters is of minor importance for the resulting age solution.
Figure 5 shows the influence of the exponent ![]() in the density distribution of the
ambient medium and of the source axial ratio
in the density distribution of the
ambient medium and of the source axial ratio
![]() on the age
estimate. (Though the AR parameter is the observed one, it is much less precisely
measured than the source linear size D.). The influence of the unknown inclination angle
on the age
estimate. (Though the AR parameter is the observed one, it is much less precisely
measured than the source linear size D.). The influence of the unknown inclination angle
![]() on the age is also small. Comparison of Eqs. (1) and (3) yields
on the age is also small. Comparison of Eqs. (1) and (3) yields
![]() .
Thus, t increases no more than 1.21 and 1.15
for
.
Thus, t increases no more than 1.21 and 1.15
for ![]() and
and ![]() ,
respectively, if
,
respectively, if ![]() decreases from 90
decreases from 90
![]() to
60
to
60
![]() .
We conclude that the influence of
.
We conclude that the influence of ![]() on t is comparable to that
caused by the uncertainty in the AR determination.
on t is comparable to that
caused by the uncertainty in the AR determination.
As noted in Sect. 4.1, the fitted jet power increases with decreasing age (hence
with increasing
![]() )
for a given
size and brightness of the source (see Figs. 1 and 2). In Fig. 6 we show both
the fitted
jet power and the age of Cyg A as a function of
)
for a given
size and brightness of the source (see Figs. 1 and 2). In Fig. 6 we show both
the fitted
jet power and the age of Cyg A as a function of
![]() for the two extreme
values of
for the two extreme
values of
![]() considered in this section. As the parameters
considered in this section. As the parameters
![]() and t depend on
and t depend on
![]() in the opposite way, there is always a minimum value
of the product
in the opposite way, there is always a minimum value
of the product
![]() .
This product gives the kinetic energy delivered to
the cocoon by the jet. The fitting procedure thus indicates that this total
energy has a minimum for some specific value of
.
This product gives the kinetic energy delivered to
the cocoon by the jet. The fitting procedure thus indicates that this total
energy has a minimum for some specific value of
![]() and fixed observational
parameters.
and fixed observational
parameters.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6121fig6.ps}\end{figure}](/articles/aa/full/2007/04/aa6121-06/Timg97.gif) |
Figure 6:
Diagram of the jet power
|
| Open with DEXTER | |
Based on the above effect, we consider the age corresponding to the minimum kinetic energy
as the "best solution'' for the dynamical age of a given source (see Sect. 2.4).
The "best solution'' for Cyg A gives
![]() Myr (
Myr (
![]() )
and
)
and
![]() Myr (
Myr (
![]() )
for
)
for
![]() and
and
![]() ,
respectively. Since one should expect in reality
,
respectively. Since one should expect in reality
![]() in between of the two extreme values considered here for illustrative purposes,
we safely conclude that this method indicates that the age and the injection spectral
index of Cyg A is t=6-10 Myr and
in between of the two extreme values considered here for illustrative purposes,
we safely conclude that this method indicates that the age and the injection spectral
index of Cyg A is t=6-10 Myr and
![]() -0.62, respectively,
in very good agreement with other dynamical and spectral estimates published in the literature
(see, e.g., Kino & Kawakatu 2005). In addition, the corresponding kinetic power of the Cyg A
jet is
-0.62, respectively,
in very good agreement with other dynamical and spectral estimates published in the literature
(see, e.g., Kino & Kawakatu 2005). In addition, the corresponding kinetic power of the Cyg A
jet is
![]() -
-
![]() W, which is a factor of 2-3 higher than the value
estimated by K2000 and a factor of 2 lower than the one obtained by Kino & Takahara
(2004) by means of detailed analysis of the Cyg A hotspots' radiative properties.
W, which is a factor of 2-3 higher than the value
estimated by K2000 and a factor of 2 lower than the one obtained by Kino & Takahara
(2004) by means of detailed analysis of the Cyg A hotspots' radiative properties.
Further results of the age estimation derived with our method are presented in more detail for two other sources: giant radio galaxy B 1312+698 and normal-sized galaxy 3C 55.
The appropriate
![]() vs.
vs. ![]() diagrams for the given values of
diagrams for the given values of
![]() and
and
![]() are shown in Figs. 7a and 8a, with an age related to the values of
are shown in Figs. 7a and 8a, with an age related to the values of
![]() and
and ![]() fitted
to observations at the four different frequencies. In this case, the ideal intersections of
the four curves give the precise "age solutions'', as well as the precise estimates of the
jet powers and the central core densities for both sources.
fitted
to observations at the four different frequencies. In this case, the ideal intersections of
the four curves give the precise "age solutions'', as well as the precise estimates of the
jet powers and the central core densities for both sources.
 |
Figure 7:
a)
|
| Open with DEXTER | |
The dependence of these "age solutions'' (the curves marked by t) on
![]() and
and
![]() is presented in Figs. 7b and 8b, together with the
is presented in Figs. 7b and 8b, together with the
![]() and
and
![]() curves. Clearly, the "best solutions''
exist within the theoretically acceptable range of
curves. Clearly, the "best solutions''
exist within the theoretically acceptable range of
![]() .
.
The "best solutions'' for the dynamical age of all the sources from
Table 2 with the
corresponding values of
![]() are collected in Table 3. In order to show
how these solutions depend on the assumed value of the maximum electron energies, we
give the best solution for
are collected in Table 3. In order to show
how these solutions depend on the assumed value of the maximum electron energies, we
give the best solution for
![]() and
and
![]() .
As shown, the
differences are minor. In particular, Col. 6 of Table 3 gives the ratio of the standard
deviation to the mean of the ages derived with these two different values
.
As shown, the
differences are minor. In particular, Col. 6 of Table 3 gives the ratio of the standard
deviation to the mean of the ages derived with these two different values
![]() ,
showing that the resulting age estimates differ from
,
showing that the resulting age estimates differ from ![]() 4% to
4% to ![]() 30%, mostly by only
30%, mostly by only
![]() 10%.
10%.
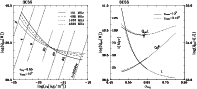 |
Figure 8: The same as in Fig. 7 but for the radio galaxy 3C 55. |
| Open with DEXTER | |
Table 3:
![]() values relating to the minimum total energy of the jet for two
different values of
values relating to the minimum total energy of the jet for two
different values of
![]() ,
and the
corresponding "best solution'' of age for the analyzed sample of FR II-type radio galaxies.
,
and the
corresponding "best solution'' of age for the analyzed sample of FR II-type radio galaxies.
One quality of the dynamical age estimated with the method presented here can be justified by
its comparison with the synchrotron (radiative) age,
![]() derived from the spectral
aging analysis (e.g. Myers & Spangler 1985; Carilli et al. 1991). In this analysis the radiative
age of emitting particles is determined from the "break'' frequency in the observed radio
spectrum and the magnetic field strength, usually computed under the equipartition conditions.
In order to find this break frequency, the
derived from the spectral
aging analysis (e.g. Myers & Spangler 1985; Carilli et al. 1991). In this analysis the radiative
age of emitting particles is determined from the "break'' frequency in the observed radio
spectrum and the magnetic field strength, usually computed under the equipartition conditions.
In order to find this break frequency, the
![]() value must be known. In most
of the published papers concerning the above analysis, the value of
value must be known. In most
of the published papers concerning the above analysis, the value of
![]() was
usually identified with the slope of the observed low-frequency spectrum. Because of a
reasonable criticism of this simple method (see Sect. 1), Murgia (1996) developed the
software SYNAGE, which allows the best fit of the spectral data to the theoretical
models of the energy losses by constraining the values of the most important model parameters,
especially a value of
was
usually identified with the slope of the observed low-frequency spectrum. Because of a
reasonable criticism of this simple method (see Sect. 1), Murgia (1996) developed the
software SYNAGE, which allows the best fit of the spectral data to the theoretical
models of the energy losses by constraining the values of the most important model parameters,
especially a value of
![]() .
.
The
![]() value for the C.I. model,
value for the C.I. model,
![]() ,
fitted to the spectrum
of the lobes of the sources from Table 2 using the SYNAGE algorithm, is given in
Col. 7 of Table 3. It is easy to see that the values of
,
fitted to the spectrum
of the lobes of the sources from Table 2 using the SYNAGE algorithm, is given in
Col. 7 of Table 3. It is easy to see that the values of
![]() are typically
higher than the values of
are typically
higher than the values of
![]() determined by minimizing the total energy as
proposed in this paper, though the errors in
determined by minimizing the total energy as
proposed in this paper, though the errors in
![]() are of the same order as
the errors in
are of the same order as
the errors in
![]() (also given in Col. 7). Only for Cyg A and (formally)
for 3C 165 are the fitted values of
(also given in Col. 7). Only for Cyg A and (formally)
for 3C 165 are the fitted values of
![]() lower than the values of
lower than the values of
![]() .
.
A discrepancy between the values of
![]() and
and
![]() for the other
sources can be explained either by (i) a lack of flux density data at frequencies below
for the other
sources can be explained either by (i) a lack of flux density data at frequencies below
![]() 100 MHz (which may be crucial for a proper determination of the slope of the initial spectrum)
and the uncertainties of the available data or by (ii) an influence of other physical processes
not taken into account in the KDA model, such as reacceleration of the relativistic particles,
non-standard evolution of the cocoon's magnetic fields, etc. Note that the
100 MHz (which may be crucial for a proper determination of the slope of the initial spectrum)
and the uncertainties of the available data or by (ii) an influence of other physical processes
not taken into account in the KDA model, such as reacceleration of the relativistic particles,
non-standard evolution of the cocoon's magnetic fields, etc. Note that the
![]() values, fitted with the SYNAGE and much higher than the effective values of
values, fitted with the SYNAGE and much higher than the effective values of
![]() determined by the minimum jet energy delivered to the source (cocoon), may lead
to a most unlikely young age and a corresponding enormously high jet-head advance velocity,
determined by the minimum jet energy delivered to the source (cocoon), may lead
to a most unlikely young age and a corresponding enormously high jet-head advance velocity, ![]() .
For example,
.
For example,
![]() for the high-redshift radio galaxy
3C 294 (see Table 3) would only yield the dynamical age of 0.25 Myr, which would imply the
unacceptable high value of
for the high-redshift radio galaxy
3C 294 (see Table 3) would only yield the dynamical age of 0.25 Myr, which would imply the
unacceptable high value of
![]() c!
c!
We note in this context that high (![]() 0.3 c) advance velocities are, in fact, observed,
however only in "compact symmetric objects'' (CSOs; see, e.g., Owsianik & Conway
1998; Polatidis & Conway 2003; Gugliucci et al. 2005). These sources, characterized by
projected linear sizes less than
0.3 c) advance velocities are, in fact, observed,
however only in "compact symmetric objects'' (CSOs; see, e.g., Owsianik & Conway
1998; Polatidis & Conway 2003; Gugliucci et al. 2005). These sources, characterized by
projected linear sizes less than ![]() 1 kpc, are believed to be young versions of the
extended radio galaxies, possibly even of the powerful classical doubles (see a review by O'Dea
1998). And indeed, the implied kinetic ages (between 100 yr and 104 yr) usually agree
closely with the spectral ages determined for some of these objects assuming energy equipartition
within the lobes (Katz-Stone & Rudnick 1997). On the other hand, it
should not be surprising that the advanced velocities of the jets in CSOs are higher than the
ones in "regular'' FR II radio galaxies, for which Scheuer (1995) gives an upper limit of
0.1 c. That is because of the differences in the lobe/jet evolution for compact and
extended objects, caused for example by the differences in the ambient medium density profiles.
In particular, Kawakatu & Kino (2006) argue for constant jet-advanced velocity of evolving
young/compact radio sources, while for the decreasing advanced velocity with increasing linear
size at later evolutionary stages (see also in this context Alexander 2000). Therefore, here
we take 0.3 c as an upper limit for the "realistic'' values of the jet-advanced velocities
in all the FR II radio galaxies considered in this paper, in agreement with Scheuer
(1995), and multi-epoch observations of young radio sources.
1 kpc, are believed to be young versions of the
extended radio galaxies, possibly even of the powerful classical doubles (see a review by O'Dea
1998). And indeed, the implied kinetic ages (between 100 yr and 104 yr) usually agree
closely with the spectral ages determined for some of these objects assuming energy equipartition
within the lobes (Katz-Stone & Rudnick 1997). On the other hand, it
should not be surprising that the advanced velocities of the jets in CSOs are higher than the
ones in "regular'' FR II radio galaxies, for which Scheuer (1995) gives an upper limit of
0.1 c. That is because of the differences in the lobe/jet evolution for compact and
extended objects, caused for example by the differences in the ambient medium density profiles.
In particular, Kawakatu & Kino (2006) argue for constant jet-advanced velocity of evolving
young/compact radio sources, while for the decreasing advanced velocity with increasing linear
size at later evolutionary stages (see also in this context Alexander 2000). Therefore, here
we take 0.3 c as an upper limit for the "realistic'' values of the jet-advanced velocities
in all the FR II radio galaxies considered in this paper, in agreement with Scheuer
(1995), and multi-epoch observations of young radio sources.
Finally, the synchrotron ages
![]() (with associated errors) for all
the sources in Table 2 - collected from the papers of Alexander & Leahy (1987), Leahy et al.
(1989), Liu et al. (1992), and Parma et al. (1999) - are given in Col. 8 of Table 3. As shown, the synchrotron ages and
our dynamical age estimates are comparable for the young sources, i.e. those whose ages are less
or much less than 10 Myr. Such behavior is in fact consistent with the conclusions of
Blundell & Rawlings (2000), who argue that the spectral aging analysis is most likely erroneous
for lobes older than 10 Myr. Indeed, in the case of the largest (and oldest) sources from
Table 3 (3C 55, 3C 103, 3C 292, B1209+745, B1312+698), the ratios of the dynamical age estimates to
the synchrotron ages (see Col. 9 of Table 3) rise to a factor of 2-4. This also agrees with
the earlier result for this ratio determined for the three giant radio galaxies: J0912+3510,
J1343+3758, and J1451+3357 (Jamrozy & Machalski 2005). The "best solution'' for the age of the analyzed radio galaxies vs. their synchrotron age is plotted in Fig. 9.
(with associated errors) for all
the sources in Table 2 - collected from the papers of Alexander & Leahy (1987), Leahy et al.
(1989), Liu et al. (1992), and Parma et al. (1999) - are given in Col. 8 of Table 3. As shown, the synchrotron ages and
our dynamical age estimates are comparable for the young sources, i.e. those whose ages are less
or much less than 10 Myr. Such behavior is in fact consistent with the conclusions of
Blundell & Rawlings (2000), who argue that the spectral aging analysis is most likely erroneous
for lobes older than 10 Myr. Indeed, in the case of the largest (and oldest) sources from
Table 3 (3C 55, 3C 103, 3C 292, B1209+745, B1312+698), the ratios of the dynamical age estimates to
the synchrotron ages (see Col. 9 of Table 3) rise to a factor of 2-4. This also agrees with
the earlier result for this ratio determined for the three giant radio galaxies: J0912+3510,
J1343+3758, and J1451+3357 (Jamrozy & Machalski 2005). The "best solution'' for the age of the analyzed radio galaxies vs. their synchrotron age is plotted in Fig. 9.
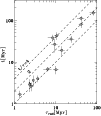 |
Figure 9: "Best solution'' age vs. the synchrotron age for the radio galaxies in Table 2. |
| Open with DEXTER | |
Given the age determined for a given source, we can derive its other physical parameters.
It was shown in Sect. 4.1 that each "age solution'' determined by the intersection
of the age curves in the
![]() diagrams (Figs. 2, 7a, and 8a) indicates
unique values of the jet power
diagrams (Figs. 2, 7a, and 8a) indicates
unique values of the jet power
![]() and the central core density
and the central core density ![]() .
It
also provides unique values of the source (cocoon) energy density and pressure,
.
It
also provides unique values of the source (cocoon) energy density and pressure, ![]() and
and ![]() ,
respectively, as well as the total radiative energy
,
respectively, as well as the total radiative energy
![]() (see
Table 1). We note, that the minimum total cocoon energy (which gives the "best solution''
of the age) naturally corresponds to the equivalent minimum of
(see
Table 1). We note, that the minimum total cocoon energy (which gives the "best solution''
of the age) naturally corresponds to the equivalent minimum of ![]() and
and ![]() .
.
Table 4: Physical parameters of the sources from Table 2.
All the physical parameters corresponding to the "best solution'' of age for the sources
considered in this paper, obtained with
![]() and given in
Table 3, are collected in Table 4. The last column of
Table 4 gives, in addition, the ratio
of the mean expansion velocity of the jet head to the speed of light, i.e. one half of
the projected linear size of a given source divided by its age estimate.
and given in
Table 3, are collected in Table 4. The last column of
Table 4 gives, in addition, the ratio
of the mean expansion velocity of the jet head to the speed of light, i.e. one half of
the projected linear size of a given source divided by its age estimate.
A justified question may be raised: starting from what age/size (or equivalently stage of the source's evolution) can the described method be applied? A priori the method is applicable to the sources for which radio emission is dominated by the lobes or cocoons evolving within a power-law ambient medium-density profile. Therefore, our method cannot be applied directly to the young (CSO-type) sources whose linear sizes are <1 kpc, because it is unlikely that their observed radio emission can be entirely attributed to the non-relativistic lobes. In particular, in many of these sources contribution from the underlying relativistic jets and bright mildly-relativistic hotspots to the total radiative output may be significant. Finally, it is also not obvious if some (small) fraction of CSOs is "frustrated'' by the dense ambient medium, as advocated by many authors (see, e.g., De Young 1993; Alexander 2000).
Slightly larger versions of CSOs, called "medium symmetric objects'' (MSOs, or "compact
steep-spectrum'' sources, CSS, if the spectral characteristics are considered), are
probably more promising in this context, since their projected linear sizes are
typically 1-10 kpc. For example, the dynamical age estimates determined with our method for two of such objects from the sample of Murgia et al. (1999) are
![]() kyr (
kyr (
![]() )
for 3C 67 with D=11 kpc and
)
for 3C 67 with D=11 kpc and
![]() kyr (
kyr (
![]() )
for 3C 186 with D=15.7 kpc.
The above dynamical age estimates are larger by a factor of 2-3 than the synchrotron
ages found by Murgia et al. (which are 51 and 113 kyr for 3C 67 and 3C 186,
respectively). However, such a discrepancy may be expected, as these synchrotron
ages were determined using the break frequency in the spectrum of the entire source.
That spectrum must be dominated by the radiation produced by the hottest regions of
a given object, probably very close to a jet terminal shock. For this reason, the
spectral ages found by Murgia et al. can be significantly lower than the dynamical ages
derived by us.
On the other hand, it is worth emphasizing that the
)
for 3C 186 with D=15.7 kpc.
The above dynamical age estimates are larger by a factor of 2-3 than the synchrotron
ages found by Murgia et al. (which are 51 and 113 kyr for 3C 67 and 3C 186,
respectively). However, such a discrepancy may be expected, as these synchrotron
ages were determined using the break frequency in the spectrum of the entire source.
That spectrum must be dominated by the radiation produced by the hottest regions of
a given object, probably very close to a jet terminal shock. For this reason, the
spectral ages found by Murgia et al. can be significantly lower than the dynamical ages
derived by us.
On the other hand, it is worth emphasizing that the
![]() values fitted by
Murgia et al. in the frame of the C.I. model and our values determined from the
minimum jet kinetic energy agree between themselves very well.
values fitted by
Murgia et al. in the frame of the C.I. model and our values determined from the
minimum jet kinetic energy agree between themselves very well.
Jets in powerful radio sources were considered as being characterized by sub- or
eventually mildly-relativistic bulk velocities on large (hundreds of kpc) scales,
![]() (e.g., Wardle & Aarons 1997). Also, advanced velocities
of their terminal features, the hotspots, were known to be non-relativistic,
(e.g., Wardle & Aarons 1997). Also, advanced velocities
of their terminal features, the hotspots, were known to be non-relativistic,
![]() (Scheuer 1995). For these reasons, it was widely assumed
that the double-shock structures formed at the heads of the jets in quasars and FR II
radio galaxies were in fact always non-relativistic phenomena. In particular, it was
argued that the non-relativistic reverse shock formed at the jet terminal point was
the place of the efficient diffusive (Fermi I) particle acceleration process, leading
to formation of the power-law particle-energy spectrum within the hotspot, injected later
into the expanding lobes/cocoons by means of the plasma backflow.
(Scheuer 1995). For these reasons, it was widely assumed
that the double-shock structures formed at the heads of the jets in quasars and FR II
radio galaxies were in fact always non-relativistic phenomena. In particular, it was
argued that the non-relativistic reverse shock formed at the jet terminal point was
the place of the efficient diffusive (Fermi I) particle acceleration process, leading
to formation of the power-law particle-energy spectrum within the hotspot, injected later
into the expanding lobes/cocoons by means of the plasma backflow.
It is known that the well-established theory for particle-shock acceleration in the
non-relativistic test-particle limit predicts a universal power-law index of the
accelerated particle continuum p = 2, weakly dependent on the plasma conditions
on both sides of the shock (e.g., Blandford & Eichler 1987). Interestingly, radio
spectral indices of powerful hotspots are indeed close to - though not always and
not exactly - the corresponding value
![]() .
Such an agreement
supported the "non-relativistic shock'' paradigm for the origin of non-thermal electrons
within heads and cocoons of FR II type radio sources. It stimulated further development
of this idea in the context of modeling the non-thermal hotspots' emission (Heavens &
Meisenheimer 1987), enabling the successful explanation of several observational features
(e.g., Meisenheimer et al. 1989, 1997). An important implication is
that, in the framework of such a "standard'' model, the injection spectral index for all
the cocoons of powerful radio sources is expected to be strictly
.
Such an agreement
supported the "non-relativistic shock'' paradigm for the origin of non-thermal electrons
within heads and cocoons of FR II type radio sources. It stimulated further development
of this idea in the context of modeling the non-thermal hotspots' emission (Heavens &
Meisenheimer 1987), enabling the successful explanation of several observational features
(e.g., Meisenheimer et al. 1989, 1997). An important implication is
that, in the framework of such a "standard'' model, the injection spectral index for all
the cocoons of powerful radio sources is expected to be strictly
![]() .
.
As mentioned in Sect. 2.3, a number of low-frequency radio observations of
FR II sources indicate that there is no universal injection spectral index for
their cocoons (see in this context Rudnick et al. 1994). This conclusion is also
supported by the detailed spectral aging studies of the few brightest
objects of this type, such as Cyg A (Carilli et al. 1991). In addition,
the standard assumption regarding non-relativistic velocities of the
large-scale jets was recently questioned by the most recent X-ray
observations (e.g., Celotti et al. 2001; Tavecchio et al.
2005). If this is indeed the
case, then one should expect significant modifications in the energy spectrum of the
accelerated particles when compared to the non-relativistic limit. Moreover, as argued
below, the assumption regarding a single power-law form of the injected electrons
is also most likely far from being realistic. For these reasons, in our analysis we decided
to treat
![]() as a basically free "effective'' parameter, which may be
different for different sources and which may be far from the canonical value of 0.5.
as a basically free "effective'' parameter, which may be
different for different sources and which may be far from the canonical value of 0.5.
In this paper we assumed that the power-law continuum of electrons injected by the hotspot
to the cocoons extends down to electron Lorentz factors
![]() .
In general, synchrotron emission of the electrons with
.
In general, synchrotron emission of the electrons with
![]() cannot be observed directly from the hotspots, since it corresponds to frequencies
<100 MHz for a typical value of the hotspots' magnetic field
cannot be observed directly from the hotspots, since it corresponds to frequencies
<100 MHz for a typical value of the hotspots' magnetic field ![]() 100
100 ![]() G.
Thus, the assumption regarding the low-energy electron spectrum cannot be verified
by observations in a simple way and should rather be constrained by the theory of
particle acceleration.
G.
Thus, the assumption regarding the low-energy electron spectrum cannot be verified
by observations in a simple way and should rather be constrained by the theory of
particle acceleration.
Unfortunately, such a theory is not yet well developed. We note in this context that
powerful jets of large scales are most likely dynamically dominated by cold
protons (see, e.g., Sikora et al. 2005, and references therein). This means that the
thickness of the terminal reverse shock should be roughly a few gyroradii of the non-
or mildly-relativistic protons, such that the energies of the electrons that
are able to undergo diffusive shock acceleration must already be ultrarelativistic,
![]() .
The questions are then (i) which process
is responsible for acceleration of
.
The questions are then (i) which process
is responsible for acceleration of
![]() -104 electrons; (ii)
if the resulting low-energy part of the electron continuum is characterized by a
power-law form at all; and (iii) if so, whether the low-energy spectral index is the same
as for the high-energy part of the electron continuum (
-104 electrons; (ii)
if the resulting low-energy part of the electron continuum is characterized by a
power-law form at all; and (iii) if so, whether the low-energy spectral index is the same
as for the high-energy part of the electron continuum (
![]() -104), originating (by assumption) from the diffusive shock acceleration process.
-104), originating (by assumption) from the diffusive shock acceleration process.
Such problems in the context of FR II hotspots were not discussed much in the literature,
with only a few papers addressing
these important issues. For example, Kino & Takahara (2004) analyze limiting possibilities
for the efficient and non-efficient temperature coupling between dynamically dominating
protons and electrons at the jet terminal shock, resulting in the formation of an
ultrarelativistic Maxwellian-type electron distribution at energies
![]() and
and
![]() ,
respectively (where
,
respectively (where
![]() is the jet bulk Lorentz factor), followed
by the shock-formed high-energy power-law tail. They argue that multiwavelength
observations of the Cyg A hotspots contradict both possibilities. This implies either an
electron-positron jet composition (as preferred by Kino & Takahara
2004) or simply more
complex (broad-band) energy spectrum of low-energy electrons (instead of an almost monoenergetical
Maxwellian distribution). In fact, formation of such a broad-band energy spectrum seems to
be more likely, since any energy/temperature coupling between protons and electrons cannot be
collisional in nature in the case of extragalactic jets, but must be mediated by the magnetic field
and plasma turbulence (see in this context Hoshino et al. 1992).
is the jet bulk Lorentz factor), followed
by the shock-formed high-energy power-law tail. They argue that multiwavelength
observations of the Cyg A hotspots contradict both possibilities. This implies either an
electron-positron jet composition (as preferred by Kino & Takahara
2004) or simply more
complex (broad-band) energy spectrum of low-energy electrons (instead of an almost monoenergetical
Maxwellian distribution). In fact, formation of such a broad-band energy spectrum seems to
be more likely, since any energy/temperature coupling between protons and electrons cannot be
collisional in nature in the case of extragalactic jets, but must be mediated by the magnetic field
and plasma turbulence (see in this context Hoshino et al. 1992).
To sum up, if the dynamical dominance of the cold protons within powerful extragalactic jets
is the case, one should expect (possibly significant) differences in the spectral shape
of the low-energy (
![]() -104) and high-energy (
-104) and high-energy (
![]() )
parts of the electron continuum formed at jet terminal shocks. Indeed, low-frequency
flattening observed in the radio emission of Cyg A hotspots (Carilli et al.
1991), as well
as the most recent analysis of the X-ray emission of the lobes of giant radio galaxy 4C 39.24
(Blundell et al. 2006), are both consistent with such an expectation. This in turn implies that
the broad-band electron spectrum injected by the hotspots to the expanding cocoons in reality does
not have a simple, single power-law form.
)
parts of the electron continuum formed at jet terminal shocks. Indeed, low-frequency
flattening observed in the radio emission of Cyg A hotspots (Carilli et al.
1991), as well
as the most recent analysis of the X-ray emission of the lobes of giant radio galaxy 4C 39.24
(Blundell et al. 2006), are both consistent with such an expectation. This in turn implies that
the broad-band electron spectrum injected by the hotspots to the expanding cocoons in reality does
not have a simple, single power-law form.
In the section above we have argued that the low-energy part of the electron distribution formed at the hotspots of powerful jets is probably broad-band, possibly even power-law, but with the (unconstrained at the moment) power-law slope most likely different from the one characterizing its high-energy part. The difference may be due to the fact that, while the low-energy part is formed by poorly known processes of energy exchange between different plasma species within the collisionless shock front, the high-energy part is supposed to originate in the "standard'' Fermi I acceleration mechanism. Yet another issue is whether this high-energy part always possesses some universal value of its power-law slope, the same for every powerful radio galaxy. We believe not since, even if the diffusive shock acceleration process is indeed responsible for formation of the latter, the expected relativistic effects will modify the resulting electron spectrum when compared to the non-relativistic test-particle model value p=2.
As already mentioned, there is growing evidence that relativistic velocities are present in large-scale FR II and quasar jets, so that the reverse shocks formed at the jet heads are at least mildly relativistic. An important fact in this context is that polarization studies usually indicate magnetic fields perpendicular to the jet axis within the hotspots (even in the case of giant-sized radio galaxies, see Machalski et al. 2006), leading to an oblique orientation of the mean magnetic field lines with respect to the reverse shock front. It was noted by Begelman & Kirk (1990) that oblique relativistic shocks are likely to be superluminal, in the sense that the shock velocity projected on the magnetic field vector exceeds the speed of light. In such a situation, a diffusive (Fermi I) acceleration process may not be possible at all, since particles moving on average along the magnetic field lines are not able to cross the shock front more than once. Moreover, as shown recently by Niemiec & Ostrowski (2004), even if the magnetic field configuration is luckily such that the diffusive particle scattering on both sides of the (mildly-)relativistic shock is in principle possible, the resulting energy spectrum of the accelerated particles strongly depends on the turbulence conditions in vicinity of the shock. As a result, a variety of spectral shapes for the accelerated particles are obtained, including different spectral indices and deviations from power-law forms. We believe that this may be partly the reason for the different values of the injection spectral index obtained here for different sources.
Multiple hotspots detected on the same sides of many FR II radio galaxies and quasars indicate that the jet terminal features are intermittent in nature (see, e.g., Scheuer 1982; Williams & Gull 1985; Leahy & Perley 1995). Typically, a pair of the hotspots is observed on one side of the cocoon, with one feature being stronger and more extended ("secondary hotspot''), and the other one weaker and more compact ("primary hotspot''), as in the famous source Cyg A. The secondary and primary hotspots are identified with "older (extinguishing)'' and "younger (recent)'' jet termination points. We note that such an intermittency may be a direct consequence of the intermittent nature of the jet phenomenon, discussed in the literature for a number of reasons (e.g., Reynolds & Begelman 1997; Stawarz et al. 2004).
Whatever the case is, the issue of interest here is that multiple hotspots differ in their multifrequency radiative and geometrical properties (see Hardcastle et al. 1998). This should in fact be expected as a natural consequence of the aging/evolutionary processes taking place in a mildly-relativistic shock front "fed'' by intermittent jet outflow. An important consequence of this fact is that the electron energy distribution injected into the cocoons by the hotspots, characterized by much shorter lifetimes than the lifetime of the whole radio source, is in fact an average over different activity phases of the jet's terminal features. As a result, the injection spectral index inferred from analyzing of the cocoon's radio continuum may differ substantially from the low-frequency spectral index of the currently active hotspot in a given radio source, as suggested in our modeling.
The above discussion, pointing out all the reasons one should not expect a single broad-band power-law shape of the electrons accelerated at the jet head and injected into the expanding cocoons agrees with the results of detailed investigation of radio continuum in FR II sources by, e.g., Rudnick et al. (1994), Treichel et al. (2001), and Young et al. (2005). By applying sophisticated technique of radio data analysis, these authors found that there is no universal injection power-law spectral index for the cocoons of powerful radio sources, that the injected population of relativistic electrons thereby is characterized by complex ("curved'') spectral shape, and that a variety of distinct spectral features exist within the extended lobes. We argue, however, that for the purpose of simple estimates of the sources' main parameters (such as ages, jet powers, etc.) as presented here, a single power-law injection spectrum may well be a relatively good approximation. The effective spectral index of such a model particle energy distribution may, however, be different for different sources. In this context we note that, somewhat surprisingly, our analysis suggests a relatively narrow range for this parameter, namely p = 2.0-2.4.
Here we propose a new approach to determining the ages of powerful radio sources, on the one hand, by exploiting the dynamical model developed for these objects by Kaiser et al. (1997; KDA), and on the other hand, using multifrequency radio observations not necessarily restricted to the high-resolution ones. The KDA model is chosen for its minimal number of free parameters when compared to the more sophisticated scenarios by Blundell et al. (1999) or Manolakou & Kirk (2002).
We applied the assumed dynamical model to a number of FR II type radio galaxies observed at different radio frequencies, and fit - for each frequency separately - the model-free parameters to the sources' observed quantities. Such a procedure, enlarging in fact a number of observables, enables us to relatively precisely determine ages and other crucial characteristics (such as the jet kinetic power) of the analyzed sources. We show that the resulting age estimates extend from about 1 Myr for the small but powerful high-redshift radio galaxies to over 100 Myr for the giant radio galaxies. The estimated ages agree very well with the ones obtained by means of the "classical'' spectral aging method for objects not older than 10 Myr, for which good-quality data are available. Meanwhile, in the case of sources older than 10 Myr, our age estimates are systematically higher (by a factor of 2-4) than the ages obtained by means of spectral aging analysis. Such behavior is in fact consistent with the conclusions of Blundell & Rawlings (2000), who argue that the spectral aging analysis is most likely erroneous for the lobes older than 10 Myr.
Interestingly, the ages of FRII-type sources estimated by using this method always correspond
to "realistic'' values of the jet-advance velocity ![]() 0.3 c, i.e. consistent with those
measured directly with the VLBI technique in many of the CSO-type sources (see Sect. 5.2). Thus,
we believe that
the method presented here is also applicable in the case of the oldest radio galaxies and/or
ones for which the only available low-resolution radio data do not allow for detailed
spectral aging studies (i.e., for majority of powerful radio sources). This implies
that the applied procedure of favoring the value of the injection spectral index that
corresponds to the minimum of the cocoons' total energy (see Sect. 4.3),
although to some level arbitrary, nevertheless gives very reasonable results.
0.3 c, i.e. consistent with those
measured directly with the VLBI technique in many of the CSO-type sources (see Sect. 5.2). Thus,
we believe that
the method presented here is also applicable in the case of the oldest radio galaxies and/or
ones for which the only available low-resolution radio data do not allow for detailed
spectral aging studies (i.e., for majority of powerful radio sources). This implies
that the applied procedure of favoring the value of the injection spectral index that
corresponds to the minimum of the cocoons' total energy (see Sect. 4.3),
although to some level arbitrary, nevertheless gives very reasonable results.
Our analysis indicates that the main factor precluding precise age determination for FR II type radio galaxies regards the poorly known shape of the initial electron energy distribution injected by the jet terminal shocks into the expanding lobes/cocoons. We considered this issue briefly and conclude that the broad-band single power-law form assumed here (and in all the other analogous models) may be accurate enough for the presented estimates, although it most likely does not strictly correspond to some well-defined realistic particle acceleration process. Instead, it should be considered as a simplest model approximation of the initial electron continuum, averaged over a very broad energy range and over the age of the source. The effective spectral index of such a distribution may be different for different sources, however within the relatively narrow range p = 2.0-2.4 suggested by our modeling.
In a subsequent paper we intend to apply this method of age determination in a large sample of FR II-type (but also younger, MSO-type) radio sources.
Acknowledgements
This project was supported by MEiN with funding for scientific research in the years 2005-2007 under contract No. 0425/P03/2005/29..S. also acknowledges support by the ENIGMA Network through grant HPRN-CT-2002-00321 and by MEiN through the grant 1-P03D-003-29 in the years 2005-2008.