A&A 459, 693-701 (2006)
DOI: 10.1051/0004-6361:20054632
A. Akylas1 - I. Georgantopoulos1 - A. Georgakakis2 - S. Kitsionas3 - E. Hatziminaoglou4
1 - Institute of Astronomy & Astrophysics, National Observatory
of Athens, I. Metaxa & B. Pavlou, Penteli, 15236, Athens, Greece
2 -
Physics Department, Imperial College of Science Technology and Medicine,
Blackett Laboratory, Prince Consort Rd, 2BZ SW7, London, UK
3 -
Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482, Potsdam, Germany
4 -
Institute de Astrofisica de Canarias, C/via Lactea s/n, 38200 La Laguna, Spain
Received 2 December 2005 / Accepted 8 June 2006
Abstract
We combine bright XMM-Newton data with the Chandra Deep Field South observations to explore the behavior of the intrinsic AGN absorption, as a function of redshift and luminosity. Our sample consists of 359 sources selected in the hard 2-8 keV band, spanning the flux range 6 ![]() 10-16-3
10-16-3 ![]() 10-13
10-13
![]() with a high rate of spectroscopic or photometric redshift completeness (100 and 85 per cent respectively for the Chandra and XMM-Newton data). We derive the column density values using X-ray spectral fits. We find that the fraction of obscured AGN falls with increasing luminosity in agreement with previous findings. The fraction of obscured AGN shows an apparent increase at high redshifts (z>2). Simulations show that this effect can most probably be attributed to the fact that at high redshifts the column densities are overestimated.
with a high rate of spectroscopic or photometric redshift completeness (100 and 85 per cent respectively for the Chandra and XMM-Newton data). We derive the column density values using X-ray spectral fits. We find that the fraction of obscured AGN falls with increasing luminosity in agreement with previous findings. The fraction of obscured AGN shows an apparent increase at high redshifts (z>2). Simulations show that this effect can most probably be attributed to the fact that at high redshifts the column densities are overestimated.
Key words: surveys - X-rays: galaxies - X-rays: general
Ultra-deep surveys with Chandra have resolved the bulk of the X-ray
background at hard energies (2-10 keV), shedding light on the nature
of the AGN population at faint fluxes (
![]()
![]() 10-16
10-16
![]() ;
Mushotzky et al. 2000; Giacconi et al. 2002; Alexander et al. 2003). These surveys have revealed luminous
unobscured QSOs, but also, more importantly, large numbers of obscured
AGN (
;
Mushotzky et al. 2000; Giacconi et al. 2002; Alexander et al. 2003). These surveys have revealed luminous
unobscured QSOs, but also, more importantly, large numbers of obscured
AGN (
![]()
![]() ). The fraction of absorbed sources rises
steeply with decreasing flux (e.g., Alexander et al. 2003) dominating
the X-ray population at the flux limit of the 2 Ms Chandra Deep Field
North (CDF-N) survey (e.g., Perola et al. 2004). At the first approximation,
this trend is in qualitative agreement with the predictions of the
X-ray background (XRB) population synthesis models (e.g., Comastri et al. 1995; Gilli et al. 2001). A more detailed quantitative comparison,
however, reveals a number of inconsistencies. For example, the models
above also predict large numbers of luminous (
). The fraction of absorbed sources rises
steeply with decreasing flux (e.g., Alexander et al. 2003) dominating
the X-ray population at the flux limit of the 2 Ms Chandra Deep Field
North (CDF-N) survey (e.g., Perola et al. 2004). At the first approximation,
this trend is in qualitative agreement with the predictions of the
X-ray background (XRB) population synthesis models (e.g., Comastri et al. 1995; Gilli et al. 2001). A more detailed quantitative comparison,
however, reveals a number of inconsistencies. For example, the models
above also predict large numbers of luminous (
![]() )
heavily obscured (
)
heavily obscured (
![]() )
type-II QSOs, although only a handful of such objects have been identified to date, despite painstaking efforts (e.g., Barger et al. 2003; Fiore et al. 2003; Szokoly et al. 2004). Parallel to the
Chandra deep fields, surveys with the XMM-Newton, probing on average
brighter fluxes, also provide a wealth of complementary information on
the nature and the evolution of the AGN population. These brighter
surveys also show a clear scarcity of obscured AGN relative to the
model expectations (e.g., Piconcelli et al. 2002; Georgantopoulos et al. 2004; Perola et al. 2004).
)
type-II QSOs, although only a handful of such objects have been identified to date, despite painstaking efforts (e.g., Barger et al. 2003; Fiore et al. 2003; Szokoly et al. 2004). Parallel to the
Chandra deep fields, surveys with the XMM-Newton, probing on average
brighter fluxes, also provide a wealth of complementary information on
the nature and the evolution of the AGN population. These brighter
surveys also show a clear scarcity of obscured AGN relative to the
model expectations (e.g., Piconcelli et al. 2002; Georgantopoulos et al. 2004; Perola et al. 2004).
Although the source of the inconsistency between observations and model
predictions remains unclear, two main scenarios are put forward to
reconcile the problem. The first argues that observational biases are
affecting our conclusions, while the second proposes major revision of
the basic assumptions of the XRB models. In the former case, it
is proposed that obscured AGN are present in current surveys, but lie
in poorly explored regions of the parameter space. For example, a large
fraction of X-ray sources, particularly in the Chandra deep
fields (about 30%, Alexander et al. 2003) are optically faint (R >
24.5 mag), and therefore, hard to study in detail. Treister et al. (2004) argue that it is precisely this poorly explored population
that comprises a large fraction of obscured AGN at high redshift. This
is because, although the energetic X-ray photons of these systems can
penetrate the large obscuring columns of gas and dust, the rest-frame
UV/optical light is heavily extincted, resulting in faint observed
optical magnitudes. Consequently the type-II AGN are difficult
spectroscopic targets, even with 10-m class telescopes, and their
intrinsic properties (including their ![]() )
remain ill constrained.
)
remain ill constrained.
Table 1: The 28 archival XMM-Newton pointings used in this study.
In the case of the model revision scenario, one of the key input
parameters to the XRB models is the intrinsic column density (![]() )
distribution of AGN. This is assumed to be that of Seyfert galaxies
(i.e., low-luminosity AGN) measured from the local Universe (Risaliti
et al. 1999). It is possible that the luminous AGN identified in
deeper surveys do not follow the same column density distribution,
leading to the failure of the population synthesis models. Indeed,
by combining sources with redshift information from
the CDF-N and brighter ASCA surveys, Ueda et al. (2003)
find that the fraction of obscured AGN diminishes with increasing
luminosity. The physical interpretation of this model could be that
the highly luminous AGN blow away the obscuring screen or they
photoionize the gas around them. More recently, La Franca et al.
(2005) estimated the fraction
of absorbed AGN as a function of luminosity combining data from the
CDF-N and Chandra Deep Field South (CDF-S) surveys as well as
bright XMM-Newton data. They also suggest a decrease of the obscured AGN fraction (hereafter F) with luminosity, as well as a possible increase with redshift, in contrast to the
standard model assumption that F is independent of
)
distribution of AGN. This is assumed to be that of Seyfert galaxies
(i.e., low-luminosity AGN) measured from the local Universe (Risaliti
et al. 1999). It is possible that the luminous AGN identified in
deeper surveys do not follow the same column density distribution,
leading to the failure of the population synthesis models. Indeed,
by combining sources with redshift information from
the CDF-N and brighter ASCA surveys, Ueda et al. (2003)
find that the fraction of obscured AGN diminishes with increasing
luminosity. The physical interpretation of this model could be that
the highly luminous AGN blow away the obscuring screen or they
photoionize the gas around them. More recently, La Franca et al.
(2005) estimated the fraction
of absorbed AGN as a function of luminosity combining data from the
CDF-N and Chandra Deep Field South (CDF-S) surveys as well as
bright XMM-Newton data. They also suggest a decrease of the obscured AGN fraction (hereafter F) with luminosity, as well as a possible increase with redshift, in contrast to the
standard model assumption that F is independent of ![]() and z.
Such studies are obviously important for furthering our understanding of the AGN unification models, and moreover, they are crucial for the
construction of X-ray background population synthesis models.
and z.
Such studies are obviously important for furthering our understanding of the AGN unification models, and moreover, they are crucial for the
construction of X-ray background population synthesis models.
In this paper, we attempt to further investigate the intrinsic absorption in AGN,
using a large X-ray sample from XMM-Newton and Chandra
with X-ray spectroscopic information.
In particular, we combine the CDF-S observations (162 sources, all with
redshift information, from Szokoly et al. 2004 and Zheng et al. 2004),
with XMM-Newton data at brighter fluxes (>3 ![]() 10-14
10-14
![]() )
from the HELLAS2XMM survey of Perola et al. (2004) (44 sources),
and our own XMM-Newton survey, which overlaps with the Sloan Digital
Sky Survey (SDSS) (153 sources). The advantages of our approach are the following:
)
from the HELLAS2XMM survey of Perola et al. (2004) (44 sources),
and our own XMM-Newton survey, which overlaps with the Sloan Digital
Sky Survey (SDSS) (153 sources). The advantages of our approach are the following:
The XMM-Newton X-ray data come from 28 public fields selected to overlap with the second data release
of the SDSS (DR2; Stoughton et al. 2002) and cover a total area of ![]() 5 sq. degrees. Eight of these fields comprise the North XMM-Newton/2dF survey (for details see Georgakakis
et al. 2003; Georgantopoulos et al. 2004). For the
fields observed more than once with XMM-Newton, we use the
deeper of the multiple observations. The observational
characteristics of the 28 XMM-Newton fields used here, obtained from Georgantopoulos & Georgakakis (2005), are listed in Table 1.
5 sq. degrees. Eight of these fields comprise the North XMM-Newton/2dF survey (for details see Georgakakis
et al. 2003; Georgantopoulos et al. 2004). For the
fields observed more than once with XMM-Newton, we use the
deeper of the multiple observations. The observational
characteristics of the 28 XMM-Newton fields used here, obtained from Georgantopoulos & Georgakakis (2005), are listed in Table 1.
The X-ray data have been analyzed using the Scientific Analysis Software (SAS v6.0). The pipeline event files, produced by the XMM-Newton Science Center, were screened for high particle background periods by rejecting time intervals with 0.5-10 keV count rates higher than 25 and 15 cts/s for the PN and the two MOS cameras, respectively. The PN and MOS good time intervals are listed in Table 1. The differences between the PN and the MOS exposure times are due to varying start and end times of the individual observations. We consider the events corresponding to patterns 0-4 for PN and 0-12 for the MOS instrument.
To increase the signal-to-noise (S/N) ratio and to reach
fainter fluxes, we have merged the MOS and the PN data into a single event file using the MERGE task of SAS. The X-ray images
have been extracted in the 2-8 keV (hard) energy band, for both
the merged and the individual event files.
We use the more sensitive (higher S/N ratio) merged image
for source extraction and flux estimation, while the individual PN
and MOS images are used to extract the spectral files. The source
detection has been performed using the EWAVELET task of SAS with
a detection threshold of 6![]() .
The choice of the threshold
minimizes the number of spurious sources
in the final catalogue without reducing the number of real detections.
All the detected sources were carefully inspected one by one to
exclude spurious detections associated with CCD gaps, hot pixels, or
sources lying close to the edge of the detector's field of view. We also
exclude the target source of each XMM-Newton
and seven sources that appear extended on the XMM-Newton EPIC images and that
are clearly associated with diffuse cluster emission from the final catalogue.
We estimate the observed flux of each source in a 18 arcsec aperture, adopting
a power-law energy distribution model with
.
The choice of the threshold
minimizes the number of spurious sources
in the final catalogue without reducing the number of real detections.
All the detected sources were carefully inspected one by one to
exclude spurious detections associated with CCD gaps, hot pixels, or
sources lying close to the edge of the detector's field of view. We also
exclude the target source of each XMM-Newton
and seven sources that appear extended on the XMM-Newton EPIC images and that
are clearly associated with diffuse cluster emission from the final catalogue.
We estimate the observed flux of each source in a 18 arcsec aperture, adopting
a power-law energy distribution model with ![]() = 1.8.
The final X-ray catalogue comprises a total of 507 sources detected
in the 2-8 keV merged (PN+MOS) images with a 6
= 1.8.
The final X-ray catalogue comprises a total of 507 sources detected
in the 2-8 keV merged (PN+MOS) images with a 6![]() ,
2-8 keV
flux limit of 5
,
2-8 keV
flux limit of 5 ![]() 10-15
10-15
![]() (see Georgakakis et al. 2006a).
For the purpose of this study, we consider only the brighter
hard X-ray sources with a 2-8 keV flux
(see Georgakakis et al. 2006a).
For the purpose of this study, we consider only the brighter
hard X-ray sources with a 2-8 keV flux ![]() (2-8) > 3
(2-8) > 3 ![]() 10-14
10-14
![]() (169 sources). This is to ensure sufficient
photon statistics to perform X-ray spectral analysis and to minimize
the number of objects without optical identifications.
The background subtracted photon count distribution of these sources
is plotted in Fig. 1.
(169 sources). This is to ensure sufficient
photon statistics to perform X-ray spectral analysis and to minimize
the number of objects without optical identifications.
The background subtracted photon count distribution of these sources
is plotted in Fig. 1.
The CDF-S X-ray data are obtained from Giacconi et al. (2002). The data from these observations include 247 hard (2-10 keV) X-ray selected sources with complete spectroscopic or photometric redshift (Szokoly et al. 2004; Zheng et al. 2004). For one source (#261), there is no redshift information and hence it is excluded from our analysis.
These data expand the 2-8 keV flux coverage of our
XMM-Newton data down to ![]() 6
6 ![]() 10-16
10-16
![]() .
To increase the photon statistics, we consider
only the sources that lie within the central CDF-S region,
and therefore overlap with all 11 Chandra pointings.
This reduces the number of the sources to 188. The vast
majority of the sources (179) contain more than 50 net
counts, sufficient for spectral analysis. Furthermore, we
exclude 26 sources identified as normal galaxy candidates
by Norman et al. (2004). Therefore, our final CDF-S AGN sample comprises 162 sources with spectroscopic (75 sources) or photometric (87 sources) redshift information. The
background subtracted photon count distribution of these
sources is plotted in Fig. 1.
.
To increase the photon statistics, we consider
only the sources that lie within the central CDF-S region,
and therefore overlap with all 11 Chandra pointings.
This reduces the number of the sources to 188. The vast
majority of the sources (179) contain more than 50 net
counts, sufficient for spectral analysis. Furthermore, we
exclude 26 sources identified as normal galaxy candidates
by Norman et al. (2004). Therefore, our final CDF-S AGN sample comprises 162 sources with spectroscopic (75 sources) or photometric (87 sources) redshift information. The
background subtracted photon count distribution of these
sources is plotted in Fig. 1.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{4632fig1.ps} \end{figure}](/articles/aa/full/2006/45/aa4632-05/Timg70.gif) |
Figure 1: The background subtracted photon count distribution for our XMM-Newton/SDSS data (dashed histogram) and the CDF-S survey (solid histogram). |
| Open with DEXTER | |
We use the SDSS DR2 catalogue to optically identify the hard X-ray detected sources using the method of Downes et al. (1986; for a detailed description of the procedure followed, see Georgakakis et al. 2004) to calculate the probability, P, that a given candidate is a spurious identification. Here we apply an upper limit in the search radius, r<7 arcsec, and a cutoff on the probability, P<0.05, to limit the optical identification to those candidates that are least likely to be spurious alignments. The cross-correlation reveals 143 coincidences. 26 sources have no optical counterpart in the SDSS limit (r < 22.5 mag), giving an 85 per cent completeness for our XMM-Newton sample. From the data above we further exclude all the sources with extended optical morphology and blue colors, i.e., g-r<0.5 mag, since the estimation of the photometric redshifts for these population is inaccurate, as we discuss below. After this selection, our catalogue comprises in total 157 hard X-ray sources. In particular, there are 45 sources with spectroscopic information, 86 with only photometric observations, and 26 optically faint sources (r>22.5 mag).
For the 86 sources with photometric information available, we
estimate photometric redshifts using the method described by
Kitsionas et al. (2005). These authors have applied the
photometric redshift estimation technique of Hatziminaoglou et al. (2000) on X-ray selected XMM-Newton samples, also using 5-band photometry from the SDSS. The method
is based on the standard ![]() minimization, using
a combination of QSO stellar and galaxy Spectral Energy Distribution
(SED) templates for the redshift estimation. In particular,
the method uses the three QSO templates of Hatziminaoglou et al. (2000) produced by varying the optical power-law spectral
index of simulated QSO spectra that include a variety of broad
emission lines between 0 and 1. It also uses four different
galaxy templates (E/S0, Sbc, Scd, Im) from Coleman et al. (1980).
minimization, using
a combination of QSO stellar and galaxy Spectral Energy Distribution
(SED) templates for the redshift estimation. In particular,
the method uses the three QSO templates of Hatziminaoglou et al. (2000) produced by varying the optical power-law spectral
index of simulated QSO spectra that include a variety of broad
emission lines between 0 and 1. It also uses four different
galaxy templates (E/S0, Sbc, Scd, Im) from Coleman et al. (1980).
Following the procedure in Kitsionas et al. (2005), we have divided the
sources in our photometric sample into point-like and extended sources
according to their SDSS optical morphology. We have estimated
photometric redshifts, using the QSO templates for the point-like
objects and the galaxy templates for the extended sources.
As explained above, we have excluded extended objects
with blue colors (g-r<0.5), since Kitsionas et al. (2005) have
shown that the photometric redshift estimations for such objects
are unreliable using template fitting techniques with the existing
QSO/galaxy templates, or even linear combinations of the two.
Moreover, point-like sources with X-ray-to-optical flux ratio
![]() (i.e., in the region occupied mostly by Galactic
stars; Stocke et al. 1991) are fitted with both QSO and stellar templates.
Kitsionas et al. (2005) have demonstrated that this method is very efficient
in identifying Galactic stars. In our sample, there are in total 4
(i.e., in the region occupied mostly by Galactic
stars; Stocke et al. 1991) are fitted with both QSO and stellar templates.
Kitsionas et al. (2005) have demonstrated that this method is very efficient
in identifying Galactic stars. In our sample, there are in total 4
![]() point-like sources that are best fitted by stellar
templates. These sources are excluded from our final catalogue.
point-like sources that are best fitted by stellar
templates. These sources are excluded from our final catalogue.
Given the fact that our sample is similar in nature to the sample
discussed by Kitsionas et al. (2005), we adopt the same probabilities
for obtaining reliable photometric redshifts. In particular, we assume
that photometric redshift estimates for QSOs in our photometric
sample have ![]() 70% probability of being within 0.3 from the source's
real redshift, whereas for red extended objects, the probability of
photometric redshift estimates being within 0.15 from the source's real
redshift is increased to
70% probability of being within 0.3 from the source's
real redshift, whereas for red extended objects, the probability of
photometric redshift estimates being within 0.15 from the source's real
redshift is increased to ![]() 75%. Our final sample, hereafter the
XMM-Newton/SDSS sample, comprises 26 sources without optical counterpart
45 sources spectroscopically classified, based on either SDSS or
NASA Extragalactic Database (NED) classification,
as QSOs, and 82 sources with photometric observations most probably
associated with an AGN.
In the case of the optically unidentified objects, we assume
a mean redshift of 1.5 to estimate the source luminosity and
the column density. Although this is clearly an arbitrary assumption,
the fact that SDSS did not detect these sources suggests that their
redshift is likely higher than 1. Indeed, galaxies with, e.g., Mr = -21,
should be detected up to a redshift of 0.7 at the SDSS magnitude
limit of r=22.5. Moreover, the vast majority of these optically
faint sources (22 out of 26) present
75%. Our final sample, hereafter the
XMM-Newton/SDSS sample, comprises 26 sources without optical counterpart
45 sources spectroscopically classified, based on either SDSS or
NASA Extragalactic Database (NED) classification,
as QSOs, and 82 sources with photometric observations most probably
associated with an AGN.
In the case of the optically unidentified objects, we assume
a mean redshift of 1.5 to estimate the source luminosity and
the column density. Although this is clearly an arbitrary assumption,
the fact that SDSS did not detect these sources suggests that their
redshift is likely higher than 1. Indeed, galaxies with, e.g., Mr = -21,
should be detected up to a redshift of 0.7 at the SDSS magnitude
limit of r=22.5. Moreover, the vast majority of these optically
faint sources (22 out of 26) present
![]() .
Previous work in both deep Chandra and shallower XMM-Newton surveys
(i.e., Alexander et al. 2002; Fiore et al. 2003)
has shown that a considerable fraction of these sources
are type-II QSOs.
.
Previous work in both deep Chandra and shallower XMM-Newton surveys
(i.e., Alexander et al. 2002; Fiore et al. 2003)
has shown that a considerable fraction of these sources
are type-II QSOs.
To increase our statistics, we have included the data from the
HELLAS2XMM survey (Perola et al. 2004) in our XMM-Newton/SDSS sample. There are 44 optically identified, hard X-ray selected QSOs in the 2-8 keV flux limit of 3 ![]() 10-14
10-14
![]() .
The conversion of their 2-10 keV intrinsic flux to our 2-8 keV band was made using an average photon index of 1.8.
.
The conversion of their 2-10 keV intrinsic flux to our 2-8 keV band was made using an average photon index of 1.8.
In Fig. 2 we plot the redshift distribution for the two datasets. Hereafter, we consider these combined observations as the XMM-Newton sample. The final XMM-Newton catalogue comprises 197 sources, of which 171 have photometric or spectroscopic information and 26 are optically unidentified sources to the flux limit of the SDSS survey.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{4632fig2.ps}\end{figure}](/articles/aa/full/2006/45/aa4632-05/Timg74.gif) |
Figure 2: The redshift distribution of our XMM-Newton/SDSS survey sample comprising 153 sources (shaded histogram), including the 26 optically unidentified sources, arbitrarily placed in the 1.0-1.5 redshift bin (see text). We also plot the redshift distribution of the 44 sources from the HELLAS2XMM survey (Perola et al. 2004, open histogram), normalized to our data. |
| Open with DEXTER | |
We explore the X-ray properties of the XMM-Newton/ SDSS sample using the
XSPEC v11.2 package to perform X-ray spectral fittings.
For the sources with adequate count statistics (net source counts
>100), we use the ![]() statistic technique. The data are grouped
to give a minimum of 15 counts per bin to ensure that Gaussian
statistics apply. We adopt an absorbed power-law model and attempt
to constrain the intrinsic absorption column density
statistic technique. The data are grouped
to give a minimum of 15 counts per bin to ensure that Gaussian
statistics apply. We adopt an absorbed power-law model and attempt
to constrain the intrinsic absorption column density ![]() (i.e., having
subtracted the Galactic absorption) and the power-law photon
index
(i.e., having
subtracted the Galactic absorption) and the power-law photon
index ![]() .
.
For the sources with limited photon statistics (net counts <100),
we use the C-statistic technique (Cash 1979) specifically developed
to extract spectral information from data with a low signal-to-noise
ratio. In this case, the data are grouped to give a minimum of 1 count per bin to avoid zero count bins. We try to constrain the intrinsic column densities using an absorbed
power-law model with ![]() fixed to 1.8.
fixed to 1.8.
In both cases, the spectral fittings are performed in the 0.3-8 keV
energy band where the sensitivity of the XMM-Newton detectors is the
highest. The estimated errors correspond to the 90 per cent
confidence level. In Table 2 we present the spectral
fitting results for the 153 sources comprising our final XMM-Newton/SDSS dataset. The spectral results for the 44 HELLAS2XMM survey sources have been obtained from Perola et al. (2004) and are not presented here. In Cols. 2 and 3 we list the source coordinates. In Col. 4, we
give the best-fit power-law photon index (when fixed to 1.8,
spectral fittings are performed using C-statistic).
In Col. 5 we present the best-fit observed column density
(uncorrected for redshift and Galactic absorption), and in Col. 6 the intrinsic 2-8 keV X-ray flux. Column 7 lists the source redshift, and Col. 8 the value of the Galactic absorption in the
direction of the pointing. In Col. 9, we present the intrinsic
column density (i.e., corrected for redshift and Galactic absorption),
and in Col. 10, the intrinsic hard (2-8 keV) X-ray luminosity, using
the K-correction appropriate for the best-fit value of ![]() .
In the last column we have included an identification key in to
distinguish between data with spectroscopic observations (id = 1),
photometric observations (id = 2), or without optical identification
(id = 3).
.
In the last column we have included an identification key in to
distinguish between data with spectroscopic observations (id = 1),
photometric observations (id = 2), or without optical identification
(id = 3).
The calculation of the intrinsic column density is based on the formula
![]() .
We have assumed a minimum value for the intrinsic column density,
.
We have assumed a minimum value for the intrinsic column density,
![]() ,
where
,
where
![]() = 1020 cm-2 is approximately the
minimum column density that can be detected in the observed 0.3-8 keV
energy range by the XMM-Newton EPIC PN or MOS CCDs. Also, in the cases
where the spectral fitting analysis indicates a very flat spectrum
(i.e.,
= 1020 cm-2 is approximately the
minimum column density that can be detected in the observed 0.3-8 keV
energy range by the XMM-Newton EPIC PN or MOS CCDs. Also, in the cases
where the spectral fitting analysis indicates a very flat spectrum
(i.e., ![]() 1.0, see the sources #50 and #85 in Table 2),
we assume that these sources are Compton thick and the
1.0, see the sources #50 and #85 in Table 2),
we assume that these sources are Compton thick and the
![]() value is arbitrarily set to 5
value is arbitrarily set to 5 ![]() 1024 cm-2.
1024 cm-2.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{4632fig3.ps} \end{figure}](/articles/aa/full/2006/45/aa4632-05/Timg80.gif) |
Figure 3: The 2-8 keV intrinsic luminosity versus redshift plot for the XMM-Newton (open circles) and the Chandra (filled triangles) sources. |
| Open with DEXTER | |
We estimate the ![]() using X-ray spectral
fittings for all 162 CDF-S sources. The spectral files and the auxiliary files were produced
from the merged CDF-S event file using the CIAO v.3.2 software, which
also corrects the auxillary files for the degradation in
the ACIS Quantum Efficiency due to molecular contamination.
We consider only the data in the 0.3-8 keV energy range.
We adopt a radius of 6 arcsec for the source count extraction and
an area 10 times larger for the background estimation. We use the DMARFADD task of CIAO to
add the ARF files from each observation separately to create a single output file for each source. Similarly, the mean RMF file for each source is extracted using the ADDRMF
task of FTOOLS.
using X-ray spectral
fittings for all 162 CDF-S sources. The spectral files and the auxiliary files were produced
from the merged CDF-S event file using the CIAO v.3.2 software, which
also corrects the auxillary files for the degradation in
the ACIS Quantum Efficiency due to molecular contamination.
We consider only the data in the 0.3-8 keV energy range.
We adopt a radius of 6 arcsec for the source count extraction and
an area 10 times larger for the background estimation. We use the DMARFADD task of CIAO to
add the ARF files from each observation separately to create a single output file for each source. Similarly, the mean RMF file for each source is extracted using the ADDRMF
task of FTOOLS.
The X-ray spectral fittings are performed using the XSPEC
v11.2 package. We use the C-statistic technique (Cash 1979).
The data are grouped to give a minimum of 1 count per bin to
avoid zero count bins. We try to constrain the intrinsic column
densities (i.e., subtract the Galactic absorption of
8 ![]() 1019 cm-2, Dickey & Lockman 1990) using an absorbed power-law model with
1019 cm-2, Dickey & Lockman 1990) using an absorbed power-law model with ![]() fixed to 1.8.
fixed to 1.8.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{4632fig4.ps} \end{figure}](/articles/aa/full/2006/45/aa4632-05/Timg81.gif) |
Figure 4:
The |
| Open with DEXTER | |
Figure 4 demonstrates that there is a large difference between
the ![]() distributions calculated from the XMM-Newton and the
Chandra data. This difference could arise as the Chandra sample probes much deeper
fluxes. It is well established (e.g., Alexander et al. 2003) that there
is a strong correlation between the average hardness ratio and the
flux, in the sense that at fainter fluxes we probe harder sources.
On the other hand, the Chandra observations reveal
intrinsically less luminous sources (by approximately an order of magnitude, see Fig. 3). Therefore, it is possible that the difference between the absorption observed
in the XMM-Newton and Chandra samples may also be explained
assuming that sources with lower luminosity present, on average,
larger amounts of absorption. Next, we will attempt to
disentangle these two possibilities.
distributions calculated from the XMM-Newton and the
Chandra data. This difference could arise as the Chandra sample probes much deeper
fluxes. It is well established (e.g., Alexander et al. 2003) that there
is a strong correlation between the average hardness ratio and the
flux, in the sense that at fainter fluxes we probe harder sources.
On the other hand, the Chandra observations reveal
intrinsically less luminous sources (by approximately an order of magnitude, see Fig. 3). Therefore, it is possible that the difference between the absorption observed
in the XMM-Newton and Chandra samples may also be explained
assuming that sources with lower luminosity present, on average,
larger amounts of absorption. Next, we will attempt to
disentangle these two possibilities.
We use the data presented above to diagnose
whether the strength of the photoelectric absorption depends
on the intrinsic luminosity. The simplest way to detect such a possible correlation is to test whether there is a significant decrease in the fraction of obscured objects as the intrinsic
luminosity increases.
This technique is affected by a selection bias. We observe the
unobscured sources within a larger volume compared to the obscured
ones, as the observed luminosity of the latter decreases
substantially due to photoelectric absorption.
To account for this effect, we calculate the fraction of absorbed
sources using the
![]() method (see Page & Carrera 2000).
For each source of a given observed 2-8 keV luminosity
method (see Page & Carrera 2000).
For each source of a given observed 2-8 keV luminosity ![]() ,
we calculate the maximum available volume using the formula:
,
we calculate the maximum available volume using the formula:
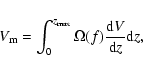
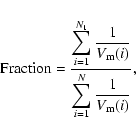
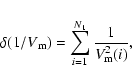
We apply this correction in both XMM-Newton and Chandra observations. The area curve of our XMM-Newton survey is constant up to
the flux limit of 3 ![]() 10-14
10-14
![]() (see Georgakakis
et al. 2006a), while the area curve for the CDF-S has been adapted
from Giacconi et al. (2002).
(see Georgakakis
et al. 2006a), while the area curve for the CDF-S has been adapted
from Giacconi et al. (2002).
In Fig. 5 we plot the estimated fraction of absorbed sources (
![]() cm-2) in a certain luminosity bin as a function of the median luminosity
of this bin for the XMM-Newton data. When we use only the 171 optically identified sources, there
is a marginal reduction in the fraction of obscuration at higher
luminosities (>1044
cm-2) in a certain luminosity bin as a function of the median luminosity
of this bin for the XMM-Newton data. When we use only the 171 optically identified sources, there
is a marginal reduction in the fraction of obscuration at higher
luminosities (>1044
![]() ). This weakens even further
when we include the 26 optically faint sources (assuming z=1.5). This is reasonable, since these sources are most probably associated with obscured sources.
). This weakens even further
when we include the 26 optically faint sources (assuming z=1.5). This is reasonable, since these sources are most probably associated with obscured sources.
In the case of the CDF-S data (Fig. 5), there is again a marginal but constant decrease of the fraction F with increasing luminosity. In a flux limited sample it is reasonable to expect a strong correlation of luminosity with redshift (see Fig. 3). We attempt to break this degeneracy by exploring the fraction of obscured Chandra sources as a function of luminosity in a thin redshift slice (0.7<z<1.2) in Fig. 5. This slice is chosen so as to maximize the number of objects. Finally, in the same panel, we plot the fraction versus luminosity for the high redshift (z>1) Chandra sources. The purpose of this is to test whether the fraction of absorbed sources increases at higher redshift. Indeed the K-correction shifts the curvature of the X-ray spectrum caused by the absorption at low energies, i.e., reduces the absorption measured at the observer's frame. This should result in an increased number of absorbed sources at higher redshift. A marginal decrease of F with increasing luminosity exists in all three cases.
![\begin{figure}
\par\hspace*{2mm} \includegraphics[height=5.95cm,width=6.2cm,clip...
...{3mm}
\includegraphics[height=5.95cm,width=6cm,clip]{4632fg5c.eps} \end{figure}](/articles/aa/full/2006/45/aa4632-05/Timg89.gif) |
Figure 5:
The fraction of obscured (
|
| Open with DEXTER | |
However, the small L-z plane coverage of the individual
samples does not allow us to provide strong constraints
on the F-L dependence. Therefore, to explore the widest luminosity and redshift
range we combine the XMM-Newton and the Chandra datasets.
Thus, we obtain a catalogue comprising 359 sources in the
2-8 keV flux range of 6 ![]() 10-16 to 4
10-16 to 4 ![]() 10-13
10-13
![]() .
In Fig. 5, we plot the fraction of the obscured sources for
the combined (XMM-Newton and Chandra) sample obtained using the
.
In Fig. 5, we plot the fraction of the obscured sources for
the combined (XMM-Newton and Chandra) sample obtained using the
![]() method. The combined data reveal a clear decrease in
the fraction of absorbed sources at higher luminosities.
The best-fit model to the data is also plotted.
The fraction of absorbed sources is related to the luminosity according to
method. The combined data reveal a clear decrease in
the fraction of absorbed sources at higher luminosities.
The best-fit model to the data is also plotted.
The fraction of absorbed sources is related to the luminosity according to
![]()
![]()
![]() .
In the same panel in Fig. 5, we also plot the
best-fit models presented in Ueda et al. (2003)
and La Franca et al. (2005).
.
In the same panel in Fig. 5, we also plot the
best-fit models presented in Ueda et al. (2003)
and La Franca et al. (2005).
In Fig. 6, we plot the fraction F against redshift for the combined XMM-Newton and
Chandra data (the optically unidentified XMM-Newton sources are excluded). It is important to note here that in this plot we are plotting the "observed'' fraction as a function of redshift, i.e. we have not applied any
![]() correction to the data. This allows a direct comparison with the models that predict the expected fraction of sources with redshift for a given survey.
correction to the data. This allows a direct comparison with the models that predict the expected fraction of sources with redshift for a given survey.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{4632fig6.ps} \end{figure}](/articles/aa/full/2006/45/aa4632-05/Timg92.gif) |
Figure 6: The observed fraction of obscured AGN as a function of redshift. The solid line gives the expected fraction, assuming the luminosity function of Ueda et al. (2003) combined with our best fit model relation between the obscured fraction of AGN and luminosity. The dotted-dashed line gives the expected fraction, assuming no dependence of F on luminosity for a ratio of obscured to unobscured AGN R=1. The long dashed line shows the input distribution of the fraction of obscured sources used in our simulations (see Appendix A), and the short dashed line the resulting one after fitting the simulated spectra. |
| Open with DEXTER | |
The dashed-dotted line model shows the expected fraction using the
Ueda et al. (2003) luminosity function, in the case
where there is no dependence of the obscured fraction
on luminosity. A value of R=1 for the ratio of
obscured to unobscured AGN has been used.
Note that the ratio R is related to the fraction F,
according to the relation F=R/(1+R).
In this case, the model predictions increase with redshift because
of the K-correction, i.e., more obscured sources are
detected as the column decreases at higher redshifts
according to
(1+z)2.65. The solid line model describes the expected fraction
of absorbed sources using the luminosity function of
Ueda et al. (2003), combined with our best-fit
![]() relation derived previously. The effect of the steep
relation derived previously. The effect of the steep
![]() relation is to roughly cancel out the K-correction
effect. The data show a significant increase in the fraction of obscured objects, F, at higher redshifts (z>2).
This behavior, if not real, may be caused by the
photometric redshift estimations, or alternatively, by small
fluctuations in the lowest energy bins, which
translate to a significant absorption at high z.
To test the first possibility, we repeat the
calculations considering the photometric and the spectroscopic data
separately. The resulting plots are very similar, and there
is still an increase of the fraction of obscured sources at high z.
Therefore, we conclude that the photometric redshifts cannot introduce this trend.
We examine the significance of the second effect by using
spectral simulations (see Appendix A for details).
In Fig. 6, the input distribution of the obscured sources used in the simulations and
the sort dashed line the resulting distribution after fitting the
simulated spectra in XSPEC are shown.
An increase in the fraction F, which is solely introduced by some fluctuations in the
lowest energy bins of the spectral files, clearly appears.
This suggests that the observed fraction of obscured sources at high z
is artificially enhanced. Consequently, there is no significant evidence for an increase in the
fraction F with redshift.
relation is to roughly cancel out the K-correction
effect. The data show a significant increase in the fraction of obscured objects, F, at higher redshifts (z>2).
This behavior, if not real, may be caused by the
photometric redshift estimations, or alternatively, by small
fluctuations in the lowest energy bins, which
translate to a significant absorption at high z.
To test the first possibility, we repeat the
calculations considering the photometric and the spectroscopic data
separately. The resulting plots are very similar, and there
is still an increase of the fraction of obscured sources at high z.
Therefore, we conclude that the photometric redshifts cannot introduce this trend.
We examine the significance of the second effect by using
spectral simulations (see Appendix A for details).
In Fig. 6, the input distribution of the obscured sources used in the simulations and
the sort dashed line the resulting distribution after fitting the
simulated spectra in XSPEC are shown.
An increase in the fraction F, which is solely introduced by some fluctuations in the
lowest energy bins of the spectral files, clearly appears.
This suggests that the observed fraction of obscured sources at high z
is artificially enhanced. Consequently, there is no significant evidence for an increase in the
fraction F with redshift.
Next we investigate the evolution of the AGN space density in different
luminosity bins as a function of redshift. For this analysis, we consider only the CDF-S data
to use a sample with complete redshift information.
The estimation of the space density is based on the 1/![]() method. The space
densities as a function of redshift are calculated in four luminosity bins in the ranges
method. The space
densities as a function of redshift are calculated in four luminosity bins in the ranges
![]() 42-43, 43-44, 44-44.5, and 44.5-45.5
42-43, 43-44, 44-44.5, and 44.5-45.5
![]() .
The results are plotted in Fig. 7 as a function of the median redshift of each redshift bin.
The 1
.
The results are plotted in Fig. 7 as a function of the median redshift of each redshift bin.
The 1![]() errors are also plotted. Figure 7 clearly shows a shift of the number
density peak with luminosity in the sense that
more luminous AGN peak occurs at an earlier era, while the less
luminous ones arise later. There is also evidence for a decline
in the density of the lower luminosity QSOs (Log
errors are also plotted. Figure 7 clearly shows a shift of the number
density peak with luminosity in the sense that
more luminous AGN peak occurs at an earlier era, while the less
luminous ones arise later. There is also evidence for a decline
in the density of the lower luminosity QSOs (Log ![]() < 44
< 44
![]() ), and especially those at 42 < Log
), and especially those at 42 < Log ![]() < 43.
This trend is known as cosmic downsizing, and it has
previously been reported by Ueda et al. (2003), Fiore et al. (2003), and
Barger et al. (2005). Hasinger et al. (2005) also found similar
results, analyzing the space density of type-I QSOs.
< 43.
This trend is known as cosmic downsizing, and it has
previously been reported by Ueda et al. (2003), Fiore et al. (2003), and
Barger et al. (2005). Hasinger et al. (2005) also found similar
results, analyzing the space density of type-I QSOs.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{4632fig7.ps} \end{figure}](/articles/aa/full/2006/45/aa4632-05/Timg94.gif) |
Figure 7:
The space density of the CDF-S AGN as a function of redshift in
four luminosity ranges, Log |
| Open with DEXTER | |
In this paper, we use the largest XMM-Newton sample with X-ray spectroscopic information available to investigate the behavior of intrinsic absorption in AGN
as a function of redshift and luminosity. We also
take advantage of the complete optical coverage
(photometric or spectroscopic) of the CDF-S observations
to extend our results at fainter fluxes
(down to ![]() 6
6 ![]() 10-16
10-16
![]() ).
).
In Fig. 5, we plot the fraction of obscured objects
as a function of luminosity separately for the XMM-Newton,
the Chandra data and their combination. Despite the weak indications of a decline of this fraction in the individual samples, the only way to unambiguously verify
this correlation is to increase the coverage of the L-z plane by combining
the two samples. It is likely that the rapid decline appearing in the combined sample
could not be easily observed in the XMM-Newton and the Chandra individual
datasets, due to the limited available volume of each independent, flux
limited survey. For example, Chandra does not cover a large enough
volume to sample a large number of luminous sources. However,
we caution that the combination of these different subsamples may
introduce some bias in favor of an
![]() correlation.
Indeed, as we move toward higher luminosities, we sample more
XMM-Newton sources and fewer Chandra sources in each luminosity bin,
according to Fig. 3. However the XMM-Newton sources are found in much
brighter fluxes in comparison with the Chandra ones. Thus, as we
move progressively to higher luminosities, we sample higher fluxes and
hence less obscured sources, according to the well known flux-absorption
correlation. This effect is summarized in Table 3 where we
list the median 2-8 keV flux for each luminosity bin presented
in Fig. 5.
correlation.
Indeed, as we move toward higher luminosities, we sample more
XMM-Newton sources and fewer Chandra sources in each luminosity bin,
according to Fig. 3. However the XMM-Newton sources are found in much
brighter fluxes in comparison with the Chandra ones. Thus, as we
move progressively to higher luminosities, we sample higher fluxes and
hence less obscured sources, according to the well known flux-absorption
correlation. This effect is summarized in Table 3 where we
list the median 2-8 keV flux for each luminosity bin presented
in Fig. 5.
The decrease of the fraction of obscured sources as a function of luminosity is consistent with the results of La Franca et al. (2005). The physical interpretation of this model could be that the radiation pressure flattens the torus in luminous objects (Königl & Kartje 1994) or increases the degree of photoionization of the gas around them. Another possible scenario is that of the "receding torus'', which has been proposed by Lawrence (1991) and has been recently updated by Simpson (2005), where, because of the effects of dust sublimation, the inner radius of the torus increases with luminosity.
One way to explore whether the relation between the absorbed
fraction and luminosity (
![]() relation) is real (or is induced
to some degree by the strong flux-absorption correlation),
is to model the number of absorbed sources as a function of flux.
In Fig. 8 we plot the fraction of obscured AGN
as a function of the flux. We plot the XMM-Newton points, the CDF-S points,
as well those from the Chandra survey in the Extended Groth Strip (Georgakakis et al. 2006b)
separately, and compare them with various model predictions.
In the above models, we use the Ueda et al. (2003)
luminosity function. The solid line gives the predictions
of our model and uses the
relation) is real (or is induced
to some degree by the strong flux-absorption correlation),
is to model the number of absorbed sources as a function of flux.
In Fig. 8 we plot the fraction of obscured AGN
as a function of the flux. We plot the XMM-Newton points, the CDF-S points,
as well those from the Chandra survey in the Extended Groth Strip (Georgakakis et al. 2006b)
separately, and compare them with various model predictions.
In the above models, we use the Ueda et al. (2003)
luminosity function. The solid line gives the predictions
of our model and uses the
![]() relation derived here.
The long dashed line corresponds to a model with a ratio of
obscured to unobscured AGN, R=4 (or F=0.8) with no
dependence on luminosity. This is the ratio derived
in the local universe by Risaliti et al. (1999)
and Maiolino & Rieke (1995). The short dashed line
corresponds to the R=1 case with no dependence on luminosity.
The R=1 model nicely represents the XMM-Newton data while the R=4 model follows the faint CDF-S data better. However, only a model that includes a decrease in the
relation derived here.
The long dashed line corresponds to a model with a ratio of
obscured to unobscured AGN, R=4 (or F=0.8) with no
dependence on luminosity. This is the ratio derived
in the local universe by Risaliti et al. (1999)
and Maiolino & Rieke (1995). The short dashed line
corresponds to the R=1 case with no dependence on luminosity.
The R=1 model nicely represents the XMM-Newton data while the R=4 model follows the faint CDF-S data better. However, only a model that includes a decrease in the
![]() relation can
explain the abrupt increase of the fraction of absorbed sources
with decreasing flux.
relation can
explain the abrupt increase of the fraction of absorbed sources
with decreasing flux.
Table 3: The median values for the 2-8 keV observed flux for each luminosity bin in the combined sample.
Previous estimates are in agreement with
our results. Piconceli et al. (2003), analyzing hard
X-ray XMM-Newton data, claimed that the observed fraction of
obscured sources at bright fluxes (>10-13
![]() )
is about 30 per cent, much lower than that predicted by
the (R=4) XRB model. La Franca et al. (2005), combining
data from different X-ray samples, studied the behavior
of obscuration in a much wider flux range. Their findings
for the fraction of obscured sources are very similar to ours
in both faint and bright fluxes.
Their proposed
)
is about 30 per cent, much lower than that predicted by
the (R=4) XRB model. La Franca et al. (2005), combining
data from different X-ray samples, studied the behavior
of obscuration in a much wider flux range. Their findings
for the fraction of obscured sources are very similar to ours
in both faint and bright fluxes.
Their proposed
![]() relation is in agreement with our
model (see Fig. 5). Note that here we have used
a power-law best-fit model instead of a linear one.
relation is in agreement with our
model (see Fig. 5). Note that here we have used
a power-law best-fit model instead of a linear one.
Figure 6 shows the dependence of F on redshift.
The fraction shows an apparent increase with redshift, with
a more abrupt increase at high redshifts, z>2.
Ueda et al. (2003) find no dependence of the fraction F
on redshift. Ballantyne et al. (2006) propose that
the obscuration may be related to star formation within
the host galaxy, and thus there may be some increase of the
obscured AGN fraction with redshift.
They test their models by comparing with the
observed type-I AGN in the CDF-N (Barger et al. 2003).
These authors find an obscured fraction F evolving as
(1+z)0.3,
together with a dependence of F on luminosity.
La Franca et al. (2005) find a dependence on redshift very
similar to ours (see their Fig. 6, right panel):
the fraction F increases from ![]() 0.2 at low redshift
to
0.2 at low redshift
to ![]() at z>2. In our case, however, our simulations
show that the lowest energy bins fluctuations can introduce
a significant artificial correlation of the fraction F with
redshift. This effect becomes particularly important at
high redshifts due to the K-correction effect.
This suggests that the observed fraction of obscured sources at high z
is erroneously enhanced.
Consequently, there is no significant evidence for an increase in the
fraction F with redshift.
at z>2. In our case, however, our simulations
show that the lowest energy bins fluctuations can introduce
a significant artificial correlation of the fraction F with
redshift. This effect becomes particularly important at
high redshifts due to the K-correction effect.
This suggests that the observed fraction of obscured sources at high z
is erroneously enhanced.
Consequently, there is no significant evidence for an increase in the
fraction F with redshift.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{4632fig8.ps} \end{figure}](/articles/aa/full/2006/45/aa4632-05/Timg102.gif) |
Figure 8:
The fraction of the sources with
|
| Open with DEXTER | |
We have combined bright XMM-Newton (from SDSS fields and the XMM1dF survey)
and faint Chandra (from CDF-S) data to form the largest
sample (359 sources in the 2-8 keV band) with X-ray spectra. Our goal is to
investigate the intrinsic AGN obscuring column density
as a function of luminosity and redshift. This bears important implications on AGN
unification models, as well as the X-ray background
population synthesis models. The CDF-S has complete redshift coverage ensuring
that there is no bias because of optically
unidentified sources at faint fluxes. At bright fluxes, the
level of redshift incompleteness is less than 15 per cent.
We use the
![]() method to estimate the fraction, F,
of obscured to unobscured AGN. This properly takes into
account the bias introduced by the fact that obscured sources are fainter in flux, and thus
are preferentially detected in smaller numbers
and at preferentially lower redshifts. Our findings can be summarized as follows:
method to estimate the fraction, F,
of obscured to unobscured AGN. This properly takes into
account the bias introduced by the fact that obscured sources are fainter in flux, and thus
are preferentially detected in smaller numbers
and at preferentially lower redshifts. Our findings can be summarized as follows:
The fraction of obscured AGN, F decreases with increasing luminosity. This confirms previous results by Ueda et al. (2003) and La Franca et al. (2005). The dependence of the fraction F on luminosity naturally reproduces the observation that the number of obscured sources increases drastically with decreasing flux.
There is tentative evidence for a increase of the fraction F with increasing redshift. However, this is mainly based on the high redshift bins (z>2), and thus should be viewed with caution. Our simulations show that these bins are affected by systematic overestimates of the column density, caused by small fluctuations in the lowest energy spectral bins.
Acknowledgements
We thank the referee Dr. A. Comastri for the valuable comments and suggestions. This work has been supported by the program Promotion of Excellence in Research, grant "X-ray Astrophysics with ESA's mission XMM'' funded jointly by the European Union and the Greek Ministry of Development. This work is based on data obtained from the XMM-Newton and CXC public data archives. We acknowledge the use of data from the Sloan Digital Sky Survey.
Table 2: The X-ray spectral fitting results for the 153 sources of our XMM-Newton/SDSS sample.
We describe here the strategy we followed to check the validity of
the derived ![]() estimations through the spectral analysis.
Given that a small fluctuation in the lowest energy bin in our Chandra spectral
files might correspond to an apparently high absorption at high z,
we tried some simulations to quantify this effect.
First we constructed 920 fake spectral files with exactly the same
redshift and flux distribution suggested from the SDF-S data.
Each spectral file presents an arbitrary amount of absorption in the
range of 1020-1023 cm-2 and a photon index of 1.8.
These fake files are fitted in XSPEC to obtain a value for the
observed column density. The obtained values are converted to the intrinsic
estimations through the spectral analysis.
Given that a small fluctuation in the lowest energy bin in our Chandra spectral
files might correspond to an apparently high absorption at high z,
we tried some simulations to quantify this effect.
First we constructed 920 fake spectral files with exactly the same
redshift and flux distribution suggested from the SDF-S data.
Each spectral file presents an arbitrary amount of absorption in the
range of 1020-1023 cm-2 and a photon index of 1.8.
These fake files are fitted in XSPEC to obtain a value for the
observed column density. The obtained values are converted to the intrinsic
![]() value based on the formula
value based on the formula
![]() .
The results are plotted in Fig. A.1. The solid line histogram
describes the initial
.
The results are plotted in Fig. A.1. The solid line histogram
describes the initial ![]() distribution of all the sources, and the
short dashed line the corresponding one, after fitting the fake data
in XSPEC. Also, the dotted line histogram shows the initial distribution
of the low redshift (z<1) sources, and the short dashed line the
resulting
distribution of all the sources, and the
short dashed line the corresponding one, after fitting the fake data
in XSPEC. Also, the dotted line histogram shows the initial distribution
of the low redshift (z<1) sources, and the short dashed line the
resulting ![]() distribution for the same population.
Clearly, the spectral fitting analysis produces a significant
increase in the number of obscured (
distribution for the same population.
Clearly, the spectral fitting analysis produces a significant
increase in the number of obscured (
![]() cm-2)
sources in comparison to the initial distribution.
The same plot suggests that this effect is almost negligible
in the low z population. Our conclusion is that high z
sources suffer from a systematic increase in the
measured column density. This overestimate is about 50 per cent
at
cm-2)
sources in comparison to the initial distribution.
The same plot suggests that this effect is almost negligible
in the low z population. Our conclusion is that high z
sources suffer from a systematic increase in the
measured column density. This overestimate is about 50 per cent
at ![]() 2.5, 20 per cent at
2.5, 20 per cent at ![]() 1.5, and becomes almost
negligible at z<1.
1.5, and becomes almost
negligible at z<1.