A&A 459, 577-588 (2006)
DOI: 10.1051/0004-6361:20054415
The Blazhko effect of RR Lyrae in 2003-2004
K. Kolenberg1,2 -
H. A. Smith3 -
K. D. Gazeas4 -
A. Elmasli5 -
M. Breger1 -
E. Guggenberger1 -
P. Van Cauteren6 -
P. Lampens7 -
P. Reegen1 -
P. G. Niarchos4 -
B. Albayrak5 -
S. O. Selam5 -
I. Özavci5 -
O. Aksu5
1 - Institute for Astronomy, University of Vienna,
Türkenschanzstrasse 17, 1180 Vienna, Austria
2 -
Instituut voor Sterrenkunde, Katholieke Universiteit Leuven,
Celestijnenlaan 200B, 3001 Leuven, Belgium
3 -
Department of Physics and Astronomy, Michigan State University,
East Lansing, MI 48824-2320, United States
4 -
Department of Astrophysics, Astronomy
and Mechanics, University of Athens, Panepistimiopolis,
157 84 Zografos, Athens, Greece
5 -
Ankara University, Faculty of Science, Dept. of Astronomy
and Space Sciences, 06100 Tandogan, Ankara, Türkiye
6 -
Beersel Hills Observatory, Belgium
7 -
Royal Observatory, Ringlaan 3, 1180 Brussel, Belgium
Received 25 October 2005 / Accepted 22 June 2006
Abstract
Aims. Extensive photometry of RR Lyr was obtained over a 421-day interval in 2003-2004, covering more than 10 Blazhko cycles in a multisite campaign. The length and density of this data set allow for a detailed analysis.
Methods. We used Fourier techniques to study RR Lyr's behavior over the pulsation and the Blazhko cycle. We propose a two-frequency model for decomposing the frequency spectrum.
Results. The light variations were fitted with the main radial frequency, its harmonics up to 11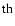 order, and the detected triplet frequencies. No significant quintuplet components were found in the frequency spectrum. Given the total time span of the measurements, we can now unambiguously conclude that the Blazhko period has become notably shorter than the previously known value of 40.8 days, whereas the main pulsation period remained roughly the same. Changes in the modulation period have been reported for other well-studied Blazhko variables. They challenge the explanations for the Blazhko effect which link the modulation period directly to the rotation period. The new photometry reveals an interval in the pulsation cycle of RR Lyr during which the star's intensity barely changes over the Blazhko cycle. This interval occurs during the infalling motion and between the supposed phases of the early and the main shock. The data also permit a more detailed study of the light curve shape at different phases in the Blazhko period through Fourier parameters.
order, and the detected triplet frequencies. No significant quintuplet components were found in the frequency spectrum. Given the total time span of the measurements, we can now unambiguously conclude that the Blazhko period has become notably shorter than the previously known value of 40.8 days, whereas the main pulsation period remained roughly the same. Changes in the modulation period have been reported for other well-studied Blazhko variables. They challenge the explanations for the Blazhko effect which link the modulation period directly to the rotation period. The new photometry reveals an interval in the pulsation cycle of RR Lyr during which the star's intensity barely changes over the Blazhko cycle. This interval occurs during the infalling motion and between the supposed phases of the early and the main shock. The data also permit a more detailed study of the light curve shape at different phases in the Blazhko period through Fourier parameters.
Key words: stars: oscillations -
stars: individual: RR Lyr
Although the time elapsed since the discovery of the Blazhko effect among the
well-known class of RR Lyrae stars approaches one century, the phenomenon
still remains a mystery.
The Blazhko effect is a periodic amplitude and/or phase modulation shown by
some 20-30 % of the galactic RRab stars (fundamental mode pulsators - see Szeidl 1988; Moskalik & Poretti 2003; Kovács 2005).
These stars, with pulsation periods of about half a day, have light curves
that are modulated on timescales of typically tens to hundreds of days.
Blazhko (1907) was the first to report this phenomenon in RW Dra.
In the LMC the occurrence rate of Blazhko stars is considerably lower
(about 12%; Alcock et al. 2003). RRc stars (first overtone pulsators) show
the Blazhko effect even less frequently (less than 5%; Alcock et al. 2000).
Nowadays, two classes of models are usually put forward as possible explanations
for the Blazhko effect. Though RR Lyrae stars have for a long time been
considered as the prototypes of purely radially pulsating stars, both
currently proposed models
involve the presence of nonradial oscillations.
In the resonance models nonradial modes of low degree 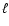 can be
nonlinearly excited through a resonance with the main radial
mode (Cox 1993; Van Hoolst et al. 1998; Nowakowski & Dziembowski 2001).
The probability of excitation is the highest for dipole (
can be
nonlinearly excited through a resonance with the main radial
mode (Cox 1993; Van Hoolst et al. 1998; Nowakowski & Dziembowski 2001).
The probability of excitation is the highest for dipole (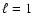 )
modes
(Van Hoolst et al. 1998).
The additional nonradial pulsation components lead to a triplet
structure in the frequency spectrum
of Blazhko variables. In the model proposed by
Nowakowski & Dziembowski (2001) the excitation of a rotationally
split
)
modes
(Van Hoolst et al. 1998).
The additional nonradial pulsation components lead to a triplet
structure in the frequency spectrum
of Blazhko variables. In the model proposed by
Nowakowski & Dziembowski (2001) the excitation of a rotationally
split 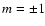 pair can cause significant amplitude and phase modulation.
In this model the modulation period is determined by the rotation rate,
but also by the Brunt-Väisälä frequency in the deepest part of the
radiative interior. As a consequence, in these models the ratio between
rotation and modulation period is not expected to be an integer number.
pair can cause significant amplitude and phase modulation.
In this model the modulation period is determined by the rotation rate,
but also by the Brunt-Väisälä frequency in the deepest part of the
radiative interior. As a consequence, in these models the ratio between
rotation and modulation period is not expected to be an integer number.
The magnetic models proposed for the Blazhko effect are similar
to the oblique pulsator model
for roAp stars (Kurtz 1982),
in which the magnetic axis of the star is inclined to its rotation axis.
The magnetic field gives rise to an additional
quadrupole component 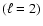 whose symmetry axis coincides with the
magnetic axis. As the star rotates, we observe the pulsation
components under different angles, which causes the observed amplitude modulation.
The additional dipole components lead to a quintuplet structure in the
frequency spectrum of a Blazhko star,
but Shibahashi & Takata (1995) also show that the quintuplet looks almost
like a triplet for certain geometrical configurations.
Depending on which of the (quintuplet) side components we observe,
the Blazhko period is supposed to be equal to the rotation
period or half the rotation period.
whose symmetry axis coincides with the
magnetic axis. As the star rotates, we observe the pulsation
components under different angles, which causes the observed amplitude modulation.
The additional dipole components lead to a quintuplet structure in the
frequency spectrum of a Blazhko star,
but Shibahashi & Takata (1995) also show that the quintuplet looks almost
like a triplet for certain geometrical configurations.
Depending on which of the (quintuplet) side components we observe,
the Blazhko period is supposed to be equal to the rotation
period or half the rotation period.
Based on the evidence that some Blazhko stars also display a long period
cycle of the order of some years besides the radial pulsation and the Blazhko
cycle (about 4 years for RR Lyr, see Detre & Szeidl 1973), several authors proposed
the existence of a magnetic cycle.
A magnetic field of the order of 1 kGauss would be required in the model of
Shibahashi & Takata (1995) to
reproduce the observed amplitude modulation.
Babcock (1958) and Romanov et al. (1994) report on the detection of a variable
magnetic field in RR Lyr with a strength up to 1.5 kGauss, but so far,
these observations have been seriously questioned.
More recently, the presence of a magnetic field of the required strength was rejected on the basis of observations carried
out over 4 consecutive years by Chadid et al. (2004), hence allowing for detection of variations over
the "4-year cycle''.
The closest match between
Blazhko stars and non-Blazhko stars occurs at the Blazhko phase which
corresponds to the largest amplitude (see diagrams in Teays 1993). These
results seem to indicate that the Blazhko effect is connected with a mechanism
which tends to suppress the normal pulsational features of the star (Szeidl
1976).
An interesting study in this respect was carried out by Jurcsik et al. (2002a),
through a comparison of the light and radial velocity amplitudes as well as the
light curve shapes (using Fourier parameters) between Blazhko stars and
so-called "normal'', non-modulated, RR Lyrae stars. They concluded that,
for Blazhko stars with large amplitude
modulation, there is no Blazhko phase that seems to be well-matched with that
of a non-modulated RRab star.
The Blazhko effect has been the frequent subject of photographic and
photometric studies, e.g., the systematic investigations carried out
at Konkoly Observatory in Budapest, Hungary (Szeidl & Kolláth 2000,
and references therein). Traditionally the phenomenon was studied by
means of O-C analysis. Therefore the
observations were in general strongly biased towards the ascending
branch and maximum phase of the primary light curve, a sampling
pernicious for Fourier analyses (see also Kovács 2001).
Photometric data sets including also other parts of the
light curve allowed for a rigorous frequency analysis, e.g., Borkowski
(1980),
Kovács (1995),
Szeidl & Kolláth (2000),
Smith et al. (2003), Jurcsik et al. (2005).
Over the past decade, the outcome of large-scale studies such as microlensing surveys (e.g., OGLE, see Moskalik &
Poretti 2003; MACHO, see Alcock et al. 2000, 2003) has yielded a much better
view of the general phenomenology of the Blazhko effect, since a large number
of previously unknown Blazhko stars were detected and analyzed.
Even though such extensive multi-target surveys have
revolutionized the
subject, long-term multi-site campaigns dedicated to particular Blazhko stars remain of
great scientific value. Only observations including complete light curves of
the target stars can reveal long-term changes in the
characteristics of the Blazhko effect (such as amplitudes, phases, and
periods). As such they can give crucial information for deciding among the
different hypotheses for the Blazhko effect.
At the end of 2003 an international collaboration (the Blazhko
Project, see also Kolenberg 2005) was set up, focused on
obtaining a better understanding of the Blazhko effect through extensive
observations of a sample of critically selected Blazhko stars.
Photometric data gathered over several Blazhko cycles ensure the required
frequency resolution. At the same time, spectroscopic data collected at
well-chosen time intervals over the Blazhko cycles of the targets can reveal
decisive information on the pulsation modes occurring in these stars.
For details on the project and for an updated status and outcome of the
ongoing campaigns we refer to the dedicated website: http://www.univie.ac.at/tops/blazhko/
One of the first main targets of the Blazhko Project was RR Lyr,
the brightest and probably the best studied RR Lyrae star. From October 2003 onwards
photometric data of this star were obtained with the 0.6-m telescope at
Michigan State University, and during the whole
observational season of 2004 six telescopes (0.13-m up to 0.8-m) acquired
photometric data.
In this paper we present the results of the photometric campaign on RR Lyr
in 2004.
In Sect. 2 we present the observations and their derived phasing. The data
analysis and its results are described in Sect. 3, with special emphasis on
new findings.
Sect. 4 is dedicated to a discussion of the results, along with the
present status of the interpretations of the Blazhko effect. Finally, some
concluding remarks are given in Sect. 5.
Our photometric observations were carried out with six different telescopes in
the northern hemisphere.
Four of the telescopes were equipped with CCD cameras, and two used
photomultipliers to obtain comparative photometry of RR Lyr. We will
discuss the combined Johnson V band photometry gathered at all the
observatories.
The time spanned by the 2003 data is 35.04 days (from HJD
2 452 915.53 to HJD 2 452 950.57); the time spanned by the 2004 data alone
is 193.99 days (from HJD 2 453 142.62 till HJD 2 453 336.61), i.e., almost 5
complete Blazhko cycles.
The total time spanned by the 2003-2004 measurements is 421.08
days, covering more than 10 Blazhko cycles.
Table 1 shows a journal of the observations. Table 2 displays the observational details.
Small zero-point shifts were carried out to combine the data gathered from
different instruments.
The resulting differential magnitudes are given with respect to
BD +42 3334.
The accuracy of an
individual differential measurement is typically 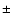 0.01-0.02 mag.
Castelaz et al. (1991) list V = 10.19 and
B-V = 0.25 for BD +42 3334 in
their table with photometry of astrometric reference stars.
0.01-0.02 mag.
Castelaz et al. (1991) list V = 10.19 and
B-V = 0.25 for BD +42 3334 in
their table with photometry of astrometric reference stars.
Table 1:
Log of the photometric Johnson V band observations of RR Lyr.
Table 2:
Observational details of the data set described in this paper.
From the 2004 measurements we determined the following ephemerides of maximum
pulsation light and maximum pulsation amplitude:
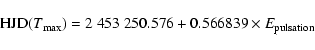 |
(1) |
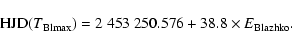 |
(2) |
Note that the Blazhko period in the new ephemeris has changed considerably
compared to previous ephemerides dating back to 1996 as given by Chadid et al. (1997).
We will discuss this in more detail in Sects. 3.1 and 4.3.
The frequency analyses were performed with Period04 (Lenz
& Breger 2005), a package applying single-frequency power spectrum and
simultaneous multi-frequency sine-wave fitting.
The fact that data were obtained from observatories at different longitudes
improved the spectral window function in the sense that one-day aliases are
much weaker (see Fig. 1).
![\begin{figure}
\par\includegraphics[bb= 64 101 499 700,width=7.7cm,clip]{4415fig1.eps}\end{figure}](/articles/aa/full/2006/44/aa4415-05/Timg14.gif) |
Figure 1:
Comparison of the spectral windows for the Michigan data only (the
largest data set, top), and the combined data, including the other
observatories ( bottom). |
| Open with DEXTER |
Given the large time gap between the 2003 and
2004 data and the relatively small number of data available
from 2003 (700 points), we started with a thorough analysis of the 2004 data
(14 002 points).
In this way, we could also verify whether the
star's behavior remained stable from one year to the next.
Extensive light and radial velocity curves of RR Lyrae Blazhko
stars exhibit in their frequency spectra either a doublet structure or an equally-spaced triplet
structure around the main pulsation frequency f0 and its harmonics kf0,
with a small
frequency separation corresponding to the Blazhko frequency 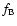 (see Kovacs
2001; Alcock et al. 2000, 2003).
Extensive light curves for RR Lyr have been published by several authors
(e.g. Balasz & Detre 1943; Szeidl et al. 1997), and it has been reported
that Fourier analyses of the light curves display a triplet structure
(e.g. Smith et al. 2003). Radial velocity curves for RR Lyr have also
been published (e.g. Struve & Blaauw 1948; and Preston et al. 1965), with
Chadid et al. (1999) reporting the existence of a triplet structure in the
radial velocity variations.
(see Kovacs
2001; Alcock et al. 2000, 2003).
Extensive light curves for RR Lyr have been published by several authors
(e.g. Balasz & Detre 1943; Szeidl et al. 1997), and it has been reported
that Fourier analyses of the light curves display a triplet structure
(e.g. Smith et al. 2003). Radial velocity curves for RR Lyr have also
been published (e.g. Struve & Blaauw 1948; and Preston et al. 1965), with
Chadid et al. (1999) reporting the existence of a triplet structure in the
radial velocity variations.
![\begin{figure}
\par\includegraphics[angle=0,width=13.5cm]{4415fig2.eps}\end{figure}](/articles/aa/full/2006/44/aa4415-05/Timg16.gif) |
Figure 2:
Fourier spectra (amplitude versus frequency) at different stages of
the period search process.
Panel a) shows the Fourier spectrum of the original data. The labeled peaks
are the main frequency f0 and its harmonics. Panel b) zooms into the
region of the right side peak frequency
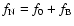 ,
the first frequency
appearing after f0 and its harmonics. Subsequently, panel c) displays the
higher order right side peak frequencies. Finally, panel d) shows the first
left side peak frequencies to appear in the Fourier spectrum after successive
prewhitening.
In all panels the unlabeled peaks of considerable amplitudes are 1-day
aliases of real frequencies. ,
the first frequency
appearing after f0 and its harmonics. Subsequently, panel c) displays the
higher order right side peak frequencies. Finally, panel d) shows the first
left side peak frequencies to appear in the Fourier spectrum after successive
prewhitening.
In all panels the unlabeled peaks of considerable amplitudes are 1-day
aliases of real frequencies. |
| Open with DEXTER |
Fourier analyses were carried out on the photometric data.
When searching for frequencies through successive prewhitening, we first
find the main frequency f0 and its first two harmonics, 2f0 and 3f0. Then the right side
peak of the triplet at the main frequency appears,
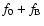 ,
followed by 4f0, and right
side peaks of higher order. The first left side peak to appear is one of
higher order,
,
followed by 4f0, and right
side peaks of higher order. The first left side peak to appear is one of
higher order,
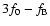 ,
closely followed by
,
closely followed by
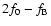 .
The left side
peak of the main frequency,
.
The left side
peak of the main frequency,
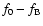 has a low but significant
amplitude. Figure 2 shows the results of successive prewhitening in the
Fourier spectrum of the data set.
For comparison with photometric results
on previous data sets of RR Lyr, we present the results expressed in
magnitudes. Table 3 list the results of a multifrequency fit to the
combined set of 2004 data, according to the formula (see also Kovács 1995):
has a low but significant
amplitude. Figure 2 shows the results of successive prewhitening in the
Fourier spectrum of the data set.
For comparison with photometric results
on previous data sets of RR Lyr, we present the results expressed in
magnitudes. Table 3 list the results of a multifrequency fit to the
combined set of 2004 data, according to the formula (see also Kovács 1995):
where we calculated amplitudes and phases up to order n=11, since the
amplitudes of the higher-order harmonics went below the significance level.
In the fit, f0 is the main pulsation frequency and 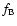 is the Blazhko
frequency.
We calculated optimum values for the
frequencies, their amplitudes and phases by minimizing the residuals.
Errors on the values for the frequencies, amplitudes and phases were
calculated following Breger et al. (1999) and
Montgomery & O'Donoghue (1999). Since correlated noise may lead to an
underestimation of these errors, we multiplied them by a factor 2 in
order to get realistic values,
following the conclusions of Handler et al. (2000) and Jerzykiewicz et al. (2005). We compared the obtained error values with those yielded by
extensive Monte
Carlo simulations, and concluded they are of the same order of magnitude.
is the Blazhko
frequency.
We calculated optimum values for the
frequencies, their amplitudes and phases by minimizing the residuals.
Errors on the values for the frequencies, amplitudes and phases were
calculated following Breger et al. (1999) and
Montgomery & O'Donoghue (1999). Since correlated noise may lead to an
underestimation of these errors, we multiplied them by a factor 2 in
order to get realistic values,
following the conclusions of Handler et al. (2000) and Jerzykiewicz et al. (2005). We compared the obtained error values with those yielded by
extensive Monte
Carlo simulations, and concluded they are of the same order of magnitude.
From this data set and with the fit according to Eq. (1), we obtained
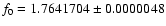 c/d for the
main radial frequency, corresponding to a period
c/d for the
main radial frequency, corresponding to a period
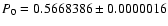 d. The right side peak at the main frequency is at
d. The right side peak at the main frequency is at
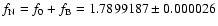 c/d. For the Blazhko frequency we then get a value of
c/d. For the Blazhko frequency we then get a value of
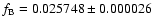 c/d, as the difference between the main peak and the side peak
in the triplet structure. The Blazhko period obtained in this way
from this data set is
thus
c/d, as the difference between the main peak and the side peak
in the triplet structure. The Blazhko period obtained in this way
from this data set is
thus
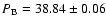 d.
This period is considerably shorter than the
previously assumed value of 40.8 days. The change in the Blazhko period will
be discussed in Sect. 4.3.
d.
This period is considerably shorter than the
previously assumed value of 40.8 days. The change in the Blazhko period will
be discussed in Sect. 4.3.
In our analyses we adopt a significance criterion of amplitude signal-to-noise
ratios of 4.0 for non-combination frequencies and 3.5 for combination
frequencies, following Breger et al. (1993).
The values in Table 3 displayed in italics
correspond to combination frequencies not exceeding a signal-to-noise level
of 3.5. Although the model proposed in Eq. (3) contains a term varying
with the modulation frequency 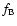 ,
the data set does not reveal any
significant variation with this frequency.
,
the data set does not reveal any
significant variation with this frequency.
Table 3:
Amplitudes and phases (in degrees) of the pulsation and modulation
frequency components of RR Lyr from the 2004 photometric data. The values displayed in italics
correspond to combination frequencies not exceeding a signal-to-noise level
of 3.5. For non-combination frequencies the signal-to-noise ratio threshold is
4.0. The residuals of the fit are at 0.021 mag, which is about the noise
level of the data set.
Though there is some remaining signal in the residuals
of the obtained fit to the data (see Fig. 8), no other frequencies were found in the data
with a signal exceeding the applied signal-to-noise ratio threshold.
From these data we observed that there is no exact repetition of the light
curve shape from one Blazhko cycle to the next. This called for caution in
directly including
the RR Lyr photometry (700 data, 11.05 h) from 2003 in the fit, since small
phase shifts or changes of the zero point would deteriorate the obtained fit.
RR Lyr is known to have a long-term cycle of about 4 years, at the end of
which the strength of the amplitude and phase modulation suddenly decreases and
then recovers (Detre & Szeidl 1973). This event is also observed to be
accompanied by a shift in the Blazhko phasing.
Chadid & Gillet (1997) noticed that the end of 1994 corresponded to the
beginning of a new "4-year cycle''. If the cycle indeed still has a period
ranging from 3.8 to 4.8 years as reported by Detre & Szeidl (1973), a new
cycle would have been likely to start between mid 2002 and mid 2004, i.e.,
it might have restarted within the time span of our observations.
At previous transitions a shift in the Blazhko
phase has been observed (Detre & Szeidl 1973).
We included the 2003 data in the solution only after
obtaining an optimal fit for the 2004 data, which show no indication of a
large shift in the Blazhko period. For this fit the obtained frequency values, their
amplitudes and phases remain the
same within the given error bars. Within the
observational errors, they agree well with the fit obtained from the 2004
data. This implies that there is no clear indication for
the beginning of a new "4-year cycle''
between November, 2003 and March, 2004. It rather seems that all
data have been obtained within the same "4-year cycle'' of RR Lyr.
![\begin{figure}
\par\includegraphics[angle=0,width=6.5cm]{4415fig3.eps}\end{figure}](/articles/aa/full/2006/44/aa4415-05/Timg74.gif) |
Figure 3:
The typical frequency spectrum of a Blazhko star (top)
can be decomposed into combinations
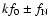 with
k=0,1,2,...
(center: sum combinations, and
bottom: difference combinations) of f0 and an additional mode with
a frequency
with
k=0,1,2,...
(center: sum combinations, and
bottom: difference combinations) of f0 and an additional mode with
a frequency 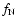 (right side peak) close to
f0. A possible explanation for the lower left side peaks is that they
result from a combination with a higher order harmonic than the right
side peaks.
(right side peak) close to
f0. A possible explanation for the lower left side peaks is that they
result from a combination with a higher order harmonic than the right
side peaks. |
| Open with DEXTER |
Equation (3) gives the commonly used frequency decomposition for Blazhko
stars, which we refer to as the "modulation model''.
This decomposition explicitly
contains the modulation or Blazhko frequency, which may result from a periodic
change of our view upon the star's pulsation, or from a beating
between two close frequencies (see Sect. 1.1).
Another mathematically equivalent way of decomposing the frequencies starts
from the
simple assumption that in reality there are only two modes present in the
star, producing the observed frequency spectrum (frequency-amplitude diagram).
On the one hand, there is the main radial mode, which in the case of a fundamental mode
RRab pulsator, has a large amplitude and hence behaves nonlinearly.
We see the harmonics of this frequency up to a high order (up to order 11 in
this case).
On the other hand, we observe a frequency 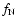 ,
close to the main frequency,
related to an additional mode.
Because of its frequency value (too close to a radial mode
frequency to be radial itself), this mode must be nonradial and, since it
has a small amplitude, it can be considered as behaving in a
linear fashion, at least in the zone where most of the pulsation takes place.
We note that a model of nonlinear
mode superposition was already proposed by Borkowski (1980) to explain the
Blazhko effect in the star AR Her as a result of double mode pulsation.
Balász & Detre (1943) also noted that the light variations of RR Lyr can
most easily be described by a superposition of two pulsations with frequencies
f0 and
,
close to the main frequency,
related to an additional mode.
Because of its frequency value (too close to a radial mode
frequency to be radial itself), this mode must be nonradial and, since it
has a small amplitude, it can be considered as behaving in a
linear fashion, at least in the zone where most of the pulsation takes place.
We note that a model of nonlinear
mode superposition was already proposed by Borkowski (1980) to explain the
Blazhko effect in the star AR Her as a result of double mode pulsation.
Balász & Detre (1943) also noted that the light variations of RR Lyr can
most easily be described by a superposition of two pulsations with frequencies
f0 and 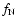 .
.
All frequencies occurring in the spectrum of RR Lyr can be explained through
combinations of the main frequency f0, its harmonics kf0
and the nonradial mode 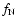 (see Fig. 3).
In this way, Eq. (3) can be rewritten as
(see Fig. 3).
In this way, Eq. (3) can be rewritten as
In this decomposition, referred to as the "two-frequency model'', the Blazhko
frequency is the result of a beating
between two real frequencies, since
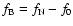 .
.
The two models expressed in Eqs. (3) and (4) are
mathematically equivalent (see also Tab. 3).
However, if the frequencies observed in the spectrum merely result from
linear combinations of f0 and 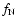 ,
the "two-frequency model'' may be more accurate.
This model explains the (equidistant) triplets in a natural way and may
even explain the unequal amplitudes in the triplet structures
observed in the majority of the Blazhko stars (see e.g.,
Alcock et al. 2003). The right side (higher frequency) peak in the triplet
at f0 corresponds
to the mode with frequency
,
the "two-frequency model'' may be more accurate.
This model explains the (equidistant) triplets in a natural way and may
even explain the unequal amplitudes in the triplet structures
observed in the majority of the Blazhko stars (see e.g.,
Alcock et al. 2003). The right side (higher frequency) peak in the triplet
at f0 corresponds
to the mode with frequency 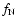 .
The right side peaks in the triplet
structures around the harmonics result from the sum combinations, whereas all
the left side (lower frequency) peaks can be explained by differences.
The left side peaks that are generally lower (and sometimes barely visible) may
be explained as the result of a combination with a higher harmonic.
This straightforward model raises a lot of complicated questions, e.g.,
concerning the nature of combination frequencies, their
amplitudes and phases, and the possible role of resonances,
but it is certainly worth further exploration.
.
The right side peaks in the triplet
structures around the harmonics result from the sum combinations, whereas all
the left side (lower frequency) peaks can be explained by differences.
The left side peaks that are generally lower (and sometimes barely visible) may
be explained as the result of a combination with a higher harmonic.
This straightforward model raises a lot of complicated questions, e.g.,
concerning the nature of combination frequencies, their
amplitudes and phases, and the possible role of resonances,
but it is certainly worth further exploration.
![\begin{figure}
\par\includegraphics[angle=0,width=8.5cm]{4415fig4.eps}\end{figure}](/articles/aa/full/2006/44/aa4415-05/Timg79.gif) |
Figure 4:
Top: the combined RR Lyr photometry of 2003-2004 folded
with the main pulsation period. The mean light curve derived
from all data is displayed as a solid line. Bottom: residuals after
subtraction of the mean light curve, clearly showing a phase interval
during which the brightness barely changes over the Blazhko cycle. |
| Open with DEXTER |
Figure 4 shows the combined RR Lyr V data folded
with the main pulsation period
f0=1.7641704 c/d (top panel), as well as
the residuals from the mean light curve (lower panel).
The mean light curve is defined by the components of the fit given in
Table 3, varying with only f0 and its 10 significant harmonics (up to 11
f0).
Figure 4 clearly displays an interval in the pulsation
cycle, roughly 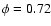 -0.82, during
which the star's intensity barely changes over the Blazhko cycle.
The "static'' phase interval is right after the bump and shortly before
the start of the steep ascending branch, during
the infalling motion and between the assumed phases of early and main shock (Gillet &
Crowe 1988).
Reduced scatter in the descending branch of Blazhko stars is a common
feature.
In the folded light curve of RR Lyrae as shown in Fig. 4, however, the
decrease in scatter is very distinct.
The folded
photographic
light curve of RR Lyr from the years 1943-1945 published by Szeidl &
Kolláth (2000, their Fig. 1) also indicates a slightly reduced scatter in
this phase interval.
The folded light curve of RR Lyr published by Smith et al. (2003) shows
the generally reduced scatter on the descending
branch, but the interval of even more reduced scatter shortly before
minimum light is
not as pronounced. This may be due to the shorter 1996 data set;
more data may have resulted in a more unambiguously "static'' phase interval.
However, other Blazhko stars seem not to show this feature, e.g.,
the folded light curve of XZ Cyg published by
LaCluyzé et al. (2004), or those of some Blazhko stars detected by the MACHO survey (see,
e.g., Kurtz et al. 2000, their Fig. 4). Is it still an open question
whether this feature is a unique, and coincidental, property of RR Lyr, or if it is also
observable in other Blazhko targets.
-0.82, during
which the star's intensity barely changes over the Blazhko cycle.
The "static'' phase interval is right after the bump and shortly before
the start of the steep ascending branch, during
the infalling motion and between the assumed phases of early and main shock (Gillet &
Crowe 1988).
Reduced scatter in the descending branch of Blazhko stars is a common
feature.
In the folded light curve of RR Lyrae as shown in Fig. 4, however, the
decrease in scatter is very distinct.
The folded
photographic
light curve of RR Lyr from the years 1943-1945 published by Szeidl &
Kolláth (2000, their Fig. 1) also indicates a slightly reduced scatter in
this phase interval.
The folded light curve of RR Lyr published by Smith et al. (2003) shows
the generally reduced scatter on the descending
branch, but the interval of even more reduced scatter shortly before
minimum light is
not as pronounced. This may be due to the shorter 1996 data set;
more data may have resulted in a more unambiguously "static'' phase interval.
However, other Blazhko stars seem not to show this feature, e.g.,
the folded light curve of XZ Cyg published by
LaCluyzé et al. (2004), or those of some Blazhko stars detected by the MACHO survey (see,
e.g., Kurtz et al. 2000, their Fig. 4). Is it still an open question
whether this feature is a unique, and coincidental, property of RR Lyr, or if it is also
observable in other Blazhko targets.
Nevertheless, this observational fact deserves a closer look; an alternative
way of approaching RR Lyrae light curves may
also provide new insight into the Blazhko problem.
From Table 3 it is clear that the right side peaks in the triplet structures
have higher amplitudes. The left side peak at
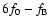 does not have
a higher signal-to-noise ratio than 3.5, and for the higher order side lobes
(from 8f0 onwards) always at least one of the side peak components
is below the 3.5-noise level.
does not have
a higher signal-to-noise ratio than 3.5, and for the higher order side lobes
(from 8f0 onwards) always at least one of the side peak components
is below the 3.5-noise level.
As Jurcsik et al. (2005) concluded from their analysis of RR Gem, the
amplitudes of the modulation components decrease much less steeply than the
amplitudes of the harmonics of the main frequency. This is also the case for
RR Lyr (see Table 3).
Table 4 lists the amplitude ratios, phase differences and their errors for
the first seven modulation component pairs, defined as
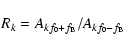 |
(5) |
and
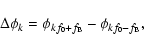 |
(6) |
where f0 is the radial mode frequency and 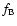 the Blazhko frequency.
In Table 4 we also display the so-called
asymmetry parameter
the Blazhko frequency.
In Table 4 we also display the so-called
asymmetry parameter
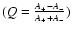 - introduced by
Alcock et al. (2003) -
to quantify the degree of asymmetry in the peaks.
For all the 731 Blazhko stars
detected by the MACHO survey, the asymmetry parameters show a rather broad
distribution and peaks at +0.3,
indicating that on
average the right side peaks in the triplets have amplitudes almost twice as
high as the left side peaks. (Note: -1.0/+1.0 refers to complete
asymmetry, 0 to a symmetric triplet.)
For the 2004 RR Lyr data, the error-weighted mean value of the asymmetry
parameter Q over the first 7 modulation component pairs is about +0.52. This
indicates a `higher-than-average' asymmetry to the right.
In this respect, however, we note that the quantification of this asymmetry is
subject to some uncertainty.
This was nicely illustrated by Jurcsik et al. (2005), who checked the
stability of their results by analyzing
different subsets of their extensive data set on the low amplitude Blazhko star
RR Gem, and concluded that the phase coverage over the Blazhko cycle affects
the amplitudes of the observed side lobes.
- introduced by
Alcock et al. (2003) -
to quantify the degree of asymmetry in the peaks.
For all the 731 Blazhko stars
detected by the MACHO survey, the asymmetry parameters show a rather broad
distribution and peaks at +0.3,
indicating that on
average the right side peaks in the triplets have amplitudes almost twice as
high as the left side peaks. (Note: -1.0/+1.0 refers to complete
asymmetry, 0 to a symmetric triplet.)
For the 2004 RR Lyr data, the error-weighted mean value of the asymmetry
parameter Q over the first 7 modulation component pairs is about +0.52. This
indicates a `higher-than-average' asymmetry to the right.
In this respect, however, we note that the quantification of this asymmetry is
subject to some uncertainty.
This was nicely illustrated by Jurcsik et al. (2005), who checked the
stability of their results by analyzing
different subsets of their extensive data set on the low amplitude Blazhko star
RR Gem, and concluded that the phase coverage over the Blazhko cycle affects
the amplitudes of the observed side lobes.
For RR Lyr, however, following the studies of Szeidl & Kollath (2000, and
references therein) and
Smith et al. (2003), all present photometric data sets of RR Lyr show the
higher-frequency side lobes to have higher amplitudes. This consistent
picture points to a real
difference in the amplitudes of the modulation components.
Table 4:
Side lobe amplitude ratios Rk, phase differences
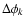 (in degrees) and asymmetry
parameters Q as defined in the
text, and their respective
errors for the 2004 photometric V data.
k denotes the multiplet order.
(in degrees) and asymmetry
parameters Q as defined in the
text, and their respective
errors for the 2004 photometric V data.
k denotes the multiplet order.
The temporal variation of the light curve shape parameters may provide
decisive information about the Blazhko mechanism that can be used to
eliminate some models for the Blazhko phenomenon.
A powerful tool for analyzing and comparing light curves of pulsating stars is
provided by Fourier decomposition, a technique first applied by Simon & Lee (1981).
![\begin{figure}
\par\includegraphics[angle=0,width=12cm]{4415fig5.eps}\end{figure}](/articles/aa/full/2006/44/aa4415-05/Timg87.gif) |
Figure 5:
Pulsation light curves (thick solid lines) constructed from the data
(dots) falling into the 0.1
phase intervals of the Blazhko cycle. The mean light curve over all Blazhko
phase intervals is also shown as a thin solid line. |
| Open with DEXTER |
The calculated Fourier parameters that are the amplitude ratios
and the epoch-independent phase differences
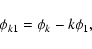 |
(8) |
offer a way to quantify the
asymmetry of
the lightcurves. Nearly sinusoidal light curves (like, e.g., of RRc stars)
lead to low amplitude ratios and large phase differences, whereas the opposite
holds for highly asymmetric light curves.
Our 2004 data were divided into 10 subsets, corresponding to uniformly
distributed phase intervals throughout the Blazhko cycle (e.g., 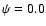 -0.1,
-0.1, 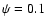 -0.2,
etc.),
where Blazhko phase
-0.2,
etc.),
where Blazhko phase 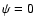 is defined as the phase of maximum
Blazhko amplitude.
The minimum and maximum numbers of data in these subsets are 797 and 3082.
The time base for each of these intervals, as well as the number of data used
to construct the mean light curves, are listed in Table 5.
For each of the Blazhko phase intervals, we determined a mean light curve.
Figure 5 shows the data for each of the intervals, the
mean light curves obtained from these data per Blazhko phase interval,
as well as the mean
light curve derived from the fit to all data.
is defined as the phase of maximum
Blazhko amplitude.
The minimum and maximum numbers of data in these subsets are 797 and 3082.
The time base for each of these intervals, as well as the number of data used
to construct the mean light curves, are listed in Table 5.
For each of the Blazhko phase intervals, we determined a mean light curve.
Figure 5 shows the data for each of the intervals, the
mean light curves obtained from these data per Blazhko phase interval,
as well as the mean
light curve derived from the fit to all data.
Table 5:
Log on the subsets of 2004 observations used to construct the light
curves at different phase intervals in the Blazhko cycle.
When defining mean light curves over a Blazhko phase interval, one has to
deal with two sources of uncertainties:
- 1.
- For RR Lyr, a Blazhko phase interval with a width of 0.1 corresponds to
almost 4 days. At some phases in the Blazhko cycle, especially
those around maximum light, the light curves change very rapidly.
Hence, we stress that the values of the Fourier parameters given in this
paper correspond to mean values per Blazhko phase interval.
- 2.
- On the other hand, it is known that the Blazhko effect changes in
strength, and that it may not exactly repeat from one cycle to the
next, as mentioned in Sect. 3.1. Additional
periodicities, as were found by Walraven (1949) and
Fringant (1961), could not be disentangled from this data set.
The variations may also be caused by
nonperiodic changes in the light curve shape. All of these factors
represent an
additional source of uncertainty in defining the
"mean light curves'' per Blazhko phase interval.
However, our data have been gathered over a rather short time span compared
to the "4-year cycle'' and the light curves from Blazhko intervals of
subsequent cycles overlap quite well.
We have based the error calculations for the Fourier parameters in this paper
on the residuals of the fit given by the mean light curve per Blazhko
interval. This implies that if the scatter around the mean light curve per
Blazhko interval is quite large, which is especially the case around maximum
Blazhko amplitude (see Fig. 5), the error bars on the mean light curve as
well as those on the derived Fourier parameters will become larger. (Note that
a higher number of fitted data points also lowers the errors.)
Nevertheless, we call for
caution in interpreting these "mean light curves'', and stress that the
light curves, and their characteristics shown in Figs. 5-7, are
representative for this data set. We cannot exclude that there is
an influence of as yet unknown periodicities on the mean light curves.
For data gathered at another time,
the picture may change. Therefore, it would be interesting to follow up on
RR Lyr and the changes in its Blazhko behavior.
A first inspection of the mean light curves at different Blazhko phases
reveals that RR Lyr shows both amplitude and phase modulation. The ascending
branch moves back and forth in the course of the Blazhko cycle.
Figure 6 shows the pulsation phases of maximum and minimum light, as a
function of the Blazhko phase, as well as the difference in phase between minimum and
maximum light.
Balázs & Detre (1943) found that the time interval
between minimum and maximum varies between 0.067 (at 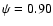 )
and
0.121 (at
)
and
0.121 (at 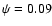 ). We find larger values ranging from 0.14 (
). We find larger values ranging from 0.14 ( 0.02) to 0.21
(
0.02) to 0.21
( 0.02), with the lower values during the first half of the Blazhko
cycle and a steep increase around the minimum of the Blazhko amplitude. This observation
illustrates that the light curves observed by Balász & Detre (1943) had
branches ascending more steeply than the ones we observed. There is no strict
repetition of the light curve shape from one Blazhko
cycle to the next, as already shown from our data set spanning 10 Blazhko
cycles. Additionally, the so-called "4-year cycle'' (Detre & Szeidl 1973)
known from the literature,
is connected with stronger and weaker phases of the Blazhko effect.
0.02), with the lower values during the first half of the Blazhko
cycle and a steep increase around the minimum of the Blazhko amplitude. This observation
illustrates that the light curves observed by Balász & Detre (1943) had
branches ascending more steeply than the ones we observed. There is no strict
repetition of the light curve shape from one Blazhko
cycle to the next, as already shown from our data set spanning 10 Blazhko
cycles. Additionally, the so-called "4-year cycle'' (Detre & Szeidl 1973)
known from the literature,
is connected with stronger and weaker phases of the Blazhko effect.
![\begin{figure}
\par\includegraphics[angle=0,width=7.7cm]{4415fig6.eps}\end{figure}](/articles/aa/full/2006/44/aa4415-05/Timg95.gif) |
Figure 6:
Pulsation phase of maximum light ( top), of minimum light ( center),
and pulsation phase interval between minimum and maximum
light ( bottom) as a function of the phase in the Blazhko cycle. |
| Open with DEXTER |
In the mean light curves (see Fig. 5), the so-called bump, the slight increase
in the brightness at a pulsation phase
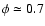 ,
gets more pronounced
at certain Blazhko phases, e.g.,
,
gets more pronounced
at certain Blazhko phases, e.g., 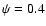 -0.5. It also seems that the
bump occurs later closer to the phase of Blazhko maximum.
A clear hump (a slight hesitation in the course of the
light increase at
-0.5. It also seems that the
bump occurs later closer to the phase of Blazhko maximum.
A clear hump (a slight hesitation in the course of the
light increase at
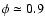 )
can be seen in the Blazhko phase
interval
)
can be seen in the Blazhko phase
interval 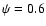 -0.8.
The bump is usually associated with the early shock in the atmospheres of
RR Lyrae stars, and the hump with the main shock, though there is no
consensus on the exact relationships between the shock waves and the
luminosity variations yet (see, e.g., Gillet & Crowe 1988; Carney et al. 1992).
-0.8.
The bump is usually associated with the early shock in the atmospheres of
RR Lyrae stars, and the hump with the main shock, though there is no
consensus on the exact relationships between the shock waves and the
luminosity variations yet (see, e.g., Gillet & Crowe 1988; Carney et al. 1992).
A higher-order harmonic fit was made to the mean light curve defined for each
of the subsets, according to:
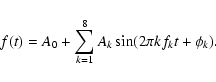 |
(9) |
The changes in the light curve shape are most pronounced in the height of
maximum which itself varies strongly. These variations occur so quickly
that for some 0.1-phase intervals the portions of light curves observed within
an interval of some days already show a rather large scatter.
Hence the fit to the curve yields mean values with larger error bars for
the Fourier parameters.
The course of the Fourier parameters over the Blazhko cycle is given in
Figure 7.
Note that the maximum in the amplitude ratios does not
occur at the highest Blazhko amplitude 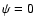 ,
but rather in the phase
interval
,
but rather in the phase
interval 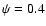 -0.5.
Indeed, the amplitudes A1 decrease more steeply towards the Blazhko minimum
than the amplitudes of the harmonics of the main frequency.
Our observed Fourier parameters fall within the range of theoretical values
calculated by Dorfi & Feuchtinger (1999) and Feuchtinger (1999).
Fitting the observed changes in the Fourier
parameters with subsequent hydrodynamical models for a given period would
be a challenging and informative confrontation between theoretical work and
observations.
Finally, we note that the value of [Fe/He] calculated from the period and
the Fourier parameter
-0.5.
Indeed, the amplitudes A1 decrease more steeply towards the Blazhko minimum
than the amplitudes of the harmonics of the main frequency.
Our observed Fourier parameters fall within the range of theoretical values
calculated by Dorfi & Feuchtinger (1999) and Feuchtinger (1999).
Fitting the observed changes in the Fourier
parameters with subsequent hydrodynamical models for a given period would
be a challenging and informative confrontation between theoretical work and
observations.
Finally, we note that the value of [Fe/He] calculated from the period and
the Fourier parameter 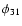 close to its lowest value around Blazhko
maximum phase (4.99 in the sine
frame, 1.85 in the cosine frame - see Fig. 7) with the formula given
by Kovács & Jurcsik
(1996) yields the known [Fe/H] = -1.39 of RR Lyr (Beers et al. 2000).
close to its lowest value around Blazhko
maximum phase (4.99 in the sine
frame, 1.85 in the cosine frame - see Fig. 7) with the formula given
by Kovács & Jurcsik
(1996) yields the known [Fe/H] = -1.39 of RR Lyr (Beers et al. 2000).
We calculated mean brightnesses and intensities for each of the phase
intervals. Unfortunately, the accuracy of this data set did not allow us to
detect a significant variation in the mean brightness or intensity of RR
Lyr over the Blazhko cycle. This implies that the mean brightness variations
do not exceed 0.02 mag.
From a survey on 731 Blazhko variables, Alcock et al. (2003) conclude that there is a
variation with the Blazhko period having an overal amplitude of about 0.006 mag
in the average brightness of the stars.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4415fig7.eps}\end{figure}](/articles/aa/full/2006/44/aa4415-05/Timg102.gif) |
Figure 7:
Fourier parameters of the V light curve in different phases of the
Blazhko cycle. Upper panel: amplitudes in mag. Middle panel: amplitude
ratios as defined in the text. Lower panel: epoch-independent phase
differences in radians and with respect to a cosine frame, to allow comparsion
with the theoretical Fourier parameters calculated by Feuchtinger (1999). |
| Open with DEXTER |
In their present form, neither of the two models discussed in Sect. 1.1
satisfactorily explains the
variety of features diplayed by Blazhko stars, though some of these
peculiarities have been partially accounted for. For instance, Van Hoolst et al. (1998)predict a higher probablity of excitation of nonradial modes for
RRab stars than for RRc stars, though not in the degree observed. A few other
examples of still insufficiently resolved characteristics are the asymmetry of
the side peaks, and the tendency of the right side peak in the triplets to be
higher, both of which were confirmed by our observations of RR Lyr.
Models should also explain why some Blazhko stars show pure amplitude
modulation, some pure phase modulation, and others both types of modulation.
RR Lyrae clearly shows both.
Note that quintuplet structures in the
frequency spectra of RR Lyrae stars have never been observed convincingly
enough to conclude their reality (Alcock et al. 2000, 2003; Moskalik & Poretti
2003). In line with the previous studies, the present data set reveals
no significant quintuplet frequencies.
It is also clear from this data set that the amplitudes of the modulation
components in the frequency spectrum decrease much less steeply than the
amplitudes of the harmonics of the main radial frequency. This observation
was already made by Jurcsik et al. (2005) in their analysis of photometric
data of the Blazhko star RR Gem. Any valid model for the Blazhko effect
should also account for this observation.
The identification of the nonradial modes in modulated RR Lyrae stars
is essential for narrowing down the possible explanations for the Blazhko
effect. High-resolution spectroscopic data are the best diagnostic for
finding and identifying nonradial modes in pulsating stars.
Earlier results obtained from spectroscopic data (Kolenberg et al. 2003)
pointed towards the presence of a nonradial mode with low degree,
in agreement with the models, but not discriminating
among them. A more precise identification was hampered by the
limited signal-to-noise ratio of the data and the incomplete sampling over the
Blazhko cycle.
A combined photometric and
spectroscopic campaign carried out over several Blazhko cycles is the best way
to observationally assess the Blazhko problem.
Our observation of a "static'' phase interval in the pulsation cycle
(Sect. 3.3), during which the
star's intensity barely changes over the Blazhko cycle, may shed
new light upon approaches to explain the Blazhko effect. It occurs between
the phases of early and main shock in the star, associated with respectively
the bump and the hump.
It would be interesting to investigate whether other Blazhko stars show a similar feature.
Furthermore, the obvious changes in the strength and position of the
bump over the Blazhko cycle, observed in RR Lyr and other Blazhko stars, deserve a more profound study. Depending on its
origin,
still a matter of controversy,
the bump can provide a clue about the
star's interior structure or its pulsational behavior.
Two competing models have been proposed to explain the bump.
For a more detailed description of the "infall hypothesis'' and the `echo
model', we refer to Gillet & Crowe (1988) and Carney et al. (1992).
From our data set, there is no clear indication of any change in the
Blazhko phase between the data recorded in 2003 and those gathered in 2004,
nor any strong indication for the end of a longer cycle during our
2004 observations.
It would be interesting to find out whether the "4-year cycle'' of RR Lyr is
still as prominent as it was over the past half century, and how well it
really describes the long-term behavior of RR Lyr. Future photometric data of
RR Lyr can serve this purpose.
Not only the amplitude but also the length of the secondary period seems to be
variable.
As was reported by Szeidl & Kolláth (2000), RR Lyr's
primary period has shown small increases and decreases since its discovery in
1901. No regularity can be found in the changes of the primary period.
An important result following from the present data set on RR Lyr is that
the Blazhko period, previously known to be about 40.8 days, has become
notably shorter. Our analysis points towards a Blazhko period of about
39 days.
A shorter Blazhko period for RR Lyr was already pointed out by Belserene
(1999) who obtained 161 differential B measurements over a total time span
of 477 days in 1993 and 1994. She finds a prominent secondary peak in the
data at 1.7897 c/d, corresponding to our
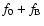 or
or 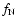 .
Her best frequencies for the main pulsation and the side peak frequency point
towards a Blazhko period of 39.2 days, though the error bars are larger than
the ones derived from the present data set.
Smith et al. (2003) analyzed 2573 differential B and 2461 differential V
data spanning a 77-day interval in 1996. From their fits to the data they find
a value of
.
Her best frequencies for the main pulsation and the side peak frequency point
towards a Blazhko period of 39.2 days, though the error bars are larger than
the ones derived from the present data set.
Smith et al. (2003) analyzed 2573 differential B and 2461 differential V
data spanning a 77-day interval in 1996. From their fits to the data they find
a value of 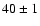 day for the Blazhko period, adding weight to the
observations made by Belserene (1999).
Our much denser data set spans 10 consecutive Blazhko cycles, and hence leads
to smaller error bars on the frequencies. We can
now safely state that the Blazhko period is about 39 days, shorter than the
previously mentioned value of 40.8 days. Belserene's (1999) data indicate
that already in 1993-1994 the Blazhko period appeared to be shorter.
day for the Blazhko period, adding weight to the
observations made by Belserene (1999).
Our much denser data set spans 10 consecutive Blazhko cycles, and hence leads
to smaller error bars on the frequencies. We can
now safely state that the Blazhko period is about 39 days, shorter than the
previously mentioned value of 40.8 days. Belserene's (1999) data indicate
that already in 1993-1994 the Blazhko period appeared to be shorter.
The changing Blazhko period of RR Lyr reminds one of the recent
results published by LaCluyzé et al. (2004) on the changing Blazhko
period of XZ Cyg.
During the first half of the 20th century, XZ Cyg had a Blazhko period of
about 57.4 days. Starting in 1965, the primary period underwent a steep decline
(in several steps), accompanied by an increase in the Blazhko period to 58.5
days.
Extensive analyses of old and new photometry of XZ Dra (Jurcsik et al. 2002b)
and RV UMa (Kanyo 1976; Kovacs 1995) confirmed that these stars also show
coincident changes in their Blazhko period and primary period. These changes
have different signs and orders of magnitude.
Any theoretical explanation that requires the Blazhko period to be exactly
equal or directly proportional to the rotation period of the star would imply
changes in the star's rotation rate.
Table 6:
Published Blazhko periods from some previous data sets of RR Lyr. If error
bars are given in the publication, they are added. We stress that
this table is far from exhaustive, but just indicative of the likely change of the
star's Blazhko period.
Throughout the literature on RR Lyr, there has always been mention of a Blazhko
period of about 41 days.
Prager (1916) was the first to find the secondary oscillation in the phases of
RR Lyr's light maxima from data by Wendell (1909, 1914). Shapley (1916) investigated the changes in spectrum,
period, and light curve of RR Lyr, and obtained a secondary period of 40
days.
Struve & Blaauw (1948) found the radial velocity curve to oscillate with a
period of approximately 75 pulsation cycles, or about 42 days.
Walraven
(1949) published the first photoelectric observations of RR Lyr, also
performed in
1947, mentioning a
41-day cycle.
Fringant (1961) describes RR Lyr's secondary cycle as the mean value of 72
primary cycles, resulting in a period of 40.8 days.
The important study by
Preston et al. (1965) makes notice of a modulation period of 41 days, and
adopts Fringant's (1961) published value.
Table 6 shows a summary of the Blazhko periods of RR Lyr quoted in
previous papers devoted to the star.
Unfortunately, error bars on the Blazhko period are rarely given.
Note that this table only contains a listing of some of the
main published data sets of RR Lyr. An exhaustive analysis of all still
available
previous data sets is beyond the scope of this paper. Nevertheless, we think
this concise overview is important to show that the Blazhko period indeed has
become shorter.
It would be interesting to know when the change in the Blazhko period began,
and whether it took place abruptly or rather continuously.
As mentioned above, data gathered in 1993 (Belserene 1999) and 1996 (Smith et al. 2003) already indicated a shorter Blazhko period.
In the cases of XZ Cyg, XZ Dra and RV UMa, the
change in the Blazhko period was associated with a change in the fundamental
period.
As with many RR Lyrae stars, the main
period of RR Lyr has been subject to strong variation, in which no regularity
can be noticed.
The O-C diagram for the primary period of RR Lyr shown in the review by
Szeidl & Kollath (2000) (their Fig. 3) spanning a century of observations
(1899-1999)
presents a series of ups and downs. The data from
Struve & Blaauw (1948) and Walraven (1949)
have been taken when the O-C diagram shows a steep decline.
The same is true for the data published by Fringant (1961), which were
gathered between 1947 and 1959.
The O-C diagrams published by Balász-Detre & Detre (1962) and by Szeidl
(1976, his Fig. 7) display that the changes in both the
pulsation period and Blazhko period in RR Lyr were at times parallel, at
other times antiparallel, which makes it hard to draw firm conclusions about
the relation between the period changes in RR Lyr.
The constancy or variability of the primary period is connected with the
interesting but still unanswered question of what initiated the change in the
Blazhko period.
![\begin{figure}
\par\includegraphics[angle=270,width=8.7cm]{4415fig8.eps}\end{figure}](/articles/aa/full/2006/44/aa4415-05/Timg112.gif) |
Figure 8:
Residuals after
subtraction of the fit to the data described in Table 3. There is an
increased scatter around the phase of maximum light. |
| Open with DEXTER |
From our data set no further significant frequencies could be detected.
However,
as Fig. 8 shows,
the residuals from the fit still show scatter, especially around the
phase of light maximum.
The enhanced scatter around maximum light may be in part a consequence of
the difficulties of fitting a steep function (the rising branch) with a
Fourier series.
On the other hand, the scatter in the residuals could also indicate
the presence of periodic or nonperiodic changes in the light curve.
But since the mean residual value (0.021 mag) is of the order of the noise
level in the data set, we can draw no conclusions about its cause.
Additional third and fourth frequencies in the light curve of RR Lyr were
identified by Walraven (1949) and Fringant (1961), but the long-term existence
of these cycles has not yet been established.
Therefore, follow-up campaigns devoted to RR Lyr are of great scientific
importance.
In this paper we present the results of a frequency analysis of an extensive
set of photometric data of the Blazhko star RR Lyr, which was obtained with
six different telescopes and over a total time span of more than 10 Blazhko
cycles in 2003 and 2004. The main results can be summarized as follows.
- The light curves spanning over 10 Blazhko cycles can be satisfactorily
represented by a Fourier sum with frequencies of the form of kf0,
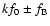 ,
with
k=0,1,...,11,
,
with
k=0,1,...,11,
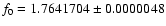 c/d, and
c/d, and
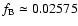 c/d.
An alternative representation was proposed in Sect. 2.2 of
this paper, decomposing the variation in terms of combinations of
the main frequency f0,
its harmonics and one additional nonradial mode connected to the frequency
c/d.
An alternative representation was proposed in Sect. 2.2 of
this paper, decomposing the variation in terms of combinations of
the main frequency f0,
its harmonics and one additional nonradial mode connected to the frequency
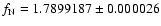 c/d, which has smaller amplitude and
behaves in a linear fashion.
c/d, which has smaller amplitude and
behaves in a linear fashion.
-
However, there is some residual scatter after subtraction of the best fit
obtained for the data. From this data set, we were not able to disentangle
additional frequencies.
-
The new data reveal that the Blazhko period, previously known
to be about 40.8 days, has become remarkably shorter with a value of about
38.8 days. Similar observations have been made for other Blazhko stars,
constraining the possible explanations for the Blazhko effect.
-
Moreover, our data show that there is a phase interval (
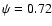 -0.82) in the
pulsation
cycle, right after the
phase of the so-called bump, during which
the star's intensity barely
changes over the Blazhko cycle.
-0.82) in the
pulsation
cycle, right after the
phase of the so-called bump, during which
the star's intensity barely
changes over the Blazhko cycle.
-
As in the majority of amplitude and phase modulated RRab stars, and as shown
by previous studies of the target, the triplet
structures observed in the frequency spectrum of RR Lyr show a strong
asymmetry to the right. This still puzzling statistical fact may be
explained by the simple Fourier decomposition into combination frequencies
proposed in Sect. 3.2, in which the left side peaks within the same
triplet result from a combination with a higher order harmonic than the
right side peaks and hence have a smaller amplitude.
The simple picture may be disturbed by resonances in the star,
which could enhance or diminish the actually observed amplitudes of the
frequencies.
-
A study of the variations of the light curve shape over the Blazhko cycle
reveals that the strong amplitude and phase modulation in RR Lyr is
accompanied by changes in the shape (and position) of the bump, and that the
hump is only observed at certain Blazhko phases.
Fourier parameters prove very useful to quantize the degree of asymmetry of the
light curves.
Data covering several complete Blazhko cycles would be needed to find
out if such changes in the light curve shape repeat similarly from one Blazhko
cycle to the next.
The data set described and analyzed in this paper was obtained in the
framework of a combined photometric and spectroscopic campaign devoted to RR
Lyrae (see Sect. 1.2).
Such combined campaigns, yielding long-term accurate photometry as well as
time-resolved, high-signal-to-noise, high-resolution spectroscopy,
carried out over
several Blazhko cycles are the best way
to observationally assess the Blazhko problem.
Acknowledgements
Part of this investigation has been supported by the Austrian Fonds zur
Förderung der wissenschaftlichen Forschung, project number P17097-N02.
HAS thanks the US National
Science Foundation for support under grant AST-0205813.
This research has made use of the SIMBAD database, operated at CDS Strasbourg,
France. KK is grateful to Bela Szeidl, Johanna Jurcsik and Geza Kovács for
fruitful discussions.
We thank the referee for useful comments and suggestions.
- Alcock, C.,
Allsman, R., Alves, D. R., et al. 2000, ApJ, 542, 257 [NASA ADS] [CrossRef] (In the text)
- Alcock, C.,
Alves, D. R., Becker, A., et al. 2003, ApJ, 589, 597 [NASA ADS] [CrossRef] (In the text)
- Balász,
J., & Detre, L. 1943, Communications of the Konkoly
Observatory, No. 18, 125
(In the text)
-
Balázs-Detre, J., & Detre, L. 1962, Veroeffentlichungen
der Remeis-Sternwarte zu Bamberg, 27, 90 [NASA ADS] (In the text)
- Beers, T. C.,
Chiba, M., Yoshii, Y., et al. 2000, AJ, 119, 2866 [NASA ADS] [CrossRef] (In the text)
-
Belserene, E. P. 1999, in Anni Mirabiles: A Symposium Celebrating
the 90th Birthday of Dorrit Hoffleit, ed. A. G. Davis Philip, W. F.
Van Altena, & A. R. Upgren, Schenectady: L. David Press,
85
(In the text)
- Blazhko, S.
N. 1907, Astron. Nachr., 173, 325 [NASA ADS] (In the text)
- Breger, M.,
Stich, J., Garrido, R., et al. 1993, A&A, 271, 482 [NASA ADS] (In the text)
- Breger, M.,
Handler, G., Garrido, R., et al. 1999, A&A, 349, 225 [NASA ADS] (In the text)
-
Borkowski, K. J. 1980, Acta Astronomica, 30, 393 [NASA ADS] (In the text)
- Carney, B. W.,
Storm, J., Trammell, S. R., & Jones, R. V. 1992, PASP, 104,
44 [NASA ADS] [CrossRef] (In the text)
- Castelaz,
M. W., Persinger, T., Stein, J. W., Prosser, J., & Powell, H.
D. 1991, Astron. J., 102, 2103 [NASA ADS] [CrossRef] (In the text)
- Chadid, M.,
& Gillet, D. 1997, A&A, 319, 154 [NASA ADS] (In the text)
- Chadid, M.,
Kolenberg, K., Aerts, C., & Gillet, D. 1999, A&A, 352,
201 [NASA ADS] (In the text)
- Chadid, M.,
Wade, G. A., Shorlin, S. L. S., & Landstreet, J. D. 2004,
A&A, 413, 1087 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Cousens, A.
1983, MNRAS, 203, 1171 [NASA ADS]
- Detre, L., &
Szeidl, B. 1973, in Variable Stars in Globular Clusters and Related
Systems, ed. J. D. Fernie (D. Reidel Publishers), 31
(In the text)
- Dorfi, E. A.,
& Feuchtinger, M. U. 1999, A&A, 348, 815 [NASA ADS] (In the text)
-
Feuchtinger, M. U. 1999, A&A, 351, 103 [NASA ADS] (In the text)
- Fringant,
A.-M. 1961, Journal des Observateurs, 44, 165 [NASA ADS] (In the text)
- Gillet, D.,
& Crowe, R. A. 1988, A&A, 199, 242 [NASA ADS] (In the text)
-
Jerzykiewicz, M., Handler, G., Shobbrook, R. R., et al. 2005,
MNRAS, 360, 619 [NASA ADS] [CrossRef] (In the text)
- Handler, G.,
Arentoft, T., Shobbrook, R. R., et al. 2000, MNRAS, 318, 511 [NASA ADS] (In the text)
- Jurcsik, J.,
& Kovács, G. 1996, A&A, 312, 111 [NASA ADS]
- Jurcsik,
J., Benko, J. M., & Szeidl, B. 2002a, A&A, 390, 133 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Jurcsik,
J., Benko, J. M., & Szeidl, B. 2002b, A&A, 396, 539 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Jurcsik, J.,
Sodor, A., Varadi, M., et al. 2005, A&A, 430, 1049 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Kanyo, S. 1976,
Comm. Konkoly Observatory Budapest, 69, 1 [NASA ADS] (In the text)
-
Kolenberg, K., Aerts, C., Fokin, A., et al. 2003a, ASP Conf. Ser.,
292, 171 [NASA ADS] (In the text)
-
Kolenberg, K. 2005, ASP Conf. Ser., 335, 95 [NASA ADS] (In the text)
- Kovács, G.
1995, A&A, 295, 693 [NASA ADS] (In the text)
- Kovács, G.
2001, in Stellar pulsation - nonlinear studies, ed. M. Takeuti
& D. D. Sasselov, Astrophysics and space science library
(Dordrecht: Kluwer Academic Publishers), 257, 61
(In the text)
- Kovács, G.
2005, A&A, 438, 227 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Kurtz, D. W.
1982, MNRAS, 200, 807 [NASA ADS] (In the text)
- Kurtz, D. W.,
Alcock, C., Allsman, R. A., et al. 2000, ASP Conf. Ser. 203, ed. L.
Szabados, & D. W. Kurtz, 291
(In the text)
-
LaCluyzé, A., Smith, H. A., Gill, E.-M., et al. 2004, AJ, 430,
1049 (In the text)
- Lenz, P., &
Breger, M. 2005, Comm. in Asteroseismology, 146, 53 [NASA ADS]
-
Montgomery, M. H., & O'Donoghue, D. 1999, Delta Scuti
Newslett., No. 13
(In the text)
- Moskalik,
P., & Poretti, E. 2003, A&A, 398, 213 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Nowakowski, R. M., & Dziembowski, W. A. 2001, Acta Astron., 51,
5 [NASA ADS] (In the text)
- Prager, R.
1916, Sitzb. Ak. Berlin, 8, 216 (In the text)
- Preston, G.
W., Smak, J., & Paczynski, B. 1965, ApJS, 12, 99 [NASA ADS] [CrossRef] (In the text)
- Romanov, Yu.
S., Udovichenko, S. N., & Frolov, M. S. 1994, Bul. Spec.
Astrophys. Obs., 38, 169 [NASA ADS] (In the text)
- Shapley, H.
1916, ApJ, 43, 217 [NASA ADS] [CrossRef] (In the text)
-
Shibahashi, H., & Takata, M. 1995, ASP Conf. Ser., 83, 42 [NASA ADS] (In the text)
- Smith, H. A.,
Barnett, M., Silbermann, N. A., & Gay, P. 1999, AJ, 118,
572 [NASA ADS] [CrossRef]
- Smith, H. A.,
Church, J. A., Fournier, J., et al. 2003, PASP, 115, 43 [NASA ADS] [CrossRef] (In the text)
- Simon, N.
R., & Lee, A. S. 1981, ApJ, 248, 291 [NASA ADS] [CrossRef]
- Struve, O.,
Blaauw, A. 1948, ApJ, 108, 60 [NASA ADS] [CrossRef] (In the text)
- Szeidl, B.
1976, in Multiple Periodic Variable Stars, ed. W. S. Fitch (D.
Reidel Publishers, ASSL, 60, 133)
(In the text)
- Szeidl, B.
1988, in Multimode Stellar Pulsations, ed. G. Kovacs, L. Szabados
& B. Szeidl, Budapest: Konkoly Observatory, Kultura, 45
(In the text)
- Szeidl, B.,
Guinan, E. F., Olah, K., & Szabados, L. 1997, Communications of
the Konkoly Observatory, No. 99
(In the text)
- Szeidl, B.,
& Kolláth, Z. 2000, ASP Conf. Ser., 203, 281 [NASA ADS] (In the text)
- Teays, T. J.
1993, in New Perspectives on Stellar Pulsations and pulsating
variable stars, ed. Nemec & Matthews, Proc. IAU Coll., 139,
410
(In the text)
- Van
Hoolst, T., Dziembowski, W. A., & Kawaler, S. D. 1998, MNRAS,
297, 536 [NASA ADS] [CrossRef] (In the text)
- Walraven,
T. 1949, Bull. Astron. Inst. Netherlands, 11, 17 [NASA ADS] (In the text)
- Wendell, O.
C. 1909, Harvard Annals, 69, Part I, 45
(In the text)
- Wendell, O.
C. 1914, Harvard Annals, 69, Part II, 124
(In the text)
Copyright ESO 2006
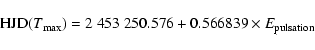
![\begin{figure}
\par\includegraphics[bb= 64 101 499 700,width=7.7cm,clip]{4415fig1.eps}\end{figure}](/articles/aa/full/2006/44/aa4415-05/Timg14.gif)
![\begin{figure}
\par\includegraphics[angle=0,width=13.5cm]{4415fig2.eps}\end{figure}](/articles/aa/full/2006/44/aa4415-05/Timg16.gif)
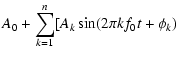
![\begin{figure}
\par\includegraphics[angle=0,width=6.5cm]{4415fig3.eps}\end{figure}](/articles/aa/full/2006/44/aa4415-05/Timg74.gif)
![\begin{figure}
\par\includegraphics[angle=0,width=8.5cm]{4415fig4.eps}\end{figure}](/articles/aa/full/2006/44/aa4415-05/Timg79.gif)
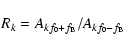
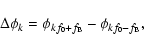
![\begin{figure}
\par\includegraphics[angle=0,width=12cm]{4415fig5.eps}\end{figure}](/articles/aa/full/2006/44/aa4415-05/Timg87.gif)
![\begin{figure}
\par\includegraphics[angle=0,width=7.7cm]{4415fig6.eps}\end{figure}](/articles/aa/full/2006/44/aa4415-05/Timg95.gif)
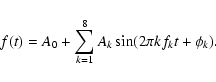
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4415fig7.eps}\end{figure}](/articles/aa/full/2006/44/aa4415-05/Timg102.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.7cm]{4415fig8.eps}\end{figure}](/articles/aa/full/2006/44/aa4415-05/Timg112.gif)