A&A 459, 391-406 (2006)
DOI: 10.1051/0004-6361:20053134
Y. Schuberth1,2 - T. Richtler2 - B. Dirsch2 - M. Hilker1 - S. S. Larsen3 - M. Kissler-Patig3 - U. Mebold1
1 - Argelander-Institut für Astronomie![]() ,
Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
,
Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
2 -
Universidad de Concepción, Departamento de Física, Casilla
160-C, Concepción, Chile
3 - European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
Received 26 March 2005 / Accepted 6 April 2006
Abstract
Context. We present the first dynamical study of the globular cluster system of NGC 4636. It is the southernmost giant elliptical galaxy of the Virgo cluster and is claimed to be extremely dark matter dominated, according to X-ray observations.
Aims. Globular clusters are used as dynamical tracers to investigate, by stellar dynamical means, the dark matter content of this galaxy.
Methods. Several hundred medium resolution spectra were acquired at the VLT with FORS 2/MXU. We obtained velocities for 174 globular clusters in the radial range
![]() ,
or
,
or
![]() in units of effective radius. Assuming a distance of 15 Mpc, the clusters are found at projected galactocentric distances in the range 4 to 70 kpc, the overwhelming majority within 30 kpc. The measured line-of-sight velocity dispersions are compared to Jeans-models.
in units of effective radius. Assuming a distance of 15 Mpc, the clusters are found at projected galactocentric distances in the range 4 to 70 kpc, the overwhelming majority within 30 kpc. The measured line-of-sight velocity dispersions are compared to Jeans-models.
Results. We find some indication of a rotation of the red (metal-rich) clusters about the minor axis. Out to a radius of 30 kpc, we find a roughly constant projected velocity dispersion for the blue clusters of
![]() .
The red clusters are found to have a distinctly different behavior: at a radius of about 3
.
The red clusters are found to have a distinctly different behavior: at a radius of about 3![]() ,
the velocity dispersion drops by
,
the velocity dispersion drops by ![]()
![]() to about
to about
![]() ,
which then remains constant out to a radius of 7
,
which then remains constant out to a radius of 7![]() .
The cause might be the steepening of the number density profile at
.
The cause might be the steepening of the number density profile at ![]()
![]() observed for the red clusters. Using only the blue clusters as dynamical tracers, we perform Jeans-analyses for different assumptions of the orbital anisotropy. Enforcing the model dark halos to be of the NFW type, we determine their structural parameters. Depending on the anisotropy and the adopted M/L-values, we find that the dark matter fraction within one effective radius can vary between 20% and 50%, with most a probable range between 20% and 30%. The ambiguity of the velocity dispersion in the outermost bin is a main source of uncertainty. A comparison with cosmological N-body simulations reveals no striking disagreement.
observed for the red clusters. Using only the blue clusters as dynamical tracers, we perform Jeans-analyses for different assumptions of the orbital anisotropy. Enforcing the model dark halos to be of the NFW type, we determine their structural parameters. Depending on the anisotropy and the adopted M/L-values, we find that the dark matter fraction within one effective radius can vary between 20% and 50%, with most a probable range between 20% and 30%. The ambiguity of the velocity dispersion in the outermost bin is a main source of uncertainty. A comparison with cosmological N-body simulations reveals no striking disagreement.
Conclusions. Although the dark halo mass still cannot be strongly constrained, NGC 4636 does not seem to be extremely dark matter dominated. The derived circular velocities are also consistent with Modified Newtonian Dynamics.
Key words: galaxies: elliptical and lenticular, cD - galaxies: kinematics and dynamics - galaxies: individual: NGC 4636 - galaxies: halos
NGC 4636 is the southernmost bright elliptical in the Virgo cluster
of galaxies. It is located 10![]() south of M 87, within the Virgo
Southern Extension. Surface brightness fluctuation (SBF) measurements
yield a distance of 15 Mpc (Tonry et al. 2001),
which we adopt throughout this paper. This value, however, has to be
considered as a lower limit, since measurements based on the globular
cluster luminosity function (GCLF) presented by Kissler et al. (1994) and Dirsch et al. (2005) point towards a larger distance of more than 17 Mpc.
Table 1 summarizes the basic properties of NGC 4636.
south of M 87, within the Virgo
Southern Extension. Surface brightness fluctuation (SBF) measurements
yield a distance of 15 Mpc (Tonry et al. 2001),
which we adopt throughout this paper. This value, however, has to be
considered as a lower limit, since measurements based on the globular
cluster luminosity function (GCLF) presented by Kissler et al. (1994) and Dirsch et al. (2005) point towards a larger distance of more than 17 Mpc.
Table 1 summarizes the basic properties of NGC 4636.
Although NGC 4636, being an elliptical galaxy, predominantly consists of an old stellar population, there are some weak indications of an intermediate age population: firstly, it is a supernova Ia host galaxy (SN 1939a: Zwicky 1939; Giclas 1939), and there are theoretical considerations that this type of supernova originates in intermediate age populations rather than in very old ones (Yungelson et al. 1995; Yoshii et al. 1996). Secondly, far infrared observations by Temi et al. (2003) hint at a recent merger that supplied NGC 4636 with extra dust.
Table 1: NGC 4636 basic data compiled from the literature (1) NED, (2) Tonry et al. (2001), (3) this work, (4) R3C, (5) Dirsch et al. (2005), (6) Bender et al. (1994), (7) Idiart et al. (2003), (8) Forman et al. (1985), and (9) Loewenstein et al. (2001).
In the 1970s, NGC 4636 was the target of several
H I-observations. Despite some claims of an extended
H I-emission (Knapp et al. 1978;
Bottinelli & Gouguenheim 1978), the deepest
observations performed by Krishna Kumar & Thonnard
(1983) yielded an upper limit of only 11.5 ![]()
![]() to the total H I mass of NGC 4636.
to the total H I mass of NGC 4636.
Because of its high X-ray luminosity, NGC 4636 has been studied extensively in this frequency range, and these observations have also been used to infer its dark matter content and distribution.
Forman et al. (1985) analyzed Einstein X-ray
data from a large sample of early-type galaxies. For NGC 4636, they found
extended emission (out to a radius of
![]() )
and derived an X-ray luminosity
of
)
and derived an X-ray luminosity
of
![]()
![]() 0.10
0.10 ![]()
![]() .
They quote a mass-to-light ratio
.
They quote a mass-to-light ratio
![]() for
for
![]() ,
the second largest value in their sample.
,
the second largest value in their sample.
Matsushita et al. (1998), using ASCA, found very
extended X-ray emission around NGC 4636 out to 60![]() .
This
corresponds to a radius of almost 300 kpc in a distance of
15 Mpc. The authors suggest that the gravitational halo of NGC 4636
itself terminates in the region between 10 and 30 kpc. They observe
an increase in mass beyond 30 kpc, forming a halo-in-halo structure
whose size is comparable to that of a galaxy group.
.
This
corresponds to a radius of almost 300 kpc in a distance of
15 Mpc. The authors suggest that the gravitational halo of NGC 4636
itself terminates in the region between 10 and 30 kpc. They observe
an increase in mass beyond 30 kpc, forming a halo-in-halo structure
whose size is comparable to that of a galaxy group.
Jones et al. (2002) used the Chandra X-Ray
Observatory Advanced CCD Imaging Spectrometer (ACIS) to study the
X-ray halo of NGC 4636 with a spatial resolution of
![]() 50 pc. The observed X-ray features are so far unique: the
images show symmetric, arm-like structures that surround a bright
central region. These structures extend
50 pc. The observed X-ray features are so far unique: the
images show symmetric, arm-like structures that surround a bright
central region. These structures extend ![]()
![]() from
the galaxy center. The leading edges of these arms show changes in
brightness by a factor of two on scales of just a few
arcseconds. While these sharp fronts might be suggestive of a merger,
the authors favor a nuclear outburst as the source of the observed
morphology. They interpret the arms as the projected edges of
paraboloidal shock fronts expanding from the nucleus. Jones et al. speculate that the unusually high X-ray luminosity of NGC 4636
might be due to the advanced state of the cooling that brought on the
outburst and may be further enhanced by the shocks. When the gas halo
returns to hydrostatic equilibrium, the X-ray luminosity could decline
by an order of magnitude or more.
from
the galaxy center. The leading edges of these arms show changes in
brightness by a factor of two on scales of just a few
arcseconds. While these sharp fronts might be suggestive of a merger,
the authors favor a nuclear outburst as the source of the observed
morphology. They interpret the arms as the projected edges of
paraboloidal shock fronts expanding from the nucleus. Jones et al. speculate that the unusually high X-ray luminosity of NGC 4636
might be due to the advanced state of the cooling that brought on the
outburst and may be further enhanced by the shocks. When the gas halo
returns to hydrostatic equilibrium, the X-ray luminosity could decline
by an order of magnitude or more.
Loewenstein & Mushotzky (2003) used the Chandra X-Ray
Observatory to measure the hot interstellar medium temperature profile
of NGC 4636. Assuming hydrostatic equilibrium, they determined the
total enclosed mass profile for the radial range
![]() .
These authors come to the conclusion that dark
matter constitutes a large fraction (between 50% and 80%) of the
total mass, even inside the effective radius.
.
These authors come to the conclusion that dark
matter constitutes a large fraction (between 50% and 80%) of the
total mass, even inside the effective radius.
Given all these peculiarities, it is of great interest to use globular clusters as dynamical tracers to evaluate the dark matter content of NGC 4636. This work continues our program on the dynamics of globular cluster systems (GCSs) around early-type galaxies. Previous papers on NGC 1399, the central galaxy of the Fornax cluster, are Richtler et al. (2004) and Dirsch et al. (2003).
The GCS of NGC 4636 has been the target of three photometric studies.
Hanes (1977) used photographic plates to assess the
number and the luminosity of the GCs.
He derived a specific frequency (i.e., the number of GCs normalized to
the host galaxy's luminosity (Harris & van den Bergh 1981) of
![]() ,
which is unusually high for a quite isolated elliptical galaxy. Most field ellipticals have
,
which is unusually high for a quite isolated elliptical galaxy. Most field ellipticals have
![]() values between 3 and 4. The first CCD-study was
performed by Kissler et al. (1994), who observed
a field of
values between 3 and 4. The first CCD-study was
performed by Kissler et al. (1994), who observed
a field of
![]()
![]()
![]() centered on NGC 4636 in one
band (Cousins V, limiting magnitude of 24.25). They estimated the
total number of GCs to be 3600
centered on NGC 4636 in one
band (Cousins V, limiting magnitude of 24.25). They estimated the
total number of GCs to be 3600 ![]() 200, which corresponds to
200, which corresponds to
![]()
![]() 2.0, hence supporting the unusually high
number of GCs.
2.0, hence supporting the unusually high
number of GCs.
The full extent of the GCS together with color information only became
apparent in the recent study of Dirsch et al. (2005). They
used the MOSAIC camera at the 4-m telescope at the Cerro Tololo
Interamerican Observatory (CTIO). The bands were Kron-Cousins R and
Washington C. The final images have a field-of-view of
![]()
![]()
![]() .
The color distribution of the GCs shows the
familiar bimodal shape. The color of the minimum of the inner sample
(
.
The color distribution of the GCs shows the
familiar bimodal shape. The color of the minimum of the inner sample
(
![]() )
was chosen to divide red (metal-rich) from blue
(metal-poor) clusters, frequently interpreted as two different
sub-populations (e.g., Ashman & Zepf 1998; Kundu
& Whitmore 2001; Larsen et al. 2001). For the
total number of globular clusters, Dirsch et al. derived 3700
)
was chosen to divide red (metal-rich) from blue
(metal-poor) clusters, frequently interpreted as two different
sub-populations (e.g., Ashman & Zepf 1998; Kundu
& Whitmore 2001; Larsen et al. 2001). For the
total number of globular clusters, Dirsch et al. derived 3700 ![]() 200,
which agrees well with the previous measurement. The specific
frequency
200,
which agrees well with the previous measurement. The specific
frequency
![]() ranges between 5.8
ranges between 5.8 ![]() 1.2 and 8.9
1.2 and 8.9 ![]() 1.2, for the GCLF and SBF distances, respectively. An interesting
feature shows up in the radial distribution of the clusters: While the
(projected) radial number density distribution of the blue clusters
can be described by one power-law (
1.2, for the GCLF and SBF distances, respectively. An interesting
feature shows up in the radial distribution of the clusters: While the
(projected) radial number density distribution of the blue clusters
can be described by one power-law (
![]() )
within 1
)
within 1![]() -8
-8![]() ,
the density distribution of the red
clusters changes the exponent within this radial interval.
At a radial distance of 7
,
the density distribution of the red
clusters changes the exponent within this radial interval.
At a radial distance of 7![]() (9
(9![]() )
for the red (blue)
clusters, the power-law exponent drops to about -5 (cf. Table 3 in
Dirsch et al. 2005) Such behavior has not been observed in any
GCS before. This abrupt decrease in number density might mark the
limit of the GCS and possibly that of the galaxy itself. The
photometric data by Dirsch et al. forms the basis of the candidate
selection for our spectroscopic observations described in the
following section.
)
for the red (blue)
clusters, the power-law exponent drops to about -5 (cf. Table 3 in
Dirsch et al. 2005) Such behavior has not been observed in any
GCS before. This abrupt decrease in number density might mark the
limit of the GCS and possibly that of the galaxy itself. The
photometric data by Dirsch et al. forms the basis of the candidate
selection for our spectroscopic observations described in the
following section.
Table 2: Summary of observations (ESO program ID 69.B-0366(B)). The seeing values were determined from the acquisition images taken just before the MXU exposures.
The observations were carried out over four nights (May 7-10, 2002)
at the European Southern Observatory (ESO) Very Large Telescope (VLT)
facility on Cerro Paranal, Chile. The VLT Unit Telescope 4 was used
with the FORS2 (FOcal Reducer/low dispersion Spectrograph) instrument
equipped with the Mask EXchange Unit (MXU). The standard resolution
collimator used for this program provided a field-of-view of
![]()
![]()
![]() .
The detector system consisted of two
4096
.
The detector system consisted of two
4096 ![]() 2048 red optimized CCDs with a pixel size of
2048 red optimized CCDs with a pixel size of
![]() .
For our observations, the chips were read out using
a 2
.
For our observations, the chips were read out using
a 2 ![]() 2 binning. The grism 600B gave a spectral resolution of
about 3 Å. The spectral coverage was dependent on the slit position
on the mask. In most cases, the usable coverage was about 2000 Å, with
limits on the red side varying between 5500 and 6500 Å. We exposed
13 spectroscopic masks, the preparation of which is described in the
next section. Flat fielding was done with internal flat lamps. A
Hg-Cd-He lamp was used for wavelength calibration. The observations
are summarized in Table 2.
2 binning. The grism 600B gave a spectral resolution of
about 3 Å. The spectral coverage was dependent on the slit position
on the mask. In most cases, the usable coverage was about 2000 Å, with
limits on the red side varying between 5500 and 6500 Å. We exposed
13 spectroscopic masks, the preparation of which is described in the
next section. Flat fielding was done with internal flat lamps. A
Hg-Cd-He lamp was used for wavelength calibration. The observations
are summarized in Table 2.
Pre-images of the 13 pointings in 7 fields (see Fig. 1)
were obtained in service mode in October 2000. Each pointing was
observed in Cousins V and I filters for 30 s. The GC candidate
selection was based upon the photometric work presented in Dirsch et al. (2005). Cluster candidates had to fulfill the following
criteria: they had to be brighter than 22.7 in R, and the allowed
color range was
![]() .
Further, the candidates should
exhibit a star-like appearance on the pre-images to distinguish them
from background galaxies. The ESO FORS Instrumental Mask Simulator
(FIMS) software was then used to select the positions, widths, and
lengths of the slits. A slit width of 1
.
Further, the candidates should
exhibit a star-like appearance on the pre-images to distinguish them
from background galaxies. The ESO FORS Instrumental Mask Simulator
(FIMS) software was then used to select the positions, widths, and
lengths of the slits. A slit width of 1
![]() was chosen according
to the sub-arcsecond seeing conditions on Paranal. To maximize the
number of GC spectra obtained per mask, we chose to observe our
targets and sky positions through separate slits of 2
was chosen according
to the sub-arcsecond seeing conditions on Paranal. To maximize the
number of GC spectra obtained per mask, we chose to observe our
targets and sky positions through separate slits of 2
![]() length. Obviously, the quality of the sky subtraction then depends on
the accuracy of the wavelength calibration. As will be shown, it
turned out to be satisfactory to obtain radial velocities with the
desired accuracy. After positioning the slits for the selected GC candidates, the remaining space on the masks (especially in the outer
fields) was used to include additional objects. Thus, background
galaxies and point sources not matching the above-mentioned criteria
were also observed.
length. Obviously, the quality of the sky subtraction then depends on
the accuracy of the wavelength calibration. As will be shown, it
turned out to be satisfactory to obtain radial velocities with the
desired accuracy. After positioning the slits for the selected GC candidates, the remaining space on the masks (especially in the outer
fields) was used to include additional objects. Thus, background
galaxies and point sources not matching the above-mentioned criteria
were also observed.
The MXU-observations of our thirteen fields have exposure times in the range of 3600 to 7200 s (see Table 2 for a summary of the observations). To minimize the effects from cosmic ray hits, the observation of each mask was divided into two exposures - with the exception of Field 1.1, for which three science images were obtained. In addition to the spectroscopic observations, calibration measurements, i.e., bias, flat fields, and wavelength calibration exposures, were obtained during the daytime.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{3134f01.eps}\end{figure}](/articles/aa/full/2006/44/aa3134-05/Timg67.gif) |
Figure 1:
Positions of the fields overlaid on a
|
| Open with DEXTER | |
The following section summarizes the reduction steps performed to
obtain the final sky-subtracted spectra. Most of the data reduction
was done within the IRAF-environment![]() .
.
The merging of the two CCD-frames was done with fsmosaic, which
is available as a part of the ESO-FIMS software. The dimension of the
combined images is 2050 ![]() 2076 pixels. For cosmic ray removal,
the task bclean from the Starlink Figaro-package was
found to perform best. Biasing and flat-fielding was done in
the standard way. Since the aim of this study is the measurement of
radial velocities rather than the measurement of line strengths, we
did not apply any response function fitting or flux calibration. To
obtain one-dimensional spectra (aperture definition, tracing, and
extraction) the IRAF task apall from the
apextract package was used.
Once the aperture positions were defined on the science images, they
were checked and - where necessary - adjusted on the flatfield divided
exposures. For the 2
2076 pixels. For cosmic ray removal,
the task bclean from the Starlink Figaro-package was
found to perform best. Biasing and flat-fielding was done in
the standard way. Since the aim of this study is the measurement of
radial velocities rather than the measurement of line strengths, we
did not apply any response function fitting or flux calibration. To
obtain one-dimensional spectra (aperture definition, tracing, and
extraction) the IRAF task apall from the
apextract package was used.
Once the aperture positions were defined on the science images, they
were checked and - where necessary - adjusted on the flatfield divided
exposures. For the 2
![]() long slits used for most sources, an aperture size of
4 pixels (=1
long slits used for most sources, an aperture size of
4 pixels (=1
![]() )
was found to yield the best results.
)
was found to yield the best results.
The one-dimensional arc lamp spectra were calibrated using the
interactive task identify from the noao.onedspec
package.
The dispersion/wavelength solution was approximated by a seventh-order Chebyshev polynomial. The residuals of this fit were inspected for outliers, and if necessary, the deviant data points were
excluded from the fit in the next step. The rms errors of the final
fits were about 0.04 Å. As described above, sky spectra were measured through separate
slits. To perform the sky subtraction for a given
GC-spectrum, two or three adjacent (within 18
![]() )
sky
spectra were combined. This combined sky spectrum was then subtracted
using the skytweak task.
)
sky
spectra were combined. This combined sky spectrum was then subtracted
using the skytweak task.
The IRAF task fxcor from the noao.rv package performs
a Fourier cross-correlation on the input object and template
spectra. This program is based upon the technique developed by
Tonry & Davis (1979). For the
cross-correlation, a template with a high S/N and a spectrum similar
to that of a globular cluster is required. NGC 4636 itself, however
is not suitable due to its high velocity dispersion of about
200
![]() .
Therefore, the velocities were measured
using a spectrum (S/N
.
Therefore, the velocities were measured
using a spectrum (S/N ![]() 30) of NGC 1396 as template. This
spectrum was obtained in Dec. 2000, during observations of the
NGC 1399 GCS, using the same FORS2 instrumental setup and has already
been used as a template for investigating the kinematics of the
NGC 1399 GCS (Dirsch et al. 2004). NGC 1396 is a dwarf
elliptical galaxy close to NGC 1399, and its spectrum resembles that
of a metal-rich globular cluster. Its velocity dispersion is only
65
30) of NGC 1396 as template. This
spectrum was obtained in Dec. 2000, during observations of the
NGC 1399 GCS, using the same FORS2 instrumental setup and has already
been used as a template for investigating the kinematics of the
NGC 1399 GCS (Dirsch et al. 2004). NGC 1396 is a dwarf
elliptical galaxy close to NGC 1399, and its spectrum resembles that
of a metal-rich globular cluster. Its velocity dispersion is only
65 ![]()
![]() (Wegner et al. 2004). We
adopted a heliocentric radial velocity of 815
(Wegner et al. 2004). We
adopted a heliocentric radial velocity of 815 ![]()
![]() (Dirsch et al. 2004). The velocities obtained with this template were checked with a second
template spectrum obtained during our observations (object 1.3:56), a bright star whose observed velocity was found to be -682
(Dirsch et al. 2004). The velocities obtained with this template were checked with a second
template spectrum obtained during our observations (object 1.3:56), a bright star whose observed velocity was found to be -682
![]() ,
with respect to the galaxy template.
The velocities measured with the two different templates agree very
well. Since the fxcor uncertainty estimates were smaller for
the galaxy template, only these velocities are used for the subsequent
analysis. The accuracy of the velocity determination depends on the
shape of the spectrum and the wavelength range for which the
cross-correlation is performed. A range of
,
with respect to the galaxy template.
The velocities measured with the two different templates agree very
well. Since the fxcor uncertainty estimates were smaller for
the galaxy template, only these velocities are used for the subsequent
analysis. The accuracy of the velocity determination depends on the
shape of the spectrum and the wavelength range for which the
cross-correlation is performed. A range of
![]() was found to be an appropriate choice in most
cases. The upper limit was chosen to avoid the night sky emission
lines found around the strong [OI] 5577 Å feature. In some
spectra however, the relatively weak nitrogen line at 5199 Å left
substantial residuals: where this was the case, the wavelength
interval was adjusted accordingly. For the velocities of the
NGC 4636 GCS, we applied a heliocentric correction of
was found to be an appropriate choice in most
cases. The upper limit was chosen to avoid the night sky emission
lines found around the strong [OI] 5577 Å feature. In some
spectra however, the relatively weak nitrogen line at 5199 Å left
substantial residuals: where this was the case, the wavelength
interval was adjusted accordingly. For the velocities of the
NGC 4636 GCS, we applied a heliocentric correction of
![]() ;
the correction for the
NGC 1396spectrum is
;
the correction for the
NGC 1396spectrum is
![]() .
The uncertainty for the velocities is estimated using:
.
The uncertainty for the velocities is estimated using:
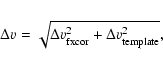
![\begin{figure}
\par\includegraphics[width=6.85cm,clip]{3134f02.eps}\end{figure}](/articles/aa/full/2006/44/aa3134-05/Timg77.gif) |
Figure 2: Histogram of the velocity uncertainties calculated by the fxcor-task. The grey histogram shows the values for the blue clusters; the black histogram shows the same for the red clusters. |
| Open with DEXTER | |
Since the wavelength calibration exposures for each mask were obtained
during the day following the observation, the mask was moved into the
focal plane again. The finite positioning accuracy of the MXU, and
shifts due to instrument flexure under gravity (all calibration
exposures are obtained with the telescope pointing at the zenith),
result in an offset between the science and the calibration
images. This offset manifests itself as a zero point shift in the
observed wavelength of the strong telluric [OI] 5577 Å emission
line. The zero point shifts in our data set were found to vary with
the position of the slit along the y-axis of the mask. To quantify
this effect, the wavelength of the 5577 Å line was measured in all
spectra for a given mask. A linear function was fit to the data and
provided a velocity correction for every aperture. These corrections
have values in the range
![]() .
.
To measure the systemic velocity of NGC 4636, we used the nine
spectra of NGC 4636 from mask 1_1 and found a heliocentric velocity
of 906 ![]()
![]() .
In the NASA/IPAC
Extragalactic Database (NED)
.
In the NASA/IPAC
Extragalactic Database (NED)![]() , one finds seven optical
velocity measurements with uncertainty estimates. The mean is 917
, one finds seven optical
velocity measurements with uncertainty estimates. The mean is 917 ![]()
![]() .
Hence, our velocity agrees very well with previous measurements.
.
Hence, our velocity agrees very well with previous measurements.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{3134f03.eps}\end{figure}](/articles/aa/full/2006/44/aa3134-05/Timg81.gif) |
Figure 3: Velocity uncertainties versus R-magnitude for the globular clusters (crosses: blue clusters; open circles: red clusters). |
| Open with DEXTER | |
Table 3: Basic properties of the globular cluster sample.
For the GCs, no trend is visible for the metal poor (blue) and the metal rich (red) subpopulations: both have very similar error distributions (see Fig. 2). Figure 3 shows the velocity uncertainties as a function of apparent R-magnitude. As expected, the measurements of fainter objects tend to have larger uncertainties. The uncertainties returned by the fxcor task are computed according to the formulae given by Tonry & Davis (1979).To check whether these uncertainties are a realistic error estimate, we compared the velocities of those 40 objects for which we had two spectra, since they were present on two masks.The mean difference for the velocity measurements was found to be very similar to the mean of the uncertainties given by fxcor. Hence, the fxcor uncertainties can be considered a good error estimate. The velocities determined for the GCs are listed in Appendix A, which is available in electronic form.
For every object with a velocity measurement, the color and magnitude
information was extracted from the photometry-database from Dirsch et al. (2005) via coordinate matching. The coordinates,
velocities, ![]() -colors and apparent R-magnitudes of these
objects are listed in Appendix A. For two clusters, neither
color nor magnitude information exists, since they happened to be
located near a bad row of the MOSAIC-CCD.
-colors and apparent R-magnitudes of these
objects are listed in Appendix A. For two clusters, neither
color nor magnitude information exists, since they happened to be
located near a bad row of the MOSAIC-CCD.
The first step was to divide our data set into GCs and foreground
stars. A compelling distinction between stars and globular clusters
would be given if the GCs could be resolved on the acquisition
images. However, only a very few, about three, of our clusters are
marginally resolved.
Guided by Fig. 4, which shows the distribution of velocity
versus color for all measured objects, a lower limit of
![]() for the radial velocity of the GCs was
chosen. However, one has to be aware that there might be a velocity
domain where this identification is doubtful. Given that the Galactic
rotation vector towards the position of NGC 4636 is
for the radial velocity of the GCs was
chosen. However, one has to be aware that there might be a velocity
domain where this identification is doubtful. Given that the Galactic
rotation vector towards the position of NGC 4636 is
![]() ,
one cannot exclude that foreground stars
have heliocentric velocities of up to
,
one cannot exclude that foreground stars
have heliocentric velocities of up to
![]() .
Neither can one rule out the presence of
GCs with radial velocities of more than
.
Neither can one rule out the presence of
GCs with radial velocities of more than
![]() relative to NGC 4636.
relative to NGC 4636.
The range in velocities occupied by foreground stars and globular
clusters is
![]() and
and
![]() ,
respectively. The data set
comprises 174 globular clusters and 175 foreground stars. The basic
properties of the GC sample are listed in Table 3. The
so-defined GCs appear in Fig. 5, which shows their
distribution around NGC 4636. The inner region is well sampled, but
due to the sharp drop-off at
,
respectively. The data set
comprises 174 globular clusters and 175 foreground stars. The basic
properties of the GC sample are listed in Table 3. The
so-defined GCs appear in Fig. 5, which shows their
distribution around NGC 4636. The inner region is well sampled, but
due to the sharp drop-off at ![]()
![]() ,
only a handful of
clusters is located outside this radius.
,
only a handful of
clusters is located outside this radius.
![\begin{figure}
\par\includegraphics[width=8.05cm,clip]{3134f04.eps}\end{figure}](/articles/aa/full/2006/44/aa3134-05/Timg96.gif) |
Figure 4:
Color vs. radial velocity. All objects with heliocentric velocities
higher than
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3134f05.eps}\end{figure}](/articles/aa/full/2006/44/aa3134-05/Timg97.gif) |
Figure 5:
Spatial distribution of the globular clusters overlaid on
a
|
| Open with DEXTER | |
For any further investigation, it is important that the color distribution of the GCs with measured
radial velocities resembles that of the entire cluster system. Indeed,
the bimodality of the color distribution found in the photometric
study by Dirsch et al. (2005) is clearly visible in our much
smaller sample (see Fig. 6). For consistency,
the same dividing color of
![]() was used. Thus, we find
97 blue and 75 red globular clusters. The color magnitude diagram
(CMD) for the GCs is shown in Fig. 6.
Although the selection of GC candidates was obviously biased towards
bright clusters, no clusters brighter than R=19 were found.
A few clusters are fainter than R=22, but
their velocities have large errors (cf. Fig. 3) and should
be considered with caution. Figure 7 shows the histogram of the apparent R-magnitudes for the globular clusters. It illustrates that our
spectroscopic study only probes the very bright part of the GCLF, well
above the turnover magnitude at 23.33 (Dirsch et al. 2005).
Furthermore, it shows that there is no significant
difference between the distributions of blue and red clusters. The
magnitude range of the GCs is
was used. Thus, we find
97 blue and 75 red globular clusters. The color magnitude diagram
(CMD) for the GCs is shown in Fig. 6.
Although the selection of GC candidates was obviously biased towards
bright clusters, no clusters brighter than R=19 were found.
A few clusters are fainter than R=22, but
their velocities have large errors (cf. Fig. 3) and should
be considered with caution. Figure 7 shows the histogram of the apparent R-magnitudes for the globular clusters. It illustrates that our
spectroscopic study only probes the very bright part of the GCLF, well
above the turnover magnitude at 23.33 (Dirsch et al. 2005).
Furthermore, it shows that there is no significant
difference between the distributions of blue and red clusters. The
magnitude range of the GCs is
![]() in Kron R. When converted to absolute magnitudes (using the distance
modulus of 30.83, Tonry et al. 2001), the
globular clusters in our sample span the range
in Kron R. When converted to absolute magnitudes (using the distance
modulus of 30.83, Tonry et al. 2001), the
globular clusters in our sample span the range
![]() in R and
in R and
![]() in V (for
in V (for
![]() ,
Dirsch et al. 2005). Assuming a typical mass-to-light ratio of
M/LV =2, one finds that the masses of the brightest
clusters are of the order 7-8
,
Dirsch et al. 2005). Assuming a typical mass-to-light ratio of
M/LV =2, one finds that the masses of the brightest
clusters are of the order 7-8 ![]()
![]() .
For
comparison, the absolute visual magnitude of
.
For
comparison, the absolute visual magnitude of ![]() Centauri
(NGC 5139) is
MV = -10.29(Harris 1996), and its mass is about 5
Centauri
(NGC 5139) is
MV = -10.29(Harris 1996), and its mass is about 5 ![]()
![]() .
.
![\begin{figure}
\par\includegraphics[width=7.55cm,clip]{3134f06.eps}\end{figure}](/articles/aa/full/2006/44/aa3134-05/Timg104.gif) |
Figure 6:
Top: Color magnitude diagram for the globular
clusters. Plotted are |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.85cm,clip]{3134f07.eps}\end{figure}](/articles/aa/full/2006/44/aa3134-05/Timg105.gif) |
Figure 7: Globular cluster luminosity distribution (bin width = 0.2 mag). The dotted line at 23.33 indicates the turnover magnitude of the GCS. Histograms for blue (solid grey) and red clusters. |
| Open with DEXTER | |
As can be seen in Fig. 5, our target clusters are not
uniformly distributed with respect to the center of NGC 4636. At the
time of the mask preparation, before the photometric data set was
fully analyzed, the projected globular cluster number density
was overestimated. Some fields
were placed at larger projected distances (see Fig. 1),
at the expense of a more uniform azimuthal coverage. Yet in total, only
15 of the 174 GCs in our sample are found at projected radii larger
than
![]() .
Thus, any measurement of the line-of-sight velocity
dispersion beyond this radius is clearly doubtful. Note that the
radius at which the power-law index of the projected globular cluster
density drops (cf. Sect. 1.2) lies in the range 7
.
Thus, any measurement of the line-of-sight velocity
dispersion beyond this radius is clearly doubtful. Note that the
radius at which the power-law index of the projected globular cluster
density drops (cf. Sect. 1.2) lies in the range 7![]() to 9
to 9![]() .
.
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{3134f08.eps}\end{figure}](/articles/aa/full/2006/44/aa3134-05/Timg106.gif) |
Figure 8:
Left: radial velocity as a function of apparent
R-magnitude. Right: radial velocity of the GCs
plotted vs. the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.4cm,clip]{3134f09.eps}\end{figure}](/articles/aa/full/2006/44/aa3134-05/Timg109.gif) |
Figure 9:
The left panels show the histograms of the GC velocities
for the entire sample, the blue subsample, and the red subsample,
respectively. In each panel, the grey histogram shows the distribution
of the corresponding error-selected (
|
| Open with DEXTER | |
In the left panel of Fig. 8, the velocities are plotted
against the R-magnitudes.
As expected, they are found to be concentrated towards the systemic
velocity. The brightest clusters, however, tend to avoid the systemic
velocity. A larger sample is needed to confirm whether this effect is
real or due to low-number statistics.
The right panel of Fig. 8 shows the velocities plotted
against the ![]() colors of the clusters. Again, no clear trend is
visible, although one notes that the five clusters with the
highest velocities are blue.
The top right panel of Fig. 9 plots all GC radial velocities
versus the projected radii in arcminutes. This figure once more shows
how few velocities were obtained for large radii. The more important
observation, however, is that the scatter of the velocities about the
systemic velocity is rather small at a radial distance of about
2
colors of the clusters. Again, no clear trend is
visible, although one notes that the five clusters with the
highest velocities are blue.
The top right panel of Fig. 9 plots all GC radial velocities
versus the projected radii in arcminutes. This figure once more shows
how few velocities were obtained for large radii. The more important
observation, however, is that the scatter of the velocities about the
systemic velocity is rather small at a radial distance of about
2![]() -4
-4![]() .
As will be shown in Sect. 7,
this translates directly into a decrease of the projected velocity
dispersion in this radial interval. On the other hand, only relatively
few GCs fall into this radial range. The middle and lower right
panels of Fig. 9 show the same diagram for blue and red
clusters, respectively. In the radial range around 2
.
As will be shown in Sect. 7,
this translates directly into a decrease of the projected velocity
dispersion in this radial interval. On the other hand, only relatively
few GCs fall into this radial range. The middle and lower right
panels of Fig. 9 show the same diagram for blue and red
clusters, respectively. In the radial range around 2![]() -4
-4![]() ,
the scatter about the systemic velocity is larger for the blue than
for the red clusters, hence the radial behavior of the velocity
dispersions for the subsamples will turn out to be rather different
(see Sect. 7).
,
the scatter about the systemic velocity is larger for the blue than
for the red clusters, hence the radial behavior of the velocity
dispersions for the subsamples will turn out to be rather different
(see Sect. 7).
Due to the inhomogeneous azimuthal coverage of our sample, it is
obvious that statements concerning rotation have to be considered with
caution. The diagnostic diagram that we have to analyze is a plot of radial
velocities vs. the position angle. Côté et al. (2001) give a useful discussion of the
relation between the intrinsic and projected rotational velocity field
of a spherical system, and we do not repeat that here. If the
intrinsic rotation velocity field is stratified on spheres, and the
galaxy is not seen pole-on, we measure radial velocities that depend
sinusoidally on the azimuth angle. Therefore, we fit the following
relation:
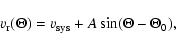 |
(1) |
![\begin{figure}
\par\includegraphics[width=7.55cm,clip]{3134f10.eps}\end{figure}](/articles/aa/full/2006/44/aa3134-05/Timg123.gif) |
Figure 10:
This plot shows radial velocity vs. the position angle (North past East). The upper panel plots the entire sample, the middle panel the blue clusters, and the lower
panel the red clusters. A marginal rotational signal is detected in
the entire sample, which is due to the stronger signal of the red
clusters, which seem to rotate around the minor axis with an amplitude of about
|
| Open with DEXTER | |
The top left panel of Fig. 9 shows the velocity distribution
of the entire velocity sample. The bin size was chosen to be
![]() ,
which is larger than the mean
uncertainty. The mean velocity of 906
,
which is larger than the mean
uncertainty. The mean velocity of 906 ![]()
![]() is in excellent agreement with the systemic velocity of NGC 4636 we
determined from the galaxy spectra (cf. Sect. 4.1). The
shape of the distribution appears Gaussian (the Anderson-Darling test
for normality yields a p-value of 0.81 (Stephens
1974)). This is what one would expect for a kinematical
sample that is close to isotropic and in dynamical equilibrium (see,
e.g., Binney & Tremaine 1987).
The most important observable that we want to extract from our data
is the projected velocity dispersion and its dependence with radius.
Throughout this analysis, it is assumed that our velocity
measurements are drawn from one normal distribution.
To calculate the velocity dispersions presented in the following
section, we employed the maximum likelihood dispersion estimator
presented by Pryor & Meylan (1993). We fixed the
systemic velocity of NGC 4636 to
is in excellent agreement with the systemic velocity of NGC 4636 we
determined from the galaxy spectra (cf. Sect. 4.1). The
shape of the distribution appears Gaussian (the Anderson-Darling test
for normality yields a p-value of 0.81 (Stephens
1974)). This is what one would expect for a kinematical
sample that is close to isotropic and in dynamical equilibrium (see,
e.g., Binney & Tremaine 1987).
The most important observable that we want to extract from our data
is the projected velocity dispersion and its dependence with radius.
Throughout this analysis, it is assumed that our velocity
measurements are drawn from one normal distribution.
To calculate the velocity dispersions presented in the following
section, we employed the maximum likelihood dispersion estimator
presented by Pryor & Meylan (1993). We fixed the
systemic velocity of NGC 4636 to
![]() .
Then, the velocity dispersion
.
Then, the velocity dispersion ![]() is calculated (by iteration)
according to:
is calculated (by iteration)
according to:
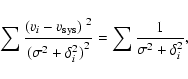 |
(2) |
![\begin{figure}
\par\includegraphics[width=16.2cm,clip]{3134f11.eps}\end{figure}](/articles/aa/full/2006/44/aa3134-05/Timg138.gif) |
Figure 11:
The left panels show the velocity dispersion versus projected
galactocentric radius for the whole, the blue, and the red cluster
samples, respectively. The right panels show the same for the
corresponding error-selected
|
| Open with DEXTER | |
The upper left panel of Fig. 11 shows the radial
dependence of the velocity dispersion for all 170 GCs within
![]() ,
For comparison, the line-of-sight velocity dispersion
measurements of the central region from Bender et al. (1994) are shown as diamonds. These authors
used a long-slit spectrum (with the slit positioned along the major
axis) to derive a central velocity dispersion of
,
For comparison, the line-of-sight velocity dispersion
measurements of the central region from Bender et al. (1994) are shown as diamonds. These authors
used a long-slit spectrum (with the slit positioned along the major
axis) to derive a central velocity dispersion of
![]()
![]()
![]() ,
and for the
average velocity dispersion measured along the major axis (
,
and for the
average velocity dispersion measured along the major axis (
![]() ), they found
), they found
![]()
![]()
![]() .
Within the
uncertainties, our data points agree with the Bender et al. measurements. Albeit consistent with a constant velocity dispersion of about
.
Within the
uncertainties, our data points agree with the Bender et al. measurements. Albeit consistent with a constant velocity dispersion of about
![]() ,
this
plot suggests a decrease of
,
this
plot suggests a decrease of ![]() by about
by about
![]() (from
(from ![]() 220 to
220 to ![]()
![]() )
in the radial distance range of roughly
2
)
in the radial distance range of roughly
2![]() -4
-4![]() .
To check whether this behavior is merely an artifact produced by velocity measurements with large uncertainties,
we next consider an error selected sample
.
To check whether this behavior is merely an artifact produced by velocity measurements with large uncertainties,
we next consider an error selected sample
![]() (cf. Fig. 9, lower panel, to see
which data points are omitted). The plot for this smaller (120 GC
velocities) sample is shown in the upper right panel of
Fig. 11. Apparently, the decline is not due to large
individual uncertainties. As will be shown next, this pattern is the
result of the different behaviors of the blue and red subpopulations.
(cf. Fig. 9, lower panel, to see
which data points are omitted). The plot for this smaller (120 GC
velocities) sample is shown in the upper right panel of
Fig. 11. Apparently, the decline is not due to large
individual uncertainties. As will be shown next, this pattern is the
result of the different behaviors of the blue and red subpopulations.
The middle and lower panels of Fig. 11 show the radial
dependence of the velocity dispersion for the blue and the red
subpopulations, respectively. The values derived for the error
selected (
![]() )
samples, which
consist of 56 blue and 56 red clusters, are shown in the right panels.
While the blue clusters show a constant velocity dispersion of
about
)
samples, which
consist of 56 blue and 56 red clusters, are shown in the right panels.
While the blue clusters show a constant velocity dispersion of
about
![]() ,
the velocity dispersion of the red
clusters drops from a value of
,
the velocity dispersion of the red
clusters drops from a value of ![]()
![]() to
to
![]()
![]() at a radius of about
2
at a radius of about
2![]() -3
-3![]() .
From this radius on, out to at least
.
From this radius on, out to at least
![]() ,
the velocity dispersion apparently remains at the constant, low
value. Considering these results for blue and red clusters, one can attribute
the drop seen for the whole error selected sample to the red
clusters.
However, the number of red clusters is rather high in the innermost
radial bins, giving the large dispersion at small radii a high degree
of confidence. On the other hand, the lower velocity dispersion at
larger distances may be uncertain for the individual bins, but that
the overall velocity dispersion is lower than for the innermost bin
can be stated with high confidence as well. This is a new feature
that has not been seen before in any of the few kinematic GC samples
of other galaxies. We offer a simple explanation in the context of the
spherical Jeans equation in the next section.
,
the velocity dispersion apparently remains at the constant, low
value. Considering these results for blue and red clusters, one can attribute
the drop seen for the whole error selected sample to the red
clusters.
However, the number of red clusters is rather high in the innermost
radial bins, giving the large dispersion at small radii a high degree
of confidence. On the other hand, the lower velocity dispersion at
larger distances may be uncertain for the individual bins, but that
the overall velocity dispersion is lower than for the innermost bin
can be stated with high confidence as well. This is a new feature
that has not been seen before in any of the few kinematic GC samples
of other galaxies. We offer a simple explanation in the context of the
spherical Jeans equation in the next section.
Table 4:
Projected velocity dispersion as a function of projected
galactocentric radius. The upper section shows the values for all, the
blue, and the red clusters. The dispersions for the corresponding
error-selected samples are listed in the lower section. The data are
shown in Fig. 11. The values in brackets are those obtained
when omitting the two (blue) GCs with velocities above
![]() .
.
The line-of-sight velocity dispersion
![]() of the GCS and its radial dependence is used to estimate the mass
profile of NGC 4636. Given that the number of spectroscopically
observed GCs is still far too low for an axisymmetric treatment, we
will assume spherical symmetry. This is justified since the deviation
from sphericity is modest in the inner parts of the galaxy (Dirsch et al. 2005) where most of our clusters are found.
A further argument is the high
of the GCS and its radial dependence is used to estimate the mass
profile of NGC 4636. Given that the number of spectroscopically
observed GCs is still far too low for an axisymmetric treatment, we
will assume spherical symmetry. This is justified since the deviation
from sphericity is modest in the inner parts of the galaxy (Dirsch et al. 2005) where most of our clusters are found.
A further argument is the high
![]() found by Kronawitter et al. (2000) (see Sect. 8.3). Given that
a flattening in the line of sight leads to an underestimation of M/L
(Magorrian & Ballantynes 2001), it is hard to imagine
that such a high value is still underestimated.
found by Kronawitter et al. (2000) (see Sect. 8.3). Given that
a flattening in the line of sight leads to an underestimation of M/L
(Magorrian & Ballantynes 2001), it is hard to imagine
that such a high value is still underestimated.
The collisionless Boltzmann equation is used to derive the
spherical, non-rotating Jeans equation
(see Binney & Tremaine 1987 for a full treatment),
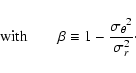
For our analysis, we use the expressions given by, e.g., Mamon &
![]() okas (2005) (see also van der Marel 1994).
Given a mass distribution M(r), a three-dimensional mass or number
density of a tracer population
okas (2005) (see also van der Marel 1994).
Given a mass distribution M(r), a three-dimensional mass or number
density of a tracer population ![]() ,
and a constant
anisotropy parameter
,
and a constant
anisotropy parameter ![]() ,
the solution to the Jeans equation (Eq. (3))
reads:
,
the solution to the Jeans equation (Eq. (3))
reads:
To assess the mass distribution of the luminous (stellar) component, we proceed as
follows: The photometric study by Dirsch et al. (2005)
provides a surface brightness profile in Kron-Cousins R. It reads:
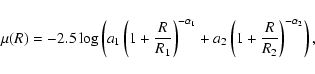 |
(6) |
To convert the cumulative luminosity into a mass profile, the stellar mass-to-light ratio is
required, i.e., M/LR. Kronawitter et al. (2000) quote a value of
M/LB = 9 for a distance of 20.5 Mpc. Because M/L is inversely
proportional to the distance, one has to apply a factor of 1.36 to get
M/LB = 12.2 at a distance of 15 Mpc. This value is
suspiciously high. Although it formally fits old, metal-rich
populations with steep mass functions, Bell et al. (2003)
quote
M/LB =10 as an upper limit found for their large
2MASS-sample. According to their relation of (B-R) versus M/LB,
NGC 4636 would have an M/LB of approximately 6. Further
uncertainties are the distance (Dirsch et al. 2005) and the
tangential anisotropy (Kronawitter et al. 2000)
of NGC 4636. Obviously, there is some freedom in adopting
the mass-to-light-ratio of the stellar population.
First, we assume
M/LB = 12.2, according to Kronawitter et al., but we shall also consider other values. To transform this mass-to-light ratio into an M/LR value, one has to
apply the factor of
![]() .
With
(B-R)4636= 1.6 and
.
With
(B-R)4636= 1.6 and
![]() ,
a factor of 0.56 results, hence
M/LR = 6.8. Further, we make the assumption that M/LR of the stellar light is constant
for the entire galaxy. This is justified since the color gradient of
NGC 4636 is relatively shallow (
,
a factor of 0.56 results, hence
M/LR = 6.8. Further, we make the assumption that M/LR of the stellar light is constant
for the entire galaxy. This is justified since the color gradient of
NGC 4636 is relatively shallow (
![]() in the range
in the range
![]() ), and the stellar populations seem to be well-mixed (Dirsch et al. 2005).
), and the stellar populations seem to be well-mixed (Dirsch et al. 2005).
For our modeling (cf. Sect. 8.6), we assume that the
stellar mass is contained within 70 kpc, yielding
![]()
![]() 1011 and 2.6
1011 and 2.6 ![]()
![]() for
M/LR=6.8 and 4.3,
respectively. The lower value shall illustrate the dependence on M/L. We adopt
M/LV=5.5 from Loewenstein & Mushotzky (2003), which results in
M/LR=4.3.
for
M/LR=6.8 and 4.3,
respectively. The lower value shall illustrate the dependence on M/L. We adopt
M/LV=5.5 from Loewenstein & Mushotzky (2003), which results in
M/LR=4.3.
Since the projected number density N(R) of the blue globular clusters
follows a double power-law, the de-projection is somewhat tricky. We
proceeded as follows: following
Zhao (1997), we adopt the double power-law
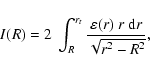 |
(9) |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{3134f12.eps}\end{figure}](/articles/aa/full/2006/44/aa3134-05/Timg200.gif) |
Figure 12: Projected radial number density of blue GCs. The data points are from Dirsch et al. (2005), the solid line is the a double power-law (cf. Eq. (8)) fit to the data, and the dashed line is the re-projected 3D number-density. It deviates only marginally from the 2D-fit. For comparison, we also show the projected light profile according to Dirsch et al. (2005). |
| Open with DEXTER | |
For simplicity, the anisotropy parameter ![]() is assumed to be
constant with radius. With our limited sample, we cannot put any
constraints on possible radial variations of
is assumed to be
constant with radius. With our limited sample, we cannot put any
constraints on possible radial variations of ![]() .
As a tracer
population, we choose the error-selected blue clusters. The red
clusters show a more complex behavior. They seem to rotate, their
projected number density is best described by three power-laws, and
the projected velocity dispersion also shows more complex features.
Therefore, we postpone any inclusion of the red clusters in the
dynamical analysis until more data becomes available.
.
As a tracer
population, we choose the error-selected blue clusters. The red
clusters show a more complex behavior. They seem to rotate, their
projected number density is best described by three power-laws, and
the projected velocity dispersion also shows more complex features.
Therefore, we postpone any inclusion of the red clusters in the
dynamical analysis until more data becomes available.
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{3134f13.eps} \end{figure}](/articles/aa/full/2006/44/aa3134-05/Timg201.gif) |
Figure 13: Mass models for a stellar M/L-ratio of 6.8. The left and right panels are distinguished by the value of the last bin. The topmost panels show the measured velocity dispersions (cf. Fig. 11 and Table 4) together with the modeled line-of-sight velocity dispersions. The second panels show the circular velocity curves of the dark matter components. Below that, the circular velocity curves for the sum of luminous and dark matter are shown. The circular velocity of the stars alone is shown as dotted line. Circles show the values derived by Kronawitter et al. (2000). The mass-to-light ratio as a function of radius is shown in the bottom panels. Different line types indicate results for different anisotropy parameters, as labeled in the second panel on the left. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{3134f14.eps} \end{figure}](/articles/aa/full/2006/44/aa3134-05/Timg202.gif) |
Figure 14: Same as Fig. 13, but for a lower stellar M/L-ratio of 4.3. See Table 5 for the model parameters. |
| Open with DEXTER | |
However, the blue clusters also pose problems. As can be seen in
Figs. 9 and 11, the velocity dispersion value of
the outermost bin is strongly affected by two outliers. Including
those objects, one obtains 227 ![]()
![]() instead
of 121
instead
of 121 ![]()
![]() .
The high value would mean an almost constant dispersion out to 7 arcmin. As seen later on, this would be inconsistent with a sharp drop of the cluster system at this radius. This issue can only be resolved
with future data. For now, we calculate our models for both values.
This argument cannot be transferred easily to the red clusters. If
they rotate, a constant velocity dispersion is plausible since we
average azimuthally.
.
The high value would mean an almost constant dispersion out to 7 arcmin. As seen later on, this would be inconsistent with a sharp drop of the cluster system at this radius. This issue can only be resolved
with future data. For now, we calculate our models for both values.
This argument cannot be transferred easily to the red clusters. If
they rotate, a constant velocity dispersion is plausible since we
average azimuthally.
For the dark component, we adopt a density profile of the form:
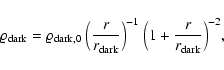 |
(10) |
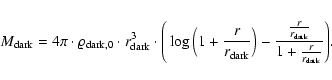 |
(11) |
Table 5:
Parameters of the dark matter halos. The first column labels
the models. The mass-to-light ratio
M/LR and
the dark matter fraction are calculated for two radii
(
![]() and
and
![]() is the radius within which the GCs used in the analysis are found).
From the NFW parameters of our model halos, we calculate the virial
radius, the virial mass, and the concentration parameter
is the radius within which the GCs used in the analysis are found).
From the NFW parameters of our model halos, we calculate the virial
radius, the virial mass, and the concentration parameter
![]() using the definitions
of Bullock et al. (2001). Then we give the total mass
within 30 kpc, the mass-to-light ratios (R-band), and the dark matter
fraction within 30 kpc and 7.5 kpc (effective radius).
Note that the virial quantities were calculated for the dark halos without adding the stellar component. Thus, the virial masses presented below are lower limits.
using the definitions
of Bullock et al. (2001). Then we give the total mass
within 30 kpc, the mass-to-light ratios (R-band), and the dark matter
fraction within 30 kpc and 7.5 kpc (effective radius).
Note that the virial quantities were calculated for the dark halos without adding the stellar component. Thus, the virial masses presented below are lower limits.
Having chosen a value for the stellar M/L and ![]() ,
we calculate
the product of radial velocity dispersion squared and the
3-dimensional number density according to Eq. (4). This we
project according to Eq. (5). For each pair of M/L and
,
we calculate
the product of radial velocity dispersion squared and the
3-dimensional number density according to Eq. (4). This we
project according to Eq. (5). For each pair of M/L and ![]() ,
we vary the dark matter parameters (
,
we vary the dark matter parameters (
![]() )
until the projected model dispersion
shows minimal residuals with regard to the observed dispersion. For
simplicity, the four data points were given equal weights and the
residuals were calculated using
)
until the projected model dispersion
shows minimal residuals with regard to the observed dispersion. For
simplicity, the four data points were given equal weights and the
residuals were calculated using
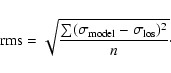 |
(12) |
Our models are displayed in Figs. 13 and 14, which show our analysis for the two different stellar M/LR-values of 6.8 and 4.3, respectively. Table 5 lists the halo parameters. The left and right panels refer to the difference in the last data bin, as seen in the topmost panels, which show the comparison between our models and the data. The observed velocity dispersion together with their statistical uncertainties are indicated. We emphasize the importance of the uncertain outermost bin, which is clearly dominated by systematics as mentioned above. The various anisotropic models are distinguished by different line styles that can be identified in the second panel, which shows the associated dark matter circular velocities. The degeneracy of potential and anisotropy is nicely visible. Only the models without dark matter, which are shown separately in Fig. 15, seem to be excluded.
The third panels show the total circular velocities, i.e., the sum of dark and luminous matter. The stellar component is indicated with a dotted line. The circular velocity values derived by Kronawitter et al. are shown as circles. Since our stellar mass-to-light ratio of 6.8 was adopted from the Kronawitter et al. analysis, it is not surprising that they do not fit well in the case of M/L=4.3.
The bottom panels show the radial dependence of the corresponding M/LR-values (cf. Table 5 for a listing of mass-to-light ratios at R= 30 and 7.5 kpc).
Of course, since the stellar M/L-value enters as a free parameter, the dark matter fraction would rise with declining M/L. However, M/LR = 4.3 is already low for an old, metal-rich stellar population. Further constraints on the M/L ratio have to come from a more precise analysis of the dynamics of the stellar body.
In all four model families, the ![]() (i.e., totally radial) models
perform worst. Besides being a poor fit to the data, these models
require very massive (
(i.e., totally radial) models
perform worst. Besides being a poor fit to the data, these models
require very massive (
![]() )
and extended dark matter halos.
)
and extended dark matter halos.
The observed GC velocity dispersion
(calculated omitting the two extreme velocities), as shown in the left
panels of Figs. 13 and 14, can be reproduced for a range of anisotropy parameters (
![]() ). The
tangential models result in less massive and more concentrated dark
halos. The isotropic model has a virial radius of about 360-400 kpc
(depending on the stellar M/L value), which is compatible to the extent
of the X-ray emission.
). The
tangential models result in less massive and more concentrated dark
halos. The isotropic model has a virial radius of about 360-400 kpc
(depending on the stellar M/L value), which is compatible to the extent
of the X-ray emission.
Although the viral masses of the dark halos differ by more than one order of magnitude, the total mass within the radial range
probed by the GC dynamics changes by only a factor of 1.5.
Hence, we can put constraints on the amount of dark matter in
NGC 4636 within 30 kpc ![]()
![]() ,
while
the shape of the halo remains largely unknown.
,
while
the shape of the halo remains largely unknown.
For completeness, we also included the values of
![]() obtained when including extreme velocities of two GCs in the last radial bin in our analysis. The resulting
almost constant line-of-sight velocity dispersion of the GCs, as
shown in the right panels of Figs. 13 and 14, can
only be reproduced with a very extended dark matter component. The
best agreement in the sense of lowest residuals is found for the
obtained when including extreme velocities of two GCs in the last radial bin in our analysis. The resulting
almost constant line-of-sight velocity dispersion of the GCs, as
shown in the right panels of Figs. 13 and 14, can
only be reproduced with a very extended dark matter component. The
best agreement in the sense of lowest residuals is found for the
![]() tangential models. The radial
tangential models. The radial
![]() models
provide rather poor fits, and the completely radial
models
provide rather poor fits, and the completely radial
![]() models (not shown), result in even poorer fits.
models (not shown), result in even poorer fits.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3134f15.eps} \end{figure}](/articles/aa/full/2006/44/aa3134-05/Timg235.gif) |
Figure 15:
Projected velocity dispersions for models without dark
matter. Upper panel:
M/LR = 6.8; lower panel: the same for
a stellar mass-to-light ratio of
M/LR= 4.3. The line
styles are the same as in Figs. 13 and 14,
i.e., the solid lines correspond to |
| Open with DEXTER | |
How do our model dark matter halos compare to cosmological N-body simulations? Is such a comparison meaningful? In particular, the less massive halos are expected to have experienced contraction during the galaxy formation process. On the theoretical side, the universality of dark matter halos is still under discussion (see Reed et al. 2004 and references therein), so that a possible disagreement may not provide a solid basis for deeper conclusions. We therefore refrain from lengthy considerations and only point out basic tendencies.
For comparison with simulations, we choose the study of
Bullock et al. (2001). They analyzed a sample of
![]() 5000 simulated halos in the range
5000 simulated halos in the range
![]() .
They found (like others) that the concentration
parameter
.
They found (like others) that the concentration
parameter
![]() decreases with growing mass, but the
scatter in the halo profiles for a given mass is still quite large. A comparison with Fig. 4 of Bullock et al. shows that for our model family shown in the left column of Fig. 13 (i.e.,
M/LR=6.8, omitting the two extreme blue
clusters), the
decreases with growing mass, but the
scatter in the halo profiles for a given mass is still quite large. A comparison with Fig. 4 of Bullock et al. shows that for our model family shown in the left column of Fig. 13 (i.e.,
M/LR=6.8, omitting the two extreme blue
clusters), the ![]() halo (model 3) best fits the
simulations. The halos corresponding to the models with tangential
bias have higher concentration parameters than halos of the same mass
shown by Bullock et al., but still may be consistent. The models with
radial anisotropies have small concentration parameters, but are as
well not excluded. This is true even for the completely radial models
(which give the worst fits to the observations). The question
therefore is whether, given the large range of permitted halo shapes
indicated by the simulations, one can meaningfully compare theoretical
simulations with observations of our kind at all, not to mention the
complications if dissipative effects of galaxy formation are taken
into account. All we can say is that our model halos do not
contradict the simulations of Bullock et al.
halo (model 3) best fits the
simulations. The halos corresponding to the models with tangential
bias have higher concentration parameters than halos of the same mass
shown by Bullock et al., but still may be consistent. The models with
radial anisotropies have small concentration parameters, but are as
well not excluded. This is true even for the completely radial models
(which give the worst fits to the observations). The question
therefore is whether, given the large range of permitted halo shapes
indicated by the simulations, one can meaningfully compare theoretical
simulations with observations of our kind at all, not to mention the
complications if dissipative effects of galaxy formation are taken
into account. All we can say is that our model halos do not
contradict the simulations of Bullock et al.
NGC 4636 has recently been a target for various X-ray studies (e.g., O'Sullivan et al. 2005; Ohto et al. 2003; Xu et al. 2002; Jones et al. 2002), emphasizing the highly disturbed
X-ray pattern. However, mass profiles derived from X-rays have, until
now, only been published by Matsushita et al. (1998)
and Loewenstein & Mushotzky (2003). Figure 16
shows the various mass profiles. The two solid lines are our models,
with the lowest and the highest mass within 30 kpc (models 1 and 14). The dotted line is the model with the highest dark matter content
within one effective radius (model 7).
The long-dashed line is the mass profile from Loewenstein &
Mushotzky (2003). The total mass enclosed within
30 kpc is for the latter profile, 1.25 ![]()
![]() ,
which is distinctly higher than our highest
value. Furthermore, the mass profile is steeper than most of our
models, rising as R1.2. However, a very concentrated dark halo,
even surpassing this X-ray profile at small radii, is not excluded.
One can speculate that the difference at larger radii might have to do
with different hydrodynamical situations at small and large radii.
,
which is distinctly higher than our highest
value. Furthermore, the mass profile is steeper than most of our
models, rising as R1.2. However, a very concentrated dark halo,
even surpassing this X-ray profile at small radii, is not excluded.
One can speculate that the difference at larger radii might have to do
with different hydrodynamical situations at small and large radii.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{3134f16.eps}\end{figure}](/articles/aa/full/2006/44/aa3134-05/Timg237.gif) |
Figure 16: Various mass profiles. This graph shows various mass profiles of NGC 4636. The solid lines are the models with the lowest and highest mass within 30 kpc, respectively (models 1 and 14). The dotted line is the model with the highest dark matter content within 30 kpc (model 7). The dashed dotted line approximates one mass profile from Matshushita et al. (1998), showing the flattening at about 10 kpc. The long-dashed line represents the mass profile from Loewenstein & Mushotzky (2003). See text for more details. |
| Open with DEXTER | |
The dashed-dotted line is the mass profile from Matsushita et al. (1998) (based on ASCA data), read off from
their log-log diagram (their Fig. 3, solid line, scaled down to our
distance of 15 Mpc), which shows the flattening of the mass profile
at 10 kpc radius most distinctly. However, their range of mass
profiles consistent with the X-ray analyses is rather large,
apparently including the possibility that there is no such flattening.
In their work, NGC 4636 is extremely dark matter dominated, with the
luminous mass already falling short by a factor of 2-3 at small
radii. Matsushita et al. quote M/L = 8 for the stellar component, but
give neither the band nor the source of their photometry, so we cannot
comment further on that. The agreement with the GC analysis out to
10 kpc is reasonably good. Outside this radius, the discrepancy is
caused by the flattening of the profile, for which we see no
indication. A similar flattening of the mass profile has been
observed with ASCA in the cases of NGC 1399 (Ikebe et al. 1996) and in Abell 1795 (Xu et al. 2002). However, it has not been seen in
the ROSAT data for NGC 1399 (Jones et al. 1997). Jones et al. (2002) interpret the high X-ray luminosity
of NGC 4636 as the transient phenomenon of an enhanced cooling rate.
Hence, it is possible that the total gravitating mass of this galaxy
cannot be accurately determined from the X-ray emission. An interesting point is the large radial extension of the X-ray emission
found by ASCA. If the dark matter fraction in NGC 4636 is low, then
this emission might indicate a dark halo not related to NGC 4636
itself. One could speculate about a dark substructure in the general
Virgo potential, formerly hosting a galaxy group, which formed NGC 4636
as the result of the merging of several galaxies. The quite abrupt
termination of the GC system between 7![]() -9
-9![]() would speak
in favor of this scenario. Stars or GCs, respectively, near their
escape energy are expected to show a drop in their radial density
profile. If NGC 4636 were embedded in a deep dark matter potential
reaching smoothly out to large radii, then one would expect to find GCs
at large radii that are still bound to NGC 4636, and accordingly, a sharp boundary would not fit into the picture. However, it is
interesting to note that the blue clusters apparently do not trace the
dark halo, as has been suggested for other galaxies, e.g., NGC 1399
(Forte et al. 2005). Deeper insight could come from a more complete sampling of GCs or Planetary Nebulae at or beyond a radius of 9
would speak
in favor of this scenario. Stars or GCs, respectively, near their
escape energy are expected to show a drop in their radial density
profile. If NGC 4636 were embedded in a deep dark matter potential
reaching smoothly out to large radii, then one would expect to find GCs
at large radii that are still bound to NGC 4636, and accordingly, a sharp boundary would not fit into the picture. However, it is
interesting to note that the blue clusters apparently do not trace the
dark halo, as has been suggested for other galaxies, e.g., NGC 1399
(Forte et al. 2005). Deeper insight could come from a more complete sampling of GCs or Planetary Nebulae at or beyond a radius of 9![]() ,
which would be a difficult observational task.
,
which would be a difficult observational task.
The CDM paradigm is the most widely accepted view of structure and
galaxy formation. Alternative concepts to explain the kinematics of
galaxies without resorting to dark matter have been minority views
until today. One of these alternative concepts is MOND (MOdified Newtonian
Dynamics), which is discussed with increasing
frequency. (e.g., Milgrom 1983; Sanders & McGaugh
2002). As a phenomenological recipe, the Newtonian
acceleration
![]() has to be replaced by the MOND acceleration
in the case of small accelerations
has to be replaced by the MOND acceleration
in the case of small accelerations ![]() through the relation
through the relation
| (13) |
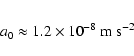
MOND proved to have an impressive predictive power (e.g., Sanders & McGaugh 2002). Many arguments have been raised against MOND, including its apparent arbitrariness, but until now, no convincing case has been found which would disprove MOND. Meanwhile, MOND also has a theoretical foundation in the work of Bekenstein (2004). Perhaps the most serious objection is that MOND does not remove the need for dark matter on cluster scales (Sanders 2003; Pointecouteau & Silk 2005). However, ignoring the pros and cons for the moment, we examine MOND's performance in the case of NGC 4636.
MOND works successfully in the cases of spiral galaxies and dwarf galaxies. Giant ellipticals are more difficult test objects, due to the fact that MOND effects start to become visible at radii where the low surface brightness is an obstacle for reliable investigations of the galaxy's dynamical behavior. However, Gerhard et al. (2001), in their sample of 21 elliptical galaxies, found the onset of increasing M/L-values at accelerations, which are a factor of 10 higher than in spiral galaxies. This would remove the universal character of a0. Milgrom & Sanders (2003) counterargued that there were discrepancies between Gerhard et al.'s analysis and that of Romanowsky et al. (2003), indicating that the last word has not been spoken yet. Therefore, it is interesting to look at the MOND rotation curve of NGC 4636 expected from the luminosity density profile and a certain M/L-ratio.
Figure 17 shows the ratio of the MOND acceleration to a0 and its
dependence on radial distance (for the "standard'' interpolation
function mentioned hereafter). An
M/LR-ratio
of 6.8 has been adopted. The graph shows that giant elliptical
galaxies like NGC 4636 are nowhere in the deep MOND regime. Thus, it is
clear that the interpolation function plays a dominant role, and the
dynamics at small radii do not tell anything about MOND without
knowledge of the transition behavior at high accelerations (for which
there is no theory). A formula that has been widely used in the case
of spiral galaxies is
![]() (Begeman et al. 1991).
(Begeman et al. 1991).
However, Famaey & Binney (2005) find that the above
interpolation does not fit the Galactic rotation curve well and propose
![]() (but see Famaey & Binney for more
detailed remarks on the shortcomings). This formula gives a smoother
transition to the MOND regime, i.e., MOND effects appear earlier.
These two formulas have no physical motivation other than giving satisfactory results.
(but see Famaey & Binney for more
detailed remarks on the shortcomings). This formula gives a smoother
transition to the MOND regime, i.e., MOND effects appear earlier.
These two formulas have no physical motivation other than giving satisfactory results.
![\begin{figure}
\par\includegraphics[angle=90,width=6.4cm,clip]{3134f17.eps}\end{figure}](/articles/aa/full/2006/44/aa3134-05/Timg245.gif) |
Figure 17: This graph shows the ratio of the MONDian acceleration to a0 as a function of galactocentric radius. Equality is reached at about 30 kpc, which already is the limit of our investigation. This means that the deep MOND regime cannot be reached by dynamical tracers and that the scheme of interpolating between the MONDian and the Newtonian regime dominates the analysis. A stellar mass-to-light ratio of M/LR=6.8 was assumed. |
| Open with DEXTER | |
Bekenstein (2004), in his relativistic TeVeS theory of
gravitation, which includes the MOND phenomenology in the limit of
small accelerations, develops the interpolation
![]() for spherical symmetry. This
interpolation is only valid for small and intermediate accelerations
and may not be valid for the full range of acceleration with which we
are dealing.
for spherical symmetry. This
interpolation is only valid for small and intermediate accelerations
and may not be valid for the full range of acceleration with which we
are dealing.
The results are shown in Fig. 18. We again adopted M/LR = 6.8 (an M/LR of 4.3 would, in any case, not be compatible with MOND). The dashed lines are the circular velocities derived from GCs with their anisotropies indicated. The dotted line is the Newtonian circular velocity due to the luminous component alone. The solid lines represent the MOND circular velocities with the uppermost one being the interpolation of Bekenstein, the middle one Famaey & Binney's, and the lower one the "standard'' interpolation. Apparently, MOND reproduces the circular velocities derived from GC kinematics quite well within the uncertainties. The minimum conclusion is that NGC 4636 does not provide a counterargument for MOND. The shape of Bekenstein's interpolation at small radii is probably irrelevant, but at large radii the deviation from our mass models is also quite large and becomes larger with declining M/L. The interpolation of Famaey & Binney works seemingly better than the "standard'' formula, however, the existent data are not sufficient to perform a critical test. A case against MOND could perhaps emerge (it only can be falsified, not verified), if the suspected drop of the velocity dispersion were to be confirmed in combination with a clear tangential bias. The necessary data set must then allow also the measurement of higher moments of the velocity dispersion. NGC 4636 has already a rich cluster system, is more or less spherical, and has a relatively isolated location. Thus, one may conclude that critical tests are difficult to perform with elliptical galaxies.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{3134f18.eps}\end{figure}](/articles/aa/full/2006/44/aa3134-05/Timg247.gif) |
Figure 18: MOND rotation curves for different interpolation schemes are shown for a stellar M/LR ratio of 6.8 (solid lines). The upper solid line is derived from Bekenstein's interpolation, the middle one from Famaey & Binney's, and the lower one from the "standard'' interpolation (see text for explanation). The dashed lines indicate the derived circular velocities from GCs for the given anisotropy parameters (models 3, 4, and 5). The dotted line is the stellar component alone with an adopted M/LR=6.8. The Famaey & Binney interpolation apparently works best. |
| Open with DEXTER | |
However, it is worth mentioning that, so far, one of the most interesting arguments comes from X-rays. Buote et al. (2002) note that the ellipticities of the X-ray isophotes around NGC 720 at larger radii are larger than those expected from the equipotential surfaces calculated from the visible mass distributions. This holds for both the Newtonian and the MOND case.
This is the first dynamical study of the globular cluster system of
the giant elliptical galaxy NGC 4636. Several hundred medium
resolution spectra were acquired at the VLT with FORS 2/MXU. We
obtained velocities for 174 globular clusters in the radial range
![]() ,
or
,
or
![]() ,
in
units of effective radius. Assuming a distance of 15 Mpc, this
corresponds to projected galactocentric distances in the range of 4 to
70 kpc. Due to the sharp decrease in the GC radial number density at
7
,
in
units of effective radius. Assuming a distance of 15 Mpc, this
corresponds to projected galactocentric distances in the range of 4 to
70 kpc. Due to the sharp decrease in the GC radial number density at
7![]() -9
-9![]() ,
about 90 percent of our clusters are found in the
range
,
about 90 percent of our clusters are found in the
range
![]() ,
i.e., within 4.5 effective
radii. This implies that the dynamics beyond this radius cannot be
determined with the current data set.
Within this radius, however, we find a roughly constant velocity
dispersion for the blue clusters.
The red clusters are found to have a distinctly different behavior: at
a radius of about 3
,
i.e., within 4.5 effective
radii. This implies that the dynamics beyond this radius cannot be
determined with the current data set.
Within this radius, however, we find a roughly constant velocity
dispersion for the blue clusters.
The red clusters are found to have a distinctly different behavior: at
a radius of about 3![]() ,
the velocity dispersion drops by
,
the velocity dispersion drops by
![]()
![]() to about
to about
![]() ,
which then remains constant out to a radius of 7
,
which then remains constant out to a radius of 7![]() .
The cause
might be the steepening of the number density profile at
.
The cause
might be the steepening of the number density profile at
![]()
![]() observed for the red clusters.
Following this line of thought, one would expect a dramatic drop in
the velocity dispersion for both red and blue clusters at
7
observed for the red clusters.
Following this line of thought, one would expect a dramatic drop in
the velocity dispersion for both red and blue clusters at
7![]() -9
-9![]() ,
corresponding to the observed change in the
power-law exponent of the GC number density. The observational
difficulty will be to pick up sufficient clusters in this region of
low surface density.
To derive a mass profile, we perform a spherical
Jeans analysis. For a given stellar mass-to-light ratio, a model dark
matter halo, and an orbital anisotropy, we calculate the projected
velocity dispersion and choose those halos that minimize the
residuals to the observational data.
The uncertain outermost data bin is an important obstacle, which
permits a large variety of halos to fit. Generally, slightly
tangential models fit better than radial ones.
Adopting the high stellar M/L value of Kronawitter et al. (2000) (M/LR = 6.8), we find an M/LR-value of 12 within 30 kpc for
,
corresponding to the observed change in the
power-law exponent of the GC number density. The observational
difficulty will be to pick up sufficient clusters in this region of
low surface density.
To derive a mass profile, we perform a spherical
Jeans analysis. For a given stellar mass-to-light ratio, a model dark
matter halo, and an orbital anisotropy, we calculate the projected
velocity dispersion and choose those halos that minimize the
residuals to the observational data.
The uncertain outermost data bin is an important obstacle, which
permits a large variety of halos to fit. Generally, slightly
tangential models fit better than radial ones.
Adopting the high stellar M/L value of Kronawitter et al. (2000) (M/LR = 6.8), we find an M/LR-value of 12 within 30 kpc for
![]() ,
corresponding
to a dark matter fraction of 27%. That being said, values as high as
26 cannot be ruled out with certainty, depending on the treatment of
the last bin.
When a lower stellar M/L value is used (Loewenstein et al. 2003) (M/LR = 4.3), the amount of dark matter
that is needed to explain the observed circular velocities increases
correspondingly. Massive dark matter halos (up to 76% dark matter) can
be required, and neither of the models can be ruled out. An important
source of uncertainty is the sparse data at the outer radius. However,
for most of the reasonable models, we found either less dark matter
than X-ray studies with ROSAT at small radii or the halos are so
concentrated that the total mass is distinctly smaller. One should
consider that the claim for the very high dark matter fraction is
based upon X-ray luminosities that arise in a region suspected to be
out of hydrostatic equilibrium, so one must proceed with caution. The
flattening of the ASCA mass profile cannot be seen. It seems that the
dark matter problem in NGC 4636 also depends, to a large extent, on the
uncertain M/L value of the luminous matter. A dynamical
re-investigation of the inner stellar region would therefore be
worthwhile. Furthermore, it would be of great interest to obtain more spectra for
globular clusters in the radial range beyond
,
corresponding
to a dark matter fraction of 27%. That being said, values as high as
26 cannot be ruled out with certainty, depending on the treatment of
the last bin.
When a lower stellar M/L value is used (Loewenstein et al. 2003) (M/LR = 4.3), the amount of dark matter
that is needed to explain the observed circular velocities increases
correspondingly. Massive dark matter halos (up to 76% dark matter) can
be required, and neither of the models can be ruled out. An important
source of uncertainty is the sparse data at the outer radius. However,
for most of the reasonable models, we found either less dark matter
than X-ray studies with ROSAT at small radii or the halos are so
concentrated that the total mass is distinctly smaller. One should
consider that the claim for the very high dark matter fraction is
based upon X-ray luminosities that arise in a region suspected to be
out of hydrostatic equilibrium, so one must proceed with caution. The
flattening of the ASCA mass profile cannot be seen. It seems that the
dark matter problem in NGC 4636 also depends, to a large extent, on the
uncertain M/L value of the luminous matter. A dynamical
re-investigation of the inner stellar region would therefore be
worthwhile. Furthermore, it would be of great interest to obtain more spectra for
globular clusters in the radial range beyond
![]() to see
whether the suspected decline in the velocity dispersion can be
confirmed. To answer the question whether the NGC 4636 globular
cluster systems rotates, it is desirable to obtain a more uniform
angular coverage.
We also investigated whether the dynamics are consistent with MOND and
answer that positively. The difficulty is that the deep MOND regime is
beyond our radial coverage. Because MOND does not predict the behavior
of the circular velocity in the transition region, one has to apply
physically unmotivated interpolation formulae. The interpolation given
by Famaey & Binney (2005) seems to work best.
to see
whether the suspected decline in the velocity dispersion can be
confirmed. To answer the question whether the NGC 4636 globular
cluster systems rotates, it is desirable to obtain a more uniform
angular coverage.
We also investigated whether the dynamics are consistent with MOND and
answer that positively. The difficulty is that the deep MOND regime is
beyond our radial coverage. Because MOND does not predict the behavior
of the circular velocity in the transition region, one has to apply
physically unmotivated interpolation formulae. The interpolation given
by Famaey & Binney (2005) seems to work best.
Acknowledgements
We thank the referee, Michael Loewenstein, for constructive criticism, which led to an improved dynamical analysis. Y.S. thanks the DAAD for supporting her stay in Concepción and acknowledges support from the Graduiertenkolleg "Galaxy Groups as Laboratories for Baryonic and Dark Matter'' and a German Science Foundation Grant (DFG-Projekt HI-855/2). T.R. and B.D. acknowledge support from the Chilean Center for Astrophysics, FONDAP No. 15010003.
The appendix lists the heliocentric velocities of globular clusters and foreground stars. The object identification follows the scheme #field.#mask #slit. The coordinates are for equinox 2000. The colors and magnitudes are from Dirsch et al. (2005).
Table A.1: Globular cluster data.
Table A.2: Star data.