A&A 456, 801-817 (2006)
DOI: 10.1051/0004-6361:20054779
Gamma-ray binaries: pulsars in disguise?
G. Dubus1,2
1 - Laboratoire Leprince-Ringuet, UMR 7638 CNRS, École Polytechnique, 91128 Palaiseau, France
2 -
Institut d'Astrophysique de Paris, UMR 7095 CNRS, Université Pierre & Marie Curie, Paris 6, 98bis Bd. Arago, 75014 Paris, France
Received 27 December 2005 / Accepted 6 May 2006
Abstract
Context. LS 5039 and LS I+61
 303 are unique amongst high-mass X-ray binaries (HMXB) for their spatially-resolved radio emission and their counterpart at >GeV gamma-ray energies, canonically attributed to non-thermal particles in an accretion-powered relativistic jet. The only other HMXB known to emit very high-energy (VHE) gamma-rays, PSR B1259-63, harbours a non-accreting millisecond pulsar.
303 are unique amongst high-mass X-ray binaries (HMXB) for their spatially-resolved radio emission and their counterpart at >GeV gamma-ray energies, canonically attributed to non-thermal particles in an accretion-powered relativistic jet. The only other HMXB known to emit very high-energy (VHE) gamma-rays, PSR B1259-63, harbours a non-accreting millisecond pulsar.
Aims. The purpose is to investigate whether the interaction of the relativistic wind from a young pulsar with the wind from its stellar companion, as in PSR B1259-63, constitutes a viable scenario for explaining the observations of LS 5039 and LS I+61
 303. Emission arises from the shocked pulsar wind material, which then flows away to large distances in a comet-shape tail, reproducing on a smaller scale what is observed in isolated, high motion pulsars interacting with the interstellar medium.
303. Emission arises from the shocked pulsar wind material, which then flows away to large distances in a comet-shape tail, reproducing on a smaller scale what is observed in isolated, high motion pulsars interacting with the interstellar medium.
Methods. The timescales for acceleration and radiation of particles at the shock between the pulsar wind and stellar wind are calculated. Simple expectations for the spectral energy distribution (SED) are derived and are shown to depend on very few input parameters. Detailed modelling of the particle evolution is attempted and compared to the observations from radio to TeV energies.
Results. Acceleration at the shock provides high-energy electrons that steadily emit synchrotron in X-rays and inverse Compton scatter stellar light to  -rays. Electrons streaming out of the system emit at IR frequencies and below. The overall aspect of the SEDs is adequately reproduced for standard values of the parameters. The morphology of the radio tail can mimic a microquasar jet. Good agreement is found with the published VLBI map of LS 5039 and predictions are made on the expected change in appearance with orbital phase.
-rays. Electrons streaming out of the system emit at IR frequencies and below. The overall aspect of the SEDs is adequately reproduced for standard values of the parameters. The morphology of the radio tail can mimic a microquasar jet. Good agreement is found with the published VLBI map of LS 5039 and predictions are made on the expected change in appearance with orbital phase.
Conclusions. The pulsar wind scenario provides a common, viable framework for interpreting the emission from all three  -ray binaries.
-ray binaries.
Key words: acceleration of particles -
stars: binaries: close -
stars: pulsars: general -
ISM: jets and outflows -
gamma rays: theory -
X-rays: binaries
X-ray binaries are systems composed of a neutron star or black hole in orbit around a high or low-mass normal star (HMXBs and LMXBs). Non-thermal radio emission has been detected in X-ray binaries and is usually associated with outflows (see Fender 2006, for a review). In a few objects, radio observations are able to follow the propagation of radio emission up to parsec scales, after initial flaring in the central source. The inferred speeds of the collimated outflow are relativistic with bulk Lorentz factors 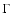 of a few. These apparently superluminal ejection events have been tentatively associated with transitions from a hard to a soft X-ray spectrum (Fender et al. 2004).
of a few. These apparently superluminal ejection events have been tentatively associated with transitions from a hard to a soft X-ray spectrum (Fender et al. 2004).
In many more objects, the radio emission has a flat spectrum and is correlated with a hard X-ray spectral state. Usually the radio emission is unresolved but imaging by very long baseline interferometry (VLBI) of Cyg X-1 in this state has revealed a compact, collimated radio outflow on a scale of a few AU (Stirling et al. 2001). Asymmetries in the surface brightness probably reflect moderate relativistic boosting (
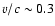 ). It is as yet unclear whether compact radio emission and superluminal ejections can be taken as different manifestations of a unique, underlying ejection mechanism.
). It is as yet unclear whether compact radio emission and superluminal ejections can be taken as different manifestations of a unique, underlying ejection mechanism.
Similar types of radio emission (compact or superluminal ejections) are seen in active galactic nuclei (AGN), prompting speculations that phenomenology known to one type of object may have its counterpart in the other. The detection of very high energy  -rays from the X-ray binary LS 5039 by the HESS collaboration would appear to vindicate this conjecture (Aharonian et al. 2005a). Observations in the 1990s have established that blazars, a subtype of AGN, emit high energy (HE, GeV) and very high energy (VHE, TeV)
-rays from the X-ray binary LS 5039 by the HESS collaboration would appear to vindicate this conjecture (Aharonian et al. 2005a). Observations in the 1990s have established that blazars, a subtype of AGN, emit high energy (HE, GeV) and very high energy (VHE, TeV)  -rays (Hoffman et al. 1999). Blazars have their jet aligned close to the line-of-sight, resulting in a very strong relativistic boosting of the jet non-thermal emission. The same configuration could be found in an X-ray binary, and this is perhaps the case in LS 5039.
-rays (Hoffman et al. 1999). Blazars have their jet aligned close to the line-of-sight, resulting in a very strong relativistic boosting of the jet non-thermal emission. The same configuration could be found in an X-ray binary, and this is perhaps the case in LS 5039.
LS 5039 is composed of a O6.5V star and an unidentified compact object in a 3.9 day orbit (McSwain & Gies 2002; McSwain et al. 2004; Casares et al. 2005b; Motch et al. 1997; Clark et al. 2001). Much of the interest in this object stems from its tentative association with the EGRET source 3EG J1824-1514 and from the fact that its radio emission was shown to be extended on a milliarcsecond scale (Paredes et al. 2000). By analogy with blazars, it is tempting to attribute the radio and  -ray emission to high-energy particles accelerated in a jet. LS 5039 is very similar to LS I+61
-ray emission to high-energy particles accelerated in a jet. LS 5039 is very similar to LS I+61
 303, an X-ray binary with a B0Ve star in a 26.5 day orbit whose association with a high-energy source dates back to COS-B (Hutchings & Crampton 1981; Casares et al. 2005a; Gregory & Taylor 1978). The associations rely purely on positional coincidence, which is fairly poor as the EGRET 99% confidence levels are roughly at 0.5
303, an X-ray binary with a B0Ve star in a 26.5 day orbit whose association with a high-energy source dates back to COS-B (Hutchings & Crampton 1981; Casares et al. 2005a; Gregory & Taylor 1978). The associations rely purely on positional coincidence, which is fairly poor as the EGRET 99% confidence levels are roughly at 0.5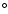 for LS 5039 and 0.2
for LS 5039 and 0.2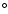 for LS I+61
for LS I+61
 303 (3EG J0241+6103). The HESS detection of VHE emission coincident to within an arcmin with the position of LS 5039 identifies this X-ray binary as the source of
303 (3EG J0241+6103). The HESS detection of VHE emission coincident to within an arcmin with the position of LS 5039 identifies this X-ray binary as the source of  -rays. By extension, it places the EGRET tentative identification on a firmer footing.
-rays. By extension, it places the EGRET tentative identification on a firmer footing.
The VHE  -ray emission is at least evidence that particles can be accelerated to very high energies in X-ray binaries. However, is it necessarily associated with blazar-like model, involving accretion of material, ejection, and non-thermal acceleration in a relativistic jet? Maraschi & Treves (1981) pointed out early on that the spindown of a young, rapidly-rotating pulsar could power the
-ray emission is at least evidence that particles can be accelerated to very high energies in X-ray binaries. However, is it necessarily associated with blazar-like model, involving accretion of material, ejection, and non-thermal acceleration in a relativistic jet? Maraschi & Treves (1981) pointed out early on that the spindown of a young, rapidly-rotating pulsar could power the  -ray emission of LS I+61
-ray emission of LS I+61
 303. The relativistic pulsar wind would be confined by the stellar wind from the massive companion. Particles accelerated at the termination shock then produce the non-thermal emission.
303. The relativistic pulsar wind would be confined by the stellar wind from the massive companion. Particles accelerated at the termination shock then produce the non-thermal emission.
There is at least one system where such a scenario is undoubtedly at work: PSR B1259-63 (=SS 2883), a 47.7 millisecond (ms) radio pulsar in a 3.4 yr orbit around a B2Ve star (Manchester et al. 1995; Johnston et al. 1994). Variable  -ray emission was detected by HESS during periastron passage (Aharonian et al. 2005b). In LS 5039 and LS I+61
-ray emission was detected by HESS during periastron passage (Aharonian et al. 2005b). In LS 5039 and LS I+61
 303, the discovery of resolved radio emission was interpreted as the signature of a relativistic jet, and recently, the attention seems to have focused on accretion/ejection scenarios (but see Martocchia et al. 2005; Leahy 2004). The pulsar scenario has become unwonted. Yet, pulsars interacting with their surrounding medium can also lead to large-scale emission, the bow shock nebula of high velocity ms pulsars even taking a comet tail appearance (e.g. Gaensler 2005). The resolved "jets'' of LS 5039 and LS I+61
303, the discovery of resolved radio emission was interpreted as the signature of a relativistic jet, and recently, the attention seems to have focused on accretion/ejection scenarios (but see Martocchia et al. 2005; Leahy 2004). The pulsar scenario has become unwonted. Yet, pulsars interacting with their surrounding medium can also lead to large-scale emission, the bow shock nebula of high velocity ms pulsars even taking a comet tail appearance (e.g. Gaensler 2005). The resolved "jets'' of LS 5039 and LS I+61
 303 might be small-scale analogues, but with the trail originating from the interaction with a companion wind rather than with the ISM.
303 might be small-scale analogues, but with the trail originating from the interaction with a companion wind rather than with the ISM.
The similarities between LS 5039 and LS I+61
 303 have long been noticed: resolved radio emission, hard steady X-ray fluxes, and EGRET emission in the GeV range at a level
303 have long been noticed: resolved radio emission, hard steady X-ray fluxes, and EGRET emission in the GeV range at a level  1035 erg s-1. LS I+61
1035 erg s-1. LS I+61
 303, located in the Northern hemisphere and inaccessible to HESS, has yet to be detected at TeV energies. While PSR B1259-63 shares the property of being a TeV emitter with LS 5039, LS I+61
303, located in the Northern hemisphere and inaccessible to HESS, has yet to be detected at TeV energies. While PSR B1259-63 shares the property of being a TeV emitter with LS 5039, LS I+61
 303 and PSR B1259-63 both have similar periodic radio outbursts that may be linked to both of them having a Be type companion. PSR B1259-63 has not been detected at GeV energies by EGRET (including at periastron passage, Tavani et al. 1996), perhaps because its long orbit only takes it close to the star for periods of time that are too limited for the sensitivity of the instrument.
303 and PSR B1259-63 both have similar periodic radio outbursts that may be linked to both of them having a Be type companion. PSR B1259-63 has not been detected at GeV energies by EGRET (including at periastron passage, Tavani et al. 1996), perhaps because its long orbit only takes it close to the star for periods of time that are too limited for the sensitivity of the instrument.
When closest, PSR B1259-63 is about 0.7 AU away from its companion, equivalent to the apastron orbital separation in LS I+61
 303. The periastron separation of 0.1 AU in LS I+61
303. The periastron separation of 0.1 AU in LS I+61
 303 is itself comparable to the orbit in the more compact LS 5039 (Table 1). There is a scaling between the three systems that, should they be governed by the same underlying processes, might lead to interesting comparisons. Indeed, their spectral energy distributions are similar in shape and luminosity (Fig. 1), suggesting the same physics might be at work in these three known examples of "
303 is itself comparable to the orbit in the more compact LS 5039 (Table 1). There is a scaling between the three systems that, should they be governed by the same underlying processes, might lead to interesting comparisons. Indeed, their spectral energy distributions are similar in shape and luminosity (Fig. 1), suggesting the same physics might be at work in these three known examples of " -ray binaries''.
-ray binaries''.
This work purports to investigate the pulsar wind scenario in light of the latest observations of these binaries. Reviewing current evidence, it is argued in Sect. 2 that there is as yet no reason to discard this possibility in LS 5039 and LS I+61
 303. The scenario is then developed in the following sections. The basic assumptions are described in Sect. 3, showing how the physical quantities scale with the parameters of the model. Simple expectations for the spectral energy distribution are derived in Sect. 4. A numerical model of the emission is elaborated in Sect. 5 and applied to the
303. The scenario is then developed in the following sections. The basic assumptions are described in Sect. 3, showing how the physical quantities scale with the parameters of the model. Simple expectations for the spectral energy distribution are derived in Sect. 4. A numerical model of the emission is elaborated in Sect. 5 and applied to the  -ray binaries in Sect. 6. It is shown that the radio emission from the shocked pulsar wind material can look like that of a compact jet emanating from an accreting microquasar. The conclusion set out in Sect. 7 is that the pulsar wind scenario provides a plausible, coherent and persuasive framework to interpret the emission from these
-ray binaries in Sect. 6. It is shown that the radio emission from the shocked pulsar wind material can look like that of a compact jet emanating from an accreting microquasar. The conclusion set out in Sect. 7 is that the pulsar wind scenario provides a plausible, coherent and persuasive framework to interpret the emission from these  -ray binaries.
-ray binaries.
Table 1:
Orbital parameters adopted for the  -ray binaries.
-ray binaries.
Several observations could securely tilt the balance towards the "black hole jet'', accretion-powered scenario, or the "pulsar wind'', rotation-powered scenario in LS 5039 and LS I+61
 303 without detailed modelling. These are examined here in turn.
303 without detailed modelling. These are examined here in turn.
A compact object mass greater than 3 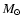 would rule out the pulsar wind scenario. Constraints have been set in both LS 5039 and LS I+61
would rule out the pulsar wind scenario. Constraints have been set in both LS 5039 and LS I+61
 303 by measuring the radial velocity of the stellar companion. This enables the measure of the period, mass function, eccentricity, and periastron angle. The mass function provides a strict lower limit to the mass of the compact object. In high-mass X-ray binaries, the mass function is too small to provide a useful constraint:
303 by measuring the radial velocity of the stellar companion. This enables the measure of the period, mass function, eccentricity, and periastron angle. The mass function provides a strict lower limit to the mass of the compact object. In high-mass X-ray binaries, the mass function is too small to provide a useful constraint:
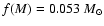 in LS 5039,
in LS 5039,
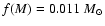 in LS I+61
in LS I+61
 303 (Casares et al. 2005b,a who have the best available datasets).
303 (Casares et al. 2005b,a who have the best available datasets).
A constraint on the compact object mass then requires additional knowledge of the mass of the stellar companion and the orbit inclination. Atmosphere fitting of the spectrum leads to an estimate for the mass (and radius) of the massive star. Accuracy requires detailed stellar models and is inherently difficult due to the high mass-loss rates of early-type stars. Lines can originate at different depths and velocities in the strong (variable) stellar wind, leading to confusing measurements of radial velocities and difficulties in spectral modelling (see e.g. discussion in Bahcall 1978). Parameters as derived have higher, probably irreducible, systematics than the quoted (statistical) errors might suggest (e.g. Table 2 of Casares et al. 2005b). In fact, the orbital period of LS I+61
 303 (26.5 days) cannot be determined from optical spectroscopy alone with high confidence, and radial velocity studies use as an a priori the well-determined radio outburst period (Hutchings & Crampton 1981; Casares et al. 2005a; Gregory 2002).
303 (26.5 days) cannot be determined from optical spectroscopy alone with high confidence, and radial velocity studies use as an a priori the well-determined radio outburst period (Hutchings & Crampton 1981; Casares et al. 2005a; Gregory 2002).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4779f1a}\par\vspace*{2mm}
\...
...4779f1b}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{4779f1c}\end{figure}](/articles/aa/full/2006/36/aa4779-05/Timg58.gif) |
Figure 1:
Observed spectral energy distributions of LS 5039, LS I+61
 303 and PSR B1259-63. Fluxes have been transformed to spectral luminosities assuming distances of 2.5 kpc (LS 5039, Casares et al. 2005b), 2.3 kpc (LS I+61 303 and PSR B1259-63. Fluxes have been transformed to spectral luminosities assuming distances of 2.5 kpc (LS 5039, Casares et al. 2005b), 2.3 kpc (LS I+61
 303, Gregory et al. 1979) and 1.5 kpc (PSR B1259-63, Johnston et al. 1994). The optical-UV emission peaking at 303, Gregory et al. 1979) and 1.5 kpc (PSR B1259-63, Johnston et al. 1994). The optical-UV emission peaking at  1 eV in the binaries is the light from the stellar companion (uncorrected for absorption by the interstellar medium). Radio to X-ray flux values in LS 5039 are taken from (in order of increasing frequency) Martí et al. (1998b), Clark et al. (2001),Martocchia et al. (2005); flux values in LS I+61 1 eV in the binaries is the light from the stellar companion (uncorrected for absorption by the interstellar medium). Radio to X-ray flux values in LS 5039 are taken from (in order of increasing frequency) Martí et al. (1998b), Clark et al. (2001),Martocchia et al. (2005); flux values in LS I+61
 303 are taken from Strickman et al. (1998), Martí & Paredes (1995),Maraschi et al. (1981), Leahy et al. (1997), Greiner & Rau (2001); in PSR B1259-63 from Johnston et al. (2005), Skrutskie et al. (2006), Marraco & Orsatti (1982). The RXTE spectrum of PSR B1259-63 obtained during the 2004 periastron passage was kindly provided by B. Giebels. The upper envelope of radio measurements in LS I+61 303 are taken from Strickman et al. (1998), Martí & Paredes (1995),Maraschi et al. (1981), Leahy et al. (1997), Greiner & Rau (2001); in PSR B1259-63 from Johnston et al. (2005), Skrutskie et al. (2006), Marraco & Orsatti (1982). The RXTE spectrum of PSR B1259-63 obtained during the 2004 periastron passage was kindly provided by B. Giebels. The upper envelope of radio measurements in LS I+61
 303 and PSR B1259-63 corresponds to values during radio outbursts. The hard X-ray BATSE points in LS 5039 and LS I+61 303 and PSR B1259-63 corresponds to values during radio outbursts. The hard X-ray BATSE points in LS 5039 and LS I+61
 303 are from Harmon et al. (2004); the OSSE bowtie is from Grove et al. (1995) and the HE 303 are from Harmon et al. (2004); the OSSE bowtie is from Grove et al. (1995) and the HE  -ray EGRET boxes are from Hartman et al. (1999); EGRET upper limits in PSR B1259-63 are from Tavani et al. (1996). The VHE -ray EGRET boxes are from Hartman et al. (1999); EGRET upper limits in PSR B1259-63 are from Tavani et al. (1996). The VHE  -ray HESS measurements are from Aharonian et al. (2005a,b) and the Whipple upper limits for LS I+61 -ray HESS measurements are from Aharonian et al. (2005a,b) and the Whipple upper limits for LS I+61
 303 from Fegan et al. (2005). 303 from Fegan et al. (2005). |
| Open with DEXTER |
The parameter space derived by Casares et al. (2005b,a) using these techniques allows for both a neutron star or a black hole in LS 5039 and LS I+61
 303. The radial velocity amplitude implies a low orbit inclination if the compact object is massive (
303. The radial velocity amplitude implies a low orbit inclination if the compact object is massive (
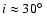 for
for
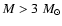 in both LS 5039 and LS I+61
in both LS 5039 and LS I+61
 303), a good omen for a model with a relativistic jet pointed close to the line-of-sight. On the other hand, a 1.4
303), a good omen for a model with a relativistic jet pointed close to the line-of-sight. On the other hand, a 1.4 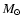 neutron star implies
neutron star implies
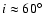 in both objects. In LS 5039, the lack of X-ray eclipses (assuming point-like emission) by a companion of
in both objects. In LS 5039, the lack of X-ray eclipses (assuming point-like emission) by a companion of 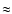
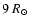 requires
requires
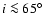 ,
consistent with the above. Line broadening of the lines gives an upper limit on their rotation speeds, which can be used to set a lower limit on the inclination for aligned spin/orbital axis since it must be lower than breakup speed. Casares et al. (2005b,a) find
,
consistent with the above. Line broadening of the lines gives an upper limit on their rotation speeds, which can be used to set a lower limit on the inclination for aligned spin/orbital axis since it must be lower than breakup speed. Casares et al. (2005b,a) find
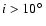 in both systems, again consistent with both a black hole and a neutron star. Since the value of
in both systems, again consistent with both a black hole and a neutron star. Since the value of 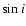 is more likely to be high than low for a random distribution of inclinations, a neutron star would seem to be favoured over a black hole.
is more likely to be high than low for a random distribution of inclinations, a neutron star would seem to be favoured over a black hole.
The binary orbit of LS 5039 is quite compact for a high-mass X-ray binary (
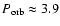 days) and is only mildly eccentric (
days) and is only mildly eccentric (
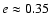 ). By comparison, LS I+61
). By comparison, LS I+61
 303 has
303 has
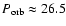 days and
days and
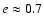 .
Orbital circularization and synchronization might be relatively advanced in LS 5039. This has prompted Casares et al. (2005b) to use their measurement of rotational broadening to constrain the orbit in LS 5039 by assuming that the massive star is corotating at the angular orbital velocity at periastron. The compact object mass then becomes 2.7-5.0
.
Orbital circularization and synchronization might be relatively advanced in LS 5039. This has prompted Casares et al. (2005b) to use their measurement of rotational broadening to constrain the orbit in LS 5039 by assuming that the massive star is corotating at the angular orbital velocity at periastron. The compact object mass then becomes 2.7-5.0 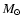 with
with
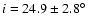 ,
probably optimistic because of the possible systematics, but in practice ruling out a neutron star.
,
probably optimistic because of the possible systematics, but in practice ruling out a neutron star.
This conclusion is not robust. Observations of the stellar companions in other high-mass X-ray binaries with similar periods do not systematically show corotation (Conti 1978). Although synchronization is undoubtedly fast by astronomical standards (some detached early-type binaries are observed to be circularized), short-lived wind-fed HMXBs do not have ages that are much greater than their typical synchronization timescale. These timescales are difficult to calculate precisely: in massive stars, they depend on excited modes in the radiative envelope (Zahn 1977). The age of the system can only be guessed at. Rotation-powered emission would probably imply an energetic pulsar with a short spindown timescale. Synchronization would then not have happened.
In both LS I+61
 303 and LS 5039, optical spectroscopy alone is unable to decide between a neutron star and black hole compact object. This work will assume a 1.4
303 and LS 5039, optical spectroscopy alone is unable to decide between a neutron star and black hole compact object. This work will assume a 1.4 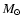 neutron star.
neutron star.
Any sign of accretion on the compact object would dismiss the pulsar wind scenario. Accretion would have to be wind-fed: Roche lobe overflow as occurs in Cyg X-1 and some other HMXBs would entail much higher X-ray luminosities. The orbits and sizes of the massive stars in LS 5039 and LS I+61
 303 support this conclusion (Casares et al. 2005b,a). The rate at which mass is accreted from the stellar wind can be estimated. The Bondi capture radius is
303 support this conclusion (Casares et al. 2005b,a). The rate at which mass is accreted from the stellar wind can be estimated. The Bondi capture radius is
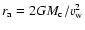 ,
where
,
where 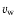 is the wind speed (about 2000 km s-1) and
is the wind speed (about 2000 km s-1) and 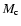 is the mass of the compact object. The Bondi mass accretion rate is then
is the mass of the compact object. The Bondi mass accretion rate is then
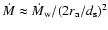 where
where
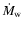 is the stellar wind mass-loss rate (about
is the stellar wind mass-loss rate (about
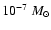 yr-1) and
yr-1) and 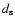 is the orbital separation. Using the LS 5039 orbital and stellar parameters in Table 1 gives between
is the orbital separation. Using the LS 5039 orbital and stellar parameters in Table 1 gives between
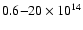 g s-1 along the orbit in LS 5039, with a time-average of
g s-1 along the orbit in LS 5039, with a time-average of
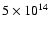 g s-1. With 10% radiative efficiency, this is too close to the sustained GeV emission at a level
g s-1. With 10% radiative efficiency, this is too close to the sustained GeV emission at a level  1035 erg s-1. In addition, although the X-ray luminosity is comparable to those of wind-fed X-ray binaries, the lightcurve does not show evidence of the large expected associated orbital variability (Bosch-Ramon et al. 2005; Reig et al. 2003). The slow, dense Be equatorial wind in LS I+61
1035 erg s-1. In addition, although the X-ray luminosity is comparable to those of wind-fed X-ray binaries, the lightcurve does not show evidence of the large expected associated orbital variability (Bosch-Ramon et al. 2005; Reig et al. 2003). The slow, dense Be equatorial wind in LS I+61
 303 allows for higher accretion rates, in better agreement with the total luminosity and the factor
303 allows for higher accretion rates, in better agreement with the total luminosity and the factor  10 variations observed in the 0.5-2 keV band lightcurve (the variability amplitudes are lower at higher energies, Harrison et al. 2000; Martí & Paredes 1995; Paredes et al. 1997).
10 variations observed in the 0.5-2 keV band lightcurve (the variability amplitudes are lower at higher energies, Harrison et al. 2000; Martí & Paredes 1995; Paredes et al. 1997).
There are no signs of the large excursions in luminosity or spectra typical of (hard or soft) X-ray transients. The X-ray spectra are reminiscent of the low/hard X-ray state of LMXBs. There are some radio/X-ray fluctuations on timescales  hour in both objects (Bosch-Ramon et al. 2005; Harrison et al. 2000); but strong, fast variability on timescales of
hour in both objects (Bosch-Ramon et al. 2005; Harrison et al. 2000); but strong, fast variability on timescales of  second, expected from a low/hard state LMXB or accreting HMXB (van der Klis 2006), has not been detected (Harrison et al. 2000; Ribó et al. 1999, although the low flux of the sources should be noted). The Thomson opacity is low in the stellar wind, hence variability might be smoothed out by scattering in a dense corona. There is no sign of such a corona in the X-ray spectra. Indeed, the apparent lack of spectral cutoffs around either 30 keV or 100 keV (see Fig. 1) sets them apart from both accreting HMXBs and low-state LMXBs. The RXTE spectra of LS 5039 did show a strong, broad Fe line (Ribó et al. 1999), but that could not be confirmed by other X-ray missions (Martocchia et al. 2005). LS 5039 lies in the Galactic Plane and the Fe line is very likely due to Ridge emission sampled by the large RXTE non-imaging aperture (Bosch-Ramon et al. 2005).
second, expected from a low/hard state LMXB or accreting HMXB (van der Klis 2006), has not been detected (Harrison et al. 2000; Ribó et al. 1999, although the low flux of the sources should be noted). The Thomson opacity is low in the stellar wind, hence variability might be smoothed out by scattering in a dense corona. There is no sign of such a corona in the X-ray spectra. Indeed, the apparent lack of spectral cutoffs around either 30 keV or 100 keV (see Fig. 1) sets them apart from both accreting HMXBs and low-state LMXBs. The RXTE spectra of LS 5039 did show a strong, broad Fe line (Ribó et al. 1999), but that could not be confirmed by other X-ray missions (Martocchia et al. 2005). LS 5039 lies in the Galactic Plane and the Fe line is very likely due to Ridge emission sampled by the large RXTE non-imaging aperture (Bosch-Ramon et al. 2005).
The radio and hard X-ray emission would be compatible with most of the emission coming from a non-thermal distribution of particles in a relativistic jet (Dermer & Böttcher 2006; Paredes et al. 2006; Romero et al. 2005). Gamma-rays would then be up-scattered photons. The puzzle is how such a jet could be fed by accretion without any of the usual signatures, most notably variability. In the  -ray binaries, the broad-band SEDs are stable even on timescales of years.
-ray binaries, the broad-band SEDs are stable even on timescales of years.
The simplest hypothesis is that accretion does not occur in LS 5039 and LS I+61
 303, as in PSR B1259-63. If the infall of material is stopped by pressure from a relativistic pulsar wind, this will produce very little emission and variability. Instead, the emission will be due to the shocked pulsar wind. As in the relativistic jet scenario, a non-thermal distribution of particles provides the necessary ingredient to explain the SED. The spindown of the pulsar provides a stable energy source on human timescales. The termination shock of the contained pulsar wind provides the conditions for particle acceleration. Only very mild variations are expected, due to fluctuations of the environment (stellar wind), consistent with observations.
303, as in PSR B1259-63. If the infall of material is stopped by pressure from a relativistic pulsar wind, this will produce very little emission and variability. Instead, the emission will be due to the shocked pulsar wind. As in the relativistic jet scenario, a non-thermal distribution of particles provides the necessary ingredient to explain the SED. The spindown of the pulsar provides a stable energy source on human timescales. The termination shock of the contained pulsar wind provides the conditions for particle acceleration. Only very mild variations are expected, due to fluctuations of the environment (stellar wind), consistent with observations.
The detection of relativistic motion in the radio emission, like that of the microquasar GRS 1915+105, would secure the jet model. The radio morphology of LS 5039 and LS I+61
 303 looks more like the compact jets seen in the low/hard X-ray state of low-mass X-ray binaries or Cyg X-1, with the significant difference that their radio spectral indices are steeper than the usual flat indices measured in the self-absorbed jets. The indices (
303 looks more like the compact jets seen in the low/hard X-ray state of low-mass X-ray binaries or Cyg X-1, with the significant difference that their radio spectral indices are steeper than the usual flat indices measured in the self-absorbed jets. The indices (
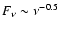 )
hint rather at optically thin synchrotron emission from a
)
hint rather at optically thin synchrotron emission from a
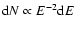 power-law distribution of electrons.
power-law distribution of electrons.
The period of the radio outbursts of LS I+61
 303 is very stable and is used as a clock for the orbital motion (Gregory 2002). The radio luminosity of LS 5039 has been steady at the same level for years (Martí et al. 1998a). The radio brightness asymmetry of LS 5039 and LS I+61
303 is very stable and is used as a clock for the orbital motion (Gregory 2002). The radio luminosity of LS 5039 has been steady at the same level for years (Martí et al. 1998a). The radio brightness asymmetry of LS 5039 and LS I+61
 303 has been used to place constraints on (de)boosting of the putative relativistic jet. This yields a mild flow velocity of 0.2-0.3c (Massi et al. 2004; Paredes et al. 2000). There is no evidence in either system of highly relativistic bulk motion directed more or less towards the line-of-sight; the main argument favouring a jet interpretation is based on the morphology of the radio emission.
303 has been used to place constraints on (de)boosting of the putative relativistic jet. This yields a mild flow velocity of 0.2-0.3c (Massi et al. 2004; Paredes et al. 2000). There is no evidence in either system of highly relativistic bulk motion directed more or less towards the line-of-sight; the main argument favouring a jet interpretation is based on the morphology of the radio emission.
As mentioned in Sect. 1, fast-moving young and old millisecond pulsars leave trails of X-ray, optical, and radio emission that can reach parsec lengths, and their properties scale with the distance where the wind terminates due to containment by the surrounding interstellar medium (Wang et al. 1993; Arons & Tavani 1993). Even the collision of standard stellar winds can produce detectable large-scale, jet-looking, radio emission (e.g. Dougherty et al. 2003). The radio emission of LS 5039 and LS I+61
 303 seems to reach scales of up to several 100 AUs (Massi et al. 2004; Paredes et al. 2002), double-sided in the case of LS 5039. Energetically speaking, this emission can easily be a pulsar nebula. However, isolated ms pulsars have time to develop long (one-sided) nebula away from their direction of proper motion. In the
303 seems to reach scales of up to several 100 AUs (Massi et al. 2004; Paredes et al. 2002), double-sided in the case of LS 5039. Energetically speaking, this emission can easily be a pulsar nebula. However, isolated ms pulsars have time to develop long (one-sided) nebula away from their direction of proper motion. In the  -ray binaries, the direction of such a nebula would be affected on short timescales by orbital motion. Radio observations of LS I+61
-ray binaries, the direction of such a nebula would be affected on short timescales by orbital motion. Radio observations of LS I+61
 303 have shown curved radio emission on a scale of 50 mas, interpreted as due to precession of a jet as in SS 433 (Massi et al. 2004). Could this morphology instead be a result of the pulsar orbital motion?
303 have shown curved radio emission on a scale of 50 mas, interpreted as due to precession of a jet as in SS 433 (Massi et al. 2004). Could this morphology instead be a result of the pulsar orbital motion?
In this work, it will be argued that the resolved radio emission in LS 5039 and LS I+61
 303 is not due to a relativistic jet akin to those of AGN or microquasars (and implying accretion), but arises instead from shocked pulsar wind material outflowing from the binary.
303 is not due to a relativistic jet akin to those of AGN or microquasars (and implying accretion), but arises instead from shocked pulsar wind material outflowing from the binary.
2.4 Can the compact object be a pulsar?
The X-ray and radio properties of LS 5039 and LS I+61
 303 sets them apart from other X-ray binaries, with no conclusive signs of accretion going on. At the same time, the luminosity, hard X-ray power law extending to high energies, weak variability, and optically thin radio emission are typical of emission from young pulsars with a high spindown power (e.g. Gaensler & Slane 2006). Examining the pulsar wind hypothesis therefore seems justified.
303 sets them apart from other X-ray binaries, with no conclusive signs of accretion going on. At the same time, the luminosity, hard X-ray power law extending to high energies, weak variability, and optically thin radio emission are typical of emission from young pulsars with a high spindown power (e.g. Gaensler & Slane 2006). Examining the pulsar wind hypothesis therefore seems justified.
In order to avoid disc or magnetospheric accretion, the relativistic wind of the pulsar must be able to quench the infall of stellar matter attracted to it (Illarionov & Sunyaev 1975). If all of the pulsar spindown power 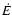 is transferred to this relativistic wind, then writing the pressures gives
is transferred to this relativistic wind, then writing the pressures gives
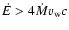 where
where 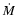 is the Bondi rate calculated above. Writing the spindown power as a function of the pulsar magnetic field B and period P, then
is the Bondi rate calculated above. Writing the spindown power as a function of the pulsar magnetic field B and period P, then
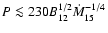 ms, with
ms, with
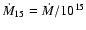 g s-1. A young, ms pulsar would push out any settling accretion flow.
g s-1. A young, ms pulsar would push out any settling accretion flow.
The young age is not problematic. Radio searches have not conclusively identified an association with a supernova remnant (Ribó et al. 2002; Frail et al. 1987; Martí et al. 1998a), but neither have they been able to do so for PSR B1259-63, which has a measured spindown age of
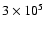 years (Johnston et al. 1992). Ribó et al. (2002) put an upper limit of about a Myr on the age of LS 5039 by tracing back the proper motion of the system to the plane. Nitrogen enrichment in the companion's atmosphere also suggests a young age in LS 5039 (McSwain et al. 2004; rotational-mixing could also explain the enrichment, Casares et al. 2005b).
years (Johnston et al. 1992). Ribó et al. (2002) put an upper limit of about a Myr on the age of LS 5039 by tracing back the proper motion of the system to the plane. Nitrogen enrichment in the companion's atmosphere also suggests a young age in LS 5039 (McSwain et al. 2004; rotational-mixing could also explain the enrichment, Casares et al. 2005b).
Detecting the radio pulse would nail down this scenario. Unfortunately, free-free absorption in the dense stellar winds of LS 5039 and LS I+61
 303 would suppress the signal. Using the Rosseland mean opacity, the radial optical depth at 1 GHz from a point at a distance d from the star is
303 would suppress the signal. Using the Rosseland mean opacity, the radial optical depth at 1 GHz from a point at a distance d from the star is
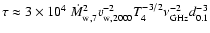 for a
for a
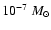 yr-1 coasting wind with a speed 2000 km s-1 and temperature 104 K; d is taken to be 0.1 AU, about the periastron orbital separation in LS 5039 and LS I+61
yr-1 coasting wind with a speed 2000 km s-1 and temperature 104 K; d is taken to be 0.1 AU, about the periastron orbital separation in LS 5039 and LS I+61
 303. High opacities are also found in LS I+61
303. High opacities are also found in LS I+61
 303 (Taylor & Gregory 1982). In PSR B1259-63, the suppression of pulsed emission is observed close to periastron (Johnston et al. 1992; Melatos et al. 1995).
303 (Taylor & Gregory 1982). In PSR B1259-63, the suppression of pulsed emission is observed close to periastron (Johnston et al. 1992; Melatos et al. 1995).
Pulsed emission in the X-ray/GeV band would serve just as well. Such a detection does not seem realistic without prior knowledge of the pulse period derivatives given the sensitivities achievable even by GLAST. In addition, the pulsed GeV signal in LS 5039 may be smoothed out by emission from the
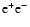 cascade initiated by absorption of TeV
cascade initiated by absorption of TeV  -rays on stellar photons (Dubus 2006).
-rays on stellar photons (Dubus 2006).
As the pulsar rotation gradually decreases, the  -ray binaries would become standard accretion-powered high-mass X-ray binaries, perhaps brighter in the X-ray sky but probably without significant emission at
-ray binaries would become standard accretion-powered high-mass X-ray binaries, perhaps brighter in the X-ray sky but probably without significant emission at  -ray energies. That three examples of such short-lived phases may have been found perhaps implies a large population of descendant HMXBs some of which might be the enshrouded hard X-ray sources discovered by INTEGRAL. Some of the unidentified EGRET sources located in the Galactic plane may also turn out to be pulsars in binaries. Massive X-ray binary population synthesis calculations by Meurs & van den Heuvel (1989) predict about 30 binaries in the brief young pulsar stage in the Galaxy, consistent with three examples being found within 3 kpc.
-ray energies. That three examples of such short-lived phases may have been found perhaps implies a large population of descendant HMXBs some of which might be the enshrouded hard X-ray sources discovered by INTEGRAL. Some of the unidentified EGRET sources located in the Galactic plane may also turn out to be pulsars in binaries. Massive X-ray binary population synthesis calculations by Meurs & van den Heuvel (1989) predict about 30 binaries in the brief young pulsar stage in the Galaxy, consistent with three examples being found within 3 kpc.
The conclusion is that LS 5039 and LS I+61
 303 could very well harbour a young pulsar with a strong relativistic wind like that of PSR B1259-63. A model based on this scenario is explored in the next sections.
303 could very well harbour a young pulsar with a strong relativistic wind like that of PSR B1259-63. A model based on this scenario is explored in the next sections.
The scenario, identical to the one proposed for PSR B1259-63, is the following: a young pulsar with a spindown rate of the order of 1036 erg s-1 generates a strong relativistic wind beyond the light cylinder (Rees & Gunn 1974). The pulsar wind is assumed to be radial, isotropic and composed of principally mono-energetic electrons/positrons with a Lorentz factor
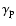 .
All the spindown power is transferred to the leptons, with a small fraction going to the magnetic field. The ratio of magnetic to kinetic energy
.
All the spindown power is transferred to the leptons, with a small fraction going to the magnetic field. The ratio of magnetic to kinetic energy 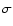 is a parameter of the model.
is a parameter of the model.
The pulsar wind is contained by the stellar wind; in a plerion like the Crab, the container is the supernova remnant material. A collisionless shock forms beyond which the leptons from the pulsar wind are accelerated and isotropized. The shocked pulsar wind material is separated from the stellar wind by a contact discontinuity across which mixing might occur (neglected here). The shock has a ``bow'' or ``comet'' shape with a tail extending away from the stellar companion. The radio emission occurs in this nebula. Studying such a complex interaction is simplified by noting that everything scales with the standoff distance (see e.g. Bucciantini et al. 2005). The standoff distance  is the radial distance from the pulsar to the star at which the ram pressures equilibrate (Sect. 3.2).
is the radial distance from the pulsar to the star at which the ram pressures equilibrate (Sect. 3.2).
Most emission occurs in the vicinity of  ,
whose value can be calculated given the orbital parameters, the stellar wind density, and the stellar wind velocity. Straightforward estimates indicate that the physical conditions at the shock are set by only three quantities: the shock distance
,
whose value can be calculated given the orbital parameters, the stellar wind density, and the stellar wind velocity. Straightforward estimates indicate that the physical conditions at the shock are set by only three quantities: the shock distance  from the pulsar, the orbital separation
from the pulsar, the orbital separation 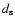 ,
and the combination
,
and the combination
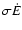 ,
which describes the pulsar wind energy and magnetization. The overall properties of the resulting spectral energy distribution are then deduced in the next section (Sect. 4). A quantitative description including emission from the nebula is given in Sects. 5, 6.
,
which describes the pulsar wind energy and magnetization. The overall properties of the resulting spectral energy distribution are then deduced in the next section (Sect. 4). A quantitative description including emission from the nebula is given in Sects. 5, 6.
The pulsar wind is described by the Lorentz factor
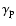 of the electrons/positrons, the spindown power
of the electrons/positrons, the spindown power 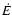 ,
and the ratio of magnetic to kinetic energy
,
and the ratio of magnetic to kinetic energy 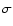 .
The (proper frame) density n1 and (observer frame) magnetic field B1 in the pulsar wind upstream of the shock are then derived from (Kennel & Coroniti 1984b)
.
The (proper frame) density n1 and (observer frame) magnetic field B1 in the pulsar wind upstream of the shock are then derived from (Kennel & Coroniti 1984b)
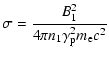 |
|
|
(1) |
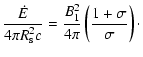 |
|
|
(2) |
Most of the energy could actually be carried by ions, which are probably a necessary ingredient to accelerate the leptons at the termination shock (Arons & Tavani 1994). Here, the kinetic energy of the wind is assumed to be only in the electrons/positrons.
In PSR B1259-63 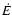 is
is
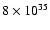 erg s-1 and the pulsar magnetic field B is about
erg s-1 and the pulsar magnetic field B is about
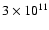 G (corresponding to a spin period P=47.7 ms and period derivative
G (corresponding to a spin period P=47.7 ms and period derivative
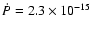 ). Thereafter,
). Thereafter, 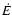 will be expected to be of the order of 1036 erg s-1. Models of the Crab plerion yield values of the order of 10-3 for
will be expected to be of the order of 1036 erg s-1. Models of the Crab plerion yield values of the order of 10-3 for 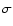 and
and
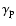 in the
105-106 range (Rees & Gunn 1974; Kennel & Coroniti 1984a). Explaining the implied conversion of electromagnetic energy (close to the pulsar) to kinetic energy (far from the pulsar) is a key question of pulsar physics. Values for
in the
105-106 range (Rees & Gunn 1974; Kennel & Coroniti 1984a). Explaining the implied conversion of electromagnetic energy (close to the pulsar) to kinetic energy (far from the pulsar) is a key question of pulsar physics. Values for 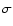 could be higher if the shock occurs closer to the pulsar than in Crab, as proposed for PSR B1259-63 by Tavani & Arons (1997); in any case,
could be higher if the shock occurs closer to the pulsar than in Crab, as proposed for PSR B1259-63 by Tavani & Arons (1997); in any case, 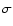 will be expected to be smaller than 1.
will be expected to be smaller than 1.
The standoff distance point  of the pulsar wind is given by
of the pulsar wind is given by
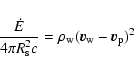 |
(3) |
where
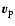 is the pulsar radial orbital speed calculated from the binary parameters,
is the pulsar radial orbital speed calculated from the binary parameters,
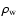 the stellar wind density, and
the stellar wind density, and
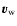 the stellar wind speed at the standoff distance. An estimate of
the stellar wind speed at the standoff distance. An estimate of  can be obtained by balancing the pressures of the two flows, assuming a stellar wind coasting at a speed
can be obtained by balancing the pressures of the two flows, assuming a stellar wind coasting at a speed 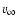 and a negligible orbital speed:
and a negligible orbital speed:
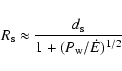 |
(4) |
where
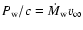 is the stellar wind momentum flux with
is the stellar wind momentum flux with
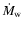 the stellar mass loss rate, supposed isotropic here, and
the stellar mass loss rate, supposed isotropic here, and 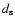 is the orbital separation. As a basis of comparison, the radiatively-driven wind of LS 5039 has
is the orbital separation. As a basis of comparison, the radiatively-driven wind of LS 5039 has
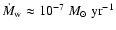 and
and
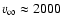 km s-1, which gives
km s-1, which gives
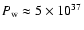 erg s-1 (McSwain et al. 2004). When the stellar wind is more powerful than the pulsar wind, in the sense that
erg s-1 (McSwain et al. 2004). When the stellar wind is more powerful than the pulsar wind, in the sense that
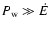 ,
then the standoff point can be written as
,
then the standoff point can be written as
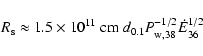 |
(5) |
where
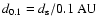 is the orbital separation (0.1 AU at periastron in LS 5039 and LS I+61
is the orbital separation (0.1 AU at periastron in LS 5039 and LS I+61
 303),
303),
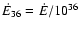 erg s-1, and
erg s-1, and
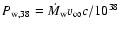 erg s-1. The standoff distance stays at about a tenth of the binary separation throughout the orbit. Writing down the dependence on the stellar wind (Eq. (5)) explicitly is easy using
erg s-1. The standoff distance stays at about a tenth of the binary separation throughout the orbit. Writing down the dependence on the stellar wind (Eq. (5)) explicitly is easy using 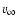 and
and 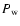 .
Equation (4) is used for the slow equatorial winds of Be stars (Sect. 6). In the following, it proved more convenient to explicitely keep
.
Equation (4) is used for the slow equatorial winds of Be stars (Sect. 6). In the following, it proved more convenient to explicitely keep  as a parameter, derived under the plausible assumptions described above. Some of the uncertainties in the geometry of the shock region or the stellar wind parameters (particularly in the wind acceleration region) are thereby hidden in
as a parameter, derived under the plausible assumptions described above. Some of the uncertainties in the geometry of the shock region or the stellar wind parameters (particularly in the wind acceleration region) are thereby hidden in  .
.
Downstream values for the magnetic field and particle density are calculated using perpendicular MHD shock jump conditions at  (Kennel & Coroniti 1984a). The post-shock magnetic field is (for
(Kennel & Coroniti 1984a). The post-shock magnetic field is (for
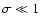 )
)
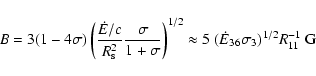 |
(6) |
where
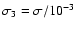 and
and
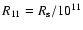 cm.
cm.
The downstream particles are assumed to be accelerated to a canonical
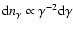 power law from a minimum energy
power law from a minimum energy
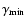 to a maximum energy
to a maximum energy
 .
For a given
.
For a given
 ,
the normalisation and lower limit
,
the normalisation and lower limit
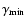 of the post-shock particle distribution are found by matching to the downstream particle and energy densities. For a
of the post-shock particle distribution are found by matching to the downstream particle and energy densities. For a
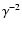 power law and
power law and
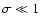 ,
,
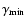 is given by (Kennel & Coroniti 1984b)
is given by (Kennel & Coroniti 1984b)
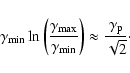 |
(7) |
For a post-shock distribution covering 2-3 decades in energy,
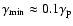 .
.
3.4 Timescales at standoff
Particles are assumed to be accelerated efficiently up to the maximum energy
 above which the timescale at which particles radiate their energy becomes shorter than the acceleration timescale. The gyroradius is used to give an estimate of the acceleration timescale to a Lorentz factor
above which the timescale at which particles radiate their energy becomes shorter than the acceleration timescale. The gyroradius is used to give an estimate of the acceleration timescale to a Lorentz factor 
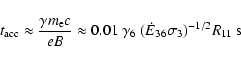 |
(8) |
using the downstream magnetic field (Eq. (6)) and writing
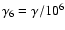 .
For ion dominated shocks (Arons & Tavani 1994), the relevant timescale is given by the ion gyroradius and the maximum electron energy is
.
For ion dominated shocks (Arons & Tavani 1994), the relevant timescale is given by the ion gyroradius and the maximum electron energy is 
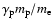 (
(
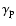 is then the upstream ion Lorentz factor). The maximum
is then the upstream ion Lorentz factor). The maximum  reached must have a smaller gyroradius than the characteristic scale of the shock
reached must have a smaller gyroradius than the characteristic scale of the shock  ,
implying
,
implying
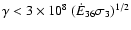 .
Particles do not reach such high
.
Particles do not reach such high  ,
as they then lose energy to radiation more rapidly than they can be accelerated.
,
as they then lose energy to radiation more rapidly than they can be accelerated.
The synchrotron timescale is
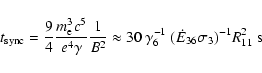 |
(9) |
so the maximum  ,
such that
,
such that
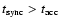 ,
is
,
is
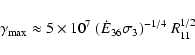 |
(10) |
which, in principle, could result in a maximum photon energy of 25 TeV. Photons up to energies 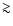 4 TeV are detected by HESS (Aharonian et al. 2005a), requiring electrons with Lorentz factors high enough that
4 TeV are detected by HESS (Aharonian et al. 2005a), requiring electrons with Lorentz factors high enough that
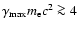 TeV, i.e.
TeV, i.e.
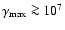 .
This is below the limit from synchrotron losses (Eq. (10)) for all plausible values of the pulsar
.
This is below the limit from synchrotron losses (Eq. (10)) for all plausible values of the pulsar 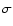 -parameter.
-parameter.
The inverse Compton timescale in the Klein-Nishina regime
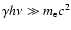 is (Blumenthal & Gould 1970)
is (Blumenthal & Gould 1970)
![\begin{displaymath}t_{\rm KN}\approx5.2~\gamma_6 \left(\frac{3~{\rm eV}}{kT_\sta...
...ma k T_\star}{m_{\rm e} c^2}\right) -1.98 \right]^{-1}~{\rm s}
\end{displaymath}](/articles/aa/full/2006/36/aa4779-05/img133.gif) |
(11) |
where the stellar (blackbody) radiation density has been lowered by geometric dilution and  is assumed to be small compared to the orbital separation
is assumed to be small compared to the orbital separation 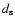 .
The stellar temperature
.
The stellar temperature 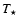 varies between
varies between
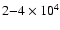 K with the stellar radius
K with the stellar radius
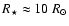 for LS 5039, LS I+61
for LS 5039, LS I+61
 303, and PSR B1259-63 so that
303, and PSR B1259-63 so that
![\begin{displaymath}t_{\rm KN}=20~\gamma_6 d_{0.1}^2 \left[\ln \gamma_6 +1.3 \right]^{-1}~T_{\star,4}^{-2} R_{\star,10}^{-2}~{\rm s}
\end{displaymath}](/articles/aa/full/2006/36/aa4779-05/img136.gif) |
(12) |
with
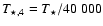 K and
K and
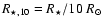 .
In the Thomson limit,
.
In the Thomson limit,
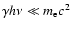 ,
then
,
then
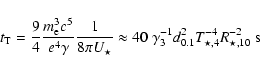 |
(13) |
where
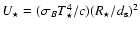 is the stellar photon density. Most of the stellar photons have an energy of 2.7
is the stellar photon density. Most of the stellar photons have an energy of 2.7
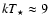 eV so that the turning point between the Thomson and Klein-Nishina regimes is for
eV so that the turning point between the Thomson and Klein-Nishina regimes is for
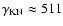 keV/
keV/
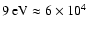 .
The interaction timescale is then at a minimum of
.
The interaction timescale is then at a minimum of 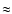 7 s (see Fig. 2).
7 s (see Fig. 2).
![\begin{figure}
\par\includegraphics[width=6cm,clip]{4779f2}
\end{figure}](/articles/aa/full/2006/36/aa4779-05/Timg145.gif) |
Figure 2:
Timescales at the standoff point as a function of the electron Lorentz factor  in LS 5039. The radiative timescale
in LS 5039. The radiative timescale
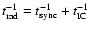 (solid lines) and the escape timescale
(solid lines) and the escape timescale
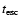 (dashed lines) are shown at periastron (black) and apastron (grey). Synchrotron cooling dominates above
(dashed lines) are shown at periastron (black) and apastron (grey). Synchrotron cooling dominates above
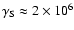 .
Inverse Compton cooling dominates below, the transition between Thomson and Klein-Nishina regimes occurring at .
Inverse Compton cooling dominates below, the transition between Thomson and Klein-Nishina regimes occurring at
 . .
 is
is
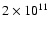 cm at periastron (d=0.1 AU) and cm at periastron (d=0.1 AU) and
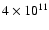 cm at apastron (d=0.2 AU) (see Table 2). cm at apastron (d=0.2 AU) (see Table 2). |
| Open with DEXTER |
The timescale for particles in the pulsar wind to reach the standoff point is
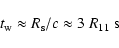 |
(14) |
which is only slightly shorter than the minimum inverse Compton timescale derived above. This is important since if the pulsar wind is composed of mono-energetic particles with
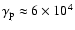 ,
then a fraction of the spindown power can be radiated by bulk inverse Compton interactions in
,
then a fraction of the spindown power can be radiated by bulk inverse Compton interactions in  -rays before reaching the termination point (Compton drag). There may then not even be a shock. (The upstream magnetic field is frozen in the MHD flow so upstream particles do not radiate synchrotron.) The resulting
-rays before reaching the termination point (Compton drag). There may then not even be a shock. (The upstream magnetic field is frozen in the MHD flow so upstream particles do not radiate synchrotron.) The resulting  -ray spectrum would display line-like emission with a strong orbital phase dependence (Ball & Kirk 2000; Bogovalov & Aharonian 2000). This possibility appears excluded by the power-law HESS spectra extending to a few TeV in LS 5039 and PSR B1259-63 (Aharonian et al. 2005a,b). Compton losses are weaker in LS I+61
-ray spectrum would display line-like emission with a strong orbital phase dependence (Ball & Kirk 2000; Bogovalov & Aharonian 2000). This possibility appears excluded by the power-law HESS spectra extending to a few TeV in LS 5039 and PSR B1259-63 (Aharonian et al. 2005a,b). Compton losses are weaker in LS I+61
 303 and PSR B1259-63 (smaller
303 and PSR B1259-63 (smaller 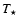 and larger separations) than in LS 5039.
and larger separations) than in LS 5039.
Downstream of the shock, the inverse Compton timescale is greater than the synchrotron timescale when
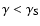 where
where
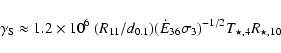 |
(15) |
using Eqs. (9) and (12). The maximum electron energy
 is indeed set by synchrotron losses (Eq. (10)) and not by inverse Compton losses. Perhaps counter-intuitively, high energy particles lose their energy mostly through synchrotron radiation, although the radiation density at
is indeed set by synchrotron losses (Eq. (10)) and not by inverse Compton losses. Perhaps counter-intuitively, high energy particles lose their energy mostly through synchrotron radiation, although the radiation density at  from the luminous stellar companion is much higher than the magnetic field energy density (
from the luminous stellar companion is much higher than the magnetic field energy density (
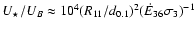 ). The difference in densities is compensated by the reduction of the inverse Compton cross-section in the Klein-Nishina regime. Note that
). The difference in densities is compensated by the reduction of the inverse Compton cross-section in the Klein-Nishina regime. Note that
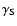 is independent of the orbital separation when the stellar wind dominates (
is independent of the orbital separation when the stellar wind dominates (
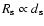 ,
see Eq. (5)).
,
see Eq. (5)).
When
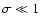 ,
the post-shock material is found from the jump conditions to initially flow away at
,
the post-shock material is found from the jump conditions to initially flow away at
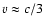 (Kennel & Coroniti 1984a) so the escape timescale is of order of
(Kennel & Coroniti 1984a) so the escape timescale is of order of
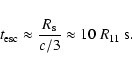 |
(16) |
Here,
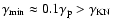 ,
so particles radiate in the Klein-Nishina regime up to
,
so particles radiate in the Klein-Nishina regime up to
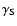 .
Their radiative timescale
.
Their radiative timescale
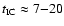 s is comparable to their escape timescale. Particles with
s is comparable to their escape timescale. Particles with
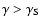 lose energy to synchrotron radiation, on a timescale
lose energy to synchrotron radiation, on a timescale
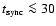 s that is, again, comparable to their escape timescale. The synchrotron radiative efficiency increases with decreasing
s that is, again, comparable to their escape timescale. The synchrotron radiative efficiency increases with decreasing  since
since
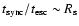 .
.
The timescales given above are sufficient to get an approximate idea of the expected high-energy emission from the pulsar wind shock region. The aim is to provide a simple framework for understanding the results from the more complex modelling presented in Sects. 5, 6.
4.1 Spectral shape
Since the radiation timescales are comparable to or (much) smaller than the flow timescale, the situation can be approximated to steady-state injection of power-law electrons interacting in the Klein-Nishina regime with an isotropic bath of quasi mono-energetic photons. Moderski et al. (2005) have studied this case, taking synchrotron emission in a uniform magnetic field into account. The overall characteristics of the spectrum emitted in the vicinity of the pulsar can be deduced from their results and the calculations above. If particle cooling is not fast enough, then particles will travel to regions of lower energy densities, modifying the spectral energy distribution from that presented here. The steady state assumption is reasonable for the high energy spectrum (Sect. 5).
Moderski et al. (2005) show that the steady-state electron distribution displays three regimes: (a) at low energies, interactions in the Thomson limit steepen the distribution by 1 in index, as usual; (b) at high energies, synchrotron emission also steepens the distribution by 1; (c) at intermediate energies, where inverse Compton interactions in the Klein-Nishina regime dominate, the decrease in cross-section is such that the distribution index is unchanged or hardened at most by 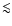 0.5. The hardening decreases with the ratio
0.5. The hardening decreases with the ratio
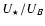 .
The change between regimes (a) and (b) occurs at the transition to the Klein-Nishina regime
.
The change between regimes (a) and (b) occurs at the transition to the Klein-Nishina regime
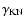 .
Case (a) does not happen here since we initially have
.
Case (a) does not happen here since we initially have
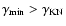 .
The change between regimes (b) and (c) occurs at
.
The change between regimes (b) and (c) occurs at
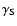 where synchrotron losses start to dominate. A
where synchrotron losses start to dominate. A
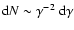 injection spectrum will therefore lead to a steady-state electron distribution going from
injection spectrum will therefore lead to a steady-state electron distribution going from
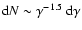 to
to
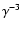 above
above
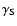 .
.
Table 2:
Characteristic frequencies of the expected spectral energy distributions.
Using the downstream magnetic field (Eq. (6)), the characteristic synchrotron frequency for an electron with an energy
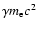 is
is
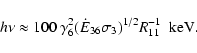 |
(17) |
The three frequencies relevant to the spectral shape, corresponding to
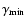 ,
,
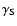 and
and
 are (using
are (using
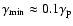 and Eqs. (10), (15)):
and Eqs. (10), (15)):
The expected synchrotron spectrum (Moderski et al. 2005) is a hard power law
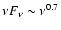 from about 1 keV initially (
from about 1 keV initially (
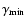 )
up to a break energy
)
up to a break energy 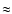 100 keV (
100 keV (
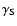 ). The spectrum then flattens, with
). The spectrum then flattens, with
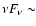 constant up to
constant up to 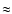 250 MeV (
250 MeV (
 ). Since
). Since
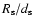 is almost constant (Eq. (5)), the break frequency changes as
is almost constant (Eq. (5)), the break frequency changes as
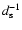 along the orbit because of the variation in the magnetic field at the standoff point. The maximum synchrotron frequency is independent of all parameters.
along the orbit because of the variation in the magnetic field at the standoff point. The maximum synchrotron frequency is independent of all parameters.
Inverse Compton interactions occur in the Klein-Nishina regime so that the characteristic frequencies are given by
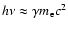
Moderski et al. (2005) find the inverse Compton spectrum for a
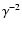 injection is constant or rising slightly in
injection is constant or rising slightly in 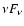 up to
up to
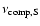 (their Fig. 6). Above an energy
(their Fig. 6). Above an energy
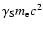 ,
the electron energy distribution steepens to
,
the electron energy distribution steepens to
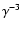 .
The spectral index steepens by
.
The spectral index steepens by 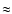 1.5 (their Eq. (31)), and
1.5 (their Eq. (31)), and
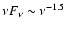 is expected above 0.6 TeV.
is expected above 0.6 TeV.
Note that photons emitted with energies above about 30 GeV can interact with stellar photons in the binary system to produce pairs
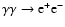 (Gould & Schréder 1967). This leads at least to a hardening (softening) of the observed VHE
(Gould & Schréder 1967). This leads at least to a hardening (softening) of the observed VHE  -ray spectrum above (below) a few 100 GeV (Dubus 2006). This can produce modifications to the electron distribution since pairs are created (this is further discussed in Sect. 6.1.1).
-ray spectrum above (below) a few 100 GeV (Dubus 2006). This can produce modifications to the electron distribution since pairs are created (this is further discussed in Sect. 6.1.1).
Assuming the situation is steady-state and that the pulsar spindown power is largely given to the particles (
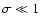 ), the synchrotron and inverse Compton luminosities should be, to order unity, equal to
), the synchrotron and inverse Compton luminosities should be, to order unity, equal to 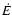 .
With a
.
With a
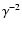 injection, the inverse Compton and synchrotron luminosities are roughly equal (Moderski et al. 2005).
injection, the inverse Compton and synchrotron luminosities are roughly equal (Moderski et al. 2005).
With such short radiative timescales, only a moderate spindown power of 1036 erg s-1 is sufficient to achieve a high radiative efficiency in X-rays and  -rays. This has little to do with the assumptions made on the pulsar wind
-rays. This has little to do with the assumptions made on the pulsar wind
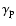 ,
,
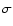 or
or 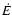 (if the wind is composed purely of electrons and positrons: a pulsar wind with a significant ion fraction would require a higher
(if the wind is composed purely of electrons and positrons: a pulsar wind with a significant ion fraction would require a higher 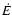 to obtain the same luminosity). The efficiency comes from the high radiation and magnetic energy densities at the standoff point that allows fast cooling of all of the injected particles. This contrasts with pulsars interacting with their supernova remnant or the interstellar medium, whose termination shock occurs much farther out, at correspondingly lower energy densities.
to obtain the same luminosity). The efficiency comes from the high radiation and magnetic energy densities at the standoff point that allows fast cooling of all of the injected particles. This contrasts with pulsars interacting with their supernova remnant or the interstellar medium, whose termination shock occurs much farther out, at correspondingly lower energy densities.
The main factor setting the high-energy luminosity is the shock distance  or, alternatively, the orbital separation
or, alternatively, the orbital separation 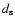 (since
(since
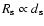 in Eq. (5)). The shock distance enters as
in Eq. (5)). The shock distance enters as
 in the synchrotron timescale compared to
in the synchrotron timescale compared to  in the escape timescale. The smaller
in the escape timescale. The smaller  ,
the more synchrotron emission dominates and the more the pulsar can be expected to be radiatively efficient. However, this is at the expense of the inverse Compton flux since the associated timescale stays constant with
,
the more synchrotron emission dominates and the more the pulsar can be expected to be radiatively efficient. However, this is at the expense of the inverse Compton flux since the associated timescale stays constant with  .
.
The dominant radiation process does not change along the orbit for a given electron energy (because
 ), but the probability that this electron can escape from the region of high
), but the probability that this electron can escape from the region of high  and UB without significant radiation increases with
and UB without significant radiation increases with  (or
(or  ). The steady-state assumption then breaks down. Conditions change as particles flow away from the shock region. The overall nebula must then be taken into account to model the emission (Sect. 5).
). The steady-state assumption then breaks down. Conditions change as particles flow away from the shock region. The overall nebula must then be taken into account to model the emission (Sect. 5).
4.3 Comparison to SEDs
The characteristic frequencies for all three  -ray binaries were calculated using the parameters in Table 1 and additional assumptions on their stellar winds. For LS 5039, the wind is radiative with
-ray binaries were calculated using the parameters in Table 1 and additional assumptions on their stellar winds. For LS 5039, the wind is radiative with
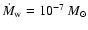 yr-1 and
yr-1 and
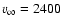 km s-1. For LS I+61
km s-1. For LS I+61
 303 and PSR B1259-63 two winds were assumed: a dense equatorial outflow and a fast polar wind similar to that in LS 5039. Details are given in Sect. 6. The standoff distances
303 and PSR B1259-63 two winds were assumed: a dense equatorial outflow and a fast polar wind similar to that in LS 5039. Details are given in Sect. 6. The standoff distances  and frequencies are given in Table 2.
and frequencies are given in Table 2.
In anticipation of Sect. 6, the pulsar was assumed to have
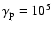 ,
,
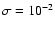 ,
and
,
and
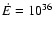 erg s-1 in all three systems. Note that
erg s-1 in all three systems. Note that 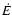 and
and 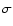 always appear in the same proportion, so that for given
always appear in the same proportion, so that for given  there are really only two parameters,
there are really only two parameters,
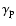 and
and
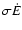 .
The characteristic frequencies are not very sensitive to
.
The characteristic frequencies are not very sensitive to
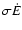 .
Interestingly, the SED is also indifferent to the exact value of
.
Interestingly, the SED is also indifferent to the exact value of
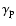 except at the low energy end of the inverse Compton spectrum.
except at the low energy end of the inverse Compton spectrum.
The expected breaks match the observed SEDs of LS 5039, LS I+61
 303 and PSR B1259-63 reasonably well, notably the rising then flattening X-ray to
303 and PSR B1259-63 reasonably well, notably the rising then flattening X-ray to  -ray spectra. An important observable feature is that, all other parameters being equal, the break frequency in X-rays
-ray spectra. An important observable feature is that, all other parameters being equal, the break frequency in X-rays 
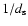 should be lower at apastron than at periastron. At higher energies, the break
should be lower at apastron than at periastron. At higher energies, the break
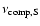 in LS I+61
in LS I+61
 303 and PSR B1259-63 occurs at frequencies that are a factor 2 lower than in LS 5039, because of the lower
303 and PSR B1259-63 occurs at frequencies that are a factor 2 lower than in LS 5039, because of the lower 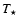 (Table 1). The TeV spectrum of PSR B1259-63 is indeed steeper than that of LS 5039. Unlike what happens with synchrotron, the spectral break in the inverse Compton emission should not change along the orbit if
(Table 1). The TeV spectrum of PSR B1259-63 is indeed steeper than that of LS 5039. Unlike what happens with synchrotron, the spectral break in the inverse Compton emission should not change along the orbit if  is proportional to
is proportional to 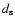 (Eq. (5)).
(Eq. (5)).
However, there are two shortcomings: the radio emission and the EGRET detections of LS 5039 and LS I+61
 303 at GeV energies (Fig. 1). The radio emission cannot be addressed by the present scheme: the minimum synchrotron frequency is
303 at GeV energies (Fig. 1). The radio emission cannot be addressed by the present scheme: the minimum synchrotron frequency is 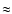 1 keV, and radiation well below must originate from particles that have cooled and escaped from the vicinity of the pulsar (see Sects. 5, 6).
1 keV, and radiation well below must originate from particles that have cooled and escaped from the vicinity of the pulsar (see Sects. 5, 6).
The GeV emission may be problematic as the model predicts a gap between 250 MeV and 50 GeV when
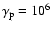 .
There is no room for increasing the synchrotron emission so as to include at least a fraction of the EGRET band: the maximum synchrotron frequency is fixed by the assumptions on
.
There is no room for increasing the synchrotron emission so as to include at least a fraction of the EGRET band: the maximum synchrotron frequency is fixed by the assumptions on
 .
Advocating higher
.
Advocating higher
 seems unreasonable. Moreover, for large orbital separations such as in PSR B1259-63 or LS I+61
seems unreasonable. Moreover, for large orbital separations such as in PSR B1259-63 or LS I+61
 303 (at apastron), the maximum electron energy is limited by the Larmor radius (supposed
303 (at apastron), the maximum electron energy is limited by the Larmor radius (supposed 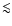
 )
rather than by radiative losses. These range from 2 MeV (apastron, polar wind) to 80 MeV (periastron, equatorial wind) for PSR B1259-63 and from 30 MeV (apastron, polar wind) to 250 MeV (periastron, equatorial wind) for LS I+61
)
rather than by radiative losses. These range from 2 MeV (apastron, polar wind) to 80 MeV (periastron, equatorial wind) for PSR B1259-63 and from 30 MeV (apastron, polar wind) to 250 MeV (periastron, equatorial wind) for LS I+61
 303. The easiest solution consists in lowering the Lorentz factor
303. The easiest solution consists in lowering the Lorentz factor
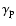 of the particles in the pulsar wind to 105. This lowers
of the particles in the pulsar wind to 105. This lowers
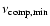 to a few GeV, while leaving the spectral breaks unchanged. The inverse Compton timescale becomes long compared to
to a few GeV, while leaving the spectral breaks unchanged. The inverse Compton timescale becomes long compared to
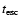 at the low energy end of the electron distribution and, as for radio, high energy emission between 250 MeV and a GeV will also come from escaping particles.
at the low energy end of the electron distribution and, as for radio, high energy emission between 250 MeV and a GeV will also come from escaping particles.
The detailed spectral energy distribution, including evolution of the physical conditions in the flow, is calculated here with the aim of accounting for the resolved radio emission, as well as providing more quantitative comparisons. The assumptions are described in this section, with LS 5039 used as an illustrative example when necessary. The application and comparison with observations are made in Sect. 6.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{4779f3}
\end{figure}](/articles/aa/full/2006/36/aa4779-05/Timg210.gif) |
Figure 3:
From left to right: evolution in the pulsar nebula of the flow speed, magnetic field and density as a function of the normalised distance z. The rightmost panel shows the time needed to reach a given distance z in the flow. At
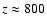 (
(
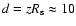 AU), the elapsed time is equal to the orbital period (dotted line). The model parameters are AU), the elapsed time is equal to the orbital period (dotted line). The model parameters are
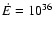 erg s-1, erg s-1,
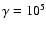 , ,
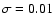 and
and
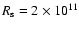 cm, appropriate for LS 5039 at periastron. cm, appropriate for LS 5039 at periastron. |
| Open with DEXTER |
Particles are continuously injected with a
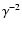 power-law energy spectrum between
power-law energy spectrum between
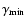 and
and
 beyond the termination shock, in an emitting region of characteristic size
beyond the termination shock, in an emitting region of characteristic size  .
Other distributions have not been considered for the sake of simplicity. The downstream particle density, in the limit of small
.
Other distributions have not been considered for the sake of simplicity. The downstream particle density, in the limit of small  ,
is given by (Kennel & Coroniti 1984b)
,
is given by (Kennel & Coroniti 1984b)
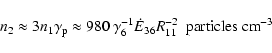 |
(24) |
using Eq. (2). The normalisation of the injected particle power-law  is then found from
is then found from
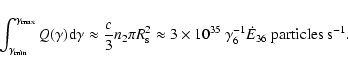 |
(25) |
Particles move downstream away from the pulsar with a speed v (initially  c/3) whilst emitting radiation. The resulting "cometary'' nebula is modelled by dividing it into small (logarithmic) subsections where the physical parameters (magnetic field, density, etc.) are homogeneous. The nebula is assumed to expand conically. The evolution of the distribution function
c/3) whilst emitting radiation. The resulting "cometary'' nebula is modelled by dividing it into small (logarithmic) subsections where the physical parameters (magnetic field, density, etc.) are homogeneous. The nebula is assumed to expand conically. The evolution of the distribution function
 along the nebula is given by
along the nebula is given by
![\begin{displaymath}\frac{\partial N}{\partial z}=\frac{\partial}{\partial \gamma...
...\frac{{\rm d}\gamma}{{\rm d} z} N \right]+Q(\gamma)\delta(z-1)
\end{displaymath}](/articles/aa/full/2006/36/aa4779-05/img215.gif) |
(26) |
where z is the distance along the nebula normalised to the standoff distance  .
The radiative and adiabatic losses for an electron (positron) are:
.
The radiative and adiabatic losses for an electron (positron) are:
![\begin{displaymath}\frac{{\rm d}\gamma}{{\rm d} z}=
\frac{R_{\rm s}}{v} \left[\l...
...t(\frac{{\rm d} \gamma}{{\rm d} t}\right)_{\rm ad}\right]\cdot
\end{displaymath}](/articles/aa/full/2006/36/aa4779-05/img216.gif) |
(27) |
The synchrotron radiation loss is the usual
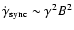 .
The energy loss to inverse Compton radiation is calculated using the Jones (1968) kernel, which is a continuous approximation, although electrons can lose significant amounts of approximation in discrete encounters with photons in the Klein-Nishina regime. Furthermore, the Jones kernel supposes an isotropic photon distribution. This should not be too bad an approximation as the angle-dependence of the cross-section is limited in the Klein-Nishina regime. The adiabatic losses for two dimensional expansion of relativistic material are
.
The energy loss to inverse Compton radiation is calculated using the Jones (1968) kernel, which is a continuous approximation, although electrons can lose significant amounts of approximation in discrete encounters with photons in the Klein-Nishina regime. Furthermore, the Jones kernel supposes an isotropic photon distribution. This should not be too bad an approximation as the angle-dependence of the cross-section is limited in the Klein-Nishina regime. The adiabatic losses for two dimensional expansion of relativistic material are
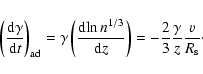 |
(28) |
The evolution of the physical parameters of the flow (B, v etc.) with z is described in the next section. Once these are determined, the differential equation governing the evolution (Eq. (26)) is numerically integrated along z using a logarithmic grid in  ,
following the scheme proposed by Chang & Cooper (1970). The results presented thereafter typically use at least 1000 points for the particle energy grid and 200 points in frequency
,
following the scheme proposed by Chang & Cooper (1970). The results presented thereafter typically use at least 1000 points for the particle energy grid and 200 points in frequency 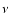 to represent emission spectra. The results have been checked to be independent of the numerical details.
to represent emission spectra. The results have been checked to be independent of the numerical details.
![\begin{figure}
\par\includegraphics[width=9.5cm,clip]{4779f4a}\hspace*{4mm}
\includegraphics[width=6.2cm,clip]{4779f4b}
\end{figure}](/articles/aa/full/2006/36/aa4779-05/Timg220.gif) |
Figure 4:
Left: evolution of the emission along the pulsar nebula. The pulsar nebula is divided into sections at various distances z with the corresponding synchrotron (black) and inverse Compton (grey) spectra shown. The first section shown is for z=1 (dz=0.01). The section dz is then increased: the fifth spectrum is at
 ,
the tenth at ,
the tenth at
 ,
the last spectrum shown is at ,
the last spectrum shown is at
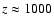 .
The total spectrum of the pulsar nebula is shown as a thick black line. The model parameters are the same as in Fig. 3. The thermal emission at .
The total spectrum of the pulsar nebula is shown as a thick black line. The model parameters are the same as in Fig. 3. The thermal emission at  1 eV is direct light from the stellar companion. Right: evolution of the particle distribution as the shocked pulsar wind moves out from the system. The sections are the same as those shown in the SED. The initial 1 eV is direct light from the stellar companion. Right: evolution of the particle distribution as the shocked pulsar wind moves out from the system. The sections are the same as those shown in the SED. The initial
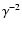 power law cools rapidly at high energies due to synchrotron radiation. Adiabatic losses dominate at large distances.
power law cools rapidly at high energies due to synchrotron radiation. Adiabatic losses dominate at large distances. |
| Open with DEXTER |
5.2 Evolution of physical conditions in the flow
The evolution of the nebular flow speed v and magnetic field B with z are computed by using the relativistic Bernouilli equation stating that
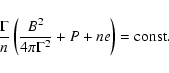 |
(29) |
along streamlines for stationary, adiabatic motion. There, 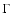 is the bulk Lorentz factor of the flow
is the bulk Lorentz factor of the flow
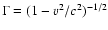 .
The additional relationships for the magnetic field B, density n, pressure P, and internal energy e come from the conservation of (toroidal) magnetic flux
.
The additional relationships for the magnetic field B, density n, pressure P, and internal energy e come from the conservation of (toroidal) magnetic flux
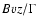 ,
of the number of particles nvz2 and the relativistic equation of state
,
of the number of particles nvz2 and the relativistic equation of state
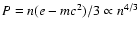 (Kennel & Coroniti 1984a).
(Kennel & Coroniti 1984a).
Close to the shock, the total energy is dominated by pressure. The density is then roughly constant, the flow speed decreases as
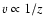 and the magnetic field increases because of flux conservation (Fig. 3). The flow becomes magnetically dominated at large radii (
and the magnetic field increases because of flux conservation (Fig. 3). The flow becomes magnetically dominated at large radii (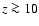 ), at which point the density varies as 1/z2, the magnetic field decreases as
), at which point the density varies as 1/z2, the magnetic field decreases as
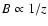 ,
and the asymptotic flow speed is
,
and the asymptotic flow speed is 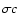 (Kennel & Coroniti 1984a).
(Kennel & Coroniti 1984a).
The present approach is admittedly simplistic. MHD simulations of a spherically symmetric pulsar wind interacting with a constant external medium exist (Bucciantini et al. 2005) and give insight into possible shortcomings. The shape of the pulsar termination shock is bullet-shaped rather than spherical. An asymmetric pulsar wind would surely change the aspect of the flow (as it does with the Crab and Vela pulsars). Shocked material flows along two channels, a fast one with material from the forward termination shock and a slower one with material from the backward-facing termination shock. The nebular flow loses energy to radiation, contradicting the adiabatic approximation. Collimation shocks may re-energise particles along the jet; mixing can occur at the surface discontinuity between the fast-moving shocked pulsar wind and the slow-moving stellar wind. Mass loading will slow down if it does not disrupt the flow. At larger distances, the flow shears because of orbital motion (Sect. 5.4), leading to additional complications. Finally, the flow merges with the stellar wind and/or ISM on scales of  0.01 pc based on the densities.
0.01 pc based on the densities.
Neglecting any effect of the orbital motion (see Sect. 5.4), the overall spectrum results from the summed contribution of the synchrotron and inverse Compton spectra (on stellar photons) calculated for subsections dz of the nebula extending away from the star. As was done for energy losses, the particle distribution and radiation fields are assumed to be spatially homogeneous and isotropic in each subsection. The inverse Compton spectrum takes the reduction of the cross-section into account for interactions in the Klein-Nishina regime via the Jones kernel. The radiation field of the stellar companion is simply diluted by the inverse square of the distance to the star (
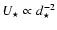 with
with
 ).
).
Figure 4 illustrates the evolution of the emission spectrum and particle distribution with increasing distance z to the pulsar in the case of LS 5039. The first 3-4 spectra show the initial evolution towards the steady-state described in Sect. 4. The particle distribution above
 cools rapidly at high energies due to synchrotron losses, resulting in a plateau down to
cools rapidly at high energies due to synchrotron losses, resulting in a plateau down to
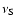 as expected. Evolution then sets in around
as expected. Evolution then sets in around 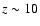 ,
with the spectral luminosity decreasing with B. The particle distribution steepens with emission sweeping the optical to IR bands. Further evolution, corresponding to peak emission in mm to radio, is set by adiabatic losses.
,
with the spectral luminosity decreasing with B. The particle distribution steepens with emission sweeping the optical to IR bands. Further evolution, corresponding to peak emission in mm to radio, is set by adiabatic losses.
Self-Compton radiation is negligible. Synchrotron emission was optically thin down to low radio frequencies in all the models computed for Sect. 6. This is a consequence of the flow geometries, which are discussed in Sect. 5.4. Still, synchrotron self-absorption might be possible in a flow directed predominantly along the line-of-sight.
In the absence of orbital motion, the spectrum seen by the observer is simply the integrated emission along the "comet'' tail nebula, just as for isolated pulsar interacting with the ISM. However, as can be deduced from Fig. 4, the radio emission originates from regions several AU away from the pulsar (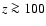 ). The time
). The time 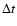 it takes for particles to reach this location, about a day here, is a significant fraction of
it takes for particles to reach this location, about a day here, is a significant fraction of
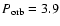 days. Orbital motion will have changed the inner boundary condition so the spectrum seen by an observer will be a composite of SEDs from all orbital phases
days. Orbital motion will have changed the inner boundary condition so the spectrum seen by an observer will be a composite of SEDs from all orbital phases 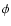 .
Here, the only parameter dependent on the orbital phase is the pulsar standoff point
.
Here, the only parameter dependent on the orbital phase is the pulsar standoff point  .
Other dependences can be envisioned if, for instance, the pulsar wind is anisotropic or if the magnetization parameter is a function of distance to the light cylinder (with higher
.
Other dependences can be envisioned if, for instance, the pulsar wind is anisotropic or if the magnetization parameter is a function of distance to the light cylinder (with higher 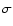 expected close to the pulsar).
expected close to the pulsar).
The relevant timescales to compare are the flow timescale
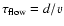 to reach a distance d from the shock and the orbital motion timescale
to reach a distance d from the shock and the orbital motion timescale
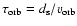 .
The orbital timescale can vary a lot for a highly eccentric orbit. Nevertheless, taking v equal to its asymptotic value
.
The orbital timescale can vary a lot for a highly eccentric orbit. Nevertheless, taking v equal to its asymptotic value 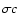 ,
the distance where orbital motion becomes important will on average be
,
the distance where orbital motion becomes important will on average be
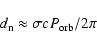 |
(30) |
and the associated timescale,
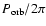 .
As it turns out, the synchrotron emission from LS 5039 depends little on the orbital phase, because
.
As it turns out, the synchrotron emission from LS 5039 depends little on the orbital phase, because
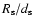 is constant with
is constant with 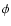 .
The spectrum seen by an observer should therefore be close to the integrated spectrum shown in Fig. 4 even at low frequencies (see Sect. 6.1).
.
The spectrum seen by an observer should therefore be close to the integrated spectrum shown in Fig. 4 even at low frequencies (see Sect. 6.1).
5.4 Appearance of the cometary nebula
On a small scale, the shocked material flows away from the binary on a straight path, following the direction given by the vector difference of the stellar wind and orbital speeds
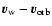 .
On a larger scale, the material "bends'' as the orbital motion becomes important at
.
On a larger scale, the material "bends'' as the orbital motion becomes important at 
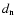 (about 1 AU for LS 5039; Eq. (30)). Parcels of material are still on outward straight paths, but the orbital motion shears the nebula. The opening angle of the flow (
(about 1 AU for LS 5039; Eq. (30)). Parcels of material are still on outward straight paths, but the orbital motion shears the nebula. The opening angle of the flow (
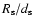 )
is small so that the width of the "comet'' tail is smaller than
)
is small so that the width of the "comet'' tail is smaller than 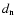 .
For a circular orbit, the large-scale appearance is then an Archimedes spiral with a step size
.
For a circular orbit, the large-scale appearance is then an Archimedes spiral with a step size
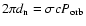 .
.
More generally, the flow speed amplitude and direction change along the orbit and the exact shape can differ from a perfect spiral. Furthermore, emission along the spiral is not constant but depends upon the distance d to the pulsar or, alternatively, upon the time elapsed since the particles left the pulsar. The flux received by the observer may also be Doppler by factors of a few (de)boosted initially, when the flow speeds are high (neglected here). Finally, the orbital orientation will also change the appearance of the nebula. For an edge-on system (
 ), the nebula will mimic a microquasar bipolar jet.
), the nebula will mimic a microquasar bipolar jet.
The trajectory of material leaving the pulsar wind termination shock can be found as a function of the elapsed time t, using polar coordinates
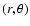 in the orbital plane. The distance d reached along the nebula is
in the orbital plane. The distance d reached along the nebula is
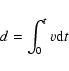 |
(31) |
where v is the flow speed calculated in Sect. 5.2. The radius r with the coordinates centred on the massive star is given by
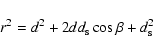 |
(32) |
where 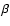 is the angle at which the shocked material flows and
is the angle at which the shocked material flows and 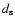 is the star-pulsar separation at t=0. If
is the star-pulsar separation at t=0. If 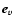 is the unit vector along the flow direction and
is the unit vector along the flow direction and 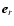 is the radial unit vector from the massive star to the pulsar location at t=0, then
is the radial unit vector from the massive star to the pulsar location at t=0, then
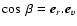 .
The angle
.
The angle 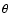 of the material is then
of the material is then
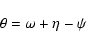 |
(33) |
where 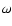 is the periastron argument,
is the periastron argument, 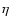 the true anomaly of the pulsar at t=0 (angle measured from the star centre,
the true anomaly of the pulsar at t=0 (angle measured from the star centre, 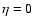 at periastron), and
at periastron), and 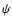 is derived from
is derived from
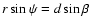 .
.
The full pattern follows from having 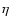 vary with time t according to the usual relationships governing orbital motion (i.e. using the eccentric anomaly). Note that v,
vary with time t according to the usual relationships governing orbital motion (i.e. using the eccentric anomaly). Note that v, 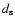 ,
and
,
and 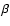 also vary with orbital phase. The result is then projected onto the plane of the sky, given the orbital inclination i.
also vary with orbital phase. The result is then projected onto the plane of the sky, given the orbital inclination i.
Figure 5 shows the spiral pattern computed for LS 5039 with
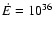 erg s-1,
erg s-1,
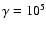 ,
,
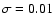 ,
and the pulsar located at periastron. The figure represents the emission from particles "ejected'' over a timescale of about an orbital period and a half. The spiral "turns'' around and outwards as the pulsar moves along the orbit. The lines illustrate the direction at which material flows out from the binary. Spacing between lines correspond to equal intervals of time; in other words, lines are spaced out more at periastron due to fast orbital motion (before projection on the plane of the sky). For very eccentric orbits (such as PSR B1259-63, see Sect. 6.3), material will tend to flow out in the direction of the major axis on the apastron side (for a radial outflow). There will be a preferred emission axis, even when the system is seen pole-on. Another effect illustrated by Fig. 5 is the bunching of lines due to the projection on the sky plane. A binary with a circular orbit but seen at some inclination will also have a preferred emission axis.
,
and the pulsar located at periastron. The figure represents the emission from particles "ejected'' over a timescale of about an orbital period and a half. The spiral "turns'' around and outwards as the pulsar moves along the orbit. The lines illustrate the direction at which material flows out from the binary. Spacing between lines correspond to equal intervals of time; in other words, lines are spaced out more at periastron due to fast orbital motion (before projection on the plane of the sky). For very eccentric orbits (such as PSR B1259-63, see Sect. 6.3), material will tend to flow out in the direction of the major axis on the apastron side (for a radial outflow). There will be a preferred emission axis, even when the system is seen pole-on. Another effect illustrated by Fig. 5 is the bunching of lines due to the projection on the sky plane. A binary with a circular orbit but seen at some inclination will also have a preferred emission axis.
Besides the orbital eccentricity and inclination, a third effect that will shape the appearance of the cometary nebula is the variation of emission with orbital phase. The amplitude can change with orbital phase. But even if the spectrum varies little along the orbit, the locus of peak emission changes, since the elapsed time depends directly on the absolute scale  (hence phase). If the standoff point is twice as far away at apastron than it is at periastron, then the spatial scale on which the radio peaks also doubles. In Fig. 5, the intensity of the 5 GHz radio emission is represented by the greyscale colouring. Note how far out material on the upper left hand side (corresponding to apastron) has a higher intensity than material on the right hand side (periastron), although the latter was emitted a shorter time ago.
(hence phase). If the standoff point is twice as far away at apastron than it is at periastron, then the spatial scale on which the radio peaks also doubles. In Fig. 5, the intensity of the 5 GHz radio emission is represented by the greyscale colouring. Note how far out material on the upper left hand side (corresponding to apastron) has a higher intensity than material on the right hand side (periastron), although the latter was emitted a shorter time ago.
All these effects combine to create radio maps that are far from trivial (see Sect. 6). Despite the complexity, there is one simple prediction: the step of the spiral should be 
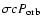 .
Therefore, the radio nebula of
.
Therefore, the radio nebula of  -ray pulsar binaries could be used to constrain the average magnetization parameter of relativistic pulsar winds. The particular cases of LS 5039, LS I+61
-ray pulsar binaries could be used to constrain the average magnetization parameter of relativistic pulsar winds. The particular cases of LS 5039, LS I+61
 303, and PSR B1259-63 are examined in the next section.
303, and PSR B1259-63 are examined in the next section.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4779f5}
\end{figure}](/articles/aa/full/2006/36/aa4779-05/Timg259.gif) |
Figure 5:
Large-scale appearance of the pulsar nebula around LS 5039 at periastron. In practice, limited angular resolution smoothes out the emission from what is shown here (see Fig. 7). The binary is located at the origin. Its size of a few tenths of AU is much smaller than the scale of the map. Material originating from the standoff point travels outwards following the direction of the comet tail at each orbital phase (shown by grey lines; the projected outflow path at apastron is indicated by a dark line). Because of the orbital motion, the emission winds up into a spiral. To illustrate this, dots are plotted at the locations reached by material expelled at regular time intervals along the orbit. The total elapsed timescale represented corresponds to almost an orbital period and a half. The greyscale codes the intensity of the 5 GHz radio emission (square root scale). At large distances, the step of the spiral tends to
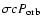 which is
which is  7 AU for the adopted parameters (same as those of Figs. 3, 4). The inclination ( 7 AU for the adopted parameters (same as those of Figs. 3, 4). The inclination (
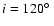 ,
corresponding to a retrograde pulsar orbit, see Sect. 6.1.2), and the major axis orientation ( ,
corresponding to a retrograde pulsar orbit, see Sect. 6.1.2), and the major axis orientation (
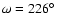 )
used here are consistent with the measurements of the companion star's radial velocity (see orbit schematic in Fig. 6 of Casares et al. 2005b). )
used here are consistent with the measurements of the companion star's radial velocity (see orbit schematic in Fig. 6 of Casares et al. 2005b). |
| Open with DEXTER |
The numerical model described in the previous section is applied to the three  -ray binaries LS 5039, LS I+61
-ray binaries LS 5039, LS I+61
 303, and PSR B1259-63. The aim is to change only the orbital parameters and stellar wind, keeping the pulsar wind identical between objects, so as to highlight the differences due to the binary environment. The spectral energy distribution, orbital variability, and radio morphology are discussed for each case.
303, and PSR B1259-63. The aim is to change only the orbital parameters and stellar wind, keeping the pulsar wind identical between objects, so as to highlight the differences due to the binary environment. The spectral energy distribution, orbital variability, and radio morphology are discussed for each case.
6.1 LS 5039
The wind of the O6.5V companion star in LS 5039 is assumed to be radiatively-driven with a velocity and density given by
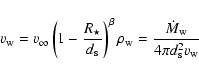 |
(34) |
with
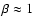 .
Spectroscopic observations of LS 5039 constrain
.
Spectroscopic observations of LS 5039 constrain
 to
to 
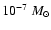 yr-1 and
yr-1 and
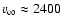 km s-1 (McSwain et al. 2004). The wind is assumed to be isotropic and purely radial. Since the orbit of the pulsar takes it to almost a stellar radius of the companion at periastron in LS 5039 and LS I+61
km s-1 (McSwain et al. 2004). The wind is assumed to be isotropic and purely radial. Since the orbit of the pulsar takes it to almost a stellar radius of the companion at periastron in LS 5039 and LS I+61
 303, more complex wind launching conditions than those assumed above could play a role in setting
303, more complex wind launching conditions than those assumed above could play a role in setting  .
A significant wind rotation might also influence the location of the standoff point and the flow direction.
.
A significant wind rotation might also influence the location of the standoff point and the flow direction.
The pulsar spindown power was taken to be
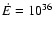 erg s-1, close to that measured in PSR B1259-63 (Sect. 6.3). Then,
erg s-1, close to that measured in PSR B1259-63 (Sect. 6.3). Then,  varies between
varies between
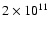 cm (periastron) and
cm (periastron) and
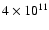 cm (apastron). The two parameters left are the pulsar wind magnetization
cm (apastron). The two parameters left are the pulsar wind magnetization 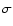 and Lorentz factor
and Lorentz factor
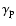 .
Low values of
.
Low values of
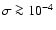 yield low downstream magnetic fields. Hence, the inverse Compton emission dominates with far too few X-rays emitted to match the SED. At the other end, values of
yield low downstream magnetic fields. Hence, the inverse Compton emission dominates with far too few X-rays emitted to match the SED. At the other end, values of
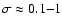 lead to overall emission inefficiency because electrons move quickly out into regions of low radiation fields (the downstream flow speed is high). Values of
lead to overall emission inefficiency because electrons move quickly out into regions of low radiation fields (the downstream flow speed is high). Values of 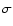 in the 0.001-0.01 range yield the best results. However, with
in the 0.001-0.01 range yield the best results. However, with
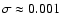 ,
the characteristic size of the radio emission (Eq. (30)) would be too small by a factor 10 to match the observed scale of
,
the characteristic size of the radio emission (Eq. (30)) would be too small by a factor 10 to match the observed scale of  10 AU (Paredes et al. 2000, see below). The best compromise was
10 AU (Paredes et al. 2000, see below). The best compromise was
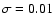 .
Coincidentally, the downstream flow speed saturates at a value (
.
Coincidentally, the downstream flow speed saturates at a value ( 3000 km s-1), which is then close to the terminal velocity of the stellar wind (
3000 km s-1), which is then close to the terminal velocity of the stellar wind ( 2000 km s-1).
2000 km s-1).
The Lorentz factor
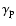 influences the lower cutoff of the particle distribution. Lower values enable the inverse Compton emission to extend down to the GeV range, as discussed in Sect. 4.3. With more low-energy electrons, the radio emission is also more easily accounted for. A value of
influences the lower cutoff of the particle distribution. Lower values enable the inverse Compton emission to extend down to the GeV range, as discussed in Sect. 4.3. With more low-energy electrons, the radio emission is also more easily accounted for. A value of
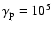 was the best compromise: at 106 the GeV emission is unaccounted for, at 104 the radio emission is overpredicted, and the downstream particle distribution then extends more than four decades in energy. The adopted values are
was the best compromise: at 106 the GeV emission is unaccounted for, at 104 the radio emission is overpredicted, and the downstream particle distribution then extends more than four decades in energy. The adopted values are
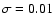 and
and
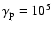 .
.
The evolution of the SED as the material flows away from the pulsar is shown in Fig. 4. The high-energy SED is very much that described in Sect. 4, with the spectral breaks in the synchrotron and inverse Compton spectra at their expected locations. Electrons in the comet tail enable the summed emission to extend down to low frequencies and also contribute to emission in the GeV domain. Comparison to the observations shows reasonable but not perfect agreement. Changes in the particle distribution, stellar, or pulsar wind could reduce the discrepancies but have not been attempted here. The purpose at this stage is to validate the model without fine-tuning and to compare the  -ray binaries under similar assumptions.
-ray binaries under similar assumptions.
Figure 6 shows the variation of the SED between periastron and apastron. Apart from the slight lowering of the synchrotron break frequency (see Sect. 4.3), the spectral energy distributions are nearly identical. This agrees with the lack of strong orbital variability observed in X-rays or radio. However, an orbital modulation is unavoidable at TeV energies because of
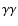 absorption (see below).
absorption (see below).
At  -ray energies, the model has plateau emission across the EGRET band and up to the HESS regime, as expected in Sect. 4. However, (1) the GeV flux is underestimated and (2) the high energy break is a factor 2-3 too low than what would be required to match the hard HESS power-law (
-ray energies, the model has plateau emission across the EGRET band and up to the HESS regime, as expected in Sect. 4. However, (1) the GeV flux is underestimated and (2) the high energy break is a factor 2-3 too low than what would be required to match the hard HESS power-law ( 2 TeV). LS 5039 is in the Galactic plane so that the EGRET flux could be overestimated (i.e. should be interpreted as an upper limit) if the diffuse
2 TeV). LS 5039 is in the Galactic plane so that the EGRET flux could be overestimated (i.e. should be interpreted as an upper limit) if the diffuse  -ray background subtracted is underestimated or if several unresolved sources contribute to the emission. That the measurements are non-contemporaneous should not be a problem in the present scenario, where variability is expected to be small (except for the possible pair cascade, see below).
-ray background subtracted is underestimated or if several unresolved sources contribute to the emission. That the measurements are non-contemporaneous should not be a problem in the present scenario, where variability is expected to be small (except for the possible pair cascade, see below).
The approximate treatment of the emission geometry may be responsible for these discrepancies. Adjusting 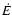 ,
,
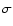 or the standoff point distance can alleviate both problems (Eq. (22)). Tweaking the accelerated distribution of particles might help, but it lacks justification. There could be a direct contribution from acceleration processes in the pulsar magnetosphere. Two other avenues can also be explored.
or the standoff point distance can alleviate both problems (Eq. (22)). Tweaking the accelerated distribution of particles might help, but it lacks justification. There could be a direct contribution from acceleration processes in the pulsar magnetosphere. Two other avenues can also be explored.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4779f6}
\end{figure}](/articles/aa/full/2006/36/aa4779-05/Timg266.gif) |
Figure 6:
Spectral energy distribution of LS 5039 at periastron (dark full line) and apastron (dark dashed line). The corresponding grey lines show the fraction received by the observer after absorption of the VHE  -rays on stellar photons. Parameters are identical to those of Figs. 3, 4 (but using -rays on stellar photons. Parameters are identical to those of Figs. 3, 4 (but using
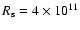 cm at apastron). Changes in the overall SED are limited and only minor variability is expected except at VHE energies where cm at apastron). Changes in the overall SED are limited and only minor variability is expected except at VHE energies where
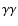 absorption strongly modulates the flux on the orbital period.
absorption strongly modulates the flux on the orbital period. |
| Open with DEXTER |
First, the anisotropy of the stellar radiation field might play a role. The outgoing energy of an up-scattered photon depends on the interaction angle with the higher energies reached at 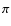 .
Even if the distribution of electrons is isotropic, the mean angle of interaction of the photons detected by the observer will depend on the orbital phase, hence there should be an energy effect. This is likely to be small at TeV energies as there is not much energy dependence on angle in the Klein-Nishina regime (Moderski et al. 2005).
.
Even if the distribution of electrons is isotropic, the mean angle of interaction of the photons detected by the observer will depend on the orbital phase, hence there should be an energy effect. This is likely to be small at TeV energies as there is not much energy dependence on angle in the Klein-Nishina regime (Moderski et al. 2005).
![\begin{figure}
\par\includegraphics[width=3.4cm,clip]{4779f7a}\hspace*{4mm}
\inc...
...]{4779f7c}\hspace*{4mm}
\includegraphics[width=3.4cm,clip]{4779f7d}
\end{figure}](/articles/aa/full/2006/36/aa4779-05/Timg268.gif) |
Figure 7:
Orbital evolution of the 5 GHz radio emission from the pulsar nebula in LS 5039. The maps were composed by summing up the contributions along the spiral nebula, as calculated for the various orbital phases 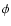 (see Fig. 5 for the
(see Fig. 5 for the 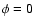 case). The maps were then smoothed by a Gaussian kernel with a full-width at half maximum (FWHM) of 0.8 mas ( case). The maps were then smoothed by a Gaussian kernel with a full-width at half maximum (FWHM) of 0.8 mas (
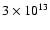 cm at 2.5 kpc). The maps share a common color scale to allow direct comparison, with contours at 50%, 25%, and 10% of the maximum orbital radio emission. The maps at cm at 2.5 kpc). The maps share a common color scale to allow direct comparison, with contours at 50%, 25%, and 10% of the maximum orbital radio emission. The maps at
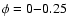 are very similar to the one observed by Paredes et al. (2000).
are very similar to the one observed by Paredes et al. (2000). |
| Open with DEXTER |
A second important effect is
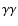 absorption (Bednarek 2006; Dubus 2006; Böttcher & Dermer 2005). High-energy
absorption (Bednarek 2006; Dubus 2006; Böttcher & Dermer 2005). High-energy  -rays are emitted in the immediate vicinity of the pulsar where they can then interact with stellar photons to produce
-rays are emitted in the immediate vicinity of the pulsar where they can then interact with stellar photons to produce
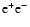 pairs. The threshold
pairs. The threshold  -ray energy is
-ray energy is  30 GeV. The transmitted flux is shown in Fig. 6 for both periastron and apastron. The calculation assumes that
30 GeV. The transmitted flux is shown in Fig. 6 for both periastron and apastron. The calculation assumes that  -ray emission is isotropic and occurs at the pulsar location (see Dubus 2006, for details). The opacity depends on orbital phase, with a maximum close to periastron passage when most of the
-ray emission is isotropic and occurs at the pulsar location (see Dubus 2006, for details). The opacity depends on orbital phase, with a maximum close to periastron passage when most of the  -ray emission between 0.1-10 TeV should be absorbed. An orbital modulation of the VHE flux measured by HESS is therefore expected. Note that this is not a discriminating feature with the accretion/jet scenario since any
-ray emission between 0.1-10 TeV should be absorbed. An orbital modulation of the VHE flux measured by HESS is therefore expected. Note that this is not a discriminating feature with the accretion/jet scenario since any  -ray emission occurring within
-ray emission occurring within 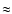 1 AU of the companion star in this system (for instance, in regions close to the black hole) would be significantly modulated.
1 AU of the companion star in this system (for instance, in regions close to the black hole) would be significantly modulated.
The average result of absorption will be a hardening of the high-energy (HESS range) spectrum. Pairs created by the absorption of  -rays can subsequently upscatter stellar photons to very high energies, thereby initiating a cascade (not taken into account in the calculation shown in Fig. 6). This can significantly increase the emission below 30 GeV as the absorbed energy is redistributed below the interaction threshold if the cascade is very strong (Aharonian et al. 2006). This would also introduce orbital variability below 30 GeV (Bednarek 2006; Dubus 2006). However, note that high energy pairs above
-rays can subsequently upscatter stellar photons to very high energies, thereby initiating a cascade (not taken into account in the calculation shown in Fig. 6). This can significantly increase the emission below 30 GeV as the absorbed energy is redistributed below the interaction threshold if the cascade is very strong (Aharonian et al. 2006). This would also introduce orbital variability below 30 GeV (Bednarek 2006; Dubus 2006). However, note that high energy pairs above
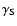 will radiate predominantly synchrotron emission instead of upscattering photons (Sect. 3.4), reducing the extent of the cascade (Aharonian et al. 2006).
will radiate predominantly synchrotron emission instead of upscattering photons (Sect. 3.4), reducing the extent of the cascade (Aharonian et al. 2006).
Understanding the exact impact of these two effects will require complex modelling, including a better representation of the shock geometry. The conclusion is that the present fairly rustic model is already able to account for the whole SED adequately, in the manner described in Sect. 4 using straightforward arguments.
The total radio intensity does not vary much along the orbit but the time/distance at which maximum radio emission is reached does depend on the orbital phase. The evolution of the radio flux with distance to the pulsar was calculated as above for various orbital phases and used together with the geometric model for the nebula (Sect. 5.4) to create emission maps of the system. Free-free absorption on the stellar wind becomes optically thin at  1 AU (see rough estimate in Sect. 2.4), close to the distance at which radio emission starts. Hence, this effect is neglected.
1 AU (see rough estimate in Sect. 2.4), close to the distance at which radio emission starts. Hence, this effect is neglected.
Figure 7 shows the evolution of the 5 GHz emission as a function of orbital phase 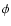 .
The first map (periastron
.
The first map (periastron  )
shown uses the same parameters as those in Fig. 5, except that the emission is smoothed by a Gaussian with FWHM of 0.8 mas to approximate the observing setup of Paredes et al. (2000). The system is seen at an inclination i=120
)
shown uses the same parameters as those in Fig. 5, except that the emission is smoothed by a Gaussian with FWHM of 0.8 mas to approximate the observing setup of Paredes et al. (2000). The system is seen at an inclination i=120 ,
i.e. 30
,
i.e. 30
 below the orbital plane (i=60
below the orbital plane (i=60 would be 30
would be 30 above the plane, the degeneracy from the radial velocity is lifted by the comparison of the curvature in the map to the VLBI observations). The contours at 50%, 25%, and 10% of the maximum surface intensity can be compared to the 5 GHz VLBI observation. The maps at
above the plane, the degeneracy from the radial velocity is lifted by the comparison of the curvature in the map to the VLBI observations). The contours at 50%, 25%, and 10% of the maximum surface intensity can be compared to the 5 GHz VLBI observation. The maps at
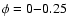 are strikingly similar to what was observed by Paredes et al. (2000), with slightly curved emission extending a few mas and the inner emission pointing in a slightly different direction. The observed very weak counter-jet would be associated with emission emitted at the previous periastron passage.
are strikingly similar to what was observed by Paredes et al. (2000), with slightly curved emission extending a few mas and the inner emission pointing in a slightly different direction. The observed very weak counter-jet would be associated with emission emitted at the previous periastron passage.
The model predicts changes in the radio maps with 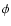 (Fig. 7), which can be verified by further VLBI observations. An animated map gives the distinct impression that blobs are alternatively ejected to the sides of the system, cunningly mimicking a microquasar. Accurate astrometry should show that the position of peak radio emission varies by a few mas. The orbital motion produces a "comma'' shape that is more pronounced at
(Fig. 7), which can be verified by further VLBI observations. An animated map gives the distinct impression that blobs are alternatively ejected to the sides of the system, cunningly mimicking a microquasar. Accurate astrometry should show that the position of peak radio emission varies by a few mas. The orbital motion produces a "comma'' shape that is more pronounced at
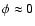 ,
when particles emitted at apastron start emitting in the radio band. Emission occurs principally along the major axis of the sky-projected system orbit. This effect shows up as a bunching of the lines representing the trajectories in the mid-plane of Fig. 5.
,
when particles emitted at apastron start emitting in the radio band. Emission occurs principally along the major axis of the sky-projected system orbit. This effect shows up as a bunching of the lines representing the trajectories in the mid-plane of Fig. 5.
On progressively larger scales, the emission becomes egg-shaped along the same axis, with the tip of the "egg'' on the apastron side as projected onto the sky. MERLIN and EVN radio observations do resolve emission on one side on a larger scale than on the other (Paredes et al. 2002). The observed emission is more linear than in the model with
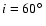 .
A higher inclination would help since emission becomes exactly line-shaped for an edge-on orbit
.
A higher inclination would help since emission becomes exactly line-shaped for an edge-on orbit
 .
However, the X-rays would then be eclipsed when the pulsar moves behind the companion; an upper limit using the orbit and assuming the X-ray emitting region is a sphere of radius
.
However, the X-rays would then be eclipsed when the pulsar moves behind the companion; an upper limit using the orbit and assuming the X-ray emitting region is a sphere of radius  gives
gives 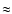
 .
The observed extent of radio emission is also larger than expected. On an equivalent map to the EVN observation, the 5 GHz intensity decreases to 1% of the peak value at 12 mas on one side and 6 mas on the other, instead of 35 mas and 25 mas. The quantitative agreement is not as good as on scales
.
The observed extent of radio emission is also larger than expected. On an equivalent map to the EVN observation, the 5 GHz intensity decreases to 1% of the peak value at 12 mas on one side and 6 mas on the other, instead of 35 mas and 25 mas. The quantitative agreement is not as good as on scales 
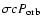 .
.
While the map in Fig. 7 basically shows only emission within an orbital timescale, maps on scales 
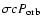 sum up emission from dozens of orbits, representing only a tiny fraction of the initial energy budget. The physics on such scales is undoubtedly more complex than the simple approach taken in Sect. 5.2: mixing occurs with the surrounding medium, recollimation shocks re-energise the electrons, shearing introduces turbulence, magnetic field changes as it is azimuthally stretched, shock conditions at earlier times were different, etc. Note that the outflow length of
sum up emission from dozens of orbits, representing only a tiny fraction of the initial energy budget. The physics on such scales is undoubtedly more complex than the simple approach taken in Sect. 5.2: mixing occurs with the surrounding medium, recollimation shocks re-energise the electrons, shearing introduces turbulence, magnetic field changes as it is azimuthally stretched, shock conditions at earlier times were different, etc. Note that the outflow length of  500 AU in Paredes et al. (2002) coincides roughly with the distance at which the stellar wind merges with the ISM. Incidentally, many of these complications are also encountered in the propagation of relativistic jets.
500 AU in Paredes et al. (2002) coincides roughly with the distance at which the stellar wind merges with the ISM. Incidentally, many of these complications are also encountered in the propagation of relativistic jets.
The conclusion is that the pulsar model provides a very good quantitative explanation for the radio emission emitted on scales of AU in LS 5039 and provides a qualitative framework to understand radio emission on larger scales. Radio observations have tremendous potential for validating the model.
The pulsar parameters 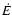 and
and
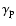 were taken as similar to those of LS 5039 for comparison purposes. A slightly higher value of
were taken as similar to those of LS 5039 for comparison purposes. A slightly higher value of
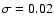 was adopted here to match the observed radio scales better (Sect. 6.2.4; note that Table 2 uses
was adopted here to match the observed radio scales better (Sect. 6.2.4; note that Table 2 uses
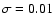 ).
).
6.2.1 Stellar wind
The stellar companion in LS I+61
 303 is a B0Ve type star that significantly complicates modelling over the case of LS 5039. Ultraviolet and infrared observations of Be stars show that their stellar wind has two components: a fast, polar outflow with properties typical of radiatively-driven winds, and a slow, equatorial outflow (Waters 1986).
303 is a B0Ve type star that significantly complicates modelling over the case of LS 5039. Ultraviolet and infrared observations of Be stars show that their stellar wind has two components: a fast, polar outflow with properties typical of radiatively-driven winds, and a slow, equatorial outflow (Waters 1986).
A typical polar wind was modelled using Eq. (34) with
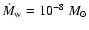 yr-1 and
yr-1 and
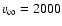 km s-1 (Waters et al. 1988). The standoff point
km s-1 (Waters et al. 1988). The standoff point  then varies between
then varies between
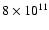 cm and
cm and
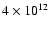 cm. The equatorial wind was modelled as
cm. The equatorial wind was modelled as
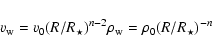 |
(35) |
with 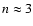 ,
,
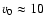 km s-1, and
km s-1, and
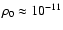 g cm-3 from the comparison to infrared observations of LS I+61
g cm-3 from the comparison to infrared observations of LS I+61
 303 (Waters et al. 1988; Martí & Paredes 1995) . This corresponds to an equatorial mass flux about a 100 times larger than the polar mass flux. The typical opening angle of the Be star equatorial outflow is 15
303 (Waters et al. 1988; Martí & Paredes 1995) . This corresponds to an equatorial mass flux about a 100 times larger than the polar mass flux. The typical opening angle of the Be star equatorial outflow is 15 .
The H
.
The H observations show the disc extends to 5-20
observations show the disc extends to 5-20 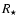 and that the terminal velocity is a few hundred km s-1. The standoff point is then between
and that the terminal velocity is a few hundred km s-1. The standoff point is then between
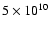 cm and
cm and
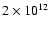 cm, smaller than the polar wind values because of the higher densities. The major difference between the two types of stellar winds will be at periastron.
cm, smaller than the polar wind values because of the higher densities. The major difference between the two types of stellar winds will be at periastron.
The resulting SEDs at periastron and apastron for both stellar winds are shown in Fig. 8. They agree well with the expectations set out in Table 2, most notably the much lower break frequencies for the equatorial outflow compared to the polar wind due to the smaller  .
.
Orbital variations in X-rays are expected to be greater than in LS 5039. Indeed, observations show variations of a factor  10 in soft X-rays (0.1-2 keV) and of smaller amplitude at higher energies. The maximum is inferred to be close to periastron (Harrison et al. 2000; Casares et al. 2005a). If consulting Fig. 8, this would seem to favour combining a small
10 in soft X-rays (0.1-2 keV) and of smaller amplitude at higher energies. The maximum is inferred to be close to periastron (Harrison et al. 2000; Casares et al. 2005a). If consulting Fig. 8, this would seem to favour combining a small  at periastron (equatorial wind) and a large
at periastron (equatorial wind) and a large  at apastron (polar wind). At apastron, the pulsar is 15
at apastron (polar wind). At apastron, the pulsar is 15  away from its stellar companion, in a region where the Be equatorial disc could already be truncated.
away from its stellar companion, in a region where the Be equatorial disc could already be truncated.
At  -ray energies, the TeV fluxes are consistent with the Whipple upper limits. Small
-ray energies, the TeV fluxes are consistent with the Whipple upper limits. Small  for the equatorial flow results in strong magnetic fields, conversely lowering the
for the equatorial flow results in strong magnetic fields, conversely lowering the  -ray emission. Non-intuitively, TeV emission will be higher at apastron than at periastron if the pulsar plows through a dense equatorial outflow close to its companion and a more tenuous wind further out. With
-ray emission. Non-intuitively, TeV emission will be higher at apastron than at periastron if the pulsar plows through a dense equatorial outflow close to its companion and a more tenuous wind further out. With  closer to the pulsar, synchrotron losses largely dominate at periastron over IC emission. This can be tested by observations with VERITAS or MAGIC. As with LS 5039, the GeV fluxes are too low to match the EGRET spectrum. An
closer to the pulsar, synchrotron losses largely dominate at periastron over IC emission. This can be tested by observations with VERITAS or MAGIC. As with LS 5039, the GeV fluxes are too low to match the EGRET spectrum. An
 cascade is unlikely to play a role here as the
cascade is unlikely to play a role here as the
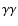 opacity is small except very close to periastron (Dubus 2006).
opacity is small except very close to periastron (Dubus 2006).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4779f8a}\par\vspace*{2mm}
\includegraphics[width=7.8cm,clip]{4779f8b}
\end{figure}](/articles/aa/full/2006/36/aa4779-05/Timg280.gif) |
Figure 8:
Spectral energy distribution of LS I+61
 303 at periastron (full black lines) and apastron (dashed black lines). The pulsar is assumed to have 303 at periastron (full black lines) and apastron (dashed black lines). The pulsar is assumed to have
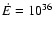 erg s-1 and erg s-1 and
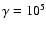 as for LS 5039, but a slightly higher
as for LS 5039, but a slightly higher
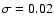 .
Top: the stellar wind is polar with a standoff point at .
Top: the stellar wind is polar with a standoff point at
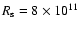 cm (periastron) and cm (periastron) and
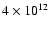 cm (apastron). Bottom: the stellar wind is equatorial with cm (apastron). Bottom: the stellar wind is equatorial with
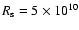 cm (periastron) and cm (periastron) and
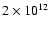 cm (apastron). Grey lines show the fraction of the emission occurring when cm (apastron). Grey lines show the fraction of the emission occurring when
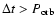 (the periastron line is visible in the top panel but not in the bottom panel).
(the periastron line is visible in the top panel but not in the bottom panel). |
| Open with DEXTER |
At low energies, the radio emission is too steep, primarily because of the value of  .
A lower value (
.
A lower value (
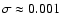 )
would yield better agreement: the downstream magnetic field is then lowered, reducing synchrotron losses and enabling stronger radio emission at large z. However, the physical extent of the associated radio emission would be smaller. A compromise would be to have
)
would yield better agreement: the downstream magnetic field is then lowered, reducing synchrotron losses and enabling stronger radio emission at large z. However, the physical extent of the associated radio emission would be smaller. A compromise would be to have  change with orbital phase. The distance of the shock to pulsar
change with orbital phase. The distance of the shock to pulsar  changes by an order-of-magnitude here (compared to a factor 2 in LS 5039) and
changes by an order-of-magnitude here (compared to a factor 2 in LS 5039) and 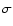 could be envisioned to decrease as
could be envisioned to decrease as  increases.
increases.
LS I+61
 303 has regular radio outbursts during which the flux increases by an order of magnitude. The outbursts last several days, peak at an orbital phase
303 has regular radio outbursts during which the flux increases by an order of magnitude. The outbursts last several days, peak at an orbital phase 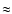 0.2-0.7 and repeat on the orbital period. There is also an X-ray orbital modulation (a factor 10 in the ROSAT band, less above) that precedes the radio peak by
0.2-0.7 and repeat on the orbital period. There is also an X-ray orbital modulation (a factor 10 in the ROSAT band, less above) that precedes the radio peak by
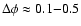 (the exact delay varies between outbursts). PSR B1259-63 has similar outbursts at periastron, associated with the pulsar crossing the Be equatorial outflow (Melatos et al. 1995). Indeed, the Be nature of the companion is the main feature distinguishing PSR B1259-63 and LS I+61
(the exact delay varies between outbursts). PSR B1259-63 has similar outbursts at periastron, associated with the pulsar crossing the Be equatorial outflow (Melatos et al. 1995). Indeed, the Be nature of the companion is the main feature distinguishing PSR B1259-63 and LS I+61
 303 from LS 5039, which has no radio outbursts.
303 from LS 5039, which has no radio outbursts.
Suppose the pulsar samples the dense equatorial disc around periastron and a more tenuous, fast wind at apastron. Changes in  ,
possibly
,
possibly 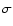 ,
are expected along the orbit; yet these do not suffice to explain the outbursts because of the timescales involved. If such were the case, the
,
are expected along the orbit; yet these do not suffice to explain the outbursts because of the timescales involved. If such were the case, the  10-day delay in the phasing of the X-ray and radio modulations would presumably be associated to the time it takes for electrons to cool from injection. The strongest radio emission would occur at apastron, when the shock is far from the pulsar and
10-day delay in the phasing of the X-ray and radio modulations would presumably be associated to the time it takes for electrons to cool from injection. The strongest radio emission would occur at apastron, when the shock is far from the pulsar and 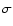 is expected to be lower. The elapsed time to radio peak is then greater than the orbital period (Fig. 8) and this would smooth out the flux modulation.
is expected to be lower. The elapsed time to radio peak is then greater than the orbital period (Fig. 8) and this would smooth out the flux modulation.
The impact of the Be star equatorial outflow is probably somewhere else. With a slow wind, the standoff point
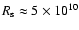 cm is very small at periastron. Moreover, the equatorial wind is very slow so that the Bondi accretion radius
cm is very small at periastron. Moreover, the equatorial wind is very slow so that the Bondi accretion radius 
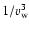 (Sect. 2.4) is actually greater than
(Sect. 2.4) is actually greater than  .
For the adopted parameters, the accretion radius is
.
For the adopted parameters, the accretion radius is 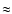
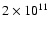 cm at periastron. Matter falls towards the compact object at a rate
cm at periastron. Matter falls towards the compact object at a rate  1017 g s-1, but is not accreted: the pulsar wind is still able to hold off the inflow of material (Sect. 2.4). However, the situation changes in a significant way from that described until now.
1017 g s-1, but is not accreted: the pulsar wind is still able to hold off the inflow of material (Sect. 2.4). However, the situation changes in a significant way from that described until now.
When the relative motions are fast (polar wind case or the high-velocity isolated pulsar case), the standoff distance is farther out than the Bondi capture radius so that the external ram pressure is mostly unidirectional. The pulsar creates a long comet tail directed away from the maximum ram pressure point. At periastron, the standoff distance is within the Bondi capture radius. The external pressure from inflowing material is more spherically distributed, as in a SNR plerion, so that the shocked pulsar wind cannot break open the surrounding medium on a short timescale.
Therefore, a possible picture would be that the shocked pulsar wind is embedded in the equatorial disc at periastron (plerion-like) and that the geometry is open (comet-like) at apastron, where the Bondi radius is smaller than  for both an equatorial or a polar wind. High-energy radiation is not affected much as it is emitted close to the pulsar in both cases. The change should be mostly in the low frequency emission as particles are constantly injected in a bubble slowly expanding in the equatorial outflow. The outburst would be associated with emission from this bubble of electrons, following an earlier suggestion by Leahy (2004). Detailed modelling is not attempted here but note that adiabatic expansion of bubbles has been shown to reproduce the radio outbursts (Leahy 2004; Taylor & Gregory 1984; Paredes et al. 1991) and, naturally, has also been proposed for the radio outbursts of PSR B1259-63 (Connors et al. 2002).
for both an equatorial or a polar wind. High-energy radiation is not affected much as it is emitted close to the pulsar in both cases. The change should be mostly in the low frequency emission as particles are constantly injected in a bubble slowly expanding in the equatorial outflow. The outburst would be associated with emission from this bubble of electrons, following an earlier suggestion by Leahy (2004). Detailed modelling is not attempted here but note that adiabatic expansion of bubbles has been shown to reproduce the radio outbursts (Leahy 2004; Taylor & Gregory 1984; Paredes et al. 1991) and, naturally, has also been proposed for the radio outbursts of PSR B1259-63 (Connors et al. 2002).
The radio emission map expected from the simple case of a polar wind is shown in Fig. 9 for 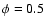 and
and
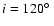 .
(Here,
.
(Here, 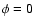 corresponds to periastron passage, to which
corresponds to periastron passage, to which 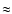 0.2 should be added if using the radio ephemeris, Gregory 2002.) The orientation of the orbit is illustrated in Fig. 2 of Casares et al. (2005a). The image does not take the radio outbursts into account but should nevertheless be indicative of the overall morphology to expect.
0.2 should be added if using the radio ephemeris, Gregory 2002.) The orientation of the orbit is illustrated in Fig. 2 of Casares et al. (2005a). The image does not take the radio outbursts into account but should nevertheless be indicative of the overall morphology to expect.
As in LS 5039, the nebula has a "comma'' shape. The physical scale is larger than in LS 5039 because of the longer orbital period. The major axis is almost parallel to the plane of the sky, defining a very clear preferred direction for emission. This is consistent with observations of one-sided radio emission on scales of 10-100 mas (Massi et al. 2001,2004). The mean position angle will increasingly vary as one goes to higher spatial resolutions, and the impact of the orbital motion becomes clearer. This could explain the almost perpendicular directions seen at 3 mas and 10 mas resolution, albeit at different epochs (Massi et al. 2001,1993). Massi et al. (2004) also find changes in structure about 50 mas away from the core emission on timescale of days during the radio outburst. This could be due to a combination of rapidly changing emission angles at periastron passage and delayed peak radio emission; a proper model for the radio outbursts would be required to verify this possibility.
![\begin{figure}
\par\includegraphics[width=3.5cm,clip]{4779f9a}\hspace*{4mm}
\includegraphics[width=3.5cm,clip]{4779f9b}
\end{figure}](/articles/aa/full/2006/36/aa4779-05/Timg285.gif) |
Figure 9:
Left: map of the 5 GHz radio emission from the pulsar nebula in LS I+61
 303 at 303 at 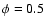 (i=120
(i=120 ). ). 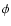 is zero at periastron passage (for which
is zero at periastron passage (for which
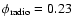 ,
Gregory 2002). Right: corresponding outflow path (as in Fig. 5 but on a linear greyscale) before smoothing (the projected outflow path at apastron is indicated by a dark line). The stellar wind is assumed to be polar (top panel of Fig. 8). The smoothing Gaussian kernel has an FWHM of 8 mas ( ,
Gregory 2002). Right: corresponding outflow path (as in Fig. 5 but on a linear greyscale) before smoothing (the projected outflow path at apastron is indicated by a dark line). The stellar wind is assumed to be polar (top panel of Fig. 8). The smoothing Gaussian kernel has an FWHM of 8 mas (
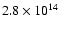 cm at 2.3 kpc). Contours are at 50%, 25%, and 10% of maximum emission. There is a preferred direction to the right, towards apastron. cm at 2.3 kpc). Contours are at 50%, 25%, and 10% of maximum emission. There is a preferred direction to the right, towards apastron. |
| Open with DEXTER |
6.3 PSR B1259-63
For PSR B1259-63, the measured 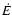 is
is
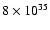 erg s-1 ( In the text
Manchester et al. 1995). The other pulsar parameters were taken to be
erg s-1 ( In the text
Manchester et al. 1995). The other pulsar parameters were taken to be
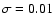 and
and
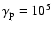 to compare with the other two systems. Emission by containment of a pulsar wind in PSR B1259-63 has previously been investigated by several authors (Tavani et al. 1994; Kirk et al. 1999; Murata et al. 2003; Melatos et al. 1995; Tavani & Arons 1997). The purpose here is to put the system in the same context as LS 5039 and LS I+61
to compare with the other two systems. Emission by containment of a pulsar wind in PSR B1259-63 has previously been investigated by several authors (Tavani et al. 1994; Kirk et al. 1999; Murata et al. 2003; Melatos et al. 1995; Tavani & Arons 1997). The purpose here is to put the system in the same context as LS 5039 and LS I+61
 303, and explore possible large-scale radio emission.
303, and explore possible large-scale radio emission.
Both an equatorial and a polar stellar wind were considered, with the same parameters as those given for LS I+61
 303 in Sect. 6.2.1. The periastron distance in PSR B1259-63 is comparable to the apastron distance in LS I+61
303 in Sect. 6.2.1. The periastron distance in PSR B1259-63 is comparable to the apastron distance in LS I+61
 303. Any equatorial outflow is then at or close to its terminal velocity, and there is little difference in
303. Any equatorial outflow is then at or close to its terminal velocity, and there is little difference in  with a polar wind (only a factor 3, see Table 2). The equatorial wind is truncated at
with a polar wind (only a factor 3, see Table 2). The equatorial wind is truncated at 
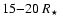 and is not considered at apastron. Only a polar wind can contain the pulsar wind at apastron.
and is not considered at apastron. Only a polar wind can contain the pulsar wind at apastron.
The spectral energy distribution at periastron and apastron is shown in Fig. 10 for the case of a polar wind. The SED at periastron for an equatorial wind (not shown) is very close to the one shown here, the difference in  being small. Unsurprisingly, the SED is essentially the same as that for LS I+61
being small. Unsurprisingly, the SED is essentially the same as that for LS I+61
 303 at apastron, the orbital separation being the same and other parameters varying little. The GeV emission from PSR B1259-63 around periastron should be detected by GLAST in the future, if only because of this similitude. The TeV slope appears in good agreement with the HESS measurement. The variations in integrated flux seen by HESS around periastron are beyond this model's present abilities (which predicts none) and will probably require taking anisotropic IC scattering into account (see Kirk et al. 1999), as well as changes in the circumstellar density to properly reproduce. There seems to be an inflection in the X-ray spectrum between 1-10 keV that might correspond to the break observed with RXTE. Very good agreement can indeed be obtained when using
303 at apastron, the orbital separation being the same and other parameters varying little. The GeV emission from PSR B1259-63 around periastron should be detected by GLAST in the future, if only because of this similitude. The TeV slope appears in good agreement with the HESS measurement. The variations in integrated flux seen by HESS around periastron are beyond this model's present abilities (which predicts none) and will probably require taking anisotropic IC scattering into account (see Kirk et al. 1999), as well as changes in the circumstellar density to properly reproduce. There seems to be an inflection in the X-ray spectrum between 1-10 keV that might correspond to the break observed with RXTE. Very good agreement can indeed be obtained when using
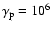 .
.
The SED at apastron is only slightly different. Despite the considerably larger orbital separation, the TeV flux is only lowered by a few factors. The photon density is indeed much lower, but the scale of the flow (set by  )
is much larger than at periastron. Particles have a longer time available to interact and this compensates for the weaker densities. Overall, the radiation efficiency is the same as at periastron, since the same amount of energy is being dissipated regardless of orbital phase. In its present simplified form, the model cannot account for the observed order-of-magnitude changes in X-ray luminosity. This was noted by Murata et al. (2003) who proposed that lowering
)
is much larger than at periastron. Particles have a longer time available to interact and this compensates for the weaker densities. Overall, the radiation efficiency is the same as at periastron, since the same amount of energy is being dissipated regardless of orbital phase. In its present simplified form, the model cannot account for the observed order-of-magnitude changes in X-ray luminosity. This was noted by Murata et al. (2003) who proposed that lowering 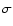 with pulsar distance might help.
with pulsar distance might help.
Emission at apastron occurs on large, resolvable scales. Figure 10 shows the amount of the total flux emitted after an elapsed time
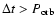 after injection. This flux is radiated several hundred AUs away and may lead to a faint arcsecond scale bowshock structure up to IR frequencies.
after injection. This flux is radiated several hundred AUs away and may lead to a faint arcsecond scale bowshock structure up to IR frequencies.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4779f10}
\end{figure}](/articles/aa/full/2006/36/aa4779-05/Timg289.gif) |
Figure 10:
Spectral energy distribution of PSR B1259-63 at periastron (solid line) and apastron (dashed line). The pulsar is assumed to have
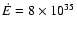 erg s-1, erg s-1,
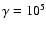 ,
and ,
and
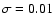 .
The stellar wind is polar (same parameters as LS I+61 .
The stellar wind is polar (same parameters as LS I+61
 303) with a standoff point at 303) with a standoff point at
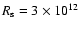 cm (periastron) and cm (periastron) and
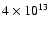 cm (apastron). With an equatorial, slow wind, the standoff point at periastron is at cm (apastron). With an equatorial, slow wind, the standoff point at periastron is at
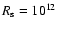 cm, not different enough from the polar wind case to significantly change the expected SED from that shown above. The grey dashed line shows the summed late time emission ( cm, not different enough from the polar wind case to significantly change the expected SED from that shown above. The grey dashed line shows the summed late time emission (
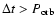 )
at apastron, which occurs on scales )
at apastron, which occurs on scales
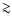 0.01 pc. 0.01 pc. |
| Open with DEXTER |
In PSR B1259-63, observations of the radio dispersion measure imply the disc is inclined with respect to the orbital plane (Melatos et al. 1995). The radio outbursts seen before and after periastron are presumably associated with the two pulsar disc crossings (Ball et al. 1999). Working by analogy, smaller separations and a coplanar equatorial outflow would explain the single outburst per orbit in LS I+61
 303. As explained above for LS I+61
303. As explained above for LS I+61
 303, the outbursts are unlikely to be due solely to a change in
303, the outbursts are unlikely to be due solely to a change in  .
The large increase in radio flux might be related to the slow expansion of a bubble of relativistic electrons formed in the dense flow. Shock-acceleration of electrons from the stellar wind itself may also play a role (Ball et al. 1999).
.
The large increase in radio flux might be related to the slow expansion of a bubble of relativistic electrons formed in the dense flow. Shock-acceleration of electrons from the stellar wind itself may also play a role (Ball et al. 1999).
It is therefore as difficult as with LS I+61
 303 to accurately predict the shape the radio emission might take. Figure 11 shows expectations at
303 to accurately predict the shape the radio emission might take. Figure 11 shows expectations at 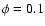 assuming PSR B1259-63 only interacts with a polar wind. The spatial scales should be easy to resolve since
assuming PSR B1259-63 only interacts with a polar wind. The spatial scales should be easy to resolve since  is large. Unfortunately there are no published radio maps to compare with. The rapid revolution of the pulsar around periastron produces an arc with two brighter "knots'' where pre- and post-periastron electrons are cooling. These two knots gradually drift apart. This takes no account of the radio outbursts. If these are localised in the equatorial wind, the impact might be only an increase in the central (unresolved) component, leaving the much fainter diffuse components described here mostly unchanged. The bow shock points away from the star in almost the same direction for most of the highly eccentric orbit.
is large. Unfortunately there are no published radio maps to compare with. The rapid revolution of the pulsar around periastron produces an arc with two brighter "knots'' where pre- and post-periastron electrons are cooling. These two knots gradually drift apart. This takes no account of the radio outbursts. If these are localised in the equatorial wind, the impact might be only an increase in the central (unresolved) component, leaving the much fainter diffuse components described here mostly unchanged. The bow shock points away from the star in almost the same direction for most of the highly eccentric orbit.
![\begin{figure}
\par\includegraphics[width=3.5cm,clip]{4779f11a}\hspace*{4mm}
\includegraphics[width=3.3cm,clip]{4779f11b}
\end{figure}](/articles/aa/full/2006/36/aa4779-05/Timg290.gif) |
Figure 11:
Left: map of 5 GHz radio emission from PSR B1259-63 close to periastron passage ( ,
i=30 ,
i=30 ), assuming only a polar-type stellar wind. Right: corresponding outflow path on the same scale before smoothing (the projected outflow path at apastron is indicated by a dark line). The smoothing Gaussian kernel has a FWHM of 0.05 ), assuming only a polar-type stellar wind. Right: corresponding outflow path on the same scale before smoothing (the projected outflow path at apastron is indicated by a dark line). The smoothing Gaussian kernel has a FWHM of 0.05
 (
(
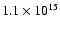 cm at 1.5 kpc). The contours are at 50%, 25%, and 10% of the maximum intensity. The tail extends to a few arcseconds. The spatial scale is large given the size of the orbit (hence cm at 1.5 kpc). The contours are at 50%, 25%, and 10% of the maximum intensity. The tail extends to a few arcseconds. The spatial scale is large given the size of the orbit (hence  ); with an even larger eccentricity than LS I+61 ); with an even larger eccentricity than LS I+61
 303, the preferred direction of the nebula towards apastron is very clear. 303, the preferred direction of the nebula towards apastron is very clear. |
| Open with DEXTER |
The pulsar wind scenario offers a tantalizing way to unite LS 5039, LS I+61
 303 and PSR B1259-63 into a new-class of young, rotation-powered
303 and PSR B1259-63 into a new-class of young, rotation-powered  -ray binaries. At present, nothing rules out that the compact object in LS 5039 and LS I+61
-ray binaries. At present, nothing rules out that the compact object in LS 5039 and LS I+61
 303 is a pulsar. The radial velocities allow it, and there are no conclusive signs of accretion. Directly unveiling a radio pulse will not be possible due to strong free-free absorption; although a difficult endeavour, an X-ray or
303 is a pulsar. The radial velocities allow it, and there are no conclusive signs of accretion. Directly unveiling a radio pulse will not be possible due to strong free-free absorption; although a difficult endeavour, an X-ray or  -ray pulse would prove the scenario.
-ray pulse would prove the scenario.
A similar relativistic pulsar wind with most of its
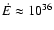 erg s-1 energy (
erg s-1 energy (
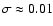 )
in electrons and positrons of Lorentz factor
)
in electrons and positrons of Lorentz factor
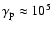 suffices to explain most properties in all three objects. The termination shock occurs at the pressure balance point. There, particles in the pulsar wind are scattered and accelerated into a non-thermal power-law distribution. The maximum energy is set by the size of the shock region and radiative losses. Downstream values in the shocked pulsar wind material (density, magnetic field) are set by the MHD jump conditions. Particles radiate synchrotron and inverse Compton whilst being advected away in a comet tail nebula. At high energies synchrotron cooling dominates, giving characteristic break frequencies between a rising and flat
suffices to explain most properties in all three objects. The termination shock occurs at the pressure balance point. There, particles in the pulsar wind are scattered and accelerated into a non-thermal power-law distribution. The maximum energy is set by the size of the shock region and radiative losses. Downstream values in the shocked pulsar wind material (density, magnetic field) are set by the MHD jump conditions. Particles radiate synchrotron and inverse Compton whilst being advected away in a comet tail nebula. At high energies synchrotron cooling dominates, giving characteristic break frequencies between a rising and flat 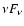 spectrum in hard X-rays and between a flat and a declining
spectrum in hard X-rays and between a flat and a declining 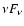 spectrum in VHE
spectrum in VHE  -rays. The VHE emission occurs close to the pulsar, and an orbital modulation of the flux in the TeV range is expected in this scenario, due to absorption (pair production) on stellar photons.
-rays. The VHE emission occurs close to the pulsar, and an orbital modulation of the flux in the TeV range is expected in this scenario, due to absorption (pair production) on stellar photons.
The small-scale radio emission is also reasonably reproduced. Radiation shifts to lower wavelengths as particles lose their energy to radiation and conditions in the flow change. Ultimately, the particles that gave rise to  -ray radiation near the star emit radio far from the binary. The flow changes from a cometary shape to a spiral-shaped nebula with a step
-ray radiation near the star emit radio far from the binary. The flow changes from a cometary shape to a spiral-shaped nebula with a step 
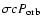 .
Matching with the observed size of radio nebula in LS 5039 and LS I+61
.
Matching with the observed size of radio nebula in LS 5039 and LS I+61
 303 implies
303 implies
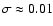 .
On large scales (several turns of the spiral), the radio emission is underestimated by the model. Changes in the flow conditions on such scales, notably velocity and magnetic field evolution, are undoubtedly more complex than the simple assumptions made here. Nevertheless, the combination of the peculiar geometry, emission at various distances, and inclination can conspire to create radio maps with seemingly bipolar ejections of material as in X-ray binary jets. Predictions are made for LS 5039 that are amenable to observation with radio interferometry.
.
On large scales (several turns of the spiral), the radio emission is underestimated by the model. Changes in the flow conditions on such scales, notably velocity and magnetic field evolution, are undoubtedly more complex than the simple assumptions made here. Nevertheless, the combination of the peculiar geometry, emission at various distances, and inclination can conspire to create radio maps with seemingly bipolar ejections of material as in X-ray binary jets. Predictions are made for LS 5039 that are amenable to observation with radio interferometry.
The present model does not provide an entirely satisfactory view of the GeV  -rays detected by EGRET in LS 5039 and LS I+61
-rays detected by EGRET in LS 5039 and LS I+61
 303. The fluxes are underproduced in both cases. The discrepancy might have an observational side with fluxes overestimated, comprising the combined emission from several sources in the wide instrumental PSF. Much more precise measurements will be made by GLAST in the future. On the theoretical side, inadequacies in the treatment of the emission region might be at work, notably anisotropies. The stellar radiation is anisotropic, the pulsar wind is anisotropic, the termination shock is not spherical, etc. If synchrotron losses are limited, IC cooling of particles will enhance the GeV yield and lower the discrepancy. The mismatch between EGRET and HESS spectra of LS 5039 is also difficult for leptonic jet models (Dermer & Böttcher 2006; Paredes et al. 2006).
303. The fluxes are underproduced in both cases. The discrepancy might have an observational side with fluxes overestimated, comprising the combined emission from several sources in the wide instrumental PSF. Much more precise measurements will be made by GLAST in the future. On the theoretical side, inadequacies in the treatment of the emission region might be at work, notably anisotropies. The stellar radiation is anisotropic, the pulsar wind is anisotropic, the termination shock is not spherical, etc. If synchrotron losses are limited, IC cooling of particles will enhance the GeV yield and lower the discrepancy. The mismatch between EGRET and HESS spectra of LS 5039 is also difficult for leptonic jet models (Dermer & Böttcher 2006; Paredes et al. 2006).
The present model also does not satisfyingly explain the nature of the radio outbursts in LS I+61
 303 and PSR B1259-63. However, the scenario provides a unifying context. As has been argued for both sources, the reason must be found in the Be nature of the companion stars. The progression of the pulsar in the slow, dense wind could lead to an enclosed geometry, rather than an open comet tail geometry. Radio emission might also be enhanced by the acceleration of particles from the stellar wind itself. There is as yet no coherent picture of the radio outbursts of LS I+61
303 and PSR B1259-63. However, the scenario provides a unifying context. As has been argued for both sources, the reason must be found in the Be nature of the companion stars. The progression of the pulsar in the slow, dense wind could lead to an enclosed geometry, rather than an open comet tail geometry. Radio emission might also be enhanced by the acceleration of particles from the stellar wind itself. There is as yet no coherent picture of the radio outbursts of LS I+61
 303 in the context of the accretion-driven/relativistic jet scenario.
303 in the context of the accretion-driven/relativistic jet scenario.
Despite these shortcomings, the explanatory scope of the model is large. Once the orbital parameters are set, the only variables that come into play are 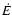 ,
,
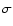 ,
,
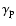 ,
and
,
and  .
The SEDs come out naturally for reasonable inputs and the comet-tail nebula produces radio emission on scales of
.
The SEDs come out naturally for reasonable inputs and the comet-tail nebula produces radio emission on scales of
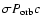 and beyond. The pulsar scenario therefore seems like a viable alternative to the accretion/jet scenario for LS 5039 and LS I+61
and beyond. The pulsar scenario therefore seems like a viable alternative to the accretion/jet scenario for LS 5039 and LS I+61
 303.
303.
Note added in proof.
Since acceptance of this article, the MAGIC collaboration has reported the detection of VHE  -ray emission from LS I+61
-ray emission from LS I+61
 303, with a higher flux at apastron than periastron as predicted in Sect. 6.2.2 (Albert et al. 2006, Science, in press [arXiv:astro-ph/0605549]).
303, with a higher flux at apastron than periastron as predicted in Sect. 6.2.2 (Albert et al. 2006, Science, in press [arXiv:astro-ph/0605549]).
Acknowledgements
I thank B. Giebels, J.-P. Lasota, M. Sikora, R. Taam, and R. Fender for their comments.
- Aharonian,
F. A., et al. (HESS collaboration) 2005a, Science, 309,
746
(In the text)
- Aharonian, F. A.,
et al. (HESS collaboration) 2005b, A&A, 442, 1
(In the text)
- Aharonian,
F. A., Anchordoqui, L. A., Khangulyan, D., &
Montaruli, T. 2006, J. Phys., Conf. Ser., 39, 408
(In the text)
- Arons, J., & Tavani,
M. 1993, ApJ, 403, 249 [NASA ADS] [CrossRef]
- Arons, J., &
Tavani, M. 1994, ApJS, 90, 797 [NASA ADS] [CrossRef] (In the text)
- Bahcall, J. N.
1978, ARA&A, 16, 241 [NASA ADS] (In the text)
- Ball, L., &
Kirk, J. G. 2000, Astropart. Phys., 12, 335 [NASA ADS] [CrossRef]
- Ball, L., Melatos, A.,
Johnston, S., & Skjaeraasen, O. 1999, ApJ, 514, L39 [NASA ADS] [CrossRef] (In the text)
- Bednarek, W. 2006,
MNRAS, 368, 579 [NASA ADS] [CrossRef]
- Blumenthal, G. R., &
Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] (In the text)
-
Bogovalov, S. V., & Aharonian, F. A. 2000, MNRAS,
313, 504 [NASA ADS] [CrossRef]
- Bosch-Ramon, V., Paredes,
J. M., Ribó, M., et al. 2005, ApJ, 628, 388 [NASA ADS] [CrossRef]
- Böttcher, M.,
& Dermer, C. D. 2005, ApJ, 634, L81 [NASA ADS] [CrossRef]
- Bucciantini,
N., Amato, E., & Del Zanna, L. 2005, A&A, 434, 189 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Casares, J., Ribas,
I., Paredes, J. M., Martí, J., & Allende Prieto, C.
2005a, MNRAS, 360, 1105 [NASA ADS] [CrossRef]
- Casares, J.,
Ribó, M., Ribas, I., et al. 2005b, MNRAS, 364, 899 [NASA ADS] [CrossRef]
- Chang,
J. S., & Cooper, G. 1970, J. Comp. Phys., 6, 1 (In the text)
- Clark, J. S.,
et al. 2001, A&A, 376, 476 [EDP Sciences] [NASA ADS] [CrossRef]
- Connors, T. W.,
Johnston, S., Manchester, R. N., & McConnell, D. 2002,
MNRAS, 336, 1201 [NASA ADS] [CrossRef] (In the text)
- Conti, P. S. 1978,
A&A, 63, 225 [NASA ADS] (In the text)
- Dermer, C. D.,
& Böttcher, M. 2006, ApJ, 643, 1081 [NASA ADS] [CrossRef]
- Dougherty,
S. M., Pittard, J. M., Kasian, L., et al. 2003,
A&A, 409, 217 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Dubus, G. 2006, A&A,
451, 9 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Fegan, S. J.,
et al. 2005, ApJ, 624, 638 [NASA ADS] [CrossRef] (In the text)
- Fender,
R. P. 2006, chapter 9 in Compact Stellar X-Ray Sources, ed. W.
H. G. Lewin, & M. van der Klis, Cambridge Astrophysics Series
39 (Cambridge University Press), 381
(In the text)
- Fender, R. P.,
Belloni, T. M., & Gallo, E. 2004, MNRAS, 355, 1105 [NASA ADS] [CrossRef] (In the text)
- Frail, D. A.,
Seaquist, E. R., & Taylor, A. R. 1987, AJ, 93,
1506 [NASA ADS] [CrossRef]
- Gaensler,
B. M. 2005, Ad. Space Res., 35, 1116 [NASA ADS] (In the text)
- Gaensler, B. M., &
Slane, P. O. 2006, ARA&A, 44, 17 [NASA ADS] (In the text)
- Gould, R. J., &
Schréder, G. P. 1967, Phys. Rev., 155, 1404 [NASA ADS] [CrossRef] (In the text)
- Gregory,
P. C. 2002, ApJ, 575, 427 [NASA ADS] [CrossRef]
- Gregory, P. C.,
& Taylor, A. R. 1978, Nature, 272, 704 [NASA ADS] [CrossRef]
- Gregory,
P. C. Taylor, A. R., Crampton, D., et al. 1979, AJ, 84,
1030 [NASA ADS] [CrossRef] (In the text)
- Greiner, J., &
Rau, A. 2001, A&A, 375, 145 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Grove, J. E.,
Tavani, M., Purcell, W. R., et al. 1995, ApJ, 447,
L113 [NASA ADS] (In the text)
- Hall, T. A.,
et al. 2003, ApJ, 583, 853 [NASA ADS] [CrossRef]
- Harmon, B. A.,
et al. 2004, ApJS, 154, 585 [NASA ADS] [CrossRef] (In the text)
- Harrison,
F. A., Ray, P. S., Leahy, D. A., Waltman,
E. B., & Pooley, G. G. 2000, ApJ, 528, 454 [NASA ADS] [CrossRef] (In the text)
- Hartman, R. C.,
Bertsch, D. L., Chen, A. W., et al. 1999, ApJS, 123, 79 [NASA ADS] [CrossRef] (In the text)
- Hoffman, C. M.,
Sinnis, C., Fleury, P., & Punch, M. 1999, Rev. Mod. Phys., 71,
897 [NASA ADS] [CrossRef] (In the text)
- Hutchings,
J. B., & Crampton, D. 1981, PASP, 93, 486 [NASA ADS] [CrossRef]
- Illarionov,
A. F., & Sunyaev, R. A. 1975, A&A, 39, 185 [NASA ADS] (In the text)
- Johnston, S.,
Manchester, R. N., Lyne, A. G., et al. 1992, ApJ,
387, L37 [NASA ADS] [CrossRef] (In the text)
- Johnston, S.,
Manchester, R. N., Lyne, A. G., Nicastro, L., &
Spyromilio, J. 1994, MNRAS, 268, 430 [NASA ADS]
- Johnston, S.,
Ball, L., Wang, N., & Manchester, R. N. 2005, MNRAS, 358,
1069 [NASA ADS] [CrossRef] (In the text)
- Jones, F. C. 1968,
Phys. Rev., 167, 1159 [NASA ADS] [CrossRef] (In the text)
- Kennel, C. F., &
Coroniti, F. V. 1984a, ApJ, 283, 694 [NASA ADS] [CrossRef]
- Kennel, C. F., &
Coroniti, F. V. 1984b, ApJ, 283, 710 [NASA ADS] [CrossRef] (In the text)
- Kirk, J. G., Ball, L.,
& Skjaeraasen, O. 1999, Astropart. Phys., 10, 31 [NASA ADS] [CrossRef]
- Leahy, D. A.
2004, A&A, 413, 1019 [EDP Sciences] [NASA ADS] [CrossRef]
- Leahy,
D. A., Harrison, F. A., & Yoshida, A. 1997, ApJ, 475,
823 [NASA ADS] [CrossRef] (In the text)
- Manchester,
R. N., Johnston, S., Lyne, A. G., et al. 1995, ApJ,
445, L137 [NASA ADS] [CrossRef]
- Maraschi, L., &
Treves, A. 1981, MNRAS, 194, 1P [NASA ADS] (In the text)
- Maraschi, L.,
Treves, A., & Tanzi, E. G. 1981, ApJ, 248, 1010 [NASA ADS] [CrossRef] (In the text)
- Marraco,
L. G., & Orsatti, A. M. 1982, Rev. Mex. Astron.
Astrofis., 5, 183 [NASA ADS] (In the text)
- Martí, J., &
Paredes, J. M. 1995, A&A, 298, 151 [NASA ADS] (In the text)
- Martí, J.,
Peracaula, M., Paredes, J. M., Massi, M., & Estalella, R.
1998a, A&A, 329, 951 [NASA ADS] (In the text)
- Martí, J.,
Paredes, J. M., & Ribó, M. 1998b, A&A, 338,
L71 [NASA ADS] (In the text)
- Martocchia, A.,
Motch, C., & Negueruela, I. 2005, A&A, 430, 245 [EDP Sciences] [NASA ADS] [CrossRef]
- Massi, M., Paredes,
J. M., Estalella, R., & Felli, M. 1993, A&A, 269,
249 [NASA ADS]
- Massi, M., Ribó,
M., Paredes, J. M., Peracaula, M., & Estalella, R. 2001,
A&A, 376, 217 [EDP Sciences] [NASA ADS] [CrossRef]
- Massi, M.,
Ribó, M., Paredes, J. M., et al. 2004, A&A, 414,
L1 [EDP Sciences] [NASA ADS] [CrossRef]
- McSwain,
M. V., & Gies, D. R. 2002, ApJ, 568, L27 [NASA ADS] [CrossRef]
- McSwain,
M. V., Gies, D. R., Huang, W., et al. 2004, ApJ,
600, 927 [NASA ADS] [CrossRef]
- Melatos, A.,
Johnston, S., & Melrose, D. B. 1995, MNRAS, 275, 381 [NASA ADS]
- Meurs,
E. J. A., & van den Heuvel, E. P. J. 1989,
A&A, 226, 88 [NASA ADS]
- Moderski, R.,
Sikora, M., Coppi, P. S., & Aharonian, F. 2005, MNRAS,
845
(In the text)
- Motch, C., Haberl, F.,
Dennerl, K., Pakull, M., & Janot-Pacheco, E. 1997, A&A,
323, 853 [NASA ADS]
- Murata, K., Tamaki, H.,
Maki, H., & Shibazaki, N. 2003, PASJ, 55, 473 [NASA ADS]
- Paredes,
J. M., Martí, J., Estalella, R., & Sarrate, J. 1991,
A&A, 248, 124 [NASA ADS]
- Paredes,
J. M., Martí, J., Peracaula, M., & Ribó, M.
1997, A&A, 320, L25 [NASA ADS] (In the text)
- Paredes, J. M.,
Martí, J., Ribó, M., & Massi, M. 2000, Science, 288,
2340 [NASA ADS] [CrossRef] (In the text)
- Paredes,
J. M., Ribó, M., Ros, E., Martí, J., & Massi, M.
2002, A&A, 393, L99 [EDP Sciences] [NASA ADS] [CrossRef]
- Paredes,
J. M., Bosch-Ramon, V., & Romero, G. E. 2006,
A&A, 451, 259 [EDP Sciences] [NASA ADS] [CrossRef]
- Rees, M. J., &
Gunn, J. E. 1974, MNRAS, 167, 1 [NASA ADS] (In the text)
- Reig, P., Ribó, M.,
Paredes, J. M., & Martí, J. 2003, A&A, 405,
285 [EDP Sciences] [NASA ADS] [CrossRef]
- Ribó, M., Reig,
P., Martí, J., & Paredes, J. M. 1999, A&A, 347,
518 [NASA ADS]
- Ribó, M., Paredes,
J. M., Romero, G. E., et al. 2002, A&A, 384,
954 [EDP Sciences] [NASA ADS] [CrossRef]
- Romero, G. E.,
Christiansen, H. R., & Orellana, M. 2005, ApJ, 632,
1093 [NASA ADS] [CrossRef]
- Skrutskie, M.F., Cutri,
R. M., Stiening, R. 2006, AJ, 131, 1163 [NASA ADS] (In the text)
- Stirling,
A. M., Spencer, R. E., de la Force, C. J.,
et al. 2001, MNRAS, 327, 1273 [NASA ADS] [CrossRef] (In the text)
- Strickman,
M. S., Tavani, M., Coe, M. J., et al. 1998, ApJ,
497, 419 [NASA ADS] [CrossRef] (In the text)
- Tavani, M., & Arons, J.
1997, ApJ, 477, 439 [NASA ADS] [CrossRef] (In the text)
- Tavani, M., Arons, J.,
& Kaspi, V. M. 1994, ApJ, 433, L37 [NASA ADS] [CrossRef]
- Tavani, M., Grove, J. E.,
Purcell, W., et al. 1996, A&AS, 120, 221 [NASA ADS] (In the text)
- Taylor, A. R.,
& Gregory, P. C. 1982, ApJ, 255, 210 [NASA ADS] [CrossRef] (In the text)
- Taylor, A. R.,
& Gregory, P. C. 1984, ApJ, 283, 273 [NASA ADS] [CrossRef]
- van der Klis, M. 2006, chapter
2 in Compact Stellar X-Ray Sources, ed. W. H. G. Lewin, & M.
van der Klis, Cambridge Astrophysics Series 39 (Cambridge
University Press), 39
(In the text)
- Wang, Q. D., Li,
Z.-Y., & Begelman, M. C. 1993, Nature, 364, 127 [NASA ADS] [CrossRef]
- Waters,
L. B. F. M. 1986, A&A, 162, 121 [NASA ADS] (In the text)
- Waters,
L. B. F. M., van den Heuvel, E. P. J.,
Taylor, A. R., Habets, G. M. H. J., &
Persi, P. 1988, A&A, 198, 200 [NASA ADS] (In the text)
- Zahn, J.-P. 1977, A&A,
57, 383 [NASA ADS] (In the text)
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4779f1a}\par\vspace*{2mm}
\...
...4779f1b}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{4779f1c}\end{figure}](/articles/aa/full/2006/36/aa4779-05/Timg58.gif)
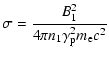
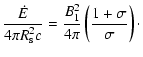
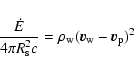
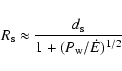
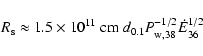
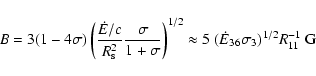
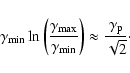
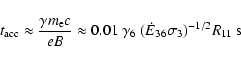
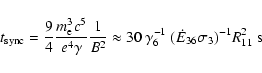
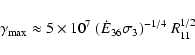
![\begin{displaymath}t_{\rm KN}\approx5.2~\gamma_6 \left(\frac{3~{\rm eV}}{kT_\sta...
...ma k T_\star}{m_{\rm e} c^2}\right) -1.98 \right]^{-1}~{\rm s}
\end{displaymath}](/articles/aa/full/2006/36/aa4779-05/img133.gif)
![\begin{displaymath}t_{\rm KN}=20~\gamma_6 d_{0.1}^2 \left[\ln \gamma_6 +1.3 \right]^{-1}~T_{\star,4}^{-2} R_{\star,10}^{-2}~{\rm s}
\end{displaymath}](/articles/aa/full/2006/36/aa4779-05/img136.gif)
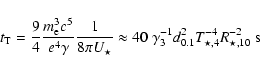
![\begin{figure}
\par\includegraphics[width=6cm,clip]{4779f2}
\end{figure}](/articles/aa/full/2006/36/aa4779-05/Timg145.gif)
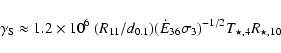
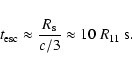
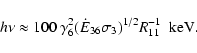
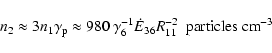
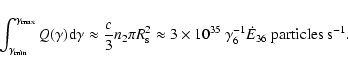
![\begin{displaymath}\frac{\partial N}{\partial z}=\frac{\partial}{\partial \gamma...
...\frac{{\rm d}\gamma}{{\rm d} z} N \right]+Q(\gamma)\delta(z-1)
\end{displaymath}](/articles/aa/full/2006/36/aa4779-05/img215.gif)
![\begin{displaymath}\frac{{\rm d}\gamma}{{\rm d} z}=
\frac{R_{\rm s}}{v} \left[\l...
...t(\frac{{\rm d} \gamma}{{\rm d} t}\right)_{\rm ad}\right]\cdot
\end{displaymath}](/articles/aa/full/2006/36/aa4779-05/img216.gif)
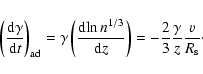
![\begin{figure}
\par\includegraphics[width=9.5cm,clip]{4779f4a}\hspace*{4mm}
\includegraphics[width=6.2cm,clip]{4779f4b}
\end{figure}](/articles/aa/full/2006/36/aa4779-05/Timg220.gif)
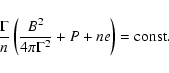
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4779f5}
\end{figure}](/articles/aa/full/2006/36/aa4779-05/Timg259.gif)
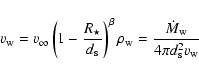
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4779f6}
\end{figure}](/articles/aa/full/2006/36/aa4779-05/Timg266.gif)
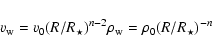
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4779f8a}\par\vspace*{2mm}
\includegraphics[width=7.8cm,clip]{4779f8b}
\end{figure}](/articles/aa/full/2006/36/aa4779-05/Timg280.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4779f10}
\end{figure}](/articles/aa/full/2006/36/aa4779-05/Timg289.gif)